Renewable Energy Utilization Analysis of Highly and Newly Industrialized Countries Using an Undesirable Output Model
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
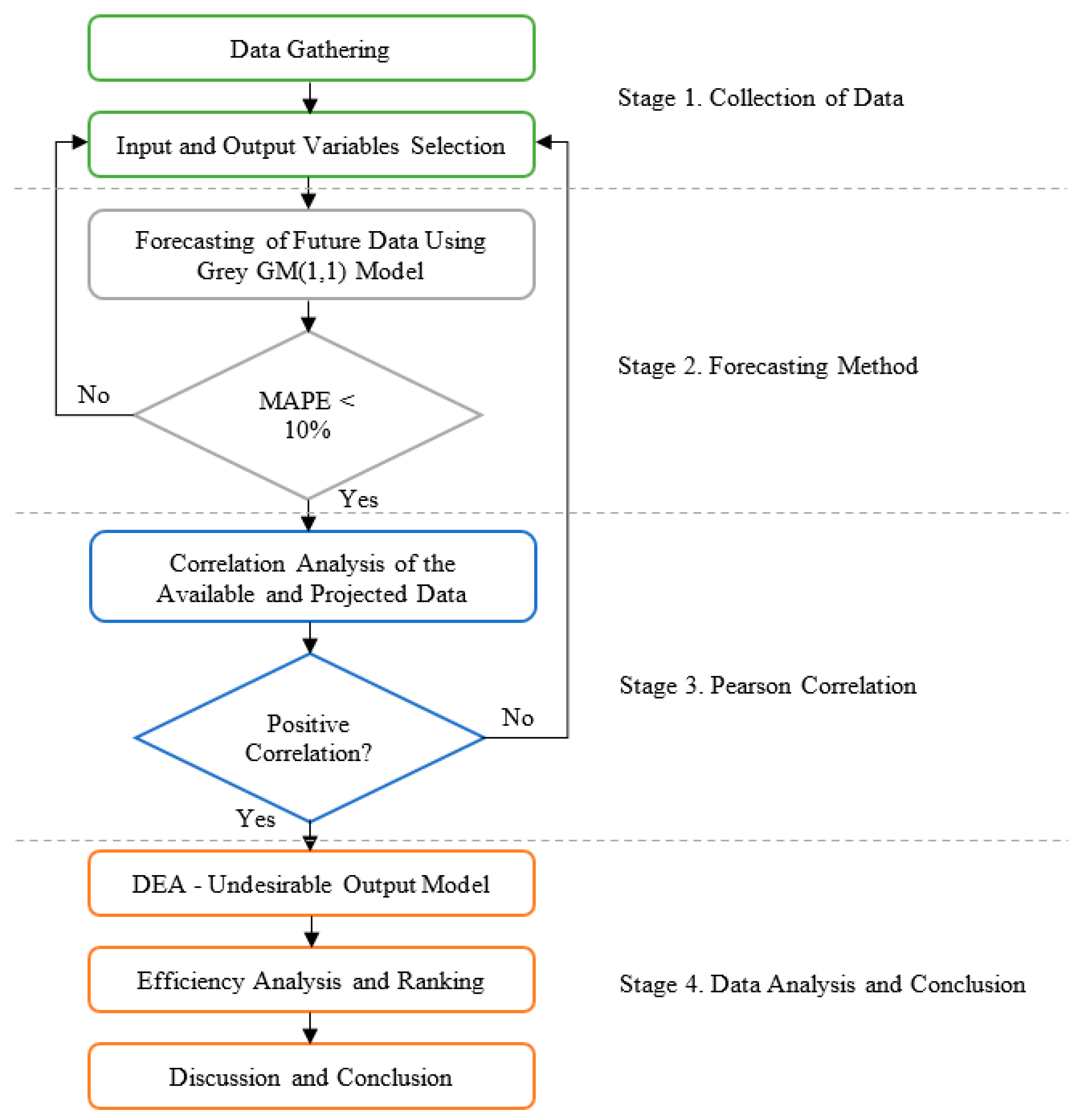
3.1. Research Process
- Stage 1. Collection of Data
- Stage 2. Grey Forecasting Method
- Stage 3. Pearson Correlation
- Stage 4. Data Analysis and Conclusion
3.2. GM (1,1) Grey Prediction Model
3.3. Data Envelopment Analysis—Undesirable Output Model
4. Results
4.1. Data Analysis of the Input and Output Factors
4.2. GM (1,1) Grey Prediction Model Results
4.3. Results of the DEA Undesirable Model for the Period 2013–2018
4.3.1. Efficiency Scores of HICs and NICs
4.3.2. Average Efficiency Scores and Overall Ranking
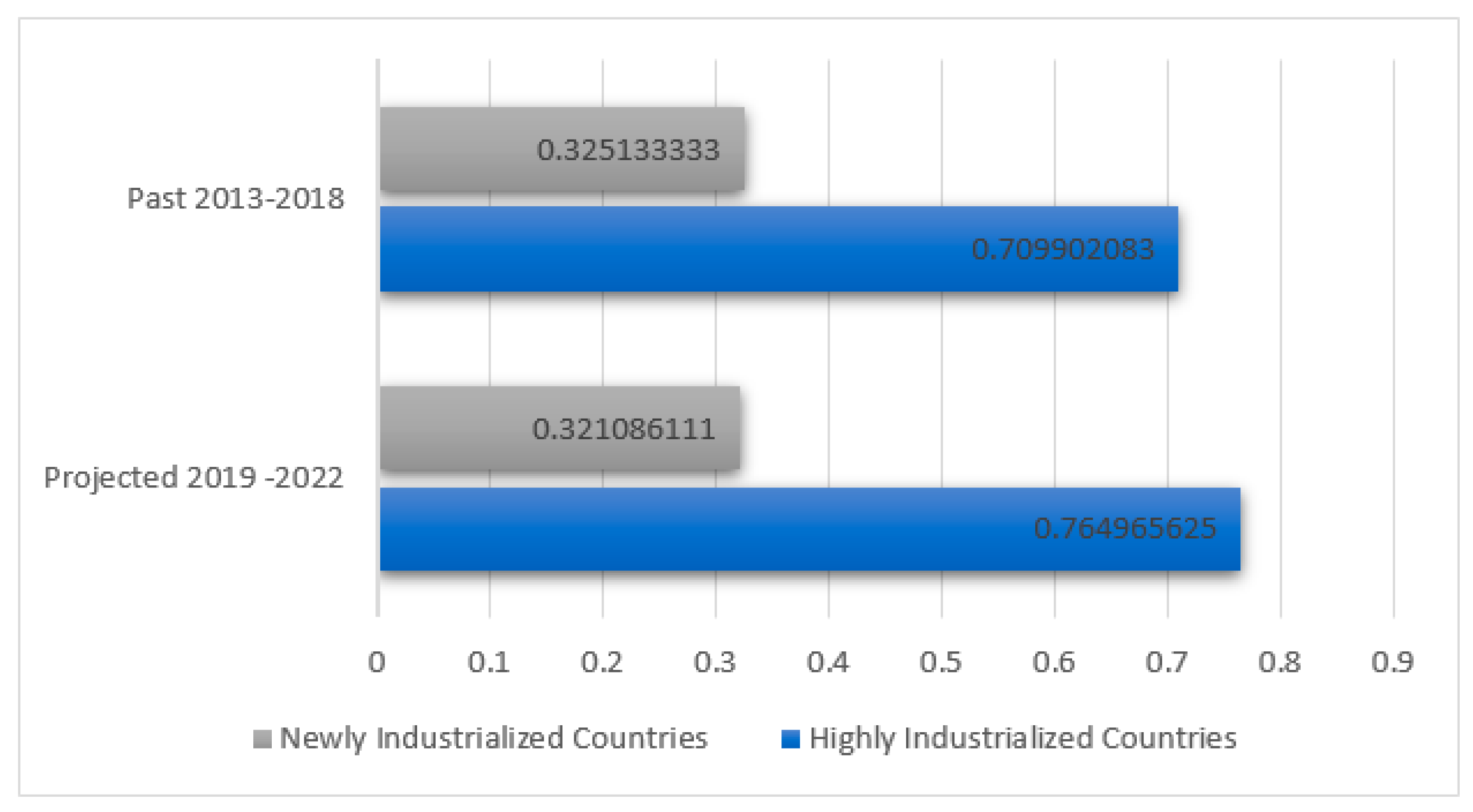
4.4. Projected Efficiency Scores for the Period 2019–2022
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Adoption of the Paris Agreement. In Proceedings of the Conference of the Parties, Paris, France, 30 November–11 December 2015. [Google Scholar]
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- The International Renewable Energy Agency (IRENA). Available online: https://www.irena.org/aboutirena (accessed on 4 December 2019).
- Laub, Z. The Group of Eight (G8) Industrialized Nations. Counsil on Foreign Relations. 2014. Available online: http://www.cfr.org/backgrounder/group-eight-g8-industrialized-nations/ (accessed on 6 December 2019).
- Szirmai, A.; Naudé, W.; Alcorta, L. Pathways to Industrialization in the Twenty-First Century: New Challenges and Emerging Paradigms; OUP Oxford: Oxford, UK, 2013. [Google Scholar]
- Cleveland, C.J.; Kaufmann, R.K.; Stern, D.I. Aggregation and the role of energy in the economy. Ecol. Econ. 2000, 32, 301–317. [Google Scholar] [CrossRef]
- Cîrstea, S.D.; Moldovan-Teselios, C.; Cîrstea, A.; Turcu, A.C.; Darab, C.P. Evaluating renewable energy sustainability by composite index. Sustainability 2018, 10, 811. [Google Scholar] [CrossRef] [Green Version]
- Iddrisu, I.; Bhattacharyya, S.C. Sustainable Energy Development Index: A multi-dimensional indicator for measuring sustainable energy development. Renew. Sustain. Energy Rev. 2015, 50, 513–530. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.W.; Zhong, J. Construction of a responsible investment composite index for renewable energy industry. Renew. Sustain. Energy Rev. 2015, 51, 288–303. [Google Scholar] [CrossRef]
- Schlör, H.; Fischer, W.; Hake, J.-F. Methods of measuring sustainable development of the German energy sector. Appl. Energy 2013, 101, 172–181. [Google Scholar] [CrossRef]
- Liu, G. Development of a general sustainability indicator for renewable energy systems: A review. Renew. Sustain. Energy Rev. 2014, 31, 611–621. [Google Scholar] [CrossRef]
- Doukas, H.; Papadopoulou, A.; Savvakis, N.; Tsoutsos, T.; Psarras, J. Assessing energy sustainability of rural communities using Principal Component Analysis. Renew. Sustain. Energy Rev. 2012, 16, 1949–1957. [Google Scholar] [CrossRef]
- Štreimikienė, D.; Šliogerienė, J.; Turskis, Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy 2016, 85, 148–156. [Google Scholar] [CrossRef]
- Ren, J.; Sovacool, B.K. Prioritizing low-carbon energy sources to enhance China’s energy security. Energy Convers. Manag. 2015, 92, 129–136. [Google Scholar] [CrossRef]
- Troldborg, M.; Heslop, S.; Hough, R.L. Assessing the sustainability of renewable energy technologies using multi-criteria analysis: Suitability of approach for national-scale assessments and associated uncertainties. Renew. Sustain. Energy Rev. 2014, 39, 1173–1184. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Fouladgar, M.M.; Zavadskas, E.K.; Moini, S.H.H. Selecting the optimal renewable energy using multi criteria decision making. J. Bus. Econ. Manag. 2013, 14, 957–978. [Google Scholar] [CrossRef]
- San Cristóbal, J. Multi-criteria decision-making in the selection of a renewable energy project in spain: The Vikor method. Renew. Energy 2011, 36, 498–502. [Google Scholar] [CrossRef]
- Kabak, M.; Dağdeviren, M. Prioritization of renewable energy sources for Turkey by using a hybrid MCDM methodology. Energy Convers. Manag. 2014, 79, 25–33. [Google Scholar] [CrossRef]
- Halkos, G.E.; Tzeremes, N.G. Measuring the effect of Kyoto protocol agreement on countries’ environmental efficiency in CO2 emissions: An application of conditional full frontiers. J. Prod. Anal. 2014, 41, 367–382. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-N.; Ho, H.-X.T.; Luo, S.-H.; Lin, T.-F. An integrated approach to evaluating and selecting green logistics providers for sustainable development. Sustainability 2017, 9, 218. [Google Scholar] [CrossRef] [Green Version]
- Oggioni, G.; Riccardi, R.; Toninelli, R. Eco-efficiency of the world cement industry: A data envelopment analysis. Energy Policy 2011, 39, 2842–2854. [Google Scholar] [CrossRef]
- Woo, C.; Chung, Y.; Chun, D.; Seo, H.; Hong, S. The static and dynamic environmental efficiency of renewable energy: A Malmquist index analysis of OECD countries. Renew. Sustain. Energy Rev. 2015, 47, 367–376. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.; Han, J. Total factor carbon emission performance: A Malmquist index analysis. Energy Econ. 2010, 32, 194–201. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, T.-D.; Yu, M.-C. Energy Use Efficiency Past-to-Future Evaluation: An International Comparison. Energies 2019, 12, 3804. [Google Scholar] [CrossRef] [Green Version]
- Zofío, J.L.; Prieto, A.M. Environmental efficiency and regulatory standards: The case of CO2 emissions from OECD industries. Resour. Energy Econ. 2001, 23, 63–83. [Google Scholar] [CrossRef]
- Xie, B.-C.; Shang, L.-F.; Yang, S.-B.; Yi, B.-W. Dynamic environmental efficiency evaluation of electric power industries: Evidence from OECD (Organization for Economic Cooperation and Development) and BRIC (Brazil, Russia, India and China) countries. Energy 2014, 74, 147–157. [Google Scholar] [CrossRef]
- Cicea, C.; Marinescu, C.; Popa, I.; Dobrin, C. Environmental efficiency of investments in renewable energy: Comparative analysis at macroeconomic level. Renew. Sustain. Energy Rev. 2014, 30, 555–564. [Google Scholar] [CrossRef]
- Wang, C.-N.; Luu, Q.-C.; Nguyen, T.-K.-L. Estimating Relative Efficiency of Electricity Consumption in 42 Countries during the Period of 2008–2017. Energies 2018, 11, 3037. [Google Scholar] [CrossRef] [Green Version]
- Chien, T.; Hu, J.-L. Renewable energy and macroeconomic efficiency of OECD and non-OECD economies. Energy Policy 2007, 35, 3606–3615. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Operat. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The economic theory of index numbers and the measurement of input, output, and productivity. Econ. J. Econ. Soc. 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lindgren, B.; Roos, P. Productivity changes in Swedish pharamacies 1980–1989: A non-parametric Malmquist approach. J. Prod. Anal. 1992, 3, 85–101. [Google Scholar] [CrossRef]
- Ahn, T.; Charnes, A.; Cooper, W.W. Some statistical and DEA evaluations of relative efficiencies of public and private institutions of higher learning. Socio-Econ. Plan. Sci. 1988, 22, 259–269. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Operat. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Introduction to Data Envelopment Analysis and its Uses: With DEA-Solver Software and References; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Wang, C.-N.; Nguyen, T.-D.; Le, M.-D. Assessing Performance Efficiency of Information and Communication Technology Industry-Forecasting and Evaluating: The Case in Vietnam. Appl. Sci. 2019, 9, 3996. [Google Scholar] [CrossRef] [Green Version]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Tseng, F.-M.; Yu, H.-C.; Tzeng, G.-H. Applied hybrid grey model to forecast seasonal time series. Technol. Forecast. Soc. Chang. 2001, 67, 291–302. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Gielen, D.; Saygin, D. REmap 2030 Renewable Energy Prospects for Russian Federation. Abu Dhabi. 2017. Available online: http://www.irena.org/remap (accessed on 6 April 2020).
- Ahmed, S.; Pourya, S.; Michael, W.; Doug, S.; Jinlei, F.; Ghislaine, K.; Verena, O.; Michael, R. Adopting and Promoting a 100% Renewable Energy Target; International Renewable Energy Agency: Vancouver, BC, Canada, 2018. [Google Scholar]
- Esteban, M.; Portugal-Pereira, J. Post-disaster resilience of a 100% renewable energy system in Japan. Energy 2014, 68, 756–764. [Google Scholar] [CrossRef]
- Share of Renewable Energy Power in Japan, 2018 (Preliminary Report); Institute for Sustainable Energy Policies: Tokyo, Japan, 2019.
- Antonelli, M.; Desideri, U.; Franco, A. Effects of large scale penetration of renewables: The Italian case in the years 2008–2015. Renew. Sustain. Energy Rev. 2018, 81, 3090–3100. [Google Scholar] [CrossRef]
- Winarno, O.T.; Alwendra, Y.; Mujiyanto, S. Policies and strategies for renewable energy development in Indonesia. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 270–272. [Google Scholar]
- Nakumuryango, A.; Inglesi-Lotz, R. South Africa’s performance on renewable energy and its relative position against the OECD countries and the rest of Africa. Renew. Sustain. Energy Rev. 2016, 56, 999–1007. [Google Scholar] [CrossRef] [Green Version]
- Vidal-Amaro, J.J.; Østergaard, P.A.; Sheinbaum-Pardo, C. Optimal energy mix for transitioning from fossil fuels to renewable energy sources—The case of the Mexican electricity system. Appl. Energy 2015, 150, 80–96. [Google Scholar] [CrossRef]
- Karagöz, G.N. Renewable Energy in Turkey: A Cleaner, Self-Sufficient Alternative to Coal; Kadir Has Üniversitesi: Istanbul, Turkey, 2019. [Google Scholar]
- de Melo, C.A.; de Martino Jannuzzi, G.; Bajay, S.V. Nonconventional renewable energy governance in Brazil: Lessons to learn from the German experience. Renew. Sustain. Energy Rev. 2016, 61, 222–234. [Google Scholar] [CrossRef]
- Khor, C.S.; Lalchand, G. A review on sustainable power generation in Malaysia to 2030: Historical perspective, current assessment, and future strategies. Renew. Sustain. Energy Rev. 2014, 29, 952–960. [Google Scholar] [CrossRef]
- Kumar, S. Assessment of renewables for energy security and carbon mitigation in Southeast Asia: The case of Indonesia and Thailand. Appl. Energy 2016, 163, 63–70. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Tran, N.N.; Tran, T.L.A. Sustainable supplier selection process in edible oil production by a hybrid fuzzy analytical hierarchy process and green data envelopment analysis for the SMEs food processing industry. Mathematics 2018, 6, 302. [Google Scholar] [CrossRef] [Green Version]



| Authors, Year [References] | Factors | Method/s | No. of Counties | |
|---|---|---|---|---|
| Inputs | Outputs | |||
| Zofio and Prieto, 2001 [26] | Energy Consumption Capital stock Labor | GDP CO2 emission | DEA | 18 |
| Xie et al., 2014 [27] | Labor Installed capacity Fuel and nuclear | Power generation CO2 emission | DEA-SBM | 26 |
| Cicea et al., 2014 [28] | GDP capita Energy intensity Investment to renewables | CO2 emission | DEA | 22 |
| Wang et al., 2018 [29] | Energy Consumption Population | GDP CO2 CH4 methane N2O nitrous oxide | DEA-Undesirable model | 42 |
| Chien and Hu, 2009 [30] | Capital stock Energy consumption Labor | GDP | DEA | 45 |
| MAPE | Forecast Categories |
|---|---|
| <10% | High Accuracy |
| 10–20% | Good |
| 20–50% | Reasonable |
| >50% | Inaccurate |
| DMU No. | Highly Industrialized Countries (HIC) | DMU No. | Newly Industrialized Countries (NIC) |
|---|---|---|---|
| CTRY1 | France | CTRY9 | South Africa |
| CTRY2 | Germany | CTRY10 | Mexico |
| CTRY3 | Italy | CTRY11 | Brazil |
| CTRY4 | United Kingdom | CTRY12 | China |
| CTRY5 | Japan | CTRY13 | India |
| CTRY6 | United States | CTRY14 | Indonesia |
| CTRY7 | Canada | CTRY15 | Malaysia |
| CTRY8 | Russia | CTRY16 | Thailand |
| CTRY17 | Turkey |
| Input Factors | Output Factors | ||||
|---|---|---|---|---|---|
| Total Renewable Energy Capacity in GW (TREC) | Labor Force In millions (LF) | Total Energy Consumption in Mtoe (TEC) | Carbon Dioxide Emission in MtCO2 (CO2) | Gross Domestic Product in $ Million (GDP) | |
| Descriptive Statistics | |||||
| Max | 479.11 | 785,372.42 | 2993.90 | 9061.26 | 18,219.3 |
| Min | 3.43 | 14,589.35 | 86.33 | 228.53 | 296.64 |
| Average | 80.98 | 124,337.42 | 560.54 | 1401.99 | 3229.5 |
| SD | 110.48 | 197,968.12 | 780.22 | 2226.36 | 4468.96 |
| Correlation Scores | |||||
| TREC | 1 | 0.8274 | 0.9191 | 0.9467 | 0.7080 |
| LF | 0.8274 | 1 | 0.8104 | 0.8515 | 0.4637 |
| TEC | 0.9191 | 0.8104 | 1 | 0.9888 | 0.8581 |
| CO2 | 0.9467 | 0.8515 | 0.9888 | 1 | 0.7941 |
| GDP | 0.7080 | 0.4637 | 0.8581 | 0.7941 | 1 |
| DMU No. | Country | TREC | LF | TEC | CO2 | GDP | Average |
|---|---|---|---|---|---|---|---|
| CTRY1 | France | 0.21% | 0.09% | 0.39% | 1.02% | 4.81% | 1.30% |
| CTRY2 | Germany | 0.34% | 0.20% | 0.85% | 0.99% | 4.60% | 1.39% |
| CTRY3 | Italy | 0.37% | 0.25% | 0.59% | 0.71% | 4.65% | 1.31% |
| CTRY4 | United Kingdom | 2.85% | 0.06% | 0.32% | 0.72% | 3.03% | 1.40% |
| CTRY5 | Japan | 2.28% | 0.19% | 0.35% | 0.44% | 2.51% | 1.15% |
| CTRY6 | United States | 0.77% | 0.14% | 1.00% | 1.37% | 0.46% | 0.75% |
| CTRY7 | Canada | 1.24% | 0.14% | 0.80% | 0.63% | 4.57% | 1.48% |
| CTRY8 | Russia | 0.13% | 0.21% | 1.42% | 1.29% | 12.82% | 3.17% |
| CTRY9 | South Africa | 5.17% | 0.43% | 1.14% | 1.38% | 5.29% | 2.68% |
| CTRY10 | Mexico | 1.51% | 0.09% | 0.62% | 1.39% | 4.51% | 1.62% |
| CTRY11 | Brazil | 0.31% | 0.14% | 0.89% | 1.26% | 8.10% | 2.14% |
| CTRY12 | China | 0.52% | 0.07% | 0.94% | 0.83% | 2.12% | 0.90% |
| CTRY13 | India | 1.06% | 0.08% | 0.47% | 1.07% | 2.14% | 0.96% |
| CTRY14 | Indonesia | 0.40% | 0.28% | 0.96% | 1.49% | 2.01% | 1.03% |
| CTRY15 | Malaysia | 3.33% | 0.08% | 1.21% | 0.53% | 5.40% | 2.11% |
| CTRY16 | Thailand | 1.96% | 0.17% | 0.34% | 0.55% | 2.84% | 1.17% |
| Input Factors | Output Factors | ||||
|---|---|---|---|---|---|
| Total Renewable Energy Capacity in GW (TREC) | Labor Force In millions (LF) | Total Energy Consumption in Mtoe (TEC) | Carbon Dioxide Emission in MtCO2 (CO2) | Gross Domestic Product in $ Million (GDP) | |
| Descriptive Statistics | |||||
| Max | 1025.678 | 788,934.32 | 3265.25 | 9,616.34 | 22,840.18 |
| Min | 9.79 | 16,459.70 | 94.97 | 240.41 | 347.94 |
| Average | 142.74 | 130,441.84 | 604.62 | 1475.28 | 3965.78 |
| SD | 233.78 | 203,616.31 | 839.58 | 2342.19 | 5920.01 |
| Correlation Scores | |||||
| TREC | 1 | 0.8531 | 0.9110 | 0.9512 | 0.7194 |
| LF | 0.8531 | 1 | 0.8212 | 0.8597 | 0.5379 |
| TEC | 0.9110 | 0.8212 | 1 | 0.9888 | 0.8774 |
| CO2 | 0.9512 | 0.8597 | 0.9888 | 1 | 0.8226 |
| GDP | 0.7194 | 0.5379 | 0.8774 | 0.8226 | 1 |
| Countries | Year Periods and Rankings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2013 | Rank | 2014 | Rank | 2015 | Rank | 2016 | Rank | 2017 | Rank | 2018 | Rank | |
| Highly Industrialized Countries (HICs) | ||||||||||||
| CTRY1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY2 | 0.7030 | 6 | 0.6277 | 5 | 0.5518 | 6 | 0.6498 | 6 | 0.7326 | 5 | 1.0000 | 1 |
| CTRY3 | 0.7783 | 4 | 0.6829 | 4 | 0.5860 | 4 | 0.6794 | 5 | 0.7358 | 4 | 0.7325 | 5 |
| CTRY4 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY5 | 0.7341 | 5 | 0.5928 | 6 | 0.5647 | 5 | 0.7187 | 4 | 0.7153 | 6 | 0.6770 | 6 |
| CTRY6 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY7 | 0.5117 | 7 | 0.4115 | 7 | 0.3648 | 7 | 0.3945 | 7 | 0.4341 | 7 | 0.4157 | 7 |
| CTRY8 | 0.2215 | 8 | 0.1887 | 8 | 0.1417 | 8 | 0.1531 | 8 | 0.1852 | 8 | 0.1904 | 8 |
| Newly Industrialized Countries (NICs) | ||||||||||||
| CTRY9 | 1.0000 | 1 | 1.0000 | 1 | 0.3000 | 3 | 0.2600 | 4 | 0.2760 | 4 | 0.2748 | 4 |
| CTRY10 | 0.3574 | 2 | 0.3439 | 2 | 0.3455 | 2 | 0.3518 | 2 | 0.4020 | 2 | 0.3873 | 2 |
| CTRY11 | 0.3362 | 4 | 0.2718 | 5 | 0.2050 | 6 | 0.2338 | 5 | 0.2791 | 3 | 0.2266 | 6 |
| CTRY12 | 0.1338 | 8 | 0.1315 | 8 | 0.1500 | 8 | 0.1668 | 8 | 0.1811 | 8 | 0.1840 | 8 |
| CTRY13 | 0.1001 | 9 | 0.0993 | 9 | 0.1150 | 9 | 0.1351 | 9 | 0.1537 | 9 | 0.1411 | 9 |
| CTRY14 | 0.2993 | 5 | 0.2877 | 3 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY15 | 0.2285 | 6 | 0.2185 | 6 | 0.2049 | 7 | 0.2309 | 6 | 0.2568 | 7 | 0.2810 | 3 |
| CTRY16 | 0.2055 | 7 | 0.1876 | 7 | 0.2104 | 5 | 0.2291 | 7 | 0.2626 | 6 | 0.2716 | 5 |
| CTRY17 | 0.3363 | 3 | 0.2793 | 4 | 0.2634 | 4 | 0.2806 | 3 | 0.2653 | 5 | 0.2152 | 7 |
| DMU No. | Countries | Average Efficiency Score | Overall Ranking |
|---|---|---|---|
| Highly Industrialized Countries | |||
| CTRY1 | France | 1.0000 | 1 |
| CTRY4 | United Kingdom | 1.0000 | 1 |
| CTRY6 | United States | 1.0000 | 1 |
| CTRY2 | Germany | 0.7108 | 4 |
| sCTRY3 | Italy | 0.6992 | 5 |
| CTRY5 | Japan | 0.6671 | 6 |
| CTRY7 | Canada | 0.4221 | 7 |
| CTRY8 | Russia | 0.1801 | 8 |
| Newly Industrialized Countries | |||
| CTRY14 | Indonesia | 0.7645 | 1 |
| CTRY9 | South Africa | 0.5185 | 2 |
| CTRY10 | Mexico | 0.3647 | 3 |
| CTRY17 | Turkey | 0.2734 | 4 |
| CTRY11 | Brazil | 0.2588 | 5 |
| CTRY15 | Malaysia | 0.2368 | 6 |
| CTRY16 | Thailand | 0.2278 | 7 |
| CTRY12 | China | 0.1579 | 8 |
| CTRY13 | India | 0.1241 | 9 |
| Countries | Year Periods and Rankings | |||||||
|---|---|---|---|---|---|---|---|---|
| 2019 | Rank | 2020 | Rank | 2021 | Rank | 2022 | Rank | |
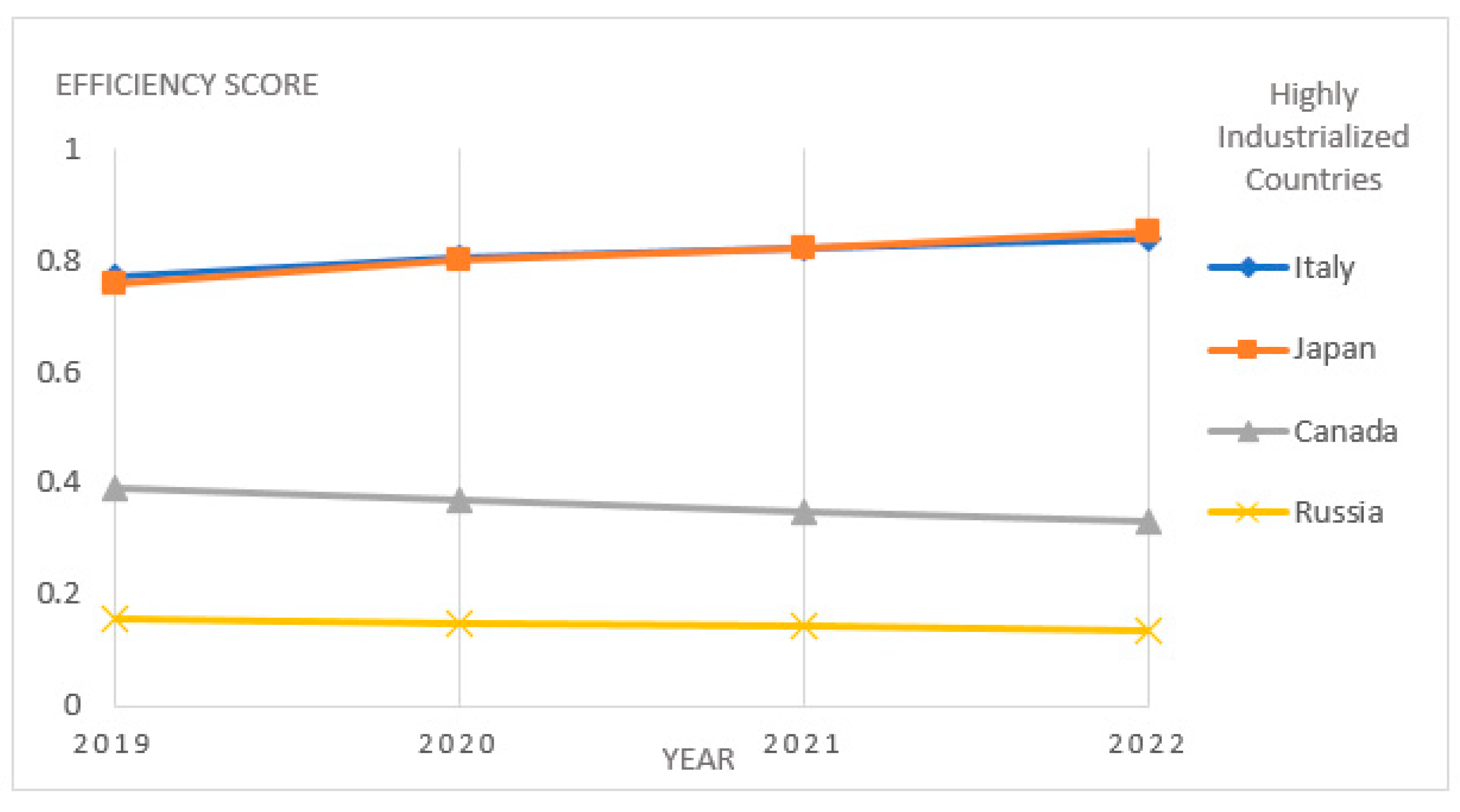
| Highly Industrialized Countries (HICs) | ||||||||
| CTRY1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY2 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY3 | 0.7687 | 5 | 0.8030 | 5 | 0.8208 | 5 | 0.8381 | 6 |
| CTRY4 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY5 | 0.7577 | 6 | 0.7977 | 6 | 0.8207 | 6 | 0.8493 | 5 |
| CTRY6 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY7 | 0.3909 | 7 | 0.3686 | 7 | 0.3482 | 7 | 0.3295 | 7 |
| CTRY8 | 0.1580 | 8 | 0.1498 | 8 | 0.1423 | 8 | 0.1356 | 8 |
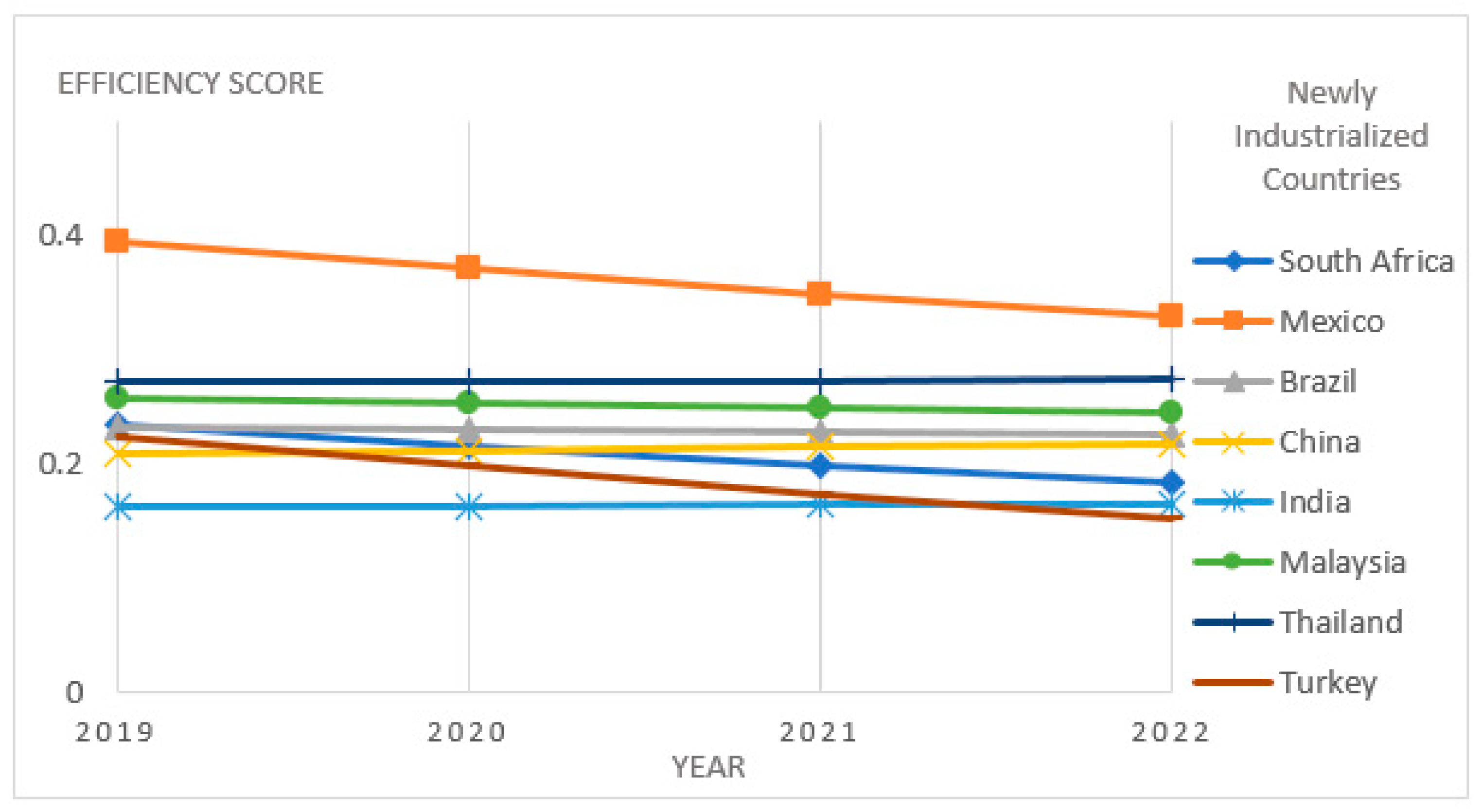
| Newly Industrialized Countries (NICs) | ||||||||
| CTRY9 | 0.2342 | 5 | 0.2152 | 6 | 0.1983 | 7 | 0.1834 | 7 |
| CTRY10 | 0.3958 | 2 | 0.3717 | 2 | 0.3495 | 2 | 0.3288 | 2 |
| CTRY11 | 0.2332 | 6 | 0.2308 | 5 | 0.2286 | 5 | 0.2261 | 5 |
| CTRY12 | 0.2101 | 8 | 0.2126 | 7 | 0.2149 | 6 | 0.2173 | 6 |
| CTRY13 | 0.1627 | 9 | 0.1639 | 9 | 0.1651 | 9 | 0.1664 | 8 |
| CTRY14 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 | 1.0000 | 1 |
| CTRY15 | 0.2576 | 4 | 0.2532 | 4 | 0.2489 | 4 | 0.2447 | 4 |
| CTRY16 | 0.2720 | 3 | 0.2728 | 3 | 0.2737 | 3 | 0.2747 | 3 |
| CTRY17 | 0.2248 | 7 | 0.1999 | 8 | 0.1748 | 8 | 0.1534 | 9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-N.; Tibo, H.; Duong, D.H. Renewable Energy Utilization Analysis of Highly and Newly Industrialized Countries Using an Undesirable Output Model. Energies 2020, 13, 2629. https://doi.org/10.3390/en13102629
Wang C-N, Tibo H, Duong DH. Renewable Energy Utilization Analysis of Highly and Newly Industrialized Countries Using an Undesirable Output Model. Energies. 2020; 13(10):2629. https://doi.org/10.3390/en13102629
Chicago/Turabian StyleWang, Chia-Nan, Hector Tibo, and Duy Hung Duong. 2020. "Renewable Energy Utilization Analysis of Highly and Newly Industrialized Countries Using an Undesirable Output Model" Energies 13, no. 10: 2629. https://doi.org/10.3390/en13102629
APA StyleWang, C.-N., Tibo, H., & Duong, D. H. (2020). Renewable Energy Utilization Analysis of Highly and Newly Industrialized Countries Using an Undesirable Output Model. Energies, 13(10), 2629. https://doi.org/10.3390/en13102629






