An Energy Preservation Index for Evaluating the Rockburst Potential Based on Energy Evolution
Abstract
:1. Introduction
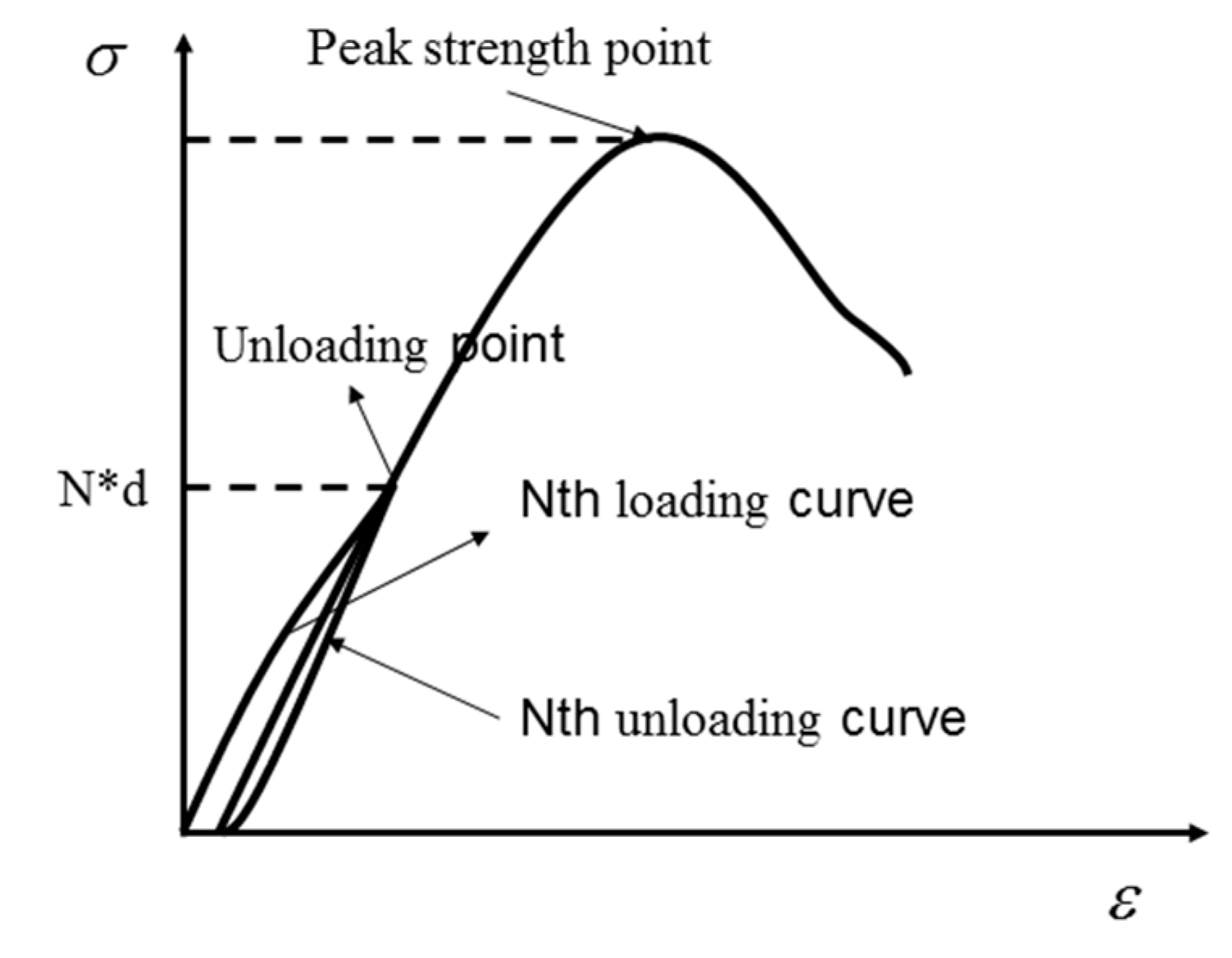
2. Strain Energy Calculation of One Cycle
3. Test Materials and Methods
3.1. Specimen Preparation
3.2. Experimental Instrument and Method
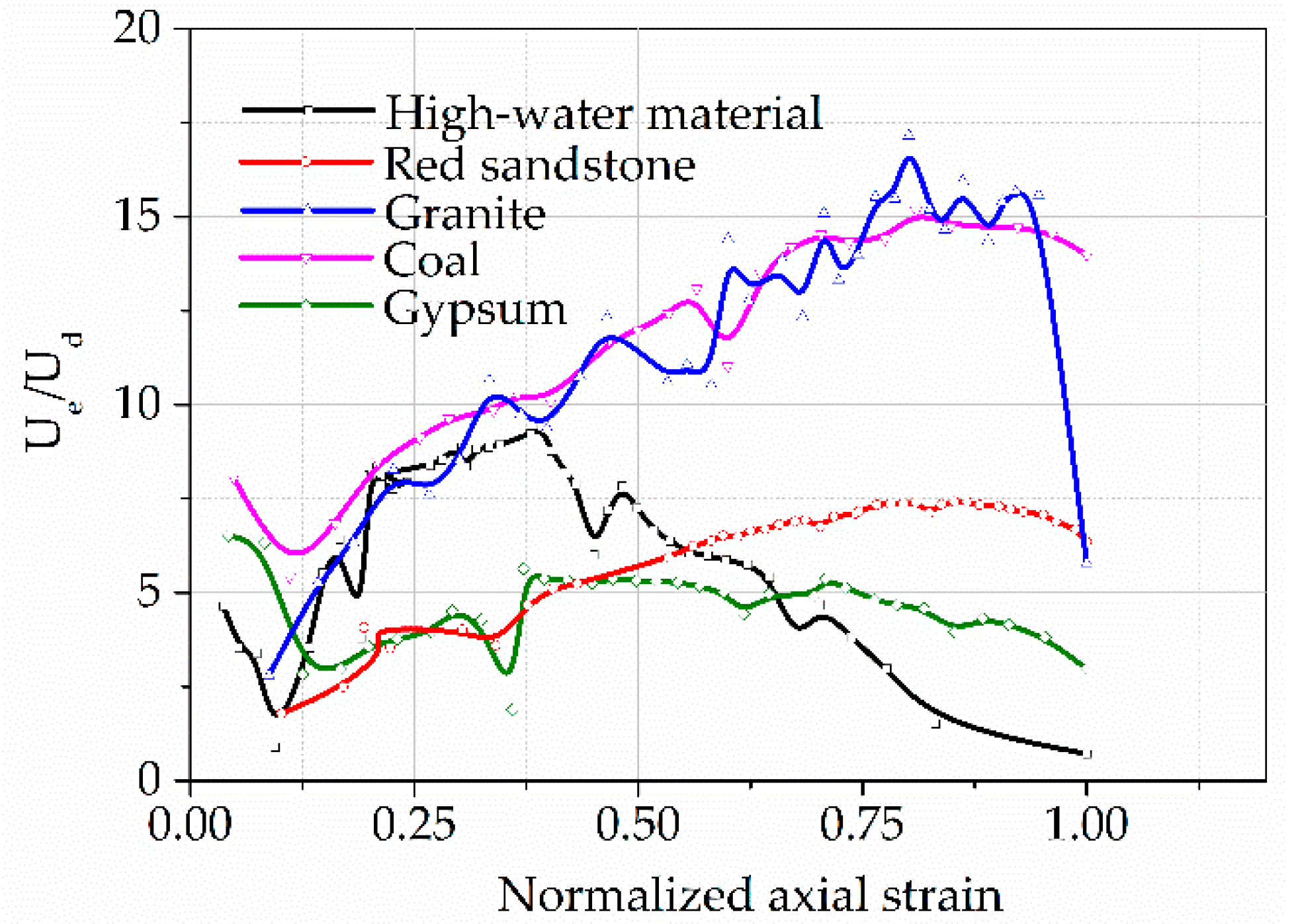
4. Experimental Results and Analysis
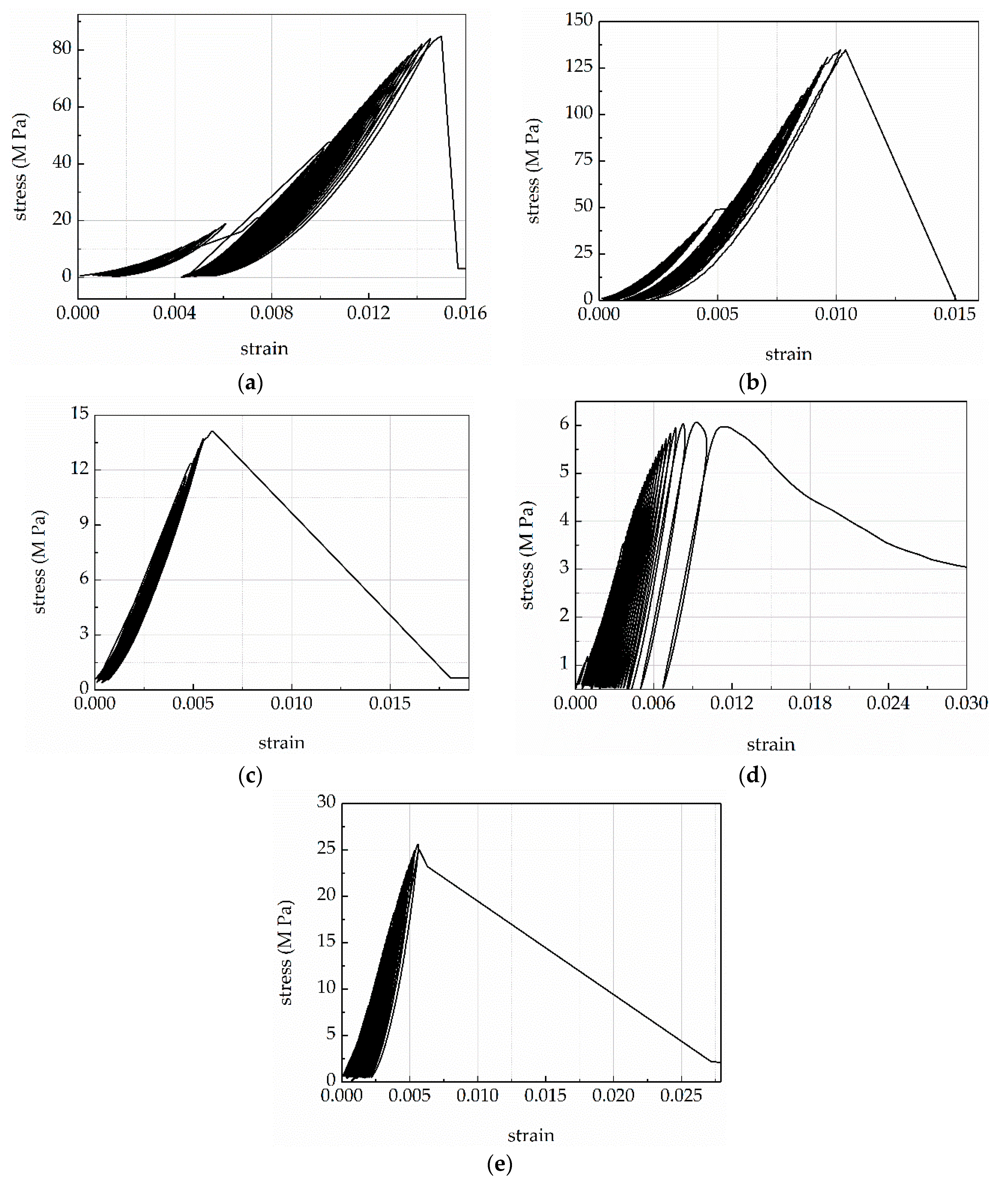
4.1. Stress–Strain Curves Characteristics
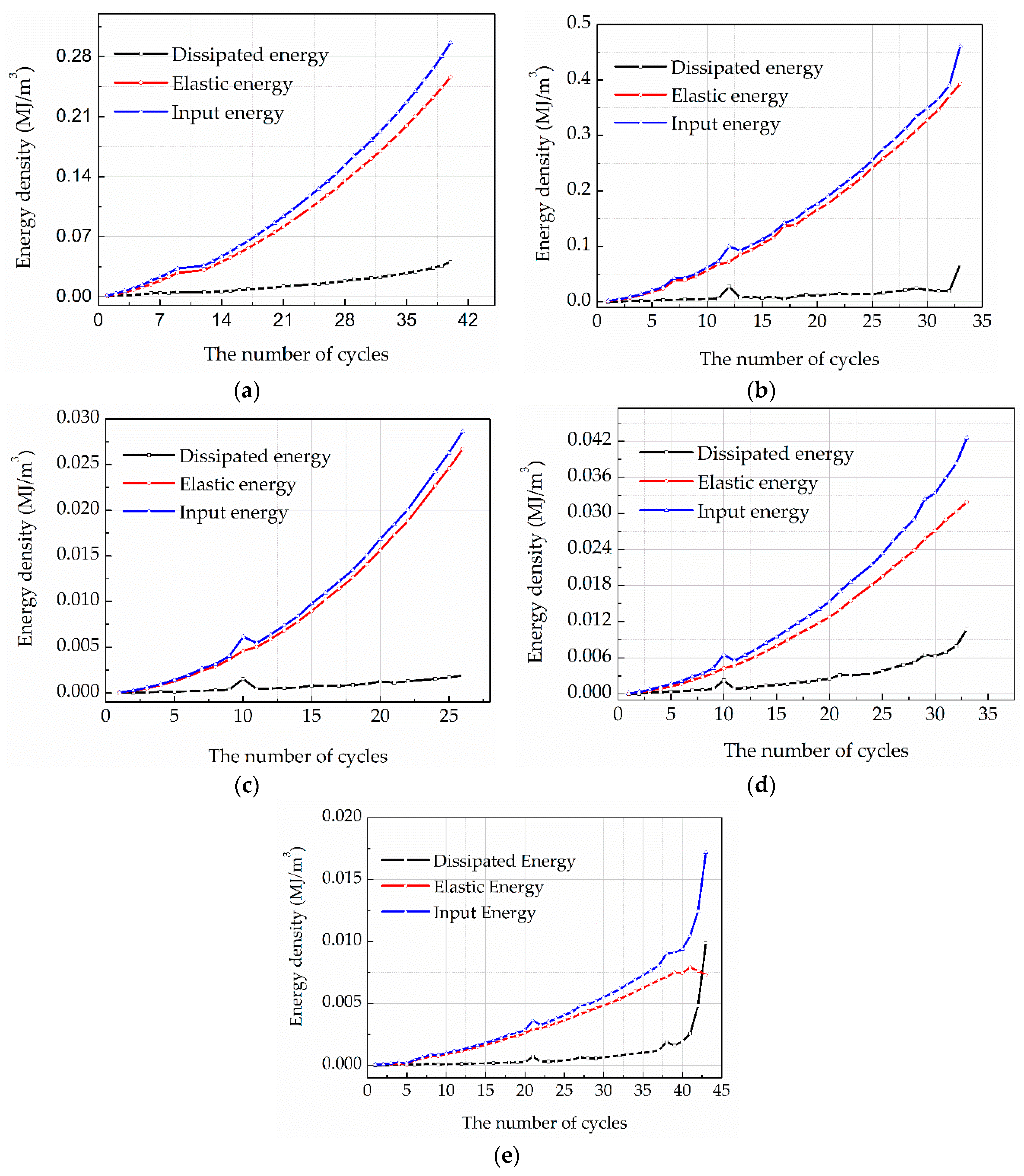
4.2. Energy Evolution Characteristics
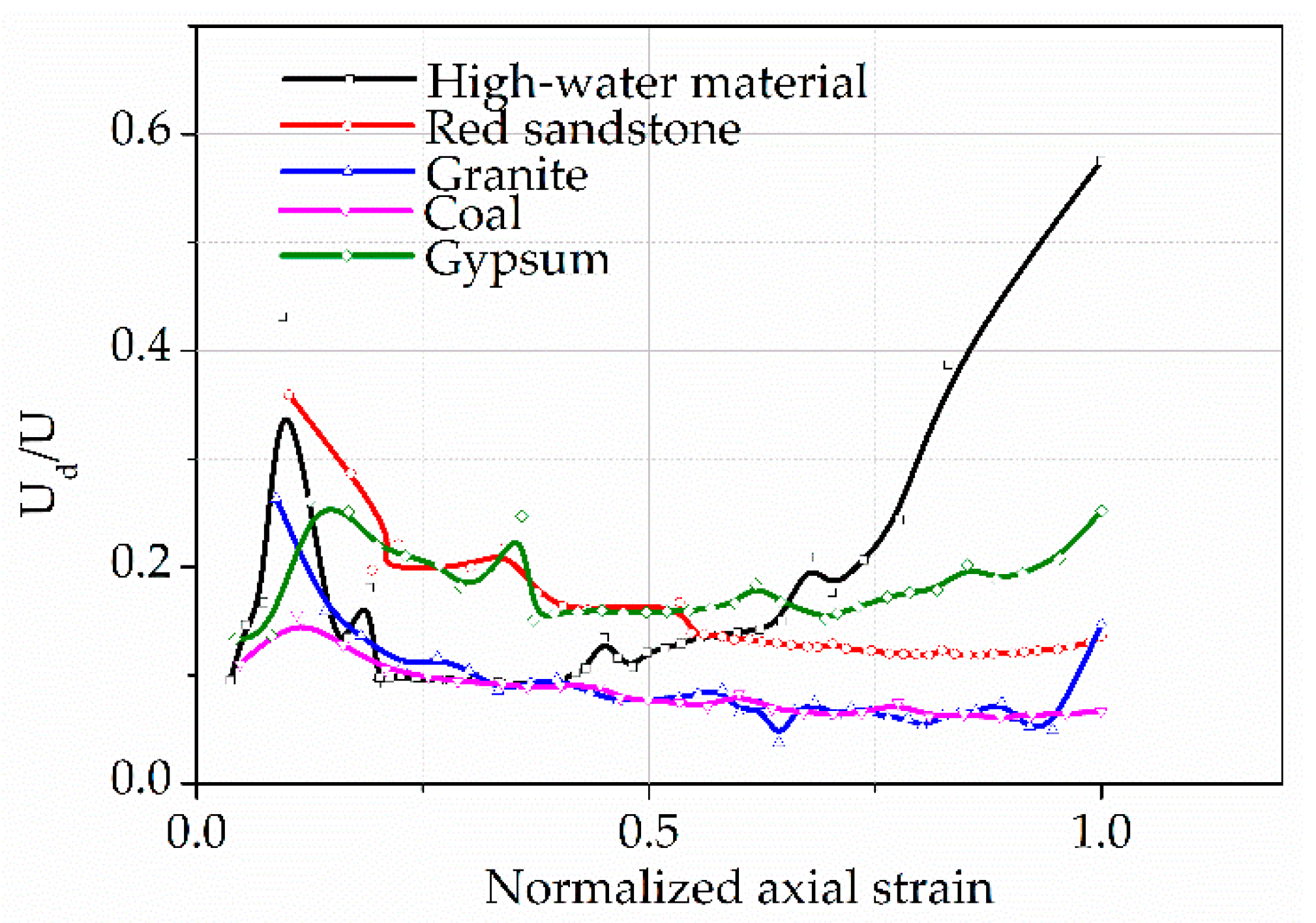
4.3. The Energy Preservation Index
5. Analysis of Rockburst Based on
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cai, W.; Dou, L.; Zhang, M.; Cao, W.; Shi, J.; Feng, L. A fuzzy comprehensive evaluation methodology for rock burst forecasting using microseismic monitoring. Tunn. Undergr. Sp. Tech. 2018, 80, 232–245. [Google Scholar] [CrossRef]
- Xie, H. Research framework and anticipated results of deep rock mechanics and mining theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar]
- Jiang, Y.; Zhao, Y.; Wang, H.; Zhu, J. A review of mechanism and prevention technologies of coal bumps in China. J. Rock. Mech. Geotec. Eng. 2017, 9, 180–194. [Google Scholar] [CrossRef]
- Li, Z.; He, X.; Dou, L.; Song, D.; Wang, G.; Xu, X. Investigating the mechanism and prevention of coal mine dynamic disasters by using dynamic cyclic loading tests. Saf. Sci. 2019, 115, 215–228. [Google Scholar] [CrossRef]
- Wang, G.; Gong, S.; Dou, L.; Cai, W.; Yuan, X.; Fan, C. Rockburst mechanism and control in coal seam with both syncline and hard strata. Saf. Sci. 2019, 115, 320–328. [Google Scholar] [CrossRef]
- Zhang, C.; Canbulant, I.; Tahmasebinia, F.; Hebblewhite, B. Assessment of energy release mechanisms contributing to coal burst. Int. J. Min. Sci. Technol. 2017, 27, 43–47. [Google Scholar] [CrossRef]
- Zhai, S.; Su, G.; Yin, S.; Zhao, B.; Yan, L. Rockburst characteristics of several hard brittle rocks: A true triaxial experimental study. J. Rock. Mech. Geotec. Eng. 2020, 12, 279–296. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock. Mech. Geotec. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Peng, R.; Ju, Y.; Wang, J.; Xie, H.; Gao, F.; Mao, L. Energy dissipation and release during coal failure under conventional triaxial compression. Rock. Mech. Rock. Eng. 2015, 48, 509–526. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Fang, X.; Wang, P. Energy dissipation and damage evolution analyses for the dynamic compression failure process of red-sandstone after freeze-thaw cycles. Eng. Geol. 2017, 221, 104–113. [Google Scholar] [CrossRef]
- Hou, P.; Gao, F.; Yang, Y.; Zhang, X.; Zhang, Z. Effect of the layer orientation on mechanics and energy evolution characteristics of shales under uniaxial loading. Int. J. Min. Sci. Technol. 2016, 26, 857–862. [Google Scholar] [CrossRef]
- Kidybinski, A. Bursting liability indices of coal. Int. J. Rock. Mech. Min. 1981, 18, 295–304. [Google Scholar] [CrossRef]
- Gong, F.; Yan, J.; Li, X.; Luo, S. A peak-strength strain energy storage index for rockburst potential of rock materials. Int. J. Rock. Mech.Min. 2019, 117, 76–89. [Google Scholar] [CrossRef]
- Cook, N.G.M. The design of underground excavations. In Proceedings of the Eighth Rock Mechanics Symposium, Minneapolis, MN, USA, 15–17 September 1966. [Google Scholar]
- Xiao, Q.; Liu, J.; Lei, S.; Gao, B. A new method for calculating energy release rate in tunnel excavation subjected to high in situ stress. Perspec. Sci. 2016, 7, 292–298. [Google Scholar]
- Pan, J. Relationship between deformation and failure of coal and its burst potential under uniaxial compression. Saf. Coal Mines 2006, 37, 1–4. [Google Scholar]
- Zhu, F.; Pan, C.; Guo, R. A new rock burst index–effective impact energy index. J. Min. Saf. Eng. 2002, 19, 83–84. [Google Scholar]
- Tang, L.; Pan, C.; Wang, W. Surplus energy index for analyzing rockburst potential. J. Cent. South Univ. 2002, 33, 129–132. [Google Scholar]
- Xu, J.; Jiang, J.; Xu, N.; Liu, Q.; Gao, Y. A new energy index for evaluating the potential of rockburst and its engineering application. Eng. Geol. 2017, 230, 46–54. [Google Scholar] [CrossRef]
- Zhang, X.; Feng., G.; Kang, L.; Yang, S. Method to determine burst potential of coal rock by residual energy emission speed. J. China Coal Soc. 2009, 34, 1165–1168. [Google Scholar]
- Beck, D.A.; Brady, B.H.G. Evaluation and application of controlling parameters for seismicity events in hard-rock mines. Int. J. Rock Mech. Min. Sci. 2002, 39, 633–642. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, X.; Xiang, T.; Su, G. Rockburst characteristics and numerical simulation based on a new energy index: A case study of a tunnel at 2500 m depth. Bull. Eng. Geol. Environ. 2010, 69, 381–388. [Google Scholar] [CrossRef]
- Wang, J.; Park, H.D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn. Undergr. Space Technol. 2016, 16, 49–57. [Google Scholar] [CrossRef]
- Mansurov, V.A. Prediction of rockbursts by analysis of induced seismicity data. Int. J. Rock Mech. Min. Sci. 2001, 38, 893–901. [Google Scholar] [CrossRef]
- Hua, A.; You, M. Rock failure due to energy release during unloading and application to underground rock burst control. Tunn. Undergr. Space Technol. 2001, 16, 241–246. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, Q.; Li, W. Numerical simulation of rock burst in circular tunnels under unloading conditions. J. China Univ. Min. Technol. 2007, 17, 552–556. [Google Scholar] [CrossRef]
- Xie, H.; Ju, Y.; Li, L.; Peng, R. Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 2008, 27, 1729–1740. [Google Scholar]
- Liang, C.; Wu, S.; Li, X.; Xin, P. Effects of strain rate on fracture characteristics and mesoscopic failure mechanisms of granite. Int. J. Rock Mech. Min. 2015, 76, 146–154. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, F. Energy evolution mechanism in process of sandstone failure and energy strength criterion. J. Appl. Geophys. 2018, 154, 21–28. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Wang, E. Quantitative study on stress-strain hysteretic behaviors in rocks. Chin. J Rock Mech. Eng. 2007, 26, 4066–4072. [Google Scholar]
- Chen, Y.; Wang, S. Elastoplastic response of saturated rocks subjected to multilevel cyclic loading. Rock Soil Mech. 2010, 31, 1030–1034. [Google Scholar]
- Zhang, D.; Ranjith, P.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: a review. J. Petrol Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Li, Z.; Chen, P.; Yang, X.; Liu, Y. Energy distribution and fractal characterization of acoustic emission (AE) during coal deformation and fracturing. Measurement 2019, 136, 122–131. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Nie, T. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Blagoveshchenskii, V.V.; Panin, I.G. Acoustic emission at interaction of gliding deformation with point obstacles. Phys. Solid State 2017, 59, 1554–1556. [Google Scholar] [CrossRef]
- Wang, X.; Wu, S.; Ge, H.; Sun, Y.; Zhang, Q. The complexity of the fracture network in failure rock under cyclic loading and its characteristics in acoustic emission monitoring. J. Geophys. Eng. 2018, 15, 2091–2103. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Wang, E.; Kong, X.; Wang, X.; Zhang, C.; Jia, H.; Wang, H.; Qian, J. Fractal characteristics of acoustic emissions from coal under multi-stage true-triaxial compression. J. Geophys. Eng. 2018, 15, 2021–2032. [Google Scholar]
- Kim, J.S.; Lee, K.S.; Cho, W.J.; Choi, H.J.; Cho, G.C. A comparative evaluation of stress-strain and acoustic emission methods for quantitative damage assessments of brittle rock. Rock Mech. Rock Eng. 2015, 48, 495–508. [Google Scholar] [CrossRef]









| Lithology | Specimen Number | Diameter/mm | Height/mm | Weight/g | Longitudinal Wave Speed/Km·s−1 |
|---|---|---|---|---|---|
| Red sandstone | S1 | 49.49 | 100.33 | 474.56 | 2.358 |
| S2 | 49.35 | 100.38 | 481.47 | 2.632 | |
| S3 | 49.70 | 100.22 | 475.53 | 2.315 | |
| Gypsum | G1 | 49.32 | 100.20 | 439.99 | 4.808 |
| G2 | 49.30 | 100.30 | 434.33 | 4.032 | |
| G3 | 49.33 | 100.10 | 438.22 | 4.630 | |
| Granite | g1 | 50.00 | 100.30 | 510.31 | 3.676 |
| g2 | 49.70 | 100.16 | 506.56 | 3.731 | |
| g3 | 49.90 | 100.23 | 508.49 | 3.676 | |
| Coal | C1 | 49.30 | 100.00 | 231.52 | 1.852 |
| C2 | 49.16 | 99.60 | 232.64 | 1.838 | |
| C3 | 49.19 | 99.74 | 235.55 | 1.880 | |
| High-water material | H1 | 49.42 | 98.64 | 238.55 | 1.724 |
| H2 | 47.90 | 96.72 | 236.55 | 1.724 | |
| H3 | 48.30 | 98.22 | 237.64 | 1.761 |
| Lithology | Red Sandstone | Gypsum | Granite | Coal | High-Water Material |
|---|---|---|---|---|---|
| UCS/M Pa | 60 | 25 | 120 | 15 | 6 |
| Loading step/KN | 4.00 | 1.5 | 8 | 1 | 0.5 |
| Loading rate/(KN/s) | 1 | 1 | 1 | 1 | 1 |
| Rock Type | Granite | Red Sandstone | Coal | Gypsum | High-Water Material |
|---|---|---|---|---|---|
| Total input energy (MJ/mm3) | 0.461 | 0.297 | 0.0286 | 0.0426 | 0.0172 |
| Elastic energy (MJ/mm3) | 0.393 | 0.256 | 0.0267 | 0.0319 | 0.0073 |
| Accumulative dissipated energy (MJ/mm3) | 0.409 | 0.659 | 0.0242 | 0.0969 | 0.0369 |
| Rock Type | Granite | Red Sandstone | Coal | Gypsum | High-Water Material |
|---|---|---|---|---|---|
| 15.94 | 7.42 | 15.17 | 5.36 | 9.393 | |
| 15.58 | 6.33 | 13.99 | 2.96 | 0.703 | |
| (%) | 97.8 | 85.4 | 92.2 | 55.4 | 7.6 |
| Rock Type | Granite | Coal | Red Sandstone | Gypsum | High-Water Material |
|---|---|---|---|---|---|
| Step amplitude at failure | 1.57 × 105 | 8.34 × 104 | 1.94 × 104 | 1.15 × 103 | 4.93 × 103 |
| Failure duration (s) | 0.5 | 1 | 0.8 | 1.5 | 8 |
| Released energy per unit time | 3.14 × 105 | 8.34 × 104 | 2.43 × 104 | 7.67 × 102 | 6.16 × 102 |
| Rock Type | AE Energy | Failure Mode | Rockburst Proneness | |
|---|---|---|---|---|
| Granite | Great | Numerous fragments | 0.978 | High |
| Coal | Relatively great | Numerous fragments | 0.922 | Relatively high |
| Red sandstone | Relatively great | Numerous fragments | 0.854 | Relatively high |
| Gypsum | Minor | A macroscopic | 0.554 | Low |
| High-water material | Minimum | Small cracks | 0.076 | No |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Gao, F.; Xing, Y.; Zhang, Z. An Energy Preservation Index for Evaluating the Rockburst Potential Based on Energy Evolution. Energies 2020, 13, 3636. https://doi.org/10.3390/en13143636
Gao L, Gao F, Xing Y, Zhang Z. An Energy Preservation Index for Evaluating the Rockburst Potential Based on Energy Evolution. Energies. 2020; 13(14):3636. https://doi.org/10.3390/en13143636
Chicago/Turabian StyleGao, Lin, Feng Gao, Yan Xing, and Zhizhen Zhang. 2020. "An Energy Preservation Index for Evaluating the Rockburst Potential Based on Energy Evolution" Energies 13, no. 14: 3636. https://doi.org/10.3390/en13143636






