Smoothed Particle Hydrodynamics Simulation of High Velocity Impact Dynamics of Molten Sand Particles
Abstract
:1. Introduction
2. Numerical Model
2.1. Method
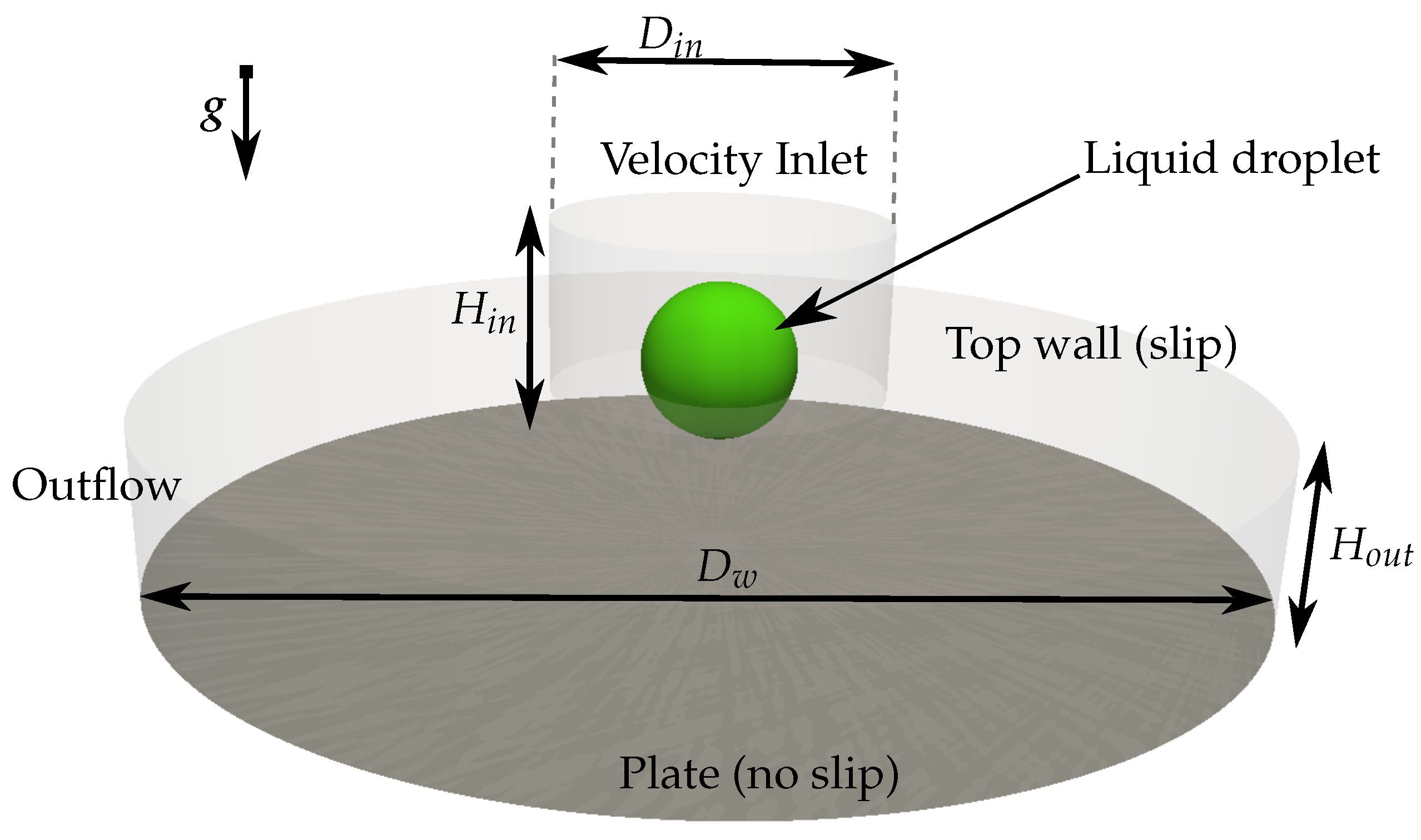
2.2. Geometry
2.3. Initial Conditions
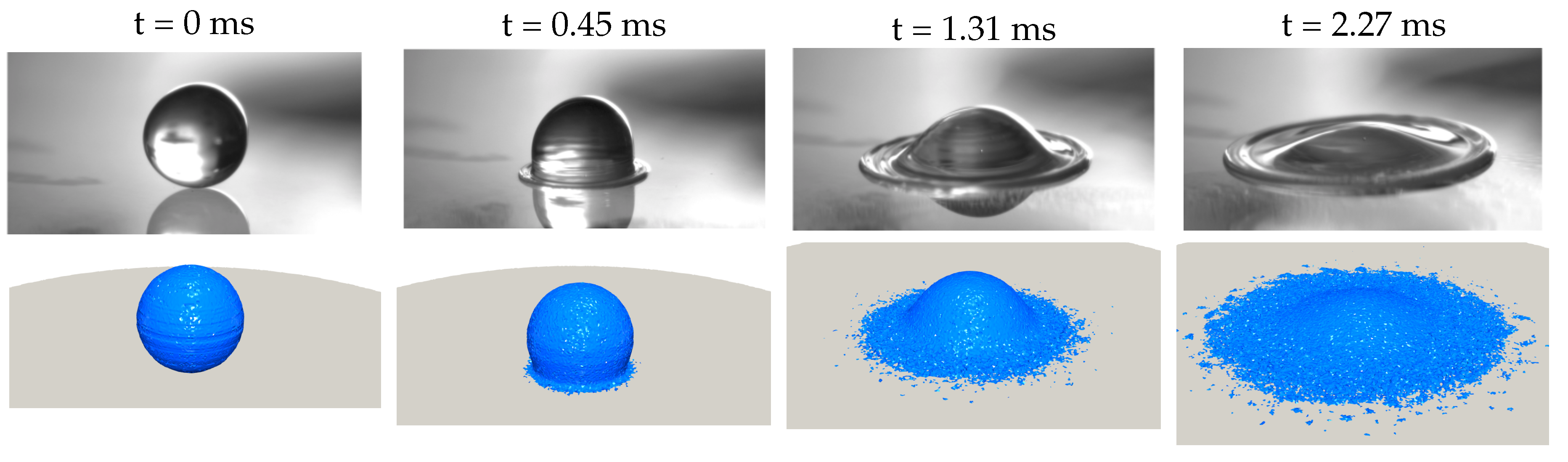
3. Validation with a Liquid Droplet
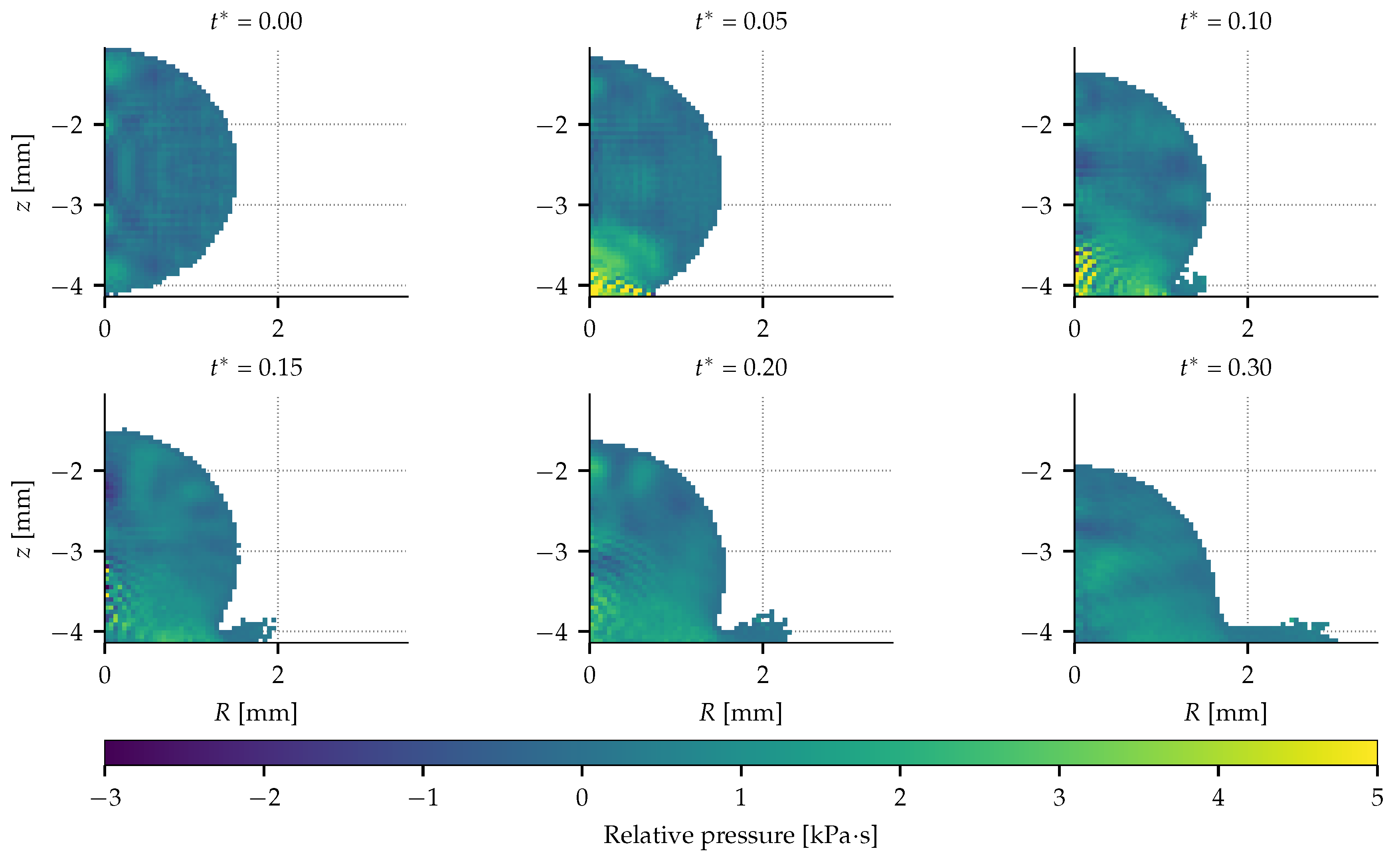
3.1. Phenomenology and Scaling of the Early Phase
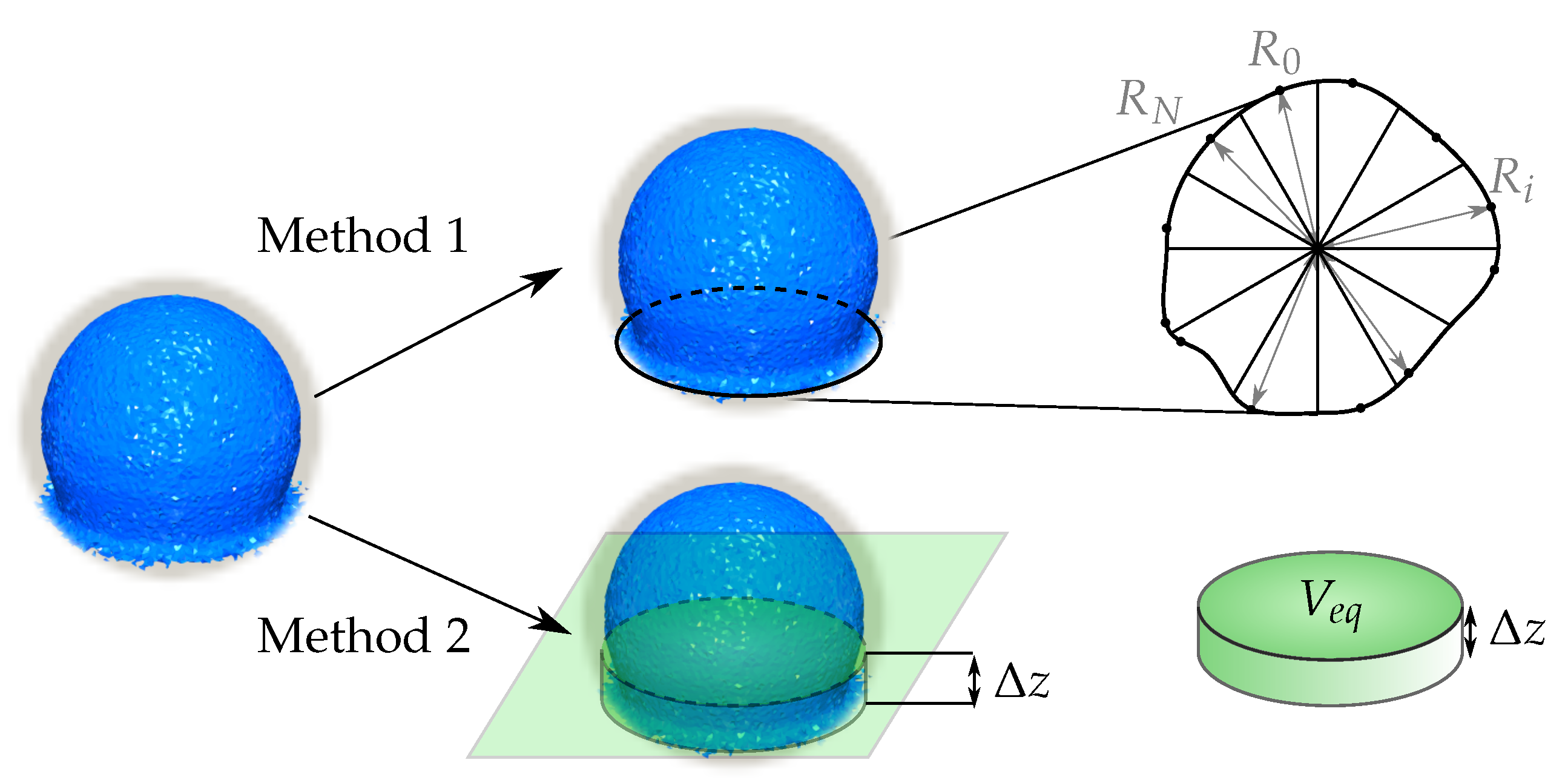
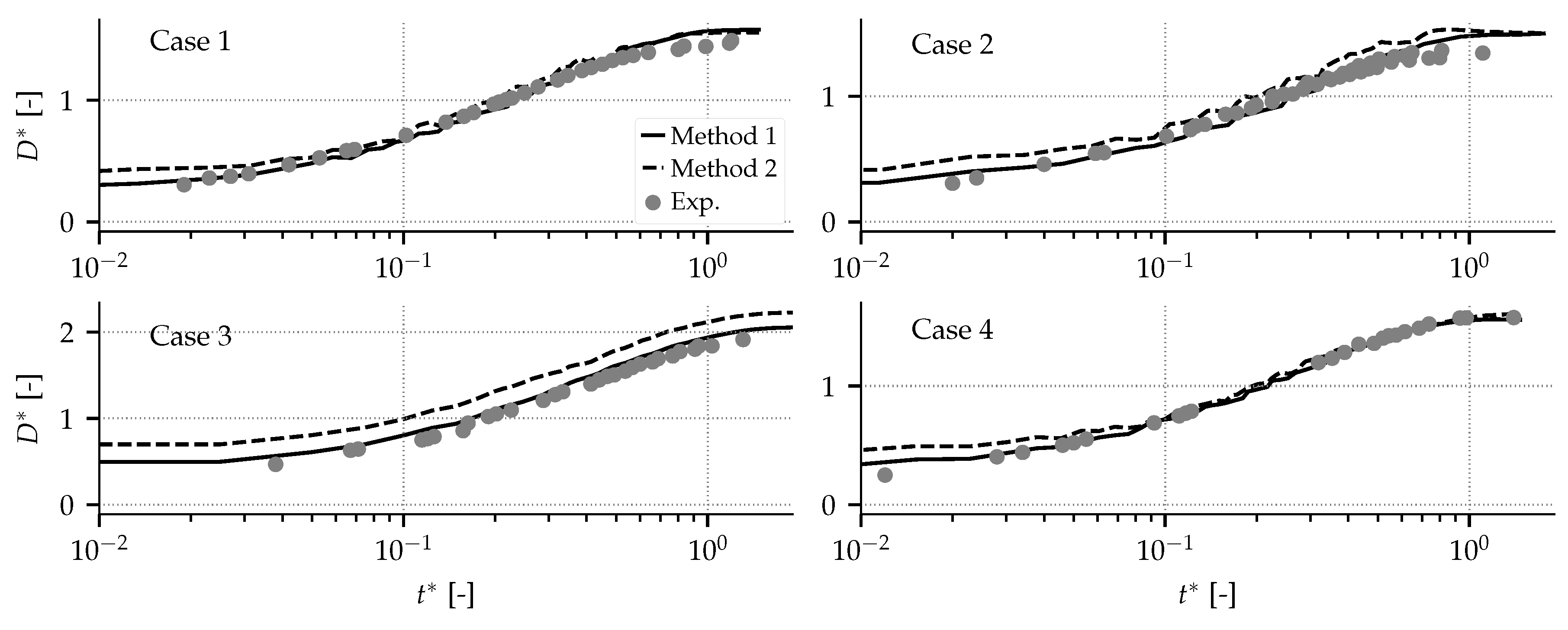
3.2. Results
4. Application to Realistic Operating Conditions
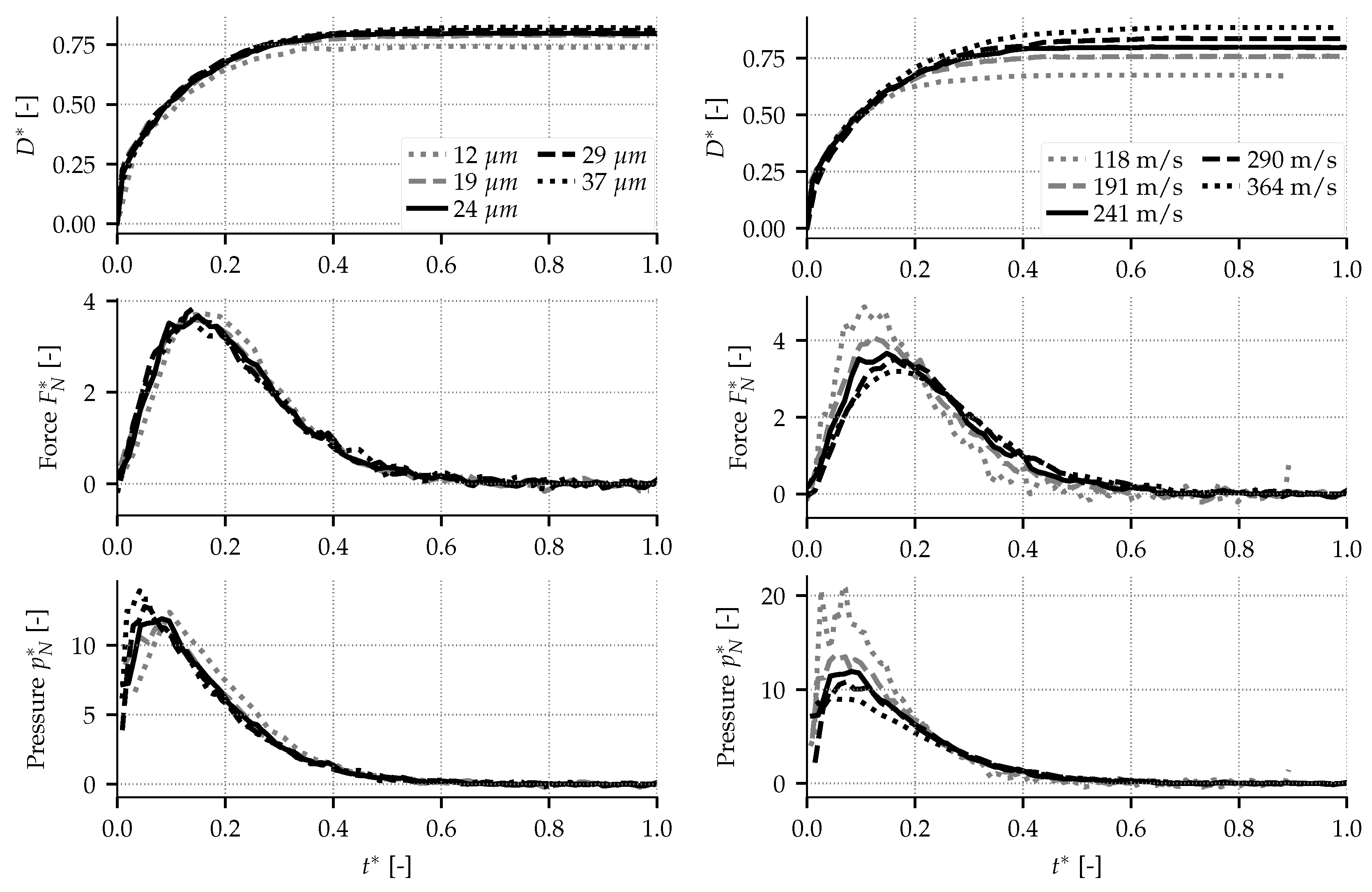
4.1. Influence of Impact Conditions of a Spherical Particle during Normal Impact
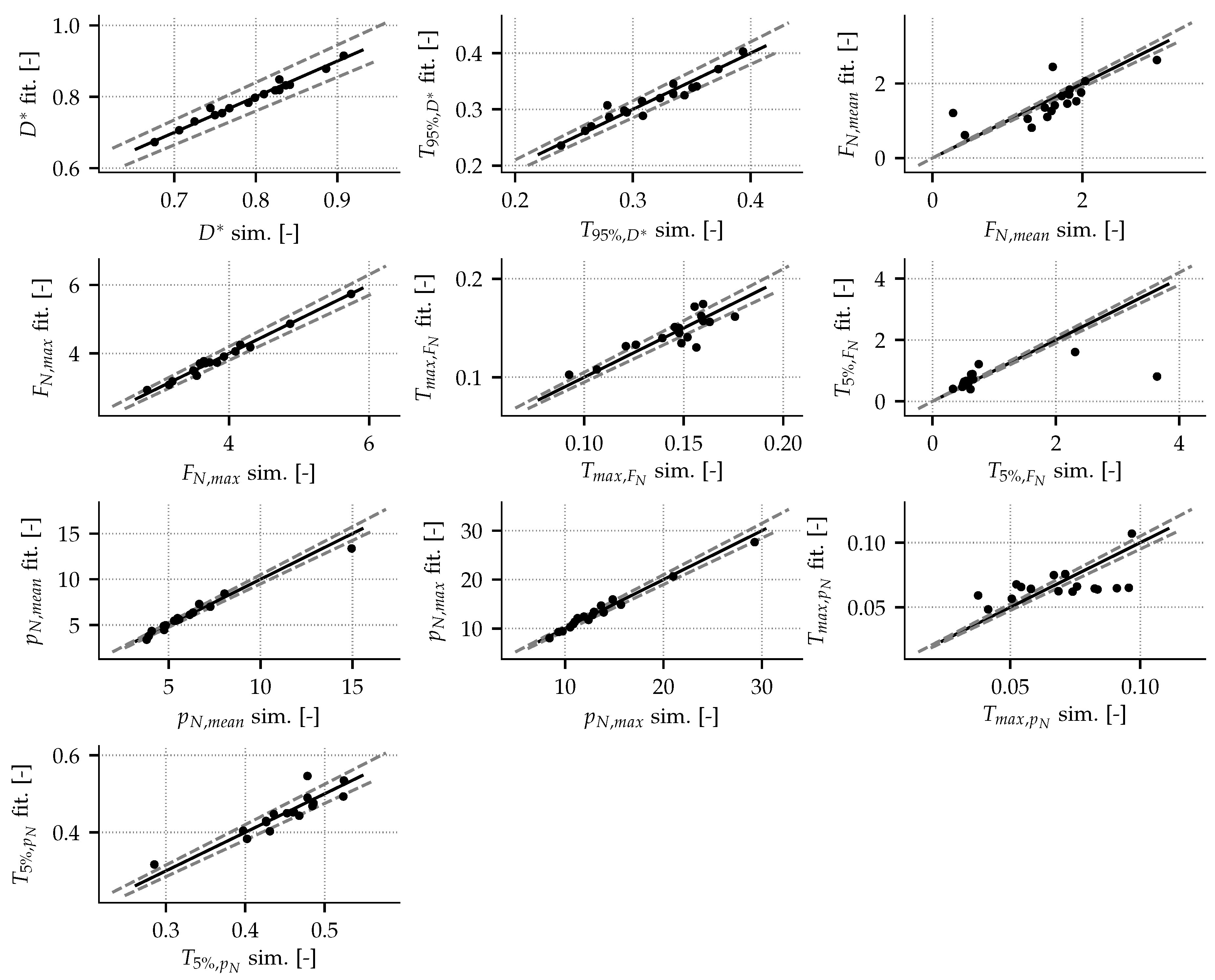
4.2. Correlation Characterizing the Normal Impact
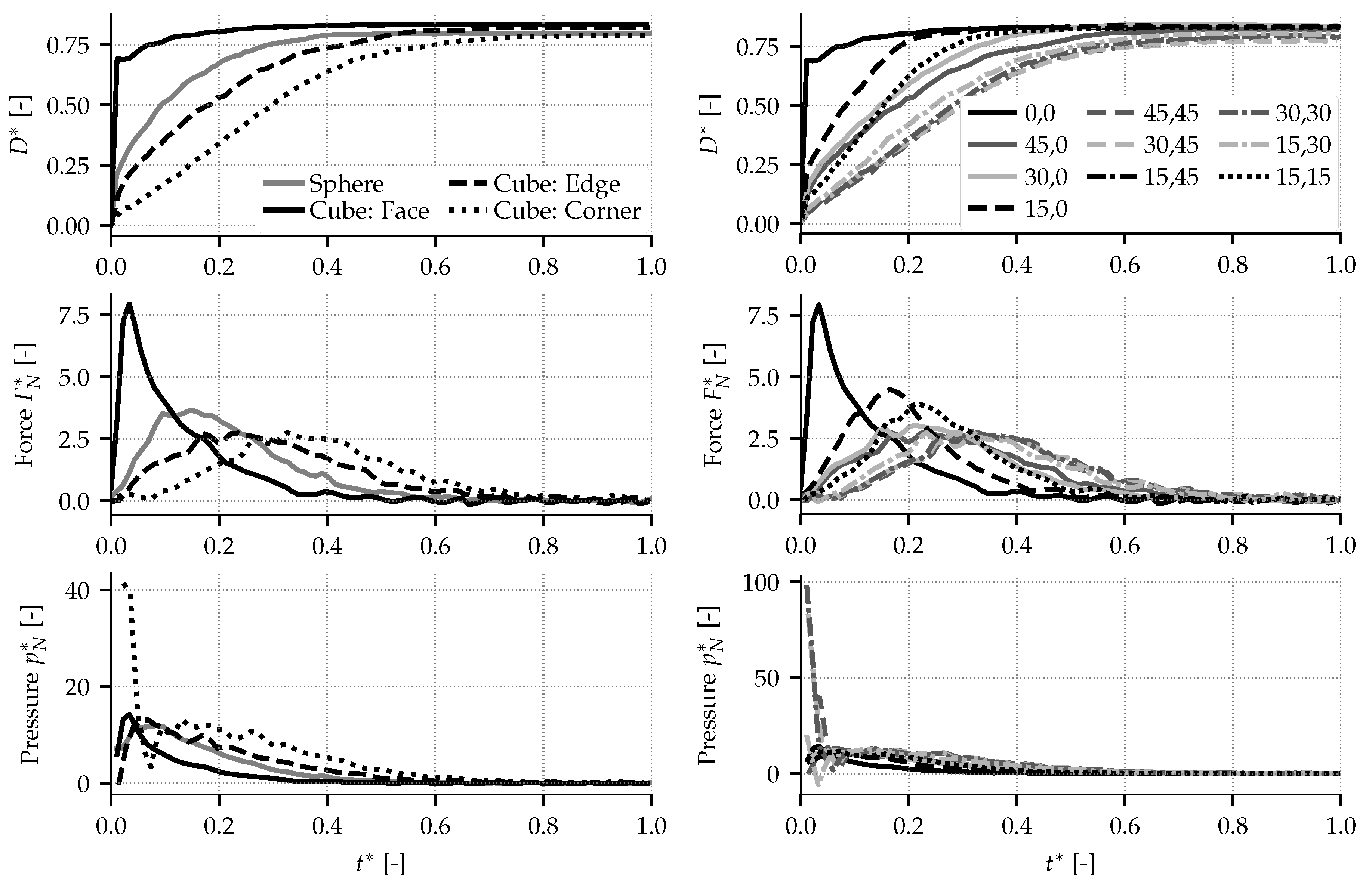
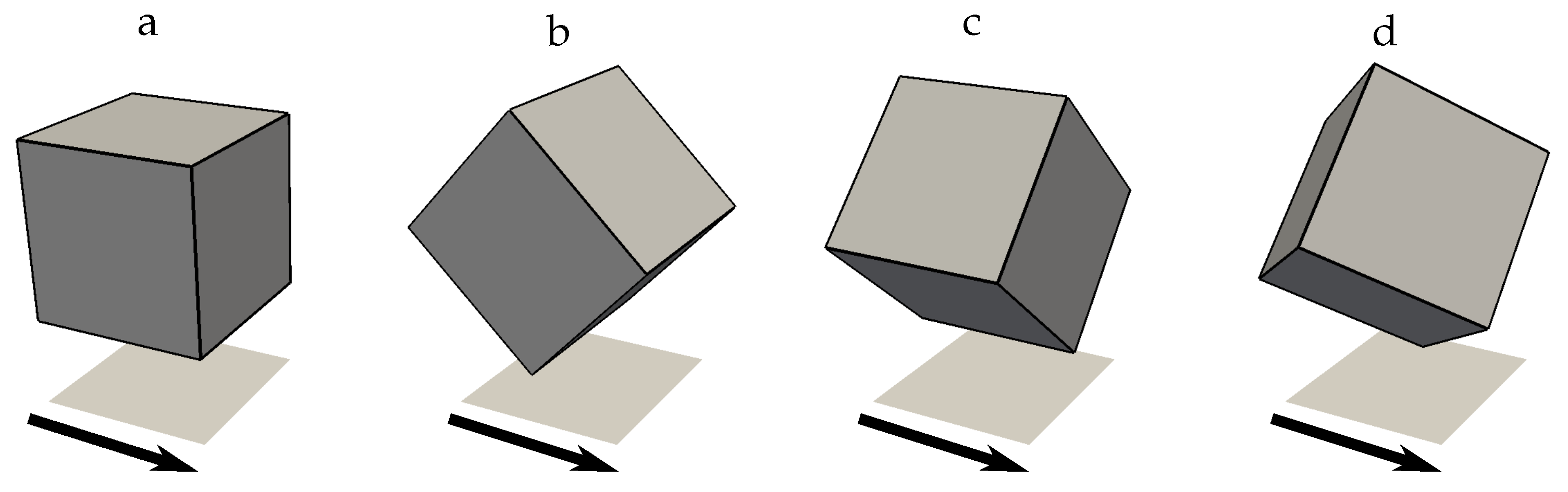
4.3. Influence of the Particle Shape
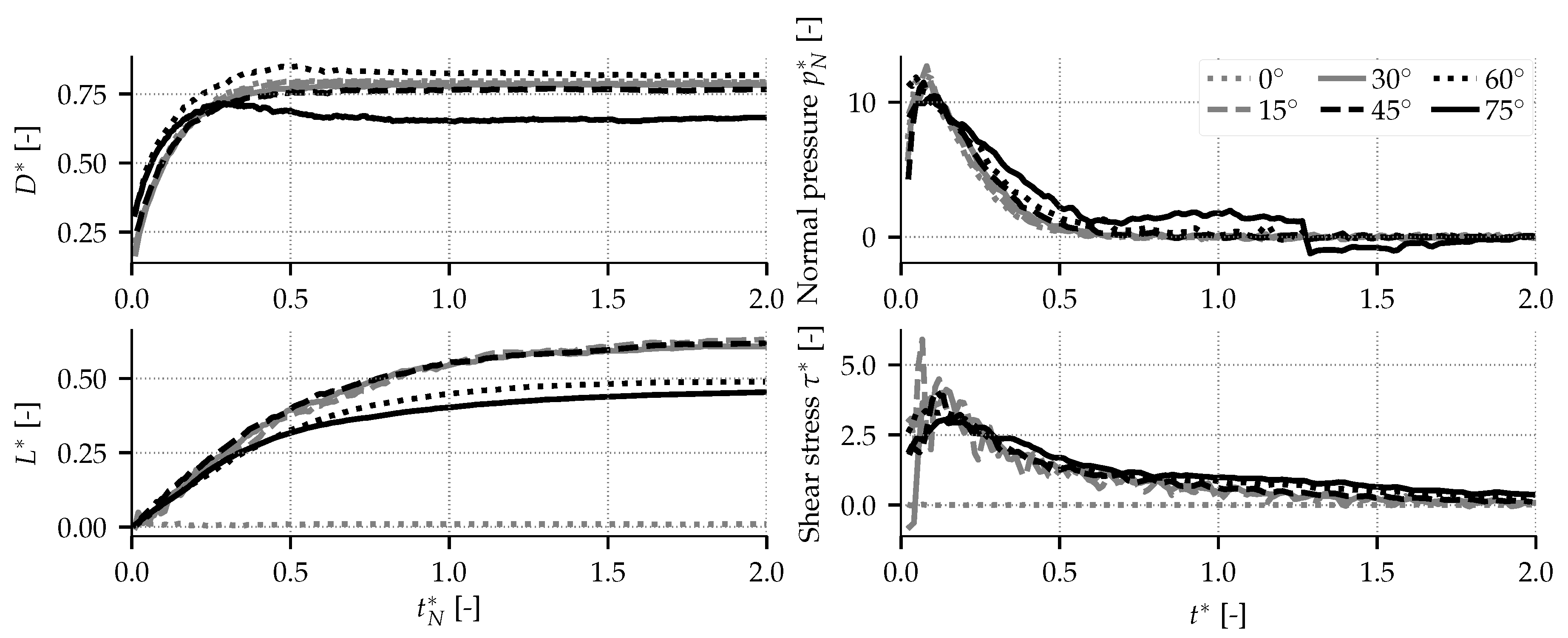
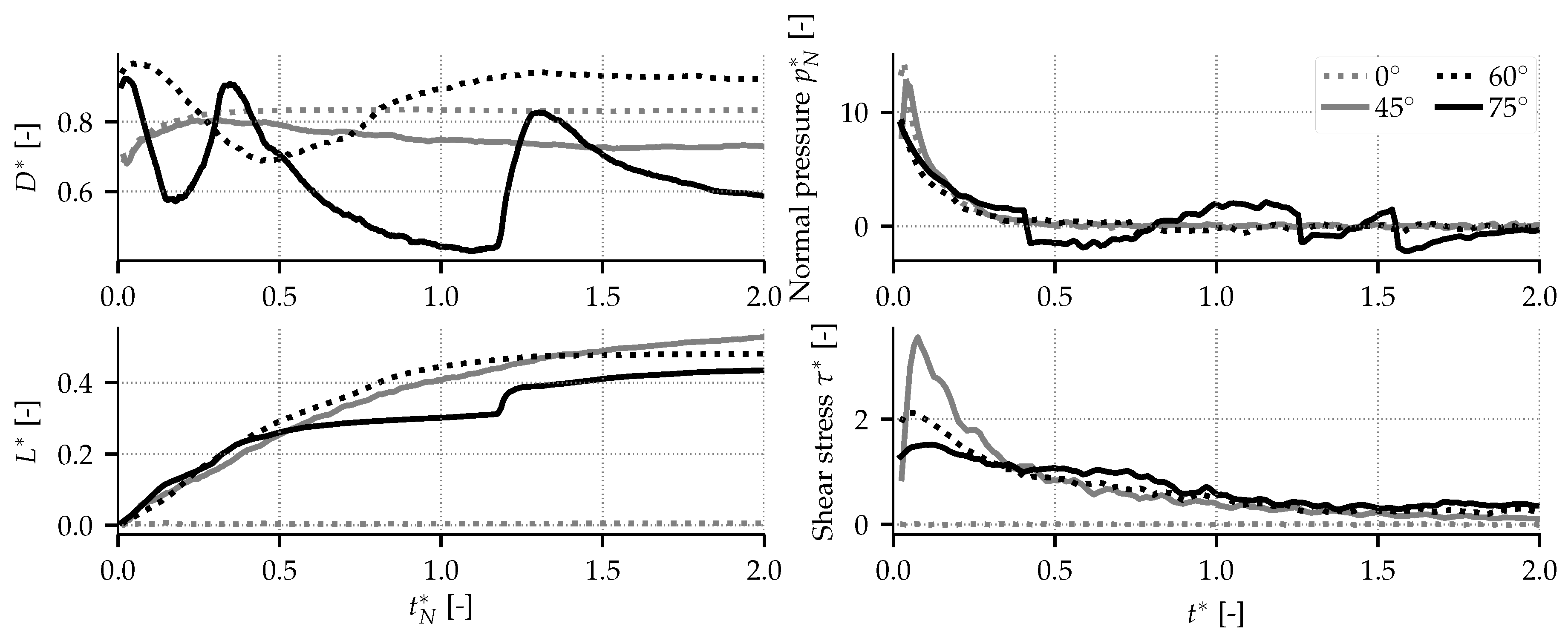
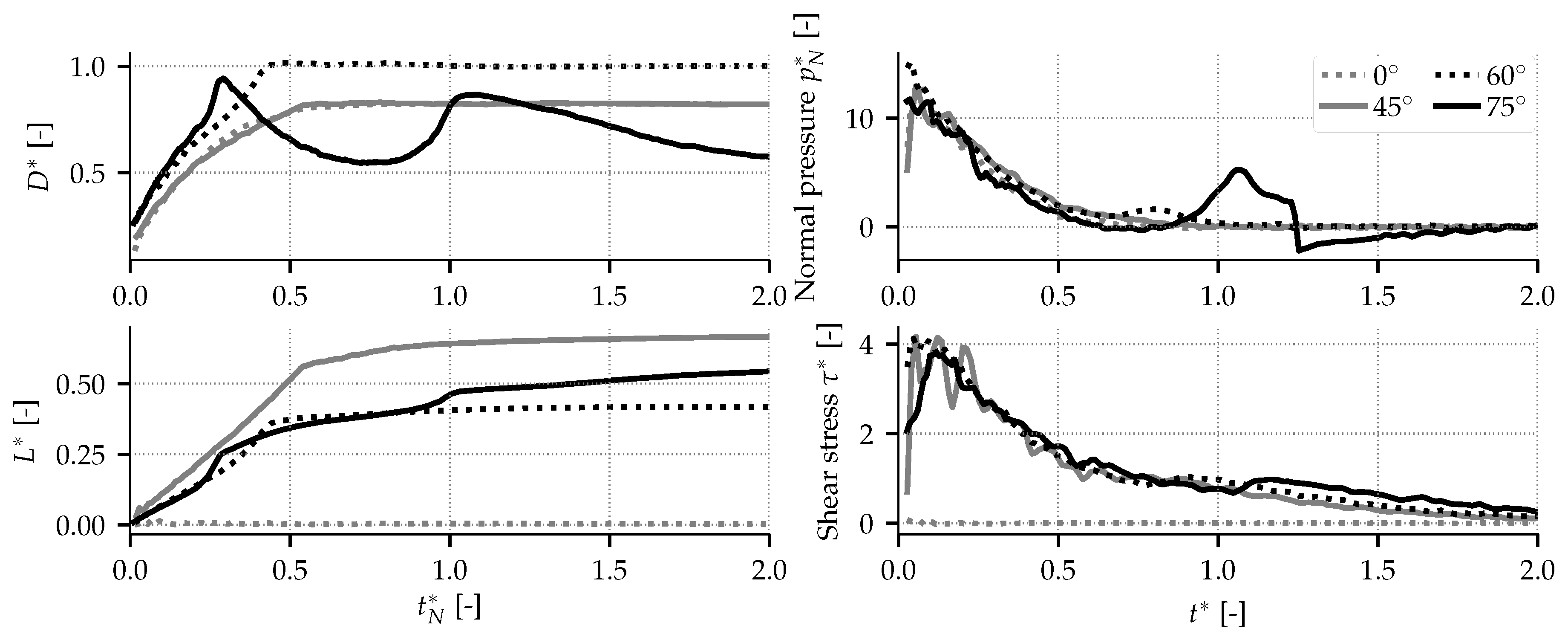
4.4. Oblique Impacts for Spherical and Cubic Particles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CMAS | Calcium-Magnesium-Aluminosilicate |
| LES | Large Eddy Simulation |
| SPH | Smoothed Particle Hydrodynamics |
| T/EBC | Thermal/Environmental Blade Coating |
References
- Hamed, A.; Tabakoff, W.C.; Wenglarz, R. Erosion and Deposition in Turbomachinery. J. Propuls. Power 2006, 22, 350–360. [Google Scholar] [CrossRef] [Green Version]
- Filippone, A.; Bojdo, N. Turboshaft engine air particle separation. Prog. Aerosp. Sci. 2010, 46. [Google Scholar] [CrossRef]
- Ghoshal, A.; Murugan, M.; Walock, M.J.; Nieto, A.; Barnett, B.D.; Pepi, M.S.; Swab, J.J.; Zhu, D.; Kerner, K.A.; Rowe, C.R.; et al. Molten Particulate Impact on Tailored Thermal Barrier Coatings for Gas Turbine Engine. J. Eng. Gas Turbines Power 2018, 140. [Google Scholar] [CrossRef]
- Bravo, L.; Jain, N.; Khare, P.; Murugan, M.; Ghoshal, A.; Flatau, A. Physical aspects of CMAS particle dynamics and deposition in gas turbine engines. J. Mater. Res. 2020, 35, 2249–2259. [Google Scholar] [CrossRef]
- Aygun, A.; Vasiliev, A.L.; Padture, N.P.; Ma, X. Novel thermal barrier coatings that are resistant to high-temperature attack by glassy deposits. Acta Mater. 2007, 55, 6734–6745. [Google Scholar] [CrossRef]
- Drexler, J.M.; Shinoda, K.; Ortiz, A.L.; Li, D.; Vasiliev, A.L.; Gledhill, A.D.; Sampath, S.; Padture, N.P. Air-plasma-sprayed thermal barrier coatings that are resistant to high-temperature attack by glassy deposits. Acta Mater. 2010, 58, 6835–6844. [Google Scholar] [CrossRef]
- Ganti, H.; Khare, P.; Bravo, L. Binary Collision of CMAS Droplets—Part I: Equal Sized Droplets. J. Mater. Res. 2020, 1–15. [Google Scholar] [CrossRef]
- Ganti, H.; Khare, P.; Bravo, L. Binary Collision of CMAS Droplets—Part II: Unequal Sized Droplets. J. Mater. Res. 2020, 1–13. [Google Scholar] [CrossRef]
- Singh, S.; Tafti, D. Particle deposition model for particulate flows at high temperatures in gas turbine components. Int. J. Heat Fluid Flow 2015, 52, 72–83. [Google Scholar] [CrossRef]
- Delimont, J.M.; Murdock, M.K.; Ng, W.F.; Ekkad, S.V. Effect of Near Melting Temperatures on Microparticle Sand Rebound Characteristics at Constant Impact Velocity. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Düsseldorf, Germany, 16–20 June 2014; American Society of Mechanical Engineers: New York, NY, USA; Volume 45578. [Google Scholar] [CrossRef]
- Murugan, M.; Ghoshal, A.; Walock, M.J.; Barnett, B.D.; Pepi, M.S.; Kerner, K.A. Sand particle-Induced deterioration of thermal barrier coatings on gas turbine blades. Adv. Aircr. Spacecr. Sci. 2017, 4, 37–52. [Google Scholar] [CrossRef]
- Jain, N.; Bravo, L.; Bose, S.; Kim, D.; Murugan, M.; Ghoshal, A.; Flatau, A. Turbulent multiphase flow and particle deposition of sand ingestion for high-temperature turbine blades. In Proceedings of the Summer Program; Center for Turbulence Research: Stanford, CA, USA, 2018; p. 11. [Google Scholar]
- Ai, W.; Fletcher, T.H. Computational Analysis of Conjugate Heat Transfer and Particulate Deposition on a High Pressure Turbine Vane. J. Turbomach. 2012, 134. [Google Scholar] [CrossRef] [Green Version]
- Gingold, R.; Monaghan, J.J. Smoothed particle hydrodynamics-theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Peng, C.; Xu, G.; Wu, W.; Yu, H.s.; Wang, C. Multiphase SPH modeling of free surface flow in porous media with variable porosity. Comput. Geotech. 2017, 81, 239–248. [Google Scholar] [CrossRef]
- Tofighi, N.; Ozbulut, M.; Rahmat, A.; Feng, J.; Yildiz, M. An incompressible smoothed particle hydrodynamics method for the motion of rigid bodies in fluids. J. Comput. Phys. 2015, 297, 207–220. [Google Scholar] [CrossRef]
- Monaghan, J.J. A turbulence model for Smoothed Particle Hydrodynamics. Eur. J. Mech. B/Fluids 2011, 30, 360–370. [Google Scholar] [CrossRef] [Green Version]
- Federrath, C.; Banerjee, R.; Clark, P.; Klessen, R. Modeling collapse and accretion in turbulent gas clouds: Implementation and comparison of sink particles in AMR and SPH. Astrophys. J. 2010, 713, 269–290. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Bai, L.; Li, L.; Zhao, M. SPH modeling of droplet impact on solid boundary. Trans. Tianjin Univ. 2014, 20, 112–117. [Google Scholar] [CrossRef]
- Shigorina, E.; Kordilla, J.; Tartakovsky, A.M. Smoothed particle hydrodynamics study of the roughness effect on contact angle and droplet flow. Phys. Rev. E 2017, 96, 033115. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Kong, S.C. 3D Simulation of Drop Impact on Dry Surface Using SPH Method. Int. J. Comput. Methods 2018, 15, 1850011. [Google Scholar] [CrossRef]
- Yang, X.; Ray, M.; Kong, S.C.; Kweon, C.B.M. SPH simulation of fuel drop impact on heated surfaces. Proc. Combust. Inst. 2019, 37, 3279–3286. [Google Scholar] [CrossRef] [Green Version]
- Das, R.; Cleary, P.W. Effect of rock shapes on brittle fracture using Smoothed Particle Hydrodynamics. Theor. Appl. Fract. Mech. 2010, 53, 47–60. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Español, P.; Revenga, M. Smoothed dissipative particle dynamics. Phys. Rev. E 2003, 67, 026705. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Adams, N. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Chaussonnet, G.; Braun, S.; Wieth, L.; Koch, R.; Bauer, H.J. Influence of particle disorder and smoothing length on SPH operator accuracy. In Proceedings of the 10th International SPHERIC Workshop, Parma, Italy, 16–18 June 2015. [Google Scholar]
- Cleary, P.W. Modelling confined multi-material heat and mass flows using SPH. Appl. Math. Model. 1998, 22, 981–993. [Google Scholar] [CrossRef] [Green Version]
- Szewc, K.; Pozorski, J.; Minier, J.P. Analysis of the incompressibility constraint in the smoothed particle hydrodynamics method. Int. J. Numer. Methods Eng. 2012, 92, 343–369. [Google Scholar] [CrossRef] [Green Version]
- Chaussonnet, G.; Braun, S.; Dauch, T.; Keller, M.; Sänger, A.; Jakobs, T.; Koch, R.; Kolb, T.; Bauer, H.J. Toward the Development of a Virtual Spray Test-Rig using the Smoothed Particle Hydrodynamics Method. Comput. Fluids 2019, 180, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Brackbill, J.; Kothe, D.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.; Adams, N. A new surface-tension formulation for multi-phase SPH using a reproducing divergence approximation. J. Comput. Phys. 2010, 229, 5011–5021. [Google Scholar] [CrossRef]
- Cole, R.H. Underwater Explosions; Dover Publications: Ann Arbor, MI, USA, 1965. [Google Scholar]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Colagrossi, A.; Bouscasse, B.; Antuono, M.; Marrone, S. Particle packing algorithm for SPH schemes. Comput. Phys. Commun. 2012, 183, 1641–1653. [Google Scholar] [CrossRef] [Green Version]
- Rioboo, R.; Tropea, C.; Marengo, M. Outcomes from a Drop Impact on Solid Surfaces. At. Sprays 2001, 11. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef] [Green Version]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef] [Green Version]
- Rioboo, R. Impact de gouttes sur surfaces solides et seches. Ph.D. Thesis, Physique Paris 6, Université Pierre et Marie Curie, Paris, France, 2001. [Google Scholar]
- Wiesner, V.L.; Vempati, U.K.; Bansal, N.P. High temperature viscosity of calcium-magnesium-aluminosilicate glass from synthetic sand. Scr. Mater. 2016, 124, 189–192. [Google Scholar] [CrossRef]



| Case | |||||
|---|---|---|---|---|---|
| - | [mm] | [mm] | [mm] | [mm] | [m] |
| Validation | 5 | 17 | 1.9 | 2 | 50 |
| Real conditions | 0.05 | 0.12 | 0.03 | 0.03 | 0.6 |
| Case | Liquid Type | Velocity | Diameter | Viscosity | Density | Surf. Tens. | Re | We | Oh |
|---|---|---|---|---|---|---|---|---|---|
| - | - | [m/s] | [mm] | [Pa·s] | [kg/m] | [kg/s] | [−] | [−] | [−] |
| 0 | Water | 1.18 | 3.04 | 0.001 | 1000 | 0.072 | 3587 | 59 | |
| 1 | Glycerin | 0.96 | 2.64 | 0.1 | 1260 | 0.063 | 32 | 49 | 0.22 |
| 2 | Glycerin | 2.70 | 2.65 | 0.1 | 1260 | 0.063 | 90 | 386 | 0.22 |
| 3 | Glycerin | 0.97 | 2.08 | 0.1 | 1260 | 0.063 | 25 | 39 | 0.25 |
| 4 | Silicone oil | 0.89 | 2.84 | 0.1 | 963 | 0.021 | 24 | 103 | 0.42 |
| Velocity | Diameter | Viscosity | Density | Surf. Tens. | Re | We | Oh |
|---|---|---|---|---|---|---|---|
| [m/s] | [m] | [Pa·s] | [kg/m] | [kg/s] | [−] | [−] | [−] |
| 250 | 25 | 11 | 2665 | 0.4 | 1.83 | 12,600 | 61 |
| a | |||||
|---|---|---|---|---|---|
| Ref. Value | - | m/s | m | Pa·s | kg/m |
| 0.807 | 0.238 | 0.072 | −0.205 | 0.160 | |
| 0.319 | 0.407 | 0.094 | −0.366 | 0.240 | |
| 1.865 | −0.184 | 1.263 | 0.848 | −0.822 | |
| 3.745 | −0.379 | 0.022 | 0.278 | −0.596 | |
| 0.139 | 0.416 | −0.195 | −0.167 | 0.468 | |
| 0.520 | 0.169 | −1.284 | −0.864 | 0.691 | |
| 5.629 | −0.594 | 0.068 | 0.560 | −1.224 | |
| 12.833 | −0.715 | 0.137 | 0.416 | −1.098 | |
| 0.056 | −0.211 | −0.716 | 0.052 | −0.018 | |
| 0.447 | 0.225 | −0.027 | −0.254 | 0.486 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaussonnet, G.; Bravo, L.; Flatau, A.; Koch, R.; Bauer, H.-J. Smoothed Particle Hydrodynamics Simulation of High Velocity Impact Dynamics of Molten Sand Particles. Energies 2020, 13, 5134. https://doi.org/10.3390/en13195134
Chaussonnet G, Bravo L, Flatau A, Koch R, Bauer H-J. Smoothed Particle Hydrodynamics Simulation of High Velocity Impact Dynamics of Molten Sand Particles. Energies. 2020; 13(19):5134. https://doi.org/10.3390/en13195134
Chicago/Turabian StyleChaussonnet, Geoffroy, Luis Bravo, Alison Flatau, Rainer Koch, and Hans-Jörg Bauer. 2020. "Smoothed Particle Hydrodynamics Simulation of High Velocity Impact Dynamics of Molten Sand Particles" Energies 13, no. 19: 5134. https://doi.org/10.3390/en13195134





