New Protection Scheme in Loop Distribution System with Distributed Generation
Abstract
:1. Introduction
- (1)
- A method for calculating the fault location in a loop distribution system with DG based on the equivalent circuit of the system is proposed.
- (2)
- After the fault location is calculated, a protection scheme to separate the fault section and supply the normal current to the healthy sections in the distribution line is proposed.
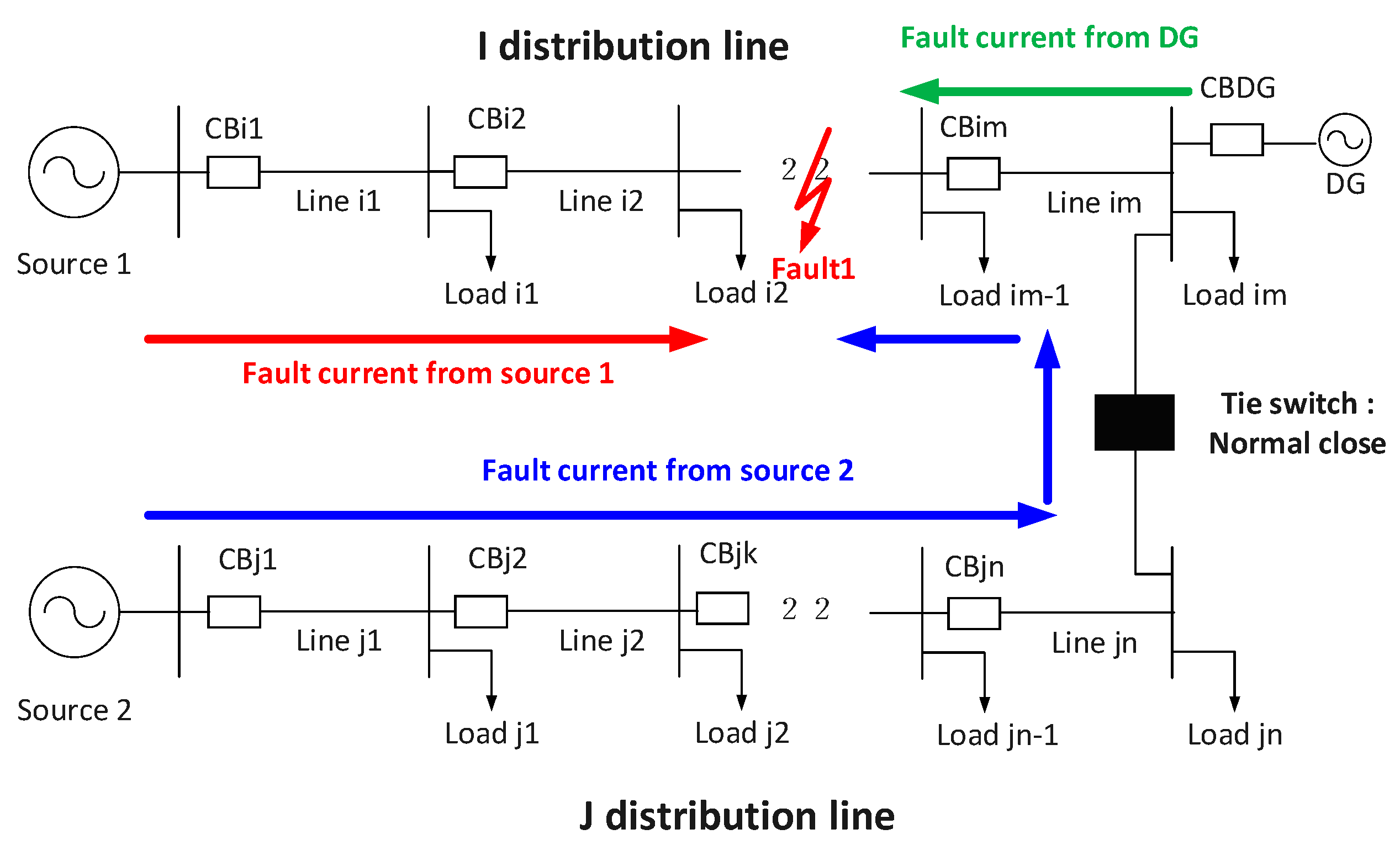
2. Considerations for Protection in Loop Distribution System with DG
- (1)
- Because the fault current is injected from both directions, the current flowing to the fault point can increase.
- (2)
- The injection of a bidirectional fault current makes it impossible to supply the normal current, even though the J distribution line is not faulty. In addition, during a fault, it is impossible to supply a normal current from the DG system to the J distribution line.
- (3)
- Despite the fault at the I distribution line, it is possible for the protection devices of the J distribution line to operate by detecting the fault current. Therefore, the protection devices of both distribution lines are operated so that the outage section can be expanded.
- (4)
- In a conventional radial distribution system, because the current flows in one direction, the directionality is not applied to the protection device. As shown in Figure 1, the fault current by the fault of the I distribution line is injected from the J distribution line and DG as well as from the I distribution line. However, if the protection device does not have directionality, maloperation of the protective devices located after the fault section in the I distribution line and protective devices located in the J distribution line is possible.
3. New Protection Scheme in Loop Distribution System with DG
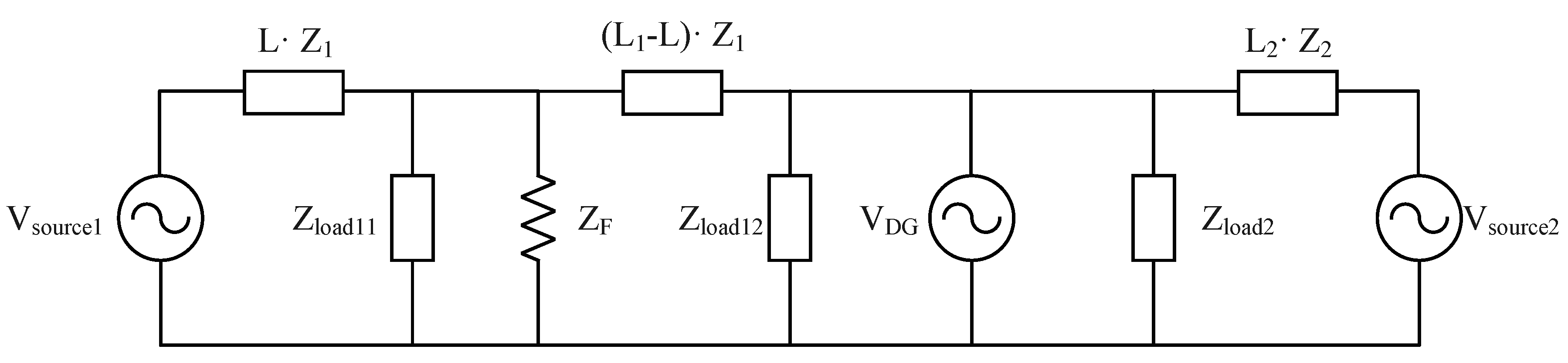
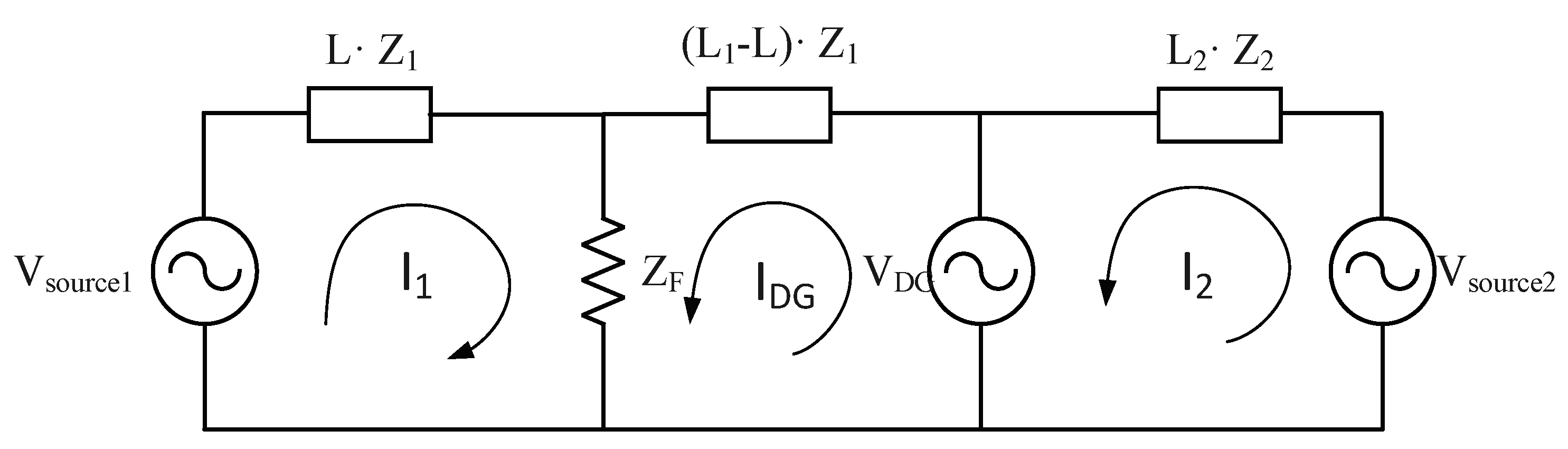
3.1. Detection Method of Fault Section
- Vsource1: Magnitude of voltage source in the I distribution line;
- Vsource2: Magnitude of voltage source in the J distribution line;
- VDG: Magnitude of voltage at the connecting point of DG;
- L1: Total line length of the I distribution line;
- L2: Total line length of the J distribution line;
- L: Length from source to fault point in the I distribution line;
- Z1: Impedance per length in the I distribution line;
- Z2: Impedance per length in the J distribution line;
- Zload11: Equivalent impedance of loads from source to fault point in the I distribution line;
- Zload12: Equivalent impedance of loads after fault point in the I distribution line I;
- Zload2: Equivalent impedance of loads in the J distribution line;
- ZF: Fault resistance.
3.2. New Protection Scheme in Loop Distribution System Considering DG
- (1)
- Through accurate determination of the fault section and its separation from the system, it is possible to supply normal power to the healthy section in the distribution line. Therefore, other protection devices do not malfunction, and the outage section can be reduced.
- (2)
- It is possible to supply normal power from the main source as well as DG because the fault section is quickly separated from the system. If the DG cannot supply normal power, the DG is separated from the distribution system by the proposed protection scheme.
4. Simulations and Discussion
4.1. System Model
4.2. Simulation Conditions
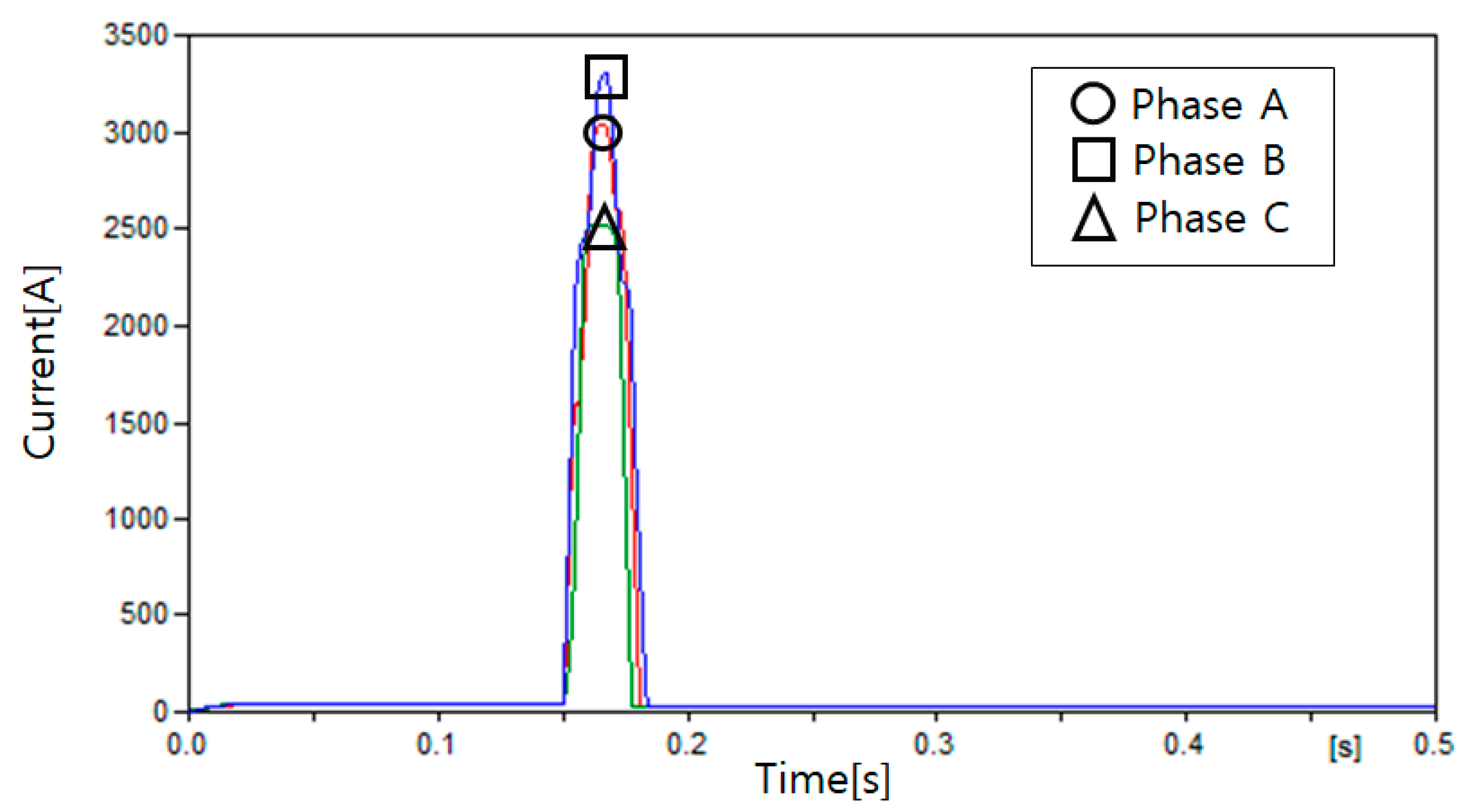
4.3. Simulation Results
4.3.1. Case 1
4.3.2. Case 2
4.3.3. Case 3
4.3.4. Case 4
4.3.5. Case 5
4.3.6. Case 6
4.3.7. Case 7
4.3.8. Case 8
5. Conclusions
Funding
Conflicts of Interest
References
- Seo, H.-C. Protection Scheme based on IoT in Loop Distribution System. Trans. Korean Inst. Electr. Eng. 2020, 69, 752–758. [Google Scholar] [CrossRef]
- Seo, H.-C. Novel Protection Scheme considering Tie Switch Operation in Open Loop Distribution System using Wavelet Transform. Energies 2019, 12, 1725. [Google Scholar] [CrossRef] [Green Version]
- Seo, H.-C. New Protection Scheme Based on Coordination with Tie Switch in an Open-Loop Microgrid. Energies 2019, 12, 4756. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.; Singh, R.K.; Choudhary, N.K. Performance Analysis of Optimization Technique for Protection Coordination in Single and Multi-Loop Distribution System. In Proceedings of the International Conference on Electrical Electronics and Computer Engineering, Aligarh, India, 8–10 November 2019. [Google Scholar]
- Zhang, Z.H.; Xu, B.Y.; Crossley, P.; Li, L. Positive-sequence-fault-component-based blocking pilot protection for closed-loop distribution network with underground cable. Int. J. Electr. Power Energy Syst. 2018, 94, 57–66. [Google Scholar] [CrossRef]
- Ngaopitakkul, A.; Leelajindakrairerk, M. Application of probabilistic neural network with transmission and distribution protection schemes for classification of fault types on radial, loop, and underground structures. Electr. Eng. 2018, 100, 461–479. [Google Scholar]
- Zhang, A.; Li, Y.; Huang, Y.; Huang, F.; Liu, Z. Research on Wide-Area Protection and Control Scheme for Closed-Loop Distribution Network. In Proceedings of the International Conference on Power System Technology, Guangzhou, China, 6–8 November 2018. [Google Scholar]
- Xue, S.; Liu, C. Fault location principle and 2-step isolation scheme for a loop-type DC grid. IET Gener. Transm. Distrib. 2018, 12, 2937–2943. [Google Scholar] [CrossRef]
- Islam, F.R.; Prakash, K.; Mamun, K.A.; Lallu, A.; Pota, H.R. Aromatic network: A novel structure for power distribution system. IEEE Access 2017, 5, 25236–25257. [Google Scholar] [CrossRef]
- Borgnino, A.; Manuel, C. Comparison of the performance of different directional polarizing methods in cross country fault protection of a MV loop. In Proceedings of the Power Systems Computation Conference, Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Dashti, R.; Salehizadeh, S.M.; Shaker, H.R.; Tahavori, M. Fault location in double circuit medium power distribution networks using an impedance-based method. Appl. Sci. 2018, 8, 1034. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Shahidehpour, M.; Li, Z.; Liu, X.; Cao, Y.; Tian, W. Protection scheme for loop-based microgrids. IEEE Trans. Smart Grid 2016, 8, 1340–1349. [Google Scholar] [CrossRef]
- Yu, P.; Venkatesh, B.; Yazdani, A.; Singh, B.N. Optimal location and sizing of fault current limiters in mesh networks using iterative mixed integer nonlinear programming. IEEE Trans. Power Syst. 2016, 31, 4776–4783. [Google Scholar] [CrossRef]
- Mishra, M.; Rout, P.K. Detection and classification of micro-grid faults based on HHT and machine learning techniques. IET Gener. Transm. Distrib. 2017, 12, 388–397. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Lee, W.G.; Kim, H.M.; Yang, H.S. Fault Analysis and Design of a Protection System for a Mesh Power System with a Co-Axial HTS Power Cable. Energies 2020, 13, 220. [Google Scholar] [CrossRef] [Green Version]
- Gush, T.; Bukhari, S.B.; Haider, R.; Admasie, S.; Oh, Y.S.; Cho, G.J.; Kim, C.H. Fault Detection and Location in a Microgrid using Mathematical Morphology and Recursive Least Square Methods. Int. J. Electr. Power Energy Syst. 2018, 102, 324–331. [Google Scholar] [CrossRef]
- Kim, W.I.; Kim, E.A.; Ko, Y.J.; Song, J.S.; Yoon, C.H.; Moon, S.H.; Kim, C.S.; Baek, S.K. Technical Trend and Challenging Issues for Celluar-Based Industrial IoT. Electron. Telecommun. Trends 2018, 33, 51–63. [Google Scholar]
- Seo, H.C. New adaptive reclosing technique using second order difference of THD in distribution system with BESS used as uninterruptible power supply. Int. J. Electr. Power Energy Syst. 2017, 90, 315–322. [Google Scholar] [CrossRef]
- Seo, H.C.; Rhee, S.B. Novel adaptive reclosing scheme using wavelet transform in distribution system with battery energy storage system. Int. J. Electr. Power Energy Syst. 2018, 97, 186–200. [Google Scholar] [CrossRef]
- Oh, Y.S.; Kim, C.H.; Gwon, G.H.; Noh, C.H.; Bukhari, S.B.; Haider, R.; Gush, T. Fault detection scheme based on mathematical morphology in last mile radial low voltage DC distribution networks. Int. J. Electr. Power Energy Syst. 2019, 106, 520–527. [Google Scholar] [CrossRef]
- Gwon, G.H.; Kim, C.H.; Oh, Y.S.; Noh, C.H.; Jung, T.H.; Han, J. Mitigation of voltage unbalance by using static load transfer switch in bipolar low voltage DC distribution system. Int. J. Electr. Power Energy Syst. 2017, 90, 157–167. [Google Scholar] [CrossRef]


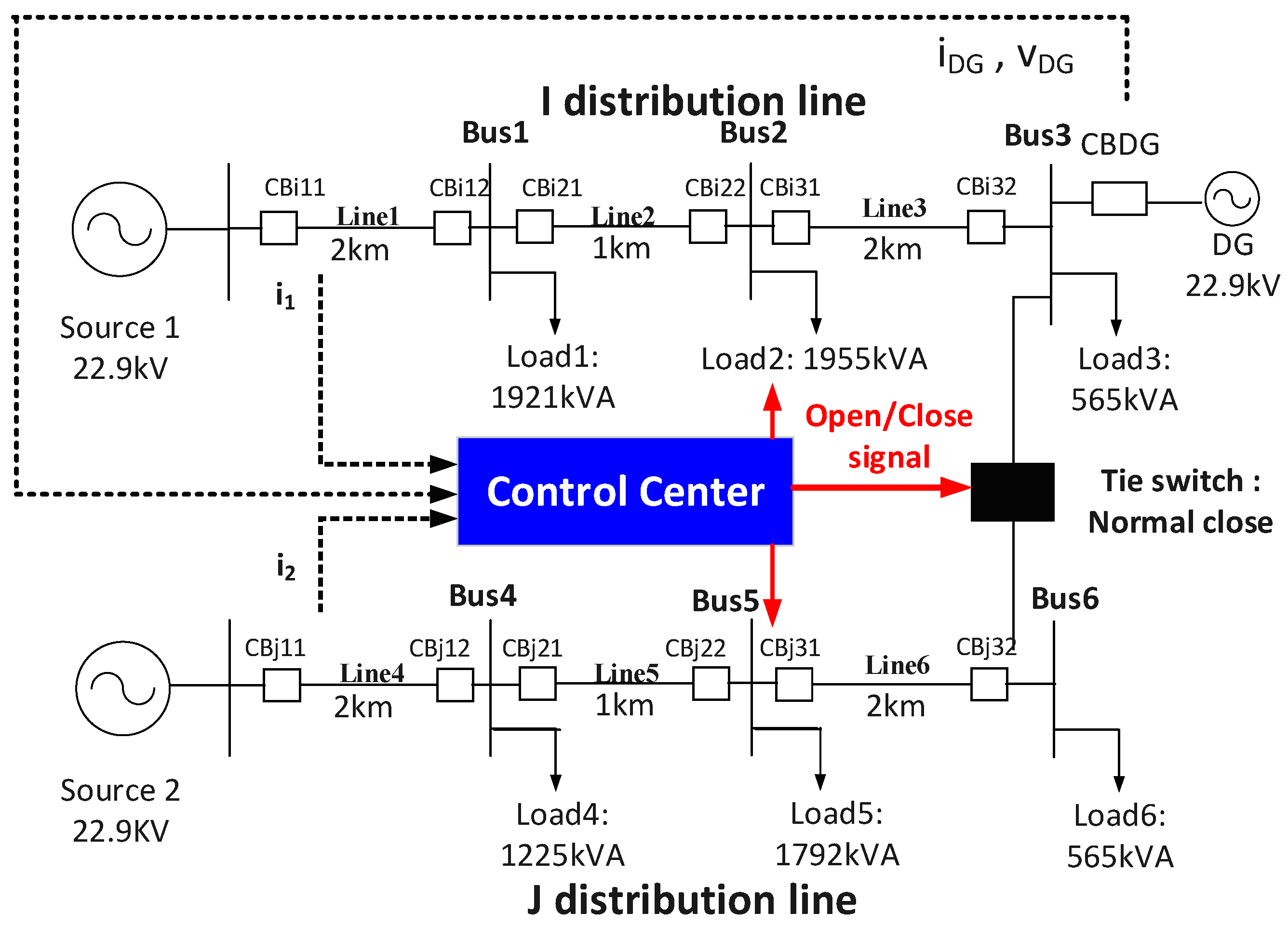
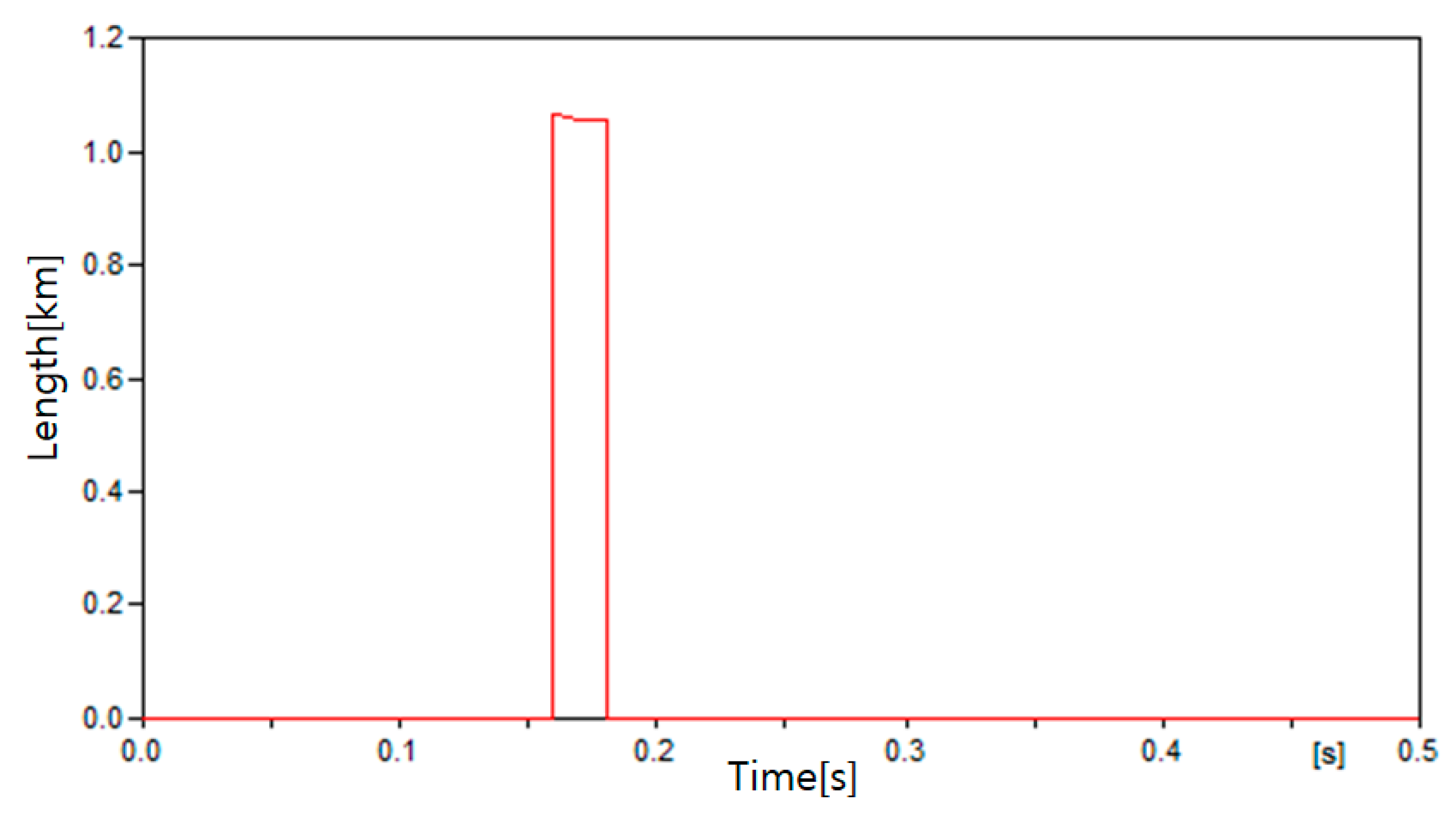
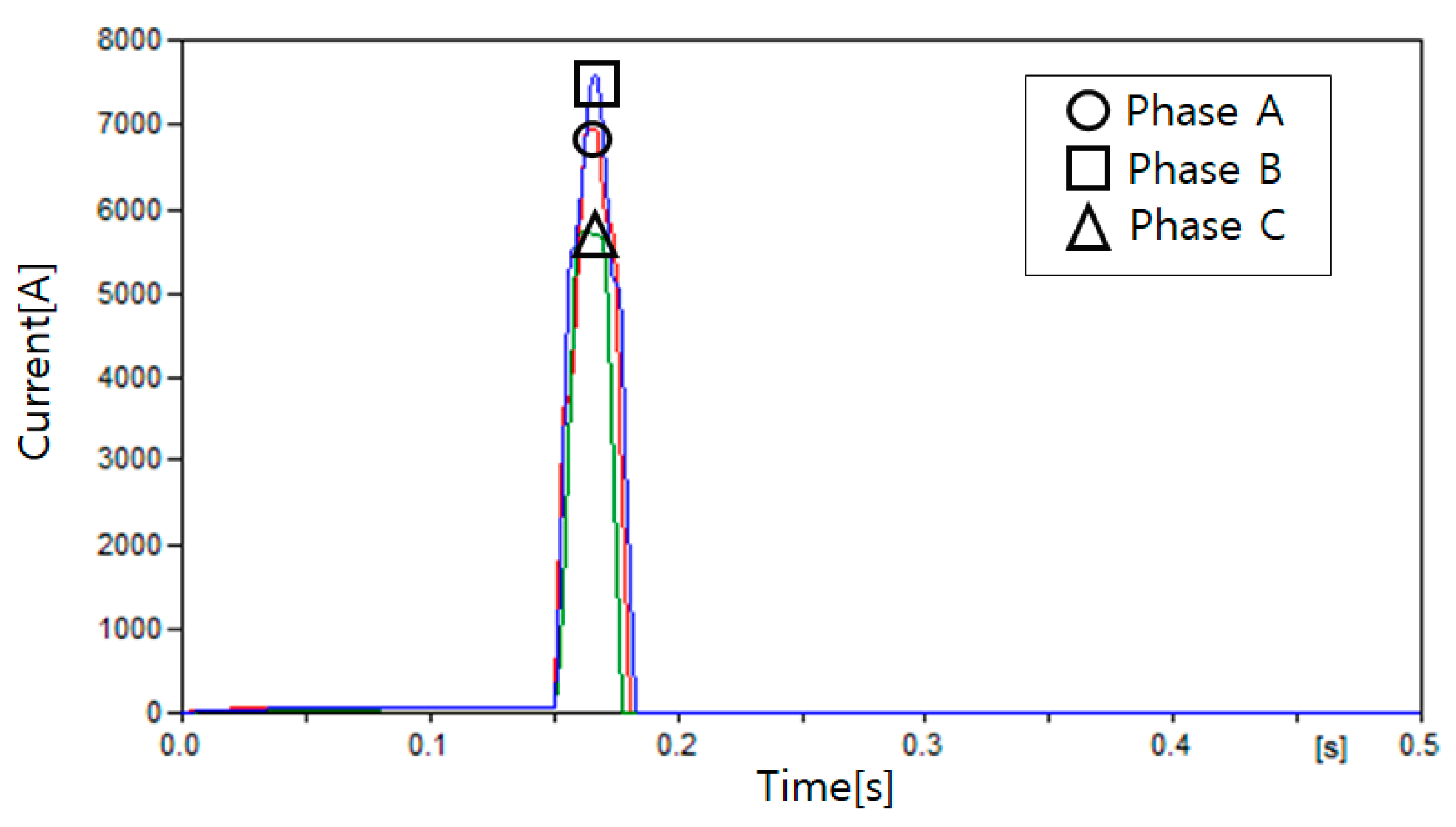


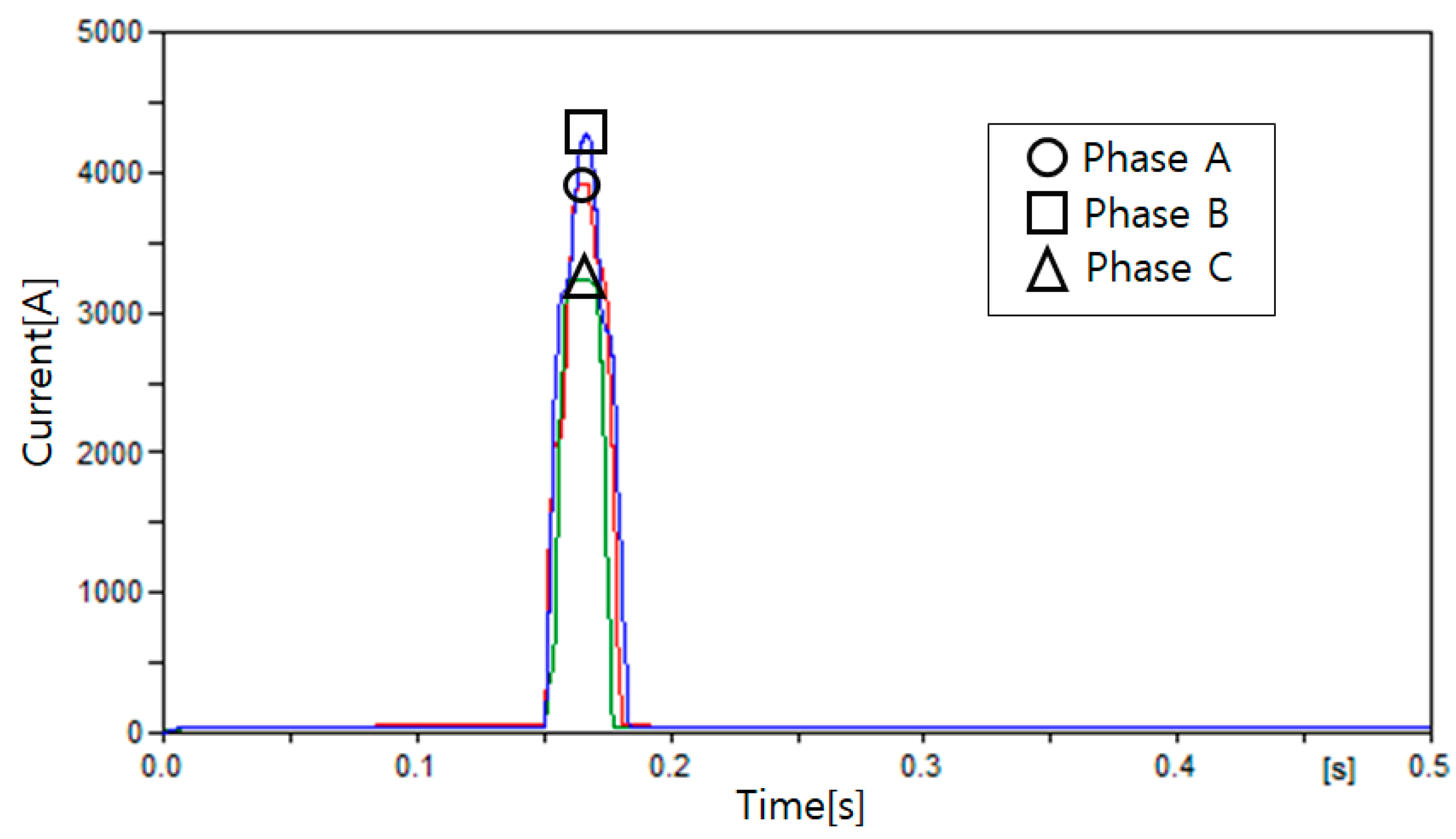

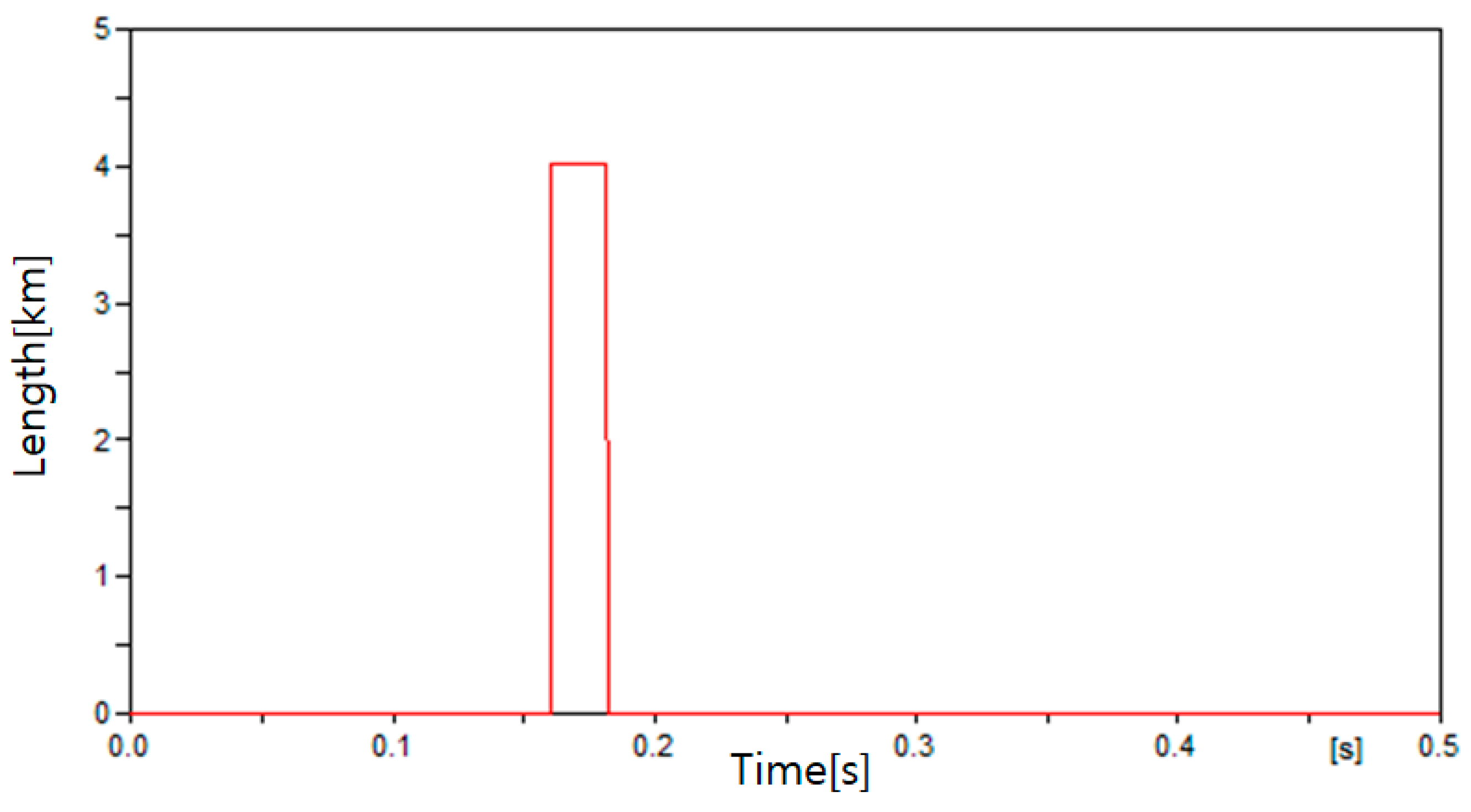


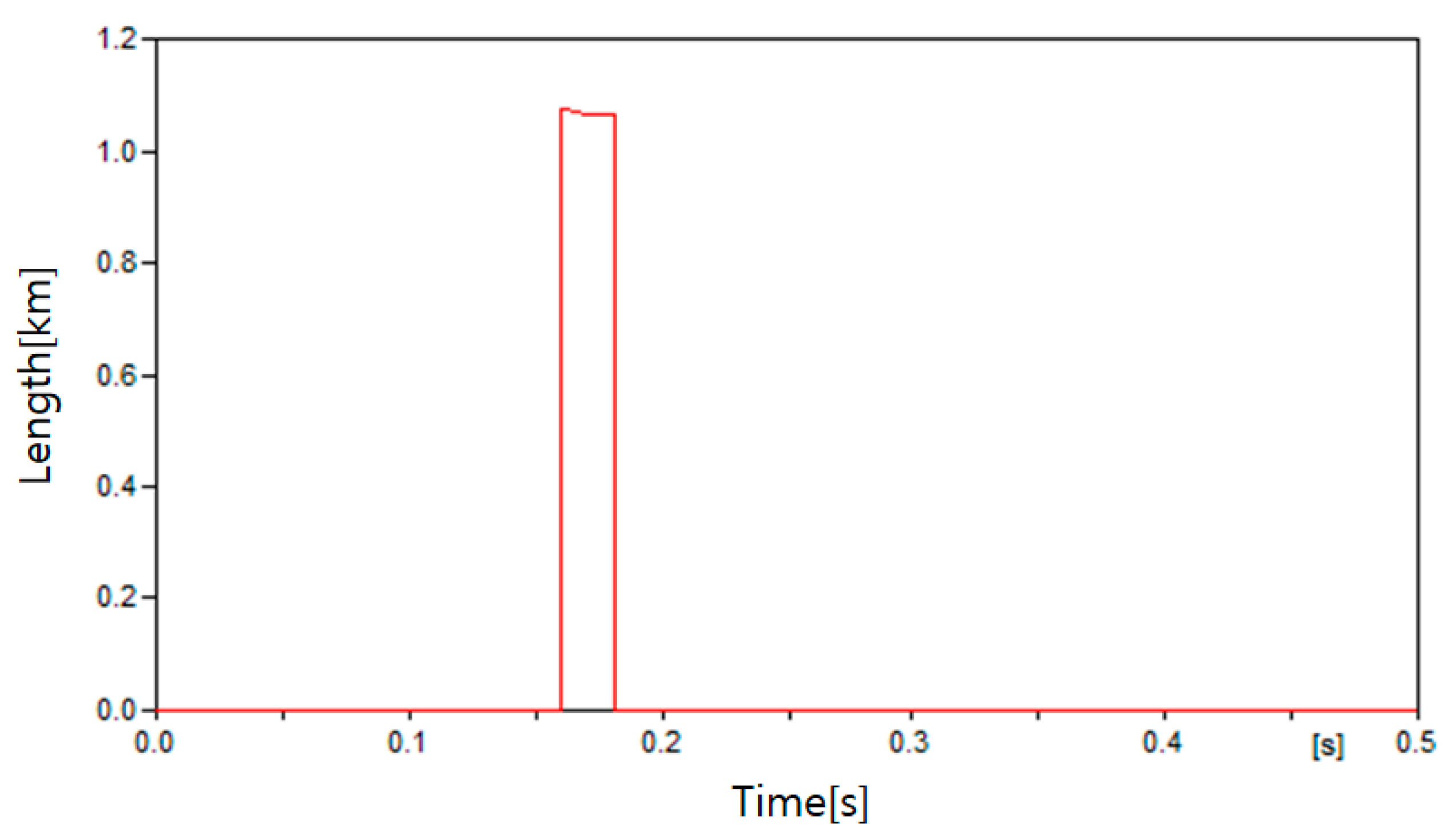
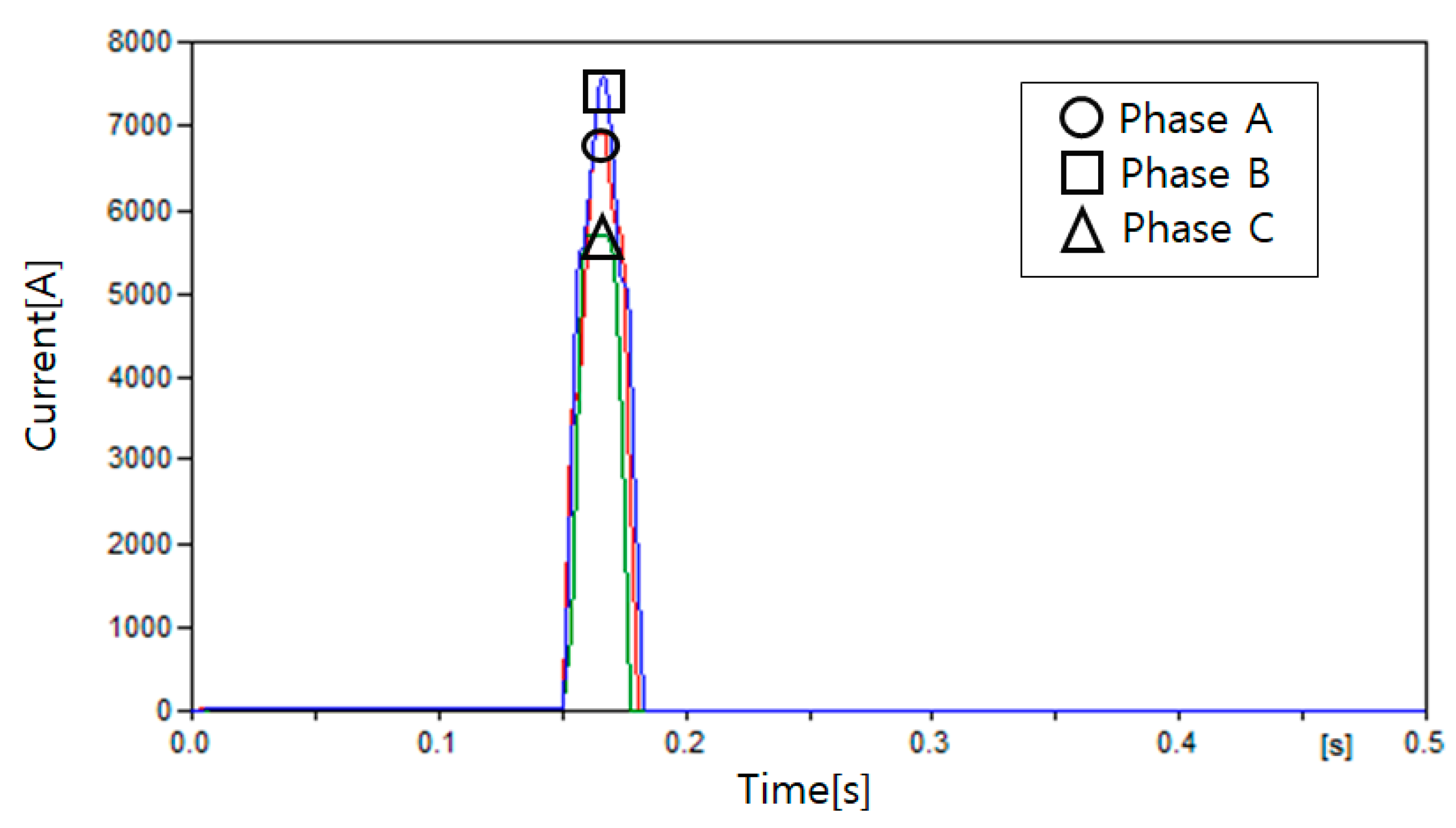

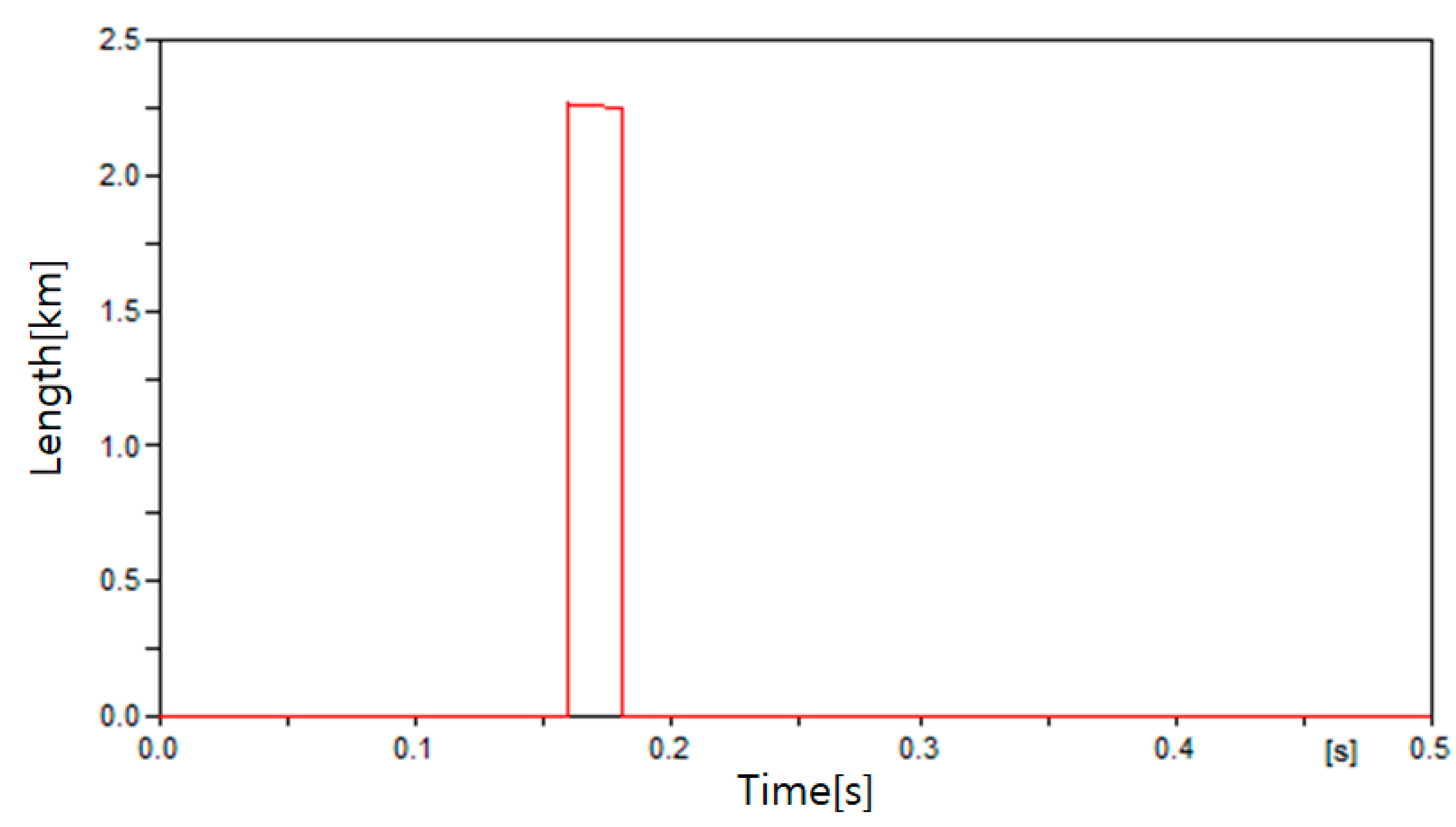


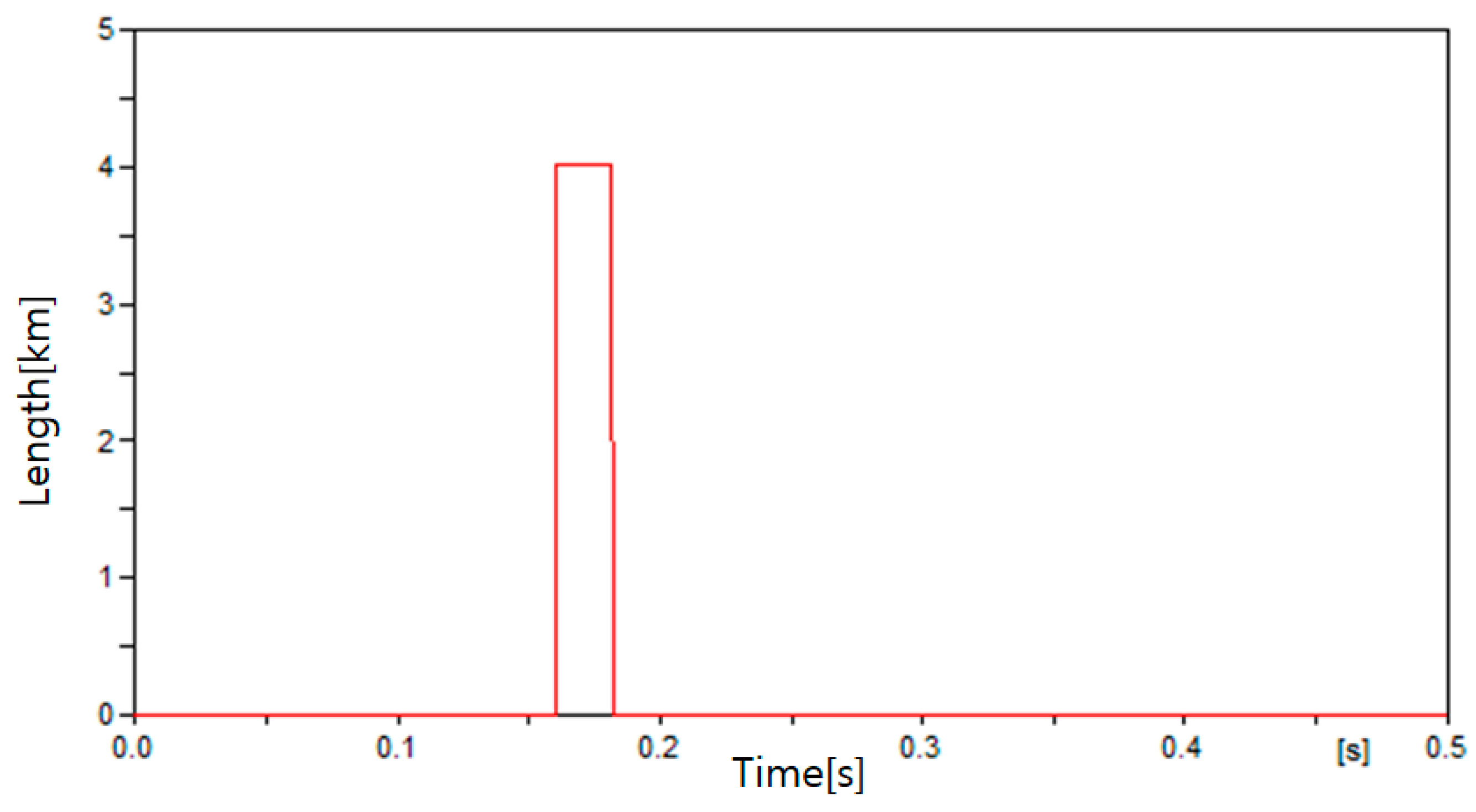
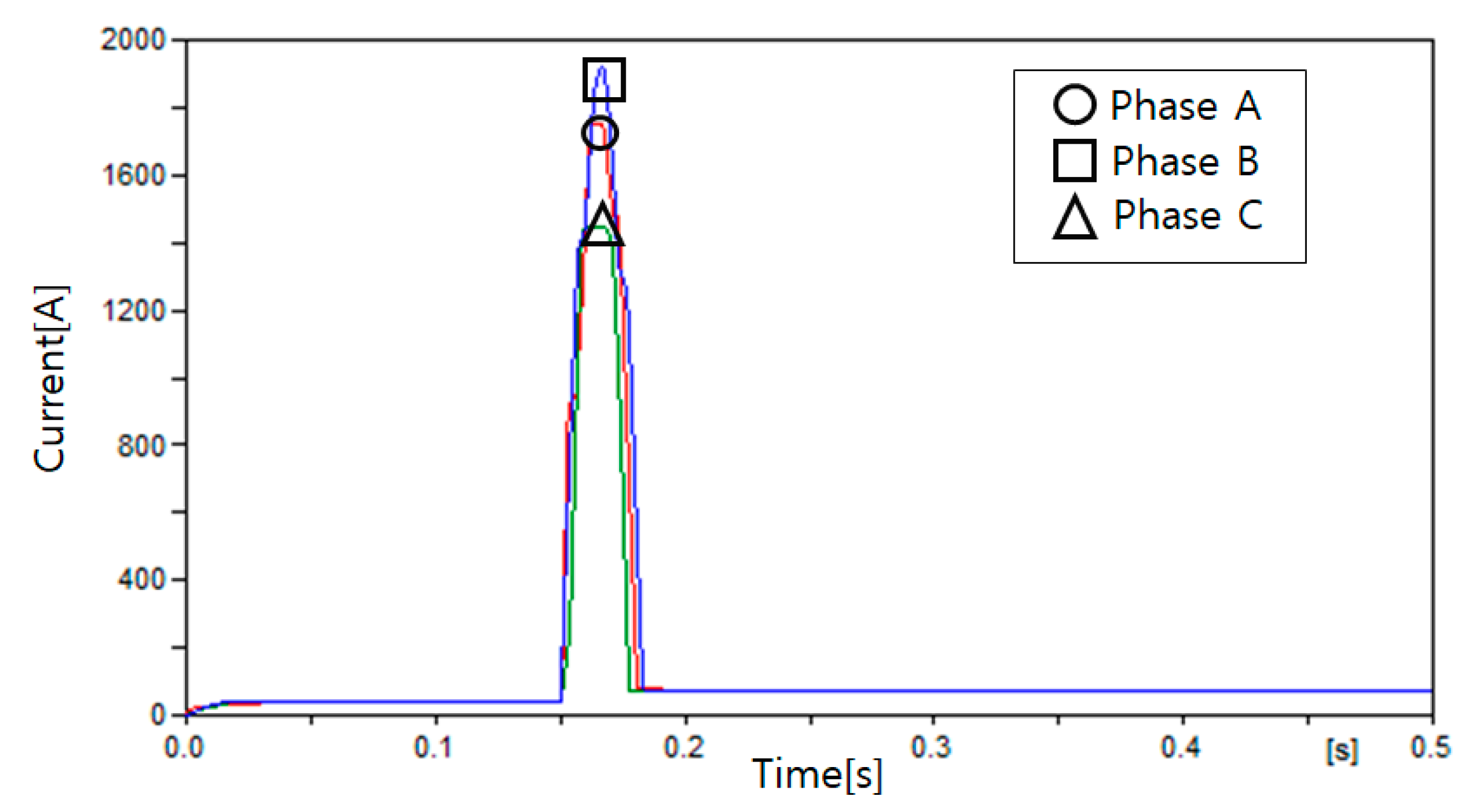
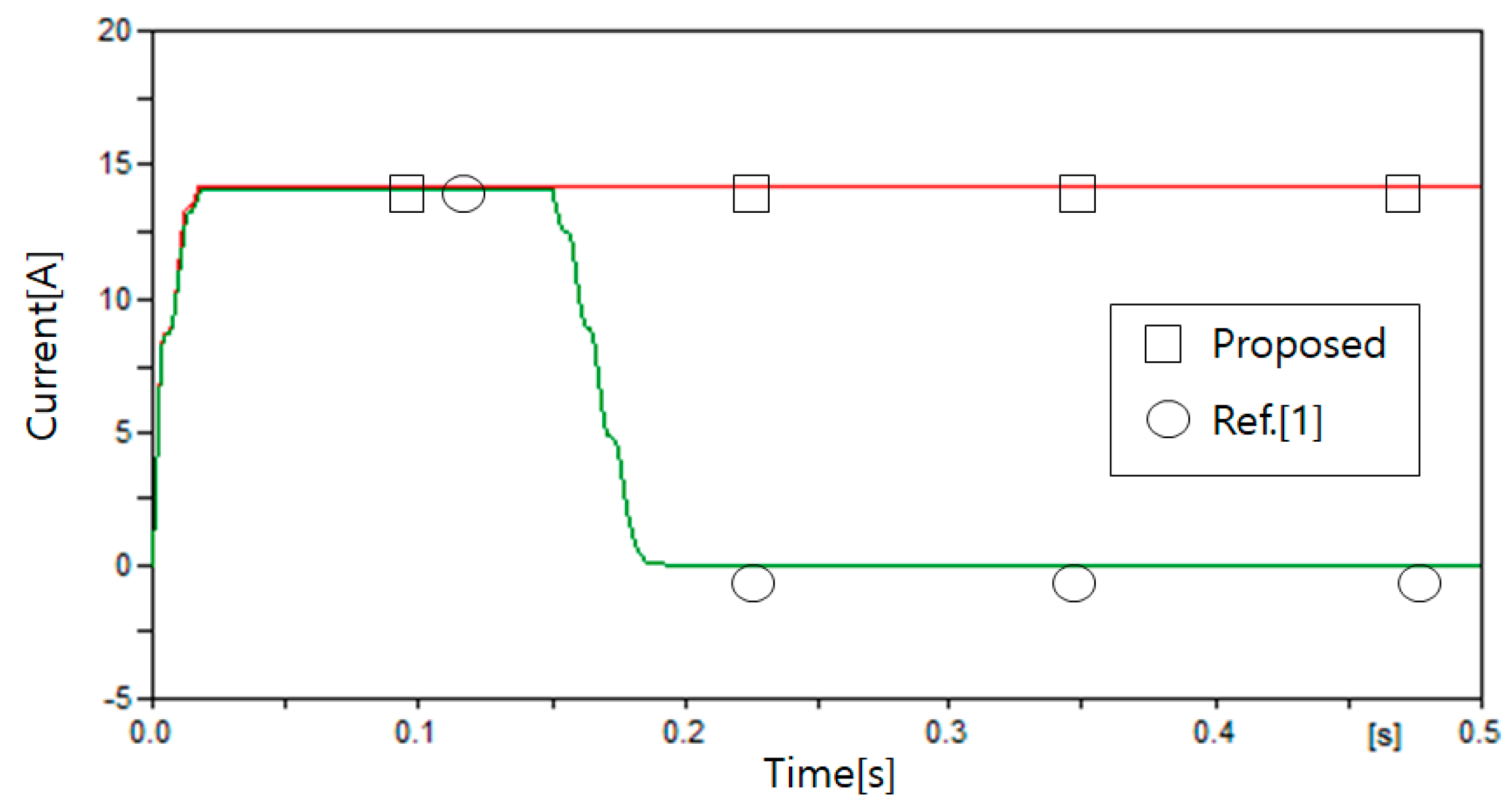
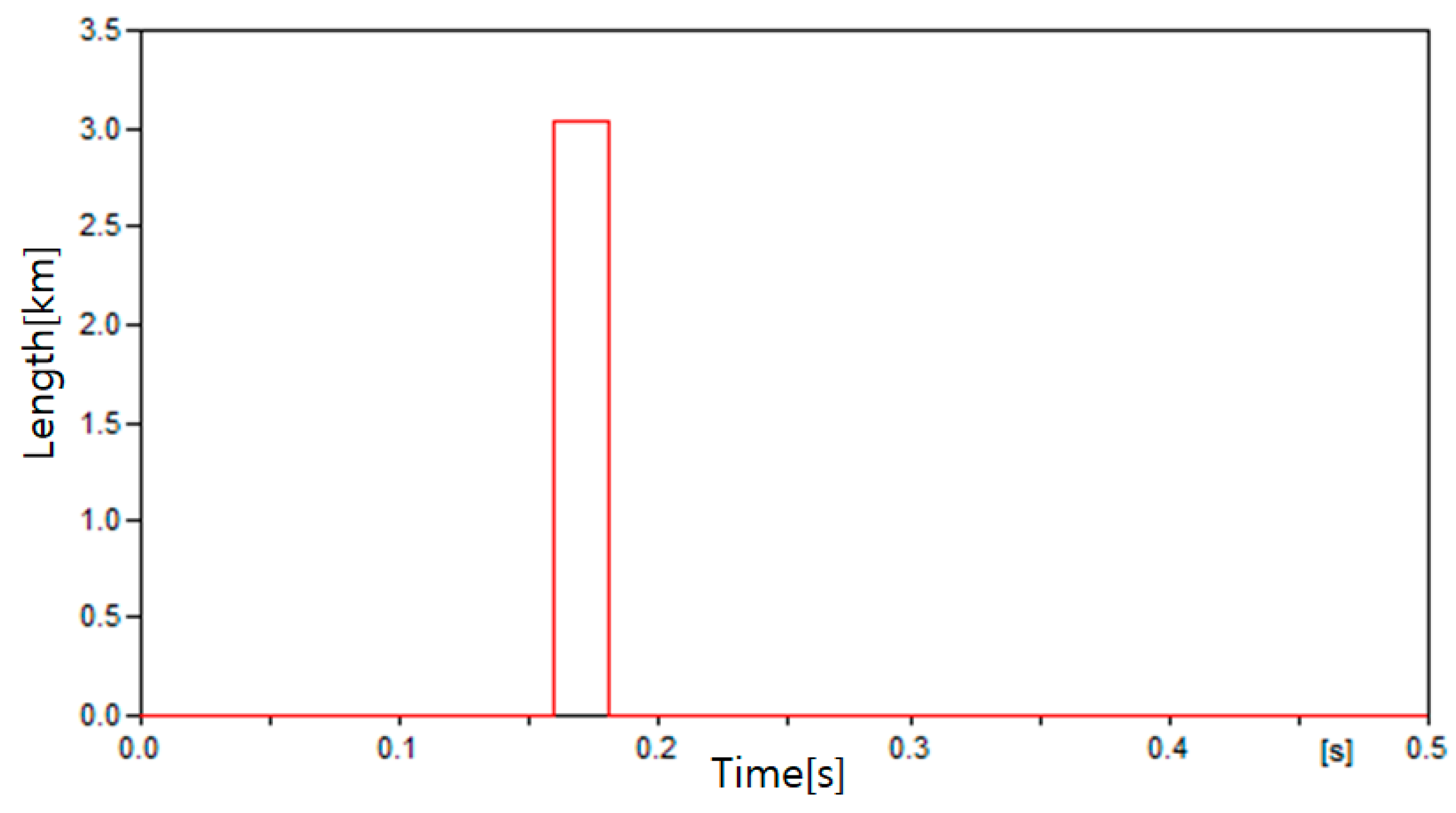


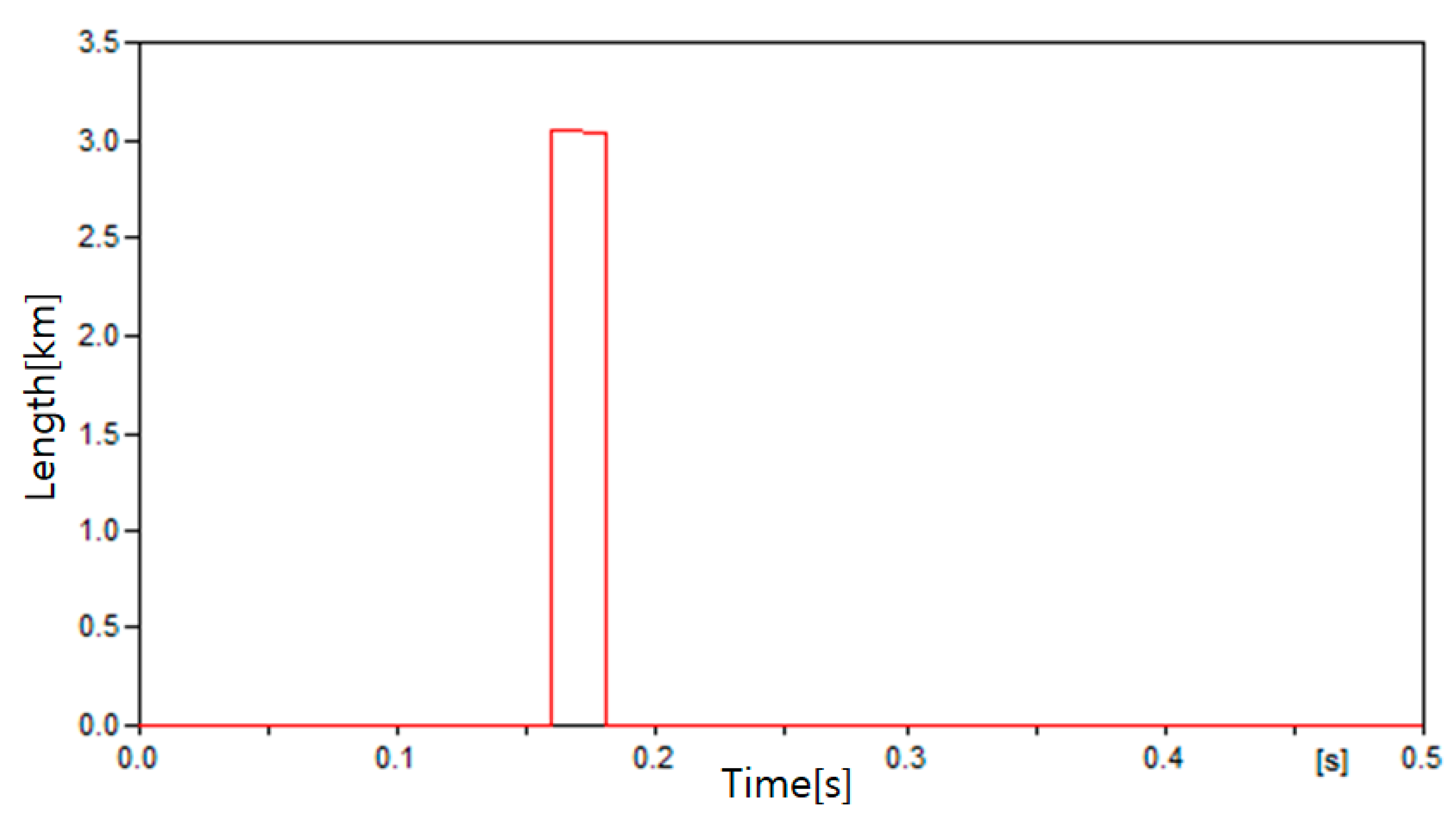

| Case | Fault Location |
|---|---|
| Case 1 | 1 km point in Line 1 (1 km from Source 1) |
| Case 2 | 0.8 km in Line 2 (2.8 km from Source 1) |
| Case 3 | 1 km point in Line 3 (4 km from Source 1) |
| Case 4 | 1 km point in Line 4 (1 km from Source 2) |
| Case 5 | 0.2 km in Line 5 (2.2 km from Source 2) |
| Case 6 | 1 km point in Line 6 (4 km from Source 2) |
| Case 7 | Bus 2 (3 km from Source 1) |
| Case 8 | Bus 5 (3 km from Source 1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, H.-C. New Protection Scheme in Loop Distribution System with Distributed Generation. Energies 2020, 13, 5897. https://doi.org/10.3390/en13225897
Seo H-C. New Protection Scheme in Loop Distribution System with Distributed Generation. Energies. 2020; 13(22):5897. https://doi.org/10.3390/en13225897
Chicago/Turabian StyleSeo, Hun-Chul. 2020. "New Protection Scheme in Loop Distribution System with Distributed Generation" Energies 13, no. 22: 5897. https://doi.org/10.3390/en13225897





