Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty †
Abstract
:1. Introduction
- Development and application of a novel robust MPC Method based on zonotopes extending classical tube-based approaches for tackling an uncertain energy dispatch problem in smart micro-grids including several heterogeneous generators and storage elements.
- Assessing the suitability and reliability of Economic MPC paradigm to incorporate the developed robust MPC method.
- The proposed method tackles the effect of demand uncertainty by tightening the system constraints in real-time as the uncertainty propagates throughout the prediction horizon.
2. Problem Statement
2.1. Control-Oriented Modelling
2.2. Control Objectives
2.2.1. Economic Cost
2.2.2. Safety Storage Levels
- -
- Upper safety level:
- -
- Lower safety level:where and are the lower and upper safety limit violations that are included as the following soft constraint
2.2.3. Smoothness of the Control Actions
2.3. Formulation of the Nominal Economic MPC Controller
3. Robustyfing the MPC Controller
3.1. Decomposition of the Control Variables
3.2. Decomposition of the State Variables
4. Formulation of the Robust MPC
4.1. Open-Loop Approach
4.2. Closed-Loop Approach
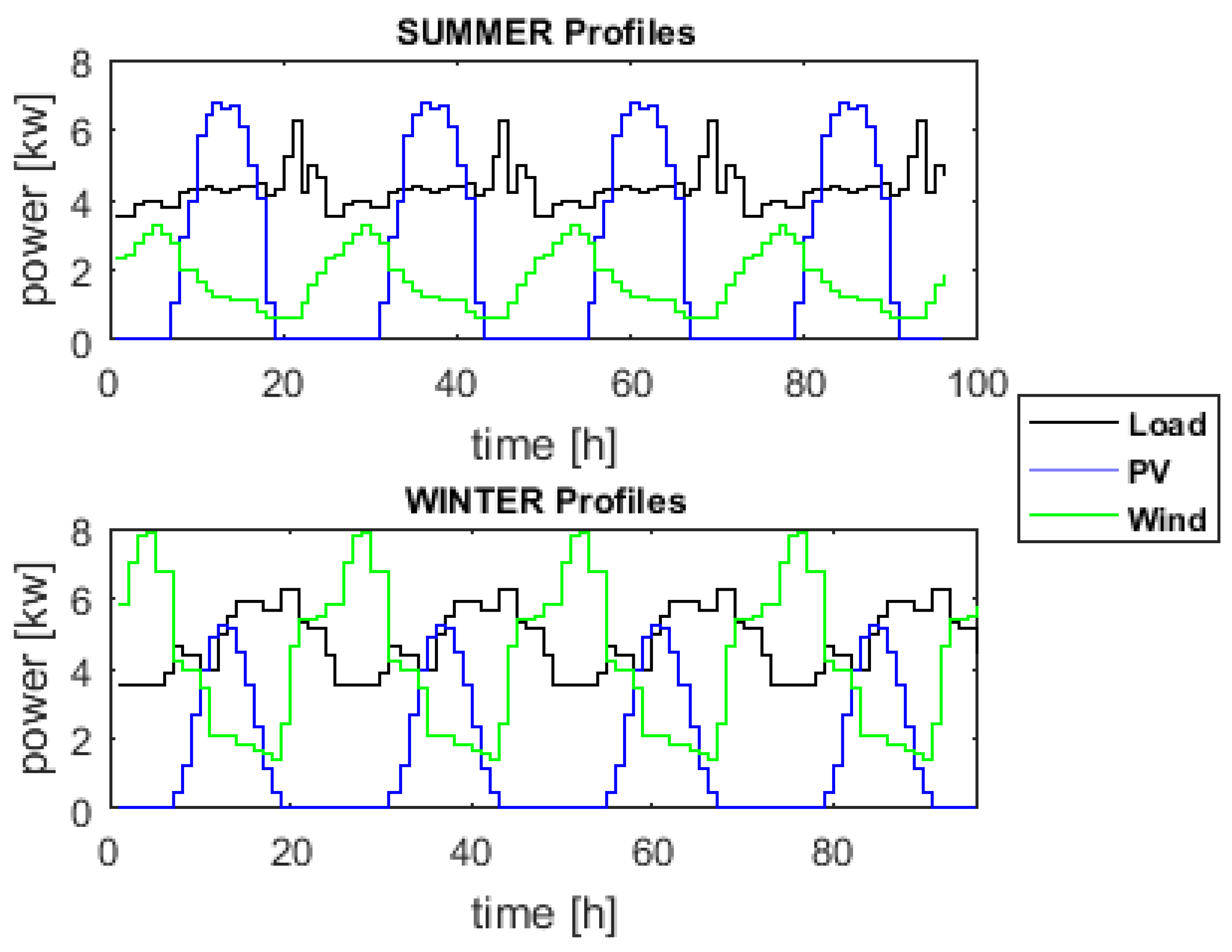
5. Application
5.1. Description
5.2. Control-Oriented Model
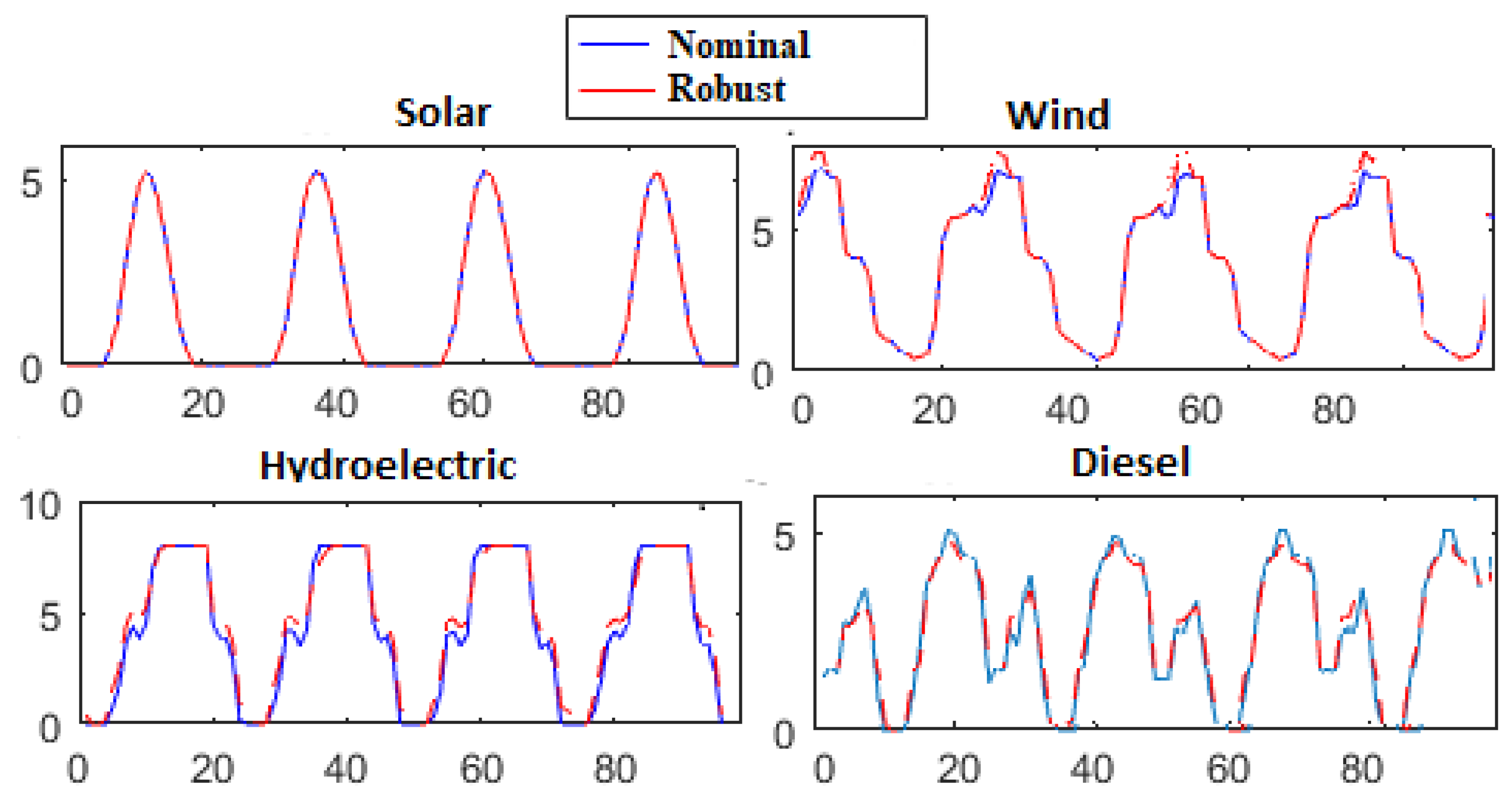
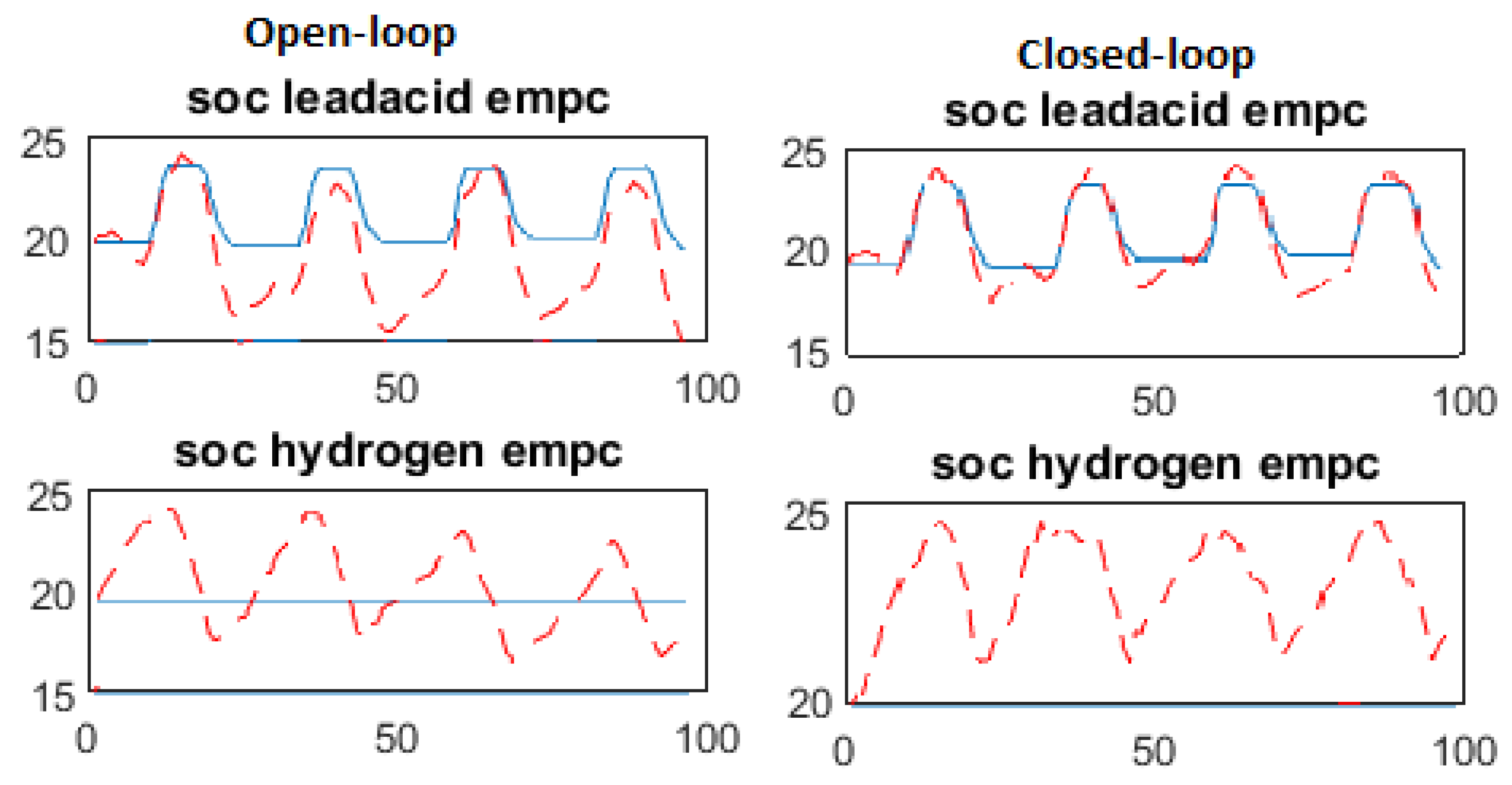
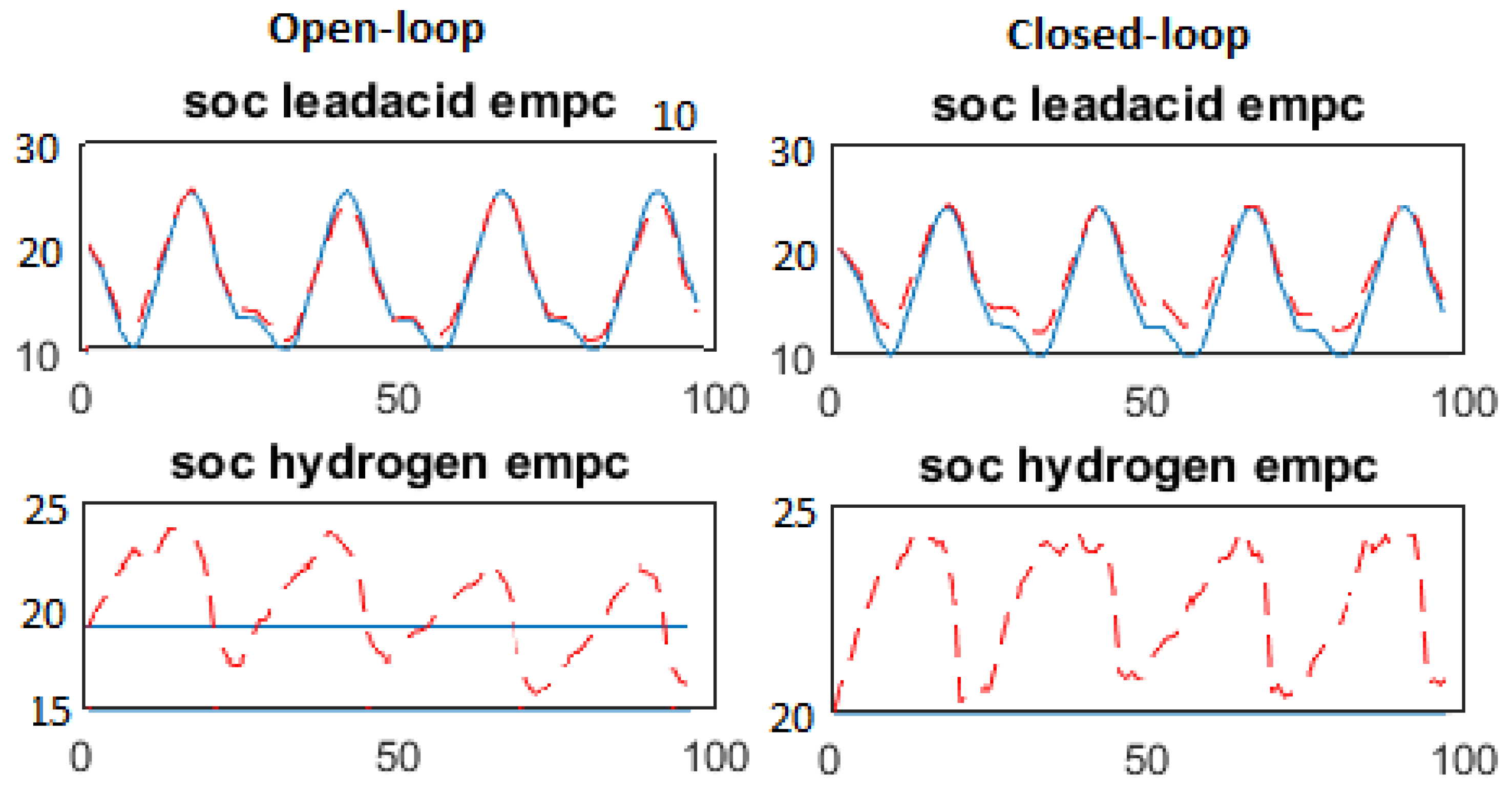
5.3. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grosso, J.M.; Ocampo-Martínez, C.; Puig, V.; Joseph, B. Chance-constrained model predictive control for large-scale Networks. J. Process Control 2014, 24, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Ocampo-Martínez, C.; Puig, V.; Cembrano, G.; Creus, R.; Minoves, M. Improving water management efficiency by using optimization-based control strategies: The Barcelona case study. Water Sci. Technol. Water Supply 2009, 9, 565–575. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Moura, S.; Yin, X.; Pickert, V. Stochastic control of smart home energy management with plug-in electric vehicle battery energy storage and photovoltaic array. J. Power Sources 2016, 333, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Maciejowski, M.J. Predictive Control with Constraints; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Åström, K.J. Control System Design; University of California Santa Barbara: Santa Barbara, CA, USA, 2002. [Google Scholar]
- Qi, W.; Liu, J.; Christofides, P. Supervisory Predictive Control of an Integrated Wind/Solar Energy Generation and Water Desalination System. In Proceedings of the 9th International Symposium on Dynamics and Control of Process Systems, Leuven, Belgium, 5–7 July 2010. [Google Scholar]
- Halvgaard, R. Model Predictive Control for Smart Energy Systems. Ph.D. Thesis, DTU Denmark, Lyngby, Denmark, 2014. [Google Scholar]
- Prodan, I.; Zio, E. A model predictive control framework for reliable microgrid energy management. Electr. Power Energy Syst. 2014, 61, 399–409. [Google Scholar] [CrossRef]
- Abate, A.; El Ghaoui, L. Robust model predictive control through adjustable variables: An application to path planning. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No. 04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 3, pp. 2485–2490. [Google Scholar]
- Bemporad, A.; Morari, M. Robust model predictive control: A survey. In Robustness in Identification and Control; Springer: Berlin/Heidelberg, Germany, 1999; pp. 207–226. [Google Scholar]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99, 351–376. [Google Scholar] [CrossRef]
- Löfberg, J. Automatic robust convex programming. Optim. Methods Softw. 2012, 27, 115–129. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Tazvinga, H.; Xia, X. Switched Model Predictive Control for Energy Dispatching of a Photovoltaic-DieselBattery Hybrid Power System. IEEE Trans. Control Syst. Technol. 2015, 23, 1229–1236. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.; Limon, D.; Alamo, T.; Valverde, L. Application of Periodic Economic MPC to a Grid-Connected Micro-grid. IFAC-PapersOnLine 2015, 48, 513–518. [Google Scholar] [CrossRef]
- Puig, V.; Costa, R.; Sampietro, L. Economic MPC for the Energy Management of Hybrid Vehicles including Fuel Cells and Supercapacitors. In Proceedings of the 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016. [Google Scholar]
- Nassourou, M.; Puig, V.; Blesa, J. Robust optimization based energy dispatch in smart grids considering demand uncertainty. J. Phys. Conf. Ser. 2017, 783, 012033. [Google Scholar] [CrossRef]
- Nassourou, M.; Puig, V.; Blesa, J. Robust optimization based energy dispatch in smart grids considering simultaneously multiple uncertainties: Load demands and energy prices. IFAC-PapersOnLine 2017, 50, 6755–6760. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust convex optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef]
- Vandenberghe, L.; Boyd, S. Semidefinite programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef] [Green Version]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009. [Google Scholar]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2012, 24, 1156–1178. [Google Scholar] [CrossRef]
- Scokaert, P.O.M.; Mayne, D.Q. min–max Feedback Model Predictive Control for Constrained Linear Systems. IEEE Trans. Autom. Control 2012, 43, 1136–1142. [Google Scholar] [CrossRef]
- Nassourou, M.; Blesa, J.; Puig, V. Robust Economic Model Predictive Control for Energy Dispatch in Smart Micro-grids Considering Demand Uncertainty. In Proceedings of the 24th IEEE Conference on Emerging Technologies and Factory Automation, Zaragoza, Spain, 10–13 September 2019. [Google Scholar]
- Grosso, J. On model predictive control for economic and robust operation of generalised flow-based networks. Ph.D. Thesis, UPC, Barcelona, Spain, 2014. [Google Scholar]
- Blesa, J.; Puig, V.; Saludes, J. Identification for passive robust fault detection using zonotope-based set-membership approaches. Int. J. Adapt. Control Signal Process. 2011, 25, 788–812. [Google Scholar] [CrossRef]
- Blesa, J.; Puig, V.; Saludes, J. Robust identification and fault diagnosis based on uncertain multiple input–multiple output linear parameter varying parity equations and zonotopes. J. Process Control 2012, 22, 1890–1912. [Google Scholar] [CrossRef] [Green Version]
- Montes de Oca, S.; Puig, V.; Blesa, J. Robust fault detection based on adaptive threshold generation using interval LPV observers. Int. J. Adapt. Control Signal Process. 2012, 26, 258–283. [Google Scholar] [CrossRef] [Green Version]
- Blesa, J.; Puig, V.; Saludes, J.; Fernández-Cantí, R.M. Set-membership parity space approach for fault detection in linear uncertain dynamic systems. Int. J. Adapt. Control Signal Process. 2016, 30, 186–205. [Google Scholar] [CrossRef] [Green Version]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Interval analysis. In Applied Interval Analysis; Springer: Berlin/Heidelberg, Germany, 2001; pp. 11–43. [Google Scholar]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004. [Google Scholar]
- Wang, Y.; Muñoz de la Peña, D.; Puig, V.; Cembrano, G. Robust economic model predictive control based on a periodicity constraint. Int. J. Robust Nonlinear Control 2019, 29, 3296–3310. [Google Scholar] [CrossRef] [Green Version]





| Model Parameters | Energy Prices (e.u) | ||
|---|---|---|---|
| 0.90 | Lead-acid battery charging: | 0.34 | |
| 1 | Lead-acid battery discharging: | 0.34 | |
| 0.90 | Hydrogen battery charging: | 0.34 | |
| 1.0 | Hydrogen battery discharging: | 0.34 | |
| Power flow between node: | 0.34 | ||
| External grid selling: | 4.3 | ||
| 24 | External grid buying: | 4.3 | |
| 2500 | Diesel: | 8.9 | |
| 12 | Hydroelectric: | 1.95 | |
| 0.1 | Wind: | 3.7 | |
| Solar: | 3.1 | ||
| Nominal EMPC (Zero Uncertainty) | Robust Closed-Loop EMPC | Robust Open-Loop EMPC | |
|---|---|---|---|
| Summer | 1125.2 | 1154.4 | 1143.6 |
| Winter | 1428.7 | 1448.4 | 1437.1 |
| Nominal EMPC (Zero Uncertainty) | Robust Closed-Loop EMPC | Robust Open-Loop EMPC | |
|---|---|---|---|
| Summer | 1131.7 | 1184.0 | unfeasible |
| Winter | 1433.6 | 1466.2 | unfeasible |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nassourou, M.; Blesa, J.; Puig, V. Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty. Energies 2020, 13, 696. https://doi.org/10.3390/en13030696
Nassourou M, Blesa J, Puig V. Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty. Energies. 2020; 13(3):696. https://doi.org/10.3390/en13030696
Chicago/Turabian StyleNassourou, Mohamadou, Joaquim Blesa, and Vicenç Puig. 2020. "Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty" Energies 13, no. 3: 696. https://doi.org/10.3390/en13030696





