Distribution Power Loss Reduction of Standalone DC Microgrids Using Adaptive Differential Evolution-Based Control for Distributed Battery Systems

Abstract

With high penetrations of renewable energy sources (RES), distributed battery systems (DBS) are widely adopted in standalone DC microgrids to stabilize the bus voltages by balancing the active power. This paper presents an Adaptive Differential Evolution (ADE)-based hierarchical control for DBS to achieve online distribution power loss mitigation as well as bus voltage regulations in standalone DC microgrids. The hierarchical control comprises two layers, i.e., ADE for the secondary layer and local proportional-integral (PI) control for the primary layer. The secondary layer control provides the bus voltage references for the primary control by optimizing the fitness function, which contains the parameters of the bus voltage deviations and the power loss on the distribution lines. Simultaneously, the state-of-charge (SoC) of the battery packs are controlled by local controllers to prevent over-charge and deep-discharge. Case studies using a Real-Time Digital Simulator (RTDS) validate that the proposed ADE-based hierarchical control can effectively reduce the distribution power loss and regulate the bus voltages within the tolerances in DC microgrids.

1. Introduction

Due to higher efficiency and easier interconnections for renewable energy sources (RES), DC microgrids have been gaining more attention than their AC counterparts in recent years [1,2,3]. DC microgrids can be either grid-connected or standalone [4]. For the emerging applications of DC microgrids in data centers, electric ships and smart buildings, etc., standalone DC microgrids seem to be more popular and encourage intensified research activities [5,6,7]. Typical standalone DC microgrids comprise distributed RES, energy storage systems (ESS), and various types of loads and power electronics interfaces [1,2,3,4,5,6,7,8,9]. Distributed RES, such as wind energy conversion systems (WECS) and photovoltaic (PV) systems, are the major power supplies of standalone DC microgrids. Various types of loads, such as constant impedance loads, constant power loads and constant current loads, are the main power consumptions of standalone DC microgrids. Due to the intermittent nature of RES, power imbalance between the power supplies and consumption may frequently occur in standalone DC microgrids, which result in undesirable bus voltage fluctuations. To tame the fluctuations, ESS, such as batteries, supercapacitors and flywheels, etc., must be introduced to compensate for the power gap. Generally, power electronics interfaces are required for most RES, ESS, and some types of loads to meet the rated bus voltages.

Owing to the high-power density and relatively mature technique, batteries are the most widely used ESS in standalone DC microgrids nowadays [10]. As the batteries are usually installed in a distributed manner over the standalone DC microgrids, they are also known as distributed battery systems (DBS). So far, various control strategies have been investigated to control DBS in standalone DC microgrids. Most of these control strategies are droop control and its variants to achieve accurate power/current sharing, state-of-charge (SoC) balance, efficiency optimization of power conversions and economic dispatch etc., [11,12,13,14,15,16,17,18,19]. In [11], a conventional droop control is adopted to generate output voltage references for local controllers to restore the DC bus voltages based on the output voltages and currents of DBS. However, the conventional droop control may lead to current sharing imbalance when the parameter deviates. Therefore, several adaptive droop control schemes are proposed to eliminate the inequal current sharing of DBS in [12,13,14,15]. Besides, the SoC of DBS is balanced by a double-quadrant droop control in order to prolong the lifetime and avoid overuse of batteries in [16]. A multiagent supervisory control is designed to precisely manage the power flow of various isolated DC microgrids in [17]. A multi-objective algorithm is proposed to minimize the cost and lifecycle emissions of standalone PV–wind–diesel systems with battery storage systems in [18]. Economic dispatch of the components in DC microgrids are achieved by minimizing the total operating cost of DBS in [19]. However, mitigating power loss on the distribution lines of standalone DC microgrids have not yet been fully investigated. Similar investigations on DC electric springs in DC microgrids, AC electric springs and DBS in AC microgrids are conducted in [20,21,22]. However, control of DBS to reduce the distribution power loss reduction of standalone DC microgrids have not been studied.

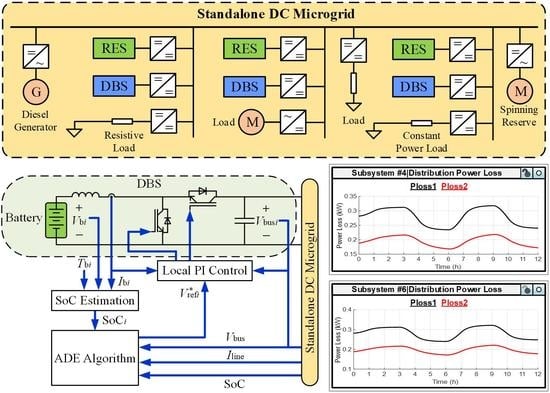
To bridge the research gap, an adaptive different evolution (ADE)-based centralized control is proposed in this paper to reduce the power loss on distribution lines of standalone DC microgrids online. ADE is a stochastic direct search and global optimization algorithm developed by Storn and Price for continuous space optimization, which overcomes the drawbacks of conventional heuristic algorithms, i.e., Genetic Algorithm (GA) and Particle Swarm Optimization (PSO), etc. [23]. The advantages of ADE over the conventional heuristic algorithms include that (i) ADE can avoid being trapped in local optimum; (ii) ADE uses fewer tuning parameters. Only population size, maximum generation, differential weight (F) bounds and crossover rate (CR) bounds are adopted without resorting to an external probability density function; (iii) ADE exhibits better performance in exploration and exploitation by dynamically adjusting F and CR [24,25,26,27]. In this paper, the ADE is adopted to optimize the objective function, which comprise the terms of distribution power loss and bus voltage deviations. Consequently, the proposed control can concurrently (i) regulate the bus voltages within the tolerances and (ii) reduce the distribution power loss on the distribution lines. This is possible, since the bus voltages of DC microgrids are generally allowed to have a certain degree of deviation, e.g., 5%. The weighting factors of the two terms in the objective function are automatically tuned by the adaptive algorithm in [22], which further reduces the distribution power loss as compared to the weighting factors with fixed values. The proposed control consists of two layers. The secondary layer control is implemented by the ADE algorithm to provide bus voltage references for the primary layer control based on the measurements of bus voltages, line currents, and SoC of the batteries, while the primary layer control is achieved by local proportional-integral (PI) control to track the bus voltage references. SoC of the batteries are strictly controlled within the tolerances by including them in the constraints of the objective function. Verifications of the proposed control method are carried out in a 5-bus 48 V DC microgrid using a Real-Time Digital Simulator (RTDS). The proposed control method can also be used for larger-scale higher-voltage level DC microgrids. Compared to the conventional droop-based local control schemes, the cost saving from the distribution power loss mitigation by the proposed control scheme is more prominent than the additional installation and maintenance costs of the communication devices.

The major contribution of this paper is to mitigate the distribution power loss of DC microgrids by controlling the DBS, which has never been reported before. The novelty of the paper also includes the ADE-based control strategy with adaptive weighting factors, which is different from the traditional algorithms being exhibited in [20,21,22].

2. Overview of the Investigated System and Control

2.1. Overview of a Standalone-DC Microgrid

Figure 1 shows a typical architecture of a standalone DC microgrid, which comprises RES, DBS, and grid-connected converters, etc. The DBS are adopted to compensate the active power flow. When the supplied power by the RES is higher than the power demand by the loads, the DBS absorb the excessive power in the charging mode. Conversely, the DBS provide the deficient power in the discharging mode. However, the SoC of the battery packs in DBS are required to be controlled within the tolerances to prevent over-charge and deep-discharge. Thus, the spinning reserve activates when any one of the SoCs of the battery packs in DBS are higher than the upper limit. Conversely, the diesel generator activates when any one of the SoCs of the battery packs in DBS are lower than the lower limit.

2.2. Overview of a DBS with the Proposed Control Scheme in a Standalone-DC Microgrid

The circuitry of a typical DBS in a standalone DC microgrid is depicted in Figure 2. A non-isolated boost converter is adopted as the grid-connected converter for the DBS. The proposed control scheme comprises two layers. The secondary layer is based on the measurements of all the bus voltages (i.e., V_bus), line currents (i.e., I_line) and SoC of the battery packs (i.e., SoC) to provide bus voltage reference (i.e., V*_refi) for the i-th DBS. The primary layer is based on the local measurements of the inductor current (i.e., I_bi) and bus voltage (i.e., V_busi) of the i-th DBS.

The flowchart of the proposed control scheme is shown in Figure 3. Initially, V_bus, I_line and output voltage, current and temperature of the i-th battery pack (i.e., V_bi, I_bi and T_bi) are measured. The measured V_bi, I_bi and T_bi are used to estimate the initial SoC of the battery pack (i.e., SoC_i(0)) using a look-up table [28]. Then, the real-time SoC of the battery pack can be calculated by the Coulomb-counting method,

$${\mathrm{SoC}}_i={\mathrm{SoC}}_i\left(0\right)-\frac{1}{C_{\mathrm{e}i}}\int I_{\mathrm{b}i}dt$$

(1)

where C_ei is the capacity of the battery unit i. In practice, such a method of using both the look-up table and the Coulomb-counting method is widely adopted for industrial applications of batteries.

Once the SoC of the DBS are monitored, they can be used to be compared with upper and lower limits, i.e., SoC_max and SoC_min, respectively. If any one of the monitored SoCs of the DBS is greater than the upper limit (i.e., SoC_max), the spinning reserves will operate to absorb redundant energy until all the SoCs of the DBS are within the tolerances. On the contrary, if any one of the monitored SoCs of the DBS is less than the lower limit (i.e., SoC_min), then the diesel generators will operate to provide sufficient energy until all the SoCs of the DBS are within the tolerances. The monitored SoC of the batteries in DBS and the measured V_bus and I_line are fed back to ADE algorithm, which generates V*_refi for the local PI controllers. Since the grid-connected converter are boost converters, the classic cascaded current and voltage control strategy can be used based on V*_refi and the feedback signals of I_bi and V_busi, as shown in Figure 4. Here, K_p1i and K_s1i are the tuning coefficients of the bus voltage PI controller. I_brefi is the inductor current reference of the i-th DBS. K_p2i and K_s2i are the tuning coefficients of the inductor current PI controller. d_i is the duty ratio of the boost converter of the i-th DBS. The time sequence of the proposed control scheme is plotted in Figure 5. Note that, the ADE optimization is conducted online. No additional offline training is required.

3. Proposed ADE Algorithm

Heuristic algorithms are widely adopted to solve the optimization problems with multiple objective constraints. However, the conventional heuristic algorithms, e.g., GA, run the risk of being trapped in local optimums. The unstable performances of the conventional heuristic algorithms are frequently observed with strong randomness. Beyond that, it is hard to choose parameters such as the number of population size, generations, crossover rate, and mutation rate to guarantee the path to be optimal. Instead, ADE can overcome these drawbacks of the conventional heuristic algorithms [24,25,26,27]. The proposed ADE algorithm consists of three stages: (i) initialization stage; (ii) iteration stage; (iii) final stage.

[Initialization Stage]

During this stage, the values of population size (i.e., P_size), generation maximum (max_gen) and stopping criteria in iterations are initialized. A random population of P_size individuals (i.e., V_bus) is formed within the search-space bounds (i.e., [V_busmin, V_busmax]). Here, V_busmin and V_busmax are the lower bound and upper bound of bus voltage (Generally, V_busmin = 0.95 V_bus and V_busmax = 1.05 V_bus).

[Iteration Stage]

For the conventional evolutionary algorithm (i.e., DE), the mutual operation performs at a low predefined probability (i.e., at 0.2) while the crossover operation is applied using a high value (i.e., 0.8). It is better to start with a high probability of mutation in the early generations and decrease it gradually. To achieve this, ADE adopts the adaptive mutual rate (i.e., p_m) and adaptive crossover rate (i.e., p_c), such that the algorithm is apt to more explorations of individual diversity in the early stage and is inclined to the exploitation afterwards.

The iteration stage of ADE comprises adaptive mutation, adaptive crossover, and selection operations. The main objective of mutation operation is to add some diversity by introducing more genetic materials into the population, to avoid the local optimum trap. For each individual V_busi, the mutation operation modifies V_busi by a small differential variation to create a mutant V_busmi. As a result, the perturbation defines the direction and length of the search space. Specifically, three distinct individuals V_busp1, V_busp2, V_busp3 are randomly selected with p1 ≠ p2 ≠ p3, and the difference vector, V_busp2 − V_busp3, is calculated, and the mutant individual V_busmi is then calculated as

$$V_{\mathrm{busm}i}=V_{\mathrm{busp}1}+p_{\mathrm{m}i}\left(V_{\mathrm{busp}2}-V_{\mathrm{busp}3}\right)$$

(2)

where p_mi(V_busp2 − V_busp3) represents the mutation step size. All the mutants V_busmi are recorded in a mutant vector V_busm. p_mi is the mutation rate used to control the amplification of the differential variation. Compared to the conventional Differential Evolution (DE) of using a fixed value of p_m, the mutation rate of the ADE is adaptively generated for each individual as

$$p_{\mathrm{m}i}=F_{\min }+\left(F_{\max }-F_{\min }\right)\frac{f_2-f_1}{f_3-f_1}$$

(3)

where F_min and F_max are the minimum and maximum mutation rate. f₁, f₂ and f₃ (f₁ < f₂ < f₃) are the fitness values of V_busp1(g), V_busp2(g), V_busp3(g) based on the objective function

$$\begin{gathered} \min J=\alpha {\displaystyle \sum }_{r=1}^m\left|V_{\mathrm{rate}}-V_{\mathrm{bus}i}\right|+\left(1-\alpha \right){\displaystyle \sum }_{i,j=1}^m{I}_{\mathrm{line}ij}\left|V_{\mathrm{bus}i}-V_{\mathrm{bus}j}\right| \\ s.t.0\le \alpha \le 1 \\ {V}_{\mathrm{busmin}}\le V_{\mathrm{bus}i}\le V_{\mathrm{busmax}} \\ {\mathrm{SoC}}_{\min }\le {\mathrm{SoC}}_i\le {\mathrm{SoC}}_{\max } \end{gathered}$$

(4)

where V_rate is the rated DC bus voltage. I_lineij is the line current between the bus i and the bus j. V_busi and V_busj are the DC bus voltages of the bus i and the bus j. α is the weighting factor, which is tuned by the adaptive algorithm in [22]. The flowchart of the adaptive weighting factor tuning algorithm is depicted in Figure 6. The weighting factor is initialized and adopted to the objective function first. Then, all the bus voltages are checked. If all the bus voltages are within the tolerances, the weighting factor is reduced by Δα (i.e., α(κ + 1) = α(κ) − Δα) in case of α(κ) – Δα ≥ 0 or keeps invariant (i.e., α(κ + 1) = α(κ)) in case of α(κ) – Δα < 0 at the next sampling time κ + 1. This process reiterates until one of the bus voltages is beyond the tolerances. If so, the weighting factor is increased by Δα (i.e., α(κ + 1) = α(κ) + Δα) in case of α(κ) + Δα ≤ 1 or keeps invariant (i.e., α(κ + 1) = α(κ)) in case of α(κ) – Δα > 1 at the next sampling time κ + 1. This process reiterates until all the bus voltages are within the tolerances. The adaptive weighting factor tuning algorithm guarantees that the power loss on the distribution lines can be approximately optimized at different power generation and load conditions by searching out the optimal α for the objective function.

Then, the crossover operator amalgamates the mutant vector V_busm and the parent vector V_bus to create a trial vector V_bust. Generally, the crossover operation can be implemented in either binomial or exponential. Due to that the binomial being more straightforward and more frequently used, it is adopted for the crossover operation in this paper as

$$V_{\mathrm{bust}i}=\left\{\begin{array}{c}{V}_{\mathrm{busm}i}, r<p_{ci}\\ V_{\mathrm{bus}i}, \mathrm{others}\end{array}\right.$$

(5)

where r~N(0,1) is a normal distribution. All the trial individuals V_busti are recorded in a trial vector V_bust. Each offspring is a stochastic linear combination of three randomly selected individuals when r < p_ci. Otherwise, the offspring inherits from the parent vector. Superior to the conventional DE of using a fixed value of p_c, the crossover rate of the ADE is adaptively generated for each individual as

$$p_{\mathrm{c}i}=\left\{\begin{array}{c}{p}_{\min }+\frac{\left(p_{\max }-p_{\min }\right)\left(f_i-f_{\min }\right)}{f_{\min }-f_{\min }}, f_i<f\\ p_{\min },\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_i\ge f\hfill \end{array}\right.$$

(6)

where p_min and p_max are the minimum and maximum crossover rate. f_min, f_max and f are the minimum, maximum and average objectives of V_busp1(g), V_busp2(g), V_busp3(g). f_i is the fitness values of the current individual. Since the crossover rate p_ci is adaptive, it makes better offspring that are more likely to survive until the next generation, as compared to the fixed crossover rate. The successful crossover rate of the last generation would be used to guide the generation of new offspring.

The third operation of ADE in the iteration stage is selection, which is similar to the elitism operation of the conventional heuristic algorithms. Selection operation is conducted based on one-to-one competition between the individuals in the parent vector and the trial vector at every generation. Better individuals are chosen for the next generation. Specifically, if the fitness value of the objective function based on the trial vector is less than or equal to that of the parent vector V_bus, the trial vector will survive and be used for the next generation. Otherwise, the parent vector will be adopted for the next generation.

[Final Stage]

Two terminal criteria of ADE include the maximum generation max_gen and the maximum deviation rate max_dr. In the final stage, the algorithm stops when any one of the terminal criteria is satisfied. Pseudocode of the whole ADE Algorithm (Algorithm 1) is provided as follows:

Algorithm 1: The ADE algorithm
Input: dimension dim(Vbusi), population size Psize, crossover rate bound (Pmin, Pmax), mutation rate bound (Fmin, Fmax), maximum generation maxgen, maximum deviation rate maxdr
Output: optimal solutions Vbusi, optimal fitness J
1.	Begin
2.	G←1   // g: generation number
3.	\\ Initialization
4.	Vbusi(g) = initialization ();
5.	\\ Iteration
6.	While the terminal criteria not met do
7.	J = fitness (Vbusi(g)); // J: fitness of the objective function
8.	// mutation operation Vbusmi(g) = mutation (Vbusi(g))
9.	J = fitness (Vbusmi(g))
10.	// crossover operation Vbusti(g) = crossover (Vbusi(g), Vbusmi(g))
11.	J = fitness (Vbusti(g))
12.	// selection operation Vbusi(g) = selection (Vbusi(g), Vbusti(g))
13.	End while
14.	\\ The final stage
15.	Output optimal solution Vbusi; optimal fitness J
16.	End

4. Case Studies

To verify the performance of the proposed ADE-based control strategy, A 5-bus 48 V DC microgrid is built in RSCAD and tested using the RTDS with a sampling frequency of 1 kHz. RSCAD is the proprietary simulation software package that is used to configure the simulations that are then run on parallel processing hardware in RTDS. In this paper, the measured voltages and currents in RSCAD are exported to the Matlab, in which the ADE algorithm calculates the optimal bus voltages. Then, the calculated optimal bus voltages are exported from Matlab to RSCAD for local bus voltage regulations. The topology of the 5-bus DC microgrid is shown in Figure 7. The sampling frequency and switching frequency of the grid-connected boost converter 20 kHz and 10 kHz, respectively. The communication delay of the signals from the measurements to the ADE algorithm is uniformly set to be 0.5 s. The capacity of the battery packs (i.e., C_ei) are identical for all the DBS, which is 100 Ah. SoC_min and SoC_max for all the DBS are 20% and 90%, respectively. The initial weighting factor (i.e., α(0)) is 1. The weighting factor difference (i.e., Δα) for the adaptive weighting factor algorithm is 0.1, which can guarantee both significant power loss and fast computation speed.

In the 5-bus DC microgrid, two RES are installed at the at buses 2 and 4, respectively. The diesel generator is installed at the bus 1. Spinning reserves are installed at bus 5. All the buses are connected with loads. The specifications of the 5-bus DC microgrid and the parameters of the adopted controllers are listed in

Table 1. Specifications of the 5-bus DC microgrid.

Parameter	Value	Parameter	Value
R12	0.2 Ω	R13	0.2 Ω
R23	0.3 Ω	R24	0.45 Ω
R25	0.4 Ω	R34	0.2 Ω
R45	0.2 Ω	Load 1	5 Ω
Load 2	10 Ω	Load 3	1.5 kW
Load 4	0.5 kW	Load 5	1 kW
Vbusmin	45.6 V	Vbusmax	50.4 V

and

Table 2. Parameters of the adopted control.

Parameter	Value
Population size Psize	18
Maximum generation maxgen	400
Lower limit of the mutation rate Fmin	0.4
Upper limit of the mutation rate Fmax	0.8
Lower limit of the crossover rate Pmin	0.1
Upper limit of the crossover rate Pmax	0.6
Kp1	0.2
Ki1	0.1
Kp2	0.1
Ki2	0.1

, respectively. Here, the tuning parameters of the local PI controllers (i.e., K_p1, K_i1, K_p2 and K_i2) are identical for all the DBS.

When the power of RES at buses 2 and 4 (i.e., P_g1 and P_g2) fluctuate in 12 h, as shown in Figure 8a, the bus voltages will fluctuate if no DBS is installed. The corresponding bus voltages are shown in Figure 8b. Apparently, the bus voltages will exceed the tolerances.

However, when DBS are installed at the buses 2, 4 and 5 with the initial SoC of 50%, 40% and 60%, respectively. The DBS are only controlled by the local PI controllers to track the rated bus voltage, while the ADE algorithm is not activated. Here, the local PI controllers are designed based on the control method in Figure 4 by incorporating an SoC outer loop control. Details of the local PI controllers being adopted here can be found in [9]. Besides, the flowchart of the control algorithm also includes the check of SoC whether beyond the tolerances or not. If the SoC of the battery packs are greater than the upper limit, the spinning reserve operates. Conversely, if the SoC of the battery packs are less than the lower limit, the diesel generator activates. The waveforms of the bus voltages are shown in Figure 9. Apparently, the fluctuations of the bus voltages are mitigated by the local PI controllers.

Then, the ADE algorithm with adaptive weighting factor is executed (the initial SoC of the DBS at the buses 2, 4 and 5 are 50%, 40% and 60%, respectively). Figure 10 shows the resulting bus voltages in 12 h. Obviously, all the bus voltages are still regulated within the tolerances. The corresponding fitness value, adaptive weighting factor and SoC of the battery packs are plotted in Figure 11 and Figure 12, respectively. SoC2, SoC4 and SoC5 indicate the SoC of the battery packs at buses 2, 4 and 5. In Figure 12, all the SoC of the battery packs are controlled within the boundaries, i.e., SoC_min = 20% and SoC_max = 90%.

The comparative waveforms of the distribution power loss of the 5-bus DC microgrid between the DBS with only local PI control (i.e., Ploss1) and with the proposed control (i.e., Ploss2) are shown in Figure 13. Apparently, the distribution power loss are reduced by the proposed control. By integrating the distribution power loss over the 12-h period, the distribution energy loss can be calculated. The distribution energy loss for the DBS with only local PI control and the proposed control are 3.35 kWh and 2.35 kWh, respectively. The energy saving is about 29.85% by using the proposed control in lieu of DBS with only local PI control.

The proposed ADE algorithm is also adopted to reduce the distribution power loss of the 5-bus DC microgrid with both RES variations and load changes. The fluctuations of RES power at buses 2 and 4 are shown in Figure 8a, while load 3, load 5, and load 2 are changed from 1.5 kW to 3 kW, 1 kW to 0.5 kW, and 10 Ω to 20 Ω at the 3rd-, 6th-, and 9th-hour, respectively. The initial SoC of the DBS at buses 2, 4 and 5 are 50%, 40% and 60%, respectively. Figure 14 shows the corresponding bus voltages in 12 h. Obviously, all the bus voltages are regulated within the tolerances.

The corresponding SoC of the battery packs are shown in Figure 15. Apparently, all the SoC of the battery packs are regulated within the tolerances, i.e., SoC_min = 20% and SoC_max = 90%. The comparative waveforms of the distribution power loss between the conventional local PI control and the proposed control are depicted in Figure 16. Obviously, the distribution power loss is mitigated for the 5-bus DC microgrid with both RES and load variations. By integrating the distribution power loss over the 12-h period, the distribution energy loss for both control methods are 3.82 kWh and 2.41 kWh, respectively. The energy saving is about 36.91%.

From the case study on the 5-bus 48 V DC microgrid, the proposed ADE-based control scheme is validated, showing that it reduces the distribution power loss on the distribution lines of DC microgrids while still regulating the bus voltages within the tolerances. The SoC of the battery packs in DBS are also stringently controlled within the boundaries, such that the lifespan of the battery packs can be prolonged over long-time operations. The average time consumed by the ADE algorithm is only about 10 s. The period time consumed by the proposed control method, which includes the measurement time of voltages and currents, calculation time of SoC, computation time of the ADE algorithm, and the operating time of local PI controllers, is negligible as compared to the variation time of the renewable energy power.

5. Conclusions

Unlike the conventional droop control to only regulate the bus voltages and state-of-charge (SoC) of the battery packs in standalone DC microgrids, an Adaptive Differential Evolution (ADE)-based control scheme is proposed in this paper to further mitigate the power loss on the distribution lines online. This might be the first paper to report the mitigation of the distribution power loss as well as bus voltage regulations by controlling DBS in DC microgrid. Being different from the existing algorithms to reduce the distribution power loss in DC microgrids, the adopted control strategy uses the ADE algorithm with adaptive weighting factors, and therefore the numbers of tuning parameters are decreased. Case studies using a Real-Time Digital Simulator (RTDS) reveal that the distribution energy loss can save about 29.85% and 36.91% for 5-bus 48 V DC microgrids with only RES fluctuations and with both RES and load variations by the proposed control, as compared to the conventional local proportional-integral (PI) control, while the bus voltages and the SoC of the battery packs are still regulated within the tolerances.