Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mechanical Tests of Corrugated Cardboard
2.2. Coefficient of Determination and Estimation Error
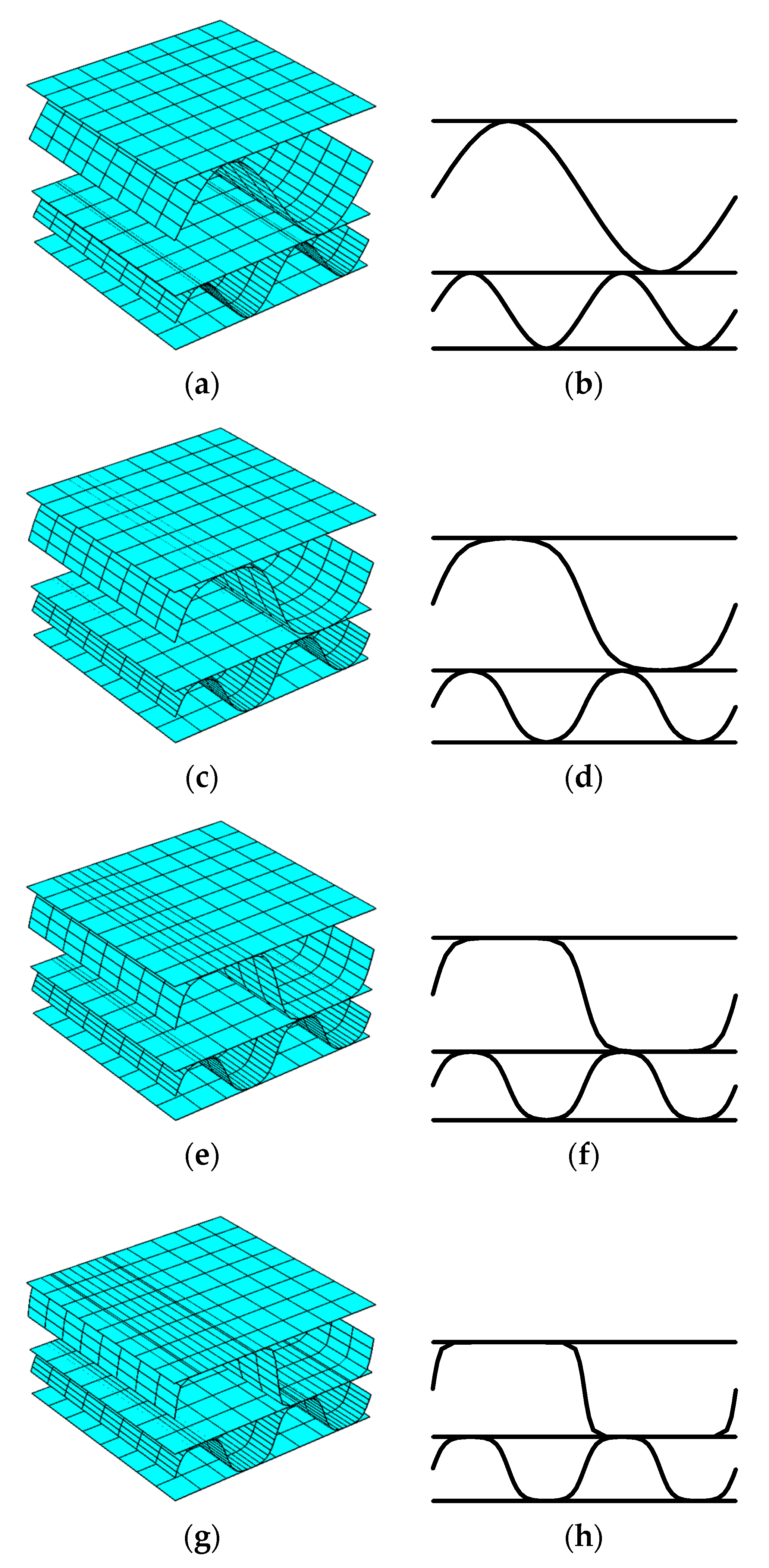
2.3. Numerical–Analytical Approach for Modeling Crushing
- Building the initial geometry of the intact corrugated cardboard (Stage a);
- Defining the shape of the crushed corrugated cardboard by a numerical–analytical approximation (Stage a–b);
- Building the material stiffness matrix using the geometry of crushed corrugated cardboard (Stage c–d);
- Homogenizing the structure to a single layered composite with effective properties according to the method presented by Garbowski and Gajewski [31] (Stage d–e);
- Computing packaging compressive strength for simple flap boxes with various dimensions via an analytical formula proposed by Garbowski et al. [23], using composite properties acquired in the previous stage (Stage f).
3. Results
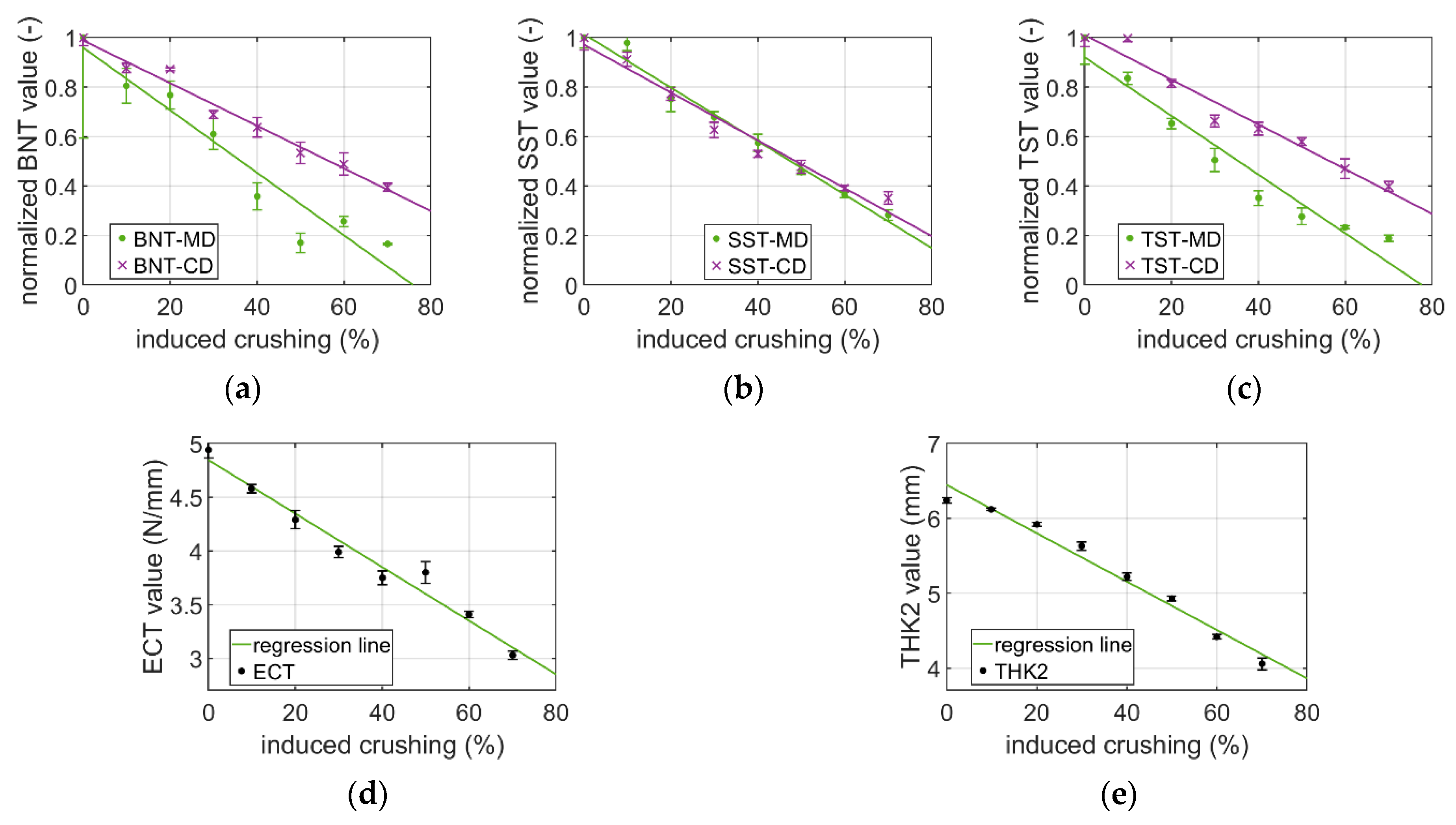
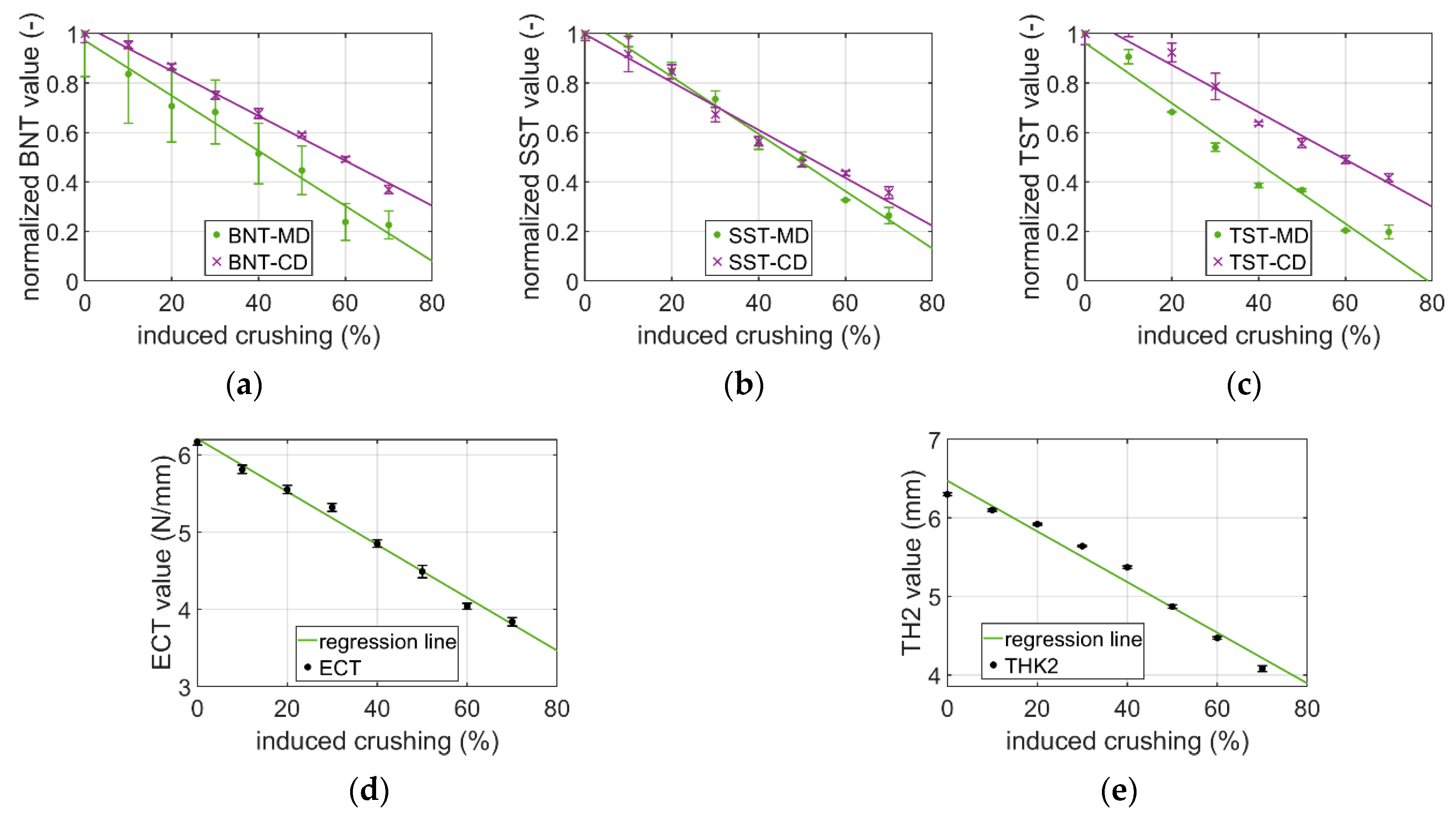
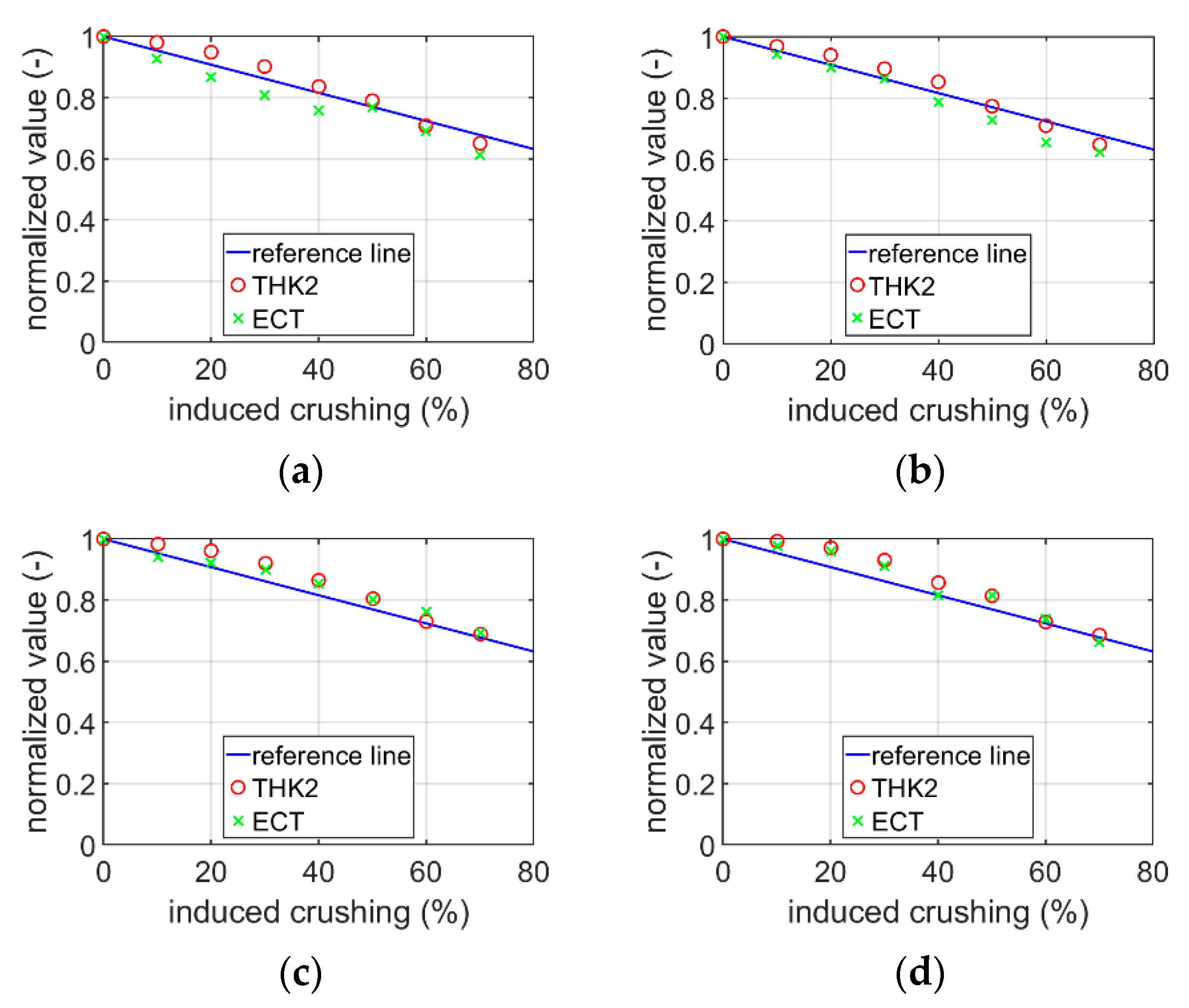
3.1. Experimental Study
3.2. Modeling Crushing in Estimating Compressive Strength of Packaging
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of the finite element analysis to predict the mechanical 490 strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Gallo, J.; Cortés, F.; Alberdi, E.; Goti, A. Mechanical Behavior Modeling of Containers and Octabins Made of Corrugated Cardboard Subjected to Vertical Stacking Loads. Materials 2021, 14, 2392. [Google Scholar] [CrossRef]
- Henry, W.; Haslach, J.R. The moisture and rate-dependent mechanical properties of paper: A review. Mech. Time Depend. Mater. 2000, 4, 169–210. [Google Scholar] [CrossRef]
- Östlund, S. Three-dimensional deformation and damage mechanisms in forming of advanced structures in paper. In Advances in Pulp and Paper Research; Batchelor, W., Söderberg, D., Eds.; FRC: Manchester, UK, 2018; pp. 489–594. [Google Scholar] [CrossRef]
- Shick, P.E.; Chari, N.C.S. Top-to-bottom compression for double wall corrugated boxes. TAPPI J. 1965, 48, 423–430. [Google Scholar]
- Chen, J.; Zhang, Y.; Sun, J. An overview of the reducing principle of design of corrugated box used in goods packaging. Procedia Environ. Sci. 2011, 10, 992–998. [Google Scholar] [CrossRef] [Green Version]
- Pathare, P.B.; Opara, U.L. Structural design of corrugated boxes for horticultural produce: A review. Biosyst. Eng. 2014, 125, 128–140. [Google Scholar] [CrossRef]
- Wolf, M. New equation helps pin down box specifications. Package Eng. 1972, 17, 66–67. [Google Scholar]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Batelka, J.J.; Smith, C.N. Package Compression Model. IPST Project 3746, Final Report; Institute of Paper Science and Technology: Atlanta, GA, USA, 1993. [Google Scholar]
- Urbanik, T.J.; Frank, B. B. Box compression analysis of world-wide data spanning 46 years. Wood Fiber. Sci. 2006, 38, 399–416. [Google Scholar]
- Ristinmaa, M.; Ottosen, N.S.; Korin, C. Analytical Prediction of Package Collapse Loads-Basic considerations. Nord. Pulp Pap. Res. J. 2012, 27, 806–813. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef] [PubMed]
- Schrampfer, K.E.; Whitsitt, W.J.; Baum, G.A. Combined Board Edge Crush (ECT) Technology; Institute of Paper Chemistry: Appleton, WI, USA, 1987. [Google Scholar]
- Nordstrand, T.; Carlssoon, L.A. Evaluation of transverse shear stiffness of structural core sandwich plates. Compos. Struct. 1997, 37, 145–153. [Google Scholar] [CrossRef]
- Nordstrand, T. Basic Testing and Strength Design of Corrugated Board and Containers. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Popil, R.E.; Coffin, D.W.; Habeger, C.C. Transverse shear measurement for corrugated board and its significance. Appita J. 2008, 61, 307–312. [Google Scholar]
- Avilés, F.; Couoh-Solís, F.; Carlsson, L.A.; Hernández-Pérez, A. Experimental determination of torsion and shear properties of sandwich panels and laminated composites by the plate twist test. Compos. Struct. 2011, 93, 1923–1928. [Google Scholar] [CrossRef]
- Avilés, F.; Carlsson, L.A.; May-Pat, A. A shear-corrected formulation for the sandwich twist specimen. Exp. Mech. 2012, 52, 17–23. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and Transversal Stiffness of Orthotropic Sandwich Panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Role of transverse shear modulus in the performance of corrugated materials. Materials 2020, 13, 3791. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Mrówczyński, D.; Jędrzejczak, R. Crushing of Single-Walled Corrugated Board during Converting: Experimental and Numerical Study. Energies 2021, 14, 3203. [Google Scholar] [CrossRef]
- Jamsari, M.A.; Kueh, C.; Gray-Stuart, E.M.; Dahm, K.; Bronlund, J.E. Modelling the impact of crushing on the strength performance of corrugated fibreboard. Packag. Technol. Sci. 2020, 33, 159–170. [Google Scholar] [CrossRef]
- Jamsari, M.A.; Kueh, C.; Gray-Stuart, E.; Martinez-Hermosilla, G.A.; Dahm, K.; Bronlund, J.E. A technique to quantify morphological damage of the flute profile in the midplane of corrugated fibreboard. Packag. Technol. Sci. 2019, 32, 213–226. [Google Scholar] [CrossRef]
- Martinez-Hermosilla, G.A.; Kueh, C.; Dahm, K.; Bronlund, J.E. Combined modelling methodology for optimisation of box design based on hybrid genetic algorithm. Packag. Technol. Sci. 2018, 31, 709–722. [Google Scholar] [CrossRef]
- Berry, T.M.; Fadji, T.S.; Defraeyea, T.; Opara, U.L. The role of horticultural carton vent hole design on cooling efficiency and compressions trength: A multi-parameter approach. Postharvest Biol. Technol. 2017, 124, 62–67. [Google Scholar] [CrossRef]
- FEMat Systems-BSE. Available online: http://fematsystems.pl/bse-system_en/ (accessed on 15 May 2021).
- FEMat Systems-CRS. Available online: http://fematsystems.pl/crs_en/ (accessed on 15 May 2021).
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef] [PubMed]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Compos. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Torres, A.; Penta, R.; Rodriguez-Ramos, R.; Grillo, A. Effective properties of hierarchical fiber-reinforced composites via a three-scale asymptotic homogenization approach. Math. Mech. Solids 2019, 24. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Merodio, J.; Sabina, F.J.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Preziosi, L.; Grillo, A. Three scales asymptotic homogenization and its application to layered hierarchical hard tissues. Int. J. Solids Struct. 2018, 130–131, 190–198. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Di Stefano, S.; Grillo, A.; Rodríguez-Ramos, R.; Merodio, J.; Penta, R. An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non Linear Mech. 2018, 106, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Jian, Z.; Hengyang, L.; Gengdong, C.; Yuanwu, C. On predicting the effective elastic properties of polymer nanocomposites by novel numerical implementation of asymptotic homogenization method. Compos. Struct. 2016, 135, 297–305. [Google Scholar] [CrossRef]
- Yuanwu, C.; Liang, X.; Gengdong, C. Novel numerical implementation of asymptotic homogenization method for periodic plate structures. Int. J. Solids Struct. 2014, 51, 284–292. [Google Scholar] [CrossRef] [Green Version]
- Gengdong, C.; Yuanwu, C.; Liang, X. Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech. Sin. 2013, 29, 550–556. [Google Scholar]
- Marek, A.; Garbowski, T. Homogenization of sandwich panels. Comput. Assist. Methods Eng. Sci. 2015, 22, 39–50. [Google Scholar]
- Xin, L.; Khizar, R.; Peng, B.; Wenbin, Y. Two-Step Homogenization of Textile Composites Using Mechanics of Structure Genome. Compos. Struct. 2017, 171, 252–262. [Google Scholar] [CrossRef]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 2. Numerical homogenization. Pol. Pap. Rev. 2014, 70, 390–394. (In Polish) [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Numerical strength estimate of corrugated board packages. Part 1. Theoretical assumptions in numerical modeling of paperboard packages. Pol. Pap. Rev. 2014, 70, 219–222. (In Polish) [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Numerical strength estimate of corrugated board packages. Part 2. Experimental tests and numerical analysis of paperboard packages. Pol. Pap. Rev. 2014, 70, 277–281. (In Polish) [Google Scholar]
- Maier, G.; Bolzon, G.; Buljak, V.; Garbowski, T.; Miller, B. Synergic Combinations of Computational Methods and Experiments for Structural Diagnoses. In Computer Methods in Mechanics. Advanced Structured Materials; Kuczma, M., Wilmanski, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1, pp. 453–476. [Google Scholar] [CrossRef]
- Aboura, Z.; Talbi, N.; Allaoui, S.; Benzeggagh, M.L. Elastic behaviour of corrugated cardboard: Experiments and modeling. Compos. Struct. 2004, 63, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Talbi, N.; Batti, A.; Ayad, R.; Guo, Y.Q. An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 2009, 88, 280–289. [Google Scholar] [CrossRef]
- Miehe, C.; Koch, A. Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. 2002, 72, 300–317. [Google Scholar] [CrossRef]
- Lebée, A.; Sab, K. Homogenization of thick periodic plates: Application of the Bending-Gradient plate theory to a folded core sandwich panel. Int. J. Solids Struct. 2012, 49, 2778–2792. [Google Scholar] [CrossRef]
- Lebée, A.; Sab, K. Homogenization of cellular sandwich panels. Comptes Rendus Mec. 2012, 340, 320–337. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Xu, B.; Chen, M.; He, R.; Wen, W.; Cheng, T.; Fang, D. Optimization design of built-up thermal protection system based on validation of corrugated core homogenization. Appl. Therm. Eng. 2017, 3. [Google Scholar] [CrossRef] [Green Version]









| Layers | ||||||
|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (-) | (MPa) | (MPa) | (MPa) | |
| liners | 3326 | 1694 | 0.34 | 859 | 429.5 | 429.5 |
| fluting | 2614 | 1532 | 0.32 | 724 | 362 | 362 |
| Crushing Level, (%) | Parameter (-) | Parameter (-) |
|---|---|---|
| 0 | 1.11 | 0.0238 |
| 5 | 1.39 | 0.0091 |
| 10 | 1.68 | 0.0028 |
| 15 | 2.04 | 0.0006 |
| 20 | 2.49 | 0.0001 |
| 25 | 3.13 | 0 |
| 30 | 4.09 | 0 |
| 35 | 5.65 | 0 |
| 40 | 8.58 | 0 |
| 45 | 15.54 | 0 |
| 50 | 45.98 | 0 |
| Cardboard Index | THK2 * | ECT * | BNT-MD * | BNT-CD * | SST-MD * | SST-CD * | TST-MD * | TST-CD * |
|---|---|---|---|---|---|---|---|---|
| BC-480 | 0.000 | 0.302 | 0.591 | 0.956 | 0.989 | 0.993 | 0.566 | 0.954 |
| BC-580 | 0.014 | 0.304 | 0.898 | 0.917 | 0.976 | 0.998 | 0.704 | 0.877 |
| EB-560 | 0.000 | 0.000 | 0.981 | 0.727 | 0.989 | 0.965 | 0.726 | 0.888 |
| EB-670 | 0.000 | 0.000 | 0.915 | 0.770 | 0.988 | 0.957 | 0.695 | 0.931 |
| Cardboard Index | BNT * | SST * | TST * |
|---|---|---|---|
| BC-480 | 0.951 | 0.995 | 0.949 |
| BC-580 | 1.000 | 0.996 | 0.987 |
| EB-560 | 0.892 | 0.994 | 0.982 |
| EB-670 | 0.859 | 0.993 | 0.974 |
| Cardboard Index | |
|---|---|
| BC-480 | 0.977 |
| BC-580 | 0.967 |
| EB-560 | 0.941 |
| EB-670 | 0.930 |
| 0% Crushing | 10% Crushing | 20% Crushing | 30% Crushing | |
|---|---|---|---|---|
| 19,514 | 17,598 | 15,751 | 14,006 | |
| 14,326 | 12,759 | 11,273 | 9876 | |
| 3438 | 3094 | 2763 | 2453 | |
| 5629 | 5069 | 4517 | 3993 | |
| 77.3 | 52.1 | 39.5 | 30.5 | |
| 237.0 | 211.7 | 187.6 | 164.7 | |
| ECT (kN/m) | 8.0 | 7.6 | 7.2 | 6.8 |
| Box Dimensions | Box Compressive Strength Due to Crushed Cardboard | |||||
|---|---|---|---|---|---|---|
| b (mm) | c (mm) | a (mm) | 0% Crushing (N) | 10% Crushing (N) | 20% Crushing (N) | 30% Crushing (N) |
| 500 | 500 | 500 | 6001 | 5613 | 5227 | 4848 |
| 500 | 1000 | 500 | 6933 | 6490 | 6049 | 5616 |
| 300 | 900 | 500 | 5805 | 5433 | 5064 | 4701 |
| 250 | 1000 | 500 | 5894 | 5516 | 5141 | 4772 |
| 200 | 1000 | 500 | 5685 | 5320 | 4958 | 4602 |
| 600 | 900 | 500 | 7132 | 6676 | 6223 | 5777 |
| 500 | 500 | 750 | 6177 | 5773 | 5373 | 4979 |
| 500 | 1000 | 750 | 6469 | 6052 | 5638 | 5230 |
| 300 | 900 | 750 | 5378 | 5031 | 4686 | 4347 |
| 250 | 1000 | 750 | 5367 | 5021 | 4679 | 4341 |
| 200 | 1000 | 750 | 5156 | 4824 | 4494 | 4170 |
| 600 | 900 | 750 | 6686 | 6256 | 5828 | 5406 |
| 500 | 500 | 1000 | 6001 | 5613 | 5227 | 4848 |
| 500 | 1000 | 1000 | 6257 | 5854 | 5453 | 5059 |
| 300 | 900 | 1000 | 5295 | 4952 | 4611 | 4276 |
| 250 | 1000 | 1000 | 5218 | 4880 | 4545 | 4215 |
| 200 | 1000 | 1000 | 5004 | 4680 | 4358 | 4042 |
| 600 | 900 | 1000 | 6646 | 6218 | 5793 | 5373 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajewski, T.; Garbowski, T.; Staszak, N.; Kuca, M. Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes. Energies 2021, 14, 4321. https://doi.org/10.3390/en14144321
Gajewski T, Garbowski T, Staszak N, Kuca M. Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes. Energies. 2021; 14(14):4321. https://doi.org/10.3390/en14144321
Chicago/Turabian StyleGajewski, Tomasz, Tomasz Garbowski, Natalia Staszak, and Małgorzata Kuca. 2021. "Crushing of Double-Walled Corrugated Board and Its Influence on the Load Capacity of Various Boxes" Energies 14, no. 14: 4321. https://doi.org/10.3390/en14144321







