An Optimal Control Scheme for Load Bus Voltage Regulation and Reactive Power-Sharing in an Islanded Microgrid
Abstract
:1. Introduction
- This study is conducted in a radial feeder system accompanied by three load buses connected with two grid forming nodes.
- The approximated impedance information of all load-buses is estimated through local load agents, which reduces the bandwidth data requirement.
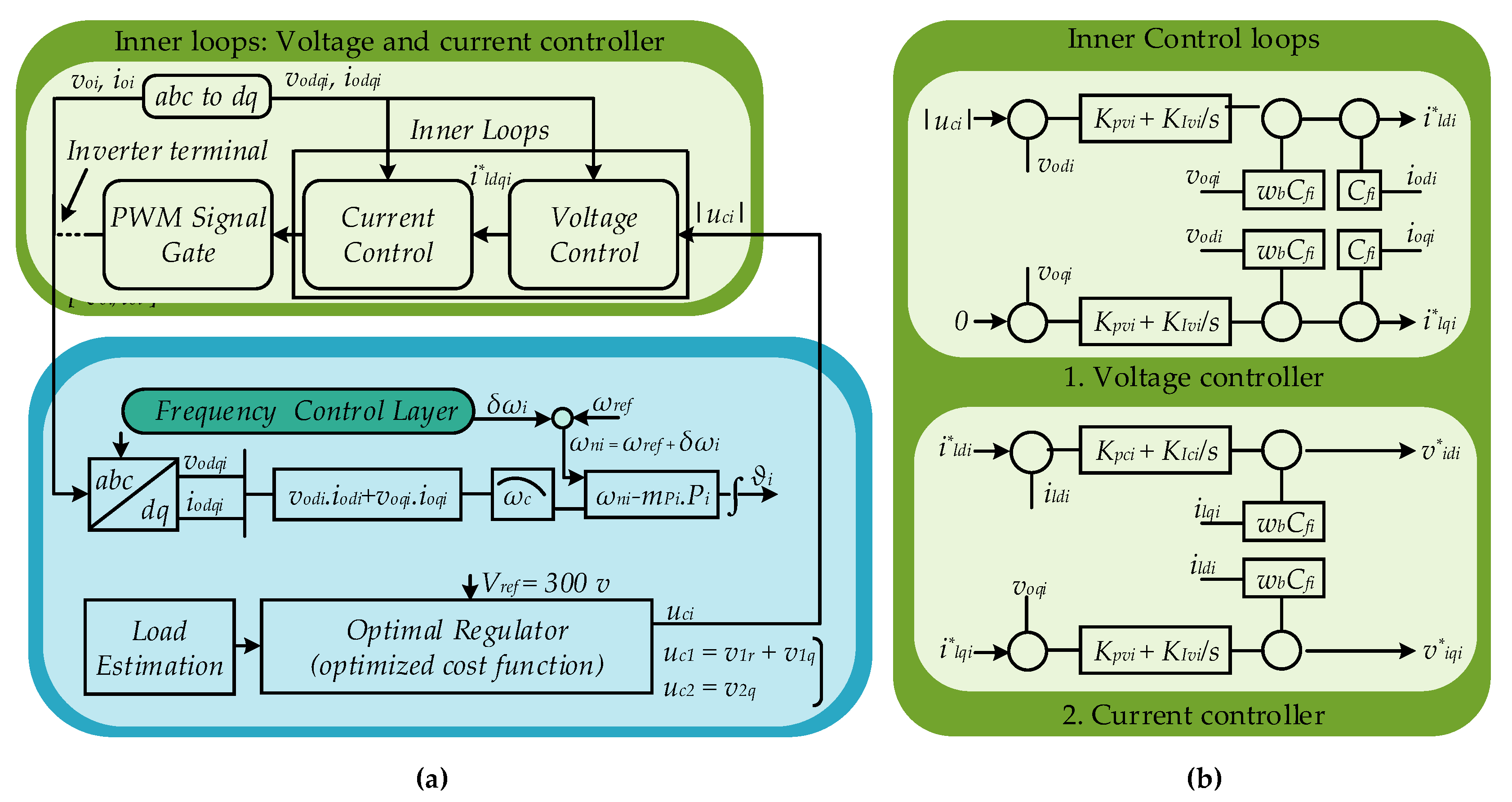
- An optimal regulator, an optimized cost function, is constructed to send optimal control commands to the inner layer of each DG unit. Moreover, the secondary control layer is responsible to restore the frequency deviations.
- The MATLAB/Simulink (R2018a, product registered with TJU, China) and experiment results show the effectiveness of the proposed methodology. For the stability analysis, separate Simulink and a linear analysis tool are considered to analyze the complex system by perturbing dynamical equations of the same.
2. Design Procedure
3. Proposed Optimal Control Strategy
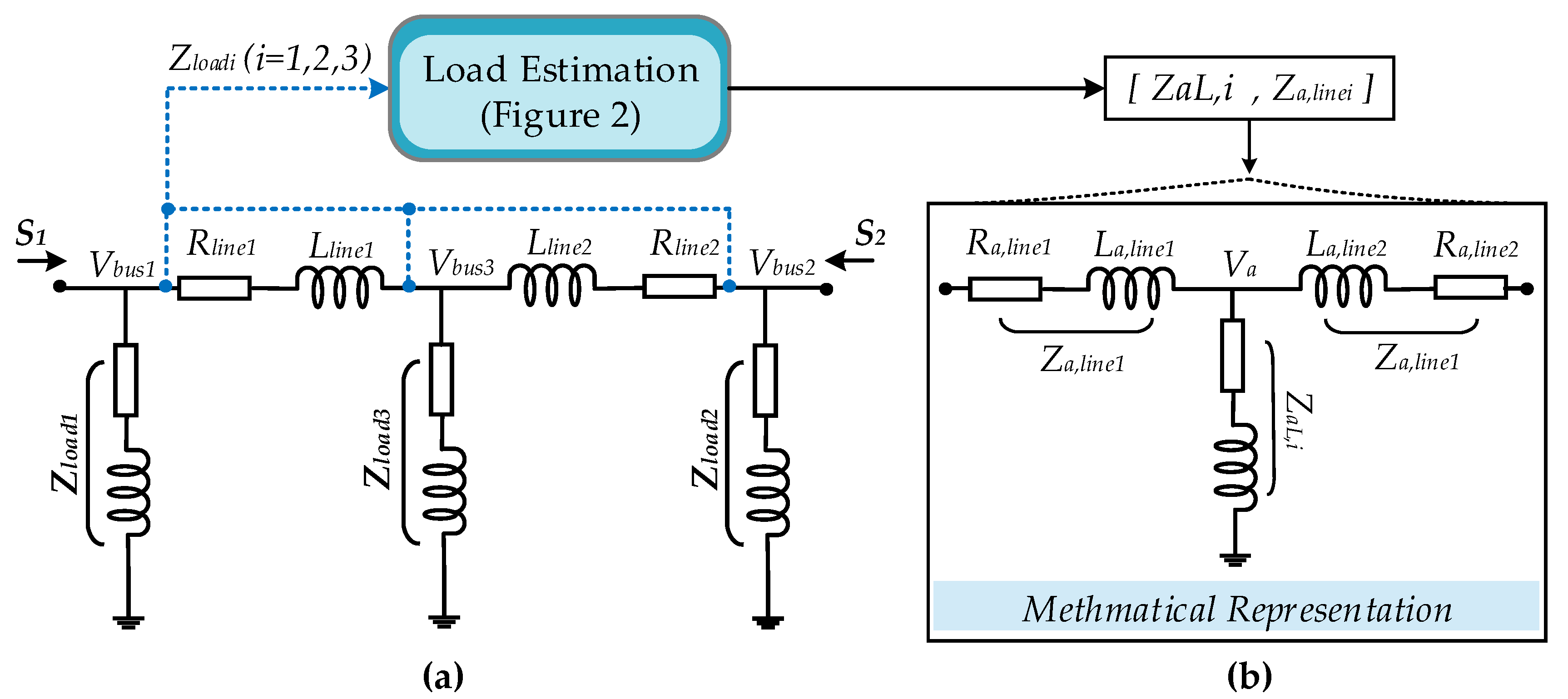
3.1. Load Estimation: The Approximation of Grid Impedance
3.2. Optimal Regulator and Algorith Flowchart
3.3. MG Power Flow Control
3.4. Mechanism of Phasor Implementation and Reactive Power Sharing
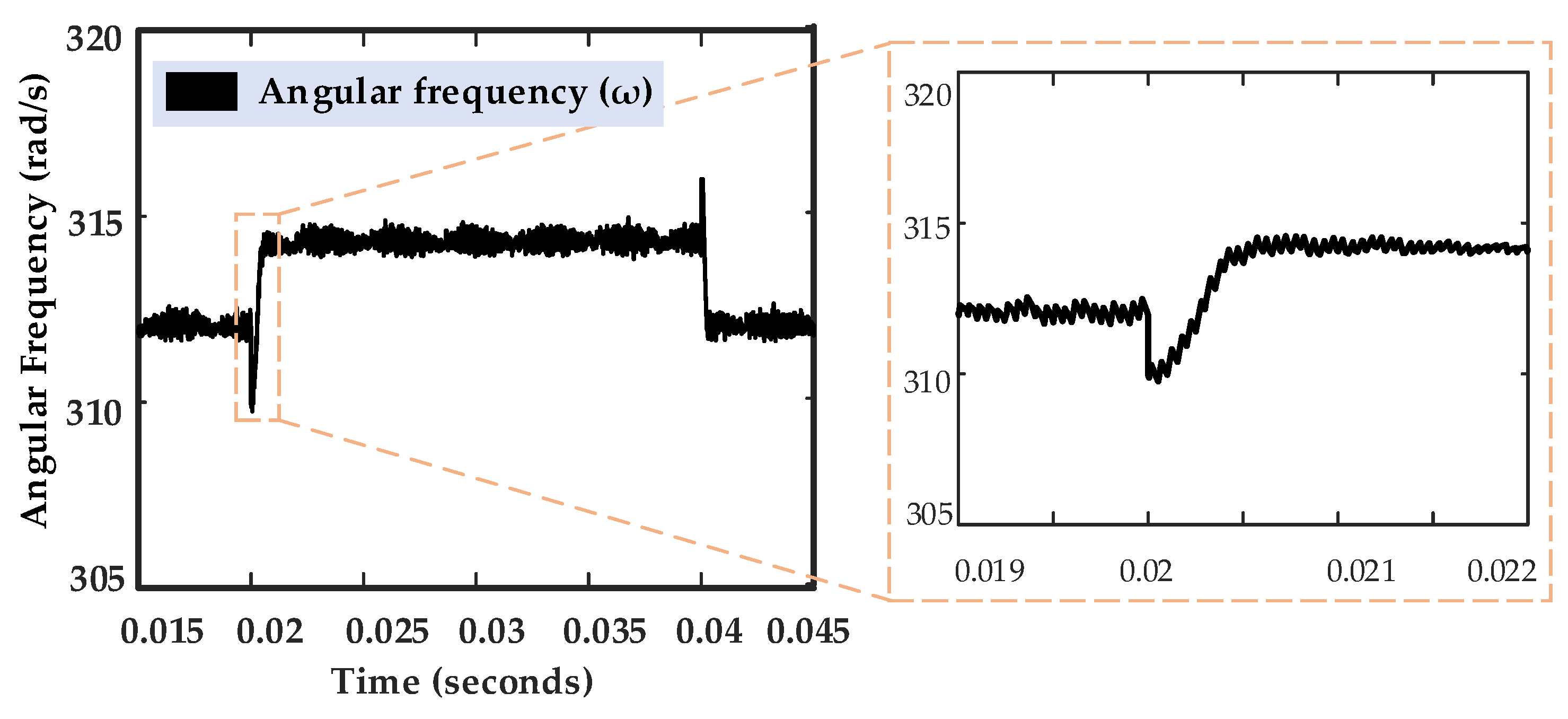
3.5. Secondary Layer: The Frequency Restoration Methodology
4. Small Signal Analysis of the MG System
4.1. Power Controller
4.2. Complete MG Model
5. Stability, Simulation, and Experimental Verification
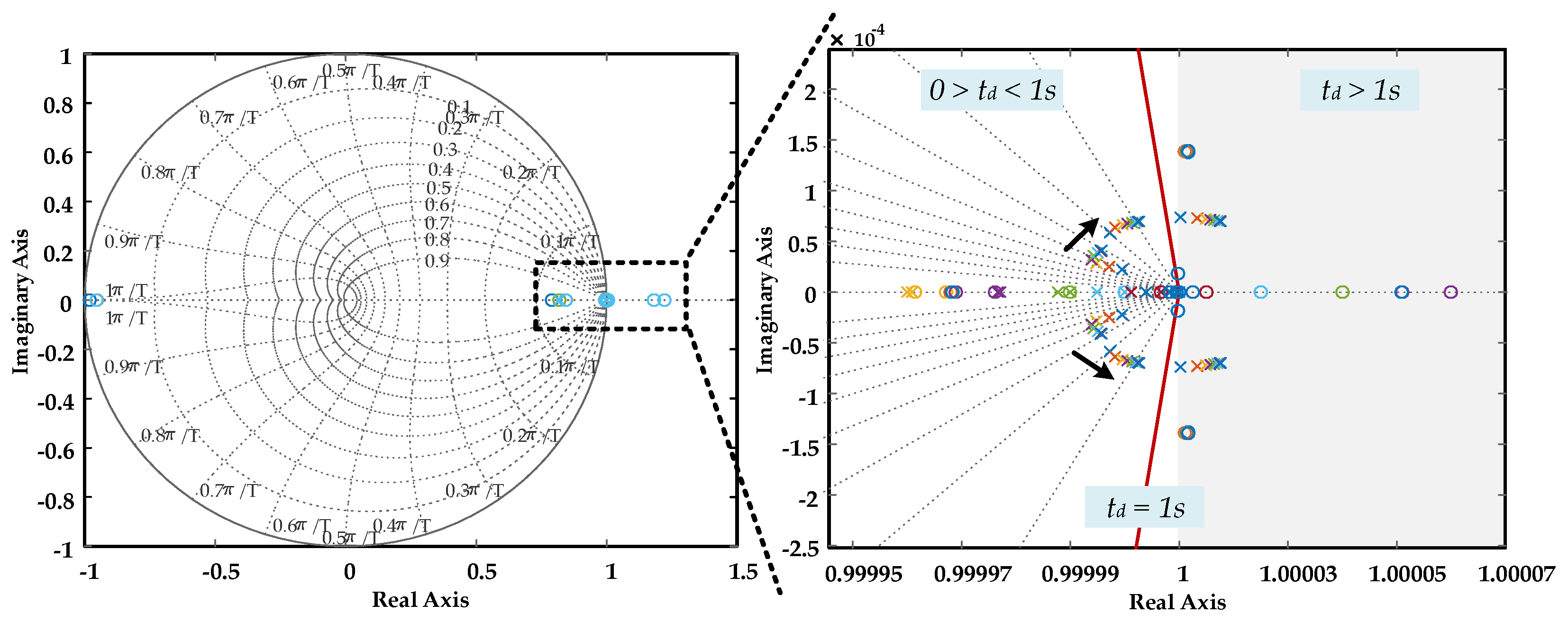
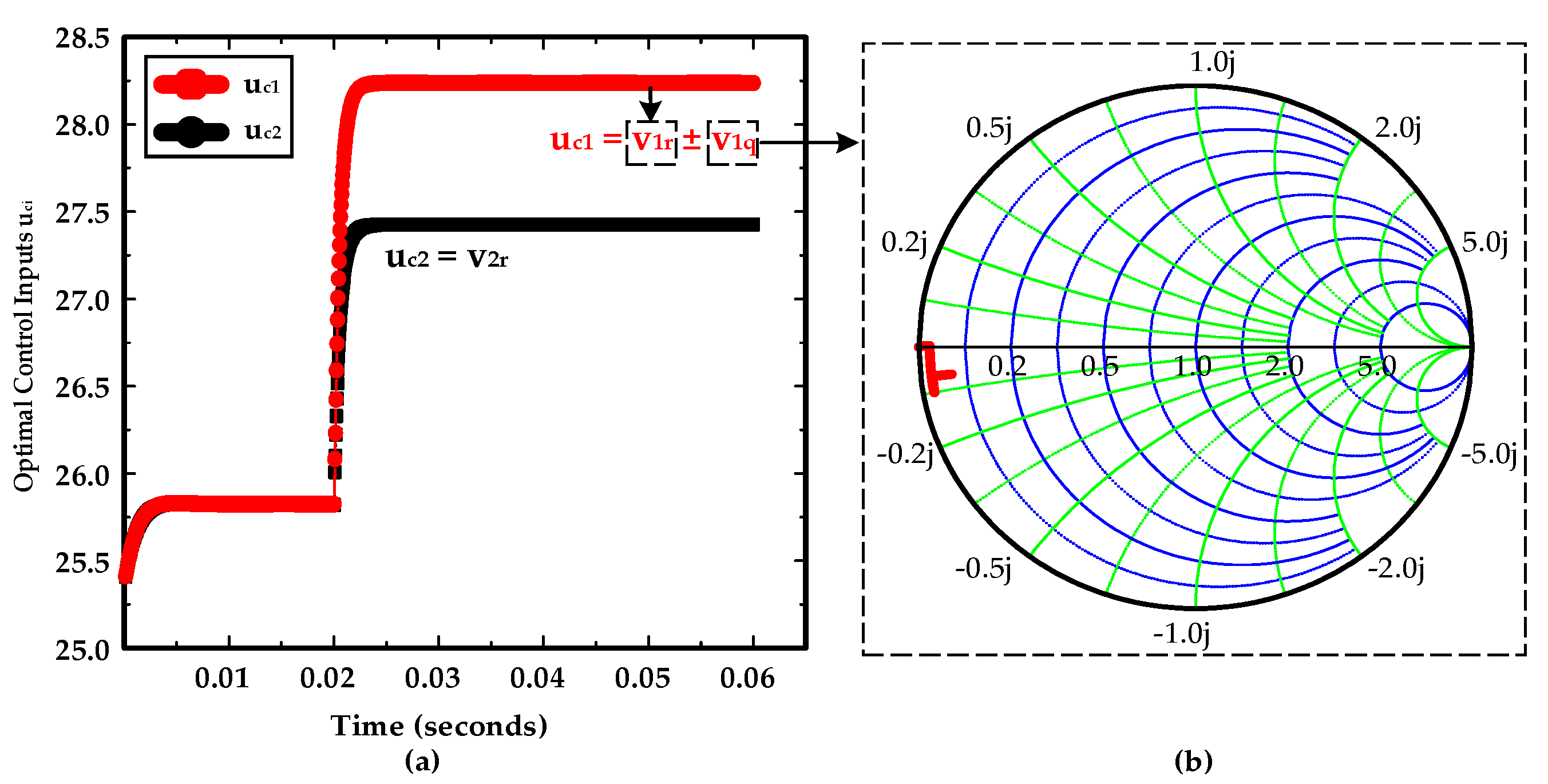
5.1. Stability Analysis Results
5.2. Case Simulation Studies
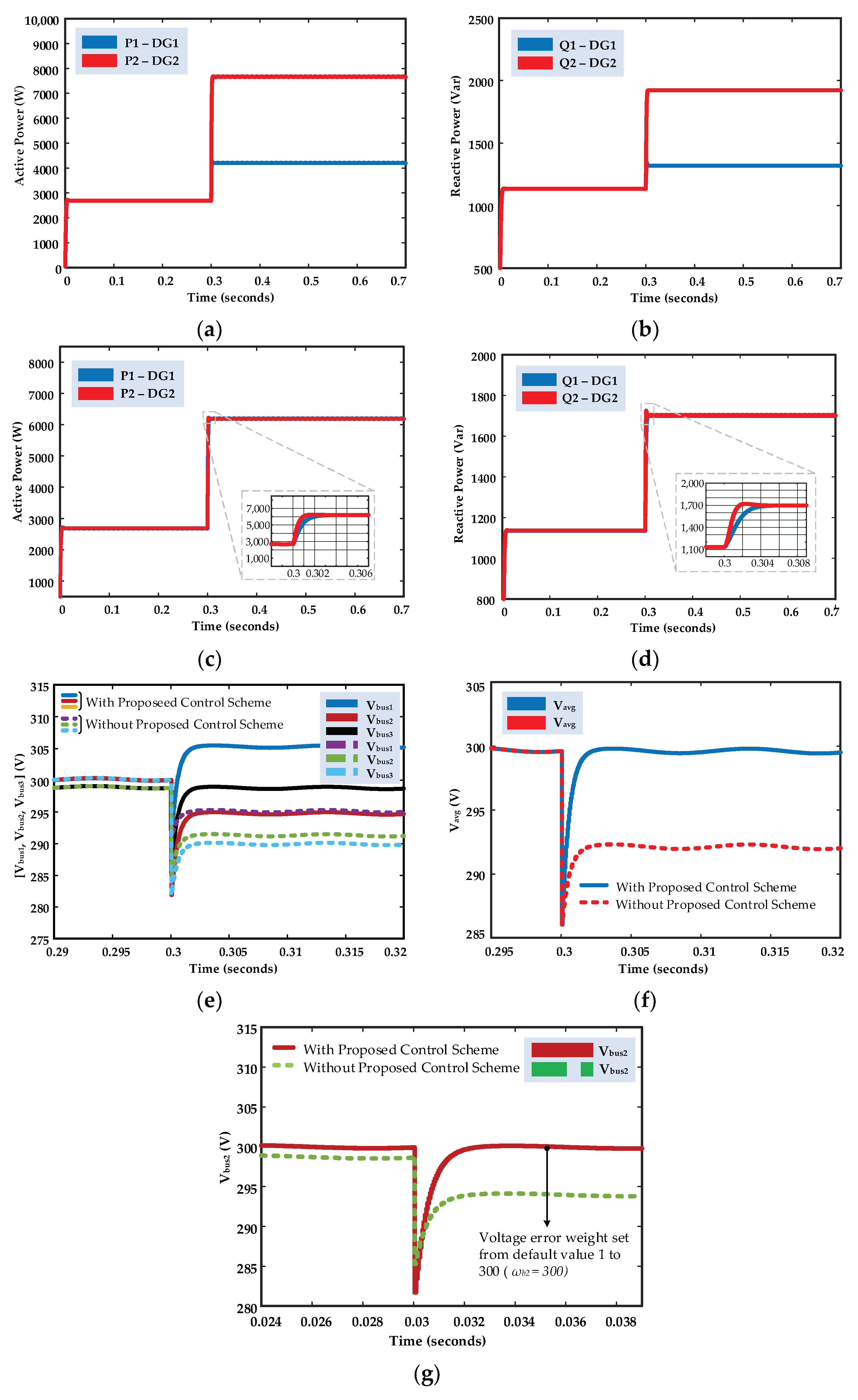
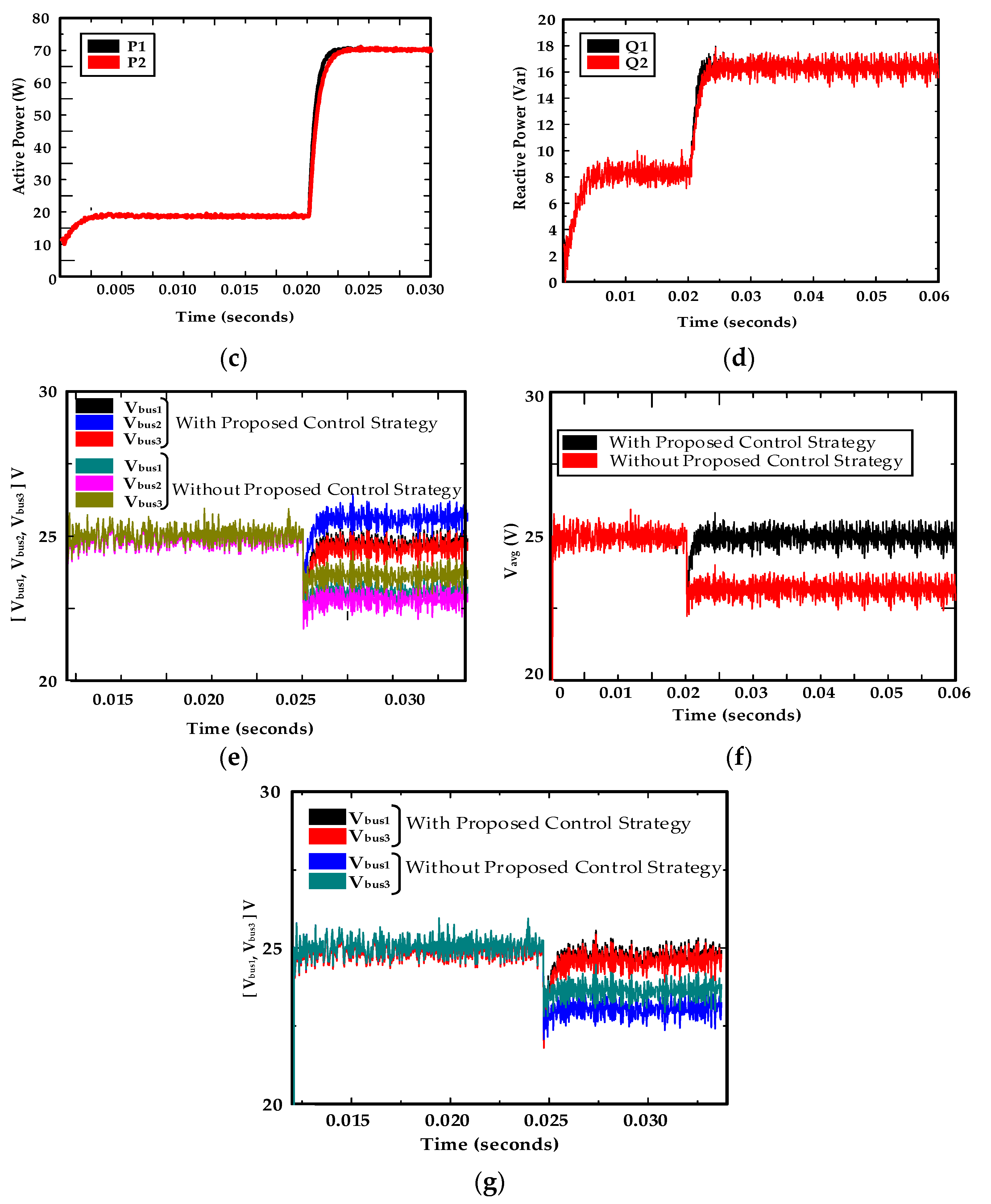
5.2.1. Case 1: Power Sharing and Bus 2 Voltage Control
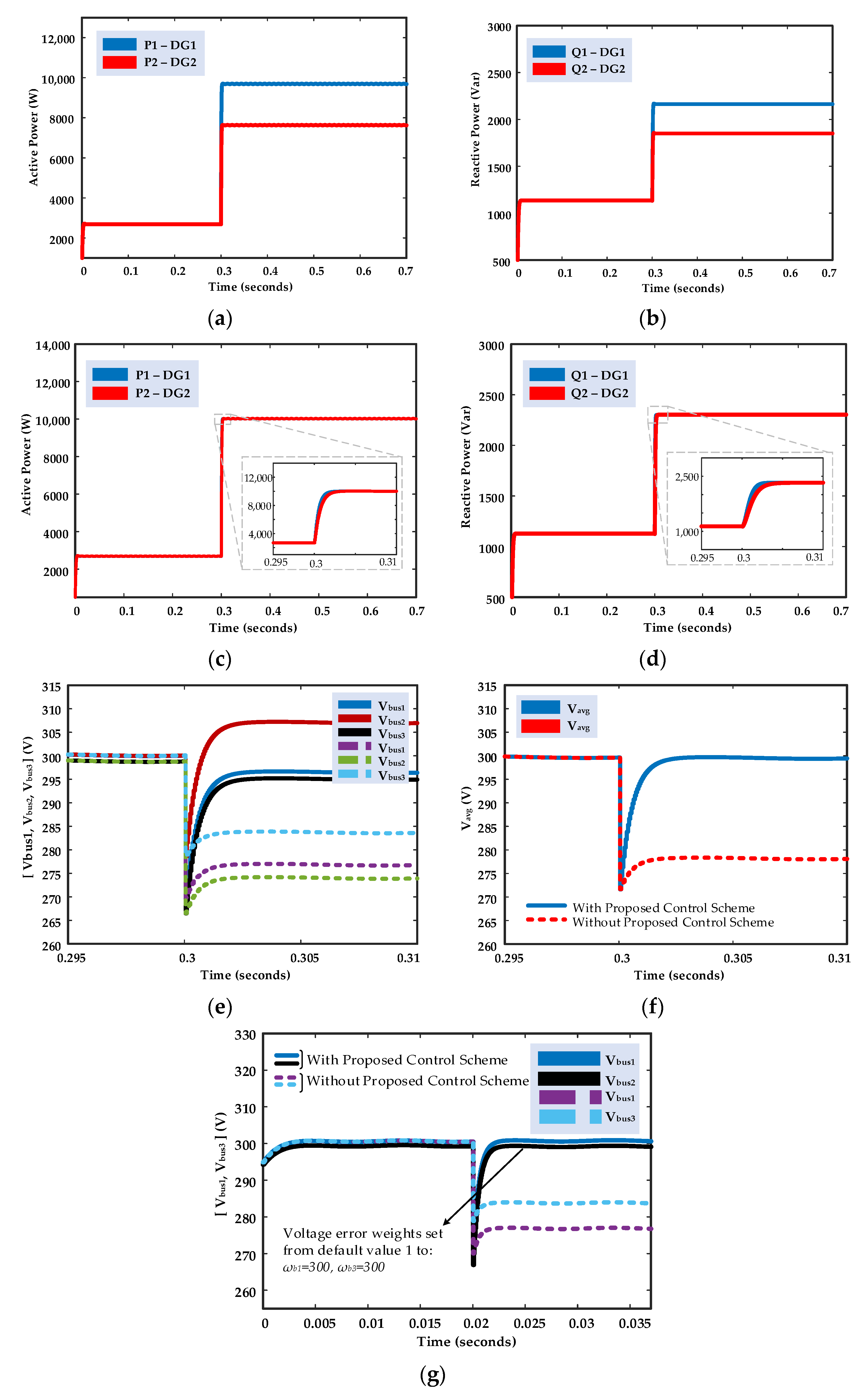
5.2.2. Load Variation at Bus 1 and Bus 2 Simultaneously
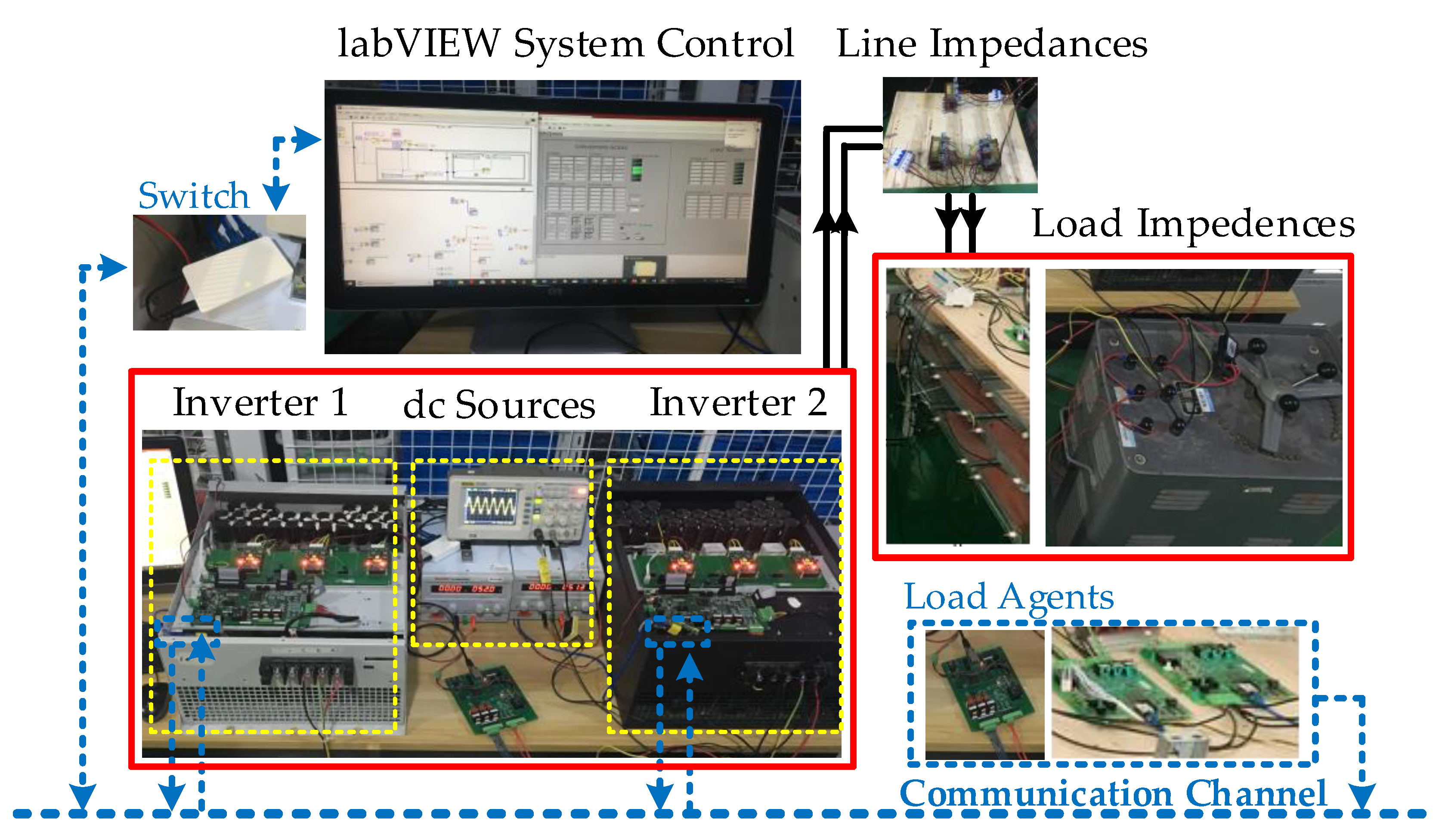
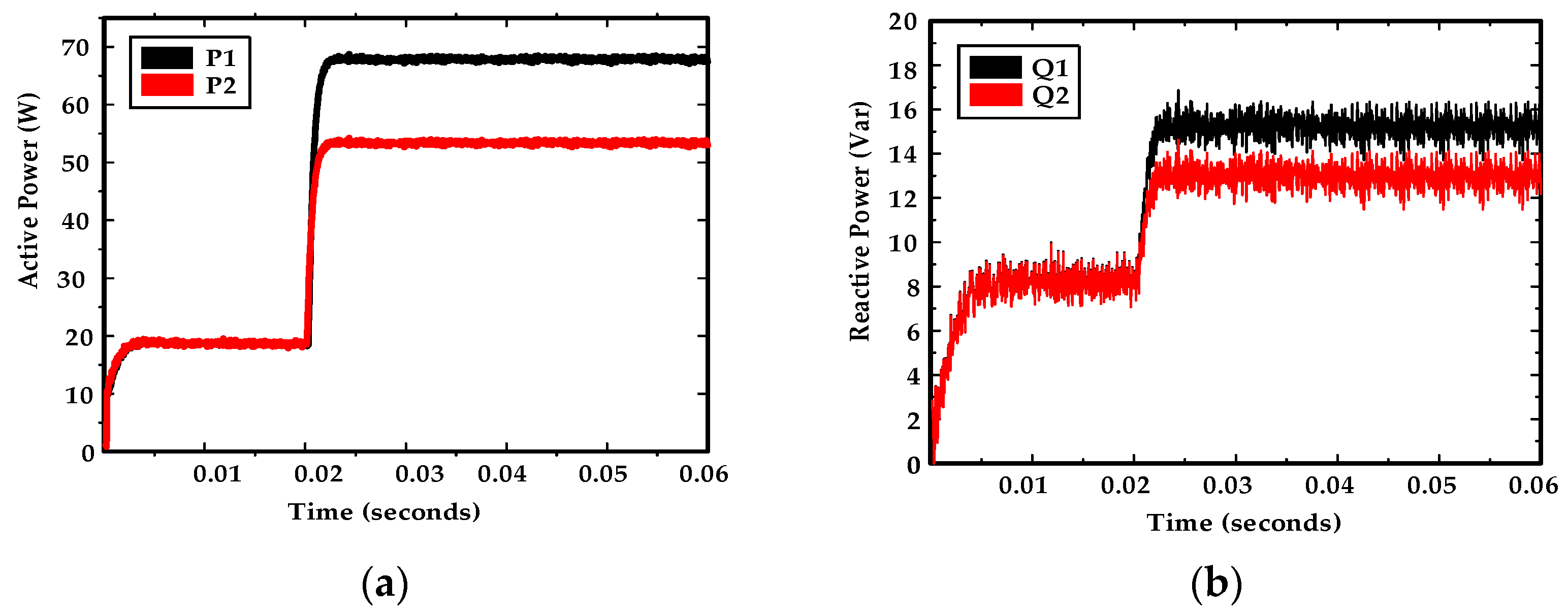
5.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B. Transformation Matrices
Appendix C. Grid Side Filter Model
Appendix D. Complete Model of an ith Inverter
Appendix E. Combined Model of N Inverters
Appendix F. Network and Load Model
References
- Khan, M.Z.; Mu, C.; Habib, S.; Alhosaini, W.; Ahmed, E.M. An Enhanced Distributed Voltage Regulation Scheme for Radial Feeder in Islanded Microgrid. Energies 2021, 14, 6092. [Google Scholar] [CrossRef]
- Ali, S.; Kazmi, A.; Shahzad, M.K.; Khan, A.Z.; Shin, D.R. Smart Distribution Networks: A Review of Modern Distribution Concepts from a Planning Perspective. Energies 2017, 10, 501. [Google Scholar]
- Habib, S.; Khan, M.M.; Abbas, F.; Ali, A.; Hashmi, K.; Shahid, M.U.; Bo, Q.; Tang, H. Risk Evaluation of Distribution Networks Considering Residential Load Forecasting with Stochastic Modeling of Electric Vehicles. Energy Technol. 2019, 7, 1900191. [Google Scholar] [CrossRef]
- Abdalla, O.H.; Fayek, H.H.; Ghany, A.; Ghany, M.A. Secondary and Tertiary Voltage Control of a Multi-Region Power System. Electricity 2020, 1, 37–59. [Google Scholar] [CrossRef]
- Baran Junior, A.R.; Piazza Fernandes, T.S.; Borba, R.A. Voltage Regulation Planning for Distribution Networks Using Multi-Scenario Three-Phase Optimal Power Flow. Energies 2020, 13, 159. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.Z.; Khan, M.M.; Jiang, H.; Hashmi, K.; Shahid, M.U. An improved control strategy for three-phase power inverters in islanded ac microgrids. Inventions 2018, 3, 47. [Google Scholar] [CrossRef] [Green Version]
- Eid, B.M.; Rahim, N.A.; Selvaraj, J.; El Khateb, A.H. Control Methods and Objectives for Electronically Coupled Distributed Energy Resources in Microgrids: A Review. IEEE Syst. J. 2016, 10, 446–458. [Google Scholar] [CrossRef]
- Hashmi, K.; Khan, M.M.; Shahid, M.U.; Nawaz, A.; Khan, A.; Jun, J.; Tang, H. An energy sharing scheme based on distributed average value estimations for islanded AC microgrids. Int. J. Electr. Power Energy Syst. 2020, 116, 105587. [Google Scholar] [CrossRef]
- Hashmi, K.; Khan, M.M.; Xu, J.; Shahid, M.U.; Habib, S.; Faiz, M.T.; Tang, H. A Quasi-average estimation aided hierarchical control scheme for power electronics-based islanded microgrids. Electronics 2019, 8, 39. [Google Scholar] [CrossRef] [Green Version]
- Habib, S.; Khan, M.M.; Abbas, F.; Numan, M.; Ali, Y.; Tang, H.; Yan, X. A framework for stochastic estimation of electric vehicle charging behavior for risk assessment of distribution networks. Front. Energy 2019, 14, 298–317. [Google Scholar] [CrossRef]
- Shahid, M.U.; Khan, M.M.; Yuning, J.; Hashmi, K.; Mumtaz, M.A.; Khan, M.Z. An adaptive droop technique for load sharing in islanded DC micro grid with faulty communication. EPE J. 2021, 1–15. [Google Scholar] [CrossRef]
- Tuladhar, A.; Jin, H.; Unger, T.; Mauch, K. Control of Parallel Inverters in Distributed AC Power Systems with Consideration of Line Impedance Effect. IEEE Trans. Ind. Appl. 2000, 36, 131–138. [Google Scholar] [CrossRef]
- Pei, Y.; Jiang, G.; Yang, X.; Wang, Z. Auto-Master-Slave Control Technique of Par allel Inverters in Distributed AC Power Systems and UPS. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 2050–2053. [Google Scholar]
- Microgrids, V. Decentralized Cooperative Control Strategy of Microsources for Stabilizing Autonomous VSC-based microgrids. IEEE Trans. Power Syst. 2012, 27, 1949–1959. [Google Scholar]
- Vandoorn, T.L.; de Kooning, J.D.M.; Meersman, B.; Vandevelde, L. Review of primary control strategies for islanded microgrids with power-electronic interfaces. Renew. Sustain. Energy Rev. 2013, 19, 613–628. [Google Scholar] [CrossRef]
- Sun, X.; Lee, Y.; Xu, D. Modeling, Analysis, and Implementation of Parallel Multi-Inverter Systems with Instantaneous average-current-sharing scheme. IEEE Trans. Power Electron. 2003, 18, 844–856. [Google Scholar]
- Guerrero, J.M.; Matas, J.; de Vicuña, L.G.; Castilla, M.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance. IEEE Trans. Ind. Electron. 2007, 54, 994–1004. [Google Scholar] [CrossRef]
- Yao, W.; Chen, M.; Matas, J.; Guerrero, J.M.; Qian, Z.M. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing. IEEE Trans. Ind. Electron. 2011, 58, 576–588. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Guerrero, J.M.; Blaabjerg, F.; Vasquez, J.C. An Islanding Microgrid Power Sharing Approach Using Enhanced Virtual Impedance Control Scheme. IEEE Trans. Power Electron. 2013, 28, 5272–5282. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.W. Decoupled Power Control for an Inverter Based Low Voltage Microgrid in Autonomous Operation. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; Volume 3, pp. 2490–2496. [Google Scholar]
- Habib, S.; Khan, M.M.; Abbas, F.; Ali, A.; Faiz, M.T.; Ehsan, F.; Tang, H. Contemporary Trends in Power Electronics Converters for Charging Solutions of Electric Vehicles. CSEE J. Power Energy Syst. 2020, 6, 911–929. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.W. Power management of inverter interfaced autonomous microgrid based on virtual frequency-voltage frame. IEEE Trans. Smart Grid 2011, 2, 30–40. [Google Scholar] [CrossRef]
- Perreault, D.J.; Selders, R.L.; Kassakian, J.G. Frequency-Based Current-Sharing Techniques for Paralleled Power Converters. IEEE Trans. Power Electron. 1998, 13, 626–634. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. An Enhanced Microgrid Load Demand Sharing Strategy. IEEE Trans. Power Electron. 2012, 27, 3984–3995. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.; Luna, A.; Rodriguez, P.; Teodorescu, R. Adaptive Droop Control Applied to Voltage-Source Inverters Operating in Grid-Connected and Islanded Modes. IEEE Trans. Ind. Electron. 2009, 56, 4088–4096. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. An accurate reactive power sharing control strategy for DG units in a microgrid. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 551–556. [Google Scholar] [CrossRef]
- Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Angle Droop versus Frequency Droop in a Voltage Source Converter Based Autonomous Microgrid. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Majumder, R.; Chaudhuri, B.; Ghosh, A.; Majumder, R.; Ledwich, G.; Zare, F. Improvement of Stability and Load Sharing in an Autonomous Microgrid Using Supplementary Droop Control Loop. IEEE Trans. Power Syst. 2010, 25, 796–808. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of power sharing control strategies for islanding operation of AC microgrids. IEEE Trans. Smart Grid 2016, 7, 200–215. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, J.M. Review of Active and Reactive Power Sharing Strategies in Hierarchical Controlled Microgrids. IEEE Trans. Power Electron. 2017, 32, 2427–2451. [Google Scholar] [CrossRef] [Green Version]
- Raj, D.C.; Gaonkar, D.N. Frequency and Voltage Droop Control of Parallel Inverters in Microgrid. In Proceedings of the 2016 2nd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 28–30 January 2016; Volume 2, pp. 407–411. [Google Scholar]
- Zhong, Q. Robust Droop Controller for Accurate Proportional Load Sharing Among Inverters Operated in Parallel. IEEE Trans. Ind. Electron. 2013, 60, 1281–1290. [Google Scholar] [CrossRef]
- Khan, M.Z.; Khan, M.M.; Xiangming, X.; Khalid, U.; Rasool, M.A.U. An optimal control load demand sharing strategy for multi-feeders in islanded microgrid. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 18–25. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Lee, C.T.; Chu, C.C.; Cheng, P.T. A new droop control method for the autonomous operation of distributed energy resource interface converters. IEEE Trans. Power Electron. 2013, 28, 1980–1993. [Google Scholar] [CrossRef]
- Matas, J.; Castilla, M.; De Vicuña, L.G.; Miret, J.; Vasquez, J.C. Virtual impedance loop for droop-controlled single-phase parallel inverters using a second-order general-integrator scheme. IEEE Trans. Power Electron. 2010, 25, 2993–3002. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2015, 30, 7019–7037. [Google Scholar] [CrossRef]
- Guerrero, J.M.; de Vicuña, L.G.; Matas, J.; Miret, J.; Castilla, M. Output impedance design of parallel-connected UPS inverters. IEEE Int. Symp. Ind. Electron. 2004, 2, 1123–1128. [Google Scholar] [CrossRef]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Wang, X.; Tian, Y.; Tan, Y. An Estimator-Based Distributed Voltage-Predictive Control Strategy for AC Islanded Microgrids. IEEE Trans. Power Electron. 2015, 30, 3934–3951. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Distributed Optimal Control of Reactive Power and Voltage in Islanded Microgrids. IEEE Trans. Ind. Appl. 2017, 53, 340–349. [Google Scholar] [CrossRef]




| Sr. | Components | Units | Components | Units |
|---|---|---|---|---|
| 1 | Nominal frequency | 50 Hz | Lload1/Rload1 | 80 mH/60 Ω |
| 2 | Simulations Vref Experiments Vref | 300 V 25 V | Lload2/Rload2 Lload3/Rload3 | 80.5 mH/61 Ω 120 mH/80 Ω |
| 3 | Switching Frequency | 16 KHz | - | - |
| 4 | Lc1/Lc2 Lline1/Rline1 Lline2/Rline2 | 1 mH/1 mH 0.5 mH/0.75 Ω 0.5 mH/0.75 Ω | Ld1/Rd1 Ld2/Rd2 Ld3/Rd3 | 10.5 mH/19 Ω 9.5 mH/20.5 Ω 10 mH/21 Ω |
| 5 | mP1/mP2 | 1.5 × 10−4/0.5 × 10−2 | ωb1, ωb2, ωb3 | 300, 500, 300 |
| Sr. No. | Control Parameters for Stability Analysis | |||
| 1 | Droop gains | Min | Max | |
| mP | 0.02 | 0.32 | ||
| 2 | Frequency restoration | |||
| kpf | 0.45 | 2.9 | ||
| kif | 0.2 | 0.9 | ||
| 3 | Voltage restoration | |||
| kpV | 0.3 | 2.5 | ||
| kiV | 0.08 | 0.48 | ||
| 4 | Time delay | |||
| τdelay | 0 | 6 | ||
| Sr. No. | Control Parameters for Experimental Prototype | |||
| Components | Units | Components | Units | |
| 1. | Operating frequency | 50 Hz | Sampling rate | 1 ms |
| 2. | DG units’ ratings | 3 A, 30 V | jXi1, jXi2 | 200 uH |
| 3. | jXc1, jXc2 | 20 uF | jXg1, jXg2 | 60 uH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.Z.; Mu, C.; Habib, S.; Hashmi, K.; Ahmed, E.M.; Alhosaini, W. An Optimal Control Scheme for Load Bus Voltage Regulation and Reactive Power-Sharing in an Islanded Microgrid. Energies 2021, 14, 6490. https://doi.org/10.3390/en14206490
Khan MZ, Mu C, Habib S, Hashmi K, Ahmed EM, Alhosaini W. An Optimal Control Scheme for Load Bus Voltage Regulation and Reactive Power-Sharing in an Islanded Microgrid. Energies. 2021; 14(20):6490. https://doi.org/10.3390/en14206490
Chicago/Turabian StyleKhan, Muhammad Zahid, Chaoxu Mu, Salman Habib, Khurram Hashmi, Emad M. Ahmed, and Waleed Alhosaini. 2021. "An Optimal Control Scheme for Load Bus Voltage Regulation and Reactive Power-Sharing in an Islanded Microgrid" Energies 14, no. 20: 6490. https://doi.org/10.3390/en14206490









