Why Should We Test the Wideband Transformation Accuracy of Inductive Current Transformers?
Abstract
:1. Introduction
- Comparison of the values of current error and phase displacement determined in the frequencies ranging from 50 Hz to 5 kHz of two inductive CTs,
- Impact of the self-generation phenomenon on the wideband metrological performance of the inductive CTs,
- Analysis of the frequency characteristic of the current error and phase displacement,
- Analysis of the factors affecting the values of the self-generated low-order higher harmonics,
- Establishment of the starting point to define the limiting values of current error and phase displacement for the future wideband accuracy class extension for inductive CTs,
- Justification of the inductive CTs applicability for transforming the distorted current and distorted power meeting and power quality evaluation.
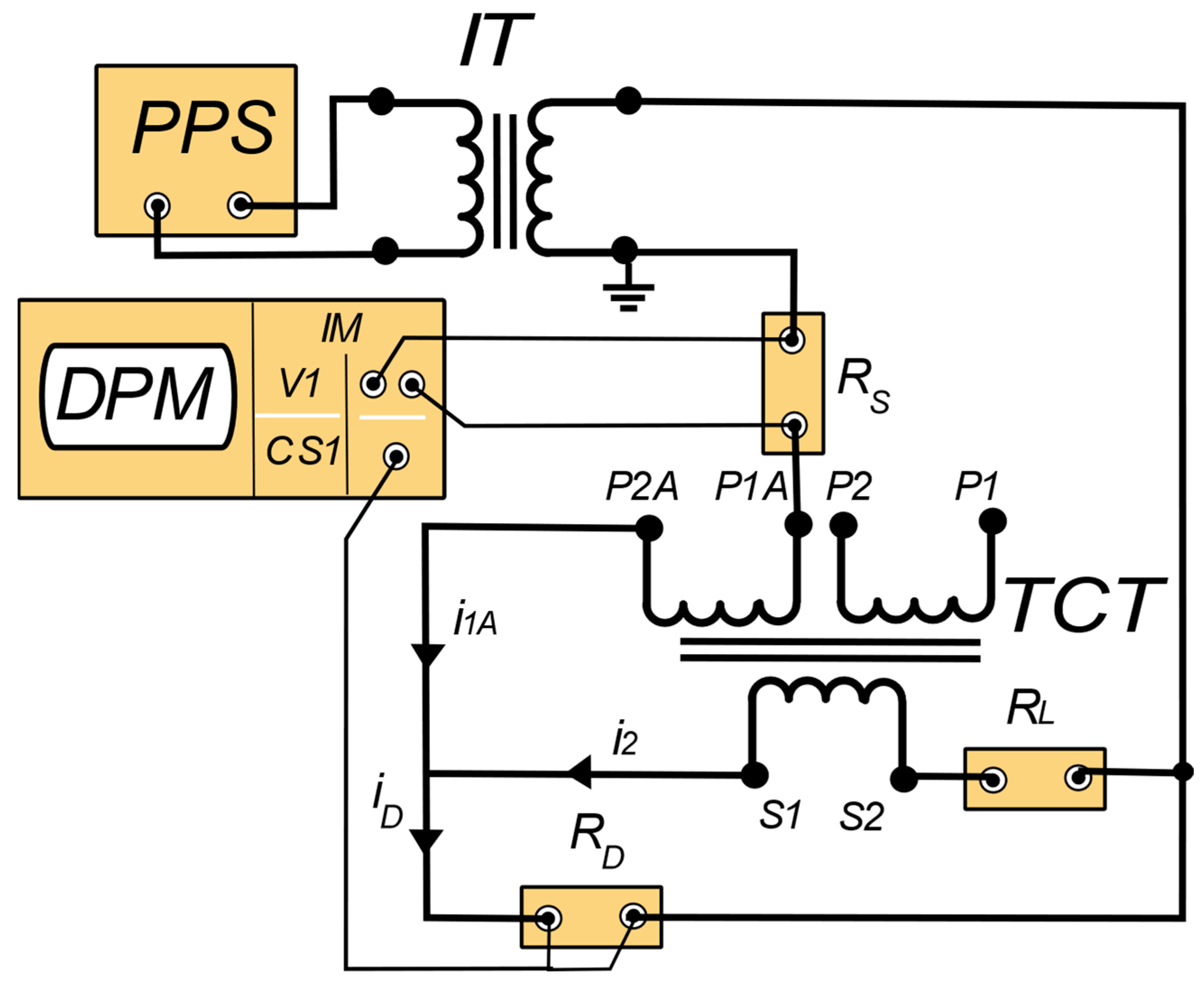
2. The Measuring Circuit and the Objects of the Research
- The RMS value of current I1Ahk in additional primary winding specified for a given hk harmonic,
- The RMS value of differential current IDhk between additional primary and secondary winding,
- The phase angle between differential current ID and current I1A flowing in additional primary winding specified for a given hk harmonic ϕhk.
- ΔIhk—the percentage value of the current error specified for its given hk harmonic,
- ε%Ihk—the percentage value of the composite error specified for its given hk harmonic.
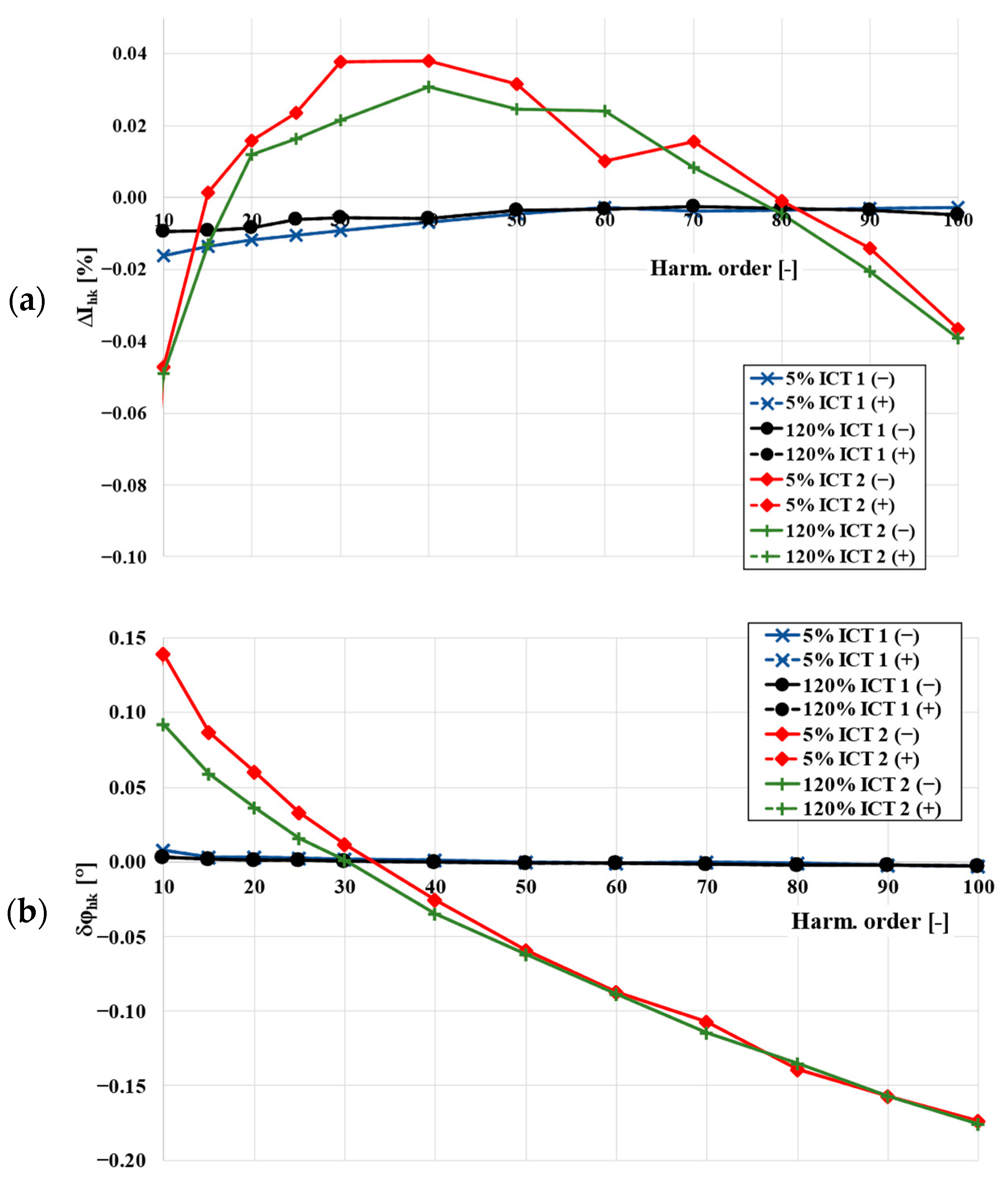
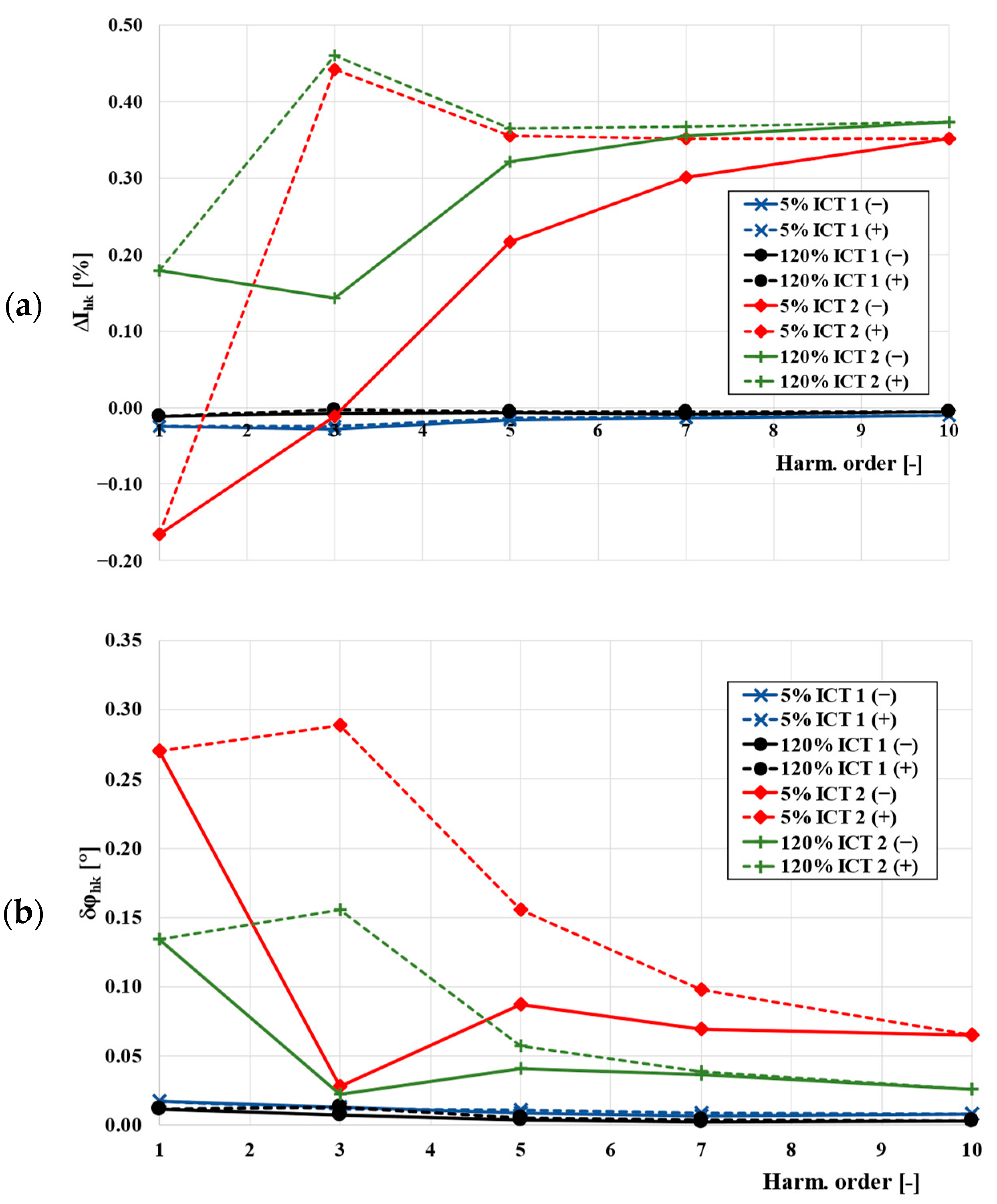
3. Metrological Performance of the CTs in the Wide Frequencies Range
- Ighk—the RMS value of the self-generated low-order higher harmonic determined for the transformation of sinusoidal current.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaczmarek, M.; Stano, E. Why Should We Test the Wideband Transformation Accuracy of Medium Voltage Inductive Voltage Transformers? Energies 2021, 14, 4432. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Stano, E. Proposal for extension of routine tests of the inductive current transformers to evaluation of transformation accuracy of higher harmonics. Int. J. Electr. Power Energy Syst. 2019, 113, 842–849. [Google Scholar] [CrossRef]
- Mingotti, A.; Peretto, L.; Bartolomei, L.; Cavaliere, D.; Tinarelli, R. Are inductive current transformers performance really affected by actual distorted network conditions? An experimental case study. Sensors 2020, 20, 927. [Google Scholar] [CrossRef] [Green Version]
- Mingotti, A.; Bartolomei, L.; Peretto, L.; Tinarelli, R. On the long-period accuracy behavior of inductive and low-power instrument transformers. Sensors 2020, 20, 5810. [Google Scholar] [CrossRef]
- Murray, R.; De Kock, J. Instrument transformers influence on harmonic measurements for grid code compliance. In Proceedings of the 2018 IEEE 4th Global Electromagnetic Compatibility Conference (GEMCCON), Stellenbosch, South Africa, 7–9 November 2018. [Google Scholar]
- Kaczmarek, M.; Stano, E. Measuring system for testing the transformation accuracy of harmonics of distorted voltage by medium voltage instrument transformers. Measurement 2021, 181, 109628. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Stano, E. Nonlinearity of Magnetic Core in Evaluation of Current and Phase Errors of Transformation of Higher Harmonics of Distorted Current by Inductive Current Transformers. IEEE Access 2020, 8, 118885–118898. [Google Scholar] [CrossRef]
- Frigo, G.; Agustoni, M. Calibration of a Digital Current Transformer Measuring Bridge: Metrological Challenges and Uncertainty Contributions. Metrology 2021, 1, 93–106. [Google Scholar] [CrossRef]
- Xiao, X.; Song, H.; Li, H. A High Accuracy AC+DC Current Transducer for Calibration. Sensors 2022, 22, 2214. [Google Scholar] [CrossRef]
- Platiše, U.; Kanalec, T.; Mohorčič, M. High precision wide bandwidth dc current transducer based on the platiše flux sensor. Sensors 2020, 20, 4197. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Wu, Z.; Abu-Siada, A.; Tao, Y. Study of current measurement method based on circular magnetic field sensing array. Sensors 2018, 18, 1439. [Google Scholar] [CrossRef] [Green Version]
- Siegenthaler, S.; Mester, C. A computer-controlled calibrator for instrument transformer test sets. IEEE Trans. Instrum. Meas. 2017, 66, 1184–1190. [Google Scholar] [CrossRef]
- Draxler, K.; Styblikova, R. Using instrument transformers in a wider frequency range. In Proceedings of the 2011 IEEE Instrumentation and Measurement Technology Conference, Hangzhou, China, 10–12 May 2011; pp. 1207–1210. [Google Scholar]
- IEC 61869-2; Instrument Transformers—Additional Requirements for Current Transformers. IEC: Geneva, Switzerland, 2012.
- IEC 61869-3; Instrument Transformers—Additional Requirements for Voltage Transformers. IEC: Geneva, Switzerland, 2011.
- IEC 61869-6; Instrument Transformers—Additional General Requirements for Low-Power Instrument Transformers. IEC: Geneva, Switzerland, 2016.
- IEC 61869-10; Instrument Transformers—Additional Requirements for Low-Power Passive Current Transformers. IEC: Geneva, Switzerland, 2017.
- IEC 61869-103; Instrument Transformers—the Use of Instrument Transformers for Power Quality Measurement. IEC: Geneva, Switzerland, 2010.
- Cristaldi, L.; Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. A Low-Cost Generator for Testing and Calibrating Current Transformers. IEEE Trans. Instrum. Meas. 2019, 68, 2792–2799. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Kaczmarek, P. Comparison of the wideband power sources used to supply step-up current transformers for generation of distorted currents. Energies 2020, 13, 1849. [Google Scholar] [CrossRef]
- Brodecki, D.; Stano, E.; Andrychowicz, M.; Kaczmarek, P. Emc of wideband power sources. Energies 2021, 14, 1457. [Google Scholar] [CrossRef]
- Kaczmarek, M.L.; Stano, E. Application of the inductive high current testing transformer for supplying of the measuring circuit with distorted current. IET Electr. Power Appl. 2019, 13, 1310–1317. [Google Scholar] [CrossRef]
- McLyman, C.W.T. Transformer and Inductor Design Handbook; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ryłko, M.S.; Hartnett, K.J.; Hayes, J.G.; Egan, M.G. Magnetic material selection for high power high frequency inductors in DC-DC converters. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 2043–2049. [Google Scholar]
- Stano, E.; Kaczmarek, M. Wideband self-calibration method of inductive cts and verification of determined values of current and phase errors at harmonics for transformation of distorted current. Sensors 2020, 20, 2167. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, M.; Stano, E. The Influence of the 3rd Harmonic of the Distorted Primary Current on the Self-Generation of the Inductive Current Transformers. IEEE Access 2022, 10, 55876–55887. [Google Scholar] [CrossRef]
- Lesniewska, E.; Rajchert, R. 3D field-circuit analysis of measurement properties of current transformers with axially and radially connected cores made of different magnetic materials. Prog. Electromagn. Res. M 2012, 28, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Prochazka, R.; Hlavacek, J.; Draxler, K. Impulse current transformer with a nanocrystalline core. IEEE Trans. Magn. 2013, 49, 77–80. [Google Scholar] [CrossRef]
- Salach, J.; Hasse, L.; Szewczyk, R.; Smulko, J.; Bieńkowski, A.; Frydrych, P.; Kolano-Burian, A. Low current transformer utilizing co-based amorphous alloys. IEEE Trans. Magn. 2012, 48, 1493–1496. [Google Scholar] [CrossRef]
- Stano, E. The Method to Determine the Turns Ratio Correction of the Inductive Current Transformer. Energies 2021, 14, 8602. [Google Scholar] [CrossRef]
- Kaczmarek, M. Estimation of the inductive current transformer derating for operation with distorted currents. Bull. Polish Acad. Sci. Tech. Sci. 2014, 62, 363–366. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, M. Wide frequency operation of the inductive current transformer with Ni80Fe20 toroidal core. Electr. Power Compon. Syst. 2014, 42, 1087–1094. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stano, E.; Kaczmarek, P.; Kaczmarek, M. Why Should We Test the Wideband Transformation Accuracy of Inductive Current Transformers? Energies 2022, 15, 5737. https://doi.org/10.3390/en15155737
Stano E, Kaczmarek P, Kaczmarek M. Why Should We Test the Wideband Transformation Accuracy of Inductive Current Transformers? Energies. 2022; 15(15):5737. https://doi.org/10.3390/en15155737
Chicago/Turabian StyleStano, Ernest, Piotr Kaczmarek, and Michal Kaczmarek. 2022. "Why Should We Test the Wideband Transformation Accuracy of Inductive Current Transformers?" Energies 15, no. 15: 5737. https://doi.org/10.3390/en15155737





