The Investigation of the Bubble Behaviors on the Vertical Heat Exchange Tube

Abstract

In the boiling process, the growth, separation, and movement of bubbles are expeditious. The visualization experiment of nucleate boiling was carried out with the help of high-speed photography. The evolution of the entire bubble life cycle is clearly observed at the nucleation site without interference from the leading and neighboring bubbles. Bubble behavior at the local heating surface has strong randomness due to the influence of the wall micro-structure, convection intensity, heating surface geometry configuration, heat flux density, and so on, but bubble behavior also has a certain regularity. In this paper, the behavior characteristics of bubbles were analyzed, with a particular focus on the evolution of bubbles. Under lower load (ΔT_sat = 8~9 °C) in study conditions, nucleation sites have a long enough time interval. In addition, the bubble separation and rising velocity obviously increase due to the change of pool boiling flow characteristics in the restricted space. The setting of confined space increases the bubble escape velocity and the rising velocity, and decreases the diameter of bubbles escaping from the wall. The results will provide some help for the understanding of bubble behavior mechanisms and numerical research.

1. Introduction

As an efficient heat transfer mechanism, boiling heat transfer has been applied in many industrial fields. Due to the transient fluctuation of pressure drop and heat transfer coefficient, it is difficult to obtain stable operation of boiling heat transfer [1]. In addition, exceedingly intense boiling can lead to critical heat flux (CHF), in which steam blocking the heated surface leads to a rapid rise in temperature, which can deteriorate the entire system of heat transfer and even cause damage [2,3].

Bubble behavior is of great importance to the boiling heat transfer process. In the boiling phenomenon, the behavior of bubbles on and near the heated surface will disturb the thermal boundary layer and velocity boundary layer, which is one of the principal mechanisms for enhancing heat transfer [4,5]. Over the decades, the behavior of bubbles during boiling has been studied extensively, both experimentally and numerically. It is a known fact that bubbles go through three main stages before leaving the heated surface: bubble growth, bubble detachment, and bubble buoyancy. On the one hand, the study of bubble behavior is of great importance to the understanding of bubble dynamics and the establishment of bubble dynamics theory. On the other hand, the study of bubble behavior and bubble diameter is helpful in understanding the mechanisms of bubble behavior and can allow for the prediction of its evolution [6]. A great deal of research has been performed regarding bubble behavior during boiling; however, limited by experimental techniques and measurement tools, experimental data related to bubble dynamics are still few and random [6,7]. In the research by Yoo [8,9], the experimental results indicated that sliding bubble dynamics from a single nucleation site have a direct impact on the level of wall heat transfer enhancement, especially for the bubble behavior near the nucleation site. The evolution of the bubble from the same nucleation site directly affects the heat and mass transfer process between the vapor and liquid phases, which are crucial for analyzing near-wall heat transfer and flow characteristics. The parameters, i.e., the velocity of sliding or rising bubbles, the diameter of the bubble, and the void of the vapor phase, are crucial for establishing a realizable boiling heat transfer mechanism model and achieving a more accurate numerical simulation [10].

There are still many questions about the underlying heat transfer mechanism during nucleate boiling. There are many complex interactions between the bubble motion, fluid motion, and heat transfer in the base layer. As the heating surface temperature increases, the number of bubbles increases, and the interaction becomes more complex. Bubble motions are complex, and are dependent upon the forces on the bubble. Studies have also shown that the interfacial tension and thermocapillary force also play essential roles. If the bubble has a movement relative to the bulk liquid, the viscous force stunts the bubble from moving, and as the bubble grows, the force or inertial effect of the surrounding liquid can not be ignored [11,12,13]. Furthermore, there are additional considerations of the impact of the Marangoni force in super-cooling conditions, especially in high sub-cooling conditions. An apparent temperature gradient is formed in the liquid around the growing bubble due to the temperature gradient between the heating surface and far away from the surface. In general, the surface tension decreases as the temperature increases, which subsequently leads to an upward thermal capillary convection flow. This can exert a reverse force on the bubble (namely, the Marangoni force), which prevents the departure of the bubble from the surface [14,15]. Wang [16] proposed that the traditional force balance model modified through a Marangoni force still can not precisely predict the bubble departure radius, especially in a low heat flux regime. Even after extensive research for several decades, there is still no generalized correlation for bubble departure radius on boiling surfaces. Moreover, the error is usually very large when using the correlations developed based on the data. The coalescence of bubbles has a significant effect on fluid flow and heat transport. Bonjour et al. [17] conducted an experimental study on coalescence by measuring three artificial nucleation sites with different spacing on vertical heating walls. The results show that bubble binding at all three sites had a higher heat transfer coefficient than boiling at a single site. Coulibaly et al. [18] also studied the effect of coalescence on bubble movement and heat transfer. The merged bubbles move and oscillate on the heated surface and show significant heat transfer changes before leaving. The size and frequency of coalescence and detachment decrease with the increase of subcooling degree. Compared with single bubble boiling, the heat flux fluctuation of coalescence boiling is much larger. A. Coulibaly, et al. [19] measured the heat flux under a nucleating bubble with a microheater much smaller than the bubble size. Peak heat flux is dynamically correlated with bubble behavior for nucleation, coalescence, and separation. The results show that the oscillation of bubbles on the heated surface results in frequent rewetting of the heated surface, or the combination with nearby bubbles, both of which increase the surface heat transfer. This indicates that in the boiling cycle, transient heat conduction after nucleation and separation is often considered to be an important heat transfer mechanism. However, microlayer evaporation and bubble movement after coalescence are also important heat transfer mechanisms.

The researchers also studied the flow characteristics around bubbles. M. Takeyama and T. Kunugi [20] used a particle tracking visualization method to quantitatively analyze the particle movement around a single bubble, and studied the flow near the base at the early stage of bubble growth and in the process of bubble escape. The results show that only the flow parallel to the heated substrate surface exists, but not perpendicular to the substrate surface. Although the departure of bubbles causes a swirling motion, the fluids do not mix vertically. Based on these results, nucleation/departure of a single bubble has very little effect on the convection of boiling heat transfer. However, the convective heat transfer can be enhanced by the flow interaction between adjacent boiling bubbles. Presently, experiments regarding boiling bubble interaction are conducted by local laser heating [21], artificial cavity [22], and microarray heater [23]. According to the measurement results of the study, this stripping effect only occurs when the junction is less than 1 mm from the heated surface [24]. In actual boiling, this flow interacts with adjacent bubbles to form complex eddies. Therefore, various bubbles are of great significance in understanding the mechanism of boiling heat transfer enhancement.

In addition, a high-speed camera is a common means to study bubble dynamics in the boiling process during visualization research, whether directly through fluid shadow structure or transparent heating substrate [25,26]. Sarker et al. [27] focused on the relationship between surface conditions and bubble waiting time, and recorded bubble behavior on vertical heaters. The results show that the bubble waiting time for conditions of high wettability and rough surface is shorter. Narayan et al. [28] studied the defrothing characteristics of single steam bubbles under ascending substrate and undercooling conditions. The bubble case is divided into stable bubble, oscillating bubble, and oscillation leaving bubble. According to S. Ahmadi et al. [29], the study experimentally investigates the heat transfer enhancement of high-voltage, high-frequency electric field upward flow boiling. The zigzag bubble motion disrupts the thermal boundary layer at the wall, thereby enhancing the bulk flow mixing, which results in an augmented heat transfer rate. Furthermore, the acting electro-hydrodynamic forces also tend to mitigate the coalescence process and change the slug flow to a bubbly flow regime for the full extent of the test.

After many years of research, the empirical relation of heat transfer coefficient has a large error band. Most of the errors are caused by the sensitivity of nucleate boiling to the micro geometry and the wettability of the micron surface. However, it is difficult to find a way to quantify these characteristics properly. There is still disagreement about the physical mechanism of heat transfer. Existing models of nucleate boiling are no more dominant than empirical relations. Heat is transferred to the liquid in the tank by the movement of the bubbles leaving the wall, or there may be some super-heated liquid around each bubble, or turbulence in the fluid. The development of efficient heat transfer techniques by control and optimization of the turbulent thermal boundary layer and turbulence continues to be a subject of interest [30]. Boiling heat transfer is no exception.

Given the complexity of phase transition mechanisms encountered in many modern applications, there is an urgent need to greatly improve the ability of computational tools to deal with related phenomena, including important interfacial dynamics and heat transfer phenomena such as bubble growth and separation, interfacial ripples, and turbulence. Due to the influence of wall micro-structure, heat convection intensity, and heat flux density, the boiling phenomenon is stochastic, and complicated bubble behavior appears at the local heating surface. However, bubble behavior also has certain regularity. Researchers pay little attention to the bubble separation velocity and the change of bubble base. In this paper, the behavior of nucleated boiling bubbles on the vertical heat exchange tubes is analyzed, including nucleation growth, slippage, and separation.

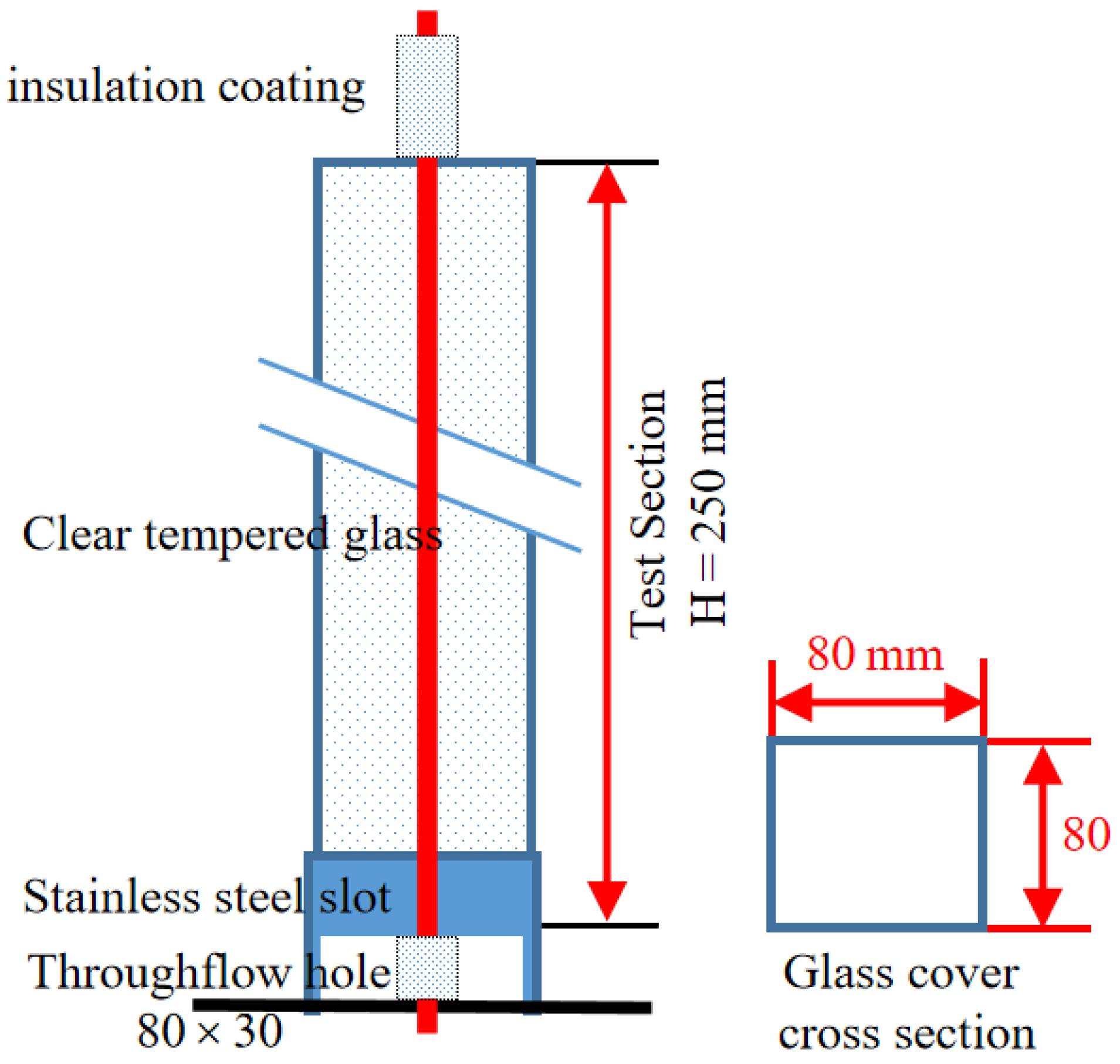
2. Experimental Facility

The experiment is conducted on the experimental platform shown in Figure 1. The experimental working mediums in the tube and the tank are conduction oil and deionized water, respectively. Heat conduction oil realizes heat circulation through an electric heating oil furnace. The outer diameter of the experimental pipe section is 20 mm and the length is 250 mm. To reduce the influence of measuring points on vapor phase distribution in the direction of height, three points of H/D = 1.25, 5, and 10 were set for the thermocouple, and two temperature measuring points were set in the circumferential direction of each height. The thermocouple is buried in the landfill. The inner diameter of the water tank is 500 mm to create a pool boiling effect. The experiment was carried out under atmospheric pressure. In addition, in order to reduce the influence of the upper and lower ends of the heat exchange tube on the experimental pipe section, the upper and lower ends of the tube were coated with thermal insulation coating. The water tank is provided with a visual toughened glass window with a diameter of 100 mm in the front and side directions in a flange direction. Temperature data collection is a temperature measurement, including the outer wall temperature of the experimental pipe section, the water bath temperature in the water tank and the inlet and outlet temperature of the thermal oil. The thermocouple was calibrated in a thermostatic water bath. The thermocouple is connected to the cable box and the data are processed by the acquisition device FLUKE NetDAQ 2640A before being imported to the private computer. The present experiment is carried out with a water temperature of 100 °C (T_∞) in the tank. The super-heat temperature ΔT is the difference between the wall temperature T_w and the water temperature T_∞ in the tank.

3. Analysis of the Bubble Characteristics in Open Space

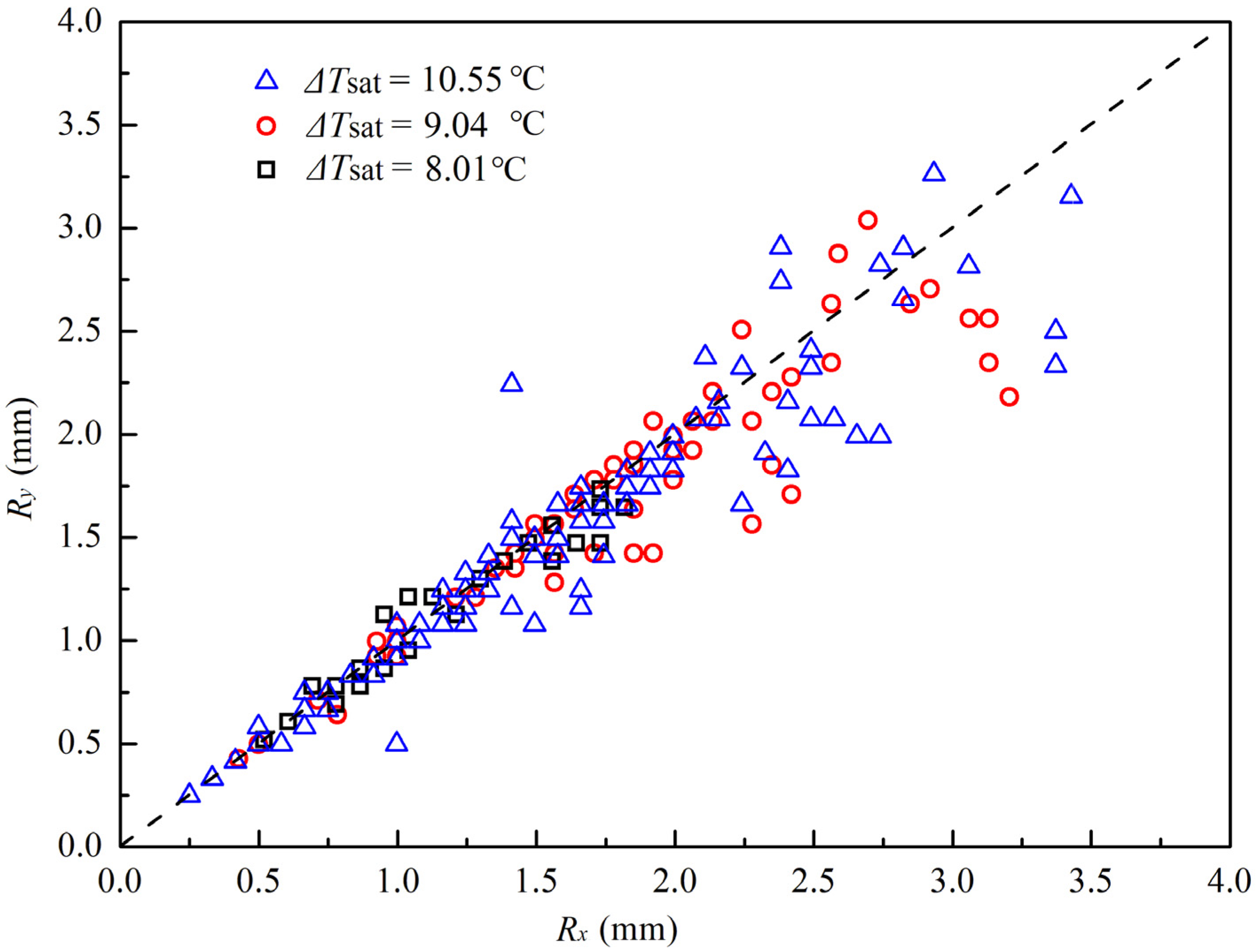
3.1. Bubble Characteristics and Bubble Definition

In the present study, the wall super-heat temperature is determined to be between 8 °C and 10 °C. The evolution of the entire bubble life cycle was clearly observed at the nucleation site. The growth of beaded bubbles can be observed along the vertical tube. Isolated and intermittent nucleation sites can be observed. The bubbles bounce and float along the wall. The bubbles are adsorbing on the tube wall and growing at the same time. The growth of the sliding bubble follows a straight trajectory on the tube wall. In addition, some bubbles are separating from the tube wall and rise in an uncertain direction in the liquid phase. The bubble size decreases in the super-cooled water. Bubble buoyancy is concentrated in the near-wall water area.

The growth and evolution process of beaded bubbles can be divided into two types (Figure 2), namely track ① and ②. Track ① includes three stages. The first stage is the independent growth stage (a) (b). In the second stage (c), (d), and (e), pairwise amalgamation occurs near the bubbles as the bubbles absorb heat. The bubble size is small, and the rising velocity of the bubble is dominated by the velocity of bulk phase in the thermal boundary layer. With the growth of bubbles, the gap between bubbles decreases, resulting in mutual absorption amalgamation. Based on the analysis of thermal-hydraulic characteristics, bubbles grow rapidly at the nucleation point. And bubbles are swept off by the liquid motion, sliding at low speed and growing rapidly. Then, the bubbles merge and enter the third stage. The spacing increases, and the size becomes larger. The rising velocity increases in the meantime. After track ①, the frequency of bubble nucleation at the nucleation point decreases. The bubbles enter the stage of independent growth and evolution, namely track ②.

Calibration is conducted with the pipe diameter (D = 20 mm). The spatial resolution of the imaging process is 0.03 mm/pixel. The error for bubble diameter is within 1 pixel. The maximum error of length is limited to 0.03 mm. The minimum time interval is 0.238 ms. For the following analysis, based on the images recorded by the high-speed camera (as shown in Figure 3), the formula for defining the bubble diameter R is as follows:

R = s(R_x + R_y)/2

R_x: The difference between horizontal coordinate

R_y: The difference between vertical coordinate

s: Size factor 0.03

Based on the definition of bubble diameter, the radial and axial dimensions (tube as a reference) of bubbles are measured under different wall super-heat temperatures. The radial versus axial dimensions of bubbles are plotted, as shown in Figure 4. The results show that bubbles are mainly spherical. Under high heat load, the radial scale is more dominant due to the effect of buoyancy convection in the near-wall water area. Because of the velocity difference between the near wall water and the far wall water, the bubbles deviating from the near wall water are more likely to be elongated in the axial direction. When the wall super-heat temperature ΔT = 8.01 °C, the bubble shape is closer to that of a sphere. The bubble interaction and wall turbulence intensity increase with the increasing of the super-heat temperature, which is not conducive to the observation of bubble behavior. Therefore, the condition of the wall super-heat temperature ΔT = 8.01 °C is selected to further analyze the bubble separation, buoyancy, and merger behaviors.

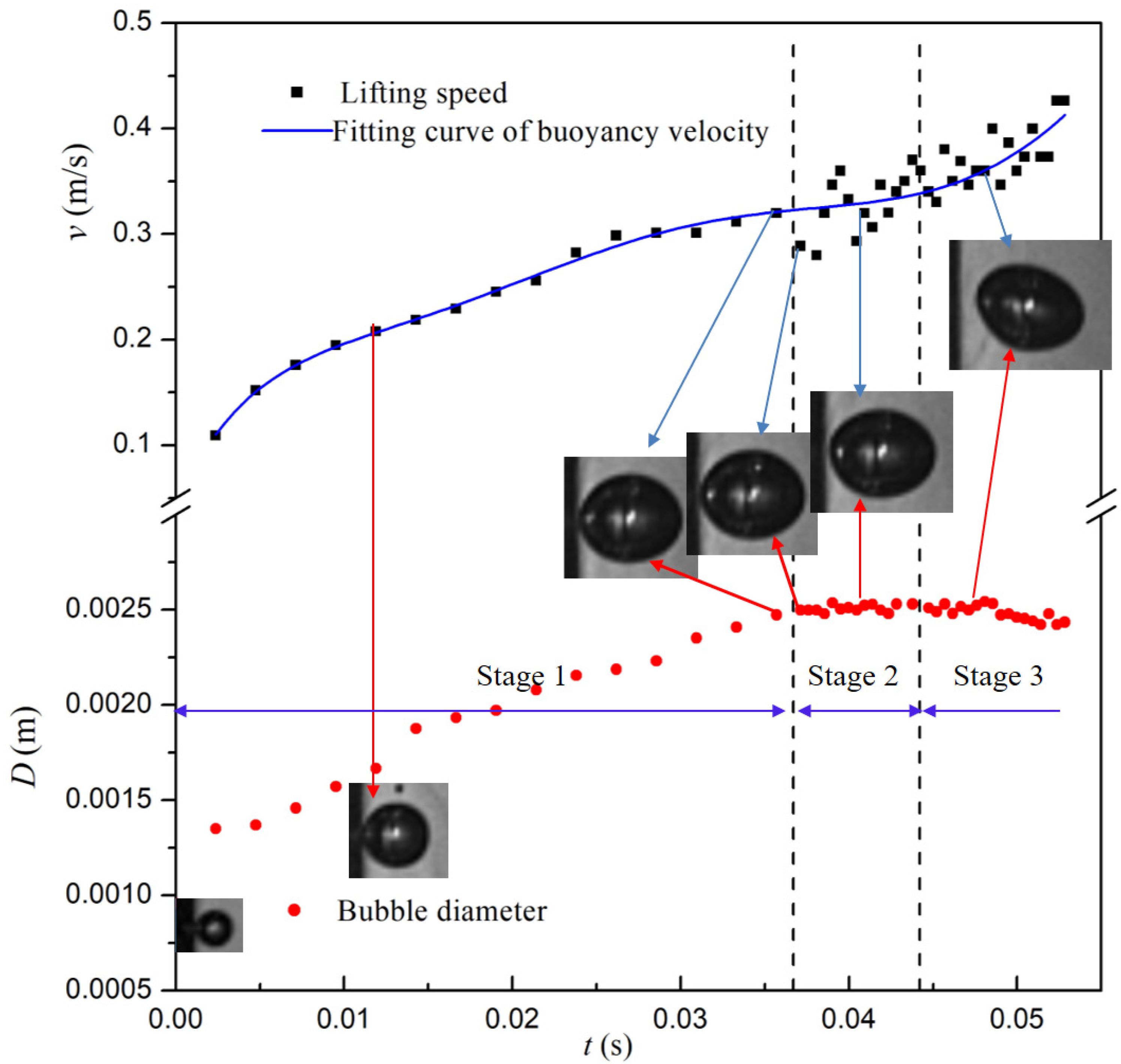
3.2. Growth Process of Single Bubble

Bubble slippage and buoyancy are the main behaviors of the dynamic evolution of a single bubble. Figure 5 shows the evolution of bubble diameter and rising velocity, to understand the bubble departure. In general, the separation of bubbles is conducive to heat transfer. According to the velocity of the bubble and the diameter at different times, the evolution of bubbles can be divided into three stages. Stage 1: Bubble departs from the nucleate point and slides on the vertical tube wall. The velocity of sliding increases with the increase of bubble diameter. Stage 2: The bubble enters the stage of escaping from the wall, and the bubble’s rising speed is relatively stable. Stage 3: After escaping from the wall, the bubble first enters the super-heat boundary layer near-wall water region. The bubble diameter has a short period of stability. When the bubble deviates further from the super-heat boundary layer and enters the super-cold water region, the bubble is condensed until it disappears from the water. Therefore, the enhancement of heat transfer can be achieved by shortening the bubble wall slip time and increasing the bubble separation speed.

Bubble departure criteria are usually derived using force balance [31,32]. The equations and the direction of the forces on the bubble have been proposed in the literature. Figure 6 shows the directions of different forces. Buoyancy F_b, unsteady resistance F_du, quasi-steady resistance F_qs, surface tension F_s, shear lift F_sL, contact pressure F_cp and hydrodynamic pressure forces F_h have been comprehensively explained by some researchers [33,34]. The force expressions of bubbles are as follows [33]:

$$\begin{gathered} F_{sx}=-1.25d_w\sigma \frac{\pi \left(\alpha -\beta \right)}{{\pi }^2-{\left(\alpha -\beta \right)}^2}\left[\sin \alpha +\sin \beta \right] \\ {F}_{sy}=-d_w\sigma \frac{\pi }{\alpha -\beta }\left[\cos \alpha -\cos \beta \right]d_w \end{gathered}$$

(1)

$$F_{du}=-{\rho }_l\pi R^2\left(\frac{3}{2}{C}_s{\dot{R}}^2+R\ddot{R}\right), C_s=1$$

(2)

$$F_b=\frac{4}{3}\pi R^3\left({\rho }_l-{\rho }_v\right)g$$

(3)

$$F_{qs}=6\pi v{\rho }_l\Delta vR\left\{\frac{2}{3}+{\left[{\left(\frac{12}{R{e}_b}\right)}^n+{0.796}^n\right]}^{-1/n}\right\}$$

(4)

$$F_{sL}=\frac{1}{2}{\rho }_l\Delta v^2\pi R^2\left\{3.877G_s^{1/2}+{\left[R{e}_b^{-2}+0.014G_s^2\right]}^{1/4}\right\}$$

(5)

$$F_h=\frac{9}{8}{\rho }_l\Delta v^2\frac{\pi d_w^2}{4}$$

(6)

$$F_{cp}=\frac{\pi d_w^2}{4}\frac{2\sigma }{5R}$$

(7)

According to the force analysis, when the sum of the forces along the flow direction is greater than zero, the bubble will be separated from the wall of the nucleation point. For the vertical surface, the main forces resulting in bubble departure are F_b, F_s, F_du, and F_qs [35]. Based on the force balance formula of bubbles, when bubbles grow from the nucleation point on the surface of the heater without separation, the sum of forces in the x and y directions must be equal to zero. When either of these equilibrium directions is disturbed, the bubble will leave the nucleation point. That is, the separation force is greater than the force that tends to keep bubbles attached to the surface.

To analyze the bubble separation speed, this paper processed the image through boundary filtering technology to determine the bubble separation state, as shown in Figure 7. d_w is defined as the contact diameter before the bubble breaks away from the wall, and s is defined as the distance which bubble breaks away from the wall. That is, the bubble separation process is defined as the bubble from the contact base diameter d_w as the reference to the contact base diameter d_w = 0. Considering the image resolution and processing errors, the d_w is set as 0.06 mm in the present study. The influence of bubble size on separation and rising velocity is analyzed at the same nucleation point.

The bubble separation velocity is defined as follows:

v’ = s/t

s is defined as the distance which bubble breaks away from the wall, t is the time for the vertical distance to be s.

The “two points” option was used to measure the dimensions of a bubble center in one image with respect to its new position in any subsequent image. The bubble lifting velocity is defined as follows:

v = S/dt

S: Distance between the two selected points, dt = [time of the second point frame] − [time of the the first point frame].

During the observation period, more bubbles grow to the maximum diameter along the wall and finally break away from the wall. As shown by data point 1 in Figure 8, bubble detachment occurs at the nucleation point. According to the literature data [31,36], as the force instability occurs first in the y direction, bubbles will escape from the heating wall rather than slip. Additionally, the diameter of the bubble base is small in the initial growth stage. The surface tension F_s is a weak force, which is the key force for maintaining the balance of forces on the bubble in the x direction. As the force in the x direction is not equal to 0 before the instability in the y direction, bubbles will slip along the heating wall corresponding to data points 2, 3, and 4 in Figure 8. At data point 2, bubble slippage rises along the wall for a short distance and then escapes. At data points 3 and 4, bubble slippage grows along the wall for a long distance until it reaches the maximum bubble size under the study condition.

Based on the empirical buoyancy formula, this is directly related to the diameter of the bubble and the velocity difference between liquid and vapor. When the vapor–liquid velocity difference is relatively constant, the buoyancy force increases with the growth of bubbles, which promotes the increase of bubble buoyancy velocity. The main macroscopic factor affecting surface tension is the contact diameter of bubbles (d_w). The contact diameter of sliding bubbles on the wall increases with the rapid growth of bubbles in the initial stage of bubble growth. For data points 1 and 2, the early detachment from the wall is mainly caused by turbulence near the wall. The Gr number derived from the momentum differential equation is used to determine the change in the heat transfer law. The natural convection outside the vertical tube changes to turbulence in the range of 10⁹ < Gr < 10¹⁰ [37]. The wall super-heat temperature of the current study condition is in the range of 8~10 °C, and the flow near the wall has completely entered the transition region of heat transfer law, according to the Gr criterion. The convection in the near wall boundary layer is turbulent. The fluctuation of wall super-heat temperature results in the change of turbulence strength in the thermal boundary layer. Turbulence overcomes the main binding surface tension, and the bubble dissociates the wall. However, as the bubble grows, the bubble base diameter increases, and the near-wall disturbance is not enough to overcome the binding force and change the upward trajectory of the subject. Then, the bubble will slip along the wall and grow. With the increase of bubble size, it is necessary to overcome the large upward buoyancy force when the bubble is free from the wall. Consequently, the separation velocity of the bubble from the wall will decrease.

With the increase of bubble size, bubble rising velocity increases, and the separation speed decreases. Given the smaller the scale of the bubbles, it becomes easier for themn to escape from the wall. For bubbles with a larger diameter, buoyancy in the y direction is dominant, and the bubble separation is delayed from the tube wall. Therefore, promoting the force imbalance in the x direction of the bubble is conducive to the early bubble separation. While a bubble is not fully grown, the x direction force on the bubble is more prone to imbalance.

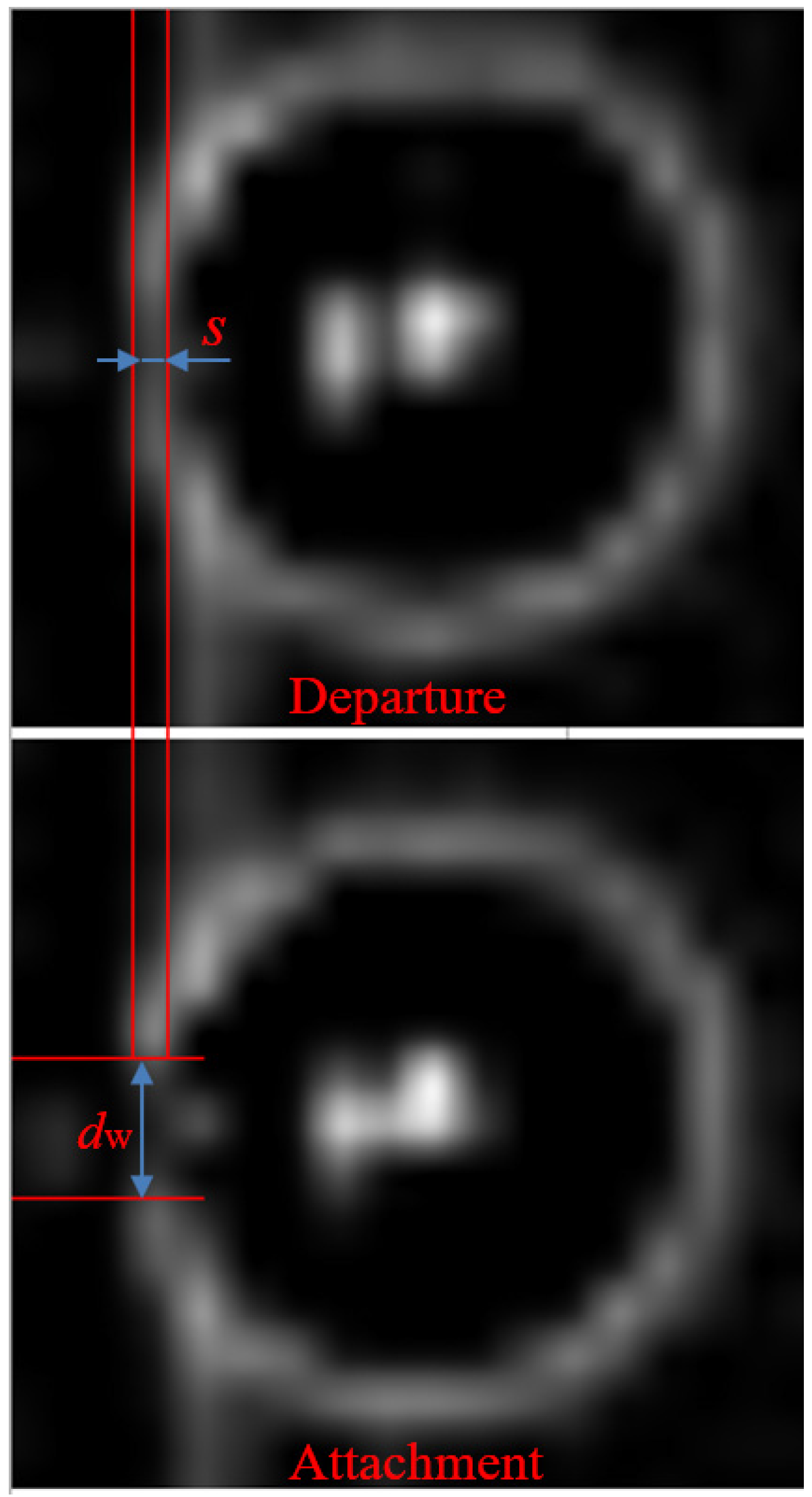
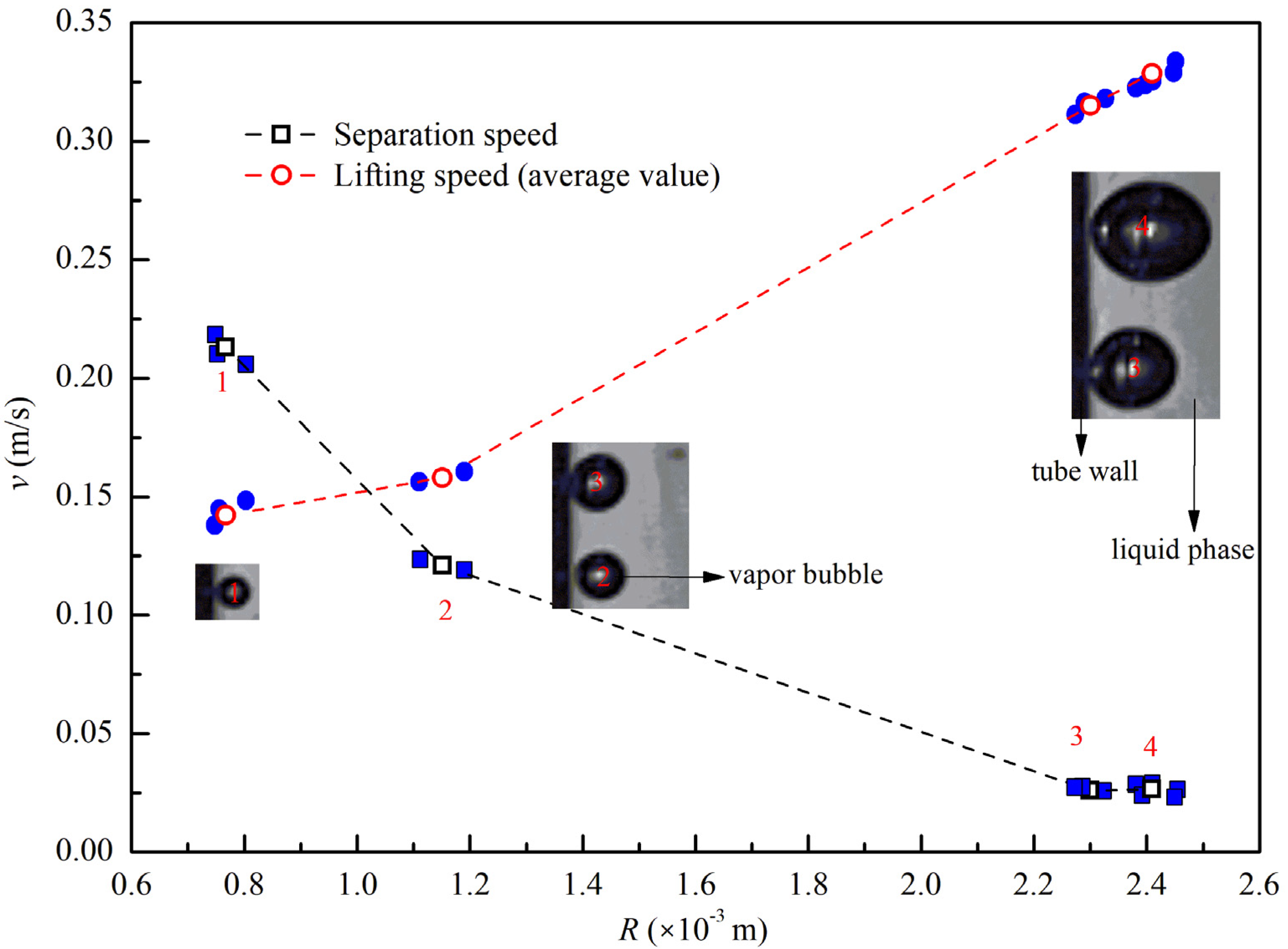
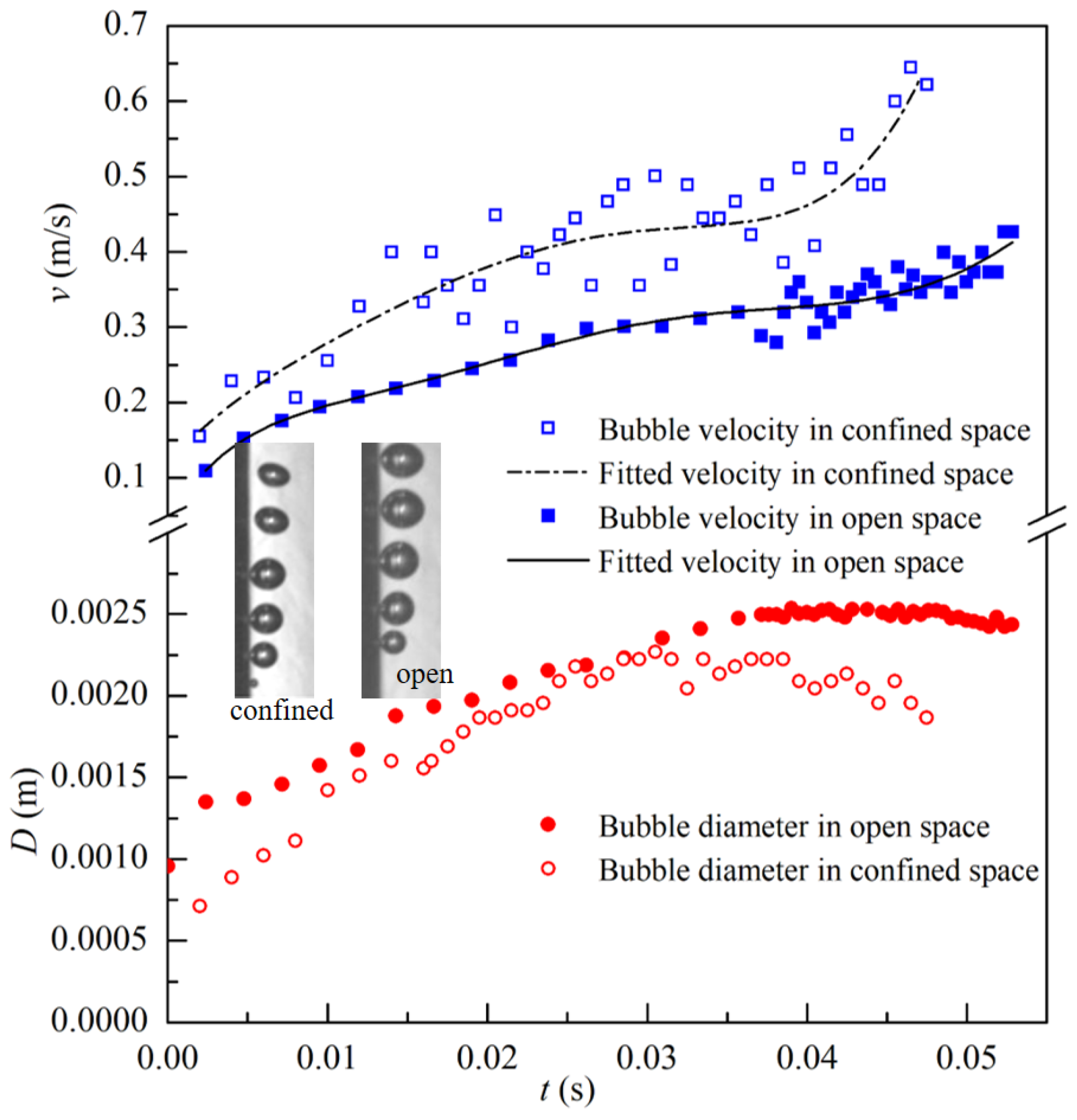
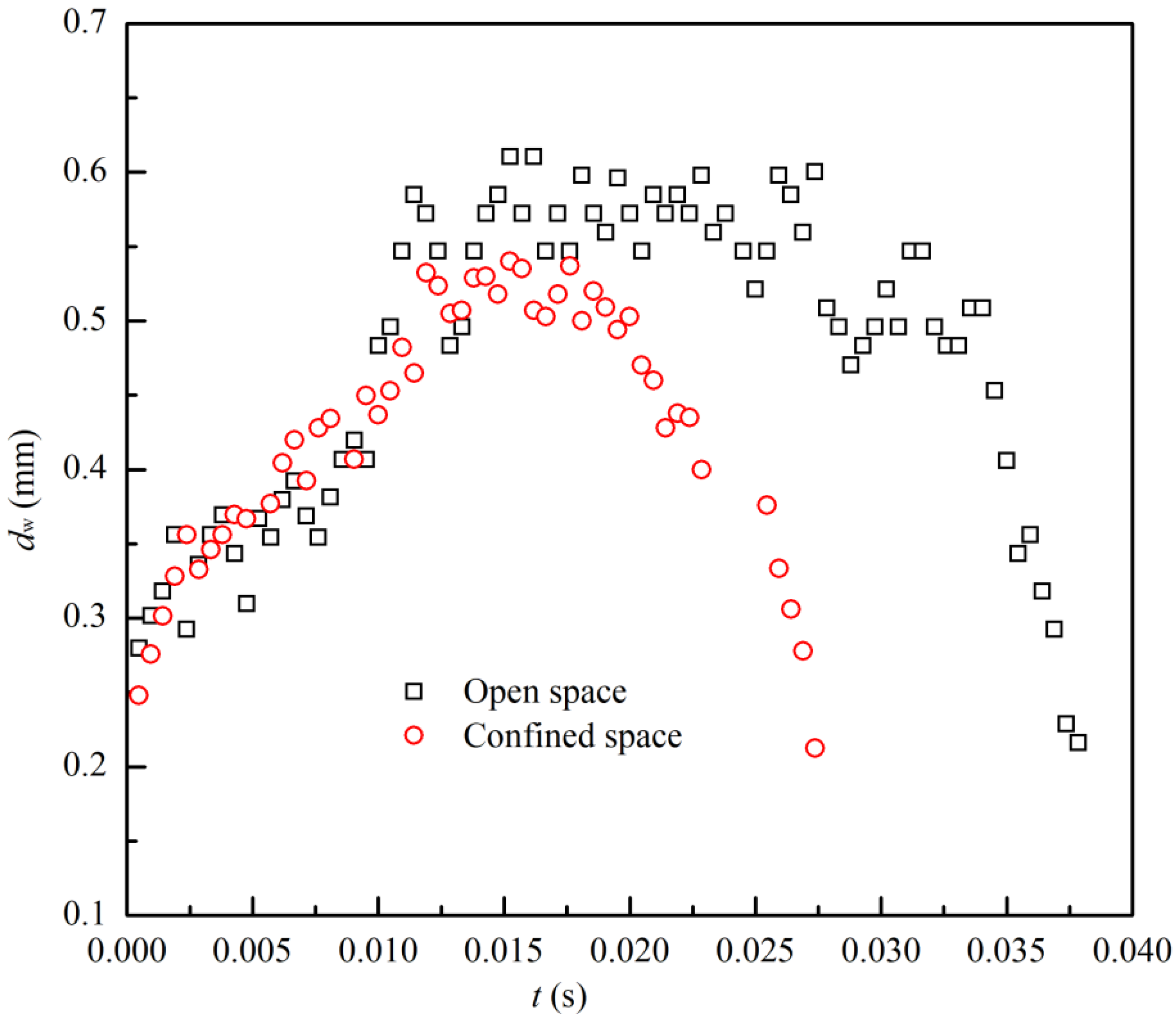
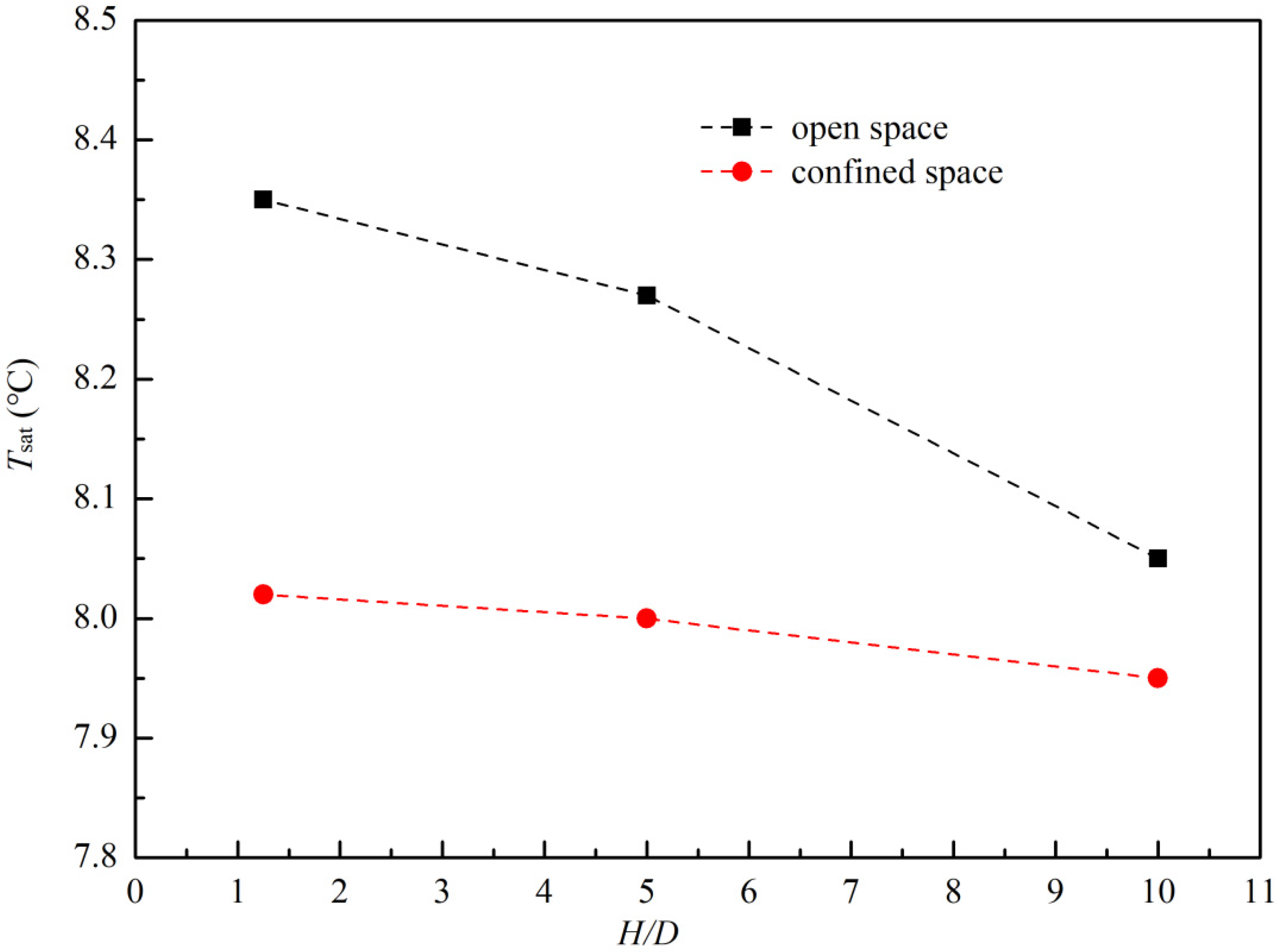
4. Analysis of Bubble in Confined Space

Increasing the bubble separation and rising speed is beneficial to heat transfer. In order to improve the separation speed and rising speed of bubbles on the heating tube, a 4D × 4D square glass space is set outside the vertical heat exchange tube, as shown in Figure 9. The glass cover is arranged on the steel flow frame, and the fluid inside and outside the glass cover can flow smoothly. The height of the glass cover is the same as that of the effective test section.

The preliminary study [38] shows that there is stratified convection in the large pool under the open space, showing progressive and conductive circulation. The restricted space limits the transverse convection between the inside and outside the glass enclosure. Circulatory convection forms between the top and bottom of the tank, thereby breaking the thermal stratification. Moreover, the velocity near the wall increases. Figure 10 depicts the separation velocity and buoyancy velocity of bubbles in confined and open space under the same inlet temperature of the heat exchange tube. The results show that the rising velocity and escape velocity increase obviously in the restricted space, and the bubble escape diameter decreases. The separated bubble dissolves rapidly in the liquid phase. That is, it is condensed. The longitudinal convection in the confined space is enhanced. The adhesion rate of bubbles on the wall is relatively low. In the open space, the amount of time that bubbles slide along the wall is longer due to transverse convection. In addition, the bubbles can easily reattach.

Figure 11 depicts the change of bubble base diameter in open space and confined space. The evolution of bubble base diameter is consistent with bubble growth and wall detachment. Compared to open space, the maximum bubble base diameter decreases in restricted space (as shown in Figure 11). In the restricted space, the passive convection effect is formed, and the single-phase and wall boiling convection enhance the restricted space convection. The reinforcement of passive convection reduces the diameter of the bubble base and accelerates the bubble wall separation.

In addition, as shown in Figure 12, there are four behavior trajectories of bubbles after they are detached: (1) The dotted green line; a bubble leaves the wall, and enters the liquid phase to condense. The bubble reattaches to the wall and grows. Furthermore, the bubble exhibits secondary detachment and condensation, and secondary attachment and growth. (2) The blue dotted line; after the vapor amalgamation between the escaped bubble and the attached bubble, the amalgamated bubble adheres to the tube wall and slips with growth. (3) The orange dotted line; the separated bubble merges with another bubble during condensation. (4) The red dotted line; after escaping from the wall and entering the super-cooled liquid region, the bubbles are condensed and disappear. The strengthening convective effect promotes bubble separation, bubble merger, and bubble buoyancy. Figure 13 shows the changes of super-heat at monitoring points at different heights on the outer wall of the heat exchange tube. Compared with confined space, the change of wall super-heat temperature is more obvious in open space. The coalescence of bubbles formed in the upper part of the heat exchange tube strengthens the convection on the upper wall. Therefore, heat transfer increases in the upper part of the open space. In the confined space, the frequency of bubble shedding is high. The duration of bubble slippage along the wall is short. And the merging behavior between bubbles is reduced. Bubbles from the wall enter the super-cooled water to condense and release heat, and the temperature difference is small between the upper and lower parts of the heat transfer tubes.

5. Conclusions

In this paper, experimental work is carried out to study the characteristics of the pool boiling on the vertical tube at atmospheric pressure. The growth, slippage, and coalescence characteristics of bubbles in the super-heat range of 8~9 °C are investigated. The research results are summarized, as follows:

• In the study of nucleate boiling outside the vertical heat exchange tube, it is found that the long growth period of a bubble along the vertical heat exchange surface is not conducive to the enhancement of wall heat transfer. Shortening the slip distance on the wall surface and increasing the separation speed of bubbles can effectively enhance the heat transfer.
• Based on the empirical formula of force on the bubble, the experimental results show that the increases of bubble base and bubble diameter are not conducive to bubble wall separation. The setting of confined space increases the flow rate in the near wall region, and the bubble separation diameter on the wall decreases at a higher liquid flow rate. The gliding mechanism and force analysis of bubbles show that the bubbles slip along the wall due to the lack of driving force in the Y direction from the wall into the liquid water. The bubble shape changes during the sliding process and the bubbles are driven away from the wall by the inertial proliferation of liquid flow under the bubble base.
• Under the condition of low velocity flow near the wall, the force on the flow direction breaks more easily with the growth of bubbles. The bubbles will slide along the heating wall after leaving the nucleation point. When the flow near the wall is enhanced, it will accelerate the force imbalance in the y direction (vertical flow direction) and cause the bubble to break away from the wall.