Heat Transfer in 3D Laguerre–Voronoi Open-Cell Foams under Pulsating Flow
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Voronoi Foam Generation
2.2. Governing Equations and Boundary Conditions
2.3. Detail of Solution Methodology
2.4. Grid Independency Test and Verification of Mathematical Model
3. Results and Discussion
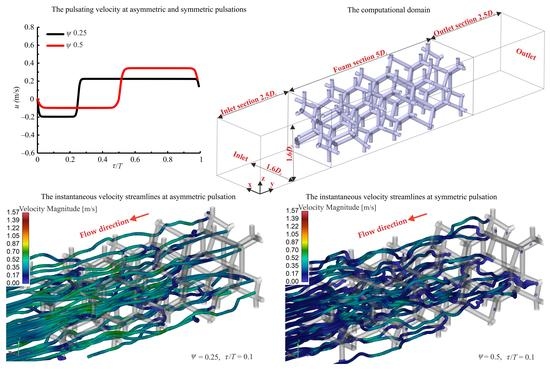
3.1. The Velocity Streamlines and Contours Plots
3.2. The Effect of Pulsations on the Nusselt Number Ratio
3.3. The Effect of Pulsation on the Friction Factor Ratio
3.4. The Effect of Pulsations on the Thermal Performance Factor
3.5. The Empirical Correlation for Predicting the Heat Transfer Enhancement, Friction Factor Ratio and TPF
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Dimensional amplitude of pulsation [m] |
| A/Ds | Dimensionless relative amplitude of pulsation [–] |
| asv | Surface area per unit of volume [m–2 m–3] |
| Ds | Strut diameter [m] |
| f | Frequency of pulsation [Hz] |
| h | Interstitial heat transfer coefficient [W m–2 K–1] |
| k | Thermal conductivity [W m−1 K−1] |
| Nu | Nusselt number based on strut diameter [–] |
| Pr | Prandtl number |
| PPI | Pore number per linear inch (pores in–1) |
| q | Heat flux [W m−2] |
| Re | Reynolds numbers based on strut diameter [–] |
| St | Strouhal number based on strut diameter [–] |
| tair | Mean air temperature [K] |
| tw | Mean wall temperature [K] |
| u | Inlet velocity [m s−1] |
| ymax/Ds | Maximum mesh size related to the cell diameter [–] |
| T | Period of the pulsation [s] |
| T1 | First half-period of the pulsation [s] |
| T2 | Second half-period of the pulsation [s] |
| Greek symbols | |
| μ | Dynamic viscosity [Pa s] |
| ρ | Density [kg m3] |
| ψ | Duty cycle [–] |
| ε | Porosity [–] |
| ξ | Friction factor [–] |
| ΔP | Pressure drop [Pa] |
| τ | Time [s] |
| Subscripts | |
| δ | Enhancement factor |
| cor | Correlation |
| num | Numerical |
| p | Pulsating flow |
| st | Steady flow |
| Abbreviations | |
| LVT | Laguerre–Voronoi tessellation |
| TPF | Thermal Performance Factor |
| VF | Voronoi foam |
| Notations | |
| 〈〉 | Averaged value over one period of the pulsation |
References
- Hmad, A.A.; Dukhan, N. Cooling Design for PEM Fuel-Cell Stacks Employing Air and Metal Foam: Simulation and Experiment. Energies 2021, 14, 2687. [Google Scholar] [CrossRef]
- De Schampheleire, S.; De Jaeger, P.; Huisseune, H.; Ameel, B.; T’Joen, C.; De Kerpel, K.; De Paepe, M. Thermal Hydraulic Performance of 10 PPI Aluminium Foam as Alternative for Louvered Fins in an HVAC Heat Exchanger. Appl. Therm. Eng. 2013, 51, 371–382. [Google Scholar] [CrossRef]
- Golosnoy, I.O.; Cockburn, A. Metal Fiber Network Materials for Compact Heat Exchangers. In Comprehensive Composite Materials II; Elsevier: Amsterdam, The Netherlands, 2018; pp. 397–424. ISBN 978-0-08-100534-7. [Google Scholar]
- Dyga, R.; Brol, S. Pressure Drops in Two-Phase Gas–Liquid Flow through Channels Filled with Open-Cell Metal Foams. Energies 2021, 14, 2419. [Google Scholar] [CrossRef]
- Simescu-Lazar, F.; Chaieb, T.; Pallier, S.; Veyre, L.; Philippe, R.; Meille, V. Direct Coating of Carbon-Supported Catalysts on Monoliths and Foams—Singular Behaviour of Pd/MWCNT. Appl. Catal. A Gen. 2015, 508, 45–51. [Google Scholar] [CrossRef] [Green Version]
- Myung, C.-L.; Kim, J.; Jang, W.; Jin, D.; Park, S.; Lee, J. Nanoparticle Filtration Characteristics of Advanced Metal Foam Media for a Spark Ignition Direct Injection Engine in Steady Engine Operating Conditions and Vehicle Test Modes. Energies 2015, 8, 1865–1881. [Google Scholar] [CrossRef] [Green Version]
- Trilok, G.; Srinivas, K.E.S.; Harikrishnan, D.; Gnanasekaran, N.; Mobedi, M. Correlations and Numerical Modeling of Stacked Woven Wire-Mesh Porous Media for Heat Exchange Applications. Energies 2022, 15, 2371. [Google Scholar] [CrossRef]
- Dukhan, N. Equivalent Parallel Strands Modeling of Highly-Porous Media for Two-Dimensional Heat Transfer: Application to Metal Foam. Energies 2021, 14, 6308. [Google Scholar] [CrossRef]
- Wang, H.; Guo, L.; Chen, K. Theoretical and Experimental Advances on Heat Transfer and Flow Characteristics of Metal Foams. Sci. China Technol. Sci. 2020, 63, 705–718. [Google Scholar] [CrossRef]
- Tikadar, A.; Kumar, S. Investigation of Thermal-Hydraulic Performance of Metal-Foam Heat Sink Using Machine Learning Approach. Int. J. Heat Mass Transf. 2022, 199, 123438. [Google Scholar] [CrossRef]
- Durmus, F.Ç.; Maiorano, L.P.; Molina, J.M. Open-Cell Aluminum Foams with Bimodal Pore Size Distributions for Emerging Thermal Management Applications. Int. J. Heat Mass Transf. 2022, 191, 122852. [Google Scholar] [CrossRef]
- Sun, M. Forced Convection Heat Transfer: A Comparison between Open-Cell Metal Foams and Additive Manufactured Kelvin Cells. Int. Commun. Heat Mass Transf. 2022, 9, 106407. [Google Scholar] [CrossRef]
- Chen, K.; Wang, X.; Chen, P.; Wen, L. Numerical Simulation Study on Heat Transfer Enhancement of a Heat Exchanger Wrapped with Metal Foam. Energy Rep. 2022, 8, 103–110. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Bahiraei, M.; Torabi, A.; Valadkhani, M. A Critical Review on Pulsating Flow in Conventional Fluids and Nanofluids: Thermo-Hydraulic Characteristics. Int. Commun. Heat Mass Transf. 2021, 120, 104859. [Google Scholar] [CrossRef]
- Ye, Q.; Zhang, Y.; Wei, J. A Comprehensive Review of Pulsating Flow on Heat Transfer Enhancement. Appl. Therm. Eng. 2021, 196, 117275. [Google Scholar] [CrossRef]
- Ni, M.; Peng, H.; Sultan, U.; Luo, K.; Xiao, G. A Quantitative Method to Describe the Flow Characteristics of an Oscillating Flow Including Porous Media. Int. J. Heat Mass Transf. 2018, 119, 860–866. [Google Scholar] [CrossRef]
- Leong, K.C.; Jin, L.W. Characteristics of Oscillating Flow through a Channel Filled with Open-Cell Metal Foam. Int. J. Heat Fluid Flow 2006, 27, 144–153. [Google Scholar] [CrossRef]
- Leong, K.C.; Jin, L.W. An Experimental Study of Heat Transfer in Oscillating Flow through a Channel Filled with an Aluminum Foam. Int. J. Heat Mass Transf. 2005, 48, 243–253. [Google Scholar] [CrossRef]
- Leong, K.C.; Jin, L.W. Effect of Oscillatory Frequency on Heat Transfer in Metal Foam Heat Sinks of Various Pore Densities. Int. J. Heat Mass Transf. 2006, 49, 671–681. [Google Scholar] [CrossRef]
- Kahaleras, M.S.; Layes, G.; Lanzetta, F.; Djetel-Gothe, S. Experimental Thermofluidic Characterization of Different Metallic Regenerators Crossed by Alternating Air Flow. Appl. Sci. 2022, 12, 4264. [Google Scholar] [CrossRef]
- Dellali, E.; Bégot, S.; Lanzetta, F.; Gavignet, E.; Rauch, J.Y. Pressure Drop Analysis of Oscillating Flows through a Miniature Porous Regenerator under Isothermal and Nonisothermal Conditions. Exp. Therm. Fluid Sci. 2019, 103, 394–405. [Google Scholar] [CrossRef]
- Bayomy, A.M.; Saghir, M.Z. Heat Transfer Characteristics of Aluminum Metal Foam Subjected to a Pulsating/Steady Water Flow: Experimental and Numerical Approach. Int. J. Heat Mass Transf. 2016, 97, 318–336. [Google Scholar] [CrossRef]
- Bağcı, Ö.; Dukhan, N. Impact of Pore Density on Oscillating Liquid Flow in Metal Foam. Exp. Therm. Fluid Sci. 2018, 97, 246–253. [Google Scholar] [CrossRef]
- Bağcı, Ö.; Dukhan, N.; Özdemir, M. Characteristics of Oscillating Liquid Flow in Foam-like Highly-Porous Media: An Experimental Study. Exp. Therm. Fluid Sci. 2015, 60, 96–105. [Google Scholar] [CrossRef]
- Bağcı, Ö.; Arbak, A.; De Paepe, M.; Dukhan, N. Investigation of Low-Frequency-Oscillating Water Flow in Metal Foam with 10 Pores per Inch. Heat Mass Transf. 2018, 54, 2343–2349. [Google Scholar] [CrossRef]
- Kim, S.-M.; Ghiaasiaan, S.M. Numerical Modeling of Laminar Pulsating Flow in Porous Media. J. Fluids Eng. 2009, 131, 41203. [Google Scholar] [CrossRef]
- Dai, Q.; Yang, L. LBM Numerical Study on Oscillating Flow and Heat Transfer in Porous Media. Appl. Therm. Eng. 2013, 54, 16–25. [Google Scholar] [CrossRef]
- Chen, S.; Huang, Q.; Liang, M.; Chen, H.; Chen, L.; Hou, Y. Numerical Study on the Heat Transfer Characteristics of Oscillating Flow in Cryogenic Regenerators. Cryogenics 2018, 96, 99–107. [Google Scholar] [CrossRef]
- Ghafarian, M.; Mohebbi-Kalhori, D.; Sadegi, J. Analysis of Heat Transfer in Oscillating Flow through a Channel Filled with Metal Foam Using Computational Fluid Dynamics. Int. J. Therm. Sci. 2013, 66, 42–50. [Google Scholar] [CrossRef]
- Habib, R.; Yadollahi, B.; Karimi, N.; Doranegard, M.H. On the Unsteady Forced Convection in Porous Media Subject to Inlet Flow Disturbances—A Pore-Scale Analysis. Int. Commun. Heat Mass Transf. 2020, 116, 104639. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D Representative Volume Elements for Heterogeneous Materials: A Review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Storm, J.; Abendroth, M.; Emmel, M.; Liedke, T.; Ballaschk, U.; Voigt, C.; Sieber, T.; Kuna, M. Geometrical Modelling of Foam Structures Using Implicit Functions. Int. J. Solids Struct. 2013, 50, 548–555. [Google Scholar] [CrossRef] [Green Version]
- Abishek, S.; King, A.J.C.; Mead-Hunter, R.; Golkarfard, V.; Heikamp, W.; Mullins, B.J. Generation and Validation of Virtual Nonwoven, Foam and Knitted Filter (Separator/Coalescer) Geometries for CFD Simulations. Sep. Purif. Technol. 2017, 188, 493–507. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Anisotropic Convective Heat Transfer in Open-Cell Metal Foams: Assessment and Correlations. Int. J. Heat Mass Transf. 2020, 154, 119682. [Google Scholar] [CrossRef]
- Diani, A.; Bodla, K.K.; Rossetto, L.; Garimella, S.V. Numerical Investigation of Pressure Drop and Heat Transfer through Reconstructed Metal Foams and Comparison against Experiments. Int. J. Heat Mass Transf. 2015, 88, 508–515. [Google Scholar] [CrossRef] [Green Version]
- Solovev, S.A.; Soloveva, O.V.; Akhmetova, I.G.; Vankov, Y.V.; Paluku, D.L. Numerical Simulation of Heat and Mass Transfer in an Open-Cell Foam Catalyst on Example of the Acetylene Hydrogenation Reaction. ChemEngineering 2022, 6, 11. [Google Scholar] [CrossRef]
- Park, S.-H.; Jeong, J.H. Analytical Fin Efficiency Model for Open-Cell Porous Metal Fins Based on Kelvin Cell Assumption. Int. J. Heat Mass Transf. 2022, 196, 123283. [Google Scholar] [CrossRef]
- Sinn, C.; Wentrup, J.; Pesch, G.R.; Thöming, J.; Kiewidt, L. Structure-Heat Transport Analysis of Periodic Open-Cell Foams to Be Used as Catalyst Carriers. Chem. Eng. Res. Des. 2021, 166, 209–219. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D.; Ventikos, Y. Simulations of Flow through Open Cell Metal Foams Using an Idealized Periodic Cell Structure. Int. J. Heat Fluid Flow 2003, 24, 825–834. [Google Scholar] [CrossRef]
- Rambabu, S.; Parthasarathy, P.; Ratna Kishore, V. A Numerical Study of Forced Convection in Ideal and Randomized Reticulated Porous Structures and a Proposal for a New Correlation. Int. J. Heat Mass Transf. 2022, 184, 122292. [Google Scholar] [CrossRef]
- Moon, C.; Kim, H.D.; Kim, K.C. Kelvin-Cell-Based Metal Foam Heat Exchanger with Elliptical Struts for Low Energy Consumption. Appl. Therm. Eng. 2018, 144, 540–550. [Google Scholar] [CrossRef]
- Suleiman, A.S.; Dukhan, N. Long-Domain Simulation of Flow in Open-Cell Mesoporous Metal Foam and Direct Comparison to Experiment. Microporous Mesoporous Mater. 2014, 196, 104–114. [Google Scholar] [CrossRef]
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. Direct Simulation of Transport in Open-Cell Metal Foam. J. Heat Transf. 2006, 128, 793–799. [Google Scholar] [CrossRef]
- Krishnan, S.; Garimella, S.V.; Murthy, J.Y. Simulation of Thermal Transport in Open-Cell Metal Foams: Effect of Periodic Unit-Cell Structure. J. Heat Transf. 2008, 130, 24503. [Google Scholar] [CrossRef] [Green Version]
- Lacroix, M.; Nguyen, P.; Schweich, D.; Pham Huu, C.; Savin-Poncet, S.; Edouard, D. Pressure Drop Measurements and Modeling on SiC Foams. Chem. Eng. Sci. 2007, 62, 3259–3267. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Modeling Structures of Open Cell Foams. Comput. Mater. Sci. 2017, 131, 160–169. [Google Scholar] [CrossRef] [Green Version]
- Nie, Z.; Lin, Y.; Tong, Q. Numerical Investigation of Pressure Drop and Heat Transfer through Open Cell Foams with 3D Laguerre-Voronoi Model. Int. J. Heat Mass Transf. 2017, 113, 819–839. [Google Scholar] [CrossRef]
- Das, S.; Sneijders, S.; Deen, N.G.; Kuipers, J.A.M. Drag and Heat Transfer Closures for Realistic Numerically Generated Random Open-Cell Solid Foams Using an Immersed Boundary Method. Chem. Eng. Sci. 2018, 183, 260–274. [Google Scholar] [CrossRef]
- Haibullina, A.; Khairullin, A.; Balzamov, D.; Ilyin, V.; Bronskaya, V.; Khairullina, L. Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow. Energies 2022, 15, 5571. [Google Scholar] [CrossRef]
- Sailor, D.J.; Rohli, D.J.; Fu, Q. Effect of Variable Duty Cycle Flow Pulsations on Heat Transfer Enhancement for an Impinging Air Jet. Int. J. Heat Fluid Flow 1999, 20, 574–580. [Google Scholar] [CrossRef]
- Ilyin, V.K.; Sabitov, L.S.; Haibullina, A.I.; Hayrullin, A.R. External Heat Transfer in Corridor and Staggered Tube Bundles of Different Configuration under the Application of Low-Frequency Pulsations. IOP Conf. Ser. Mater. Sci. Eng. 2017, 240, 12027. [Google Scholar] [CrossRef]
- Hayrullin, A.; Haibullina, A.; Sinyavin, A. Heat Transport Phenomena in Voronoi Foam Due to Pulsating Flow. Transp. Res. Procedia 2022, 63, 1236–1243. [Google Scholar] [CrossRef]
- Syamlal, M.; Rogers, W.; O‘Brien, T.J. MFIX Documentation Theory Guide. No. DOE/METC-94/1004; USDOE Morgantown Energy Technology Center: Morgantown, WV, USA, 1993; p. 48. [Google Scholar]
- Rycroft, C.H. VORO++: A Three-Dimensional Voronoi Cell Library in C++. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haibullina, A.I.; Sabitov, L.S.; Hayrullin, A.R.; Ilyin, V.K. Energy Efficiency of Pulsating Flows at Heat-Transfer Enhancement in a Shell-and-Tube Water Oil Cooler. IOP Conf. Ser. Mater. Sci. Eng. 2018, 412, 12026. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Diani, A.; Rossetto, L. Air Forced Convection through Metal Foams: Experimental Results and Modeling. Int. J. Heat Mass Transf. 2013, 62, 112–123. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced Convection in High Porosity Metal Foams. J. Heat Transf. 2000, 122, 557–565. [Google Scholar] [CrossRef]
- Mulcahey, T.I.; Pathak, M.G.; Ghiaasiaan, S.M. The Effect of Flow Pulsation on Drag and Heat Transfer in an Array of Heated Square Cylinders. Int. J. Therm. Sci. 2013, 64, 105–120. [Google Scholar] [CrossRef]
- Webb, R.L. Performance Evaluation Criteria for Use of Enhanced Heat Transfer Surfaces in Heat Exchanger Design. Int. J. Heat Mass Transf. 1981, 24, 715–726. [Google Scholar] [CrossRef]
- Haibullina, A.I.; Ilyin, V.K.; Sabitov, L.S.; Zinnatullin, N.H.; Hayrullin, A.R.; Dolgova, A.N. Thermal and Hydraulic Efficiency of the Staggered Tube Bundle in Pulsating Flow. IOP Conf. Ser. Mater. Sci. Eng. 2018, 412, 12027. [Google Scholar] [CrossRef]






















| Tested VF | PPI [in–1] | ε [–] | Ds [mm] | Dc [mm] | asv [m2 m−3] |
|---|---|---|---|---|---|
| VF-0.743 | 2 | 0.743 | 6.5 | 25.4 | 145 |
| VF-0.864 | 2 | 0.864 | 4.5 | 25.4 | 115 |
| VF-0.954 | 2 | 0.954 | 2.5 | 25.4 | 72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khairullin, A.; Haibullina, A.; Sinyavin, A.; Balzamov, D.; Ilyin, V.; Khairullina, L.; Bronskaya, V. Heat Transfer in 3D Laguerre–Voronoi Open-Cell Foams under Pulsating Flow. Energies 2022, 15, 8660. https://doi.org/10.3390/en15228660
Khairullin A, Haibullina A, Sinyavin A, Balzamov D, Ilyin V, Khairullina L, Bronskaya V. Heat Transfer in 3D Laguerre–Voronoi Open-Cell Foams under Pulsating Flow. Energies. 2022; 15(22):8660. https://doi.org/10.3390/en15228660
Chicago/Turabian StyleKhairullin, Aidar, Aigul Haibullina, Alex Sinyavin, Denis Balzamov, Vladimir Ilyin, Liliya Khairullina, and Veronika Bronskaya. 2022. "Heat Transfer in 3D Laguerre–Voronoi Open-Cell Foams under Pulsating Flow" Energies 15, no. 22: 8660. https://doi.org/10.3390/en15228660