Model-Based Investigations of Porous Si-Based Anodes for Lithium-Ion Batteries with Effects of Volume Changes
Abstract
:1. Introduction
2. Model Development
2.1. Real-Time Porosity Model
2.2. Electrode Performance
3. Results and Discussion
3.1. Validation of the Real-Time Porosity Model
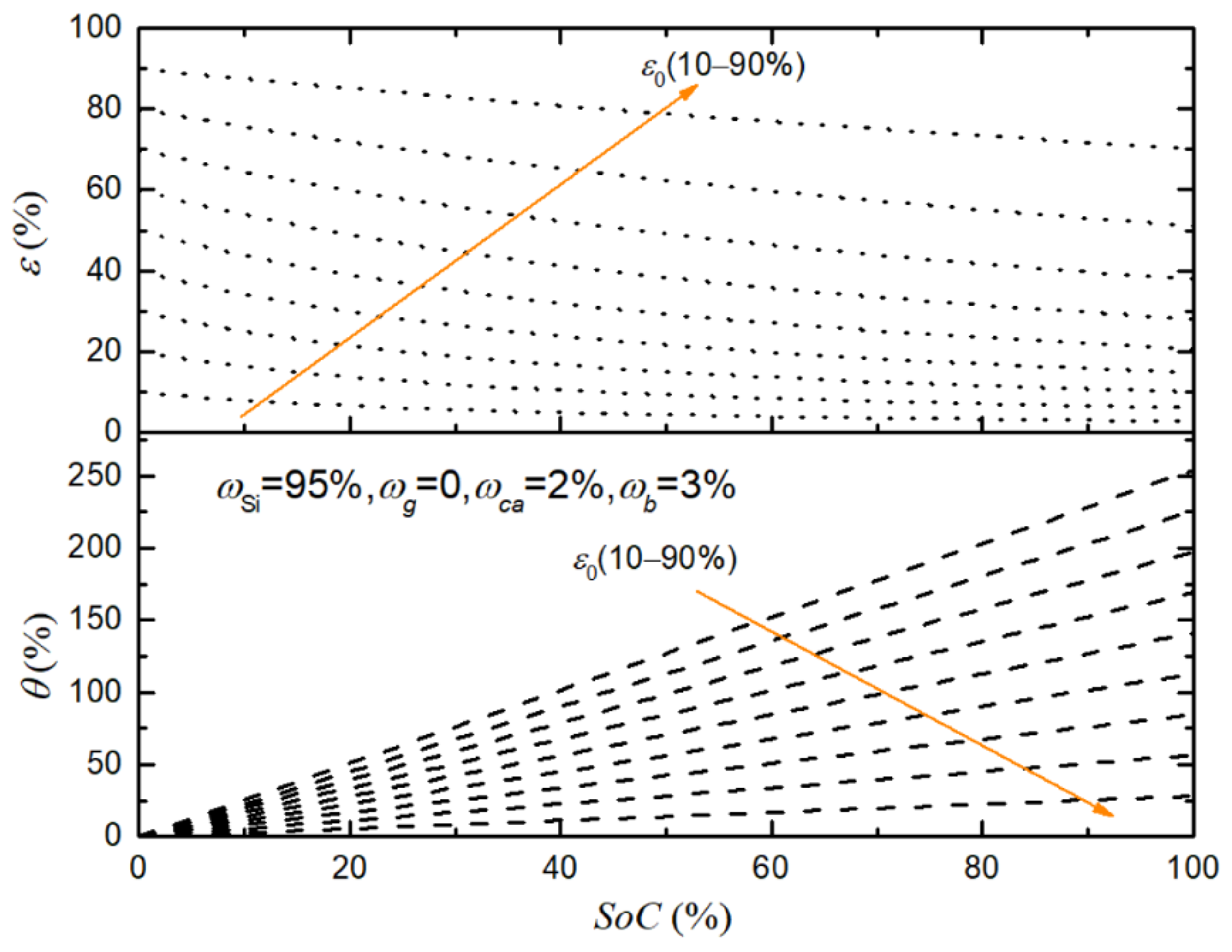
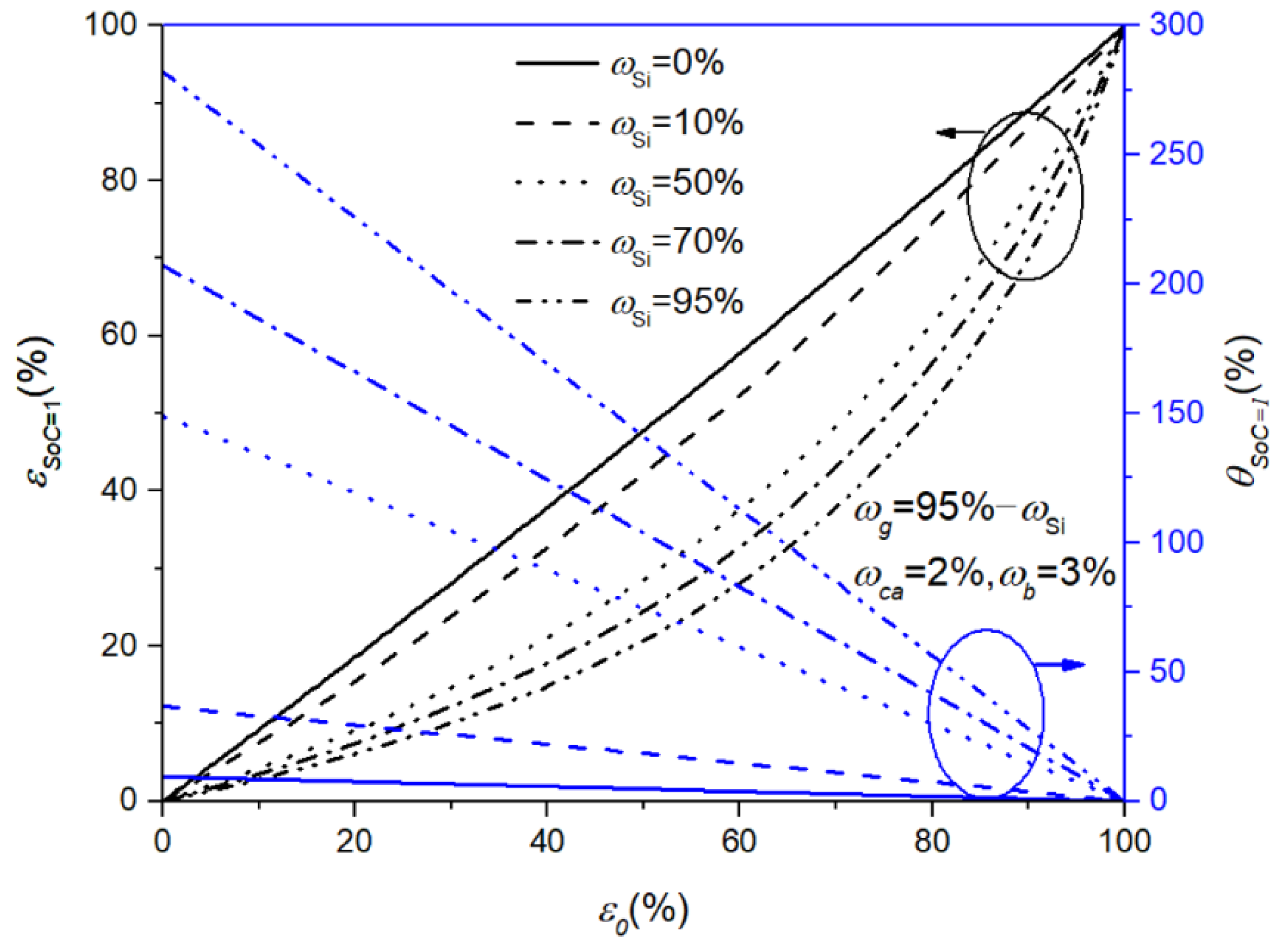
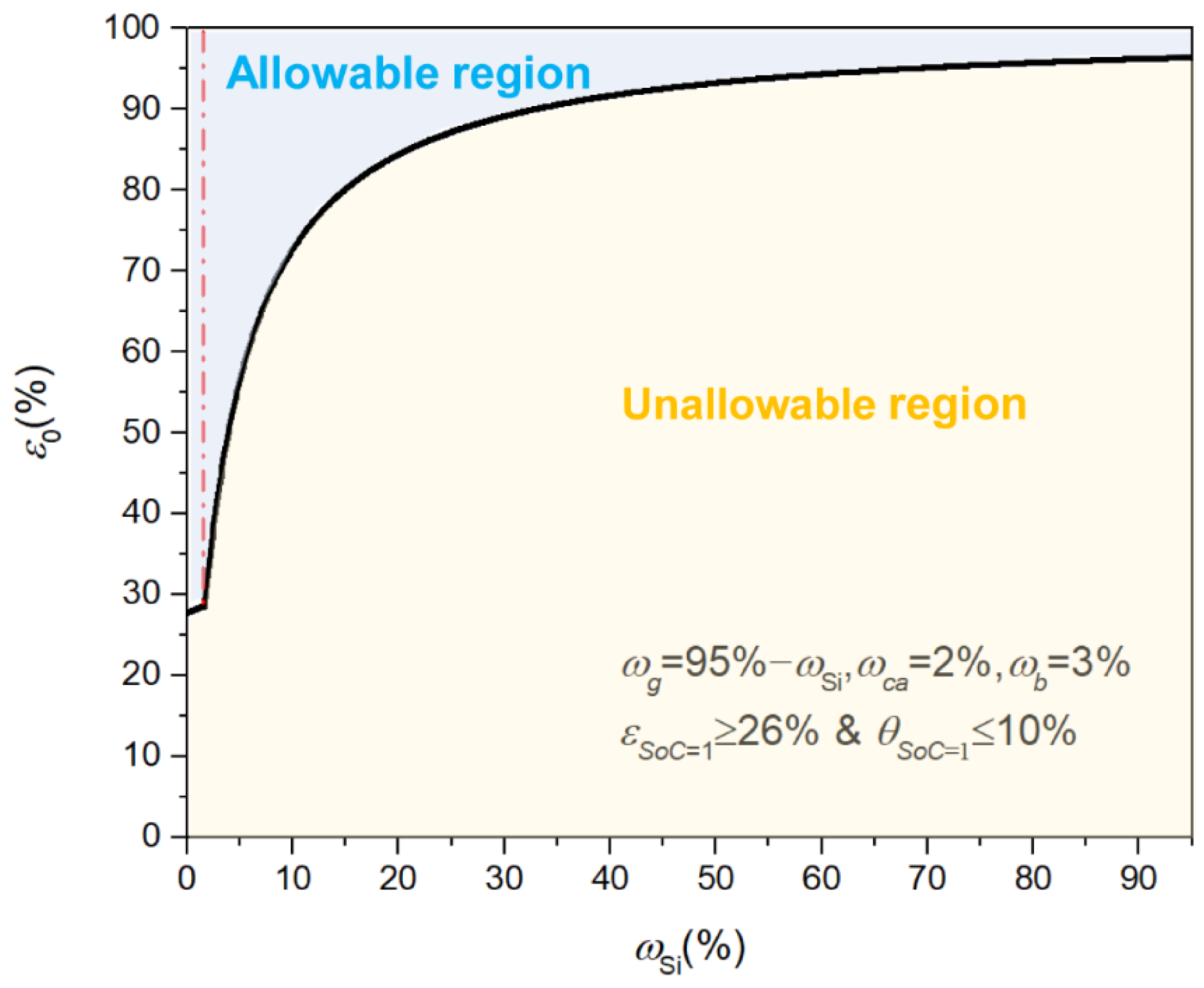
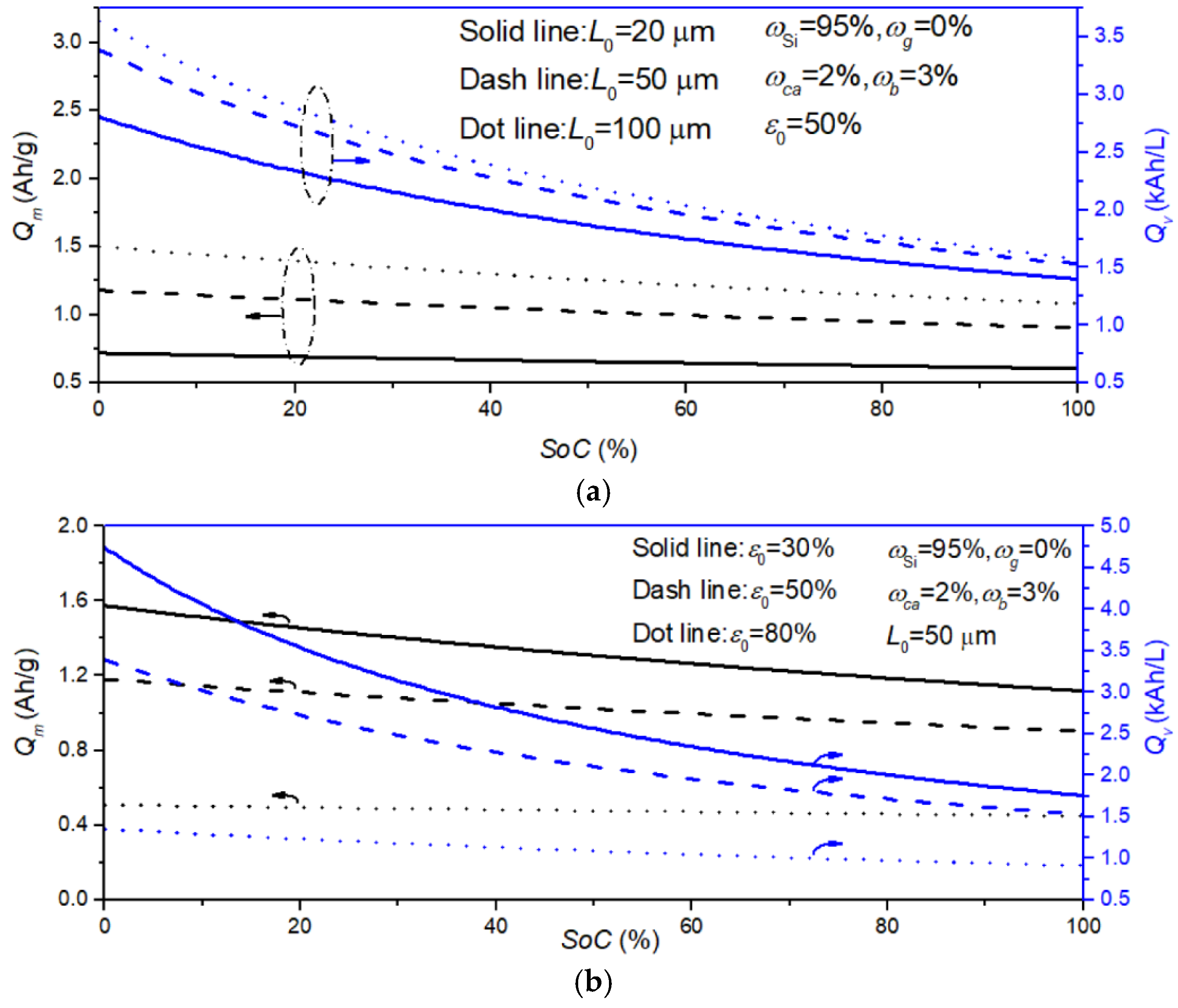
3.2. Model-Based Investigations
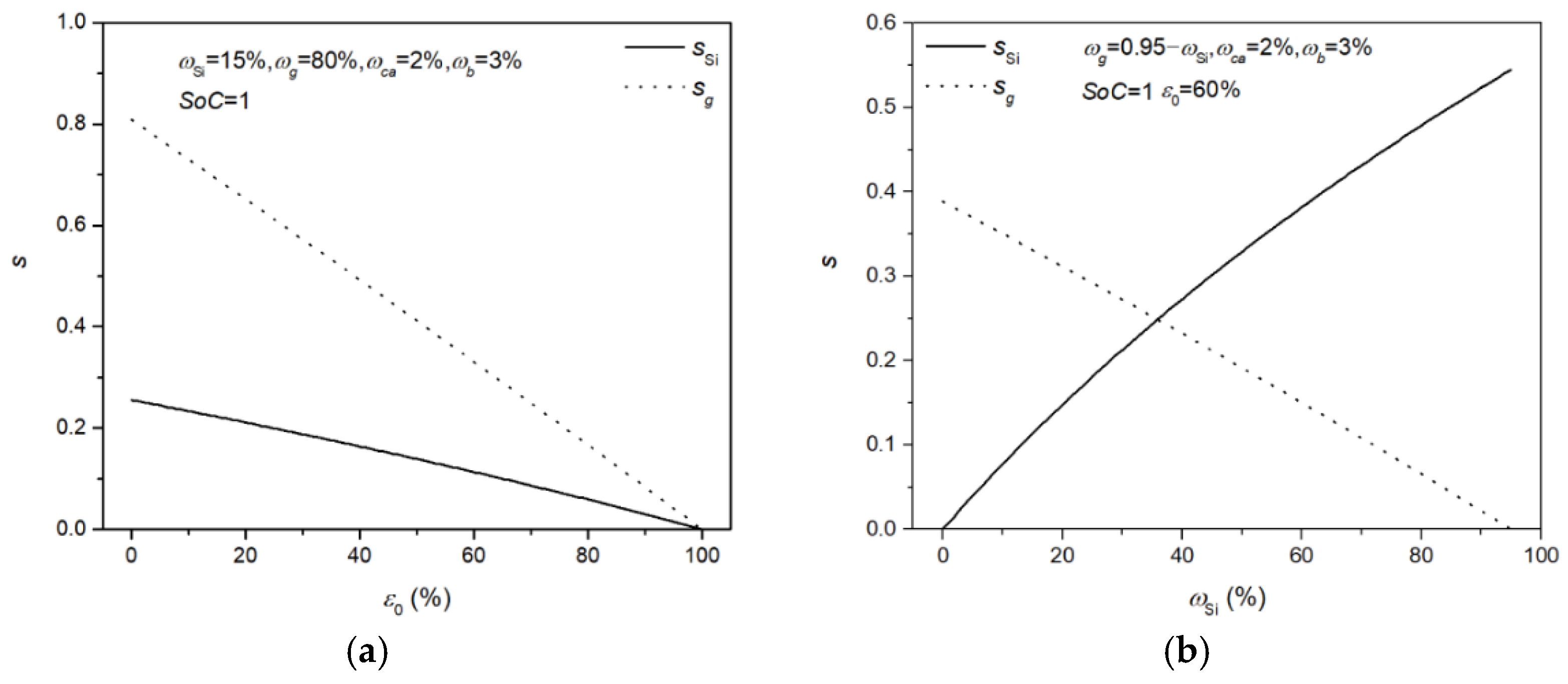
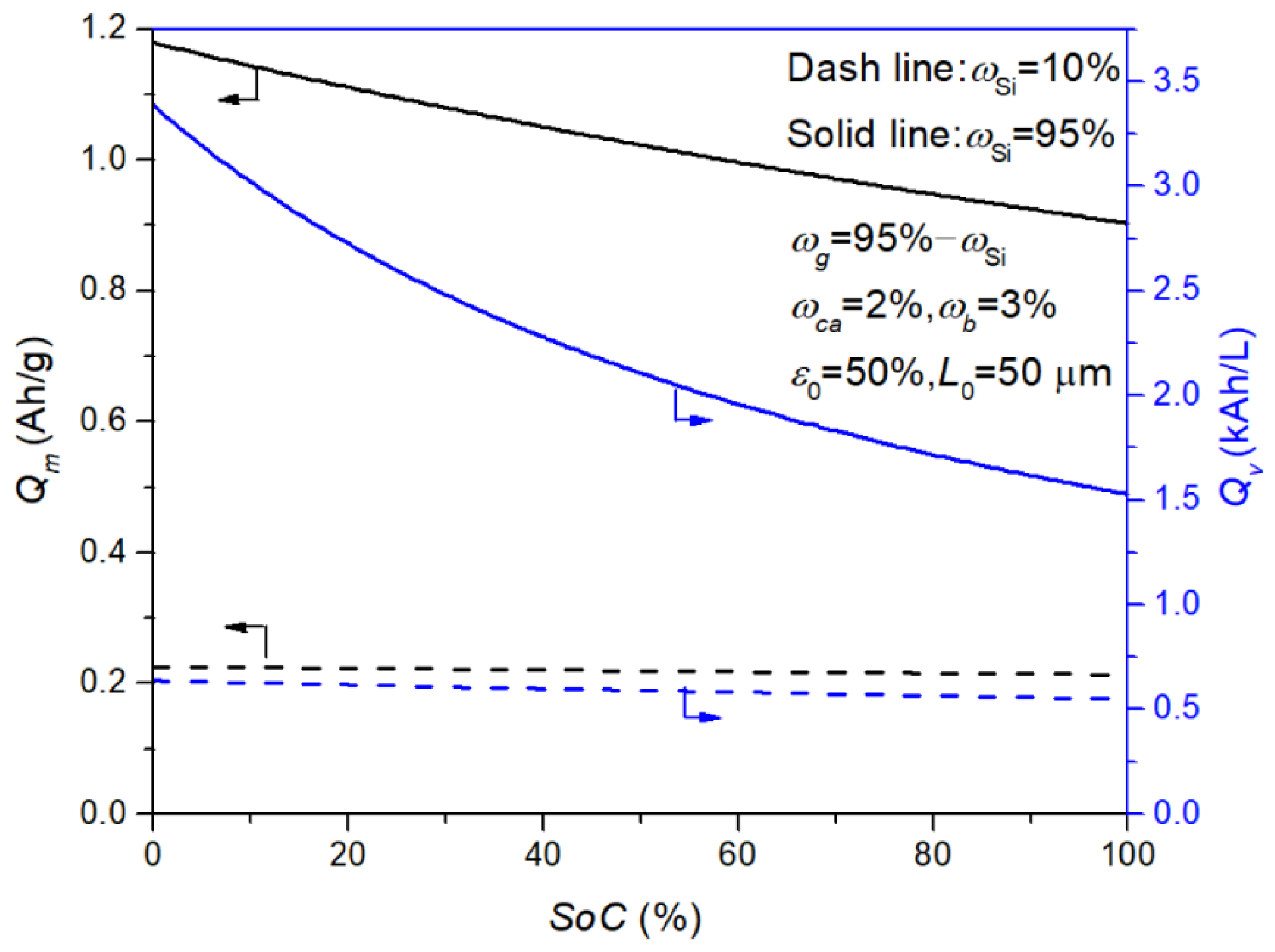
3.3. Estimation of Electrode Performance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xia, H.; Tang, Y.; Malyi, O.I.; Zhu, Z.; Zhang, Y.; Zhang, W.; Ge, X.; Zeng, Y.; Chen, X. Deep cycling for high-capacity Li-ion batteries. Adv. Mater. 2021, 33, 2004998. [Google Scholar] [CrossRef]
- Mabokela, T.E.; Nwanya, A.C.; Ndipingwi, M.M.; Kaba, S.; Ekwere, P.; Werry, S.T.; Ikpo, C.O.; Modibane, K.D.; Iwuoha, E.I. Review—Recent advances on high-capacity Li ion-rich layered manganese oxide cathodes. J. Electrochem. Soc. 2021, 168, 70530. [Google Scholar] [CrossRef]
- Jiang, M.; Danilov, D.L.; Eichel, R.A.; Notten, P.H.L. A review of degradation mechanisms and recent achievements for Ni-rich cathode-based Li-ion batteries. Adv. Energy Mater. 2021, 11, 2103005. [Google Scholar] [CrossRef]
- Lin, Q.; Guan, W.; Meng, J.; Huang, W.; Wei, X.; Zeng, Y.; Li, J.; Zhang, Z. A new insight into continuous performance decay mechanism of Ni-rich layered oxide cathode for high energy lithium ion batteries. Nano Energy 2018, 54, 313–321. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, R.; Wang, J.; Wang, Y. Current and future lithium-ion battery manufacturing. iScience 2021, 24, 102332. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Yue, F.S.; Li, S.C.; Zhang, Y.; Tian, Z.R.; Xu, Q.; Xin, S.; Guo, Y.G. Advances of polymer binders for silicon-based anodes in high energy density lithium-ion batteries. InfoMat 2021, 3, 460–501. [Google Scholar] [CrossRef]
- Li, P.; Kim, H.; Myung, S.; Sun, Y. Diverting exploration of silicon anode into practical way: A review focused on silicon-graphite composite for lithium ion batteries. Energy Storage Mater. 2021, 35, 550–576. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Wang, F.; Han, J.; Bai, S.; Tan, J.; Liu, J.S.; Li, F. Challenges and recent progress on silicon-based anode materials for next-generation lithium-ion batteries. Small Struct. 2021, 2, 2100009. [Google Scholar] [CrossRef]
- De Sutter, L.; Berckmans, G.; Marinaro, M.; Smekens, J.; Firouz, Y.; Wohlfahrt-Mehrens, M.; van Mierlo, J.; Omar, N. Comprehensive aging analysis of volumetric constrained lithium-ion pouch cells with high concentration silicon-alloy anodes. Energies 2018, 11, 2948. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Ma, L.; Li, T.; Li, J.; Yuan, C. Life cycle assessment of silicon-nanotube-based lithium ion battery for electric vehicles. ACS Sustain. Chem. Eng. 2019, 7, 599–610. [Google Scholar] [CrossRef]
- Zhang, X.; Bao, Y.; Chen, J.; Chen, H. Heterogeneous effects on chemo-mechanical coupling behaviors at the single-particle level. J. Electrochem. Soc. 2022, 169, 010522. [Google Scholar] [CrossRef]
- Tan, D.; Chen, Y.T.; Yang, H.; Bao, W.; Sreenarayanan, B.; Doux, J.M.; Li, W.; Lu, B.; Ham, S.Y.; Sayahpour, B.; et al. Carbon-free high-loading silicon anodes enabled by sulfide solid electrolytes. Science 2021, 373, 1494–1499. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, X.; Yang, L.; Wu, Y.; Chen, H.; Song, W.; Fang, D. Electrochemomechanical coupled behaviors of deformation and failure in electrode materials for lithium-ion batteries. Sci. China Technol. Sci. 2019, 62, 1277–1296. [Google Scholar] [CrossRef]
- Moyassari, E.; Roth, T.; Kucher, S.; Chang, C.C.; Hou, S.C.; Spingler, F.B.; Jossen, A. The role of silicon in silicon-graphite composite electrodes regarding specific capacity, cycle stability, and expansion. J. Electrochem. Soc. 2022, 169, 010504. [Google Scholar] [CrossRef]
- Li, P.; Hwang, J.Y.; Sun, Y.K. Nano/microstructured silicon-graphite composite anode for high-energy-density Li-ion battery. ACS Nano 2019, 13, 2624–2633. [Google Scholar] [CrossRef]
- Si, Q.; Mori, D.; Takeda, Y.; Yamamoto, O.; Imanishi, N. Silicon-carbon composite electrode materials prepared by pyrolysis of a mixture of manila hemp, silicon powder, and flake artificial graphite for lithium batteries. Energies 2017, 10, 1803. [Google Scholar] [CrossRef] [Green Version]
- Fu, R.; Ji, J.; Yun, L.; Jiang, Y.; Zhang, J.; Zhou, X.; Liu, Z. Graphene wrapped silicon suboxides anodes with suppressed Li-uptake behavior enabled superior cycling stability. Energy Storage Mater. 2021, 35, 317–326. [Google Scholar] [CrossRef]
- Li, G.; Li, J.; Yue, F.; Xu, Q.; Zuo, T.; Yin, Y.; Guo, Y. Reducing the volume deformation of high capacity SiOx/G/C anode toward industrial application in high energy density lithium-ion batteries. Nano Energy 2019, 60, 485–492. [Google Scholar] [CrossRef]
- Yu, Y.Y.; Zhu, J.D.; Zeng, K.; Jiang, M.J. Mechanically robust and superior conductive n-type polymer binders for high-performance micro-silicon anodes in lithium-ion batteries. J. Mater. Chem. A 2021, 9, 3472–3481. [Google Scholar] [CrossRef]
- Jeong, Y.K.; Huang, W.; Vilá, R.A.; Huang, W.; Wang, J.; Kim, S.C.; Kim, Y.S.; Zhao, J.; Cui, Y. Microclusters of Kinked Silicon Nanowires Synthesized by a Recyclable Iodide Process for High-Performance Lithium-Ion Battery Anodes. Adv. Energy Mater. 2020, 10, 2002108. [Google Scholar] [CrossRef]
- An, W.; Gao, B.; Mei, S.; Xiang, B.; Fu, J.; Wang, L.; Zhang, Q.; Chu, P.K.; Huo, K. Scalable synthesis of ant-nest-like bulk porous silicon for high-performance lithium-ion battery anodes. Nat. Commun. 2019, 10, 1447. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.; Li, X.; Song, J.; Zhang, X.; Luo, L.; He, Y.; Li, B.; Cai, Y.; Hu, S.; Xiao, X.; et al. Hierarchical porous silicon structures with extraordinary mechanical strength as high-performance lithium-ion battery anodes. Nat. Commun. 2020, 11, 1474. [Google Scholar] [CrossRef] [Green Version]
- Baggetto, L.; Danilov, D.; Notten, P.H. Honeycomb-structured silicon: Remarkable morphological changes induced by electrochemical (de)lithiation. Adv. Mater. 2011, 23, 1563–1566. [Google Scholar] [CrossRef]
- Louli, A.J.; Li, J.; Trussler, S.; Fell, C.R.; Dahn, J.R. Volume, pressure and thickness evolution of Li-ion pouch cells with silicon-composite negative electrodes. J. Electrochem. Soc. 2017, 164, A2689–A2696. [Google Scholar] [CrossRef]
- McDowell, M.T.; Lee, S.W.; Harris, J.T.; Korgel, B.A.; Wang, C.M.; Nix, W.D.; Cui, Y. In situ TEM of two-phase lithiation of amorphous silicon nanospheres. Nano Lett. 2013, 13, 758–764. [Google Scholar] [CrossRef]
- Timmons, A.; Dahn, J.R. In situ optical observations of particle motion in alloy negative electrodes for Li-ion batteries. J. Electrochem. Soc. 2006, 153, A1206–A1210. [Google Scholar] [CrossRef]
- Yu, D.; Zhao, M.; Hoster, H.E. Suppressing vertical displacement of lithiated silicon particles in high volumetric capacity battery electrodes. ChemElectroChem 2015, 2, 1090–1095. [Google Scholar] [CrossRef]
- Profatilova, I.; De Vito, E.; Genies, S.; Vincens, C.; Gutel, E.; Fanget, O.; Martin, A.; Chandesris, M.; Tulodziecki, M.; Porcher, W. Impact of silicon/graphite composite electrode porosity on the cycle life of 18650 lithium-ion cell. ACS Appl. Energy Mater. 2020, 3, 11873–11885. [Google Scholar] [CrossRef]
- Bridel, J.S.; Azaïs, T.; Morcrette, M.; Tarascon, J.M.; Larcher, D. Key parameters governing the reversibility of Si/carbon/CMC electrodes for Li-ion batteries. Chem. Mater. 2010, 22, 1229–1241. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, D.; Li, D.; Hu, J.; Cheng, Y. Influence of polymeric binders on mechanical properties and microstructure evolution of silicon composite electrodes during electrochemical cycling. J. Power Source 2019, 425, 170–178. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Wang, Y.; Chen, T.; Al-Shroofy, M.; Cheng, Y.T. Unveiling the critical role of polymeric binders for silicon negative electrodes in lithium-ion full cells. ACS Appl. Mater. Interfaces 2017, 9, 3562–3569. [Google Scholar] [CrossRef]
- Ai, W.; Kirkaldy, N.; Jiang, Y.; Offer, G.; Wang, H.; Wu, B. A composite electrode model for lithium-ion batteries with silicon/graphite negative electrodes. J. Power Source 2022, 527, 231142. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, Z.; Offer, G.; Xuan, J.; Wang, H. Insights into the role of silicon and graphite in the electrochemical performance of silicon/graphite blended electrodes with a multi-material porous electrode model. J. Electrochem. Soc. 2022, 169, 020568. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, L.; Guo, F.; Liu, D.; Wang, H.; Lu, J.; Zheng, J.; Yu, X.; Li, H. Mechanical-electrochemical modeling of silicon-graphite composite anode for lithium-ion batteries. J. Power Source 2022, 527, 231178. [Google Scholar] [CrossRef]
- Zhang, X.; Klinsmann, M.; Chumakov, S.; Li, X.; Kim, S.U.; Metzger, M.; Besli, M.M.; Klein, R.; Linder, C.; Christensen, J. A modified electrochemical model to account for mechanical effects due to lithium intercalation and external pressure. J. Electrochem. Soc. 2021, 168, 20533. [Google Scholar] [CrossRef]
- Heubner, C.; Langklotz, U.; Michaelis, A. Theoretical optimization of electrode design parameters of Si based anodes for lithium-ion batteries. J. Energy Storage 2018, 15, 181–190. [Google Scholar] [CrossRef]
- Gomadam, P.M.; Weidner, J.W. Modeling volume changes in porous electrodes. J. Electrochem. Soc. 2006, 153, A179–A186. [Google Scholar] [CrossRef] [Green Version]
- Dasari, H.; Eisenbraun, E. Predicting Capacity Fade in Silicon Anode-Based Li-Ion Batteries. Energies 2021, 14, 1448. [Google Scholar] [CrossRef]
- Wang, M.; Xiao, X.; Huang, X. A multiphysics microstructure-resolved model for silicon anode lithium-ion batteries. J. Power Source 2017, 348, 66–79. [Google Scholar] [CrossRef]
- Dhillon, S.; Hernández, G.; Wagner, N.P.; Svensson, A.M.; Brandell, D. Modelling capacity fade in silicon-graphite composite electrodes for lithium-ion batteries. Electrochim. Acta 2021, 377, 138067. [Google Scholar] [CrossRef]
- Sturm, J.; Rheinfeld, A.; Zilberman, I.; Spingler, F.B.; Kosch, S.; Frie, F.; Jossen, A. Modeling and simulation of inhomogeneities in a 18650 nickel-rich, silicon-graphite lithium-ion cell during fast charging. J. Power Source 2019, 412, 204–223. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekaran, R.; Fuller, T.F. Analysis of the lithium-ion insertion silicon composite electrode/separator/lithium foil cell. J. Electrochem. Soc. 2011, 158, A859–A871. [Google Scholar] [CrossRef]
- Gao, X.; Lu, W.; Xu, J. Modeling framework for multiphysics-multiscale behavior of Si–C composite anode. J. Power Source 2020, 449, 227501. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Li, J.; Jiang, H.; Yin, S.; Xu, J. Multiphysics coupled computational model for commercialized Si/graphite composite anode. J. Power Source 2020, 450, 227667. [Google Scholar] [CrossRef]
- Shah, S.R.; de Vasconcelos, L.S.; Zhao, K.J. Computational modeling of electrochemomechanics of high-capacity composite electrodes in Li-ion batteries. J. Appl. Mech. 2022, 89, 081005. [Google Scholar] [CrossRef]
- Michael, H.; Iacoviello, F.; Heenan, T.M.M.; Llewellyn, A.; Weaving, J.S.; Jervis, R.; Brett, D.J.L.; Shearing, P.R. A dilatometric study of graphite electrodes during cycling with X-ray computed tomography. J. Electrochem. Soc. 2021, 168, 10507. [Google Scholar] [CrossRef]
- Yao, K.P.C.; Okasinski, J.S.; Kalaga, K.; Almer, J.D.; Abraham, D.P. Operando quantification of (de)lithiation behavior of silicon–graphite blended electrodes for lithium-ion batteries. Adv. Energy Mater. 2019, 9, 1803380. [Google Scholar] [CrossRef]
- Fu, R.; Xiao, M.; Choe, S. Modeling, validation and analysis of mechanical stress generation and dimension changes of a pouch type high power Li-ion battery. J. Power Source 2013, 224, 211–224. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Jossen, A. Strain propagation in lithium-ion batteries from the crystal structure to the electrode level. J. Electrochem. Soc. 2016, 163, A1595–A1606. [Google Scholar] [CrossRef]
- Zhang, X.; He, J.; Zhou, J.; Chen, H.; Song, W.; Fang, D. Thickness evolution of commercial Li-ion pouch cells with silicon-based composite anodes and NCA cathodes. Sci. China Technol. Sci. 2021, 64, 83–90. [Google Scholar] [CrossRef]
- Beaulieu, L.Y.; Eberman, K.W.; Turner, R.L.; Krause, L.J.; Dahn, J.R. Colossal reversible volume changes in lithium alloys. Electrochem. Solid-State Lett. 2001, 4, A137–A140. [Google Scholar] [CrossRef]
- Pereira, D.J.; Weidner, J.W.; Garrick, T.R. The effect of volume change on the accessible capacities of porous silicon-graphite composite anodes. J. Electrochem. Soc. 2019, 166, A1251–A1256. [Google Scholar] [CrossRef]
- Kim, H.; Chou, C.; Ekerdt, J.G.; Hwang, G.S. Structure and properties of Li−Si alloys: A first-principles study. J. Phys. Chem. C 2011, 115, 2514–2521. [Google Scholar] [CrossRef]
- Doh, C.; Han, B.; Jin, B.; Gu, H. Structures and formation energies of LixC6 (x = 1–3) and its homologues for lithium rechargeable batteries. Bull. Korean Chem. Soc. 2011, 32, 2045–2050. [Google Scholar] [CrossRef] [Green Version]
- Woodford, W.H.; Carter, W.C.; Chiang, Y. Design criteria for electrochemical shock resistant battery electrodes. Energy Environ. Sci. 2012, 5, 8014–8024. [Google Scholar] [CrossRef]
- Qi, Y.; Guo, H.; Hector, L.G.; Timmons, A. Threefold increase in the young’s modulus of graphite negative electrode during lithium intercalation. J. Electrochem. Soc. 2010, 157, A558–A566. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Schmalz, J.; Reinhart, G.; Jossen, A. Multi-scale investigation of thickness changes in a commercial pouch type lithium-ion battery. J. Energy Storage 2016, 6, 213–221. [Google Scholar] [CrossRef]
- Pietsch, P.; Westhoff, D.; Feinauer, J.; Eller, J.; Marone, F.; Stampanoni, M.; Schmidt, V.; Wood, V. Quantifying microstructural dynamics and electrochemical activity of graphite and silicon-graphite lithium ion battery anodes. Nat. Commun. 2016, 7, 12909. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Lee, H.M.; Ahn, S. Battery dimensional changes occurring during charge/discharge cycles—thin rectangular lithium ion and polymer cells. J. Power Source 2003, 119–121, 833–837. [Google Scholar] [CrossRef]
- Chen, C.; Brosa Planella, F.; O’Regan, K.; Gastol, D.; Widanage, W.D.; Kendrick, E. Development of experimental techniques for parameterization of multi-scale lithium-ion battery models. J. Electrochem. Soc. 2020, 167, 80534. [Google Scholar] [CrossRef]
- Zhang, X.; Hui, Z.; King, S.; Wang, L.; Ju, Z.; Wu, J.; Takeuchi, K.J.; Marschilok, A.C.; West, A.C.; Takeuchi, E.S.; et al. Tunable porous electrode architectures for enhanced li-ion storage kinetics in thick electrodes. Nano Lett. 2021, 21, 5896–5904. [Google Scholar] [CrossRef]
- Kuang, Y.; Chen, C.; Kirsch, D.; Hu, L. Thick electrode batteries: Principles, opportunities, and challenges. Adv. Energy Mater. 2019, 9, 1901457. [Google Scholar] [CrossRef]
- Zheng, H.; Li, J.; Song, X.; Liu, G.; Battaglia, V.S. A comprehensive understanding of electrode thickness effects on the electrochemical performances of Li-ion battery cathodes. Electrochim. Acta 2012, 71, 258–265. [Google Scholar] [CrossRef]



| Symbol | Explanation | Value [Unit] |
|---|---|---|
| Mi | Molar mass of the element i (MLi = 6.94, MSi = 28.09, MC = 12.01) | [g mol−1] |
| ηi | volume expansion coefficient of the component i (ηSi = 3, ηg = 0.1, ηca = 0, ηb = 0) | [-] or [%] |
| ρi | Mass density of the component i (ρSi = 2.33, ρg = 2.20, ρca = 2.20, ρb = 1.80) | [g cm−3] |
| ωi | Mass fractions of the component i (ωSi = variable, ωg = 0.95 − ωSi, ωca = 2%, wb = 3%) | [-] or [%] |
| Qm,i | Theoretical specific capacity of the component i (Qm,Si = 3579, Qm,g = 370) | [mAh g−1] |
| Lcc | Thickness of the current collector (Lcc = 8) | [μm] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, J.; Bao, Y. Model-Based Investigations of Porous Si-Based Anodes for Lithium-Ion Batteries with Effects of Volume Changes. Energies 2022, 15, 8848. https://doi.org/10.3390/en15238848
Zhang X, Chen J, Bao Y. Model-Based Investigations of Porous Si-Based Anodes for Lithium-Ion Batteries with Effects of Volume Changes. Energies. 2022; 15(23):8848. https://doi.org/10.3390/en15238848
Chicago/Turabian StyleZhang, Xingyu, Jian Chen, and Yinhua Bao. 2022. "Model-Based Investigations of Porous Si-Based Anodes for Lithium-Ion Batteries with Effects of Volume Changes" Energies 15, no. 23: 8848. https://doi.org/10.3390/en15238848






