Research on Low Voltage Ride through Control of a Marine Photovoltaic Grid-Connected System Based on a Super Capacitor
Abstract
:1. Introduction
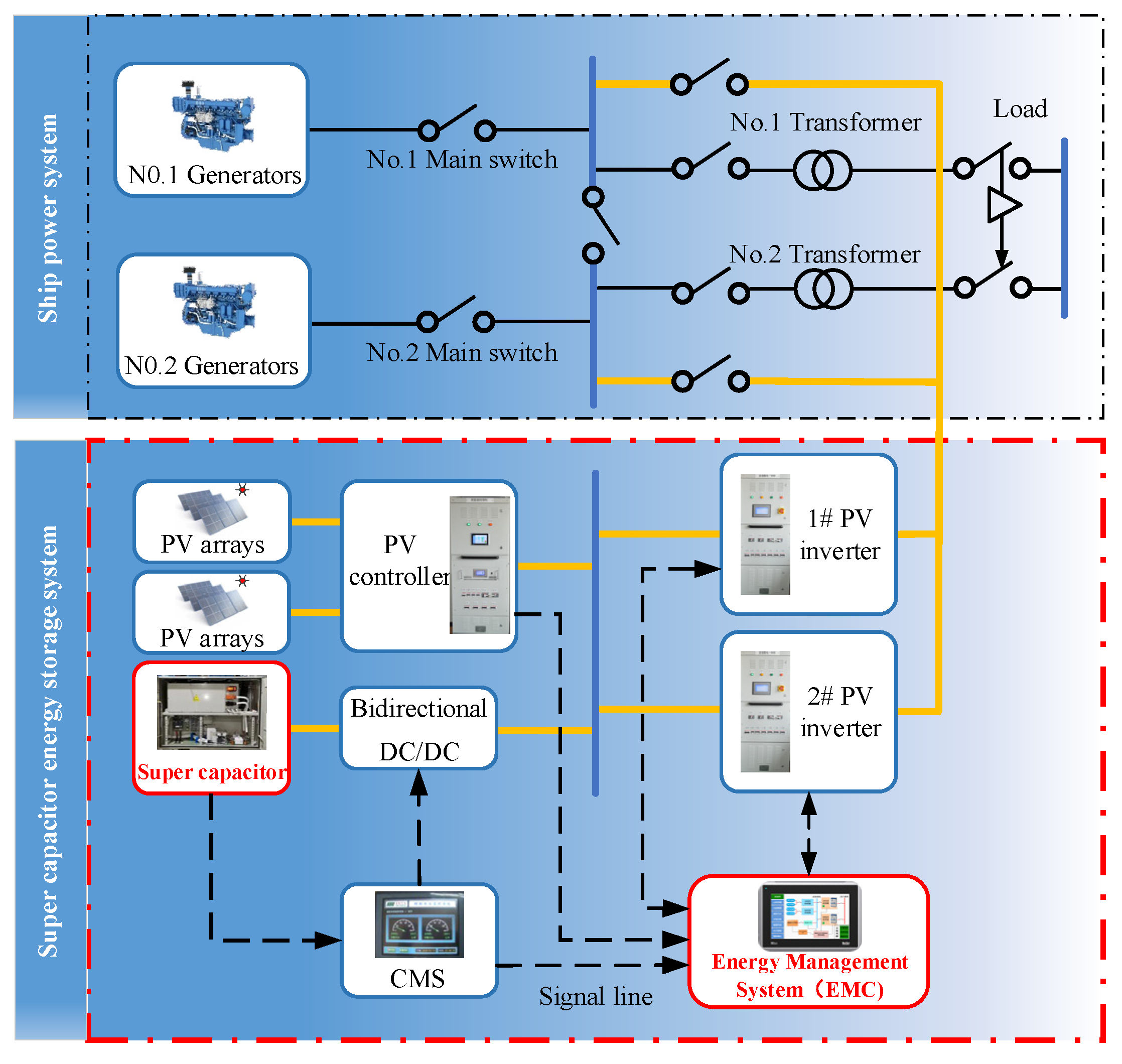
2. Structure of Marine Photovoltaic Grid-Connected System
3. Model and Control Strategy
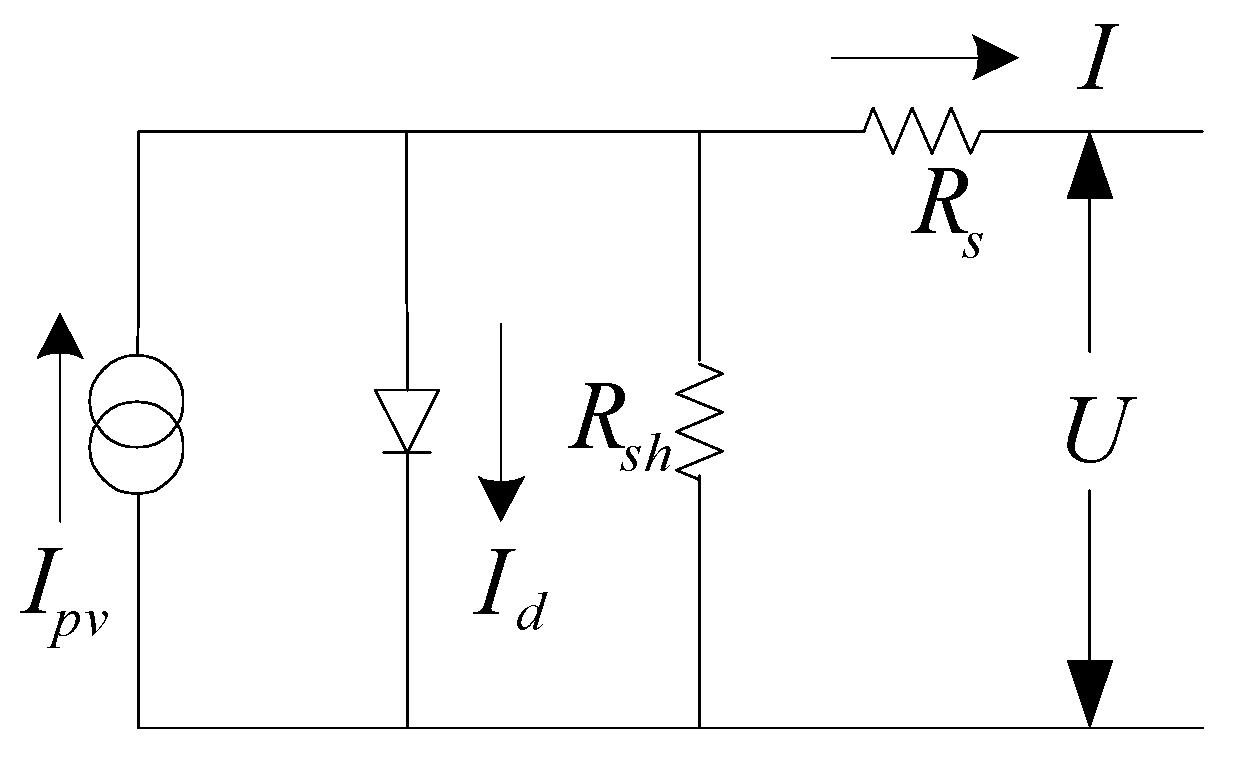
3.1. Mathematical Model and Maximum Power Point Tracking of the Photovoltaic Cell
3.2. Photovoltaic Cell Simulation Model
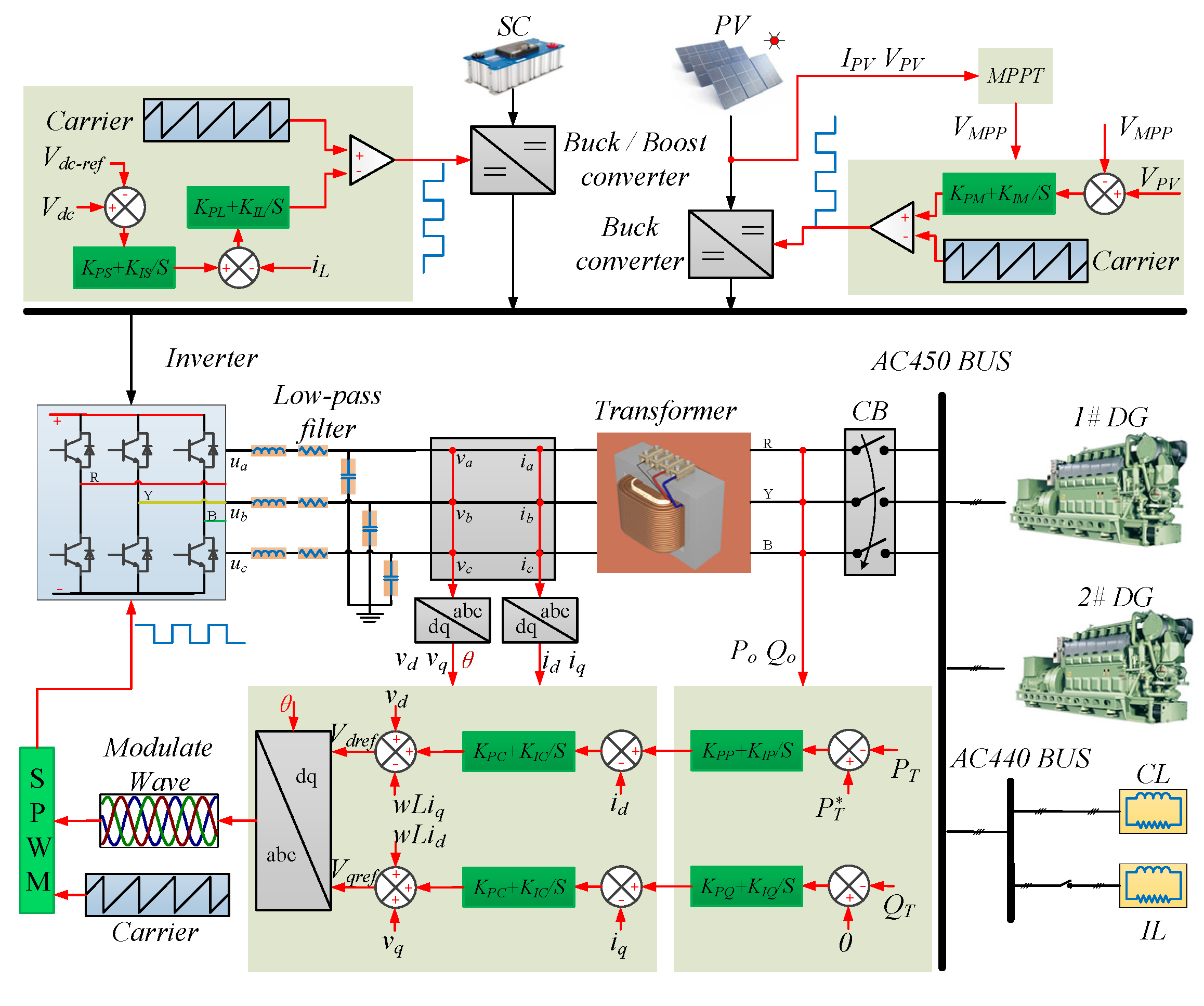
3.3. Inverter Control Strategy
3.4. Charge/Discharge Control of Super Capacitor
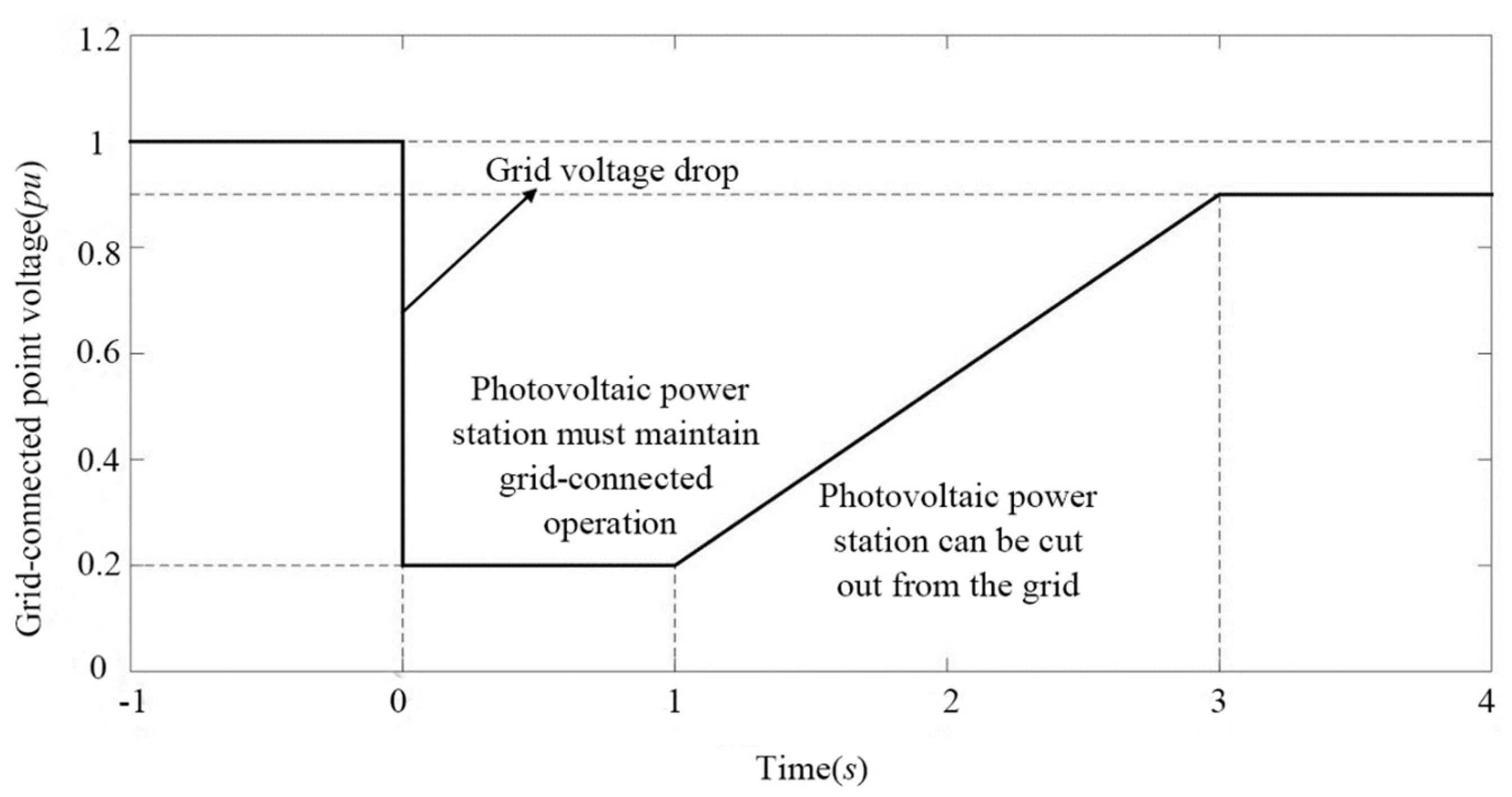
3.5. LVRT Control Strategy
4. System Simulation and Analysis
4.1. Simulation Parameters Design
4.2. Simulation Results Analysis
- (1)
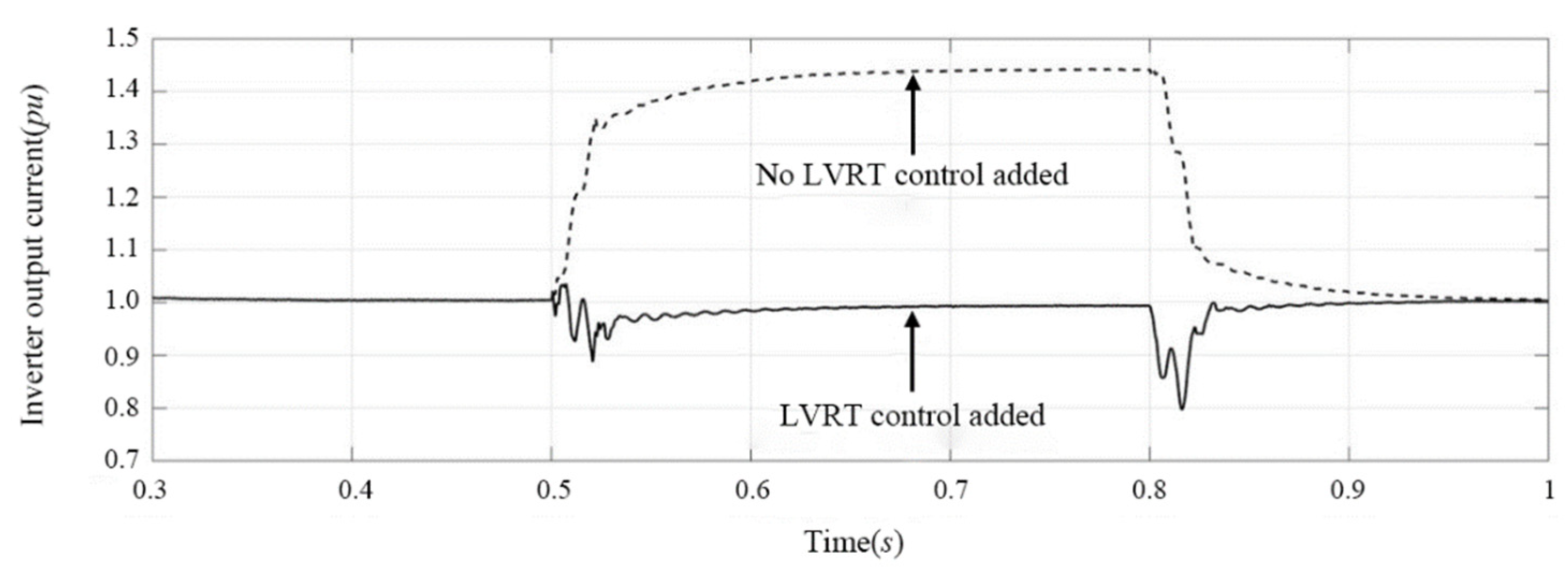
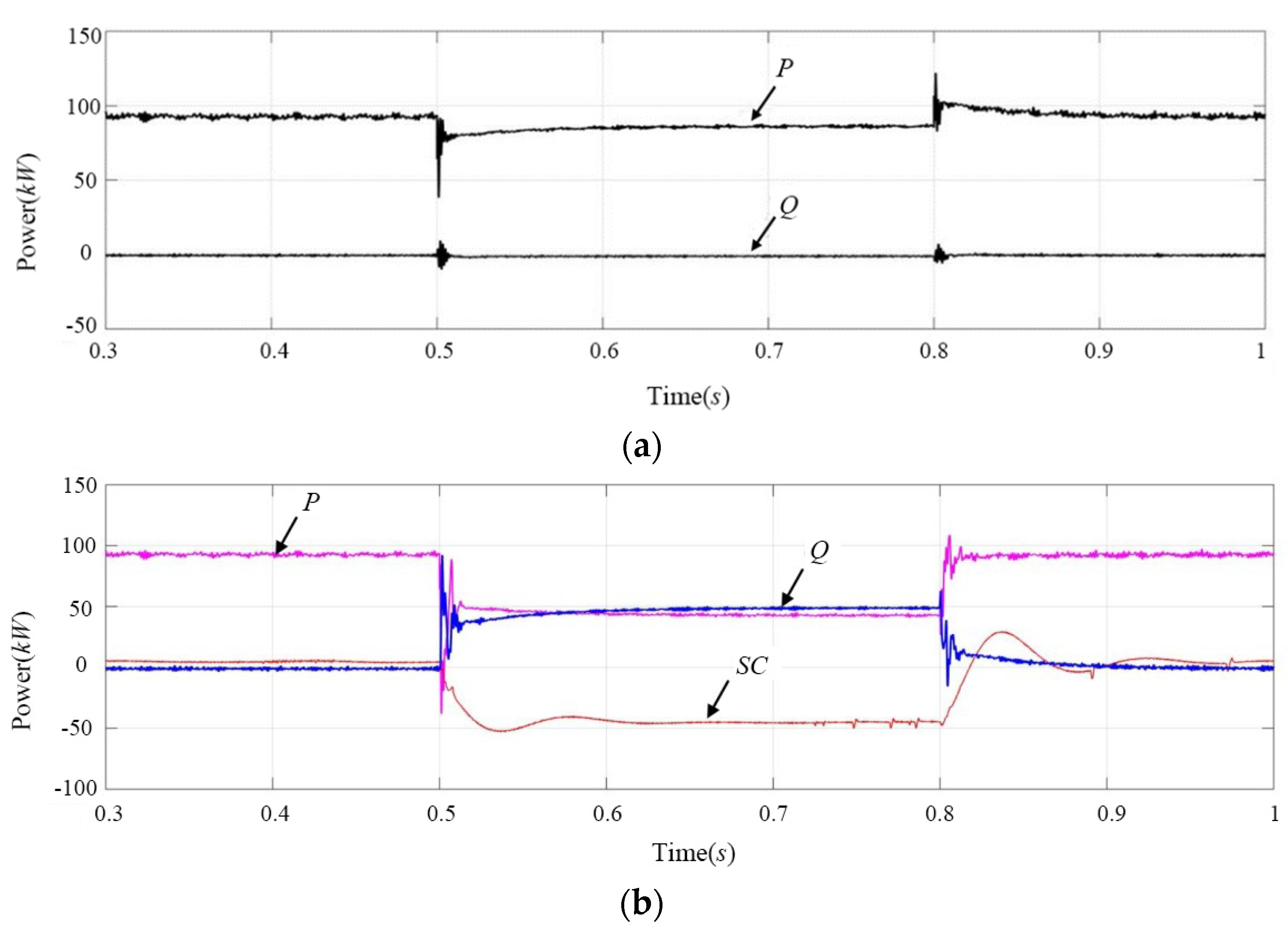
- In case of grid voltage sag, it can be seen from Figure 20a and Figure 21 that the inverter operates under unit power factor without LVRT control in grid-connected system and does not output reactive power, but the active output power drops slightly due to voltage sag. As shown in Figure 17a, Figure 18a and Figure 20a, as the photovoltaic array continues to work at the maximum power state, an imbalance between the input power and output power appears on the DC bus side, and the power difference acts on the DC bus, and the DC bus voltage presents a rapid upward trend. The DC bus voltage increases because the input power of the inverter is greater than the output power. In order to ensure the power balance between the DC input and the AC output of the inverter, the output current of the inverter will increase to 1.4 pu, which exceeds the rated operating current and causes the inverter to be off-gird due to overcurrent protection, thus increasing the fault range.
- (2)
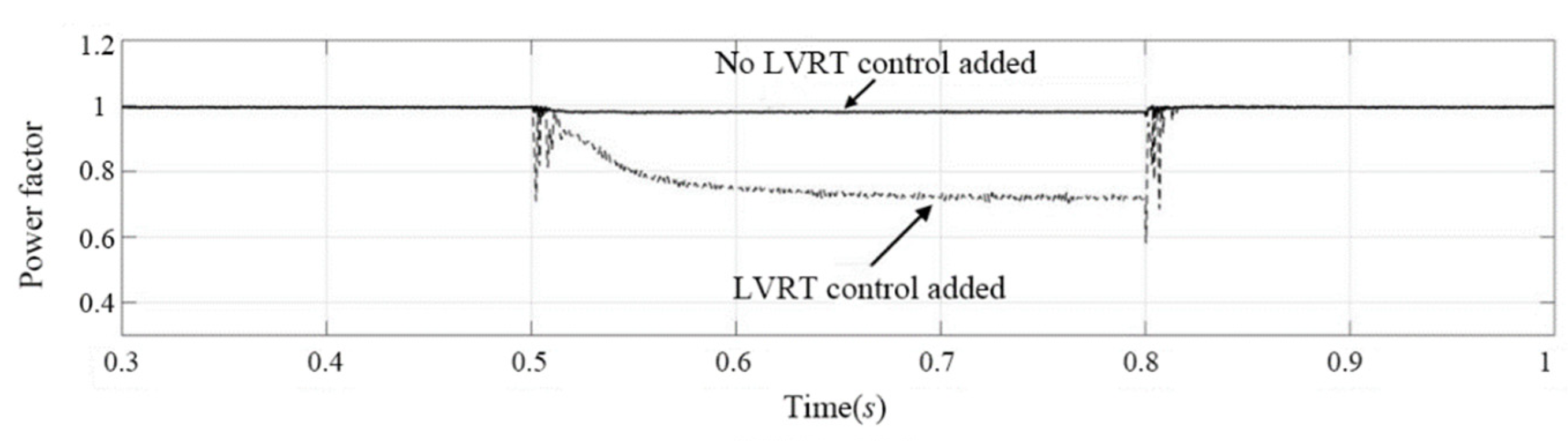
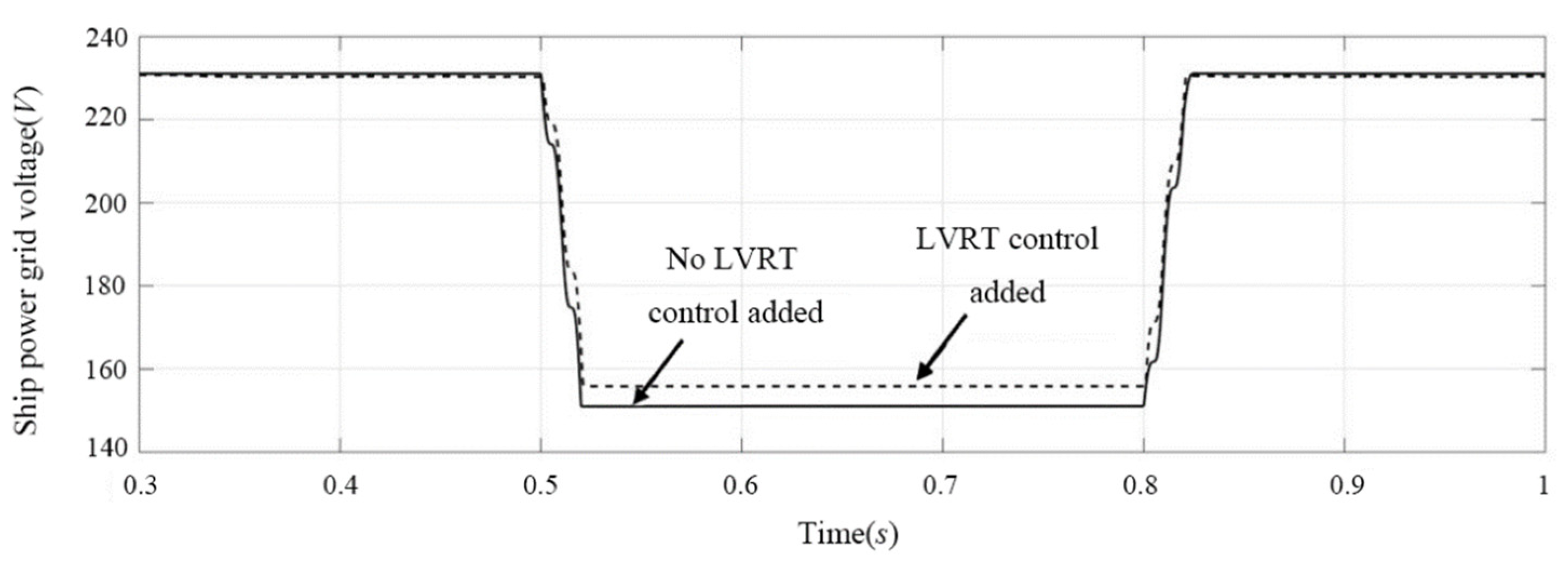
- With LVRT control, the photovoltaic controller still operates in MPPT mode during voltage sag. According to Figure 17b and Figure 18b, in order to prevent the inverter from being off-grid due to output overcurrent during voltage sag, the inverter reduces the active power output and its output current is always less than 1.1 pu. During the fault period, the super capacitor absorbs the energy difference between the inverter and the controller, so that the DC bus voltage remains stable. The dynamic and static response is ideal, with the overshoot of the DC bus less than 5%, the adjustment time less than 0.1 s, and the steady-state voltage basically remaining at 380 V. It can be seen from Figure 19 and Figure 22 that the inverter adjusts the distribution of active and reactive power when the grid voltage sags, with the power factor decreasing from 1 to 0.77 and the voltage sag increasing from 150 V to 156 V. The control strategy can absorb excess photovoltaic energy through the super capacitor adjustment system, greatly reduce the voltage rise of the DC bus of the photovoltaic power generation system, and maintain the grid-connected current below the limit current value. After the fault is removed, the marine diesel/photovoltaic grid-connected power system will quickly return to the normal working state, enhancing the low voltage ride-through capability of the system.
5. Conclusions
- (1)
- The use of super capacitors for ship energy storage can keep the DC bus voltage stable and reduce the power injected into the photovoltaic inverter.
- (2)
- The inverter can realize the independent control of dq axis current. At the same time, the feedforward compensation of the grid voltage is added, which reduces the influence of the grid voltage on the control system.
- (3)
- When the ship grid voltage fluctuates, the photovoltaic grid-connected system control strategy automatically adjusts the distribution of active power and reactive power to help restore the grid voltage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ipv,Vpv | PV source output voltage andcurrent | Reference current | |
| Id | Current flowing through the diode | is | Current of the inverter operating at unity power factor |
| Rs | Series resistance characterizing internal loss | C1 | Photovoltaic controller capacitor |
| Rsh | Bypass leakage resistance | L1 | Photovoltaic controller inductance |
| U | PV cell output voltage | D | Photovoltaic controller duty cycle |
| I | PV cell output current | Cdc | Photovoltaic controller DC bus capacitor |
| id | Stator d-axis current component | C2 | Bidirectional DC/DC converter capacitor |
| iq | Stator q-axis current component | L2 | Bidirectional DC/DC converter inductor |
| ud | Grid d-axis voltage | Kp1 | Voltage outer loop proportional coefficient |
| uq | Power grid q axis voltage | Ki1 | Integral coefficient of voltage outer loop |
| vd | Stator d-axis reference voltage | Kp2 | Current inner loop proportional coefficient |
| vq | Stator q-axis reference voltage | Ki2 | Current inner loop integral coefficient |
| Stator d-axis reference current | C3 | Inverter filter capacitor | |
| Stator q-axis reference current | L3 | Inverter filter inductor | |
| Uref | Modulated signal | Kp3 | Power outer ring proportional coefficient |
| Rc | Super capacitor model equivalent resistance | Ki3 | Power outer loop integral coefficient |
| Csc | Equivalent capacitance of the supercapacitor model |
References
- Crago, C.L.; Koegler, E. Drivers of growth in commercial-scale solar PV capacity. Energy Policy 2018, 120, 481–491. [Google Scholar] [CrossRef]
- Bolinger, M.; Seel, J.; Robson, D. Utility-Scale Solar: Empirical Trends in Project Technology, Cost, Performance, and PPA Pricing in the United States-2019 Edition; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2019. [Google Scholar]
- Barbose, G.; Darghouth, N. Tracking the Sun: Pricing and Design Trends for Distributed Photovoltaic Systems in the United States-2019 Edition; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2019. [Google Scholar]
- Hebner, R.E.; Uriarte, F.M.; Kwasinski, A.; Gattozzi, A.L.; Estes, H.B.; Anwar, A.; Cairoli, P.; Dougal, R.A.; Feng, X.; Chou, H.-M. Technical cross- fertilization between ter-restrial microgrids and ship power systems. J. Mod. Power Syst. Clean Energy 2016, 4, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhang, Q.; Qi, X.; Han, Y.; Lu, F. Estimation of PV output power in moving and rocking hybrid energy marine ships. Appl. Energy 2017, 204, 362–372. [Google Scholar] [CrossRef]
- ElNozahy, M.; Salama, M. Technical impacts of grid-connected photovoltaic systems on electrical networks—A review. J. Renew. Sustain. Energy 2013, 5, 032702. [Google Scholar] [CrossRef]
- Baggini, A. Handbook of Power Quality; John Wiely & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Hou, Y.; Magnusson, J.; Engdahl, G.; Liljestrand, L. Impact on voltage rise of PV generation in future swedish urban areas with high PV penetration. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 904–911. [Google Scholar]
- Mehrdad, T.H.; Muttaqi, K.M. Low Voltage Ride through of Wind Energy Systems; Springer: Singapore, 2017; pp. 6–15. [Google Scholar]
- Camacho, A.; Castilla, M.; Miret, J.; Borrell, A.; de Vicuña, L.G. Active and reactive power strategies with peak current limitation for distributed generation inverters during unbalanced grid faults. IEEE Trans. Ind. Electron. 2015, 62, 1515–1525. [Google Scholar] [CrossRef] [Green Version]
- Luna, A.; Rocabert, J.; Candela, J.I. Grid voltage synchronization for distributed generation systems under grid fault conditions. IEEE Trans. Ind. Appl. 2015, 51, 3414–3425. [Google Scholar] [CrossRef]
- Calle-Prado, A.; Alepuz, S.; Bordonau, J.; Nicolas-Apruzzese, J.; Cortés, P.; Rodriguez, J. Model predictive current control of grid-connected neutral point clamped converters to meet low-voltage ride-through requirements. IEEE Trans. Ind. Electron. 2015, 62, 1503–1514. [Google Scholar] [CrossRef] [Green Version]
- Saadat, N.; Choi, S.S.; Vilathgamuwa, D.M. A Statistical evaluation of the capability of distributed renewable generator energy storage system in providing load low-voltage ride-through. IEEE Trans. Power Deliv. 2015, 30, 1128–1136. [Google Scholar] [CrossRef]
- Chou, S.-F.; Lee, C.-T.; Ko, H.-C.; Cheng, P.-T. A low-voltage ride-through method with transformer flux compensation capability of renewable power grid-side converters. IEEE Trans. Power Electron. 2014, 29, 1710–1719. [Google Scholar] [CrossRef]
- Meyer, R.; Zlotnik, A.; Mertens, A. Fault ride-through control of medium-voltage converters with LCL filter in distributed generation systems. IEEE Trans. Ind. 2014, 50, 3448–3456. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Wang, B.; Wu, W.; Guerrero, J.M. Asymmetrical grid fault ride-through strategy of three-phase grid-connected inverter considering network impedance impact in low-voltage grid. IEEE Trans. Power Electron. 2014, 29, 1064–1068. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Tian, L. Research on low voltage ride through technology of grid-connected photovoltaic system. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Chengdu, China, 19–22 October 2016. [Google Scholar]
- Sadeghkhani, I.; Golshan, M.E.H.; Mehrizi-Sani, A.; Guerrero, J.M. Low-voltage ride-through of a droop-based three-phase four-wire grid-connected microgrid. IET Gener. Transm. Distrib. 2018, 12, 1906–1914. [Google Scholar] [CrossRef]
- Brandao, D.I.; Mendes, F.E.; Ferreira, R.V.; Silva, S.M.; Pires, I.A. Active and reactive power injection strategies for three-phase four-wire inverters during symmetrical/asymmetrical voltage sags. IEEE Trans. Ind. Appl. 2019, 55, 2347–2355. [Google Scholar] [CrossRef]
- Mojallal, A.; Lotfifard, S. Enhancement of grid connected PV arrays fault ride through and post fault recovery performance. IEEE Trans. Smart Grid 2019, 10, 546–555. [Google Scholar] [CrossRef]
- Yu, H.E.; Xu, Z.; Li, Y. A novel control scheme for enhancing low voltage ride through capability of solar generation. In Proceedings of the 2017 China International Electrical and Energy Conference (CIEEC), Beijing, China, 25–27 October 2017; pp. 129–134. [Google Scholar]
- Jeong, H.G.; Ro, H.S.; Lee, K.B. An improved maximum power point tracking method for wind power systems. Energies 2012, 5, 1339–1354. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.S.; Lee, K.B. New modulation techniques for a leakage current reduction and a neutral-point voltage balance in transformerless photovoltaic systems using a three-level inverter. IEEE Trans. Power Electron. 2014, 29, 1720–1732. [Google Scholar] [CrossRef]
- Espi, J.M.; Castello, J. Wind turbine generation system with optimized DC-link design and control. IEEE Trans. Ind. Electron. 2013, 60, 919–929. [Google Scholar] [CrossRef]
- Kim, M.K. Optimal control and operation strategy for wind turbines contributing to grid primary frequency regulation. Appl. Sci. 2017, 7, 927. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef] [Green Version]
- Ranaweera, I.; Midtgard, O.M. Optimization of operational cost for a grid-supporting PV system with battery storage. Renew. Energy 2016, 88, 262–272. [Google Scholar] [CrossRef]
- Reihani, E.; Motalleb, M.; Ghorbani, R.; Saoud, L.S. Load peak shaving and power smoothing of a distribution grid with high renewable energy penetration. Renew. Energy 2016, 86, 1372–1379. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.S.; Jia, Y.; Lai, L.L.; Xu, Z.; McCulloch, M.D.; Wong, K.P. A comprehensive review on large-scale photovoltaic system with applications of electrical energy storage. Renew. Sustain. Energy Rev. 2017, 78, 439–451. [Google Scholar] [CrossRef]
- Salminen, J.; Kallio, T.; Omar, N.; Van den Bossche, P.; Van Mierlo, J.; Gualous, H. Transport energy lithium ion batteries. In Future Energy, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 291–309. [Google Scholar]
- Sato, T. Science, Technology and Advanced Application of Super-Capacitors; Springer: London, UK, 2019. [Google Scholar]
- Li, J.; Cornelusse, B.; Vanderbemden, P.; Ernst, D. A SC/battery hybrid energy storage system in the microgrid. Energy Procedia 2017, 142, 3697–3702. [Google Scholar] [CrossRef]
- Paternoster, G.; Zanuccoli, M.; Bellutti, P.; Ferrario, L.; Ficorella, F.; Fiegna, C.; Magnone, P.; Mattedi, F.; Sangiorgi, E. Fabrication, characterization and modeling of a silicon solar cell optimized for concentrated photovoltaic applications. Sol. Energy Mater. Sol. Cells 2015, 134, 407–416. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. Modeling, analysis and comparison of solar photovoltaic array configurations under partial shading conditions. Sol. Energy 2015, 120, 399–418. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Khan, M.J.; Mathew, L. Different kinds of maximum power point tracking control method for photovoltaic systems: A review. Arch. Comput. Methods Eng. 2017, 24, 855–867. [Google Scholar] [CrossRef]
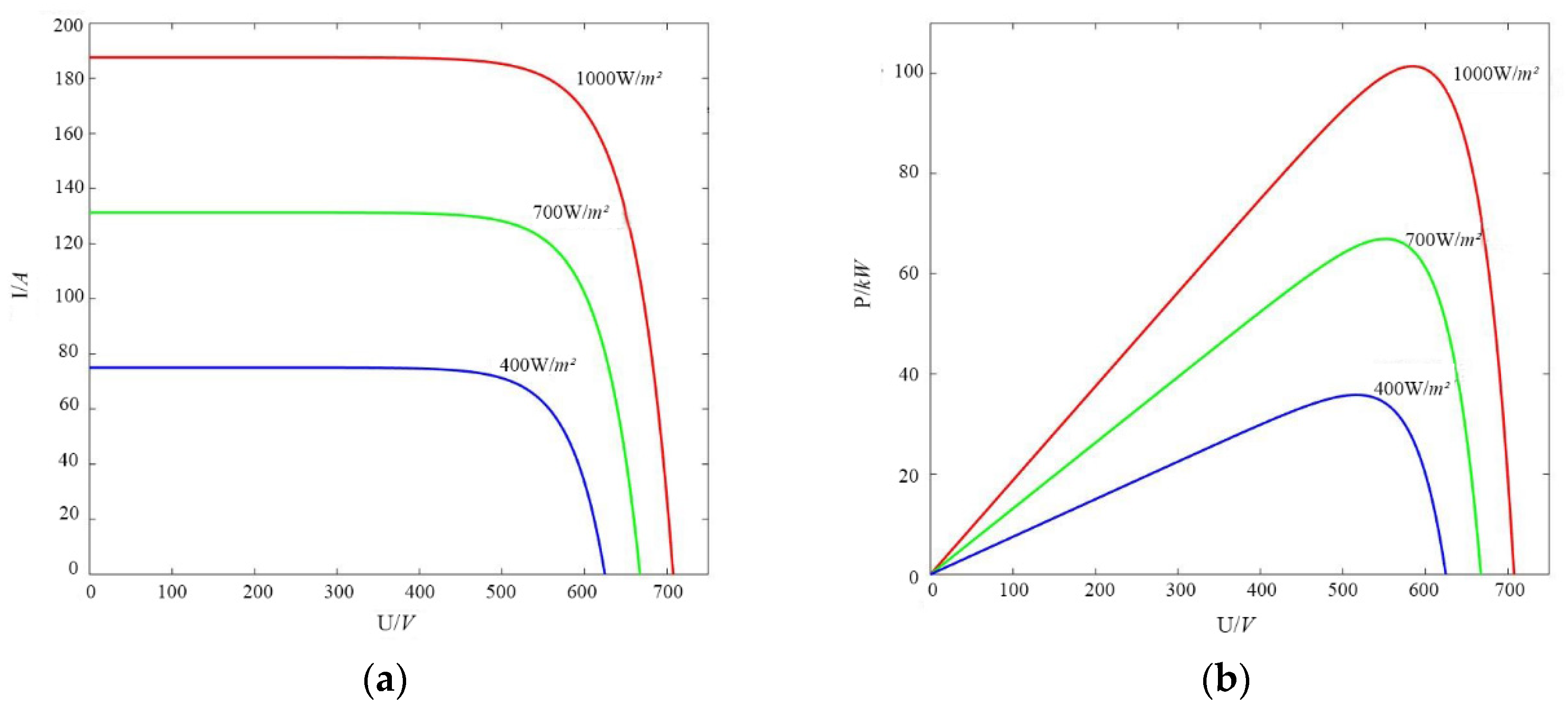
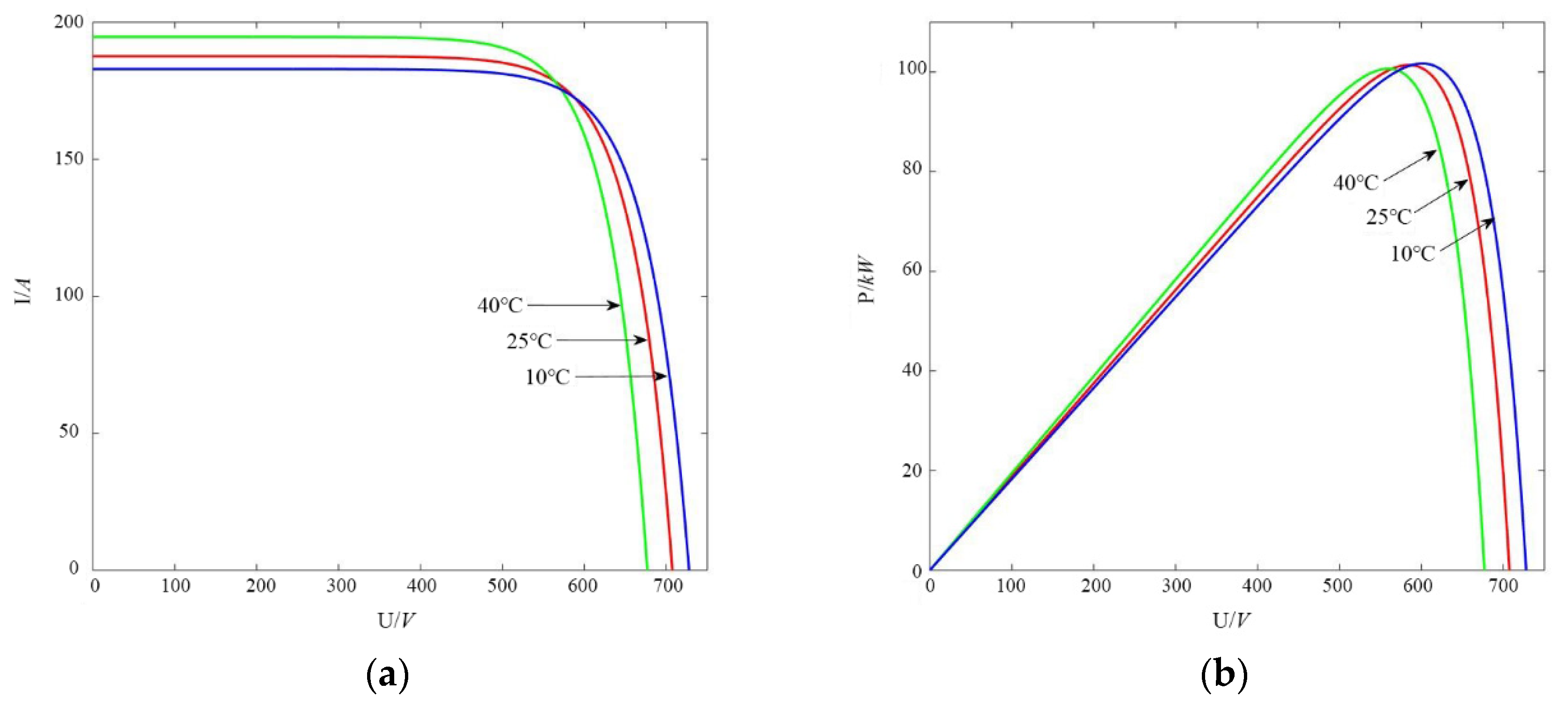
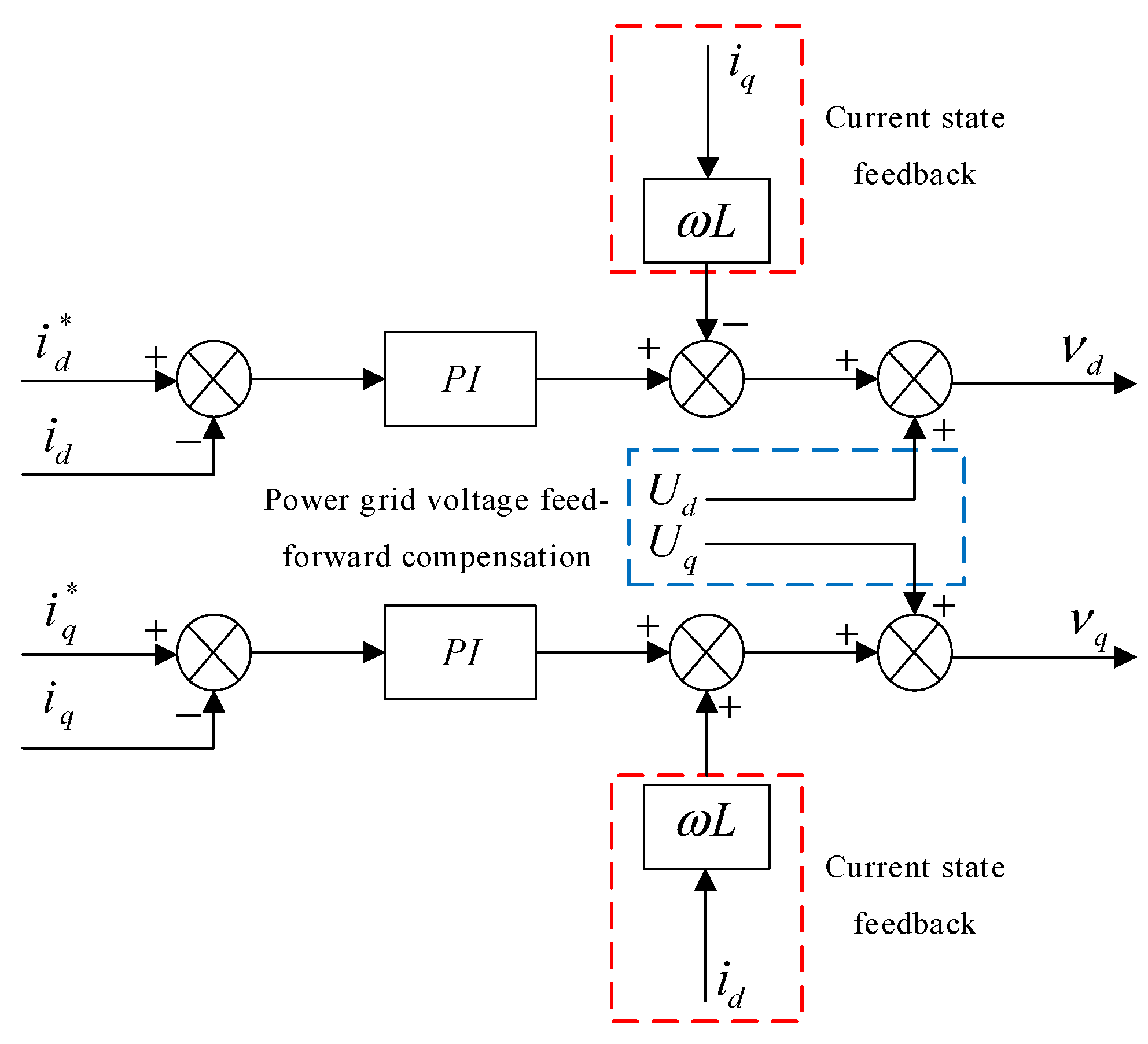
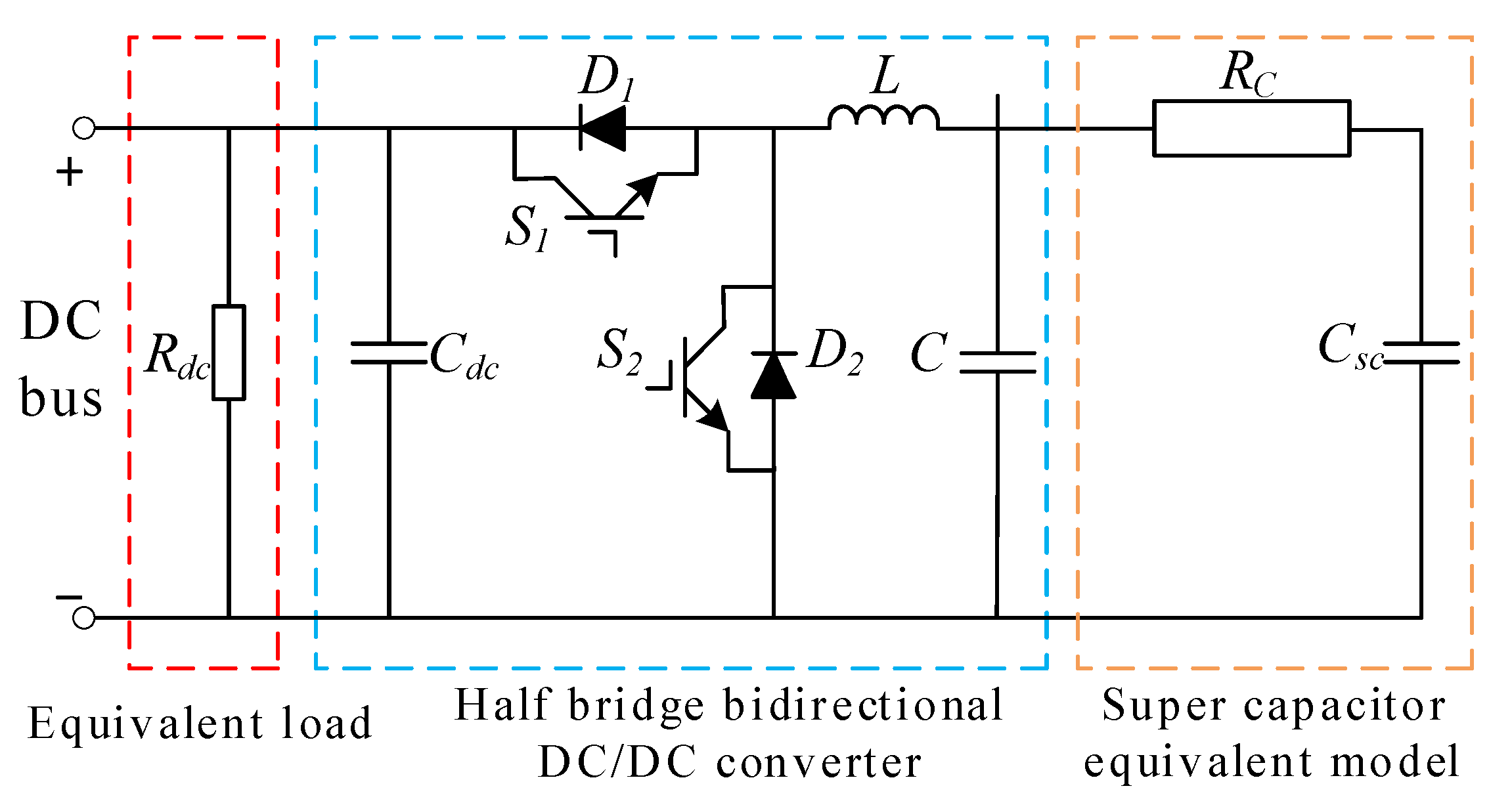



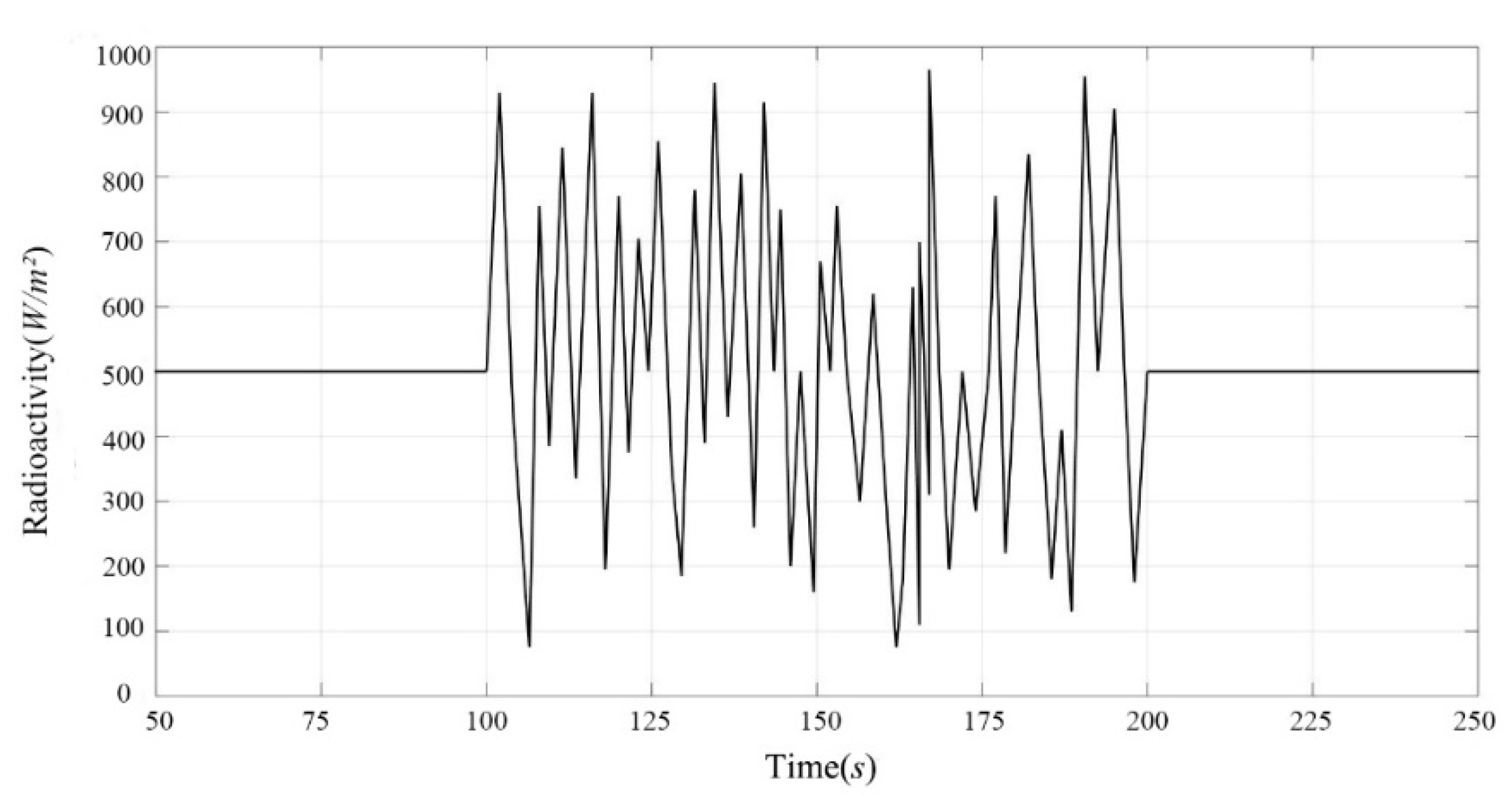

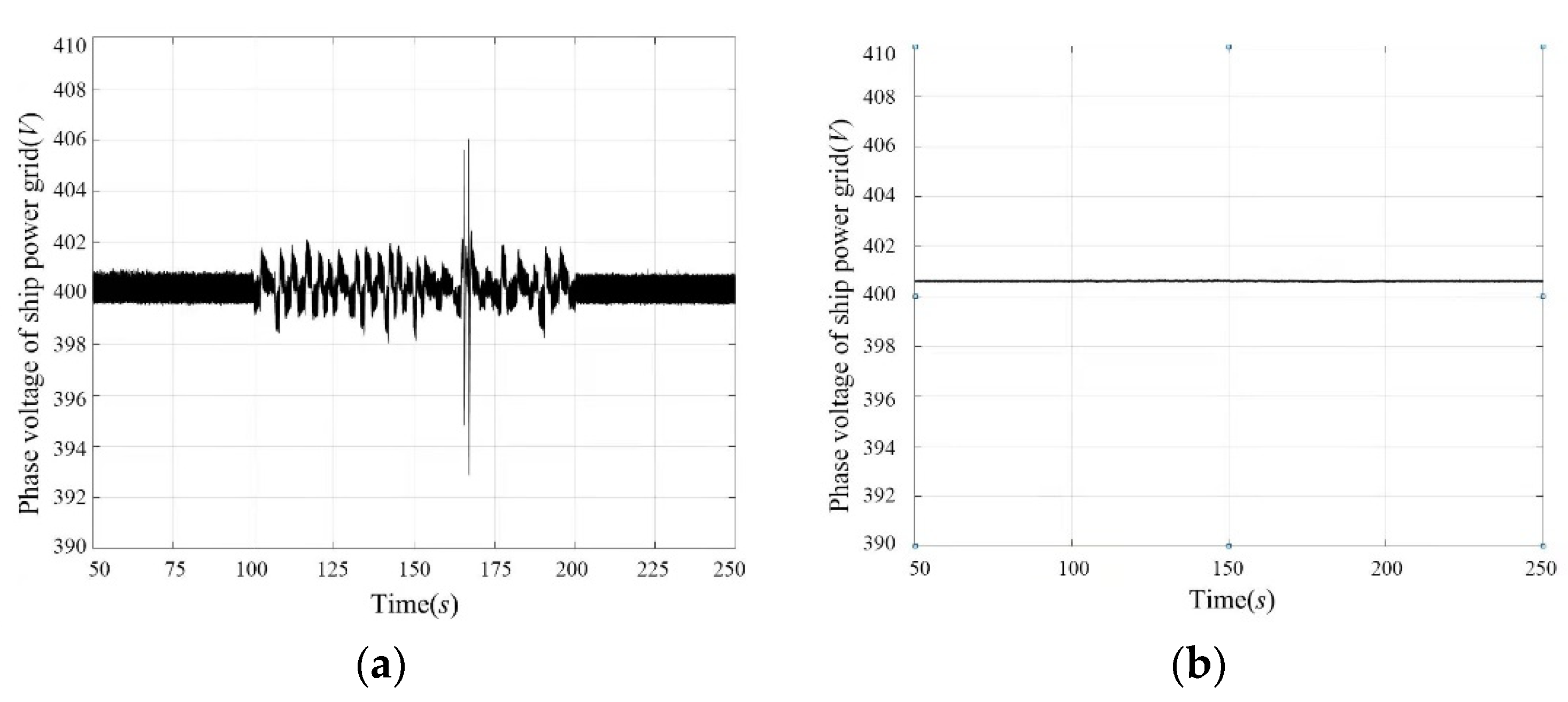
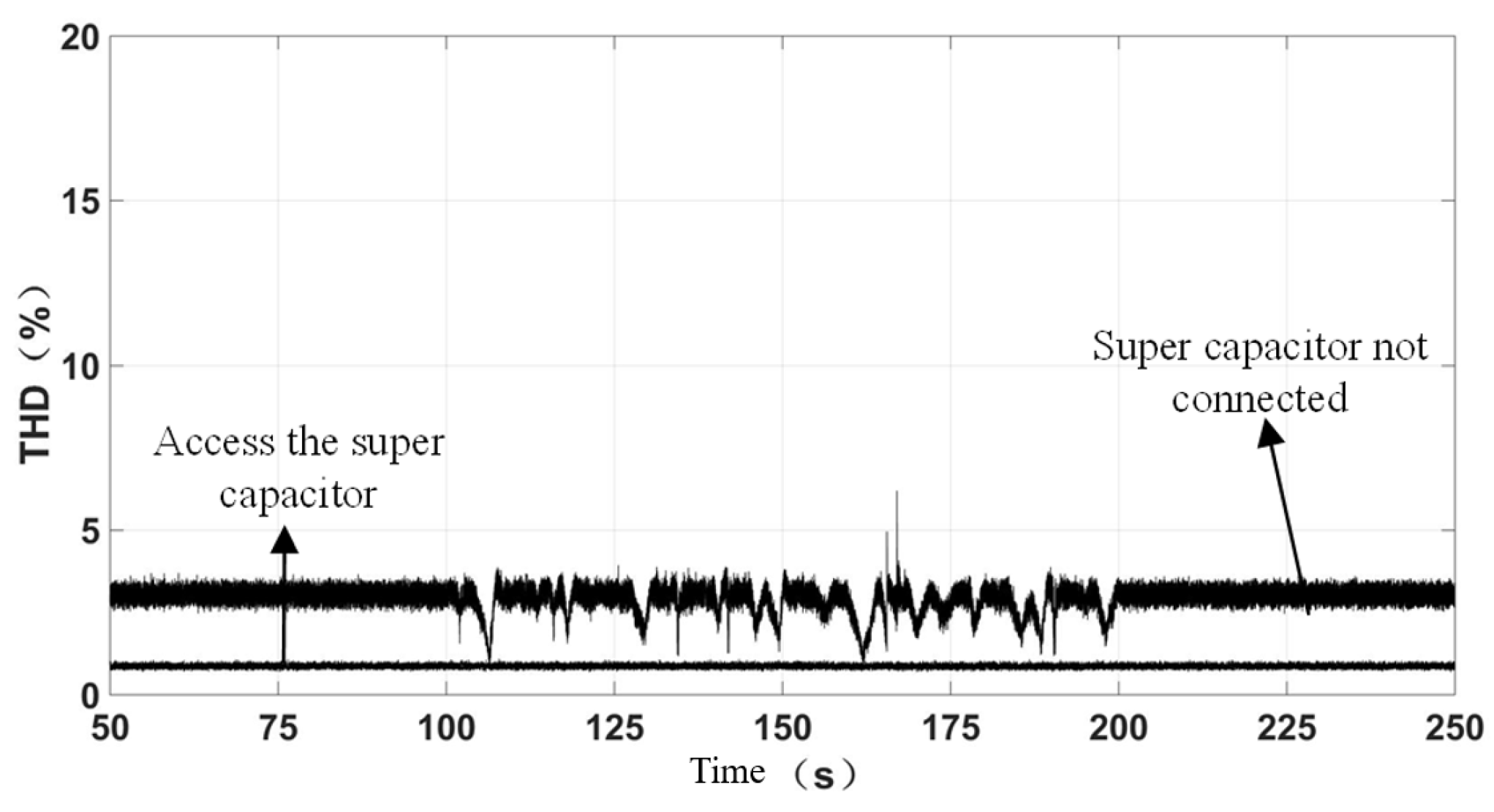




| Performance Comparison | Charging Time/(s) | Discharge Time/(s) | Power Density/(W/kg) | Charge and Discharge Efficiency/(%) | Product Maintenance | Service Life/(Years) |
|---|---|---|---|---|---|---|
| Lithium battery | (3.6~18) × 103 | (1.08~10.8) × 103 | <103 | 70–85 | high cost | 4–6 |
| Super capacitor | 0.3~30 | 0.3~30 | <104 | 85–98 | low cost | 10–15 |
| String Relationship | Total Power/kW | Open Circuit Voltage/V | Short Circuit Current/A | Peak Voltage/V | Peak Current/A |
|---|---|---|---|---|---|
| 18 series 20 parallel | 102.7 | 712.8 | 188.2 | 570.6 | 180 |
| Equipment | Parameter | Value | Unit |
|---|---|---|---|
| Photovoltaic controller | C1 | 1.7 | mF |
| L1 | 16 | µH | |
| D | 0.1% | - | |
| Cdc | 10 | mF | |
| Bidirectional DC/DC converter | IGTT switching frequency | 4 | kHz |
| C2 | 1 | mF | |
| L2 | 3 | mH | |
| Kp1 | 0.8 | - | |
| Ki1 | 100 | - | |
| Kp2 | 0.2 | - | |
| Ki2 | 30 | - | |
| Super capacitor | Operating voltage range | 240~300 | VDC |
| Energy storage capacity | 6 | kWh | |
| Maximum output current limit | 400 | A | |
| Inverter | C3 | 20 | µF |
| L3 | 0.5 | mH | |
| Kp3 | 0.01 | - | |
| Ki3 | 3 | - | |
| Kp2 | 120 | - | |
| Ki2 | 5 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Tang, X.; Liu, X.; Xu, C. Research on Low Voltage Ride through Control of a Marine Photovoltaic Grid-Connected System Based on a Super Capacitor. Energies 2022, 15, 1020. https://doi.org/10.3390/en15031020
Wang S, Tang X, Liu X, Xu C. Research on Low Voltage Ride through Control of a Marine Photovoltaic Grid-Connected System Based on a Super Capacitor. Energies. 2022; 15(3):1020. https://doi.org/10.3390/en15031020
Chicago/Turabian StyleWang, Shihao, Xujing Tang, Xionghang Liu, and Chen Xu. 2022. "Research on Low Voltage Ride through Control of a Marine Photovoltaic Grid-Connected System Based on a Super Capacitor" Energies 15, no. 3: 1020. https://doi.org/10.3390/en15031020







