Design and Performance Evaluation of SMC-Based DC–DC Converters for Microgrid Applications
Abstract
1. Introduction
2. Proposed Methodology
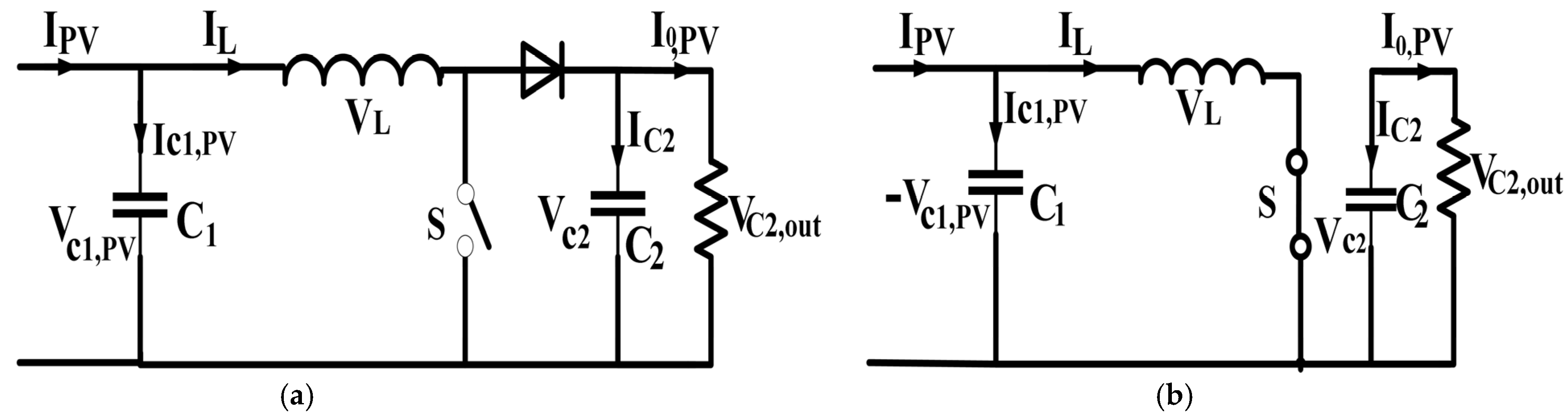
2.1. Control Signal of Step-Up Converter for the PV System
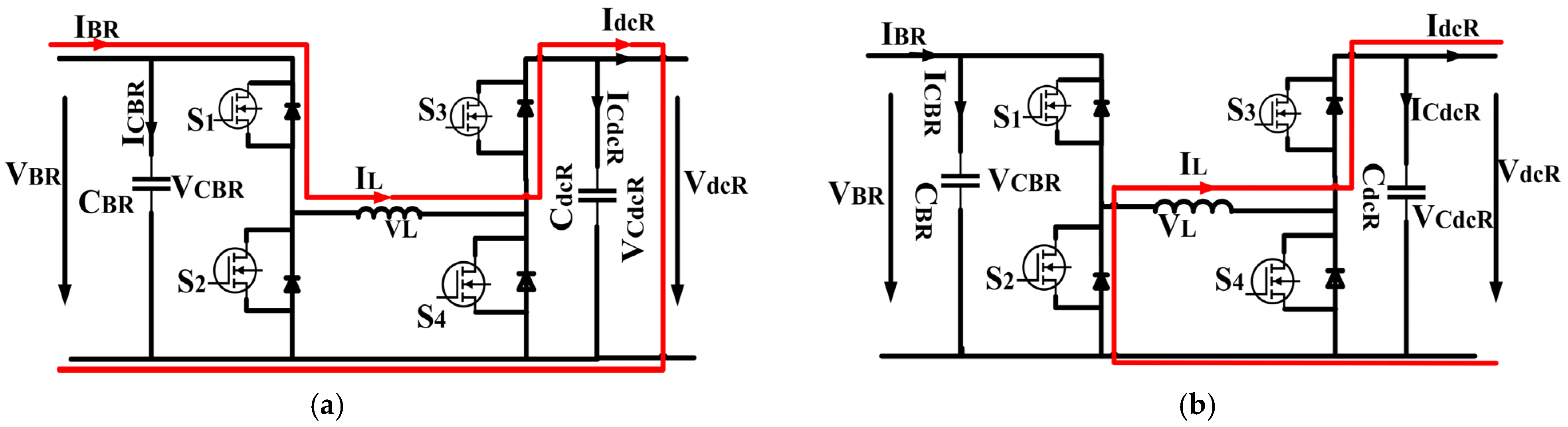
2.2. Step-Down Operational Phase for the Converter of Battery System
2.3. Boost Reverse-Operational Phase for the Converter of the Battery System
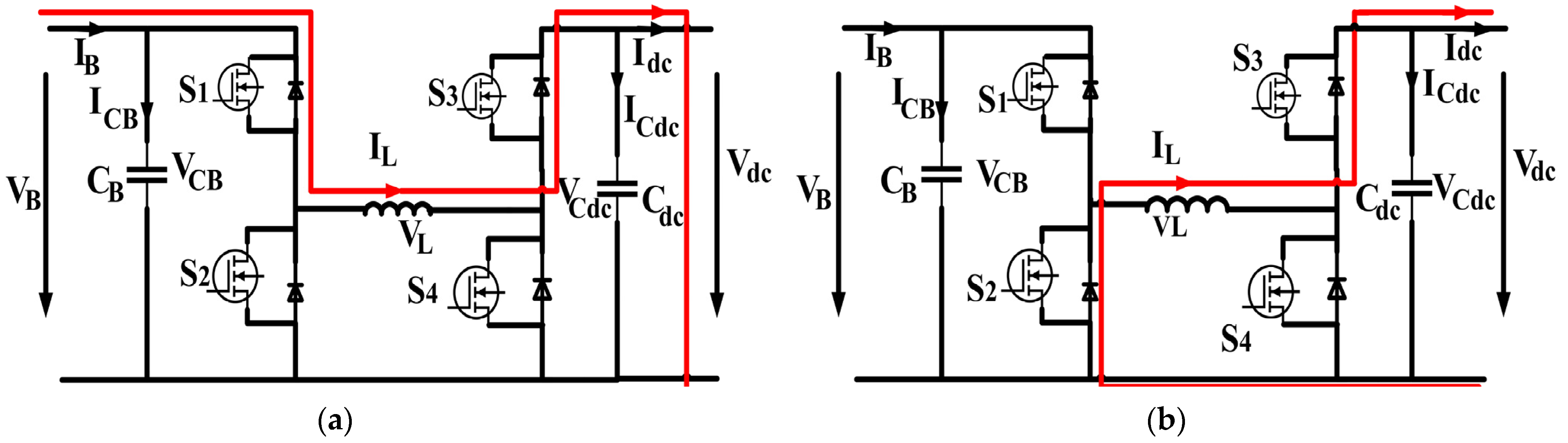
2.4. Control Signal of Buck Mode for the Load-Side Converter
2.5. Control Signal of Boost Mode for the Load-Side Converter
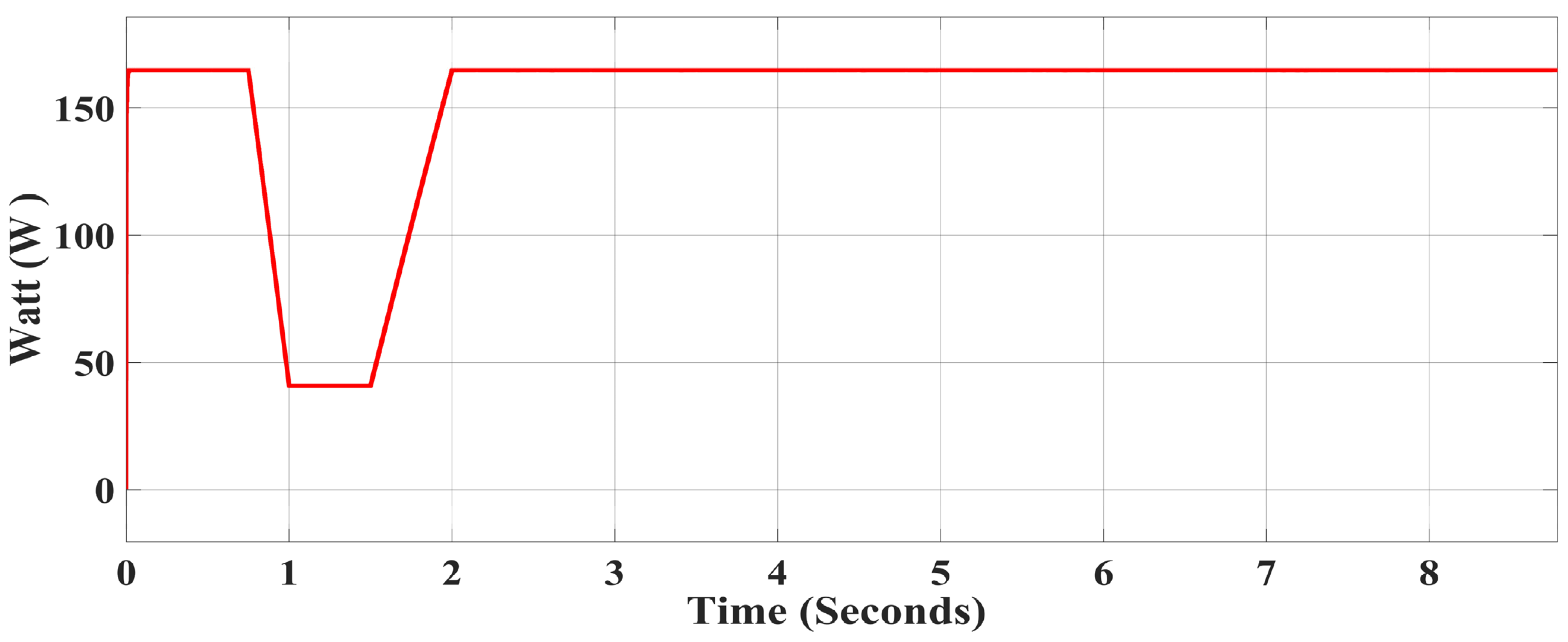
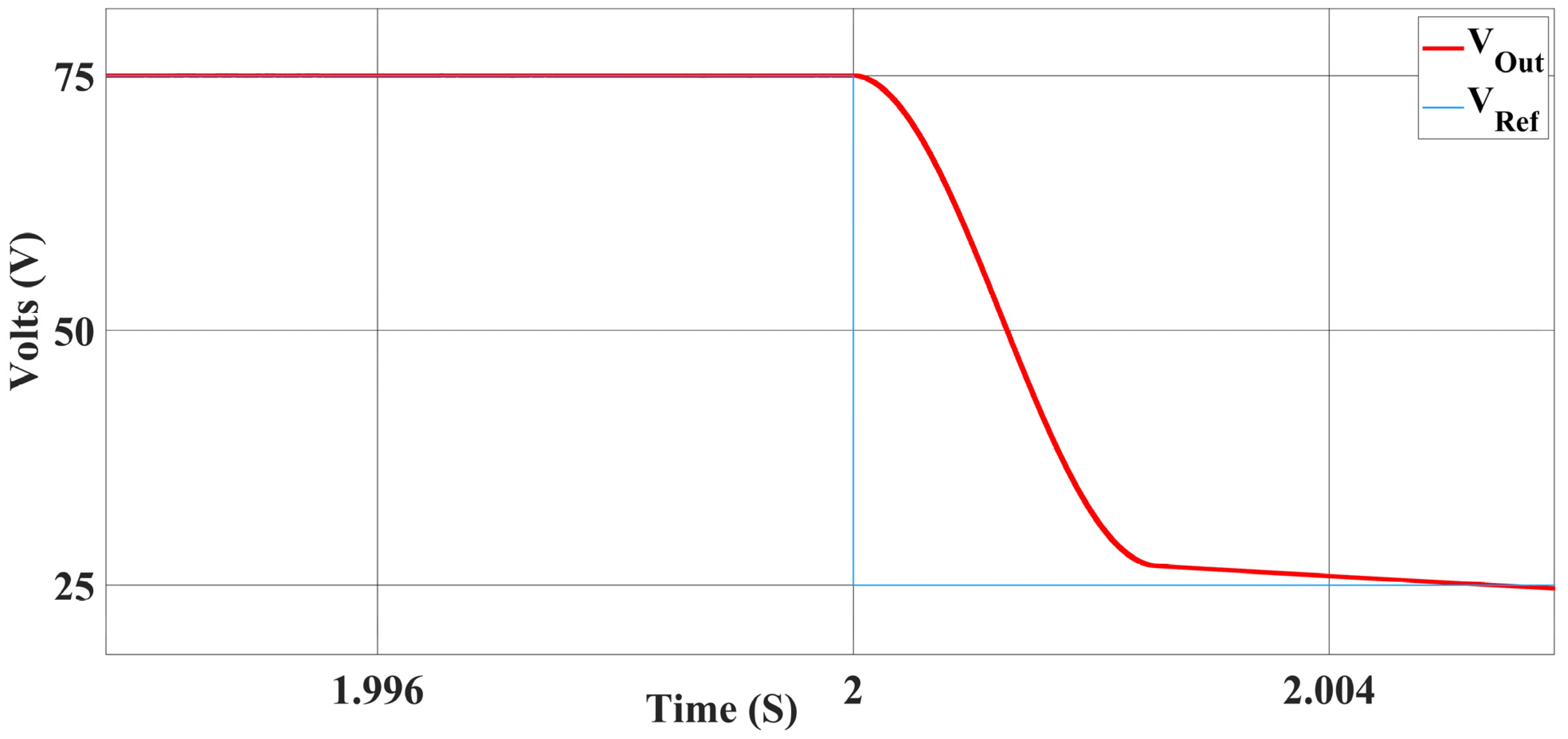
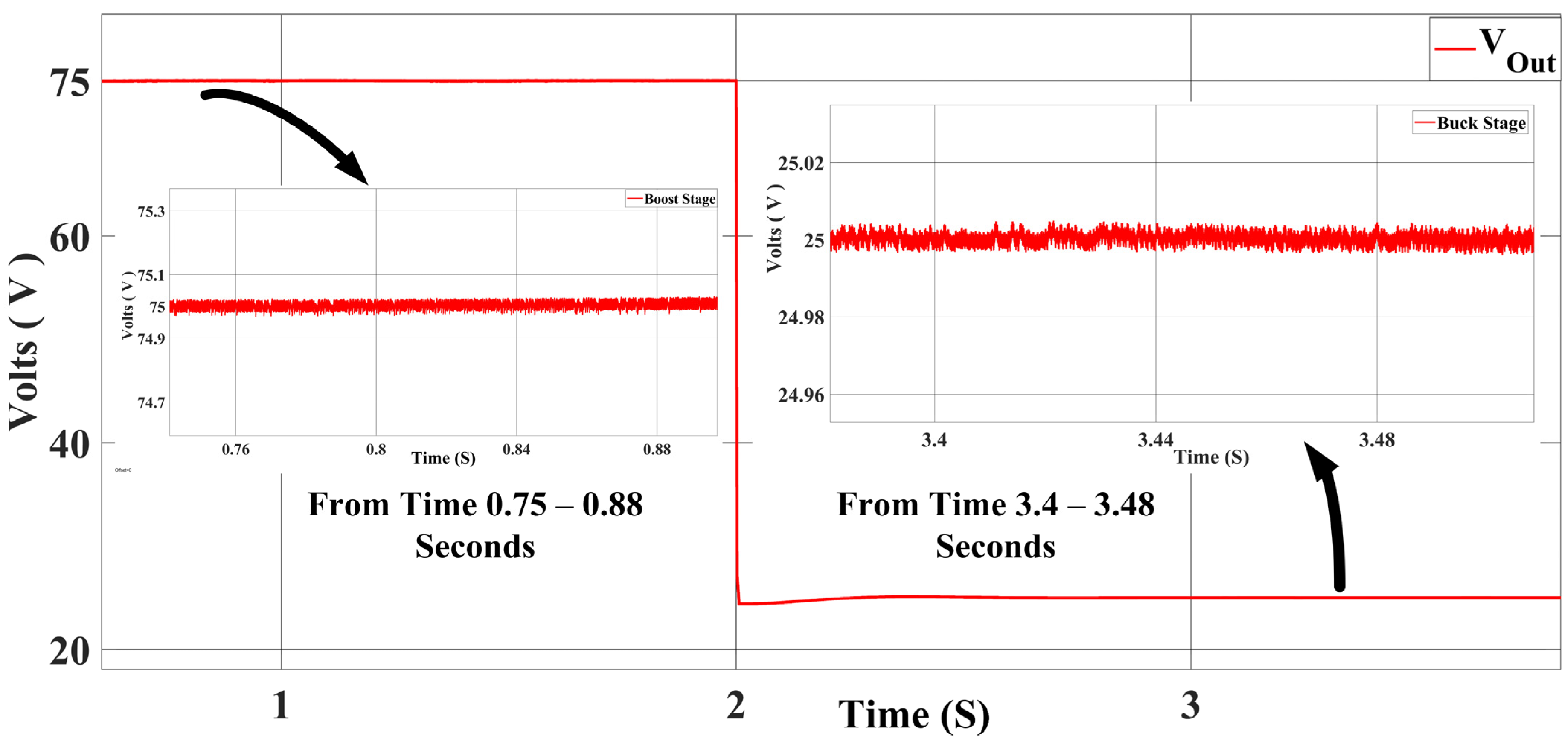
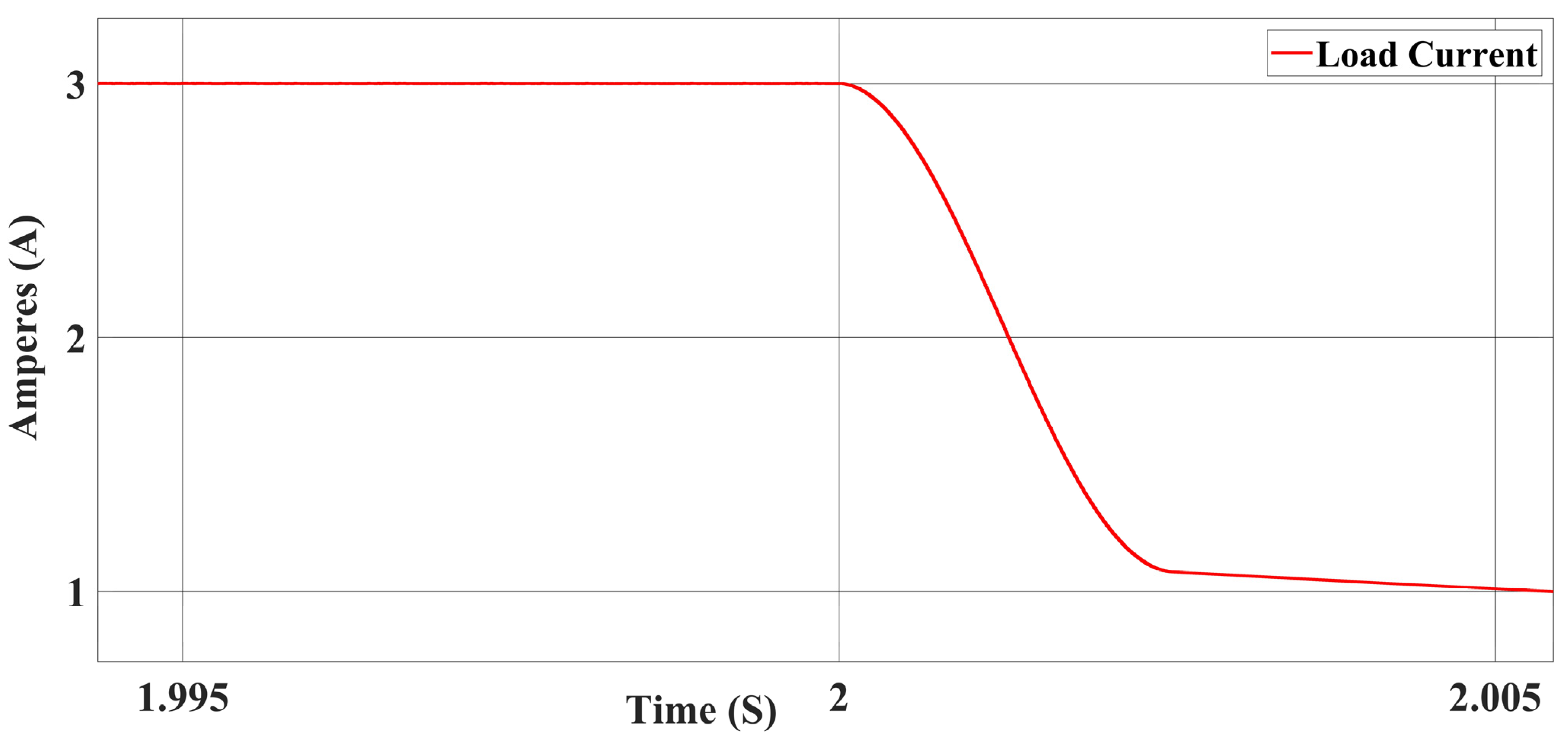
3. Simulation Results and Discussion
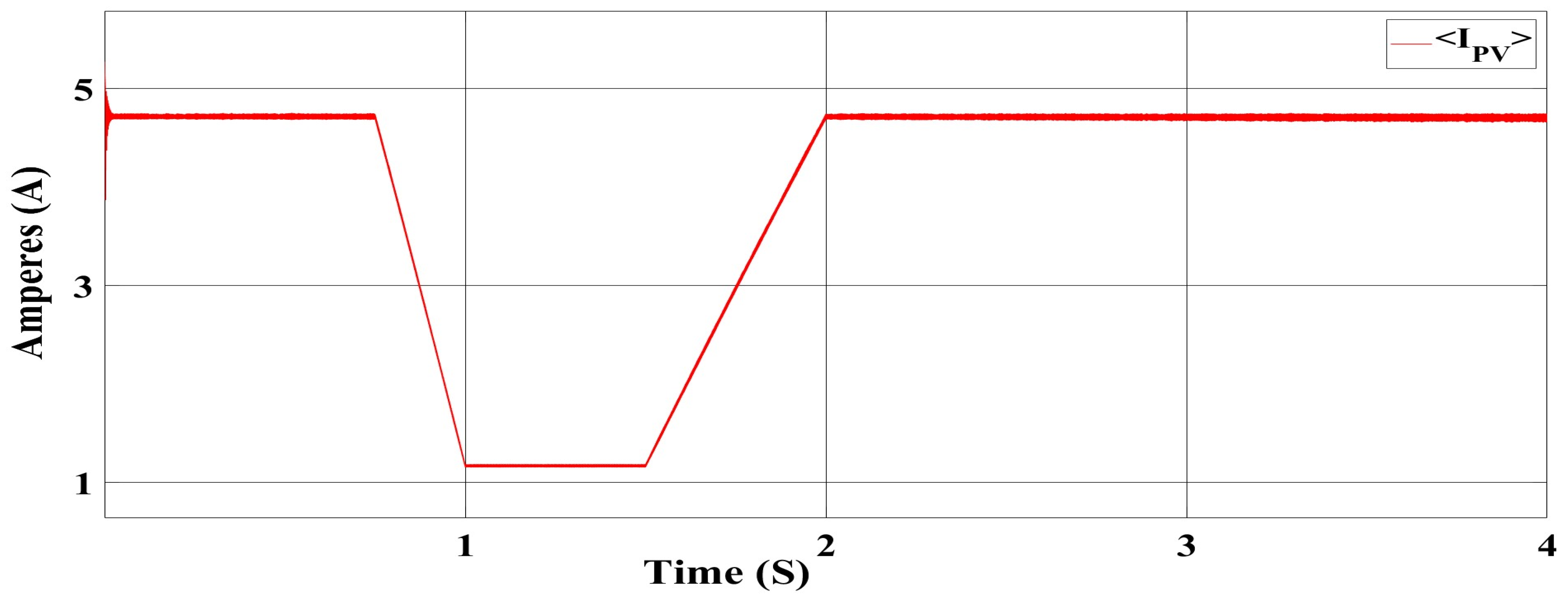
3.1. Analysis of PV-Side Converter
3.2. Analysis of Battery Converter
3.3. Results from Load-Side Converter
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anuraag, B.V.; Mahalakshmi, R.; Likhtih, S.; Bhargavi, P.; Mohanty, A. Design and Comparative Study of DC-DC Quadratic Buck-Boost Converter and Cascaded Buck-Boost Converter. In Proceedings of the 2021 International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 27–28 August 2021; pp. 642–646. [Google Scholar]
- Masood, B.; Saleem, U.; Nadeem Anjum, M.; Arshad, U. Faults Detection and Diagnosis of Transmission Lines Using Wavelet Transformed Based Technique. In Proceedings of the 2017 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies, AEECT 2017, Amman, Jordan, 11–13 October 2017. [Google Scholar]
- Eto, J.H.; Lasseter, R.; Klapp, D.; Khalsa, A.; Baktiono, S.; Schenkman, B.; Illindala, M. The CERTS Microgrid Concept, as Demonstrated at the CERTS/AEP Microgrid Test Bed Authors and Contributors; U.S. Department of Energy’s Office of Electricity: Washington, DC, USA, 2018.
- Zhao, Z.; Yang, P.; Bottrell, N.; Lai, L.L.; Green, T.C. Dynamic Modeling, Sensitivity Assessment, and Design of VSC-Based Microgrids with Composite Loads. J. Power Electron. 2020, 20, 245–259. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, D.; Zhang, J.; Liu, H.; Cai, G. A Bidirectional Dual Buck-Boost Voltage Balancer with Direct Coupling Based on a Burst-Mode Control Scheme for Low-Voltage Bipolar-Type DC Microgrids. J. Power Electron. 2015, 15, 1609–1618. [Google Scholar] [CrossRef]
- Lin, C.C.; Yang, L.S.; Wu, G.W. Study of a Non-Isolated Bidirectional DC-DC Converter. IET Power Electron. 2013, 6, 30–37. [Google Scholar] [CrossRef]
- Chen, G.; Lee, Y.S.; Hui, S.Y.R.; Xu, D.; Wang, Y. Actively Clamped Bidirectional Flyback Converter. IEEE Trans. Ind. Electron. 2000, 47, 770–779. [Google Scholar] [CrossRef]
- Li, H.; Peng, F.Z.; Lawler, J.S. A Natural ZVS Medium-Power Bidirectional DC-DC Converter with Minimum Number of Devices. IEEE Trans. Ind. Appl. 2003, 39, 525–535. [Google Scholar] [CrossRef]
- Lin, B.R.; Huang, C.L.; Lee, Y.E. Asymmetrical Pulse-Width Modulation Bidirectional DC-DC Converter. IET Power Electron. 2008, 1, 336–347. [Google Scholar] [CrossRef]
- Mi, C.; Bai, H.; Wang, C.; Gargies, S. Operation, Design and Control of Dual H-Bridge-Based Isolated Bidirectional DC-DC Converter. IET Power Electron. 2008, 1, 507–517. [Google Scholar] [CrossRef]
- Naayagi, R.T.; Forsyth, A.J.; Shuttleworth, R. High-Power Bidirectional DC-DC Converter for Aerospace Applications. IEEE Trans. Power Electron. 2012, 27, 4366–4379. [Google Scholar] [CrossRef]
- Khan, F.H.; Tolbert, L.M.; Webb, W.E. Hybrid Electric Vehicle Power Management Solutions Based on Isolated and Nonisolated Configurations of Multilevel Modular Capacitor-Clamped Converter. IEEE Trans. Ind. Electron. 2009, 56, 3079–3095. [Google Scholar] [CrossRef]
- Ko, Y.P.; Lee, Y.S.; Chao, W.H. Analysis, Design and Implementation of Fuzzy Logic Controlled Quasi-Resonant Zero-Current Switching Switched-Capacitor Bidirectional Converter. IET Power Electron. 2011, 4, 683–692. [Google Scholar] [CrossRef]
- Kim, I.D.; Paeng, S.H.; Ahn, J.W.; Nho, E.C.; Ko, J.S. New Bidirectional ZVS PWM Sepic/Zeta DC-DC Converter. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007. [Google Scholar]
- Jose, P.; Mohan, N. A Novel ZVS Bidirectional Ćuk Converter for Dual Voltage Systems in Automobiles. In Proceedings of the IECON’03. 29th Annual Conference of the IEEE Industrial Electronics Society, Roanoke, VA, USA, 3–6 November 2003. [Google Scholar]
- Wai, R.J.; Duan, R.Y. High-Efficiency Bidirectional Converter for Power Sources with Great Voltage Diversity. IEEE Trans. Power Electron. 2007, 22, 1986–1996. [Google Scholar] [CrossRef]
- Wu, T.F.; Yang, J.G.; Kuo, C.L.; Kuo, M.C. Optimal Negative Current Control for Four-Phase Interleaved Bi-Directional Buck/Boost Converters to Achieve ZVS and ZCS. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 2017–2022. [Google Scholar] [CrossRef]
- Ning, J.; Zeng, J.; Du, X. A Four-Port Bidirectional DC-DC Converter for Renewable Energy-Battery-DC Microgrid System. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition, ECCE 2019, Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar]
- Zeng, J.; Du, X.; Yang, Z. A Multiport Bidirectional DC-DC Converter for Hybrid Renewable Energy System Integration. IEEE Trans. Power Electron. 2021, 36, 12281–12291. [Google Scholar] [CrossRef]
- Zubieta, L.E.; Lehn, P.W. A High Efficiency Unidirectional DC/DC Converter for Integrating Distributed Resources into DC Microgrids. In Proceedings of the 2015 IEEE 1st International Conference on Direct Current Microgrids, ICDCM 2015, Atlanta, GA, USA, 7–10 June 2015. [Google Scholar]
- Fusheng, Z.; Naayagi, R.T. Power Converters for DC Microgrids—Modelling and Simulation. In Proceedings of the International Conference on Innovative Smart Grid Technologies, ISGT Asia 2018, Singapore, 22–25 May 2018. [Google Scholar]
- Sim, J.; Lee, J.; Choi, H.; Jung, J.H. High Power Density Bidirectional Three-Port DC-DC Converter for Battery Applications in DC Microgrids. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019. [Google Scholar]
- Sarvi, M.; Soltani, I.; NamazyPour, N.; Rabbani, N. A New Sliding Mode Controller for DC/DC Converters in Photovoltaic Systems. J. Energy 2013, 2013, 871025. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. Perturb and Observe MPPT Algorithm with a Current Controller Based on the Sliding Mode. Int. J. Electr. Power Energy Syst. 2013, 44, 346–356. [Google Scholar] [CrossRef]
- Ullah, Q.; Wu, X.; Saleem, U. Current Controlled Robust Four-Switch Buck-Boost DC-DC Converter. In Proceedings of the 2021 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 26–27 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cong, W.; Jain, P. A Quantitative Comparison and Evaluation of 48V DC and 380V DC Distribution Systems for Datacenters. In Proceedings of the 2014 IEEE 36th International Telecommunications Energy Conference (INTELEC) 2014, Vancouver, Canada, 28 September–2 October 2014. [Google Scholar] [CrossRef]
- Wu, L.; Kihinet, W.; Robelo, E.; Bezabih, E.; Longwood, K.; Tshimanga, T.; Saeedifard, M.; Lambert, F.; Harley, R. Development of a Solar-Power-Based Nanogrid System for Village Huts in Haiti Mountain Area; Development of a Solar-Power-Based Nanogrid System for Village Huts in Haiti Mountain Area. In Proceedings of the 2016 North American Power Symposium (NAPS) 2016, Denver, CO, USA, 18–20 September 2016. [Google Scholar] [CrossRef]
- Khan, H.S.; Mohamed, I.S.; Kauhaniemi, K.; Liu, L. Artificial Neural Network-Based Voltage Control of DC/DC Converter for DC Microgrid Applications. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orelans, LA, USA, 8–10 November 2021. [Google Scholar]
- Hu, Y.; Chen, H.; Xu, R.; Li, R.; Fang, Z. A Type of High Step-up DC-DC Converter. Diangong Jishu Xuebao Trans. China Electrotech. Soc. 2012, 27, 224–230. [Google Scholar] [CrossRef]
- Chen, Z.X.; Wang, J.; Ge, L.S.; Jiang, T.; Liu, Y.F.; Liu, Y.F. Double Integral Sliding Mode Control of Paralleled DC/DC Converters. In Proceedings of the 2015 10th IEEE Conference on Industrial Electronics and Applications, ICIEA 2015, Auckland, New Zealand, 15–17 June 2015; pp. 1134–1138. [Google Scholar] [CrossRef]
- Safari, A.; Ardi, H. Sliding Mode Control of a Bidirectional Buck/Boost DC-DC Converter with Constant Switching Frequency. Iran. J. Electr. Electron. Eng. 2018, 14, 69. [Google Scholar]
- Chatrenour, N.; Razmi, H.; Doagou-Mojarrad, H. Improved Double Integral Sliding Mode MPPT Controller Based Parameter Estimation for a Stand-Alone Photovoltaic System. Energy Convers. Manag. 2017, 139, 97–109. [Google Scholar] [CrossRef]
- Pradhan, R.; Subudhi, B. Double integral sliding mode MPPT control of a photovoltaic system. IEEE Trans. Contr. Syst. Technol. 2016, 24, 285–292. [Google Scholar] [CrossRef]
- Zehelein, M.; Ruthardt, J.; Nitzsche, M.; Tymosch, T.; Roth-Stielow, J. Leakage current reduction for a double-leg boost converter by switching transition synchronization. J. Eng. 2019, 2019, 3789–3792. [Google Scholar] [CrossRef]
- Mahery, H.M.; Babaei, E. Mathematical modeling of buck-boost dc-dc converter and investigation of converter elements on transient and steady state responses. Int. J. Electr. Power Energy Syst. 2013, 44, 949–963. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Xue, Y. Four-Switch Buck-Boost Converter Based on Model Predictive Control with Smooth Mode Transition Capability. IEEE Trans. Ind. Electron. 2020, 68, 9058–9069. [Google Scholar] [CrossRef]






| Parameter Name | Symbol | Value |
|---|---|---|
| Positive integer for signum function | ϕ | 0.49 |
| Coefficients of the required sliding surface | a1 | 2.1 |
| a2 | 3.2 | |
| a3 | 3.99 | |
| a4 | 1 | |
| Boundary layer’s thickness | α | 0.5 |
| Parameter Name | Symbol | Value |
|---|---|---|
| Positive integer for signum function | ϕ | 0.5 |
| Coefficients of the required sliding surface | a1 | 90 |
| a2 | 1000 | |
| a3 | 1000 | |
| a4 | 1 | |
| Boundary layer’s thickness | α | 0.5 |
| Parameter Name | Symbol | Value |
|---|---|---|
| Positive integer for signum function | ϕ | 0.5 |
| Coefficients of the required sliding surface | a1 | 85 |
| a2 | 870 | |
| a3 | 870 | |
| a4 | 1 | |
| Boundary layer’s thickness | α | 0.5 |
| Component | Symbol | Value | Unit |
|---|---|---|---|
| Input capacitor | C1 | 370 | uF |
| Inductor | L | 4 | mH |
| Output (DC bus) capacitor | CdcR | 550 | mF |
| Component | Symbol | Value | Unit |
|---|---|---|---|
| Input capacitor | CBR | 1.5 | mF |
| Inductor | L | 0.5 | mH |
| DC bus capacitor | CdcR | 550 | mF |
| Component | Symbol | Value | Unit |
|---|---|---|---|
| Resistive load | R | 25 | Ω |
| Switching frequency | f | 250 | KHz |
| DC bus capacitor | CdcR | 550 | mF |
| Inductor | L | 0.138 | mH |
| Output capacitor | Cdc | 2.5 | mF |
| Operational Stage | Input Voltage (V) | Output Voltage (V) | Output Current (A) |
|---|---|---|---|
| Buck | 48 | 36 | 1.44 |
| Buck | 48 | 25 | 1 |
| Buck | 48 | 12 | 0.48 |
| Boost | 48 | 60 | 2.4 |
| Boost | 48 | 70 | 2.8 |
| Boost | 48 | 75 | 3 |
| References | Findings | Challenges |
|---|---|---|
| [17] | Optimized control of negative current of the step-down/step-up converter | Only works ideally in DCM, with a frequency of less than 80 KHz |
| [34] | Decrease in the leakage current in the double-leg step-up electronic-power converters | Half of the switch transitions are not aligned |
| [35] | Exploration of the steady-state characteristics of buck-boost electronic-power converters | Complicated control structures |
| [36] | MPC-based FSBB converters | Increased computational challenges and DCM operation |
| Proposed Power Converter | SMC-based FSBB converters for DC MGs | This research did not encounter the challenges and limitations described above |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Q.; Busarello, T.D.C.; Brandao, D.I.; Simões, M.G. Design and Performance Evaluation of SMC-Based DC–DC Converters for Microgrid Applications. Energies 2023, 16, 4212. https://doi.org/10.3390/en16104212
Ullah Q, Busarello TDC, Brandao DI, Simões MG. Design and Performance Evaluation of SMC-Based DC–DC Converters for Microgrid Applications. Energies. 2023; 16(10):4212. https://doi.org/10.3390/en16104212
Chicago/Turabian StyleUllah, Qudrat, Tiago Davi Curi Busarello, Danilo Iglesias Brandao, and Marcelo Godoy Simões. 2023. "Design and Performance Evaluation of SMC-Based DC–DC Converters for Microgrid Applications" Energies 16, no. 10: 4212. https://doi.org/10.3390/en16104212
APA StyleUllah, Q., Busarello, T. D. C., Brandao, D. I., & Simões, M. G. (2023). Design and Performance Evaluation of SMC-Based DC–DC Converters for Microgrid Applications. Energies, 16(10), 4212. https://doi.org/10.3390/en16104212








