A Thermal Analysis of a Convective–Radiative Porous Annular Fin Wetted in a Ternary Nanofluid Exposed to Heat Generation under the Influence of a Magnetic Field
Abstract
:1. Introduction
2. Problem Formulation
- Temperature-dependent linear Q
- Temperature-dependent non-linear Q
3. Basic Concepts of DTM
4. Analytical Procedure
- The expression for temperature distribution with linear temperature-dependent Q after applying DTM properties:
- The expression for temperature distribution with non-linear temperature-dependent Q after applying DTM properties:
- For linear Qint
- For non-linear Qint
5. Results and Discussion
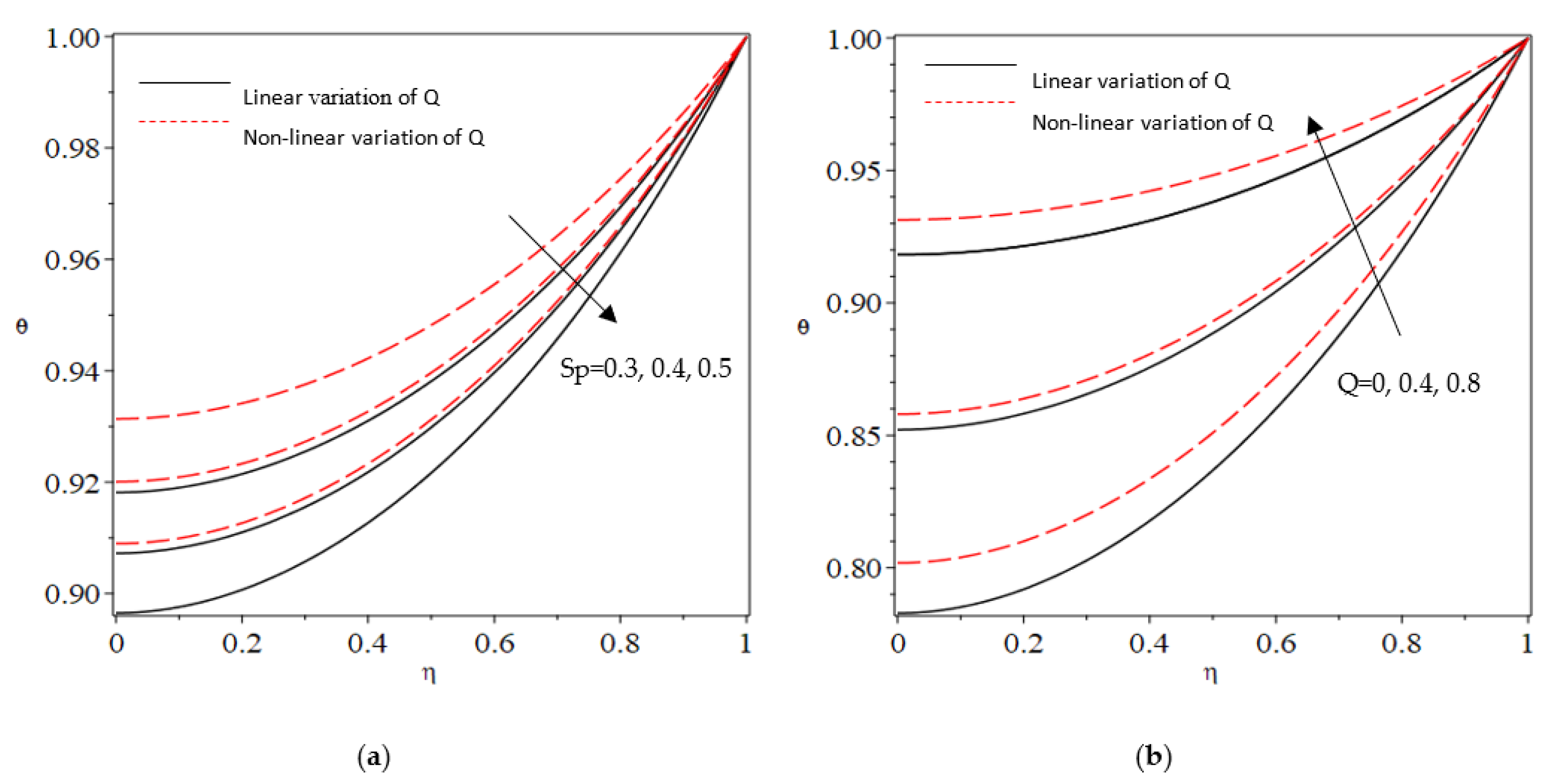
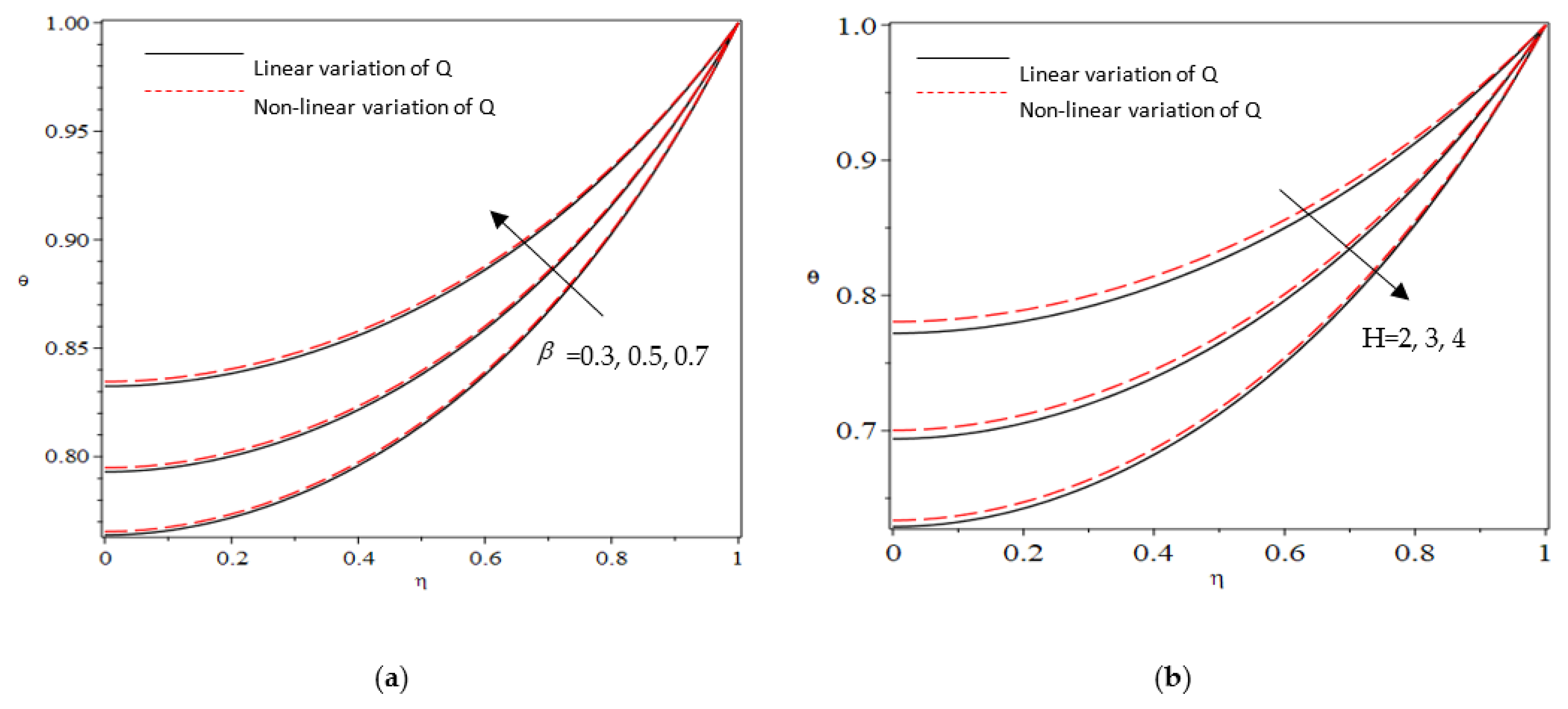
5.1. Nanoparticles Study
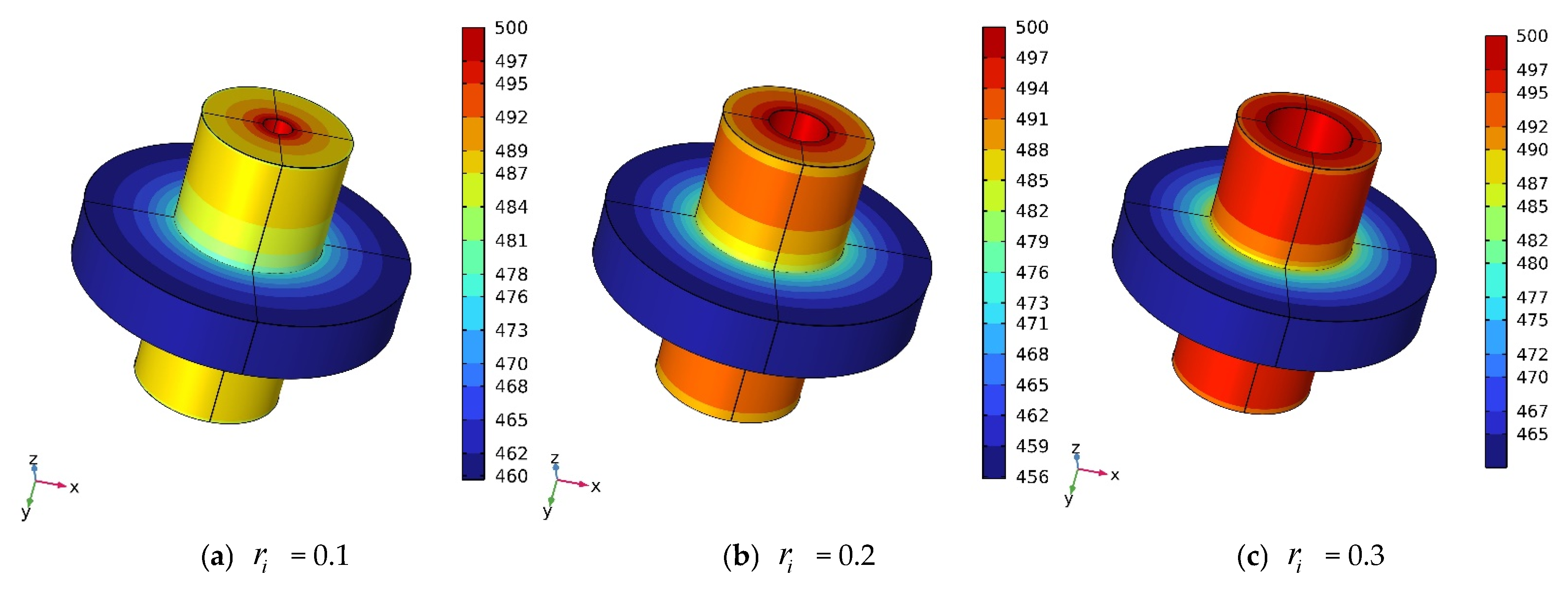
5.2. Thermal Analysis
6. Conclusions
- The heat distribution of the fin can be enhanced by incrementing the values of variable thermal conductivity;
- Non-linear variation in the internal heat source parameter elevated the thermal intensity inside the fin;
- The enhancement of the heat transfer rate is achieved by increasing both the radiative and wet porous parameters. This improvement can be attributed to the combined effects of thermal radiation and the presence of moisture in the vicinity of the fin surface;
- The thickness and inner radius of a fin are crucial factors that impact the heat transmission rate. Based on the analysis, it can be concluded that a cost-effective annular rectangular fin can be achieved by maintaining a thickness of 0.1 and an inner radius of 0.2.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| wet porous parameter | |
| convective-conductive parameter | |
| heat transfer coefficient | |
| heat generation number | |
| aspect ration | |
| specific heat | |
| width of the fin | |
| temperature | |
| emissivity | |
| length | |
| density | |
| acceleration due to gravity | |
| Hartman number | |
| Permeability | |
| density | |
| surface emissivity of fin | |
| non-dimensional temperature | |
| radiative parameter | |
| cross-sectional area | |
| Stefan-Boltzmann constant | |
| thermal conductivity | |
| fin thickness | |
| surface emissivity parameter | |
| mass flow rate | |
| current intensity | |
| fin effectiveness | |
| constants and | |
| variable parameter | |
| heat transfer coefficient at temperature | |
| dimensionless ambient temperature | |
| latent heat of water evaporation |
References
- Hosseinzadeh, K.; Roghani, S.; Mogharrebi, A.; Asadi, A.; Waqas, M.; Ganji, D. Investigation of cross-fluid flow containing motile gyrotactic microorganisms and nanoparticles over a three-dimensional cylinder. Alex. Eng. J. 2020, 59, 3297–3307. [Google Scholar] [CrossRef]
- Hayat, T.; Riaz, R.; Aziz, A.; Alsaedi, A. Influence of Arrhenius activation energy in MHD flow of third grade nanofluid over a nonlinear stretching surface with convective heat and mass conditions. Phys. A Stat. Mech. Its Appl. 2020, 549, 124006. [Google Scholar] [CrossRef]
- Koriko, O.K.; Adegbie, K.S.; Shah, N.A.; Animasaun, I.L.; Olotu, M.A. Numerical solutions of the partial differential equations for investigating the significance ofpartial slip due to lateral velocity and viscous dissipation: The case of blood-gold Carreaunanofluid and dusty fluid. Numer. Methods Partial. Differ. Equ. 2021, 1–29. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar Dusty Fluid: Coriolis Force Effects on Dynamics of MHD Rotating Fluid When Lorentz Force Is Significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Salehi, S.; Nori, A.; Hosseinzadeh, K.; Ganji, D. Hydrothermal analysis of MHD squeezing mixture fluid suspended by hybrid nanoparticles between two parallel plates. Case Stud. Therm. Eng. 2020, 21, 100650. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Madhukesh, J.K.; Shah, N.A.; Yook, S.-J. Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alex. Eng. J. 2023, 64, 969–979. [Google Scholar] [CrossRef]
- Ullah, I.; Ullah, S.; Ali, A.; Shah, S.I.; Weera, W.; Alam, M.M. Heat transfer analysis from moving convection-radiative triangular porous fin exposed to heat generation. Case Stud. Therm. Eng. 2022, 38, 102177. [Google Scholar] [CrossRef]
- Gouran, S.; Ghasemi, S.; Mohsenian, S. Effect of internal heat source and non-independent thermal properties on a convective–radiative longitudinal fin. Alex. Eng. J. 2022, 61, 8545–8554. [Google Scholar] [CrossRef]
- Kumar, R.S.V.; Kumar, R.N.; Sowmya, G.; Prasannakumara, B.C.; Sarris, I.E. Exploration of Temperature Distribution through a Longitudinal Rectangular Fin with Linear and Exponential Temperature-Dependent Thermal Conductivity Using DTM-Pade Approximant. Symmetry 2022, 14, 690. [Google Scholar] [CrossRef]
- Subray, P.V.A.; Hanumagowda, B.N.; Varma, S.V.K.; Zidan, A.M.; Alaoui, M.K.; Raju, C.S.K.; Shah, N.A.; Junsawang, P. Dynamics of Heat Transfer Analysis of Convective-Radiative Fins with Variable Thermal Conductivity and Heat Generation: Differential Transformation Method. Mathematics 2022, 10, 3814. [Google Scholar] [CrossRef]
- Lee, H.-L.; Yang, Y.-C.; Chu, S.-S. Transient thermoelastic analysis of an annular fin with coupling effect and variable heat transfer coefficient. J. Therm. Stress. 2002, 25, 1105–1120. [Google Scholar] [CrossRef]
- Ganji, D.; Ganji, Z. Determination of temperature distribution for annular fins with temperature dependent thermal conductivity by HPM. Therm. Sci. 2011, 15, 111–115. [Google Scholar] [CrossRef]
- Mallick, A.; Prasad, D.K.; Behera, P.P. Stresses in radiative annular fin under thermal loading and its inverse modeling using sine cosine algorithm (SCA). J. Therm. Stress. 2018, 42, 401–415. [Google Scholar] [CrossRef]
- Arslanturk, C. Correlation equations for optimum design of annular fins with temperature dependent thermal conductivity. Heat Mass Transf. 2008, 45, 519–525. [Google Scholar] [CrossRef]
- Das, R. Identification of materials in a hyperbolic annular fin for a given temperature requirement. Inverse Probl. Sci. Eng. 2015, 24, 213–233. [Google Scholar] [CrossRef]
- Sowmya, G.; Gamaoun, F.; Abdulrahman, A.; Kumar, R.S.V.; Prasannakumara, B.C. Significance of thermal stress in a convective-radiative annular fin with magnetic field and heat generation: Application of DTM and MRPSM. Propuls. Power Res. 2022, 11, 527–543. [Google Scholar] [CrossRef]
- Mallick, A.; Das, R. Application of Simplex Search Method for Predicting Unknown Parameters in an Annular Fin Subjected to Thermal Stresses. J. Therm. Stress. 2013, 37, 236–251. [Google Scholar] [CrossRef]
- Ranjan, R.; Mallick, A.; Prasad, D.K. Closed form solution for a conductive–convective–radiative annular fin with multiple nonlinearities and its inverse analysis. Heat Mass Transf. 2016, 53, 1037–1049. [Google Scholar] [CrossRef]
- Sarwe, D.U.; Kulkarni, V.S. Differential transformation method to determine heat transfer in annular fins. Heat Transf. 2021, 50, 7949–7971. [Google Scholar] [CrossRef]
- Kundu, B. Exact Method for Annular Disc Fins with Heat Generation and Nonlinear Heating. J. Thermophys. Heat Transf. 2017, 31, 337–345. [Google Scholar] [CrossRef]
- Reddy, N.K.; Swamy, H.K.; Sankar, M.; Jang, B. MHD convective flow of Ag–TiO2 hybrid nanofluid in an inclined porous annulus with internal heat generation. Case Stud. Therm. Eng. 2023, 42, 102719. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.M.; Kanimozhi, B.; Muthtamilselvan, M.; Abdalla, B. Combined Marangoni and Buoyancy Convection in a Porous Annular Cavity Filled with Ag-MgO/Water Hybrid Nanofluid. Curr. Nanosci. 2023, 19, 4–14. [Google Scholar] [CrossRef]
- Kundu, B.; Lee, K.-S. A proper analytical analysis of annular step porous fins for determining maximum heat transfer. Energy Convers. Manag. 2016, 110, 469–480. [Google Scholar] [CrossRef]
- Kundu, B.; Lee, K.-S. Analytical tools for calculating the maximum heat transfer of annular stepped fins with internal heat generation and radiation effects. Energy 2014, 76, 733–748. [Google Scholar] [CrossRef]
- Rostami, A.K.; Ganji, D.D. Optimization of a shell and helically finned tube heat exchanger with stepped annular fins. ZAMM Z. Fur Angew. Math. Und Mech. 2023, 103, e202200310. [Google Scholar] [CrossRef]
- Sanchouli, M.; Payan, S.; Payan, A.; Nada, S. Investigation of the enhancing thermal performance of phase change material in a double-tube heat exchanger using grid annular fins. Case Stud. Therm. Eng. 2022, 34, 101986. [Google Scholar] [CrossRef]
- Chen, H.-T.; Chiu, Y.-J.; Liu, C.-S.; Chang, J.-R. Numerical and experimental study of natural convection heat transfer characteristics for vertical annular finned tube heat exchanger. Int. J. Heat Mass Transf. 2017, 109, 378–392. [Google Scholar] [CrossRef]
- Nagarani, N.; Mayilsamy, K. Experimental heat transfer analysis on Annular Circular and Elliptical fins. Int. J. Eng. Sci. Technol. 2010, 2, 2839–2845. [Google Scholar]
- Kang, H.S.; Look, D.C. Optimization of a trapezoidal profile annular fin. Heat Transf. Eng. 2009, 30, 359–367. [Google Scholar] [CrossRef]
- Galgat, S.S.; Jadhav, N.P. Experimental Investigation of Heat Transfer Enhancement by Vortex Generators in Heat Ex-changer. Int. Eng. Res. J. 2015, 2, 5290–5294. [Google Scholar]
- Sowmya, G.; Gireesha, B.J.; Prasannakumara, B.C. Scrutinization of different shaped nanoparticle of molybdenum disulfide suspended nanofluid flow over a radial porous fin. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 3685–3699. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Bakier, A. Thermal analysis of natural convection and radiation in porous fins. Int. Commun. Heat Mass Transf. 2011, 38, 638–645. [Google Scholar] [CrossRef]
- Das, R.; Ooi, K. Predicting multiple combination of parameters for designing a porous fin subjected to a given temperature requirement. Energy Convers. Manag. 2013, 66, 211–219. [Google Scholar] [CrossRef]
- Sobamowo, M.G.; Jayesimi, L.O.; Waheed, M.A. Effects of Internal Heat Generation on the Thermal Stability of a Porous Fin. World Sci. News 2020, 149, 110–127. [Google Scholar]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Mallick, A.; Ghosal, S.; Sarkar, P.K.; Ranjan, R. Homotopy Perturbation Method for Thermal Stresses in an Annular Fin with Variable Thermal Conductivity. J. Therm. Stress. 2014, 38, 110–132. [Google Scholar] [CrossRef]
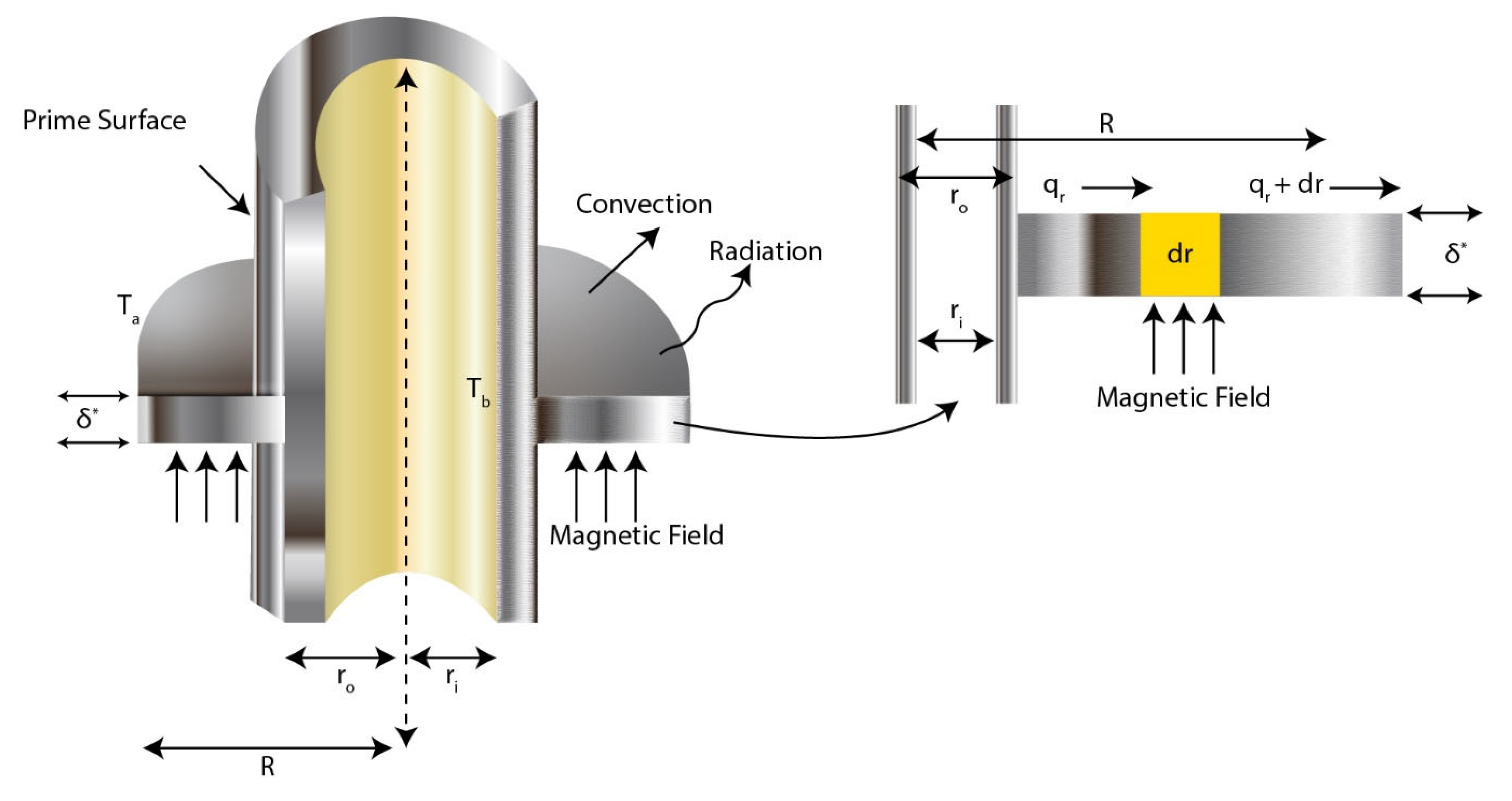



| Properties | Expressions for Ternary Nanofluid Properties |
|---|---|
| Dynamic viscosity | |
| Thermal conductivity | where , |
| Heat capacity | |
| Thermal expansion | |
| Electrical conductivity | where , |
| Basic Function | Transfigured Function |
|---|---|
| where |
| Non-Dimensional Radius | Arslanturk [14] (FDM) | Mallick et al. [36] (HPM) | Present Study (DTM) |
|---|---|---|---|
| 0 | 1.000 | 1.000 | 1.0000 |
| 0.1 | 0.9477 | 0.9455 | 0.9497 |
| 0.2 | 0.9036 | 0.9013 | 0.9054 |
| 0.3 | 0.8668 | 0.8659 | 0.8669 |
| 0.4 | 0.8365 | 0.8380 | 0.8341 |
| 0.5 | 0.8119 | 0.8165 | 0.8067 |
| 0.6 | 0.7927 | 0.8005 | 0.7849 |
| 0.7 | 0.7782 | 0.7891 | 0.7684 |
| 0.8 | 0.7682 | 0.7816 | 0.7574 |
| 0.9 | 0.7624 | 0.7775 | 0.7517 |
| 1 | 0.7605 | 0.7763 | 0.7514 |
| Physical Properties | ||||
|---|---|---|---|---|
| 997.1 | 4179 | 0.613 | 0.05 | |
| Graphene Oxide | 3600 | 765 | 3000 | |
| Cobalt | 8900 | 420 | 100 | |
| Cu | 8933 | 675 | 401 |
| Nanofluid | Hybrid Nanofluid | Ternary Nanofluid | |
|---|---|---|---|
| 0 | 8.645 | 8.648 | 8.686 |
| 0.125 | 8.660 | 8.670 | 8.707 |
| 0.250 | 8.733 | 8.734 | 8.769 |
| 0.375 | 8.831 | 8.836 | 8.869 |
| 0.500 | 8.975 | 8.979 | 9.009 |
| 0.625 | 9.161 | 9.163 | 9.188 |
| 0.750 | 9.391 | 9.392 | 9.409 |
| 0.875 | 9.663 | 9.668 | 9.678 |
| 1 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, A.; Hanumagowda, B.N.; Srilatha, P.; Ananth Subray, P.V.; Varma, S.V.K.; Chohan, J.S.; Alkarni, S.; Shah, N.A. A Thermal Analysis of a Convective–Radiative Porous Annular Fin Wetted in a Ternary Nanofluid Exposed to Heat Generation under the Influence of a Magnetic Field. Energies 2023, 16, 6155. https://doi.org/10.3390/en16176155
Sharma A, Hanumagowda BN, Srilatha P, Ananth Subray PV, Varma SVK, Chohan JS, Alkarni S, Shah NA. A Thermal Analysis of a Convective–Radiative Porous Annular Fin Wetted in a Ternary Nanofluid Exposed to Heat Generation under the Influence of a Magnetic Field. Energies. 2023; 16(17):6155. https://doi.org/10.3390/en16176155
Chicago/Turabian StyleSharma, Arushi, B. N. Hanumagowda, Pudhari Srilatha, P. V. Ananth Subray, S. V. K. Varma, Jasgurpreet Singh Chohan, Shalan Alkarni, and Nehad Ali Shah. 2023. "A Thermal Analysis of a Convective–Radiative Porous Annular Fin Wetted in a Ternary Nanofluid Exposed to Heat Generation under the Influence of a Magnetic Field" Energies 16, no. 17: 6155. https://doi.org/10.3390/en16176155





