A Second-Order Singular Perturbation for Model Simplification for a Microgrid
Abstract
:1. Introduction
2. Second-Order Singular Perturbation
2.1. Precise Model for a Microgrid
2.2. Model Simplification via Singular Perturbation
2.2.1. Timescale Seperation
2.2.2. Traditional Singular Perturbation
2.2.3. The Proposed Second-Order Singular Perturbation
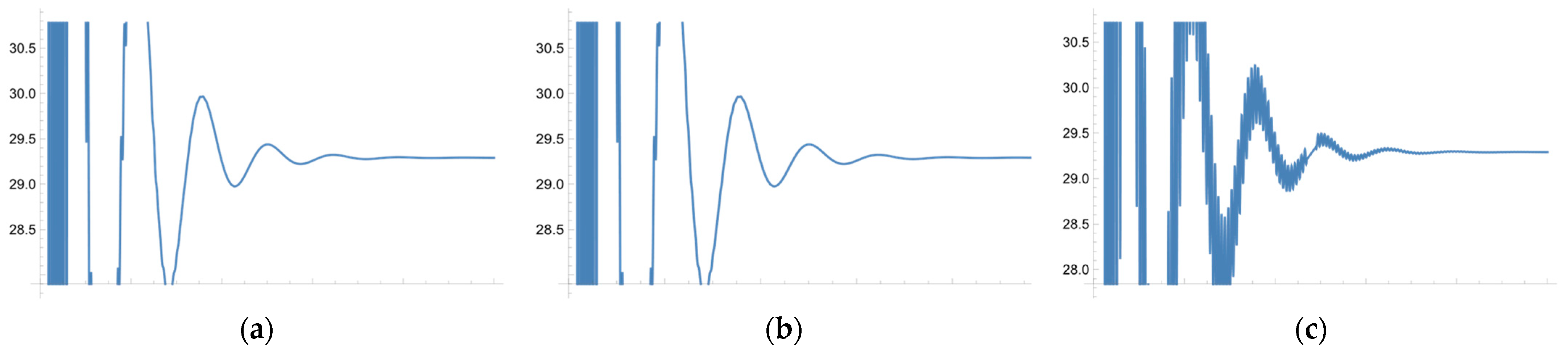
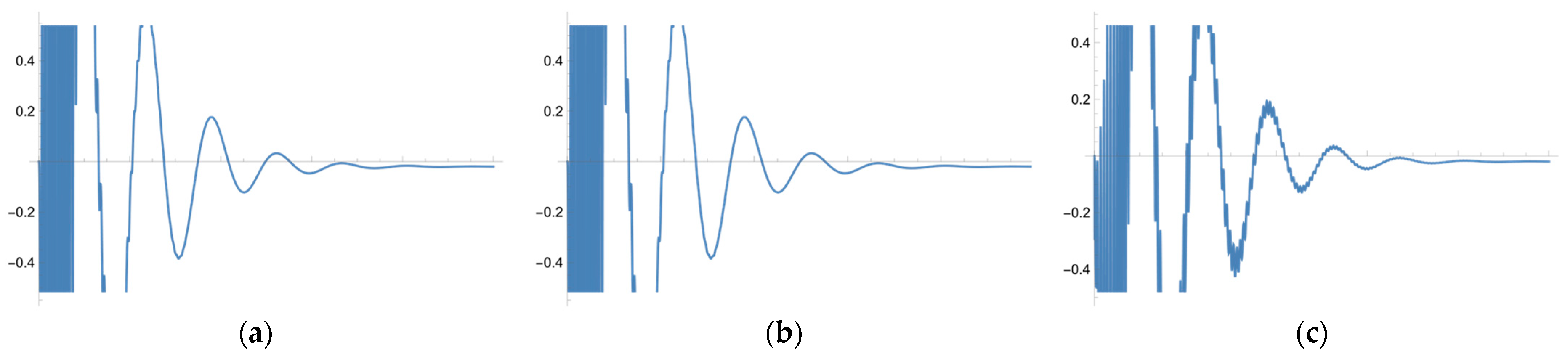
3. Parameter Setting and Experiment Results
3.1. Parameter Setting
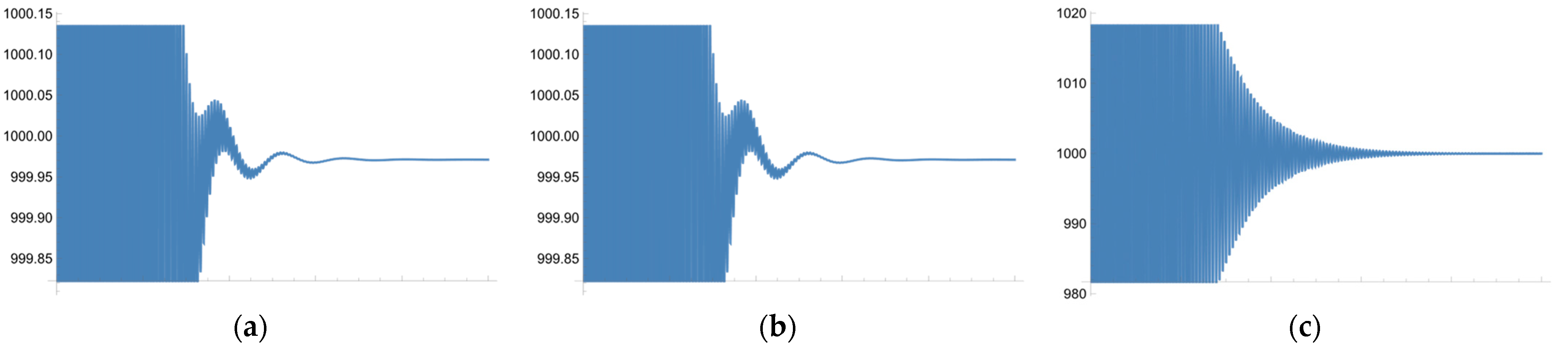
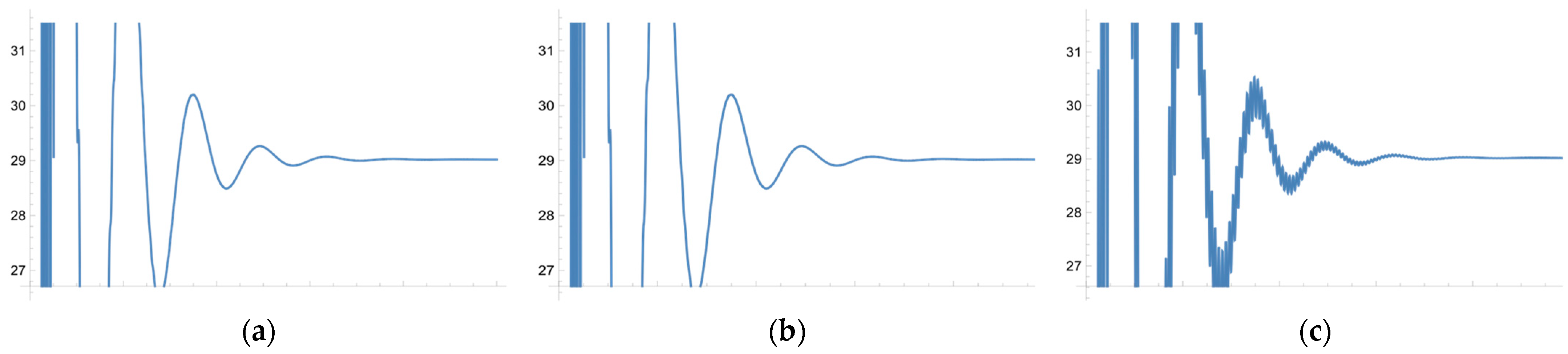
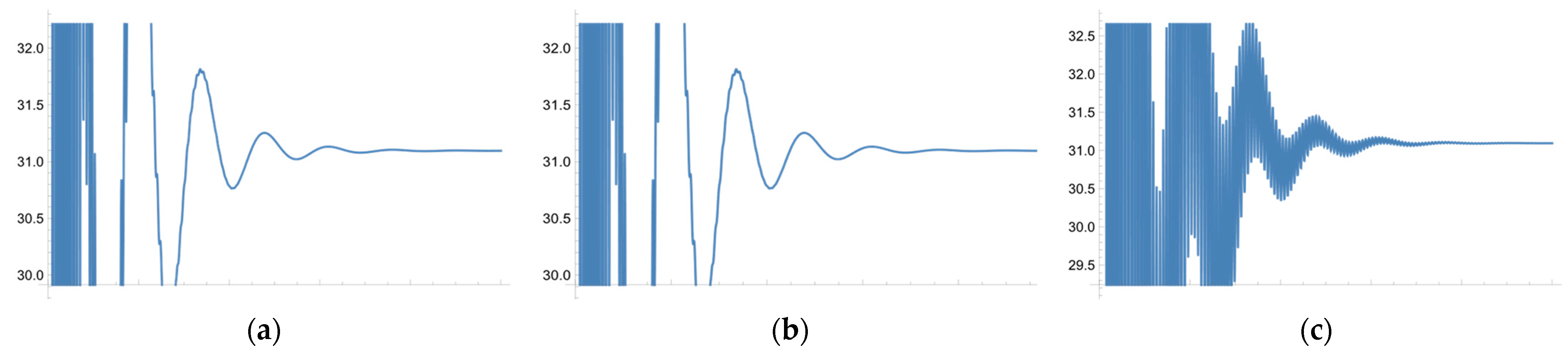
3.2. Experiment Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Zhao, X.; Lv, Y. Stability Analysis and Performance Improvement of Power Sharing Control in Islanded Microgrids. IEEE Trans. Smart Grid 2022, 13, 4665–4676. [Google Scholar] [CrossRef]
- Abdelgabir, H.; Shaheed, M.N.B.; Elrayyah, A.; Sozer, Y. A Complete Small-Signal Modelling and Adaptive Stability Analysis of Nonlinear Droop-Controlled Microgrids. IEEE Trans. Ind. Appl. 2022, 58, 7620–7633. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X.; Zhang, H.; Yang, F.; Tong, L.; Yang, Y.; Yan, D.; Yang, A.; Yu, M.; Liu, Z.; et al. Online Identification of Battery Model Parameters and Joint State of Charge and State of Health Estimation Using Dual Particle Filter Algorithms. Int. J. Energy Res. 2022, 46, 19615–19652. [Google Scholar] [CrossRef]
- Nikolakakos, I.P.; Zeineldin, H.H.; El-Moursi, M.S.; Kirtley, J.L. Reduced-Order Model for Inter-Inverter Oscillations in Islanded Droop-Controlled Microgrids. Ieee Trans. Smart Grid 2018, 9, 4953–4963. [Google Scholar] [CrossRef]
- Shuai, Z.; Peng, Y.; Liu, X.; Li, Z.; Guerrero, J.M.; Shen, Z.J. Dynamic Equivalent Modeling for Multi-Microgrid Based on Structure Preservation Method. IEEE Trans. Smart Grid 2019, 10, 3929–3942. [Google Scholar] [CrossRef]
- Rashidirad, N.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. A Simplified Equivalent Model for the Analysis of Low-Frequency Stability of Multi-Bus DC Microgrids. IEEE Trans. Smart Grid 2018, 9, 6170–6182. [Google Scholar] [CrossRef]
- Hu, W.; Wu, Z.; Lv, X.; Dinavahi, V. Robust Secondary Frequency Control for Virtual Synchronous Machine-Based Microgrid Cluster Using Equivalent Modeling. IEEE Trans. Smart Grid 2021, 12, 2879–2889. [Google Scholar] [CrossRef]
- Kontis, E.O.; Papadopoulos, T.A.; Syed, M.H.; Guillo-Sansano, E.; Burt, G.M.; Papagiannis, G.K. Artificial-Intelligence Method for the Derivation of Generic Aggregated Dynamic Equivalent Models. IEEE Trans. Power Syst. 2019, 34, 2947–2956. [Google Scholar] [CrossRef] [Green Version]
- Levron, Y.; Belikov, J. Modeling Power Networks Using Dynamic Phasors in the Dq0 Reference Frame. Electr. Power Syst. Res. 2017, 144, 233–242. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, K.; Shahidehpour, M.; He, B. Reduced-Order State Space Model for Dynamic Phasors in Active Distribution Networks. IEEE Trans. Smart Grid 2020, 11, 1928–1941. [Google Scholar] [CrossRef]
- Yu, H.; Su, J.; Wang, H.; Wang, Y.; Shi, Y. Modelling Method and Applicability Analysis of a Reduced-Order Inverter Model for Microgrid Applications. IET Power Electron. 2020, 13, 2638–2650. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Reduced-Order and Aggregated Modeling of Large-Signal Synchronization Stability for Multiconverter Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3150–3165. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xia, M.; Qin, Q.; Liu, X. Takagi-Sugeno Multimodeling-Based Large Signal Stability Analysis of DC Microgrid Clusters. IEEE Trans. Power Electron. 2021, 36, 12670–12684. [Google Scholar] [CrossRef]
- Mariani, V.; Vasca, F.; Vásquez, J.C.; Guerrero, J.M. Model Order Reductions for Stability Analysis of Islanded Microgrids With Droop Control. IEEE Trans. Ind. Electron. 2015, 62, 4344–4354. [Google Scholar] [CrossRef] [Green Version]
- Rasheduzzaman, M.; Mueller, J.A.; Kimball, J.W. Reduced-Order Small-Signal Model of Microgrid Systems. IEEE Trans. Sustain. Energy 2015, 6, 1292–1305. [Google Scholar] [CrossRef]
- Vorobev, P.; Huang, P.; Hosani, M.A.; Kirtley, J.L.; Turitsyn, K. High-Fidelity Model Order Reduction for Microgrids Stability Assessment. IEEE Trans. Power Syst. 2018, 33, 874–887. [Google Scholar] [CrossRef] [Green Version]
- Eberlein, S.; Rudion, K. Small-Signal Stability Modelling, Sensitivity Analysis and Optimization of Droop Controlled Inverters in LV Microgrids. Int. J. Electr. Power Energy Syst. 2021, 125, 106404. [Google Scholar] [CrossRef]
- Roos, M.H.; Nguyen, P.H.; Morren, J.; Slootweg, J.G. Direct-Quadrature Sequence Models for Energy-Function Based Transient Stability Analysis of Unbalanced Inverter-Based Microgrids. IEEE Trans. Smart Grid 2021, 12, 3692–3704. [Google Scholar] [CrossRef]


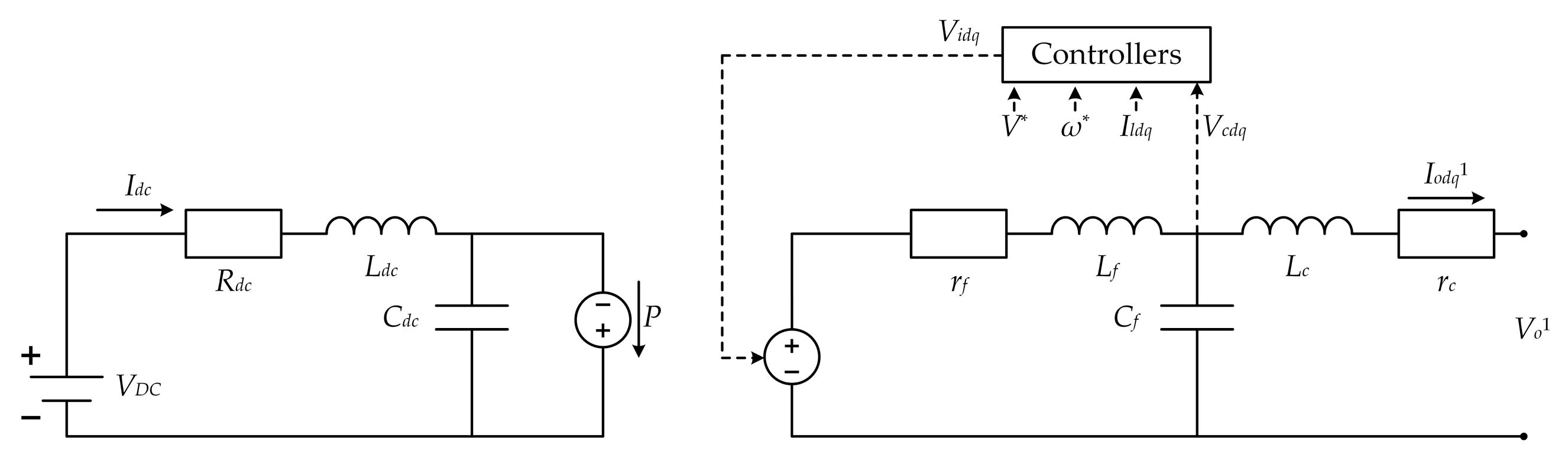

| Number | Variable | Definition |
|---|---|---|
| 1 | Idc | Current of DC side |
| 2 | VCdc | Voltage on the capacitor of DC side |
| 3 | θ | Angle of the inverter |
| 4 | P1 | Output active power after the LCL filter |
| 5 | Q1 | Output reactive power after the LCL filter |
| 6 (7) | Intermediate Variable | |
| 8 (9) | AC output current deviation from its nominal in positive sequence and d(q) frame | |
| 10 (11) | Positive-sequence component of inverter output current in positive sequence and d(q) frame | |
| 12 (13) | Voltage on the capacitor of LCL filter in positive sequence and d(q) frame | |
| 14 (15) | Output current of the LCL filter in positive sequence and d(q) frame | |
| 16 (17) | Voltage on the capacitor of LCL filter in zero sequence and d(q) frame | |
| 18 (19) | Output current of the LCL filter in zero sequence and d(q) frame | |
| 20 (21) | Voltage on the capacitor of LCL filter in negative sequence and d(q) frame | |
| 22 (23) | Output current of the LCL filter in negative sequence and d(q) frame |
| Variable | Value | Definition |
|---|---|---|
| Vtri | 1 V | Peak amplitude of the triangular signal of the PWM drive circuit |
| Rdc | 0.002 | Resistance at the DC side |
| rf | 0.001 | Input resistance of the LCL filter |
| Ldc | 2 mH | Equivalent inductance of the DC side |
| Lf | 15 mH | Input inductance of the LCL filter |
| Lc | 20 μH | Output inductance of the LCL filter |
| Cdc | 680 μF | Equivalent capacitor of the DC side |
| Cf | 300 μF | Capacitor of LCL filter |
| VDC | 1000 V | Output voltage of the DC source |
| V* | 311 V | Nominal output voltage of the inverter (amplitude) |
| ω* | 314 | Nominal output angular frequency of the inverter |
| Kic(Kpc) | 0.02 () | Current (power) gains of current controller |
| Kiv(Kpv) | 200 (0.2) | Current (power) gains of voltage controller |
| mp(nq) | P-V (Q-) droop coefficient |
| Variable Combination to Be Simplified | Variable Combination to Be Simplified |
|---|---|
| 14, 16, 18, 20, 22 | 15, 16, 18, 20, 22 |
| 14, 16, 18, 20, 23 | 15, 16, 18, 20, 23 |
| 14, 16, 18, 21, 23 | 15, 16, 18, 21, 23 |
| 14, 16, 19, 20, 22 | 15, 16, 19, 20, 22 |
| 14, 16, 19, 20, 23 | 15, 16, 19, 20, 23 |
| 14, 16, 19, 21, 22 | 15, 16, 19, 21, 22 |
| 14, 16, 19, 21, 23 | 15, 16, 19, 21, 23 |
| 14, 17, 18, 20, 23 | 15, 17, 18, 20, 23 |
| 14, 17, 18, 21, 22 | 15, 17, 18, 21, 22 |
| 14, 17, 18, 21, 23 | 15, 17, 18, 21, 23 |
| 14, 17, 19, 20, 22 | 15, 17, 19, 20, 22 |
| 14, 17, 19, 20, 23 | 15, 17, 19, 20, 23 |
| 14, 17, 19, 21, 22 | 15, 17, 19, 21, 22 |
| 14, 17, 19, 21, 23 | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.-Q.; Yang, B.-S.; Tao, J. A Second-Order Singular Perturbation for Model Simplification for a Microgrid. Energies 2023, 16, 584. https://doi.org/10.3390/en16020584
Yin X-Q, Yang B-S, Tao J. A Second-Order Singular Perturbation for Model Simplification for a Microgrid. Energies. 2023; 16(2):584. https://doi.org/10.3390/en16020584
Chicago/Turabian StyleYin, Xiao-Qi, Bao-Shun Yang, and Jun Tao. 2023. "A Second-Order Singular Perturbation for Model Simplification for a Microgrid" Energies 16, no. 2: 584. https://doi.org/10.3390/en16020584





