Abstract
Faulted phase identification is one of the segments of conventional system protection that is severely vulnerable in the presence of inverter-based resources (IBR) such as Type IV wind and solar PV power plants. The work presented in this paper investigates the effect of IBRs on the conventional phasor-based faulted phase identification methods widely implemented in contemporary commercial protection relays using theoretical analysis and simulation results. Moreover, this premise is further validated by testing commercial line protection relays using hardware-in-the-loop simulations. This paper also evaluates the applicability of recently proposed transients/incremental quantities-based techniques to overcome the deficiencies of conventional methods to correctly identify the faulted phase in systems with IBRs through real-time and control hardware-in-the-loop simulations. Comparisons with commercial relays show that transient/incremental quantities-based methods are more suitable for systems with a high penetration of IBRs.
1. Introduction
The past decade has seen exponential growth in renewable power generation around the world, both on and offshore. Several key aspects of conventional power system protection paradigms are vulnerable to the ever-increasing penetration of renewable energy generation, particularly to those involving full-rated frequency converters such as Type IV wind turbine generator (WTG) systems and solar PV systems [1,2,3,4,5,6,7,8,9,10,11,12]. These challenges are discussed and investigated in both technical reports [1,2,3,9] as well as in power system research [1,2,3,4,5,6,7,8,9,10,11,12] in general. The fault current characteristics and the factors that need to be considered when analyzing fault currents from inverter-based resources and the solutions to the challenges faced by traditional protection schemes are discussed in [1,2,3,9]. The impact on power system protection by inverter-based resources is discussed in [4,11,13], along with an analysis of some of the contemporary methods in [4]. An analysis of the impact of the negative sequence component-based protection elements communicated by assisted protection schemes and fault identification schemes has been carried out in [5]. This analysis includes case studies on protection malfunction and recommends countermeasures. A similar analysis was conducted in [10]. The impact on directional and distance elements are analyzed in [7,8,12], respectively, along with some solutions to mitigate the impact.
A Type IV WTG system, for example, converts all its output power via a full-rated AC-DC-AC frequency converter before connecting to the main grid. The dynamic behavior of most of these inverter-based resources (IBR) is significantly different from conventional synchronous generator-based power plants, particularly during faults. In a power system protection study, a synchronous generator can be accurately represented by a voltage source behind an impedance (typically using sub-transient values), and therefore, the currents during a fault can also be accurately estimated. By contrast, the electrical characteristics of its power generator have little to no effect on the fault current contribution from a Type IV WTG system. As mentioned above, Type IV WTG systems, due to their variable frequency outputs, require power electronic converters to interface with the transmission system. The control systems of these converters have a major bearing on the dynamic behavior of the plants during disturbances and the short-circuit current contributions during faults [1,6,9].
Conventional phasor-based protection algorithms often exploit and rely on the fact that the currents during faults invariably exhibit certain characteristics such as higher magnitudes (than load currents), asymmetry (for asymmetrical faults), and predictable phase angle relationships between the voltages and currents. In contrast, short circuit currents from IBRs are lower in magnitude and do not exhibit a universal behavior. Reliance on such assumptions compromises the reliability of conventional protection algorithms in the presence of IBRs. In addition, weather conditions can introduce significantly large and intermittent changes in IBR outputs, which further increases the vulnerability of system protection.
Power system protection issues associated with high levels of wind penetration have been well-studied in recent years while finding remedies to them still remains a popular area of research in electrical power engineering [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. In particular, negative sequence-based schemes, protection elements supervised by current magnitudes, phase distance, and directional elements are prone to mis operate due to IBR-induced phenomena [1]. However, it is important to state that since there is no universally accepted behavior for IBRs at present, their representation in power system studies and simulations is also not consistent. Simulation models used for many studies are proprietary black-box-type models provided by IBR manufacturers, which are often not readily available. The tests carried out with such models are understandably not reproducible and can yield conflicting results.
The accurate identification of the faulted phase is an integral part of typical line protection schemes and becomes particularly important when single-pole tripping is desired [16,17,18,19,20]. Conventional faulted phase selection algorithms can also be vulnerable in the presence of IBRs. This is mentioned as a potential issue in the relevant literature, although it is not rigorously analyzed by most of them. The work conducted in [12] analyzes one of the methods used for faulted phase selection and proposes an improved technique. It also evaluates the performance of commercial relays under IBR currents, but it is unclear what portion of the mis operation presented in the results directly results from inaccurate phase selection. In addition, there are few studies on using fault-induced transients for faulted phase selection [21,22,23,24,25,26,27]. However, the applicability of these techniques has not been tested in the presence of IBRs.
To address the above-mentioned research gaps, this paper evaluates and compares the performance of phase selection algorithms of contemporary relays and those newly proposed in the literature in the presence of IBRs. The main contributions of this paper are listed below.
- Although there is a theoretical understanding of the reasons behind the phase selection problems due to IBR penetration, the extent of the issue is not well understood. A simulation-based analysis was carried out to validate the theoretical explanations and demonstrate the deficiencies of conventional faulted phase identification algorithms in the presence of IBRs.
- The phase selection performance of commercial relays under the presence of IBR is not well documented. Thus, a few samples of commercial relays were tested in a hardware-in-the-loop (HIL) simulation setup using an electromagnetic-transient (EMT) type digital real-time simulator (DRTS) to assess the performance and further validate the theoretical premise.
- Although alternative phase selection algorithms have been proposed in the recent literature to overcome the deficiencies of conventional phasor-based techniques, most of them are only verified by using offline simulations. In order to investigate the real-time applicability of two such methods, transient-based and incremental quantities-based faulted phase identification methods were implemented in hardware and tested using HIL simulations. The paper also highlighted practical considerations that require special attention while implementing the transients-based algorithm in real hardware.
- A true direct comparison of the real-time performance of the commercial relays and novel phase selection algorithms was lacking. Therefore, the performance of traditional and transient/incremental quantities-based protection algorithms was systematically compared under the presence of IBRs, leading to clear conclusions.
The rest of the paper is organized as follows. Section 2 presents a brief overview of commonly used phase selection algorithms to explain why they are prone to mis operate in the presence of IBRs and provides a comparison between simulated fault currents generated by a conventional source and an IBR to consider their effect on conventional faulted phase identification algorithms. Section 3 details the CHIL tests carried out with two commercial line protection relays with results, which were conducted in order to validate the findings in Section 2, the applicability of a transients-based phase selection algorithm was evaluated under similar test conditions, and the results are presented along with those obtained from the incremental quantities-based method. Section 4 follows with a brief discussion and conclusions.
2. Theoretical Analysis of Contemporary Faulted Phase Selection Algorithms and the Effect of IBRs
2.1. Contemporary Faulted Phase Selection Algorithms
Several different algorithms are used in contemporary power systems relaying for faulted phase identification. These methods yield accurate results over a variety of system conditions with conventional synchronous machine-based generation. Many relay manufacturers use symmetrical component-based techniques for faulted phase identification [16,17,18,19]. Different relay manufacturers use slightly modified versions of this method, but all of its variants measure the phase angles between sequence currents and/or voltages to determine the phase(s) involved in a fault. The key aspects of such relaying algorithms are explained below.
In its most commonly implemented form, faulted phase identification using symmetrical components determines the phases involved in a fault based on the phase angle signature of ‘Phase A’ sequence currents. The symmetrical component theory and the boundary conditions at the fault dictate that the phase angle difference between ‘Phase A’ negative and the zero sequence currents lies within the distinct regions depicted in Figure 1a when the fault is one of two types indicated on the diagram. For example, the angle difference between ‘Phase A’ negative and the zero sequence current phasors during a bolted BG fault is theoretically −120°. The same relationship holds true for a CAG fault. A slightly different but distinct phase angle relationship also exists between the negative and the positive sequence current phasors during ground faults, as shown in Figure 1b.
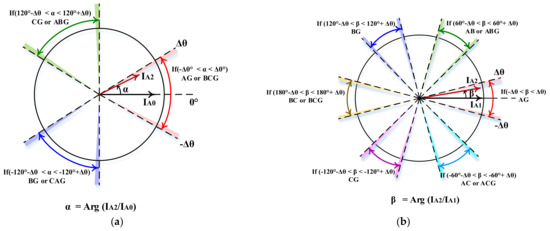
Figure 1.
(a) Angle difference between ‘Phase A’ negative and zero sequence current phasors during bolted faults (i.e., α), (b) Angle difference between ‘Phase A’ negative and positive sequence current phasors during bolted faults (i.e., β).
Various methods are employed to choose between the two possible fault types. One such method is to choose the fault type with the lower reach from the corresponding impedance element. This is based on the fact that the actual faulted loop would have a much lower impedance estimation than the other [16]. For example, the AG impedance element would yield a much lower reach than the BG or CG elements for an actual AG fault. Some manufacturers measure the phase angle signatures of all three phases and use a combined logic to single out the faulted phase 20. Certain other manufacturers combine both phase angle signatures (α and β) to determine and verify the faulted phase. It is also noteworthy that phase angle signatures of sequence voltages provide similar information about the faulted phase and can be used in phase selection algorithms.
In addition to sequence components-based fault identification techniques, there exist somewhat older methods that entirely rely upon impedance elements to determine the faulted phase [16,19]. The method uses overreaching impedance zones to develop a phase-phase-ground signal that supervises the respective zone 1 phase and ground elements while issuing trip commands accordingly. A zero-sequence pickup signal is used to discriminate between phase-phase-ground and phase-phase faults. A simplified schematic of the logic used in this method is given in [19].
In addition, line differential relays typically employ phase-segregated differential elements and determine the faulted phases based on the operated elements [11]. There are other more sophisticated techniques that use transient and/or incremental quantities for the faulted phase selection [21,22,23,24,25,26,27,28]. These approaches are typically faster than impedance-based and sequence-component-based techniques. Two such techniques, one based on transient components and the other based on incremental quantities, are presented in Section 3.2.1 and Section 3.2.2.
2.2. Effect of IBR on Faulted Phase Selection Techniques
The presence of IBRs poses significant challenges to conventional faulted phase identification techniques, particularly those that depend on the phase angle signature of sequence currents, as mentioned in Section 2. There are a few major concerns. Firstly, certain IBRs inject little to no negative sequence currents during faults (even for asymmetrical faults), which may not be enough to activate the phase identification algorithms in relays [1]. Typically, control strategies for the grid side controllers of Type IV WTG and solar PV systems suppress negative sequence currents under all conditions [1]. Even whatever little negative sequence currents are available due to imperfections in the converter controls are uncontrolled and highly transient in nature. Thus, the phase angles of these negative sequence currents not only fail to exhibit the same relationship with other sequence currents (as a conventional source) but also vary with time. As a result, most sequence-component-based faulted phase identification techniques are prone to miss-operations in the presence of IBRs with full converter interfacing.
On the other hand, techniques that completely depend on impedance elements require the fairly predictable operation of impedance elements. For example, one of the main requirements of this method is that the overreaching phase-ground element that generate the supervisory phase-phase-ground signal must operate before the zone 1 phase-ground elements. It has been shown that distance protection elements tend to produce unexpected impedance trajectories and measurements in the presence of IBRs (such as Type IV wind pants) [8]. This is of particular concern for certain types of fault conditions, such as phase-to-phase faults with a fault resistance, where the effect of the fault resistance can be greatly exaggerated and also become unpredictable and time-varying [8]. Therefore, a fault identification technique based on impedance measurements can encounter problems when used in systems with IBRs.
To demonstrate the differences between fault currents from a conventional source and a Type IV WTG system and their effects on phase selection, the system given in Figure 2 was simulated in an EMT-type DRTS. The simulation was carried out for two cases, with only one source connected at a time. In the first case, a conventional source was connected, and it was represented as a voltage source behind an impedance.
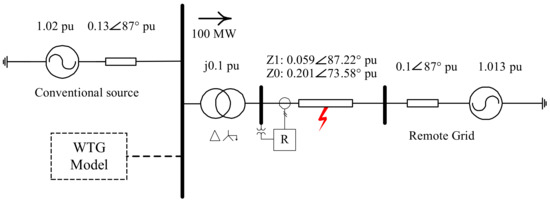
Figure 2.
Single line diagram of the power system model used for comparing a conventional source and an IBR.
In the second case, the conventional source was replaced by a Type IV WTG model. The WTG was modeled in the simulation as an averaged model using generic DQ frame current controls. The LVRT (low-voltage ride-through) strategy and other peripheral controls were based on the guidelines outlined in the IEC 61400-27-1 standard [29]. The general behavior of the WTG model was verified with those available in the published literature [1,2]. In both cases, the source was pushing 100 MW of active power at a unity power factor to a remote grid (which is also represented as a voltage source behind an impedance) via a short transmission line.
Figure 3 presents the phase currents, the magnitude of the sequence currents, and the angle difference between ‘Phase A’ negative and zero sequence current phasors observed at the relaying location (R) for each case, as indicated. The results shown are for a bolted BG fault at the mid-point (50%) of the transmission line. Here, one can observe the stark difference between fault currents produced by the conventional source and the WTG model.
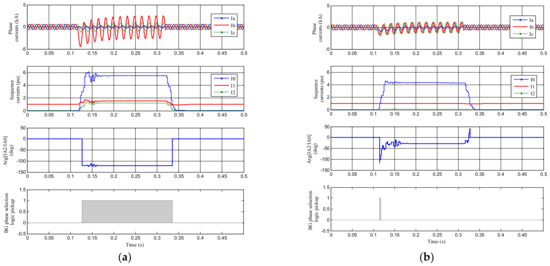
Figure 3.
(a) Results for faulted phase selection for a BG fault at the mid-point of the line with the conventional source. Results for faulted phase selection of a BG fault at the mid-point of the line with the WTG model, (b) Results for faulted phase selection of a BG fault at the mid-point of the line with the WTG model.
With the conventional source, there was a significant presence of all three sequence currents, and the phase angle difference between ‘Phase A’ negative and zero sequence currents was very close to −120° as expected. On the other hand, the fault currents observed with the WTG were dominated by the zero-sequence current produced by the wind plant transformer, which had a grounded star connection on the grid side. There was very little negative sequence current, and the magnitude of the positive sequence current remained more or less unchanged. In addition, the phase angle difference between ‘Phase A’ negative and zero sequence currents highly fluctuated with time before eventually settling down at an entirely different value from the theoretically expected −120°. However, the phase angle of the negative sequence current has little meaning in this scenario, as its magnitude was very low.
The pickup signal from a simple phase selection logic based only on the angle difference between ‘Phase A’ negative and zero sequence currents is also given in Figure 3. Understandably, the logic identifies the fault as a BG fault for the conventional source and does not respond properly to the WTG.
To investigate the impact of IBRs on impedance-based fault type identification methods, the method shown in Appendix A was implemented in the DRTS environment, and its performance was evaluated using the same methodology detailed above. The implemented logic in the simulation yielded an accurate and dependable faulted phase identification for the system with the regular voltage source, while it failed to produce accurate results when the source was replaced by an IBR. However, purely based on the results of simulation studies, this method produced better results than the sequence components algorithm (it produced a correct fault identification for some fault types under certain conditions, whereas the sequence components-based method failed in all scenarios).
It has been suggested that similar free-running phase identification methods can be implemented using (high) current measurements, however, they too are not effective against IBR-produced fault currents, which are low in magnitude and unpredictable. In principle, the traditional line differential relays are not affected by the nature of fault currents from IBR and generally perform correctly in systems with IBR [11].
3. Testing and Analysis
3.1. Performance of Commercial Relays
As the next step, two commercial line protection relays were tested to further establish the premise that the fault identification algorithms in relays were affected by the presence of IBRs. Much of the literature related to protection issues caused by IBRs base their work on simple relay functions developed in simulation environments, which can perform differently than commercial relays deployed in the field. Therefore, it is important to validate the predictions made based on theoretical analysis in laboratories using a setup that closely replicates real-world scenarios. Moreover, the manuals of commercial relays and other examples in the literature available to the public often do not contain some minor but critical details of the internal relay algorithms, such as the sensitivity thresholds used for validating signals. As a result, there is a possibility that real-world relays perform better than theoretical expectations in all scenarios, and it is important to investigate and validate this. A controller-hardware-in-the-loop test setup where commercial relays are interfaced with a DRTS is well suited for this task.
3.1.1. Test Setup
For this test, a slightly more complex (remote) system was modeled, as shown in Figure 4, to carry out tests in a more comprehensive manner. The WTG model was the same as the one explained in Section 2.2, which was rated at 100 MW and pushed power via a short 138 kV transmission line. The remote end of this line was connected to a 230 kV grid through a transformer and an adjacent transmission system. A conventional power source (a synchronous generator) was connected to the remote bus (Bus 2) via another short transmission line, as depicted in Figure 5. Both line protection relays were tested in a CHIL setup and realized using a DRTS. An abstract schematic of the test setup is presented in Figure 5.
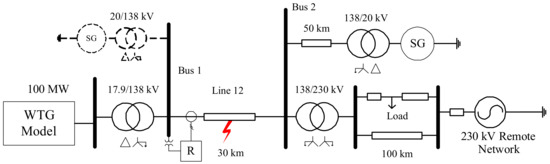
Figure 4.
Single line diagram of the power system model used for testing commercial relays.
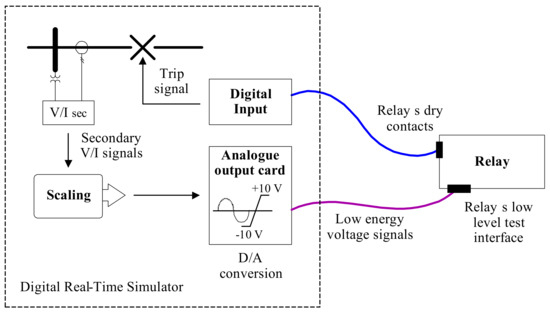
Figure 5.
Schematic of the test setup.
As shown in Figure 5, the power system was simulated in the DRTS, and both line protection relays were interfaced using low-energy analog signals and the relay’s dry contacts. High-resolution digital waveforms (secondary voltage and current transformer outputs) generated in the simulation were converted to low-energy analog voltage signals (<±10 Vpp) by the analog output card of the DRTS, which were then fed to a low-level test interface of the relays. Scaling factors for the analog output card were accurately determined in order to provide precise low-level voltages to the low-level test interface of the relays under test.
Note that the two relays were connected to the test setup one at a time and tested independently. The transmission lines were modeled using Bergeron’s line models. The positive sequence and zero sequence impedances of Line 12 were 11.3∠87.22° Ω and 38.38∠73.58° Ω, respectively. The current transformers (CT) and voltage transformers (VT) were also modeled using the standard library components available in the DRTS’s software suite. The synchronous generators were also modeled using the standard library component with typical parameters. However, note that the synchronous generator connected at Bus 1 was kept disconnected for the first part of the experiments. The remote AC network was modeled as Thevenin’s equivalent with a 230 kV source and an impedance of 20∠87° Ω. A 50 μs simulation time step was used for all simulations. Both relays were configured as distance protection relays looking into Line 12 at Bus 1 (R in Figure 5), with zone 1 enabled as a direct tripping element with an 80% reach. The faults of different types were applied along the length of Line 12.
3.1.2. Test Results and Discussion
Table 1 and Table 2, respectively, present the faulted phase identification results for low-impedance faults (Rf = 0.01 Ω) and high-impedance faults (Rf = 50 Ω). The fault inception angle was fixed at 0°. When considering the two relays, Relay 2 failed to identify the faulted phases in all test cases. Additionally, Relay 2 failed to detect phase-to-ground faults as well. However, for other types of faults, Relay 2 issued a three-phase trip signal irrespective of the type of short circuit fault applied. In comparison, Relay 1 identified a number of faults for all types.

Table 1.
Fault type identification of relays for low impedance faults.

Table 2.
Fault type identification of relays for high impedance faults.
Moreover, Relay 1 failed to detect the existence of a fault in most phase-to-ground faults. However, even when a fault was detected, Relay 1 was unable to correctly identify the faulted phase in phase-to-ground faults. In addition, both Relay 1 and Relay 2 failed to detect faults under high-impedance fault scenarios. Table 3 summarizes the performance of the two commercial relays for various ground and non-grounded faults. Both low impedance (short circuit) and high impedance faults were applied at three fault locations (at 5%, 50%, and 75% of the line length) while varying the fault inception angle from 0⁰ to 180° in one-degree steps.

Table 3.
Overall performance of relays for various fault types.
As can be seen from the results presented in Table 1, Table 2 and Table 3, both commercial relays do not reliably identify the faulted phase for IBR-generated fault currents. In particular, it was observed that the faulted phase identification for the phase to ground faults was not only incorrect (in most cases), but also the results were not reproducible with consistency when the same tests were repeated. This deficiency of existing relaying algorithms is of particular importance, considering the fact that correct faulted phase identification is imperative for the reliable use of single-pole tripping during single line-to-ground faults.
Both relays used in the experiment employed the principle of phase angle signatures of sequence currents to determine the faulted phases. However, the two relays use different methods for singling out a faulted phase(s) from two or more possibilities. One relay uses the phase angle signatures of all three phases and applies logic to single out the faulted phase, while the other uses both phase angle signatures (α and β) to determine and verify the faulted phase, as described in Section 2. However, it is difficult to attribute the differences in the performance of the two relays for low impedance faults to this aspect alone, as implementation details such as various internal checks and the thresholds used to verify the signals and decisions can also contribute to the different behavior exhibited by two relays.
Another observation made during the relay testing was the differences between the accuracies in Relay 1 for the different fault types. This can be attributed to several factors. Firstly, different fault types produce different system conditions (for example, voltages at the IBR bus vary depending on the fault type), which in turn can yield different responses from the IBR controls (for example, the behavior of the LVRT controls). Secondly, the sensitivity of relay algorithms to different types of faults might be different, resulting in varying accuracies. Further analysis of the relay data obtained from Relay 1 showed that the trip signals and phase identification signals issued by Relay 1 were transient in nature (relay pickup signals were issued transiently). Therefore, the accuracy percentages obtained from this test only provide a general idea about the relay’s behavior and not a conclusive quantitative account of their performance. Moreover, it further underlines the unpredictable behavior of conventional relays in the presence of IBRs.
The results obtained from testing the commercial relays show that the fault type identification functions in the relays are severely affected by the presence of IBRs. In an attempt to add another dimension to this study, the minimum penetration level of the synchronous generation to successfully operate the fault identification algorithms of commercial relays was investigated.
The power system model used for previous tests was modified by connecting a small synchronous generator (shown as a dashed line in Figure 5) to the WTG bus (Bus 1). Starting from 10 MVA, the synchronous generator’s apparent power was increased while applying short circuit faults at 5% of the length of the protected line. Phase-A-to-ground, phase-B-to-C-to-ground, and phase-A-to-C faults were applied, and Table 4 presents the results obtained from these tests. When the synchronous generator power level was set to 10 MVA, the performance of Relay 2 improved compared to the WTG-only case. Relay 2 started to identify the phase-A-to-ground fault correctly, while the phase-B-to-C-to-ground fault and phase-A-to-C fault were still identified as three-phase faults. As shown in Table 1, when there was no synchronous generator connected to Bus 1, Relay 2 did not identify the faulted phases for all the applied faults. On the other hand, Relay 1 did not show any improvement at a 10 MVA power level compared to the WTG-only case. At the 15 MVA power level, Relay 1 started identifying the fault type for all three types of faults applied at different fault inception angles. Relay 2 also showed some improvement by correctly identifying both phase-A-to-ground and phase-A-to-C faults. When the synchronous generator power level was increased to 20 MVA, both relays started to identify the faulted phases accurately for all the faults applied. Based on these results, it can be said that approximately 20% of the synchronous generation was required for accurate fault type identification in typical commercial relays when operating with IBR penetration.

Table 4.
Fault type identification of relays with added synchronous generation.
3.2. Transient-Based and Incremental Quantity-Based Fault Classification Schemes
In this section, two novel fault classification algorithms, one based on transient quantities and the other based on incremental quantities, are examined.
3.2.1. Transient Based Faulted Phase Selection Algorithm
A transient-based fault classification scheme has been proposed in 21 to overcome the drawbacks faced by the traditional phasor-based faulted phase identification algorithm. Fault-induced transients are generated as a result of the sudden discharge of line charges at the fault location. These transient waves propagate along the line at a velocity close to the speed of light, and they contain information about the fault type, location of the fault, and fault inception angle. Figure 6 presents the band-pass filtered three-phase currents from a conventional source and a WTG system for the same fault. The filtering is performed using a lower cutoff frequency of 1 kHz and an upper cutoff frequency of 2 kHz. Compared to the fundamental frequency components (as observed in Section 3), the effect of the type of the source is minimal on the transient current waveforms. This is particularly true during the initial time period until the current waveforms begin to distort as reflected waveforms start to reach the relaying point. This source-independent nature of the fault-induced transients helps to overcome the disadvantages faced by the phasor-based faulted phase selection algorithms.
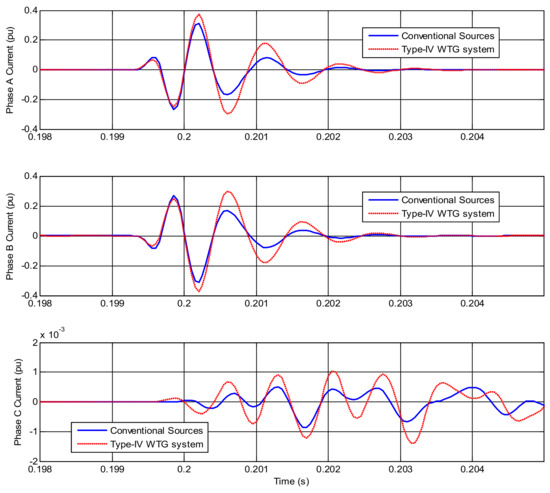
Figure 6.
Band-pass filtered phase currents for an AB fault at 5% of the line with a conventional source and a Type IV WTG system.
Even though fault-induced transients are independent of the type of source, a simple magnitude comparison-based algorithm does not provide a reliable solution since the strength of the fault-induced transient is dependent on many factors. Therefore, an algorithm based on systematic logic is required to accurately identify the faulted phases. The transient-based fault classification scheme proposed in 21 is one such systematic algorithm that has been developed to overcome the drawbacks faced by the traditional phasor-based faulted phase identification algorithms and existing transient-based faulted phase selection algorithms. The proposed method uses seven current components obtained from the measured three-phase instantaneous currents through the transformation given in (1): which is based on Clarke’s transformation. The currents, and are the instantaneous phase current band-pass filtered to remove the fundamental components and high-frequency content.
Upon detecting a fault, nine fault discrimination indices are computed, taking different ratios of the maximum rates in the change in current (ROCOC) of these filtered current components. More details of the rationale and definitions of these indices can be found in [21]. The process of identifying the fault type and faulted phases are summarized in Figure 7.
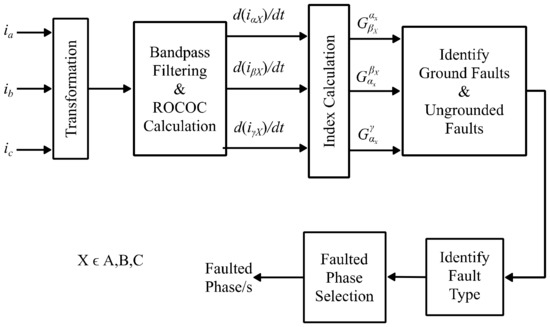
Figure 7.
Schematic of the transient-based fault classification scheme.
There are three stages in the proposed algorithm. The first stage identifies the ground faults from the ungrounded faults. The next stage identifies the fault type (phase-to-ground, phase-to-phase-to-ground, phase-to-phase, and three-phase). In the third stage, the faulted phases are identified upon identifying the fault type. The core algorithm is summarized in Appendix B for reference. There are three threshold settings in the proposed algorithm. The first threshold setting, k0, is used to identify the ground faults from the ungrounded faults. Threshold setting k1 is used to identify the fault type, and the k2 threshold setting is used to identify the faulted phase in the phase-to-ground and phase-to-phase faults. The faulted phases in phase-to-phase-to-ground faults are identified by comparing the magnitudes of the calculated indices. The accuracy of the algorithm has been verified by detailed EMT simulation studies in [21]. The method has shown promising results in accurately identifying the faulted phases in phase-to-ground faults.
3.2.2. Incremental Quantity Based Faulted Phase Classification
The incremental quantity-based faulted phase classification scheme presented in [28] was proposed as a solution to the difficulties faced by conventional faulted-phase classifications. This method relies on the phase angle signatures outlined in Section 2 to determine the fault type similar to the conventional sequence components based on the faulted-phase selection algorithms but uses estimated phase angles of the sequence currents in faulted loops and using the pure fault sequence impedances of the IBR during a fault. The algorithm uses incremental values of the local current and voltage measurements during the fault to determine pure fault sequence impedances and uses them to calculate the phase angles of the sequence currents. If the negative sequence current is not available during an asymmetric fault, the negative sequence voltage is used to calculate the negative sequence angle. A summary of equations used to estimate the phase angles of the sequence currents in this phase selection algorithm is given in Appendix B. For the theoretical background of the proposed method, please refer to the reference [28].
3.2.3. Test Setup and the Implementation of Algorithms
In an attempt to evaluate its performance with respect to commercial relays, the transient-based algorithm was tested using a test setup similar to the one used to test the commercial relays, as explained in Section 4. The method proposed in [21] was implemented as a real-time process on a different DRTS unit, as depicted in Figure 7. The algorithm, which was also developed using standard library components, received instantaneous current and voltage measurements as IEC 61850-9-2 LE sampled values (SV) from the original DRTS unit simulating the power system [30,31,32]. A schematic of the setup for testing the transient-based scheme is given in Figure 8. Note that the two DRTS units were independent and connected only through an external, real communications link that served as the IEC 61850 process bus [30,31,32]. In addition, the simulation time step of both DRTS units was synchronized to a common GNSS (global navigation satellite system) time reference.
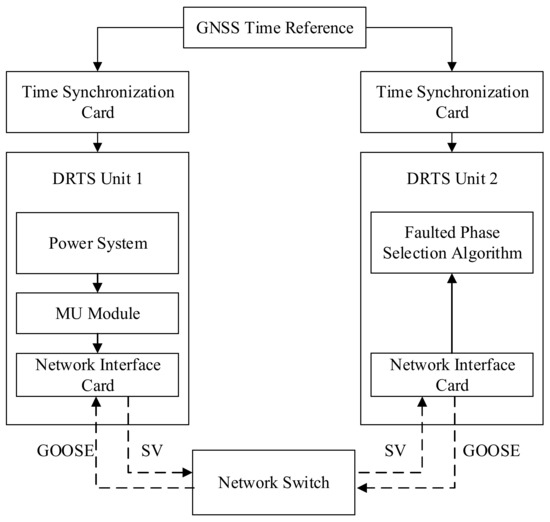
Figure 8.
Schematic of the setup for testing transient-based scheme.
IEC 61850-9-2 LE SV, published by the network interface card of the DRTS unit 1 (simulating the power system), was directed through a local area network (LAN) to DRTS unit 2, which ran the transient-based phase selection algorithm. The SV packets were published at a sampling rate of 256 samples per cycle (s/c), which translated to a sampling frequency of 15.36 kHz with a system nominal frequency of 60 Hz. The merging unit was modeled assuming an analog to digital (A/D) converter bit resolution of 24 bits. Anti-aliasing filters of the merging unit were modeled as the sixth-order low-pass Butterworth filters with the cutoff frequency set to half of the sampling frequency of 15.36 kHz. The lower and upper cutoff frequencies of the band-pass filter used in the phase selection algorithm [21] were adjusted to 2.5 kHz and 3.5 kHz, respectively. Moreover, the threshold settings k0, k1, and k2 were set as 0.05, 25, and 10, respectively. DRTS unit 2 decoded and fed the measurements in the subscribed SV to the transient-based phase selection algorithm. Upon identifying the fault type, the transient-based algorithm initiated a GOOSE message that carried the faulted phase information from DRTS unit 2 to DRTS unit 1 [33]. In order to increase the resolution of the voltage and current measurements fed to the algorithm, smaller SV channel scale factors than the ones defined in the standards IEC 61850-9-2LE/IEC 61869-9 were used. Lowering the scale factors enabled better utilization of the 32-bit representation of values used in the SV communication for this particular application, where the measurement resolution was of a higher significance than the dynamic range.
In order to provide a comparison of the transient-based faulted phase classification scheme, the incremental quantities-based phase classification scheme proposed in 33 was also implemented in the DRTS environment. Compared to the transient-based method, the incremental component-based method requires a lower sampling rate. The incremental quantities are computed using the sequence component phasors. The algorithm presented in Appendix C was implemented using standard DRTS library components. Upon computing the incremental quantities, the sequence current angles were determined as outlined in Appendix C to identify the fault type.
3.2.4. Test Results and Discussion
The power system model used to test the transient and incremental component-based schemes was identical to the one used to test the commercial relays (only the WTG was at Bus 1). The same fault was applied several times in each test case to verify the reliability of the algorithm. The results are summarized in Table 5 and Table 6.

Table 5.
Fault type identification of transient/incremental quantities-based faulted phase identification algorithms.

Table 6.
Overall performance of transient-based and incremental component-based faulted phase identification algorithms.
The results, shown in Table 5 and Table 6, show that the transient-based algorithm was able to identify the faulted phases accurately in almost all the test scenarios apart from a few phase-to-phase-to-ground faults. This is a drawback of this transient-based algorithm which has been pointed out by the authors in [21]. However, this does not affect the final trip signal since it does not identify phase-to-phase-to-ground faults as phase-to-ground faults, unlike the two commercial relays.
Table 6 shows the overall performance of the transient-based algorithm for various fault types. Similar to the commercial relay tests, both short circuit and high impedance faults were applied at three different fault locations (5%, 50%, and 75% of line length) while varying the fault inception angle from 0° to 180° in one-degree steps. Compared to the commercial relays, the current transient-based method identified the fault type with an accuracy of more than 95% for most fault types. As mentioned above, this method has a lower accuracy in identifying the faulted phases of phase-to-phase-to-ground faults compared to other fault types. However, even in this scenario, the transient-based method delivered a higher accuracy (over 70%) than the commercial relays, which yielded an accuracy below 50%. In addition to delivering a higher accuracy compared to commercial relays, the transient-based scheme was capable of identifying the faulted phase within 1 ms of fault inception. Furthermore, the average round trip time of the test loop (including the GOOSE/SV message transfer times) was approximately 4 ms.
The same number of faults given in Table 5 and Table 6 was applied to test the incremental component-based method. Compared to the commercial relays, the incremental component-based method was able to identify the faulted phases of all the faults applied, even for the high-impedance faults. The results are shown in Table 6.
Compared to the transient-based method, the incremental component-based method has better accuracy while requiring a lower sampling rate (3.84 kHz) [28]. However, this advantage comes at the expense of operating speeds. The incremental component-based method may take up to 10 ms [28] to identify the faulted phases, whereas the transient-based method makes the decision within 1 ms. Therefore, a compromise needs to be made between speed, accuracy, and computational efficiency when selecting the best method to be implemented.
4. Conclusions
The challenges of identifying the faulted phase using conventional phasor-based techniques in the presence of IBRs were investigated. First, theoretical reasoning was provided to explain the deficiency of conventional phase selection techniques, with verifications by EMT simulations. Two commercial relays were tested in a CHIL setup using a DRTS, where a power system with an IBR was simulated. The observed results were in agreement with the aforementioned theoretical reasoning and simulation results. Moreover, when the fault currents consist of contributions from a mix of conventional power generation and IBRs, a certain minimum level of conventional generation, approximately 20%, was required to ensure the correct operation of the faulted phase identification algorithms in relays.
Two methods that were recently reported in the literature to alleviate the issues caused by IBRs in faulted phase classifications were investigated. These two methods were based on transient currents and incremental quantities, respectively. The results indicated that both methods, in comparison to phasor-based techniques, have the potential to deliver significantly more accurate results for faulted phase identification in the presence of IBRs. The incremental component-based method has a better performance compared to the transient-based method even in identifying faulted phases in phase-to-phase-to-ground faults. However, from a practical perspective, both methods would work accurately since the transient-based method accurately identify the phase-to-phase-to-ground fault type from other fault types, even though it had lower accuracy in identifying the phases involved in phase-to-phase-to-ground faults. Therefore, the use of transient/incremental quantity-based methods is more suitable for systems where a higher faulted-phase selection accuracy is required, such as those with high penetration IBRs, and implement single-phase tripping.
Even though the transient-based method implemented in this paper is capable of operating with relatively low computational resources, most of the transient based methods require a higher sampling rate to operate accurately. The incremental component--based method requires a lower sampling rate compared to the transient-based method investigated in this paper. However, the low sampling rate requirement of the incremental component-based method comes at the expense of slower operating times. In general, the computational requirements of conventional methods (sequence components or impedance-based) would be lower than those of more sophisticated methods such as transients or incremental quantities-based algorithms.
Author Contributions
Conceptualization, S.K. and A.R.; methodology, S.K. and J.W.; software, S.K. and J.W.; validation, J.W.; formal analysis, S.K. and J.W.; investigation, S.K.; writing—original draft preparation, S.K. and J.W.; writing—review and editing, A.R.; visualization, J.W.; supervision, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Use of an Overreaching Impedance Zone for Phase Identification
Figure A1 presents the logic of the impedance-based phase identification method implemented in Section 2. Here, the supervising phase-phase-ground (ΦΦG) signal is produced using two overreaching phase-ground impedance zones. This compound signal is then used to block or release respective ground or phase elements, respectively.
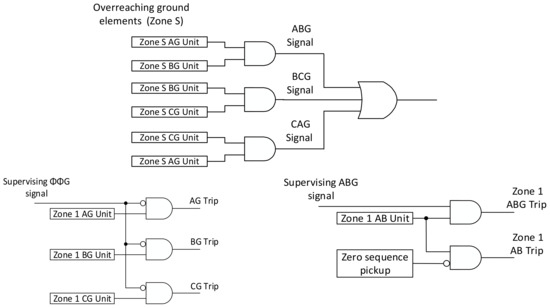
Figure A1.
Logic diagram of the implemented impedance-based phase identification technique [19].
Appendix B. Transient Based Faulted Phase Identification Algorithm
After bandpass filtering the transformed current components obtained from (1), nine fault classification indices can be defined considering their peak rate of change in currents (ROCOC) observed immediately after the fault inception as shown in (A1)–(A3), where X (∈ A, B, C) is the reference phase. The cutoff frequencies of band pass filter are selected to remove the power frequency signal components and noisy high frequency components. The maximums of the respective time derivatives are obtained within a short time window to avoid the effect of reflected secondary current waves. For more information about the signal processing involved in the method, please refer reference [21].
Using the indices defined in (A1)–(A3), the conditions are given in (A4)–(A6), respectively can be defined to identify the: (i) Ground faults from ungrounded faults, (ii) Phase-to-Ground faults from Phase-to-Phase-to-Ground faults, and (iii) Phase-to-Phase faults from Three-Phase faults.
After determining the fault type, faulted phase selection is carried out using the same indices. The criteria to identify the faulted phases are given in (A7)–(A9).
Phase selection logic diagrams are shown in Figure A2, Figure A3, Figure A4 and Figure A5. For more information about the threshold settings, setting the time window and selecting the filter frequencies please refer reference [21].
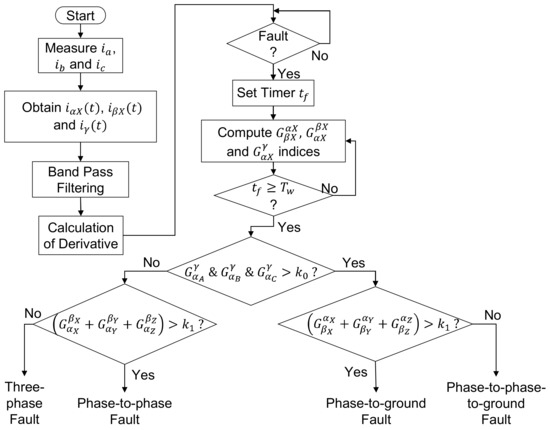
Figure A2.
Fault type identification [21].
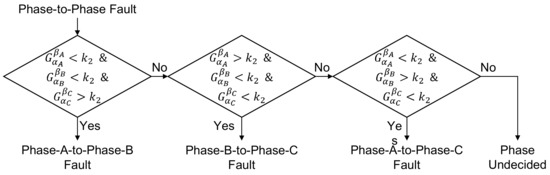
Figure A3.
Phase-to-Phase faults identification [21].
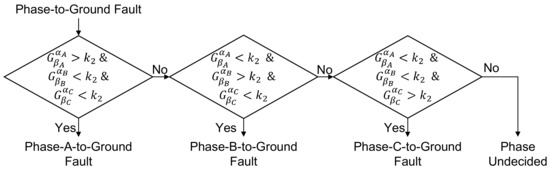
Figure A4.
Phase-to-Ground fault identification [21].
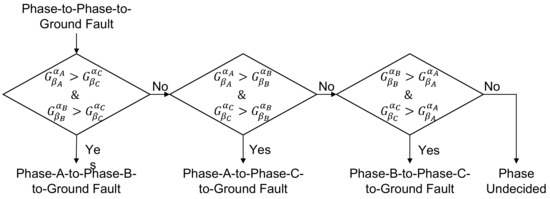
Figure A5.
Phase-to-Phase-to-Ground fault identification [21].
Appendix C. Incremental Quantity Based Phase Selection Algorithm
The incremental quantity-based phase selection algorithm proposed in [28] calculates the positive, negative and zero sequence current phase angle using positive, negative and zero sequence incremental currents and the respective pure fault source sequence impedances of the IBRs.
The pure fault sequence impedance of the IBR source impedance is calculated using (A10):
Positive sequence current angle can be calculated using (A11)
Negative sequence current angle can be calculated using either (A12) or (A13)
If negative sequence current is not available:
If negative sequence current is available:
Zero sequence current angle can be calculated using (A14)
Upon calculating the relevant phase angles, the calculated phase angles are fed into the traditional current angle phased fault classification algorithm. For further information, please refer reference [28].
References
- Nagpal, M.; Jensen, M.; Higginson, M. IEEE Power System Relaying and Control Committee Report of Working Group C32 of the System Protection Subcommittee. Protection Challenges and Practices for Interconnecting Inverter Based Resources to Utility Transmission Systems. September 2020. Available online: https://www.pes-psrc.org/kb/published/reports/Working%20Group%20C32%20Report%20Draft%208.05%20-%20Final%20-%20PSRCC%20Format.pdf (accessed on 27 December 2022).
- Brahma, S.; Farantatos, E. IEEE Power System Relaying and Control Committee Report of Working Group C24 of the System Protection Subcommittee. Modification of Commercial Fault Calculation Programs for Wind Turbine Generators. July 2020. Available online: https://www.pes-psrc.org/kb/published/reports/C24_WG_Report_Jun_2020_Final.pdf (accessed on 27 December 2022).
- NERC. 1200 MW Fault Induced Solar Photovoltaic Resource Interruption Disturbance Report—Southern California 8/16/2016 Event; NERC: Atlanta, GA, USA, 2017. [Google Scholar]
- Telukunta, V.; Pradhan, J.; Agrawal, A.; Singh, M.; Srivani, S.G. Protection challenges under bulk penetration of renewable energy resources in power systems: A review. CSEE J. Power Energy Syst. 2017, 3, 365–379. [Google Scholar] [CrossRef]
- Haddadi, A.; Kocar, I.; Farantatos, E. Impact of Inverter-Based Resources on Protection Schemes Based on Negative Sequence Components; EPRI: Palo Alto, CA, USA, 2019. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Jia, K.; Yang, Z.; Fang, Y.; Bi, T.; Sumner, M. Influence of Inverter-Interfaced Renewable Energy Generators on Directional Relay and an Improved Scheme. IEEE Trans. Power Electron. 2019, 34, 11843–11855. [Google Scholar] [CrossRef]
- Fang, Y.; Jia, K.; Yang, Z.; Li, Y.; Bi, T. Impact of Inverter-Interfaced Renewable Energy Generators on Distance Protection and an Improved Scheme. IEEE Trans. Ind. Electron. 2018, 66, 7078–7088. [Google Scholar] [CrossRef]
- Keller, J.; Kroposki, B. Understanding Fault Characteristics of Inverter-Based Distributed Energy Resources; Technical Report NREL/TP-550-46698; NREL: Golden, CO, USA, 2010. [Google Scholar]
- Haddadi, A.; Zhao, M.; Kocar, I.; Karaagac, U.; Chan, K.W.; Farantatos, E. Impact of Inverter-Based Resources on Negative Sequence Quantities-Based Protection Elements. IEEE Trans. Power Deliv. 2021, 36, 289–298. [Google Scholar] [CrossRef]
- Haddadi, A.; Farantatos, E.; Kocar, I.; Karaagac, U. Impact of inverter based resources on system protection. Energies 2021, 14, 1050. [Google Scholar] [CrossRef]
- Hooshyar, A.; Azzouz, M.; El-Saadany, E. Distance Protection of Lines Connected to Induction Generator-Based Wind Farms During Balanced Faults. IEEE Trans. Sustain. Energy 2014, 5, 1193–1203. [Google Scholar] [CrossRef]
- Chowdhury, R.; Fischer, N. Transmission Line Protection for Systems With Inverter-Based Resources—Part I: Problems. IEEE Trans. Power Deliv. 2021, 36, 2416–2425. [Google Scholar] [CrossRef]
- Chowdhury, R.; Fischer, N. Transmission Line Protection for Systems With Inverter-Based Resources—Part II: Solutions. IEEE Trans. Power Deliv. 2021, 36, 2426–2433. [Google Scholar] [CrossRef]
- Irwin, G.D.; Jindal, A.K.; Isaacs, A.L. Sub-synchronous control interactions between type 3 wind turbines and series compensated AC transmission systems. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Costello, D.; Zimmerman, K. Determining the Faulted Phase. In Proceedings of the 36th Annual Western Protective Relay Conference, Spokane, WA, USA, 20–22 October 2009. [Google Scholar]
- Carrasco, E.M.; Moreno, M.P.C.; Martínez, M.T.V.; Vicente, S.B. Improved Faulted Phase Selection Algorithm for Distance Protection under High Penetration of Renewable Energies. Energies 2020, 13, 558. [Google Scholar] [CrossRef]
- Kasztenny, B.; Campbell, B.; Mazereeuw, J. Phase Selection for Single-Pole Tripping—Weak Infeed Conditions and Cross-Country Faults. In Proceedings of the 27th Annual Western Protective Relay Conference, Spokane, WA, USA, 24–26 October 2000. [Google Scholar]
- Price, E.; Warren, B. The Performance of Faulted Phase Selectors used in Transmission Line Distance Applications. In Proceedings of the 61st Annual Conference for Protective Relay Engineers, College Station, TX, USA, 1–3 April 2008; pp. 484–490. [Google Scholar]
- L-PRO 4000 Transmission Line Protection Relay, Manual, ERLPhase Power Technologies Ltd. Available online: https://www.erlphase.com/downloads/manuals/L_PRO_4000_manual.pdf (accessed on 27 December 2022).
- Wijekoon, J.; Rajapakse, A.D.; Haleem, N.M. Fast and Reliable Method for Identifying Fault Type and Faulted Phases Using Band Limited Transient Currents. IEEE Trans. Power Deliv. 2020, 36, 2839–2850. [Google Scholar] [CrossRef]
- Dong, X.; Kong, W.; Cui, T. Fault Classification and Faulted-Phase Selection Based on the Initial Current Traveling Wave. IEEE Trans. Power Deliv. 2008, 24, 552–559. [Google Scholar] [CrossRef]
- Namdari, F.; Salehi, M. High-Speed Protection Scheme Based on Initial Current Traveling Wave for Transmission Lines Employing Mathematical Morphology. IEEE Trans. Power Deliv. 2017, 32, 246–253. [Google Scholar] [CrossRef]
- Silva, N.S.D.B.; M, K.; Souza, B.A. Fault Detection and Classification in Transmission Line Using Wavelet Transform and ANN. IEEE Trans. Power Deliv. 2006, 21, 2058–2063. [Google Scholar] [CrossRef]
- Abdullah, A. Ultrafast Transmission Line Fault Detection Using a DWT-Based ANN. IEEE Trans. Ind. Appl. 2017, 54, 1182–1193. [Google Scholar] [CrossRef]
- He, Z.; Fu, L.; Lin, S.; Bo, Z. Fault Detection and Classification in EHV Transmission Line Based on Wavelet Singular Entropy. IEEE Trans. Power Deliv. 2010, 25, 2156–2163. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, D.; Xiao, W.; Wang, W.; Zheng, Y. Research of fault phase selection on UHV transmission lines based on wavelet analysis. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies, ICSGCE 2016, Chengdu, China, 19–22 October 2016; pp. 284–289. [Google Scholar]
- Paladhi, S.; Pradhan, A.K. Adaptive Fault Type Classification for Transmission Network Connecting Converter-Interfaced Renewable Plants. IEEE Syst. J. 2020, 15, 4025–4036. [Google Scholar] [CrossRef]
- IEC 61400-27-1; Wind Energy Generation—Part 27-1: Electrical Simulation Models—Generic Models. IEC: Geneva, Switzerland, 2020.
- IEC 61850-9-2; IEC Standard for Communication Networks and Systems for Power Utility Automation, Part 9-2: Specific Communication Service Mapping (SCSM)—Sampled Values over ISO/IEC 8802-3’. IEC: Geneva, Switzerland, 2011.
- IEC 61869-9; Instrument Transformers—Part 9: Digital Interface for Instrument Transformers’. IEC: Geneva, Switzerland, 2016.
- UCA International Users Group. Implementation Guideline for DIGITAL Interface to Instrument Transformers Using IEC 61850-9-2; UCA International Users Group: Raleigh, NC, USA, 2004. [Google Scholar]
- IEC 61850-8-1; IEC Standard for Communication Networks and Systems for Power Utility Automation—Part 8-1: Specific Communication Service Mapping (SCSM—Mappings to MMS (ISO 9506-1 and ISO 9506-2) and to ISO/IEC 8802-3’. IEC: Geneva, Switzerland, 2011.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).