Distributed Energy Systems: Multi-Objective Design Optimization Based on Life Cycle Environmental and Economic Impacts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description and Modeling of Distributed Energy System
2.1.1. Photovoltaic (PV)
2.1.2. Wind Turbine
2.1.3. Combine Heat and Power (CHP)
2.1.4. Solar Thermal Collector (STC)
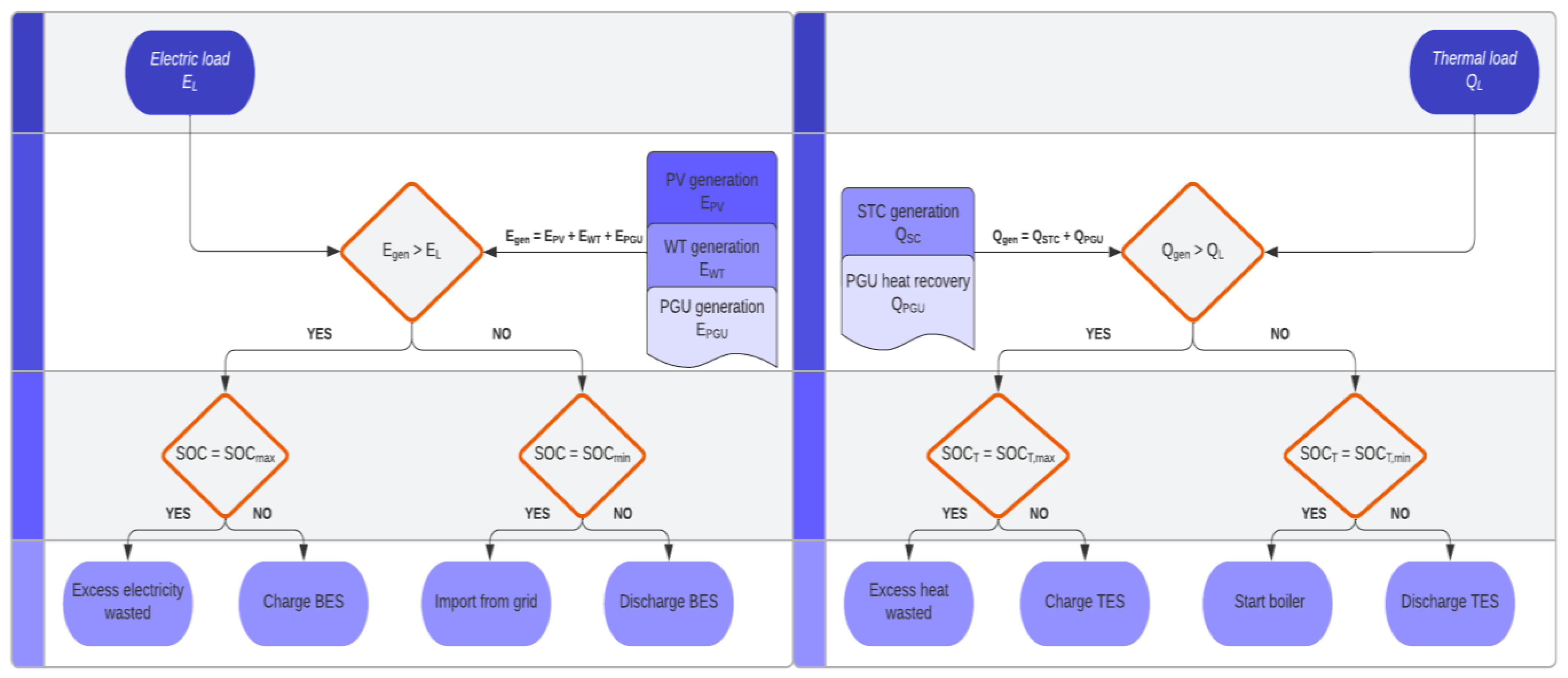
2.1.5. Energy Storage System
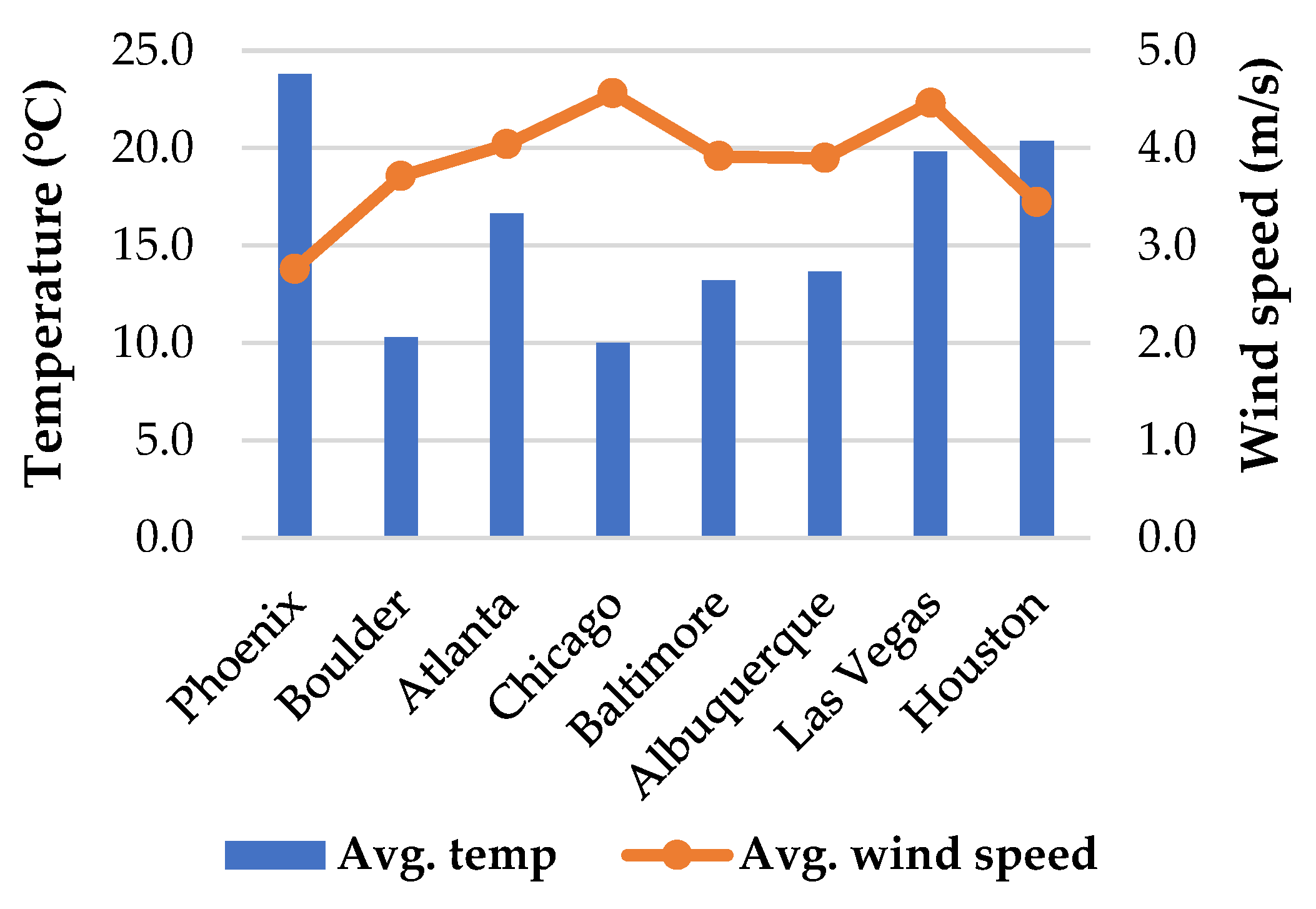
2.2. Building Model and Climate Data
2.3. Optimization Model
2.3.1. Decision Variable
- NPV: Number of PV
- NWT: Number of WT
- PPGU: PGU rated power (kW)
- EBES: Battery capacity (kWh)
- PBES: Battery rated power (kW)
- NSTC: Number of STC
- ETES: Thermal storage capacity (kWh)
2.3.2. Objective Function
2.3.3. Constraints
3. Results and Discussions
3.1. Optimization Results
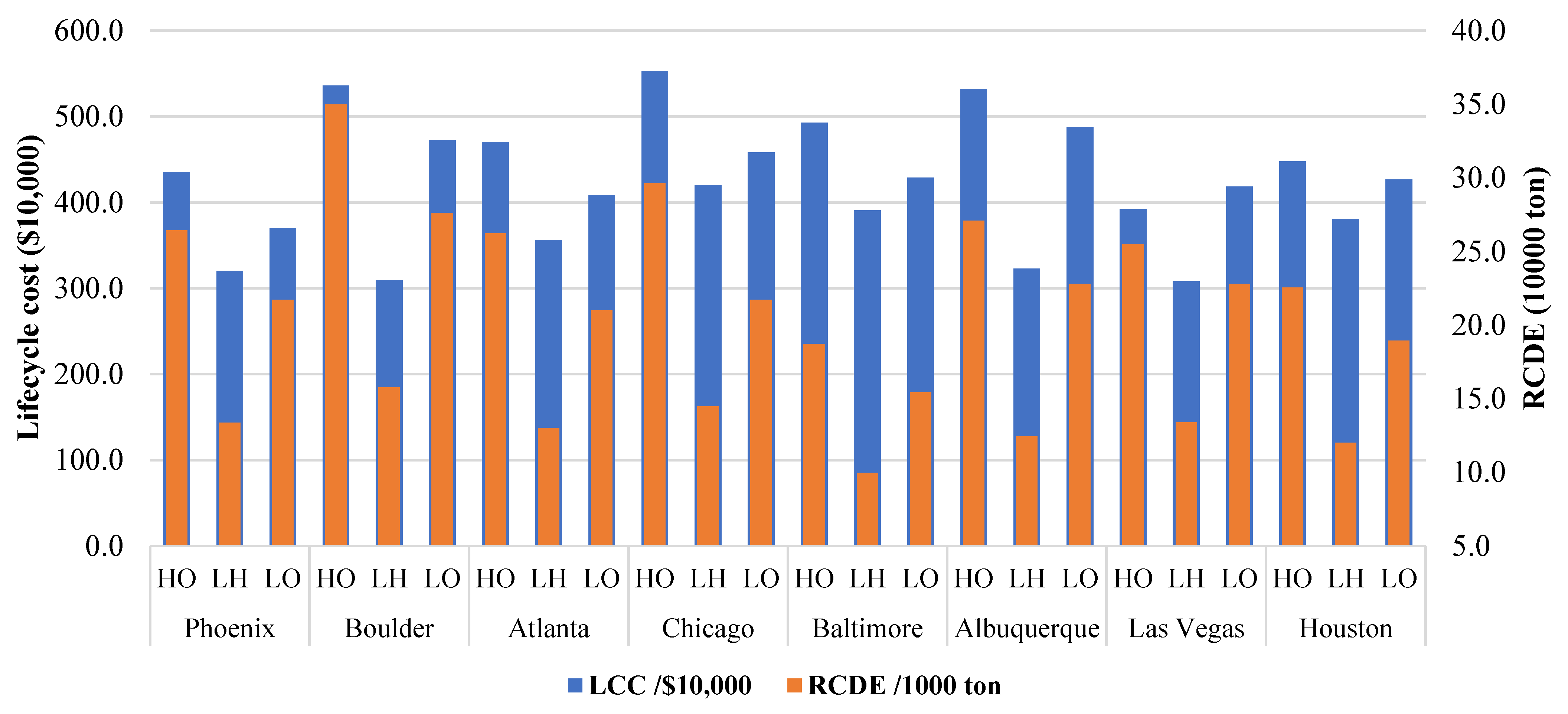
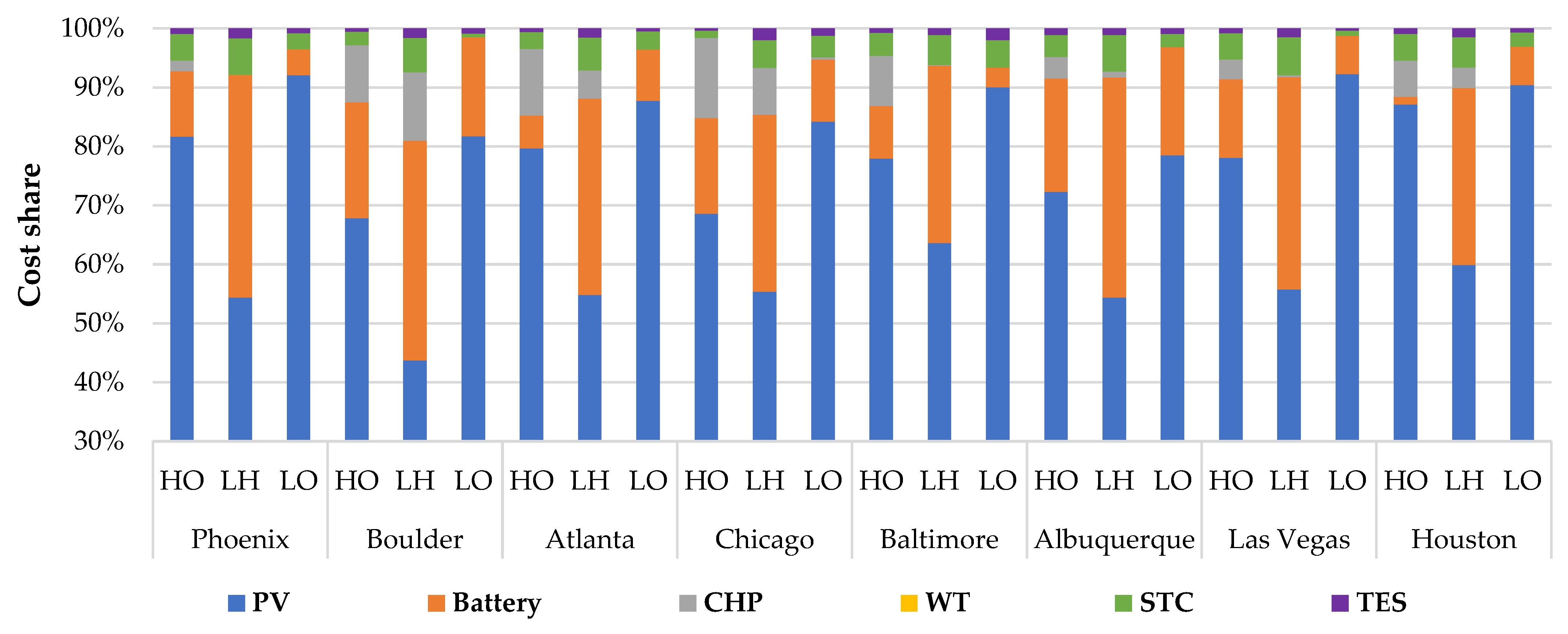
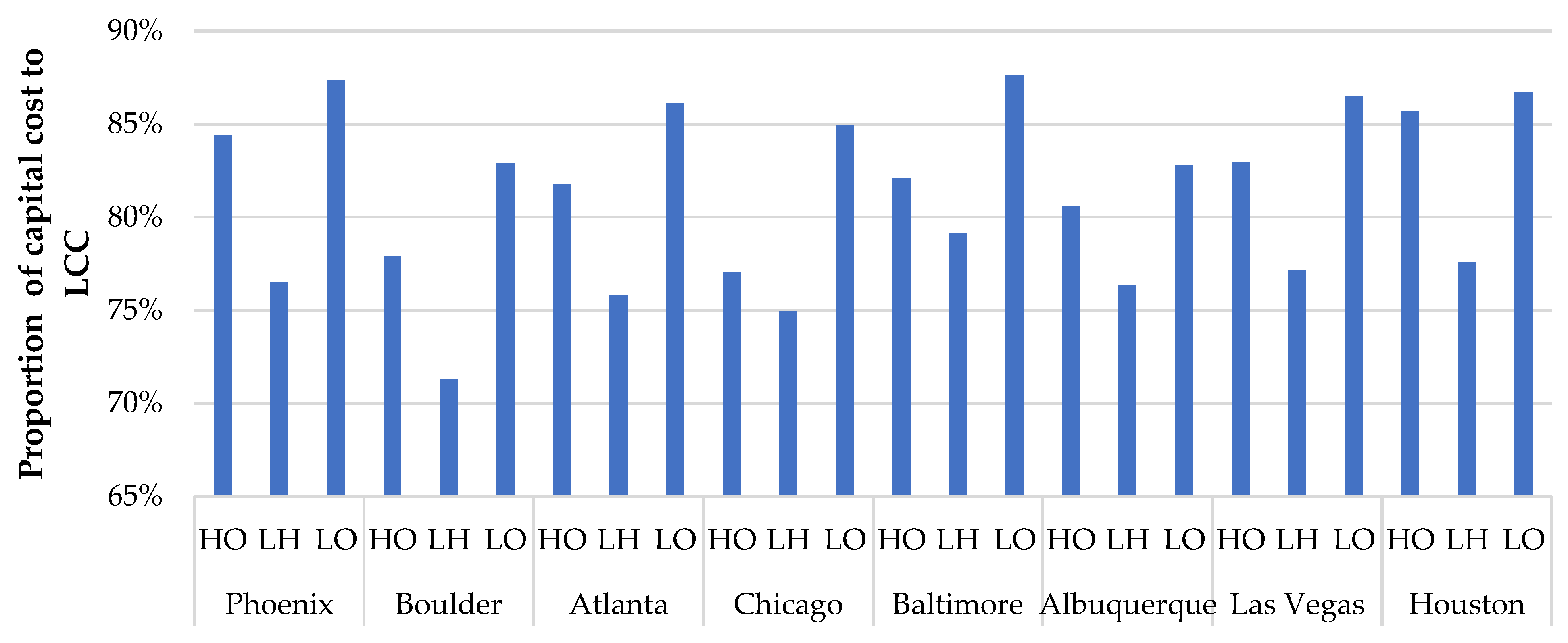
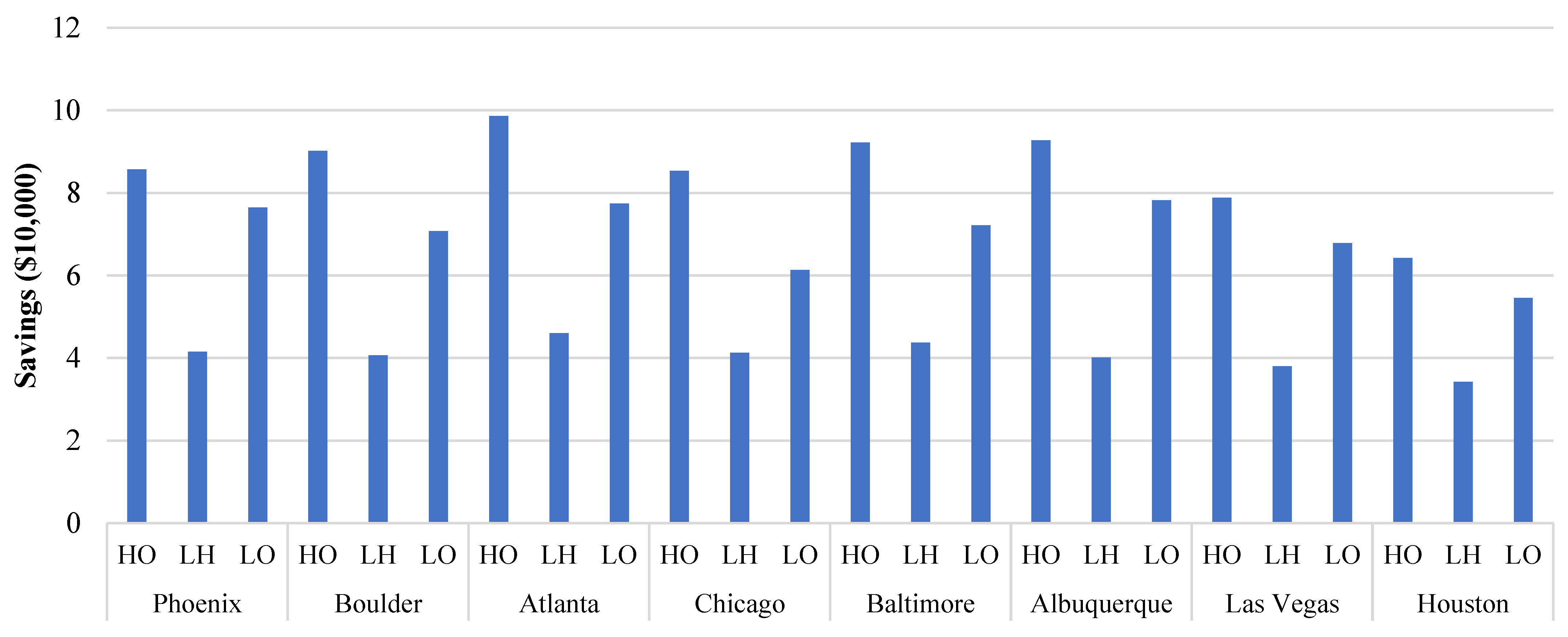
3.2. Life Cycle Cost and Reduction in Carbon Dioxide Emission of Optimized Distributed Energy System
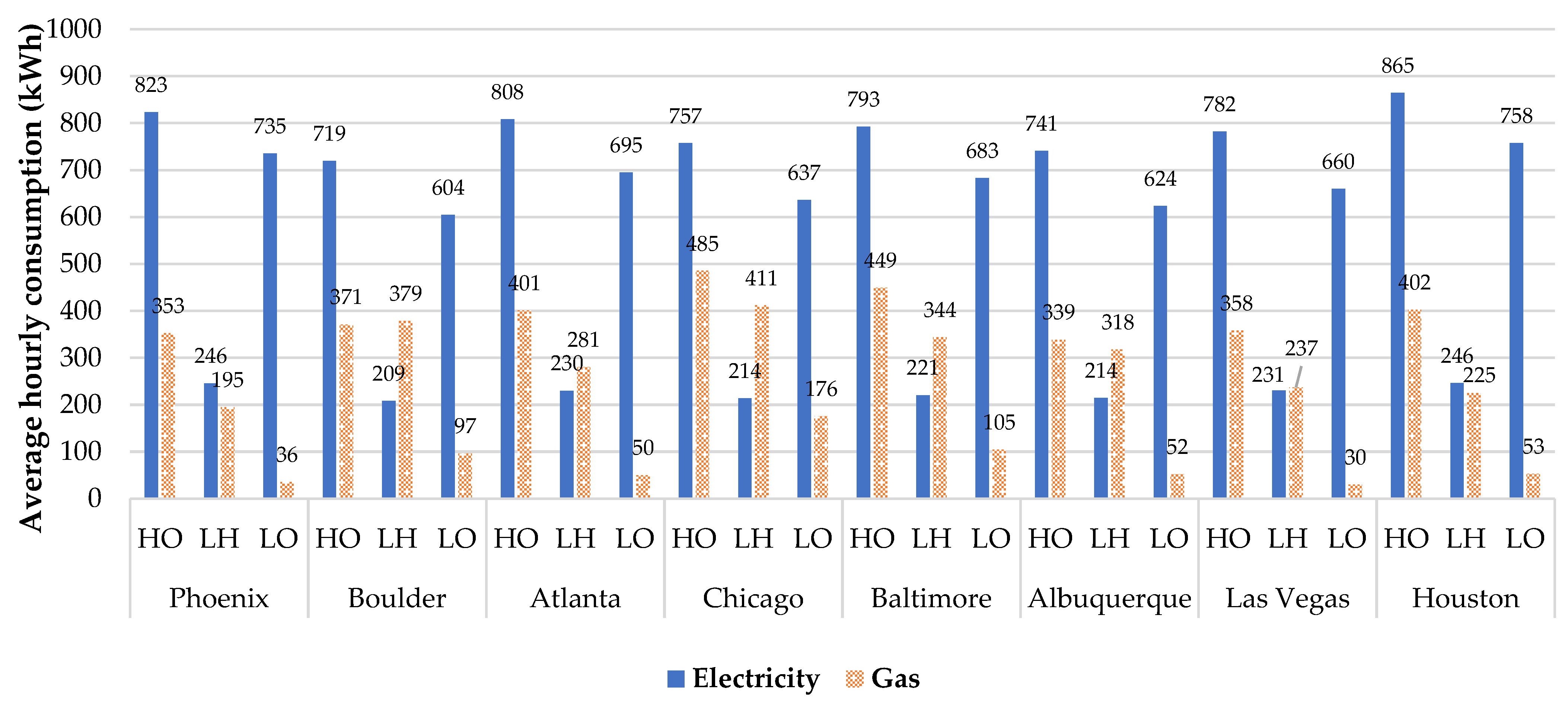
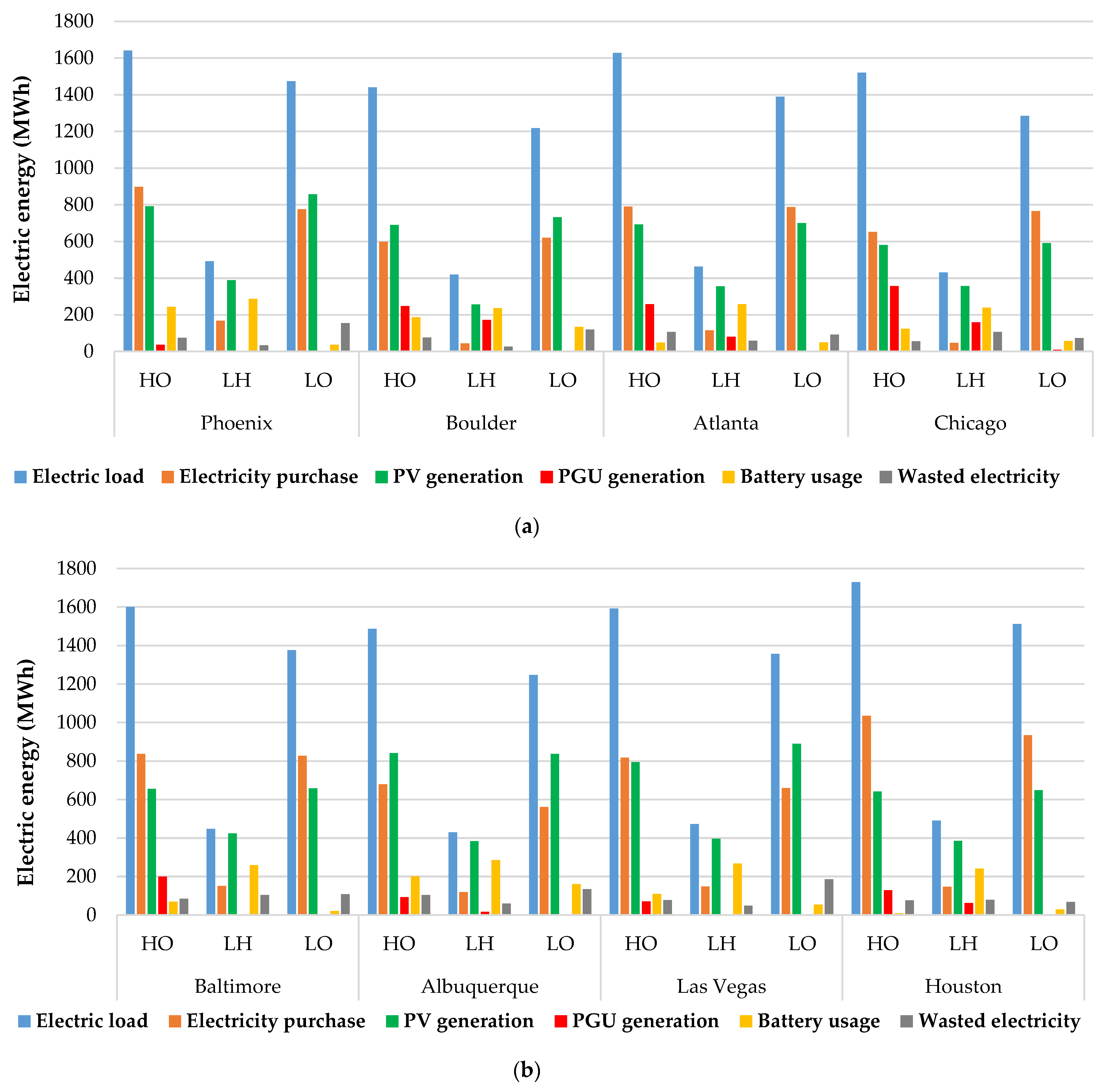
3.3. Optimized Distributed Energy System Operation Performance
4. Conclusions
- When considering the trade-offs between life cycle cost and RCDE, photovoltaic systems are favored in an optimal distributed energy system.
- The impact of optimized DES is evaluated in terms of cost savings, energy usage, carbon emission reductions, and life-cycle costs in these buildings. Among the studied locations, Boulder exhibits the highest reduction in carbon dioxide emissions for buildings of the same type.
- The cost savings derived from the implementation of DES among selected building types in different locations, hospitals, and large offices generally reap greater benefits when compared to large hotels. However, Large hotels, particularly the one located in Las Vegas, achieve the lowest life-cycle costs.
- The ratio of RCDE to LCC differs based on building type and location, with all three buildings in Boulder having the largest value, indicating a higher amount of emission reduction per dollar spent. When comparing three building types located in the same climate zone, a hospital building has the highest ratio value, followed by a large office and then a large hotel.
- The primary factor contributing to the life cycle cost of a DES is the initial capital investment, which constitutes more than 70% of the total expenditure in every instance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | CM,WT | maintenance cost of WT | |
| BES | battery energy storage | EBES | battery capacity |
| CHP | combined heat and power | Egen | total electric energy generation by DES |
| DES | distributed energy system | EL | building electric load |
| GHG | greenhouse gas | EL,DES | electricity imported with DES |
| HO | hospital | EPGU | electricity generated by the PGU |
| LCC | life cycle cost | ETES | thermal storage capacity |
| LH | large hotel | EFe | emission factor for grid electricity |
| LO | large office | EFf | emission factor for natural gas |
| MOGA | multi-objective genetic algorithm | f | active surface area fraction |
| PGU | power generation unit | FL,DES | fuel consumed with DES |
| PW | present worth | FPGU | fuel energy required to operate PGU |
| PV | photovoltaic | GT | total solar radiation |
| RCDE | reduction of carbon dioxide emission | NPV | number of PV |
| SOC | state of charge | NSTC | number of STC |
| STC | solar thermal collector | NWT | number of WT |
| TES | thermal energy storage | PBES | rated power of BES |
| WT | wind turbine | PC | charging power |
| PDC | discharging power | ||
| Variables | Pgen | electric generation power by DES | |
| As | surface area of PV module | Pload | building electric power |
| ASTC | surface area of STC | PPGU | rated power of PGU |
| Ccap | specific capacity cost of BES | PPV | PV power generation |
| Cp | rotor power coefficient | PWT | wind turbine power generation |
| CPGU | specific capital cost of PGU | Pr | present worth factor |
| Cpower | specific power cost of BES | Qboiler | thermal energy from boiler |
| CPV | specific capital cost of PV | QC | thermal energy charged by TES |
| CSTC | unit solar thermal collector cost | QDC | thermal energy discharged by TES |
| CTES | specific capacity cost of TES | QL | building heating load |
| CWT | specific capacity cost of WT | QR | recovered thermal energy |
| CapPV | capacity of the PV | QSTC | heat from solar thermal collector |
| CapWT | capacity of WT | Tamb | ambient air temperature |
| CostC | total capital cost of DES | Tin | inlet water temperature |
| Coste | cost of grid electricity | yint | y-intercept of STC |
| Costf | cost of fuel | ||
| CostM | total maintenance cost of DES | Greek | |
| CostO | total operation cost of DES | η | efficiency |
| CostR | total replacement cost of DES | ||
| CostC,BES | capital cost of BES | Subscripts | |
| CostC,PGU | capital cost of PGU | C | battery charging |
| CostC,PV | capital cost of PV | cell | module cell |
| CostC,STC | capital cost of STC | DC | battery discharging |
| CostC,TES | capital cost of TES | inverter | DC to AC conversion |
| CostC,WT | capital cost of WT | TC | TES charging |
| CM,BES | maintenance cost of BES | TDC | TES discharging efficiency |
| CM,PGU | maintenance cost of PGU | HRS | heat recovery system |
| CM,PV | maintenance cost of PV | ||
| CM,STC | maintenance cost of STC | ||
References
- Bouffard, F.; Kirschen, D.S. Centralised and distributed electricity systems. Energy Policy 2008, 36, 4504–4508. [Google Scholar] [CrossRef]
- Ding, F.; Li, P.; Wang, C.; Gao, F. Modeling and Simulation of Grid-Connected Hybrid Photovoltaic/Battery Distributed Generation System RHYTHM View Project Artificial Intelligence Driven Smart Community Control to Accelerate PV Adoption and Enhance Grid Resilience View Project Modeling and Simulation of Grid-Connected Hybrid Photovoltaic/Battery Distributed Generation System. 2010. Available online: https://www.researchgate.net/publication/241180649 (accessed on 24 September 2023).
- Kim, H.; Jung, Y.; Oh, J.; Cho, H.; Heo, J.; Lee, H. Development and evaluation of an integrated operation strategy for a poly-generation system with electrical and thermal storage systems. Energy Convers. Manag. 2022, 256, 115384. [Google Scholar] [CrossRef]
- Chen, Z.; Su, C.; Wu, Z.; Wang, W.; Chen, L.; Yang, L.; Kong, Y.; Du, X. Operation strategy and performance analyses of a distributed energy system incorporating concentrating PV/T and air source heat pump for heating supply. Appl. Energy 2023, 341, 121125. [Google Scholar] [CrossRef]
- Zhang, J.; Cho, H.; Luck, R.; Mago, P.J. Integrated photovoltaic and battery energy storage (PV-BES) systems: An analysis of existing financial incentive policies in the US. Appl. Energy 2018, 212, 895–908. [Google Scholar] [CrossRef]
- Wang, J.; Deng, H.; Qi, X. Cost-based site and capacity optimization of multi-energy storage system in the regional integrated energy networks. Energy 2022, 261, 125240. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Integration of distributed energy storage into net-zero energy district systems: Optimum design and operation. Energy 2018, 153, 575–591. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Fan, G.; Wu, D.; Guo, J.; Jin, G.; Zhang, S.; Yang, X. Co-optimization of a novel distributed energy system integrated with hybrid energy storage in different nearly zero energy community scenarios. Energy 2022, 247, 123553. [Google Scholar] [CrossRef]
- Falke, T.; Krengel, S.; Meinerzhagen, A.K.; Schnettler, A. Multi-objective optimization and simulation model for the design of distributed energy systems. Appl. Energy 2016, 184, 1508–1516. [Google Scholar] [CrossRef]
- Liu, X.; Yan, Z.; Wu, J. Optimal coordinated operation of a multi-energy community considering interactions between energy storage and conversion devices. Appl. Energy 2019, 248, 256–273. [Google Scholar] [CrossRef]
- Zhang, J.; Cho, H.; Mago, P.J.; Zhang, H.; Yang, F. Multi-Objective Particle Swarm Optimization (MOPSO) for a Distributed Energy System Integrated with Energy Storage. J. Therm. Sci. 2019, 28, 1221–1235. [Google Scholar] [CrossRef]
- Wang, B.; Yu, X.; Wu, Q.; Li, Z.; Jiang, R.; Qian, G.; Huang, R. Case studies of a distributed building energy system incorporating with EVs considering effects of random charging behaviors and time-of-use pricing in electricity. Case Stud. Therm. Eng. 2022, 38, 102297. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, R.; Zhang, B.; Zheng, Y.; An, Z. Environment dominated evaluation modeling and collocation optimization of a distributed energy system based on solar and biomass energy. Renew Energy 2023, 202, 1226–1240. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Luh, P.B.; Graditi, G.; Mongibello, L.; Naso, V. Multi-objective operation optimization of a Distributed Energy System for a large-scale utility customer. Appl. Therm. Eng. 2016, 101, 752–761. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.; Bao, Z.; Li, W.; Liu, F.; Jiang, Y. Operation optimization of a solar hybrid CCHP system for adaptation to climate change. Energy Convers. Manag. 2020, 220, 113010. [Google Scholar] [CrossRef]
- Bahlawan, H.; Morini, M.; Pinelli, M.; Spina, P.R.; Venturini, M. Simultaneous optimization of the design and operation of multi-generation energy systems based on life cycle energy and economic assessment. Energy Convers. Manag. 2021, 249, 114883. [Google Scholar] [CrossRef]
- Huang, C.; Bai, Y.; Yan, Y.; Zhang, Q.; Zhang, N.; Wang, W. Multi-objective co-optimization of design and operation in an independent solar-based distributed energy system using genetic algorithm. Energy Convers. Manag. 2022, 271, 116283. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Luo, X. Design and operation optimization of distributed solar energy system based on dynamic operation strategy. Energies 2021, 14, 69. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, W.; Du, J.; Bai, C.; Liu, W.; Chen, Z. Low-carbon optimal operation of distributed energy systems in the context of electricity supply restriction and carbon tax policy: A fully decentralized energy dispatch strategy. J. Clean. Prod. 2023, 396, 136511. [Google Scholar] [CrossRef]
- Wilcox, S.; Marion, W. Users Manual for TMY3 Data Sets. Published 2008. Available online: https://www.nrel.gov/docs/fy08osti/43156.pdf (accessed on 6 January 2022).
- Singh, M.; Santoso, S. Dynamic Models for Wind Turbines and Wind Power Plants; Subcontract Report NREL/SR-5500-52780; National Renewable Energy Laboratory: Golden, CO, USA, 2011. [Google Scholar]
- Spayde, E.; Mago, P.J.; Luck, R. Economic, energetic, and environmental performance of a solar powered organic rankine cycle with electric energy storage in different commercial buildings. Energies 2018, 11, 276. [Google Scholar] [CrossRef]
- Hodge, B.K. Alternative Energy Sources and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mitsubishi Electric. Photovoltaic Modules. Available online: https://www.mitsubishi-pv.de/datasheets/mjt-datasheet.pdf (accessed on 3 October 2023).
- Excel 10 off Grid. Bergey Windpower. 2020. Available online: http://www.bergey.com/products/off-grid-turbines/excel-10-off-grid/ (accessed on 7 January 2022).
- Warren, H.; Mago, P.J.; Knizley, A.; Luck, R. Performance enhancement of a power generation unit–organic Rankine cycle system through the addition of electric energy storage. J. Energy Storage 2017, 10, 28–38. [Google Scholar] [CrossRef]
- Certified Solar Collector. Alternate Energy Technologies. Available online: https://alternateenergycompany.com/home/pdf/AE_Collector_Brochure.pdf (accessed on 8 January 2022).
- Brusco, G.; Burgio, A.; Menniti, D.; Pinnarelli, A.; Sorrentino, N. The economic viability of a feed-in tariff scheme that solely rewards self-consumption to promote the use of integrated photovoltaic battery systems. Appl. Energy 2016, 183, 1075–1085. [Google Scholar] [CrossRef]
- Commercial Reference Buildings. U.S. Department of Energy. Available online: https://www.energy.gov/eere/buildings/commercial-reference-buildings (accessed on 9 January 2022).
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. U.S. Department of Energy Commercial Reference Building Models of the National Building Stock; National Renewable Energy Laboratory: Golden, CO, USA, 2011. [Google Scholar]
- U.S. Department of Energy (DOE). EnergyPlus Energy Simulation Software. Available online: https://energyplus.net/ (accessed on 7 January 2022).
- Mongird, K.; Viswanathan, V.; Alam, J.; Vartanian, C.; Sprenkle, V.; Baxter, R. 2020 Grid Energy Storage Technology Cost and Performance Assessment; US Department of Energy: Washinghton, DC, USA, 2020. [Google Scholar]
- Average Lifespan of a Hot Water Heater. Oliver Heating & Cooling. Available online: https://www.oliverheatcool.com/about/blog/news-for-homeowners/the-average-lifespan-of-water-heaters/ (accessed on 18 October 2023).
- Chowdhury, M.S.; Rahman, K.S.; Chowdhury, T.; Nuthammachot, N.; Techato, K.; Akhtaruzzaman, M.; Tiong, S.K.; Sopian, K.; Amin, N. An overview of solar photovoltaic panels’ end-of-life material recycling. Energy Strategy Rev. 2020, 27, 100431. [Google Scholar] [CrossRef]
- Combined Heat and Power. Energy Technology Systems Analysis Programme. May 2010. Available online: https://iea-etsap.org/E-TechDS/PDF/E04-CHP-GS-gct_ADfinal.pdf (accessed on 18 October 2023).
- Ziegler, L.; Gonzalez, E.; Rubert, T.; Smolka, U.; Melero, J.J. Lifetime extension of onshore wind turbines: A review covering Germany, Spain, Denmark, and the UK. Renew. Sustain. Energy Rev. 2018, 82, 1261–1271. [Google Scholar] [CrossRef]
- NREL Annual Technology Baseline. Commercial PV. Available online: https://atb.nrel.gov/electricity/2022/commercial_pv (accessed on 16 January 2023).
- Residential Wind Energy Systems. Bergey Windpower. Available online: http://www.bergey.com/wind-school/residential-wind-energy-systems/ (accessed on 12 January 2022).
- EIA U.S. Energy Information Administration. Capital Cost and Performance Characteristic Estimates for Utility Scale Electric Power Generating Technologies. 2020. Available online: https://www.eia.gov/analysis/studies/powerplants/capitalcost/pdf/capital_cost_AEO2020.pdf (accessed on 16 January 2023).
- Distributed Generation Renewable Energy Estimate of Costs. National Renewable Energy Laboratory (NREL). Available online: http://www.nrel.gov/analysis/tech_lcoe_re_cost_est.html (accessed on 12 January 2022).
- Mongird, K.; Fotedar, V.; Viswanathan, V.; Koritarov, V.; Balducci, P.; Hadjerioua, B. Energy Storage Technology and Cost Characterization Report; Pacific Northwest National Lab: Richland, WA, USA, 2019. [Google Scholar]
- Rockenbaugh, C.; Dean, J.; Lovullo, D.; Lisell, L.; Barker, G.; Hanckock, E.; Norton, P. High Performance Flat Plate Solar Thermal Collector Evaluation. 2016. Available online: https://www.nrel.gov/docs/fy16osti/66215.pdf (accessed on 24 September 2023).
- Natural Gas Prices. EIA U.S. Energy Information Administration. Available online: https://www.eia.gov/dnav/ng/ng_pri_sum_a_EPG0_PCS_DMcf_a.htm (accessed on 5 January 2023).
- eGRID Summary Tables 2020. EPA United States Environmental Protection Agency. Available online: https://www.epa.gov/system/files/documents/2022-01/egrid2020_summary_tables.pdf (accessed on 5 January 2023).
- Carbon Dioxide Emissions Coefficients. EIA U.S. Energy Information Administration. 2022. Available online: https://www.eia.gov/environment/emissions/co2_vol_mass.php (accessed on 13 January 2023).
- Satpathy, R.; Pamuru, V. Off-grid solar photovoltaic systems. In Solar PV Power; Elsevier: Amsterdam, The Netherlands, 2021; pp. 267–315. [Google Scholar] [CrossRef]
- Maharjan, K.; Zhang, J.; Cho, H.; Chen, Y. Distributed Energy Systems Design Optimization Based on Life Cycle Environmental and Economic Impacts. In Proceedings of the ASME 2022 16th International Conference on Energy Sustainability, ES 2022, Philadelphia, PA, USA, 11–13 July 2022. [Google Scholar] [CrossRef]



| Item | Parameters | Value |
|---|---|---|
| PV [24] | surface area of PV module, As | 1.66/m2 |
| nominal power | 250 W | |
| active surface area fraction, f | 0.85 | |
| inverter conversion efficiency, ηcell | 0.18 | |
| inverter conversion efficiency, ηinverter | 0.95 | |
| Wind Turbine [25] | rotor diameter, d | 7 m |
| cut-in wind speed | 2.5 m/s | |
| rated power | 8.9 kW at 11 m/s | |
| nominal power | 10 kW at 12 m/s | |
| rated sound level | 42.9 dB | |
| CHP [26] | PGU fuel to electric efficiency, ηPGU | 0.3 |
| heat recovery system efficiency, ηHRS | 0.8 | |
| STC [27] | y-intercept, yint | 0.76 |
| slope factor, m | 6.125 W/(m2·°C) | |
| BES and TES [28] | charge efficiencies, ηC and ηTC | 0.9 |
| discharge efficiencies, ηDC and ηTDC | 0.9 |
| Building Types | Number of Floors | Floor Area (m2) |
|---|---|---|
| Hospital (HO) | 5 | 22,422 |
| Large Hotel (LH) | 6 | 11,345 |
| Large Office (LO) | 12 | 46,320 |
| Location | Latitude | Climate Zones | Climate Type |
|---|---|---|---|
| Atlanta, GA | 33.633 | 3A | Warm Humid |
| Chicago, IL | 41.983 | 5A | Cool Humid |
| Houston, TX | 30.00 | 2A | Hot Humid |
| Phoenix, AZ | 33.45 | 2B | Hot Dry |
| Las Vegas, NV | 36.083 | 3B | Warm Dry |
| Boulder, CO | 40.13 | 5B | Cool Dry |
| Baltimore, MD | 39.167 | 4A | Mixed Humid |
| Albuquerque, NM | 35.04 | 4B | Mixed Dry |
| Decision Variable | HO | LH | LO |
|---|---|---|---|
| NPV | [0, 7000] | [0, 7000] | [0, 7000] |
| NWT | [0, 60] | [0, 60] | [0, 60] |
| PPGU | [0, 1200] | [0, 1200] | [0, 1200] |
| EBES | [0, 2000] | [0, 2000] | [0, 2000] |
| PBES | [0, 1200] | [0, 1200] | [0, 1200] |
| NSTC | [0, 100] | [0, 100] | [0, 100] |
| ETES | [0, 2000] | [0, 2000] | [0, 2000] |
| Parameter | Specific Cost |
|---|---|
| CPV | USD 1960/kW [37] |
| CO&M,PV | USD 18/kW-yr [37] |
| CWT | USD 6500/kW [38] |
| CO&M,WT | USD 0.01/kW-yr [38] |
| CPGU | USD 1810/kW [39] |
| CO&M,PGU | USD 0.02/kW-yr [40] |
| Ccap | USD 269/kWh [41] |
| Cpower | USD 350/kW [41] |
| CO&M,BES | USD 20/kW-yr [41] |
| CSTC | USD 2000/unit [42] |
| CO&M,STC | USD 100/kW-yr [42] |
| CTES | USD 31/kWh [40] |
| Location | Coste (USD/kWh) | Costf (USD/mcf) | EFe [44] (kg/kWh) | EFf [45] (kg/kWh) |
|---|---|---|---|---|
| Atlanta, GA | 0.1268 | 11.26 | 0.405 | 0.18 |
| Chicago, IL | 0.1166 | 12.20 | 0.475 | 0.18 |
| Houston, TX | 0.0926 | 11.72 | 0.369 | 0.18 |
| Phoenix, AZ | 0.1079 | 10.82 | 0.372 | 0.18 |
| Las Vegas, NV | 0.0964 | 11.05 | 0.372 | 0.18 |
| Boulder, CO | 0.1170 | 11.32 | 0.526 | 0.18 |
| Baltimore, MD | 0.1266 | 14.11 | 0.305 | 0.18 |
| Albuquerque, NM | 0.1121 | 10.36 | 0.372 | 0.18 |
| Location | Building | PV Num. | PV Cap./kW | Bat. Cap./kWh | Bat. Power/kW | CHP Power/kW | WT Num. | STC Num. | TES/kWh | LCC /USD 10,000 | RCDE/1000 ton |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Phoenix | HO | 6437 | 1609 | 741 | 187 | 18 | 0 | 98 | 793 | 435.1 | 435.1 |
| LH | 3158 | 790 | 1998 | 390 | 0 | 0 | 99 | 1026 | 320.5 | 320.5 | |
| LO | 6968 | 1742 | 306 | 60 | 0 | 0 | 56 | 649 | 370.1 | 370.1 | |
| Boulder | HO | 6593 | 1648 | 1726 | 346 | 123 | 0 | 61 | 535 | 536.2 | 536.2 |
| LH | 2452 | 613 | 1903 | 373 | 85 | 0 | 89 | 979 | 309.5 | 309.5 | |
| LO | 6992 | 1748 | 1234 | 295 | 0 | 0 | 14 | 802 | 472.3 | 472.3 | |
| Atlanta | HO | 6911 | 1728 | 387 | 115 | 128 | 0 | 68 | 558 | 470.2 | 470.2 |
| LH | 3538 | 885 | 1978 | 372 | 40 | 0 | 99 | 1084 | 356.2 | 356.2 | |
| LO | 6981 | 1745 | 646 | 116 | 0 | 0 | 67 | 407 | 408.3 | 408.3 | |
| Chicago | HO | 6870 | 1718 | 1390 | 337 | 177 | 0 | 35 | 357 | 552.7 | 552.7 |
| LH | 4217 | 1054 | 1979 | 458 | 79 | 0 | 98 | 1641 | 420.1 | 420.1 | |
| LO | 6992 | 1748 | 690 | 212 | 4 | 0 | 83 | 1084 | 458.2 | 458.2 | |
| Baltimore | HO | 6961 | 1740 | 694 | 159 | 99 | 0 | 96 | 693 | 492.9 | 492.9 |
| LH | 4504 | 1126 | 1976 | 359 | 1 | 0 | 99 | 851 | 390.7 | 390.7 | |
| LO | 6990 | 1748 | 236 | 47 | 0 | 0 | 99 | 1662 | 428.6 | 428.6 | |
| Albuquerque | HO | 6972 | 1743 | 1504 | 422 | 46 | 0 | 99 | 1137 | 532.0 | 532.0 |
| LH | 3184 | 796 | 1990 | 387 | 8 | 0 | 99 | 699 | 323.0 | 323.0 | |
| LO | 6936 | 1734 | 1551 | 252 | 0 | 0 | 54 | 855 | 487.8 | 487.8 | |
| Las Vegas | HO | 6239 | 1560 | 916 | 219 | 35 | 0 | 98 | 696 | 391.8 | 391.8 |
| LH | 3111 | 778 | 1884 | 332 | 2 | 0 | 99 | 897 | 308.1 | 308.1 | |
| LO | 6991 | 1748 | 419 | 105 | 0 | 0 | 18 | 271 | 418.4 | 418.4 | |
| Houston | HO | 6907 | 1727 | 72 | 29 | 64 | 0 | 98 | 786 | 447.8 | 447.8 |
| LH | 4136 | 1034 | 1964 | 328 | 31 | 0 | 98 | 1083 | 380.9 | 380.9 | |
| LO | 6984 | 1746 | 489 | 73 | 0 | 0 | 51 | 571 | 426.5 | 426.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maharjan, K.; Zhang, J.; Cho, H.; Chen, Y. Distributed Energy Systems: Multi-Objective Design Optimization Based on Life Cycle Environmental and Economic Impacts. Energies 2023, 16, 7312. https://doi.org/10.3390/en16217312
Maharjan K, Zhang J, Cho H, Chen Y. Distributed Energy Systems: Multi-Objective Design Optimization Based on Life Cycle Environmental and Economic Impacts. Energies. 2023; 16(21):7312. https://doi.org/10.3390/en16217312
Chicago/Turabian StyleMaharjan, Krisha, Jian Zhang, Heejin Cho, and Yang Chen. 2023. "Distributed Energy Systems: Multi-Objective Design Optimization Based on Life Cycle Environmental and Economic Impacts" Energies 16, no. 21: 7312. https://doi.org/10.3390/en16217312









