Fault Detection on Power Transmission Line Based on Wavelet Transform and Scalogram Image Analysis
Abstract
:1. Introduction
2. System Requirements and Challenges
- Fault impedance.
- Fault inception angle (FIA).
- Compensation (series and/or shunt).
- Other transmission factors such as loads, branches, transformers, etc.
- Only shunt faults are considered, while series faults are ignored. While the shunt faults have a high impact on the system, the series faults have less impact. However, both have an affect on the power system equipment life.
- Using a very simple network consisting of TL and fixed generators. Using only a simple network does not represent the real-world TL system, and the fault on such systems is not as complex as the real system. Thus, the TL that has additional components suffers their contribution to the fault as well.
- Theories are based on the TL protection to the threshold point, which differs from one network to another. This happens when the threshold is a fixed value which is different from one network to another, and may not be valuable if the system has changed by adding or removing components, load, …etc.
- Some theories utilize a supervised approach that requires a significant quantity of data and training. In general, increasing the number of datasets has the advantage of increasing the efficiency of these models, which means that it has been trained on most of the probabilistic scenario and vice versa. However, this is costly and requires time for training.
- Noise is a significant obstacle to the protection system as it can lead to misdiagnosis. This can be a major point in the diagnosis of signals. Therefore, not considering the noise in the fault analysis method causes a malfunction in the protection system as this noise is considered as a disturbance in the system, viz, it is a faulty signal.
- Fault inception angle (FIA) has an impact on the TL protection system. Without considering this factor FIA in any model lead to be a weak point for the model because the fault may occur in any FIA. That means, the future prediction results will be improper and unreliable.
- Computational cost which can be time consuming. Taking data from TL both ends costs resources and time for the fault diagnosis due to the fact that collecting data from two sides of a long transmission line needs a communication system, data preprocess, and devices besides the time to analyze.
3. The Proposed Methodology
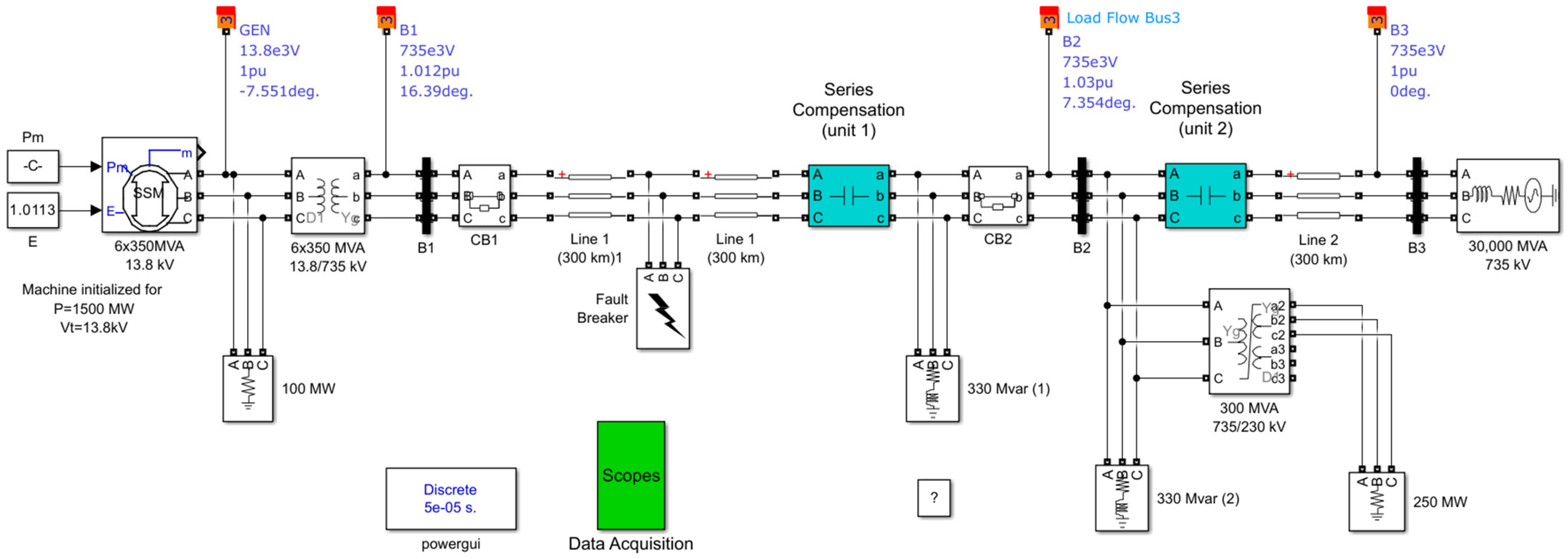
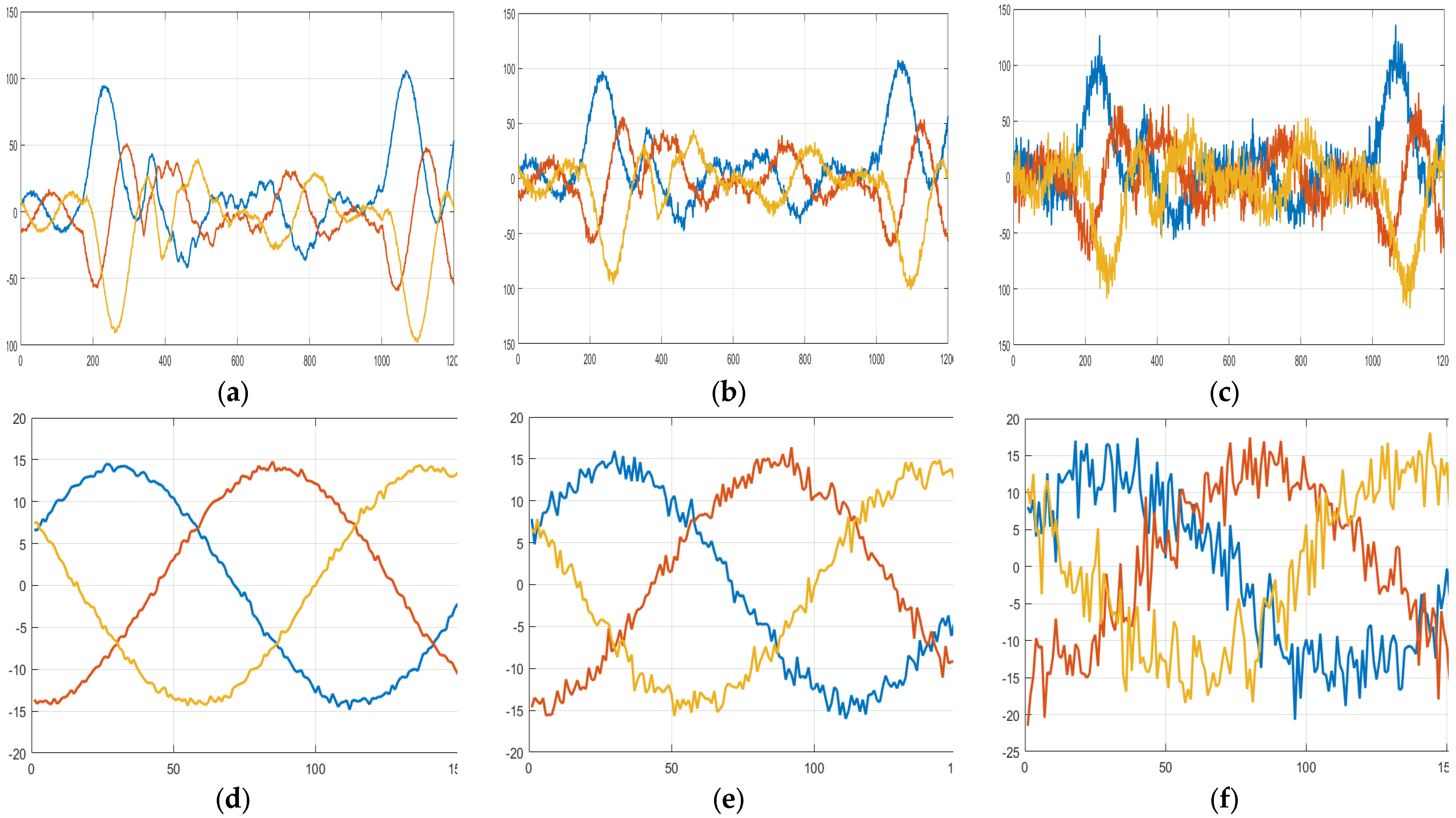
3.1. Data Collection
3.2. Contious Wavelet-Based Algorithm
- Time factor: Time does not exist for the Fourier transform, which makes it difficult to apply this theory to power systems that rely on signals traveling through time [49].
- Window limitation cannot be employed when the signal changes in a very short time or even slightly, such as when the signal passes through a transitory period [50].
- Time: it depicts the waveform with three signal spectrum fields (time, magnitude, and frequency).
- Window: the segmentation of the signal is treated as if it were a stationary signal. Consequently, STFT has a pre-defined restricted multi-window configuration.
- The window: once specified, it cannot be altered.
- Resolution pinpoint: this indicates that the window is directly proportional to frequency resolution and inversely proportional to time, and vice versa. This means that any component can result in either excellent frequency resolution or time resolution, but not both. .
- Time interval and frequency: this is regarded as the most difficult and demanding aspect of using STFT in power system analysis, particularly for transmission line protection.
- a (binary dilation or scale parameter): can compress or stretch the wavelet signal [51].
- b (binary position or translation parameter): used for shifting the wavelet signal over the original signal.
- Collect data from sending end.
- Sampling data collected.
- Applying wavelet for the signals’ feature extraction.
- Converting results in a 2D visualizing scalogram image.
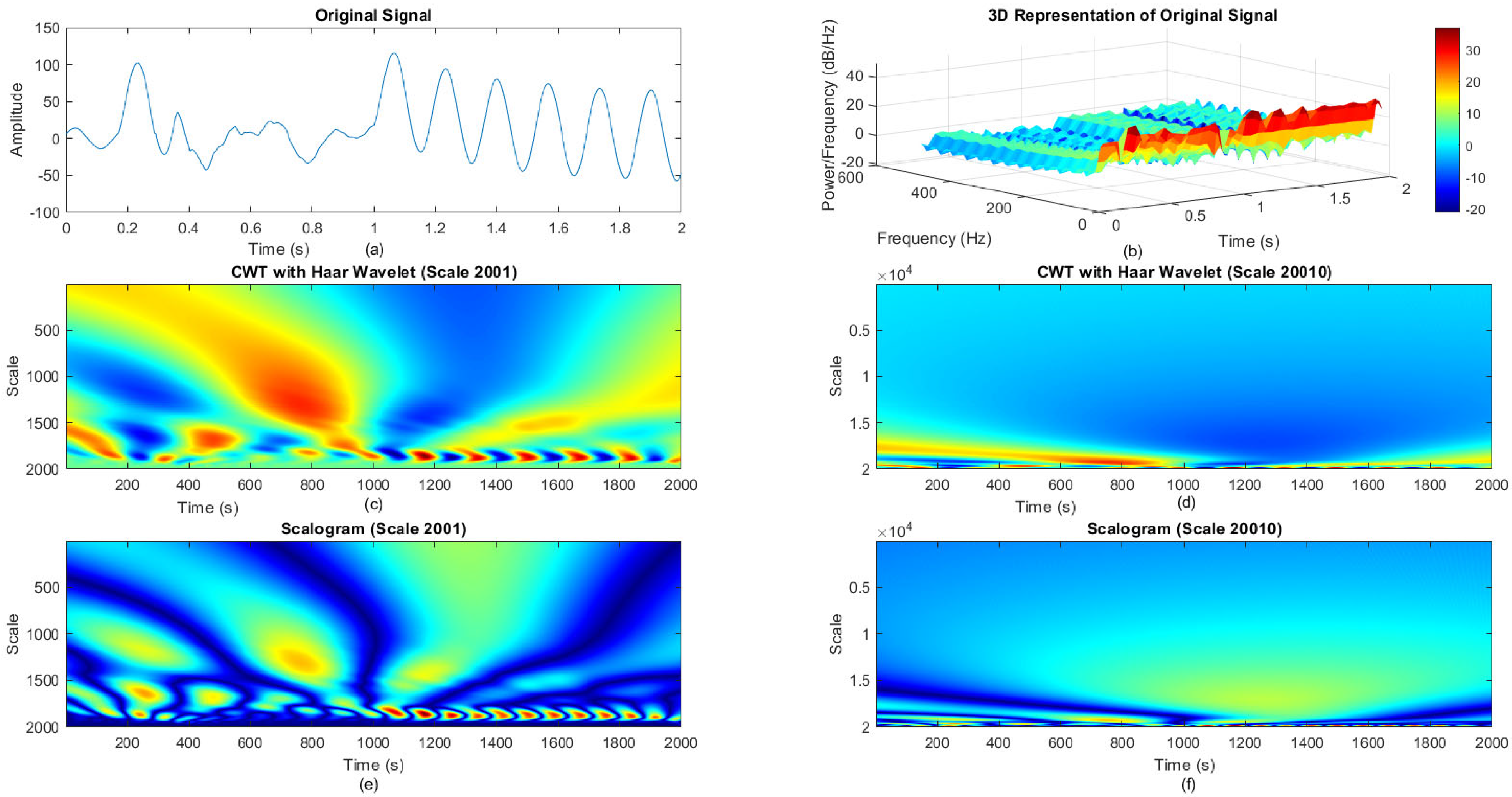
3.3. Scalogram Analysis
3.3.1. Wavelet Transform Limitations
3.3.2. Role of Scalogram Analysis
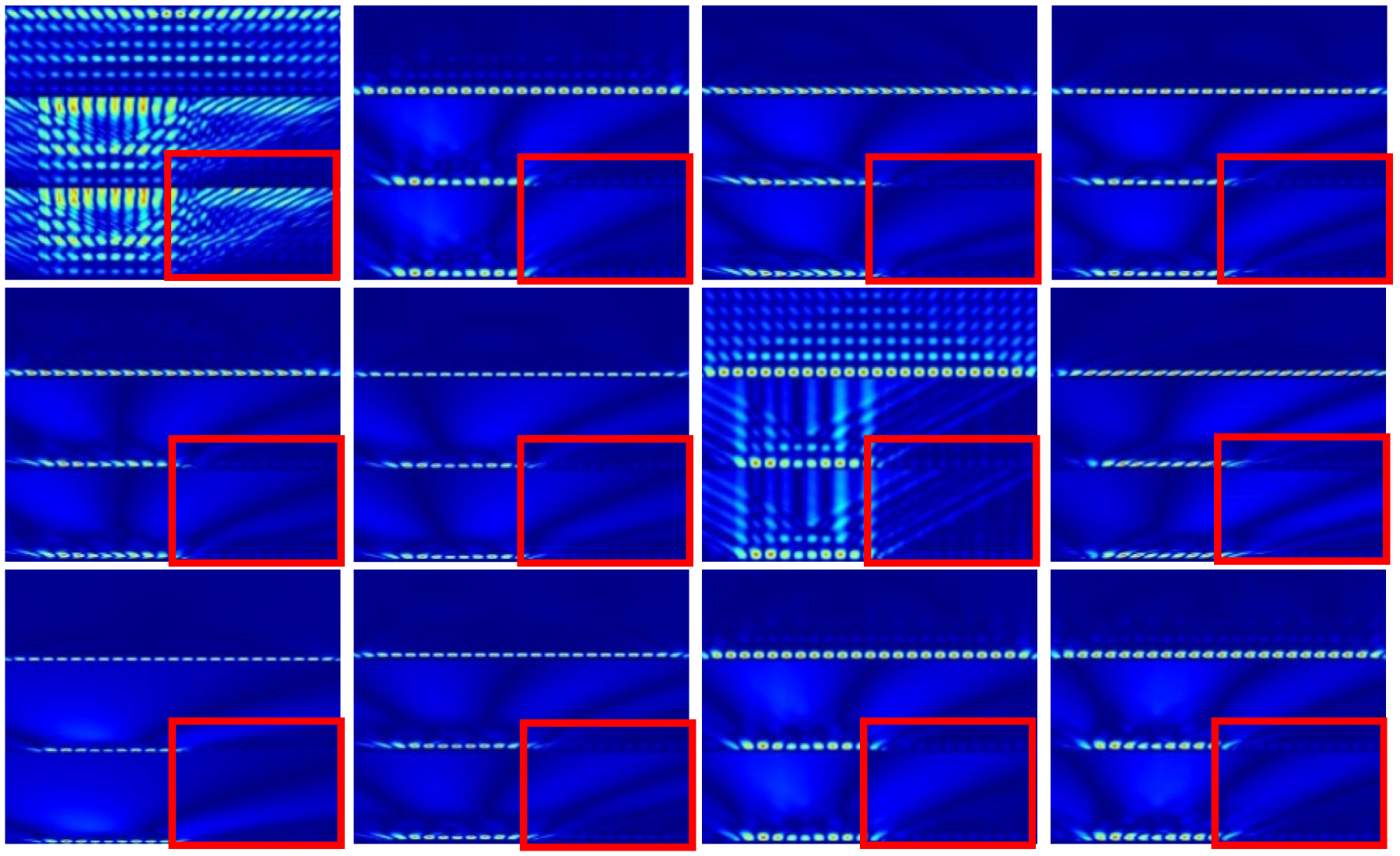
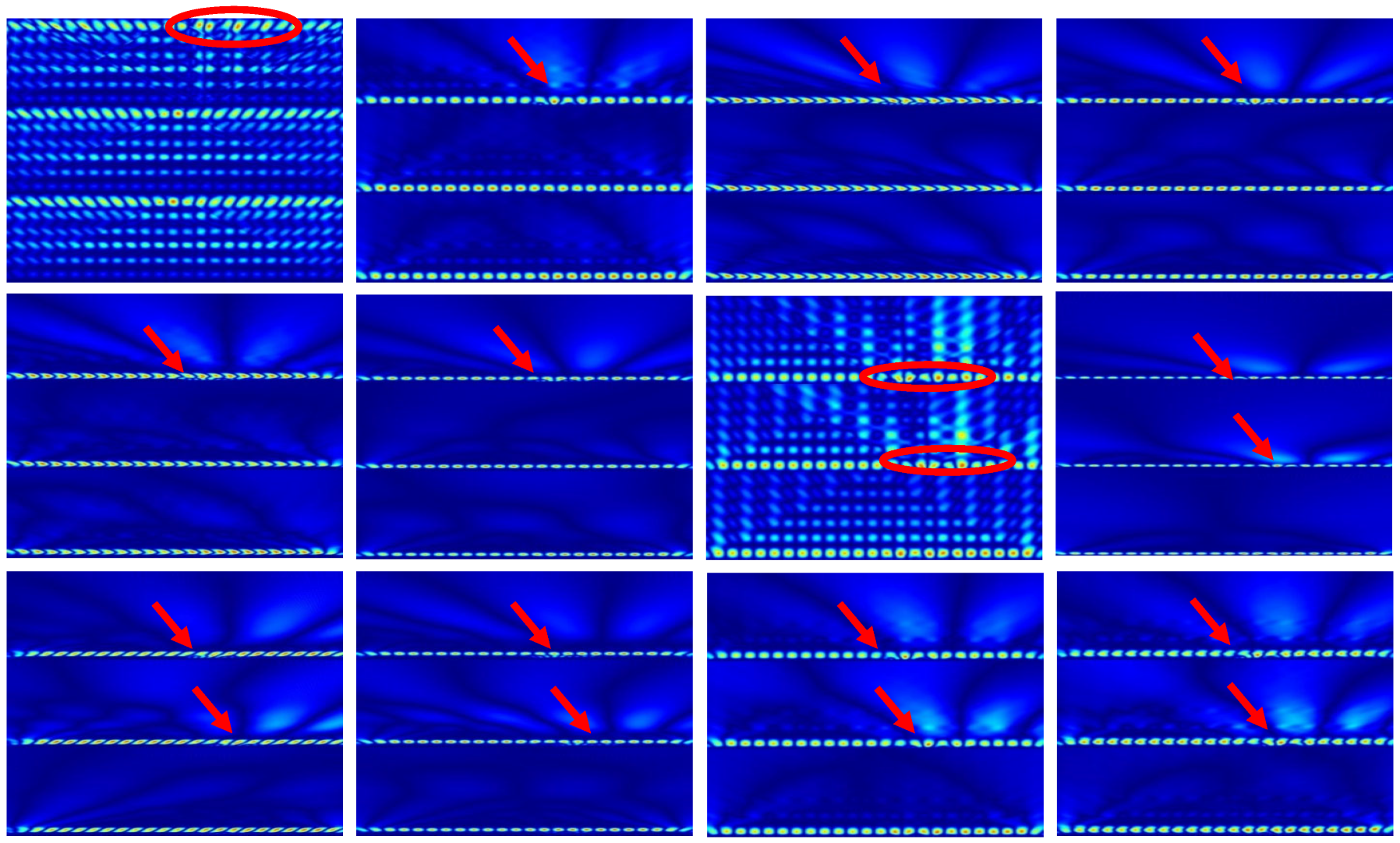
3.3.3. Scalogram Generation and Interpretation
3.3.4. Machine Learning Integration
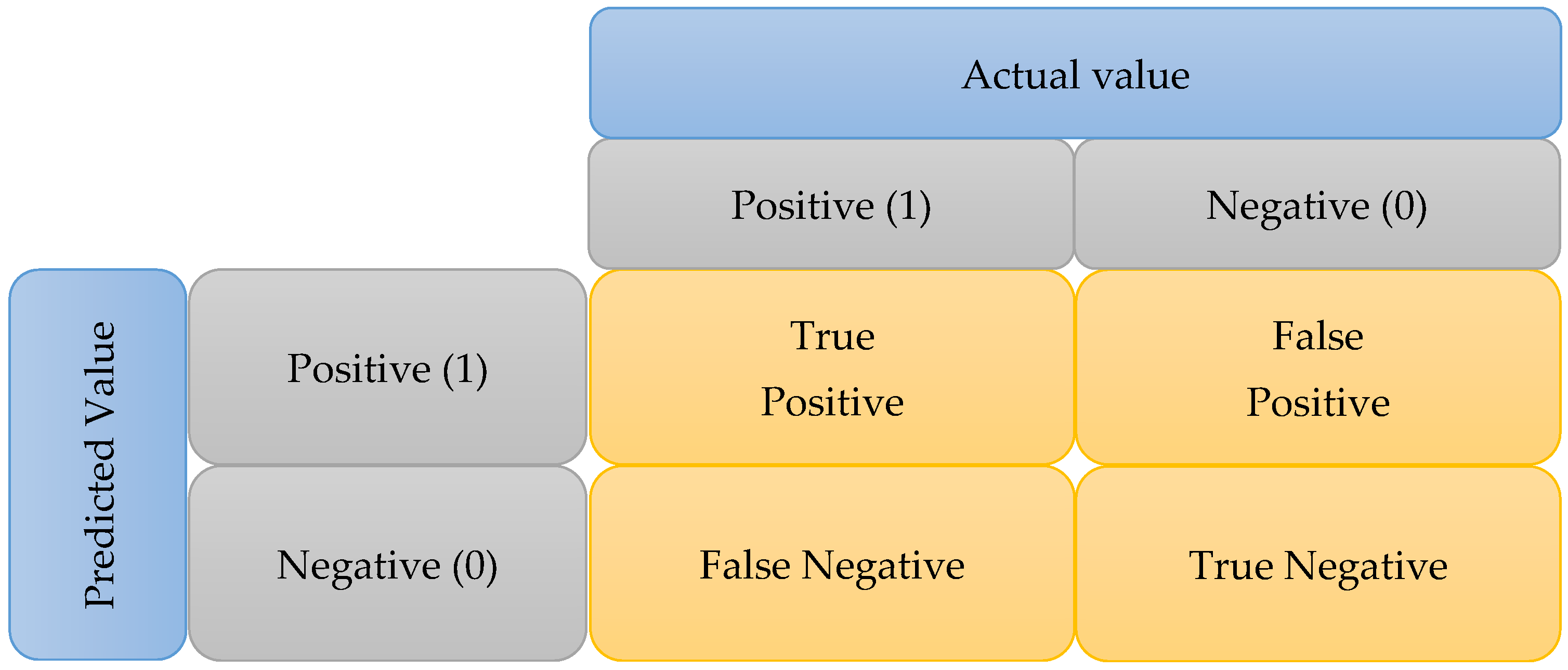
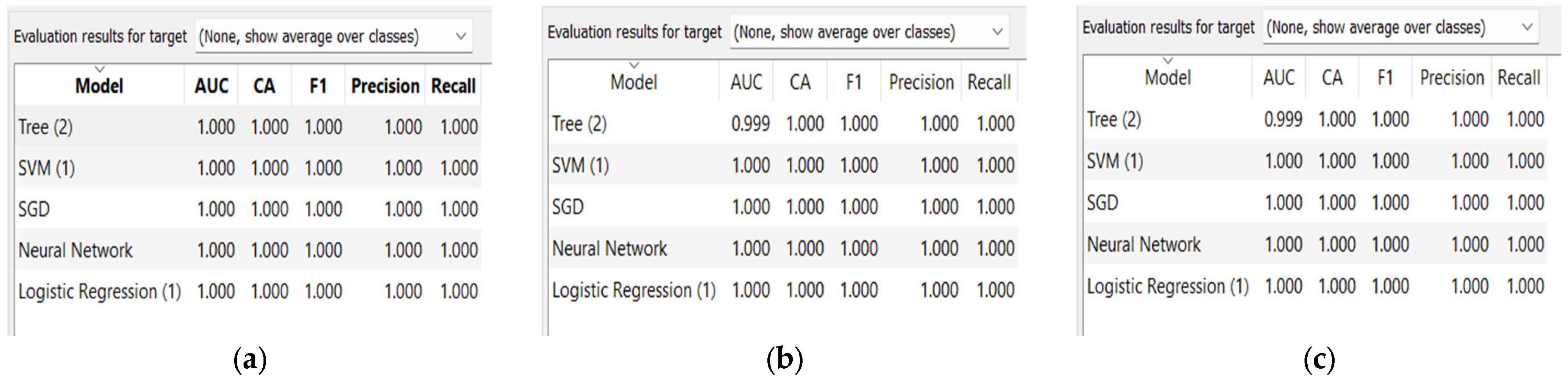
3.3.5. Validation and Performance Metrics
- Sensitivity:
- 2.
- Specificity:
- 3.
- Precision:
- 4.
- Recall:
- 5.
- F1 Score
3.3.6. Experimental Setup
- Classification based on the image features:
- 2.
- Classification based on high ranked image features:
4. Simulation Results and Discussion
4.1. Introduction to Results and Discussion
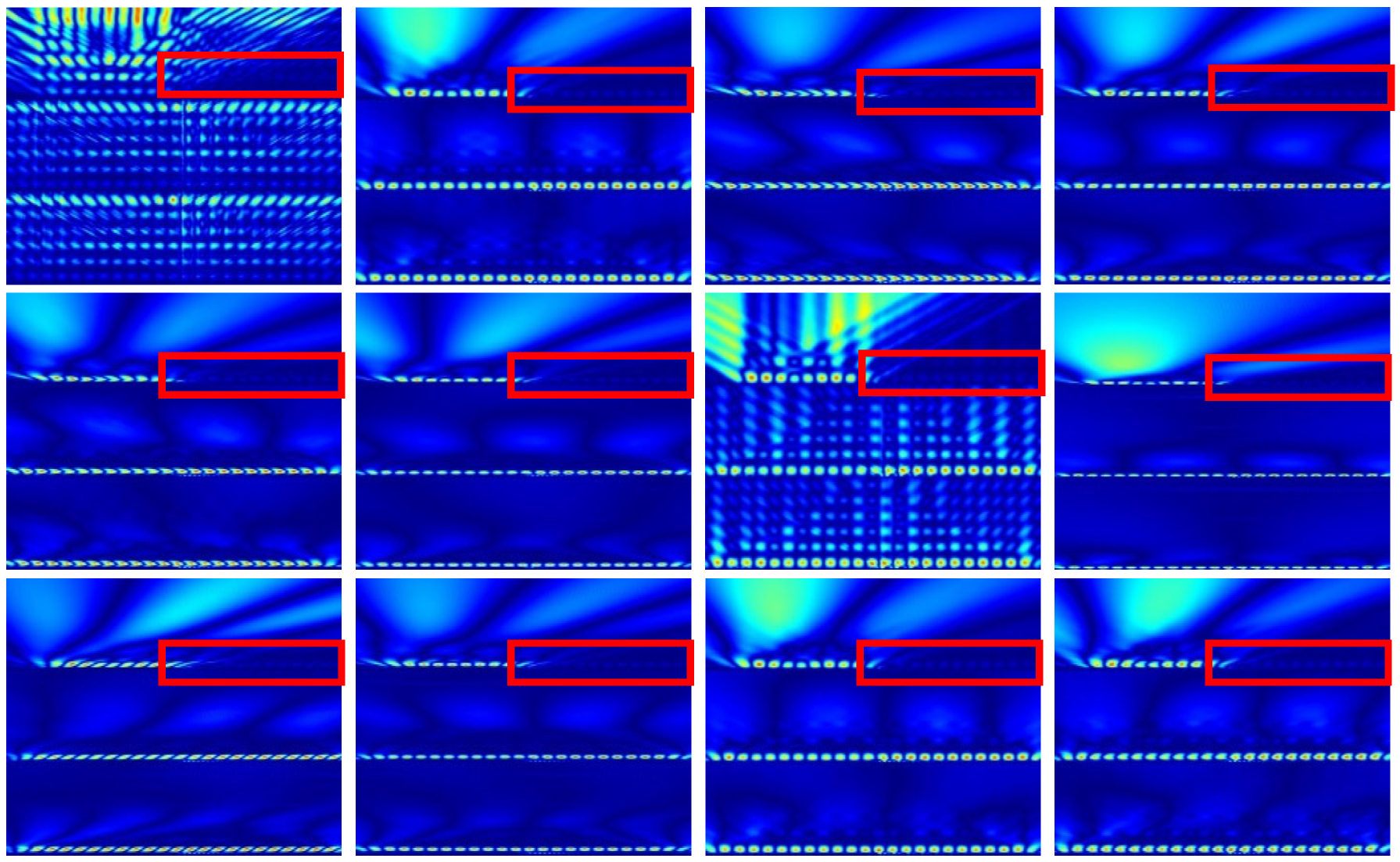
4.2. Effect of Noise
4.3. Discussion of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, P.M. Power System Protection; IEEE Press Power Engineering Series; McGraw-Hill: New York, NY, USA, 1999; ISBN 978-0-7803-3427-4. [Google Scholar]
- Rathore, B.; Mahela, O.P.; Khan, B.; Padmanaban, S. Protection Scheme Using Wavelet-Alienation-Neural Technique for UPFC Compensated Transmission Line. IEEE Access 2021, 9, 13737–13753. [Google Scholar] [CrossRef]
- Paul, M.; Debnath, S. Wavelet Based Single Ended Scheme for High Impedance Fault Classification in Transmission Lines. In Proceedings of the 2020 International Conference on Smart Technologies in Computing, Electrical and Electronics, Virtual, 9–10 October 2020. [Google Scholar]
- Fahim, S.R.; Das, S.K.; Sarker, Y.; Sheikh, R.I.; Sarker, S.K.; Datta, D. A Novel Wavelet Aided Probabilistic Generative Model for Fault Detection and Classification of High Voltage Transmission Line. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020; pp. 94–99. [Google Scholar]
- Lozada, F.I.; Quilumba, F.L.; Pérez, F.E. Detección y Clasificación de Fallas En Líneas de Transmisión Utilizando Transformada Wavelet y Máquinas de Soporte Vectorial. Rev. Técnica Energía 2018, 14, 151–158. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Karn, A.; Banerjee, S. Decision Tree Supported Distance Relay for Fault Detection and Classification in a Series Compensated Line. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Alashter, M.A.; Mrehel, O.G.; Shamekh, A.S. Design and Evaluation a Distance Relay Model Based on Artificial Neural Networks (ANN). In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunis, Tunisia, 28 September–1 October 2020; pp. 685–690. [Google Scholar]
- Hida, S.; Pradhan, V.; Naidu, O.D.; Cheriyan, E.P. A Critical Review of Distance Relaying Techniques under Power Swing Condition. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 500–505. [Google Scholar]
- Saber, A.; Emam, A.; Elghazaly, H. A Backup Protection Technique for Three-Terminal Multisection Compound Transmission Lines. IEEE Trans. Smart Grid 2018, 9, 5653–5663. [Google Scholar] [CrossRef]
- Biswas, S.; Nayak, P.K. A Fault Detection and Classification Scheme for Unified Power Flow Controller Compensated Transmission Lines Connecting Wind Farms. IEEE Syst. J. 2021, 15, 297–306. [Google Scholar] [CrossRef]
- Gangwar, A.K.; Mahela, O.P.; Rathore, B.; Khan, B.; Alhelou, H.H.; Siano, P. A Novel k-Means Clustering and Weighted k-NN-Regression-Based Fast Transmission Line Protection. IEEE Trans. Ind. Inform. 2021, 17, 6034–6043. [Google Scholar] [CrossRef]
- Singh, B.; Mahela, O.P.; Manglani, T. Detection and Classification of Transmission Line Faults Using Empirical Mode Decomposition and Rule Based Decision Tree Based Algorithm. In Proceedings of the 2018 IEEE 8th Power India International Conference (PIICON), Kurukshetra, India, 10–12 December 2018; pp. 1–6. [Google Scholar]
- Sharma, G.; Mahela, O.P.; Kumar, M.; Kumar, N. Detection and Classification of Transmission Line Faults Using Stockwell Transform and Rule Based Decision Tree. In Proceedings of the 2018 International Conference on Smart Electric Drives and Power System (ICSEDPS), Nagpur, India, 12–13 June 2018; pp. 1–5. [Google Scholar]
- Tong, H.; Qiu, R.C.; Zhang, D.; Yang, H.; Ding, Q.; Shi, X. Detection and Classification of Transmission Line Transient Faults Based on Graph Convolutional Neural Network. CSEE J. Power Energy Syst. 2021, 7, 456–471. [Google Scholar] [CrossRef]
- Swain, K.B.; Mahato, S.S.; Cherukuri, M. Expeditious Situational Awareness-Based Transmission Line Fault Classification and Prediction Using Synchronized Phasor Measurements. IEEE Access 2019, 7, 168187–168200. [Google Scholar] [CrossRef]
- Agarwal, S.; Swetapadma, A.; Panigrahi, C.; Dasgupta, A. Fault Analysis Method of Integrated High Voltage Direct Current Transmission Lines for Onshore Wind Farm. J. Mod. Power Syst. Clean Energy 2019, 7, 621–632. [Google Scholar] [CrossRef]
- Haq, E.U.; Jianjun, H.; Li, K.; Ahmad, F.; Banjerdpongchai, D.; Zhang, T. Improved Performance of Detection and Classification of 3-Phase Transmission Line Faults Based on Discrete Wavelet Transform and Double-Channel Extreme Learning Machine. Electr. Eng. 2021, 103, 953–963. [Google Scholar] [CrossRef]
- Pan, P.; Mandal, R.K.; Akanda, M.R.R. Fault Classification with Convolutional Neural Networks for Microgrid Systems. Int. Trans. Electr. Energy Syst. 2022, 2022, 8431450. [Google Scholar] [CrossRef]
- Dudhe, N.S.; Waghmare, D.B. Application of Wavelet Transform in Power System Analysis and Protection. Int. J. Eng. Res. 2017, 6, 889–892. [Google Scholar] [CrossRef]
- Rahmati, A.; Adhami, R. A Fault Detection and Classification Technique Based on Sequential Components. IEEE Trans. Ind. Appl. 2014, 50, 8. [Google Scholar] [CrossRef]
- Adhikari, S.; Sinha, N.; Dorendrajit, T. Fuzzy Logic Based On-Line Fault Detection and Classification in Transmission Line. SpringerPlus 2016, 5, 1002. [Google Scholar] [CrossRef] [PubMed]
- Pothisarn, C.; Klomjit, J.; Ngaopitakkul, A.; Jettanasen, C.; Asfani, D.A.; Negara, I.M.Y. Comparison of Various Mother Wavelets for Fault Classification in Electrical Systems. Appl. Sci. 2020, 10, 1203. [Google Scholar] [CrossRef]
- Parikh, U.B.; Das, B.; Maheshwari, R. Fault Classification Technique for Series Compensated Transmission Line Using Support Vector Machine. Int. J. Electr. Power Energy Syst. 2010, 32, 629–636. [Google Scholar] [CrossRef]
- Gayathri, K.; Kumarappan, N. Comparative Study of Fault Identification and Classification on EHV Lines Using Discrete Wavelet Transform and Fourier Transform Based ANN. Int. J. Electr. Comput. Eng. 2008, 2, 10. [Google Scholar]
- Khoker, M.Z.; Prakash Mahela, O.; Ahmad, G. A Current Based Hybrid Algorithm Using Discrete Wavelet Transform and Hilbert Transform for Detection and Classification of Power System Faults in the Presence of Solar Energy. In Proceedings of the 2020 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 22–23 February 2020; pp. 1–6. [Google Scholar]
- Jayabharata Reddy, M.; Mohanta, D.K. A Wavelet-Fuzzy Combined Approach for Classification and Location of Transmission Line Faults. Int. J. Electr. Power Energy Syst. 2007, 29, 669–678. [Google Scholar] [CrossRef]
- Youssef, O.A.S. Combined Fuzzy-Logic Wavelet-Based Fault Classification Technique for Power System Relaying. IEEE Trans. Power Deliv. 2004, 19, 582–589. [Google Scholar] [CrossRef]
- Jiang, J.-A.; Chuang, C.-L.; Wang, Y.-C.; Hung, C.-H.; Wang, J.-Y.; Lee, C.-H.; Hsiao, Y.-T. A Hybrid Framework for Fault Detection, Classification, and Location—Part I: Concept, Structure, and Methodology. IEEE Trans. Power Deliv. 2011, 26, 1988–1998. [Google Scholar] [CrossRef]
- Jiang, J.-A.; Chuang, C.-L.; Wang, Y.-C.; Hung, C.-H.; Wang, J.-Y.; Lee, C.-H.; Hsiao, Y.-T. A Hybrid Framework for Fault Detection, Classification, and Location—Part II: Implementation and Test Results. IEEE Trans. Power Deliv. 2011, 26, 1999–2008. [Google Scholar] [CrossRef]
- Jamil, M.; Sharma, S.K.; Singh, R. Fault Detection and Classification in Electrical Power Transmission System Using Artificial Neural Network. SpringerPlus 2015, 4, 334. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.K.; Badge, S.S. A Novel Fault Detection and Classification Technique for Double Circuit Transmission Line Using Artificial Neural Network. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 6–7 July 2017. [Google Scholar]
- Sharma, P.; Saini, D.; Saxena, A. Fault Detection and Classification in Transmission Line Using Wavelet Transform and ANN. Bull. Electr. Eng. Inform. 2016, 5, 284–295. [Google Scholar] [CrossRef]
- Parvez, I.; Aghili, M.; Sarwat, A.I.; Rahman, S.; Alam, F. Online Power Quality Disturbance Detection by Support Vector Machine in Smart Meter. J. Mod. Power Syst. Clean Energy 2019, 7, 1328–1339. [Google Scholar] [CrossRef]
- Hojabri, M.; Dersch, U.; Papaemmanouil, A.; Bosshart, P. A Comprehensive Survey on Phasor Measurement Unit Applications in Distribution Systems. Energies 2019, 12, 4552. [Google Scholar] [CrossRef]
- Sundaravaradan, N.A.; Mohanta, D.K. Robust Fault Analysis in Transmission Lines Using Synchrophasor Measurements. Prot. Control Mod. Power Syst. 2018, 3, 14. [Google Scholar] [CrossRef]
- Zhang, N.; Kezunovic, M. Transmission Line Boundary Protection Using Wavelet Transform and Neural Network. IEEE Trans. Power Deliv. 2007, 22, 859–869. [Google Scholar] [CrossRef]
- Chen, K.; Hu, J.; He, J. Detection and Classification of Transmission Line Faults Based on Unsupervised Feature Learning and Convolutional Sparse Autoencoder. IEEE Trans. Smart Grid 2016, 9, 1748–1758. [Google Scholar] [CrossRef]
- Bhowmik, P.S.; Purkait, P.; Bhattacharya, K. A Novel Wavelet Transform Aided Neural Network Based Transmission Line Fault Analysis Method. Int. J. Electr. Power Energy Syst. 2009, 31, 213–219. [Google Scholar] [CrossRef]
- Patel, M.; Patel, R.N. Fault Detection and Classification on a Transmission Line Using Wavelet Multi Resolution Analysis and Neural Network. Int. J. Comput. Appl. 2012, 47, 27–33. [Google Scholar] [CrossRef]
- Fan, C.; Li, K.K.; Chan, W.L.; Yu, W. Study of Protection Scheme for Transmission Line Based on Wavelet Transient Energy. Int. J. Electr. Power Energy Syst. 2006, 28, 459–470. [Google Scholar] [CrossRef]
- Aguilera, C.; Orduna, E.; Ratta, G. Adaptive Noncommunication Protection Based on Traveling Waves and Impedance Relay. IEEE Trans. Power Deliv. 2006, 21, 1154–1162. [Google Scholar] [CrossRef]
- De Souza Gomes, A.; Costa, M.A.; De Faria, T.G.A.; Caminhas, W.M. Detection and Classification of Faults in Power Transmission Lines Using Functional Analysis and Computational Intelligence. IEEE Trans. Power Deliv. 2013, 28, 1402–1413. [Google Scholar] [CrossRef]
- Tag Eldin, E.S.M. Fault Location for a Series Compensated Transmission Line Based on Wavelet Transform and an Adaptive Neuro-Fuzzy Inference System. In Proceedings of the 2010 Electric Power Quality and Supply Reliability Conference, Kuressaare, Estonia, 11–13 June 2010; pp. 229–236. [Google Scholar]
- Jain, A.; Thoke, A.S.; Patel, R.N. Fault Classification of Double Circuit Transmission Line Using Artificial Neural Network. Int. J. Electr. Syst. Sci. Eng. 2008, 2, 750–755. [Google Scholar]
- Tao, X.; Zhang, D.; Wang, Z.; Liu, X.; Zhang, H.; Xu, D. Detection of Power Line Insulator Defects Using Aerial Images Analyzed with Convolutional Neural Networks. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1486–1498. [Google Scholar] [CrossRef]
- Junfeng, L.; Min, L.; Qinruo, W. A Novel Insulator Detection Method for Aerial Images. In Proceedings of the 9th International Conference on Computer and Automation Engineering—ICCAE’17, Sydney, NSW, Australia, 18–21 February 2019; ACM Press: Sydney, NSW, Australia, 2017; pp. 141–144. [Google Scholar]
- Liu, C.; Wu, Y.; Liu, J.; Sun, Z.; Xu, H. Insulator Faults Detection in Aerial Images from High-Voltage Transmission Lines Based on Deep Learning Model. Appl. Sci. 2021, 11, 4647. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhen, Z.; Zhang, L.; Qi, Y.; Kong, Y.; Zhang, K. Insulator Detection Method in Inspection Image Based on Improved Faster R-CNN. Energies 2019, 12, 1204. [Google Scholar] [CrossRef]
- Janıcek, F.; Mucha, M.; Ostrozlık, M. A New Protection Relay Based on Fault Transient Analysis Using Wavelet Transform. J. Electr. Eng. 2007, 58, 8. [Google Scholar]
- Masood, B.; Saleem, U.; Anjum, M.N.; Arshad, U. Faults Detection and Diagnosis of Transmission Lines Using Wavelet Transformed Based Technique. In Proceedings of the 2017 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Aqaba, Jordan, 11–13 October 2017; pp. 1–6. [Google Scholar]
- Cabrelli, C.A.; Molter, U.M. Wavelet Transform of the Dilation Equation. J. Aust. Math. Soc. Ser. B Appl. Math. 1996, 37, 474–489. [Google Scholar] [CrossRef]




| System Condition | Parameters |
|---|---|
| Shunt fault | AG, BG, CG, AB, AC, BC, ABG, ACG, BCG, ABCG and NORMAL |
| Series fault | One line open, two lines open |
| Noise level | Ideal, 10, 20 and 30 dB |
| Fault inception angle | 30, 60, 90, 180, 270, 360 |
| Fault location | 20, 30, 40, 50, 75, 100, 150, 200, 280 |
| Fault resistance | 0.001, 0.005, 1, 10, 50, 75, 100, 200 |
| ‘bior’ Biorthogonal wavelets-3.1 | ‘coif’ Coiflets-2 | ‘db’ Daubechies wavelets-7 | ‘dmey’ Discrete approximation of Meyer wavelet-14 |
| ‘fk’ Fejér-Korovkin filters-14 | ‘gaus’ Gaussian wavelets-7 | ‘haar’ Haar wavelet- | ‘mexh’ Mexican hat wavelet (also known as Ricker wavelet)- |
| ‘meyr’ Meyer wavelet- | ‘morl’ Morlet wavelet- | ‘rbio’ Reverse biorthogonal wavelets-4.4 | ‘sym’ Symlets-5 |
| Classifier Type | According to Image Embedding Inputs | According to Image Features | According to 250 High Ranked Image Features | |||
|---|---|---|---|---|---|---|
| Accuracy % | Accuracy % | Accuracy % | ||||
| Ideal | With Noise 10, 20, and 30 dB | Ideal | With Noise 10, 20, and 30 dB | Ideal | With Noise 10, 20, and 30 dB | |
| Logistic regression | 100 | 100 | 100 | 100 | 100 | 100 |
| SVM | 100 | 100 | 100 | 100 | 100 | 100 |
| Random forest | 100 | 100 | 100 | 100 | 100 | 100 |
| Neural Network | 100 | 100 | 100 | 100 | 100 | 100 |
| kNN | 100 | 100 | 100 | 100 | 100 | 100 |
| AdaBoost | 100 | 100 | ||||
| Decision Tree | 100 | 100 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altaie, A.S.; Majeed, A.A.; Abderrahim, M.; Alkhazraji, A. Fault Detection on Power Transmission Line Based on Wavelet Transform and Scalogram Image Analysis. Energies 2023, 16, 7914. https://doi.org/10.3390/en16237914
Altaie AS, Majeed AA, Abderrahim M, Alkhazraji A. Fault Detection on Power Transmission Line Based on Wavelet Transform and Scalogram Image Analysis. Energies. 2023; 16(23):7914. https://doi.org/10.3390/en16237914
Chicago/Turabian StyleAltaie, Ahmed Sabri, Ammar Abbas Majeed, Mohamed Abderrahim, and Afaneen Alkhazraji. 2023. "Fault Detection on Power Transmission Line Based on Wavelet Transform and Scalogram Image Analysis" Energies 16, no. 23: 7914. https://doi.org/10.3390/en16237914
APA StyleAltaie, A. S., Majeed, A. A., Abderrahim, M., & Alkhazraji, A. (2023). Fault Detection on Power Transmission Line Based on Wavelet Transform and Scalogram Image Analysis. Energies, 16(23), 7914. https://doi.org/10.3390/en16237914









