Optimal Design of a Submodule Capacitor in a Modular Multilevel Converter for Medium Voltage Motor Drives
Abstract
:1. Introduction
- The approach of utilizing a high-frequency CMV and circulating current injection to minimize SM capacitor voltage fluctuations during low-speed or standstill operations of the motor drive is mathematically explained in detail.
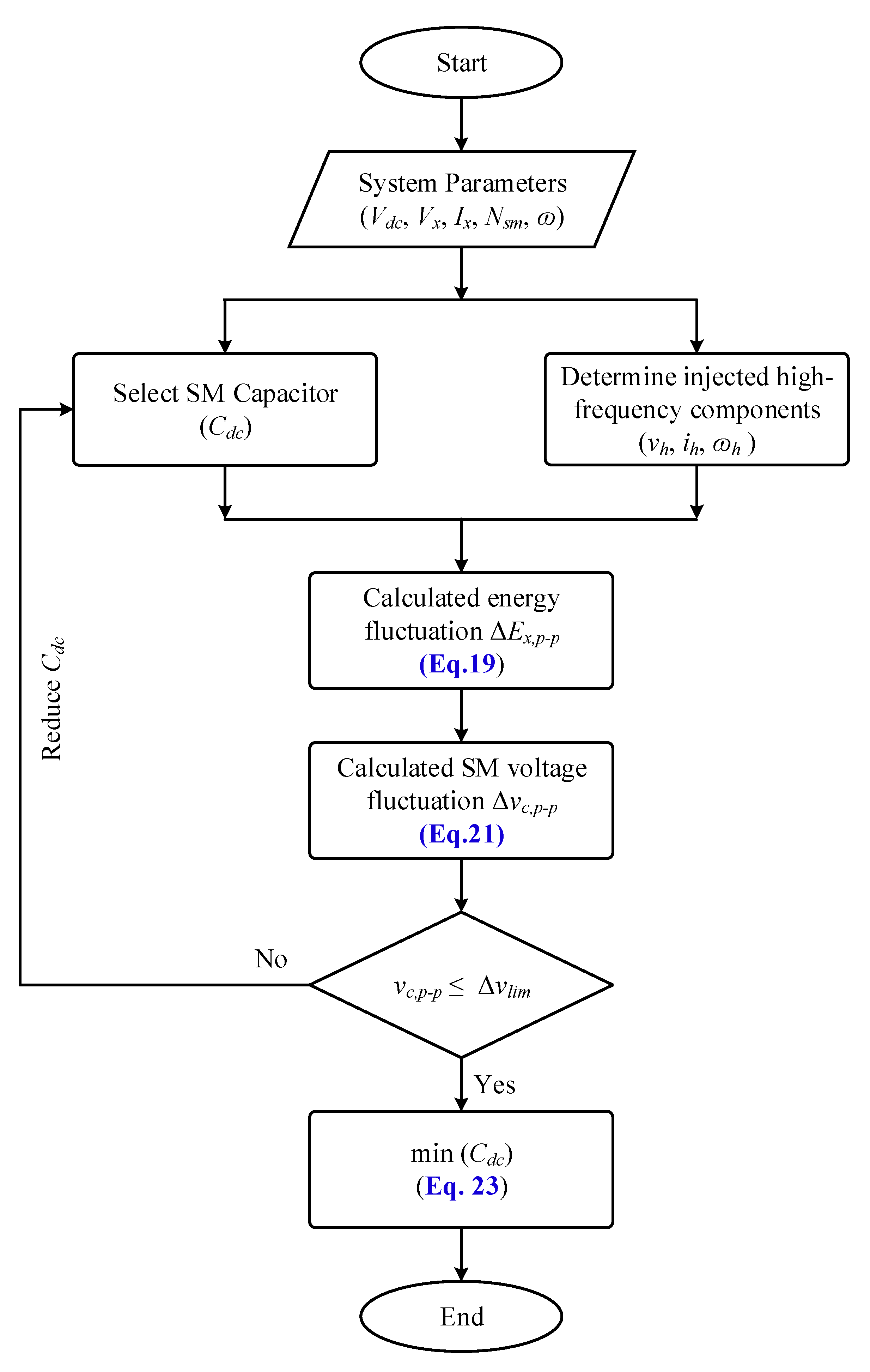
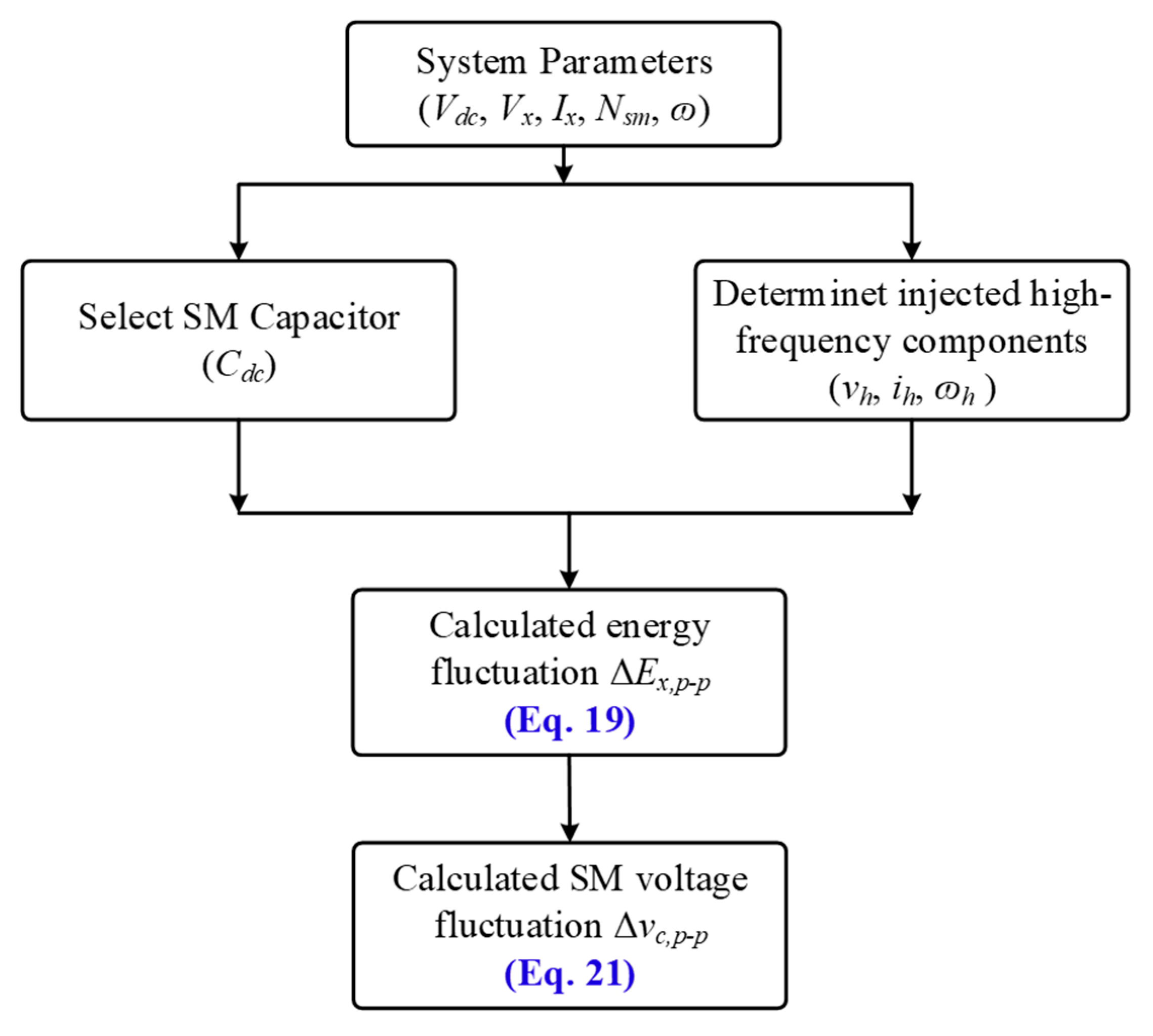
- An algorithm is formulated to estimate the SM capacitor voltage ripple, which is employed to optimize the SM capacitance in accordance with the system specifications for the allowable SM capacitor voltage ripple limit (Δvlim).
2. Circuit and Operation of Modular Multilevel Converter
2.1. Circuit Operation
2.2. Voltage Ripple Reduction under Low-Frequency Operation
3. Design SM Capacitor in Low-Speed Range of Medium Voltage Motor Drives
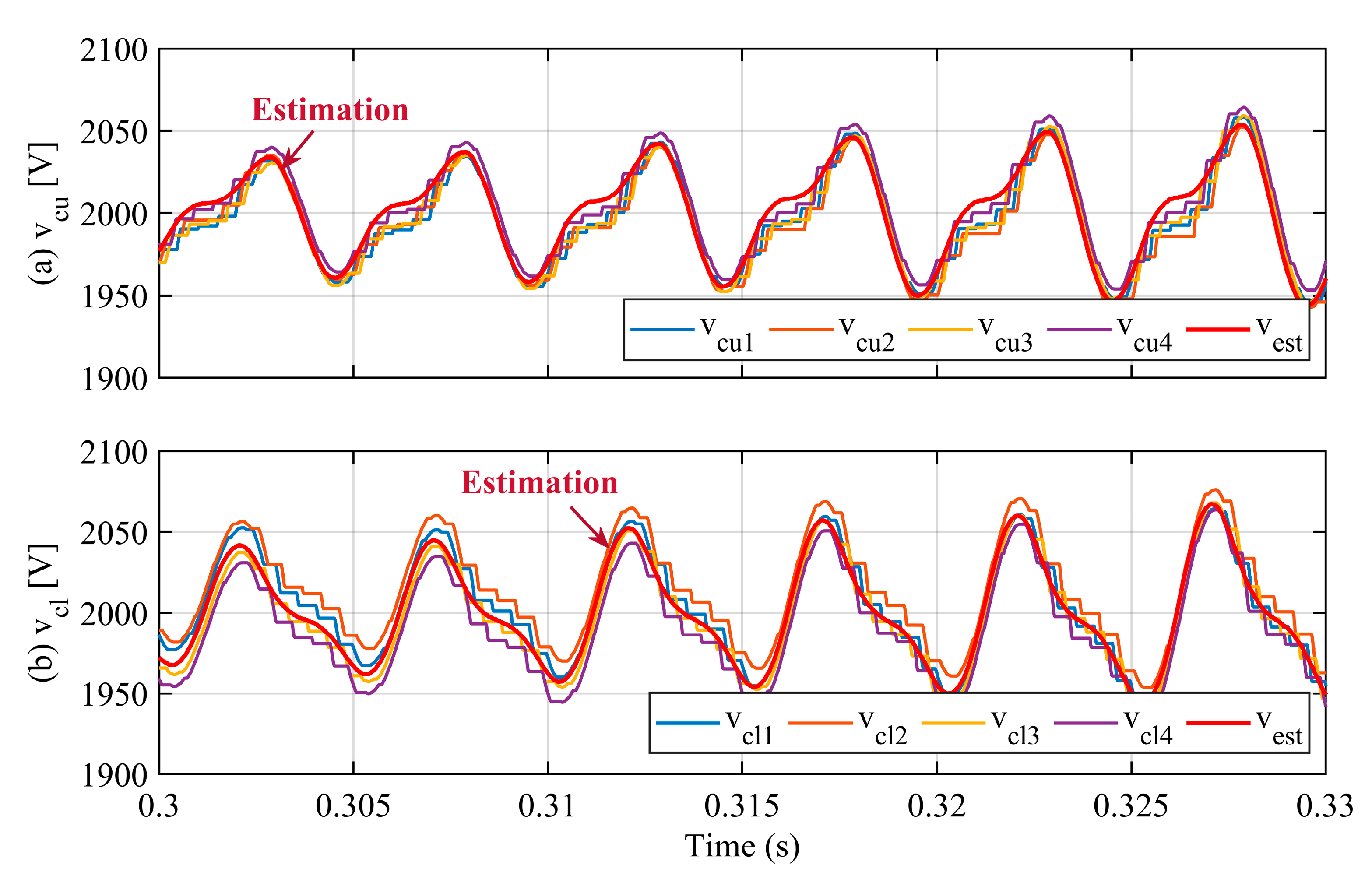
3.1. Estimation of Submodule Voltage Fluctuation
3.2. Optimal Sizing Algorithm of the SM Capacitor
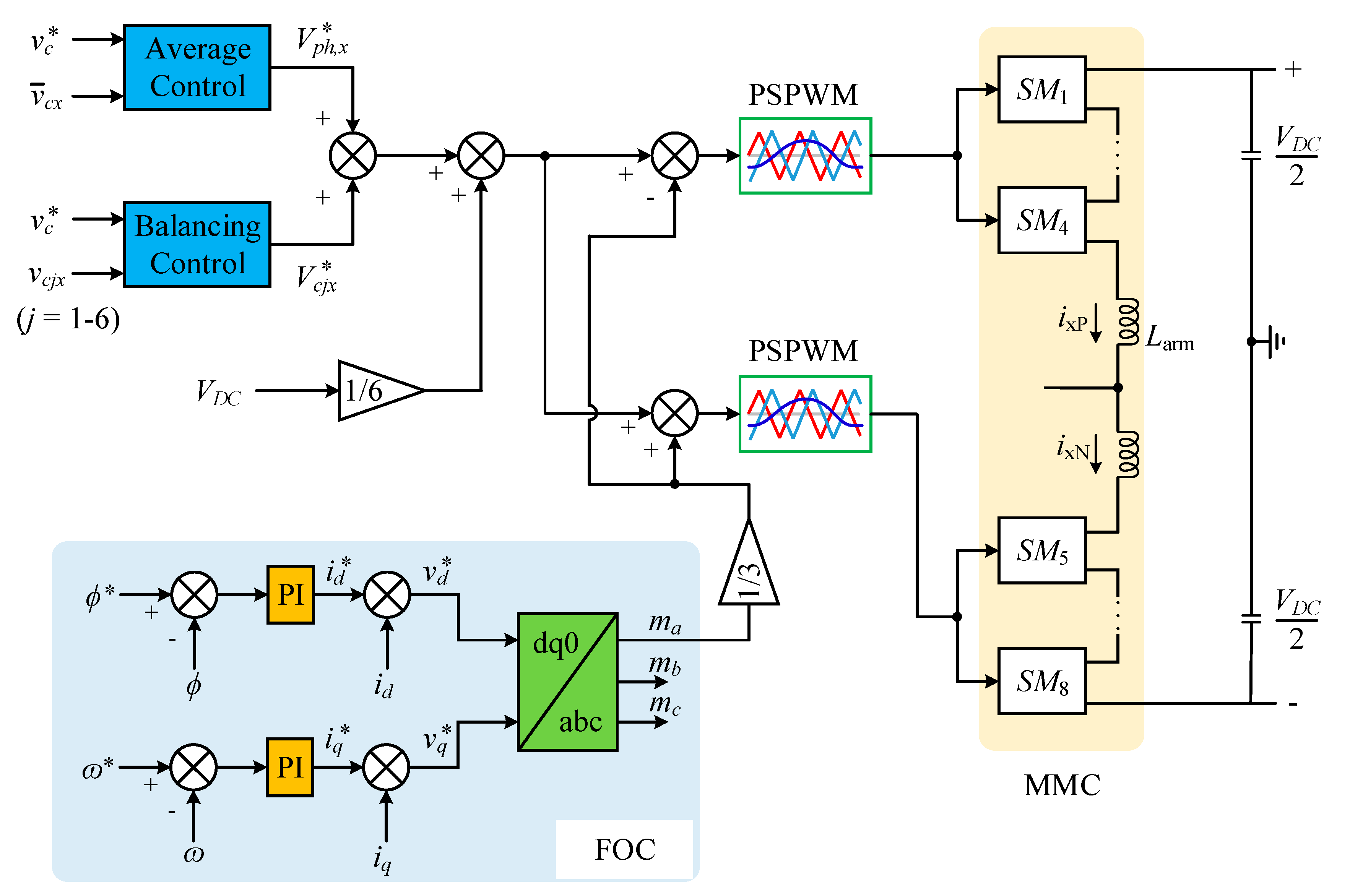
3.3. SM Voltage Balancing Control

3.4. Overall System Control
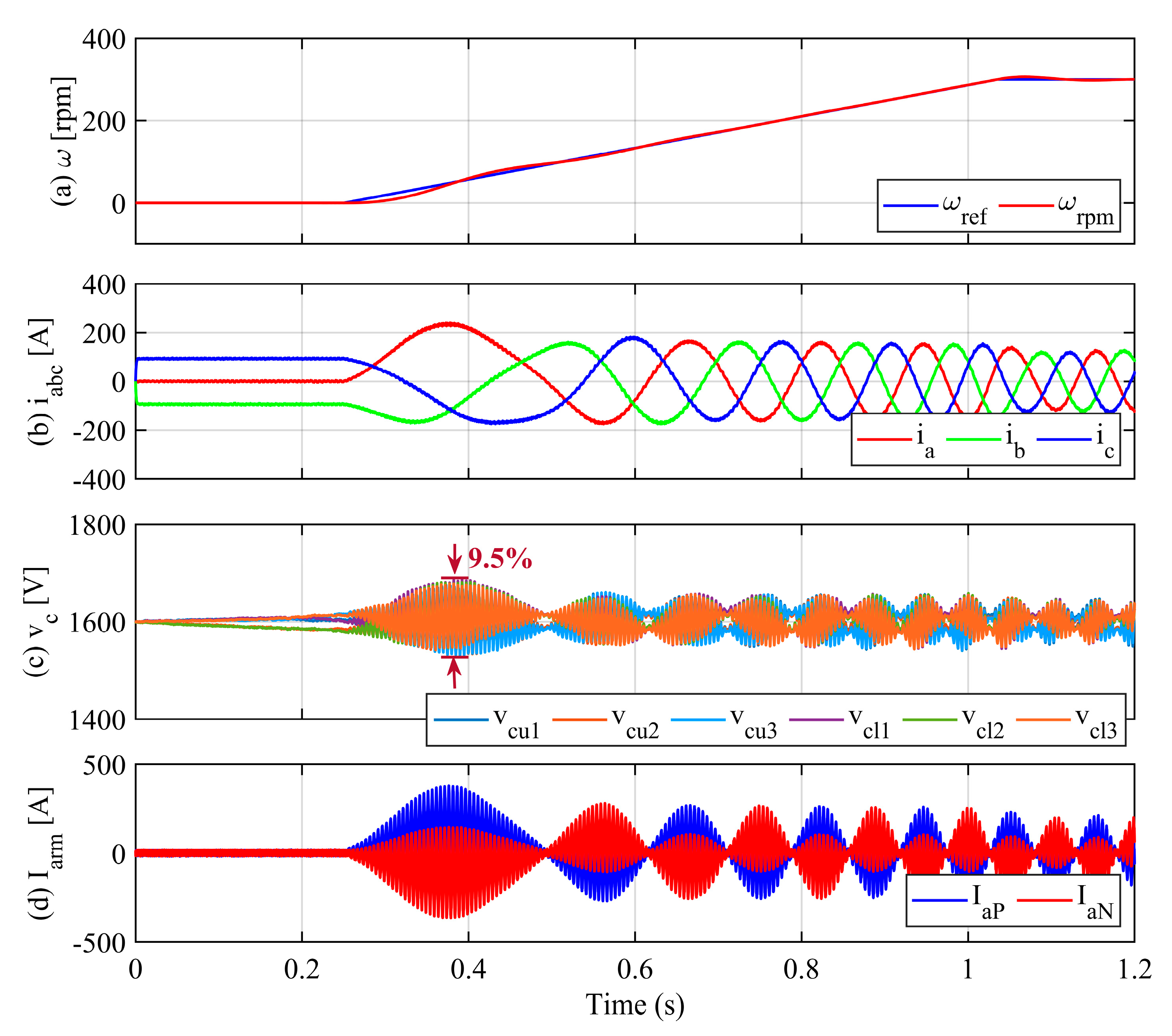
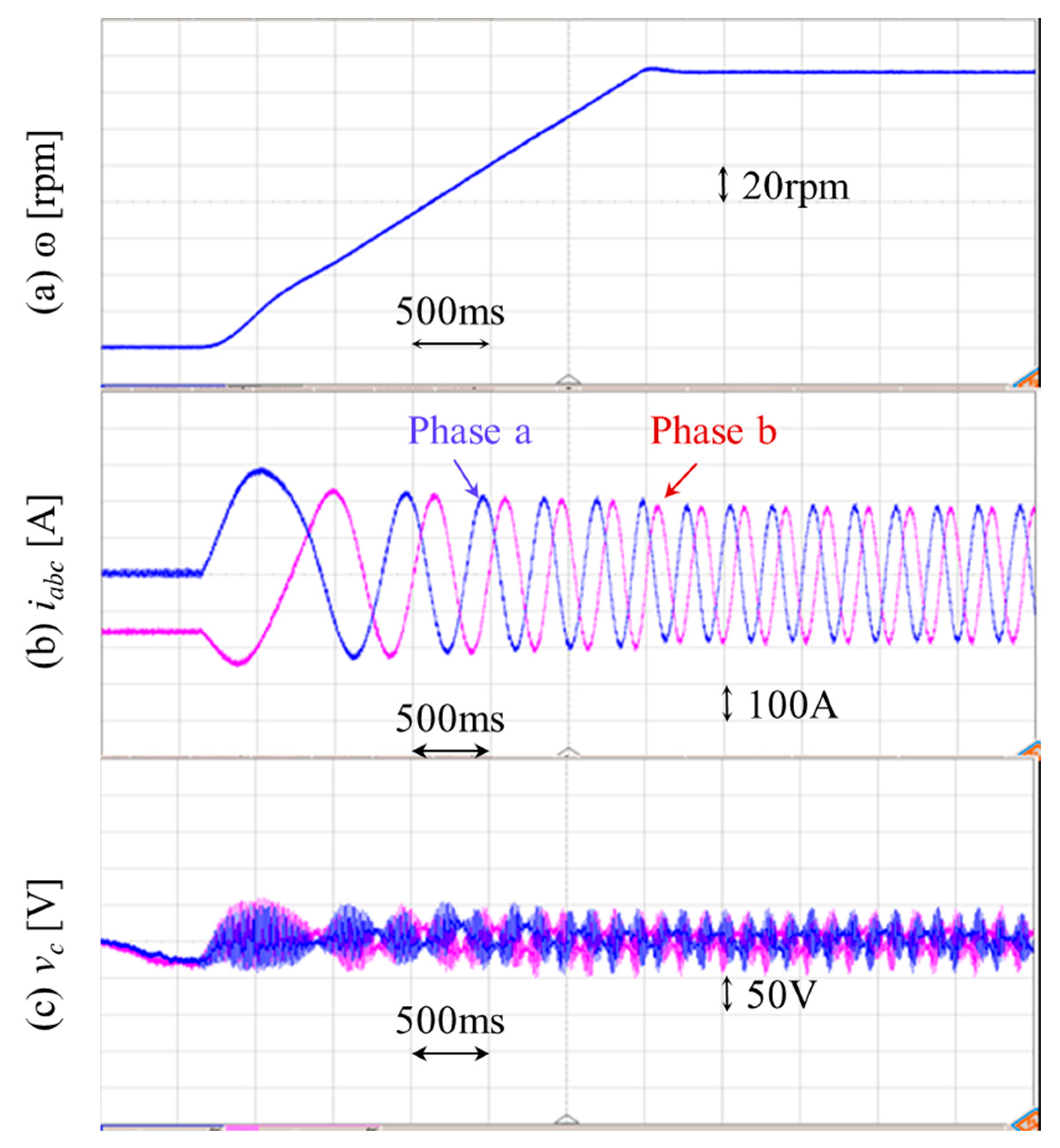
4. Simulation Results
| Frequency [fn] | Voltage Ripple Estimation | Real SM Voltage Ripple |
|---|---|---|
| 5 Hz | 9.8% | 9.5% |
| 10 Hz | 8.6% | 8.1% |
| 15 Hz | 6% | 6.6% |
| 20 Hz | 5.4% | 5.8% |
| 25 Hz | 3.6% | 4.2% |
| 30 Hz | 2.2% | 2.9% |


5. Real-Time Simulation

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Antonopoulos, A.; Ängquist, L.; Nee, H.P. On dynamics and voltage control of the modular multilevel converter. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, EPE’09, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Dekka, A.; Wu, B.; Fuentes, R.L.; Perez, M.; Zargari, N.R. Evolution of Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1631–1656. [Google Scholar] [CrossRef]
- Perez, M.A.; Bernet, S.; Rodriguez, J.; Kouro, S.; Lizana, R. Circuit Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 4–17. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R. Dynamic Performance of a Modular Multilevel Back-to-Back HVDC System. IEEE Trans. Power Deliv. 2010, 25, 2903–2912. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular Multilevel Converters for HVDC Applications: Review on Converter Cells and Functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Gnanarathna, U.N.; Gole, A.M.; Jayasinghe, R.P. Efficient Modeling of Modular Multilevel HVDC Converters (MMC) on Electromagnetic Transient Simulation Programs. IEEE Trans. Power Deliv. 2011, 26, 316–324. [Google Scholar] [CrossRef]
- Peralta, J.; Saad, H.; Dennetière, S.; Mahseredjian, J.; Nguefeu, S. Detailed and Averaged Models for a 401-Level MMC-HVDC System. IEEE Trans. Power Deliv. 2012, 27, 1501–1508. [Google Scholar] [CrossRef]
- Guan, M.; Xu, Z. Modeling and Control of a Modular Multilevel Converter-Based HVDC System under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2012, 27, 4858–4867. [Google Scholar] [CrossRef]
- Akagi, H. Classification, Terminology, and Application of the Modular Multilevel Cascade Converter (MMCC). IEEE Trans. Power Electron. 2011, 26, 3119–3130. [Google Scholar] [CrossRef]
- Hagiwara, M.; Maeda, R.; Akagi, H. Negative-Sequence Reactive-Power Control by a PWM STATCOM Based on a Modular Multilevel Cascade Converter (MMCC-SDBC). IEEE Trans. Ind. Appl. 2012, 48, 720–729. [Google Scholar] [CrossRef]
- Pereira, M.; Retzmann, D.; Lottes, J.; Wiesinger, M.; Wong, G. SVC PLUS: An MMC STATCOM for network and grid access applications. In Proceedings of the 2011 IEEE PES Trondheim PowerTech: The Power of Technology for a Sustainable Society, POWERTECH 2011, Trondheim, Norway, 19–23 June 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Lee, C.T.; Wang, B.S.; Chen, S.W.; Chou, S.F.; Huang, J.L.; Cheng, P.T.; Akagi, H.; Barbosa, P. Average Power Balancing Control of a STATCOM Based on the Cascaded H-Bridge PWM Converter with Star Configuration. IEEE Trans. Ind. Appl. 2014, 50, 3893–3901. [Google Scholar] [CrossRef]
- Diab, M.S.; Massoud, A.M.; Ahmed, S.; Williams, B.W. A Modular Multilevel Converter with Ripple-Power Decoupling Channels for Three-Phase MV Adjustable-Speed Drives. IEEE Trans. Power Electron. 2019, 34, 4048–4063. [Google Scholar] [CrossRef]
- Antonopoulos, A.; Ängquist, L.; Norrga, S.; Ilves, K.; Harnefors, L.; Nee, H.P. Modular Multilevel Converter AC Motor Drives with Constant Torque from Zero to Nominal Speed. IEEE Trans. Ind. Appl. 2014, 50, 1982–1993. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Xu, D.; Yang, R.; Xu, D.; Buccella, C.; Cecati, C. An Improved Circulating Current Injection Method for Modular Multilevel Converters in Variable-Speed Drives. IEEE Trans. Ind. Electron. 2016, 63, 7215–7225. [Google Scholar] [CrossRef]
- Jung, J.J.; Lee, H.J.; Sul, S.K. Control Strategy for Improved Dynamic Performance of Variable-Speed Drives with Modular Multilevel Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 371–380. [Google Scholar] [CrossRef]
- Antonopoulos, A.; Ängquist, L.; Harnefors, L.; Nee, H.P. Optimal Selection of the Average Capacitor Voltage for Variable-Speed Drives with Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 227–234. [Google Scholar] [CrossRef]
- Okazaki, Y.; Kawamura, W.; Hagiwara, M.; Akagi, H.; Ishida, T.; Tsukakoshi, M.; Nakamura, R. Experimental Comparisons Between Modular Multilevel DSCC Inverters and TSBC Converters for Medium-Voltage Motor Drives. IEEE Trans. Power Electron. 2017, 32, 1805–1817. [Google Scholar] [CrossRef]
- He, L.; Zhang, K.; Xiong, J.; Fan, S.; Xue, Y. Low-Frequency Ripple Suppression for Medium-Voltage Drives Using Modular Multilevel Converter With Full-Bridge Submodules. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 657–667. [Google Scholar] [CrossRef]
- Kumar, Y.S.; Poddar, G. Control of Medium-Voltage AC Motor Drive for Wide Speed Range Using Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2017, 64, 2742–2749. [Google Scholar] [CrossRef]
- Kumar, Y.S.; Poddar, G. Medium-Voltage Vector Control Induction Motor Drive at Zero Frequency Using Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2018, 65, 125–132. [Google Scholar] [CrossRef]
- Pan, J.; Ke, Z.; Al Sabbagh, M.; Li, H.; Potty, K.A.; Perdikakis, W.; Na, R.; Zhang, J.; Wang, J.; Xu, L. 7-KV 1-MVA SiC-Based Modular Multilevel Converter Prototype for Medium-Voltage Electric Machine Drives. IEEE Trans. Power Electron. 2020, 35, 10137–10149. [Google Scholar] [CrossRef]
- Korn, A.J.; Winkelnkemper, M.; Steimer, P. Low output frequency operation of the modular multi-level converter. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, ECCE 2010—Proceedings 2010, Atlanta, GA, USA, 12–16 September 2010; pp. 3993–3997. [Google Scholar] [CrossRef]
- Hagiwara, M.; Nishimura, K.; Akagi, H. A Medium-Voltage Motor Drive with a Modular Multilevel PWM Inverter. IEEE Trans. Power Electron. 2010, 25, 1786–1799. [Google Scholar] [CrossRef]
- Hagiwara, M.; Hasegawa, I.; Akagi, H. Start-up and Low-Speed Operation of an Electric Motor Driven by a Modular Multilevel Cascade Inverter. IEEE Trans. Ind. Appl. 2013, 49, 1556–1565. [Google Scholar] [CrossRef]
- Le, D.D.; Lee, D.C. Reduction of Half-Arm Current Stresses and Flying-Capacitor Voltage Ripples of Flying-Capacitor Mmcs. IEEE Access 2020, 8, 180076–180086. [Google Scholar] [CrossRef]
- Le, D.D.; Lee, D.C. Current Stress Reduction and Voltage Total Harmonic Distortion Improvement of Flying-Capacitor Modular Multilevel Converters for AC Machine Drive Applications. IEEE Trans. Ind. Electron. 2022, 69, 90–100. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Zargari, N.R. Current Stress Reduction for Flying-Capacitor Modular Multilevel Converter. IEEE Trans. Power Electron. 2019, 34, 184–191. [Google Scholar] [CrossRef]
- Oliveira, R.; Yazdani, A. An Enhanced Steady-State Model and Capacitor Sizing Method for Modular Multilevel Converters for HVdc Applications. IEEE Trans. Power Electron. 2018, 33, 4756–4771. [Google Scholar] [CrossRef]
- Tang, Y.; Ran, L.; Alatise, O.; Mawby, P. Capacitor Selection for Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2016, 52, 3279–3293. [Google Scholar] [CrossRef]
- Jo, Y.J.; Nguyen, T.H.; Lee, D.C. Capacitance Estimation of the Submodule Capacitors in Modular Multilevel Converters for HVDC Applications. J. Power Electron. 2016, 16, 1752–1762. [Google Scholar] [CrossRef]
- Merlin, M.M.C.; Green, T.C. Cell Capacitor Sizing in Multilevel Converters: Cases of the Modular Multilevel Converter and Alternate Arm Converter. IET Power Electron. 2015, 8, 350–360. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.J.; Wang, J.; Javid, Z.; Wang, M.; Sun, K. Research on Capacitance Selection for Modular Multi-Level Converter. IEEE Trans. Power Electron. 2019, 34, 8417–8434. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z.; Xu, L. Reduced Switching-Frequency Modulation and Circulating Current Suppression for Modular Multilevel Converters. IEEE Trans. Power Deliv. 2011, 26, 2009–2017. [Google Scholar] [CrossRef]
- Engel, S.P.; De Doncker, R.W. Control of the Modular Multi-Level Converter for Minimized Cell Capacitance. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, EPE 2011, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Nguyen, V.T.; Kim, J.W.; Park, J.W.; Lee, J.M.; Park, B.G. A Modified Submodule of Modular Multilevel Converter Using Active Power Decoupling Method for Reducing Capacitor Voltage Ripple under Low-Frequency Operation. IET Power Electron. 2023, 16, 868–882. [Google Scholar] [CrossRef]
- Wu, B.; Narimani, M. High-Power Converters and Ac Drives; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 9780471731719. [Google Scholar]
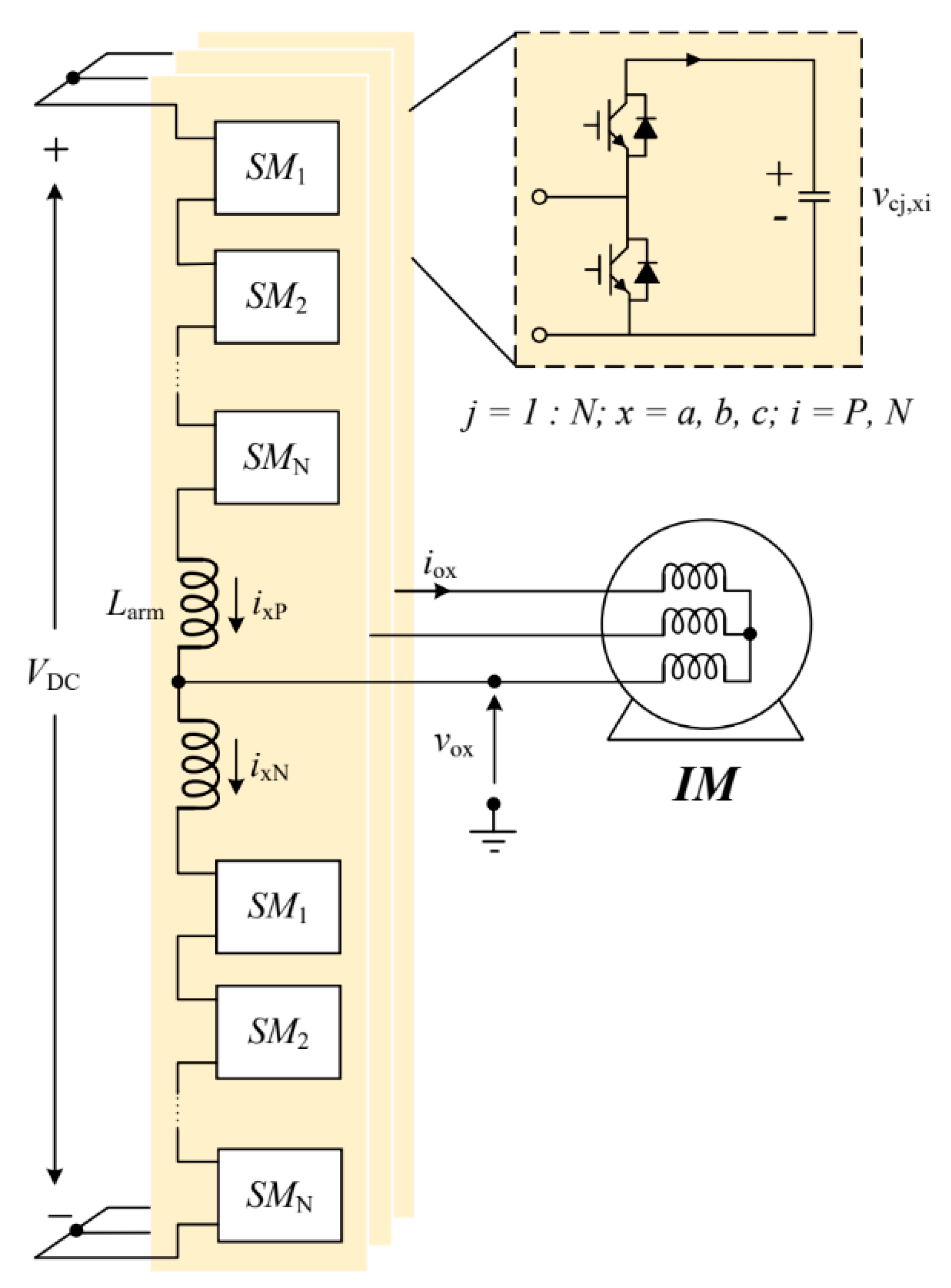




| Parameters | Symbol | Values |
|---|---|---|
| DC-link voltage | VDC | 4800 V |
| Number of SMs per arm | NSM | 3 |
| Arm inductance | Larm | 1.5 mH |
| SM capacitance | Cdc | 1000 uF |
| Switching frequency | fsw | 2000 Hz |
| Nominal frequency | fn | 60 Hz |
| Rated voltage | Vrated | 3300 V |
| Rated current | Irated | 215 A |
| Rated speed | ωrated | 1800 rpm |
| Rated torque | Trated | 5306 N.m |
| Voltage ripple limit | Δvlim | 10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-T.; Kim, J.-W.; Lee, J.-W.; Park, B.-G. Optimal Design of a Submodule Capacitor in a Modular Multilevel Converter for Medium Voltage Motor Drives. Energies 2024, 17, 471. https://doi.org/10.3390/en17020471
Nguyen V-T, Kim J-W, Lee J-W, Park B-G. Optimal Design of a Submodule Capacitor in a Modular Multilevel Converter for Medium Voltage Motor Drives. Energies. 2024; 17(2):471. https://doi.org/10.3390/en17020471
Chicago/Turabian StyleNguyen, Van-Thang, Ji-Won Kim, Jae-Woon Lee, and Byoung-Gun Park. 2024. "Optimal Design of a Submodule Capacitor in a Modular Multilevel Converter for Medium Voltage Motor Drives" Energies 17, no. 2: 471. https://doi.org/10.3390/en17020471






