Study on Proppant Transport and Placement in Shale Gas Main Fractures

Abstract

In this paper, based on the background of a deep shale reservoir, a solid–liquid two-phase flow model suitable for proppant and fracturing fluid flow was established based on the Euler method, and a large-scale fracture model was established. Based on field parameters, a proppant transport experiment was conducted. Then, on the basis of the experimental fracture model, proppant transport simulation under different influencing factors was carried out. The results show that the laboratory experiment was in good agreement with the simulated results. The process of proppant accumulation in fractures can be divided into three stages according to the characteristics of sand banks. The displacement mainly affects the sedimentation distance of the proppant in the first stage, and the viscosity of the fracturing fluid represents the strength of the fluid sand carrying performance. Compared with 40/70 mesh proppant, 70/140 mesh proppant is more easily fluidizable, the fracture width has less influence on proppant migration and placement, and the perforation location only affects the accumulation pattern at the fracture entrance, but has less influence on proppant placement in the remote well zone.

1. Introduction

The fracture pattern of deep shale is dominated by a large main fracture, and the proppant transport law in the fracture is the key to influence the placement pattern of proppant in the fracture, and the placement pattern of proppant in the fracture directly determines the final effect of fracturin. The placement of proppant in the artificial fracture is critical to the success of the operation because the uneven placement of proppant in the artificial fracture can seriously affect the fracture conductivity and stimulation. The study of the proppant transport pattern in fractures can not only optimize parameters such as construction displacement and sand ratio, and select a suitable fracturing fluid system and proppant system, but also effectively control the fracture height and width. Therefore, it is very necessary to study the transport and settlement law of proppant in large main fractures.

Laboratory physical experimentation is the key method to study the law of proppant migration and placement. In 1959, Kern et al. [1] investigated the transport and placement of proppant in fluids by constructing two Plexiglass plates. In 1976, Fredrickson et al. [2] created a narrow-slit device with a height of 0.3 m, a length of 1.83 m, and a width of 6 mm, which could be used to study the placement effect of proppant under different particle densities and fluid viscosity. In 2005, Yajun Liu et al. [3] established a parallel plate fracture model which considered the effect of wall roughness and obtained the variation law of proppant transport distance under different fluid viscosity conditions through parametric study, and analyzed the reason for proppant pointing in the lead fluid. In 2009, Adam Dayan et al. [4] studied the proppant placement pattern in fractures during fracturing for the study of shale reservoirs, and established a complex fracture model in which the small channel above the main fracture was considered to be a secondary fracture, so as to study the distribution law of proppant in the complex fractures. In 2014, Sahai et al. [5] studied the transport law of proppant in complex fractures by simplifying complex fractures into multiple fracture devices with vertical intersections of primary and secondary fractures. In 2019, Kuangsheng Zhang et al. [6] designed a piece of narrow-slit equipment with a height of 0.5 m, a length of 4 m, and an adjustable wide slit (6–12 mm), and studied the migration and settlement law of different particle size combinations of proppants in fractures through experiments. In 2021, Liaoyuan Zhang et al. [7] compared and evaluated the migration of proppants in complex fractures with different combinations of proppants using a large visual complex fracture particle migration device, considering fluid loss and roughness. Two parameters, near-well sand dune angle and near-well unfilled degree, were put forward to evaluate the laying of proppant in near-well fractures. In 2022, Jinjian Gao et al. [8] used a large visual flat vertical fracture simulation system to study the settlement and migration rule of ceramic proppant in fractures under different sand ratios, and analyzed the influence of sand ratio on the horizontal migration and settlement speed of proppant particles. In 2023, Tang Tang et al. [9] carried out proppant transport tests based on single straight flat fractures, summarized two typical stacking modes of proppant in flat fractures, and tested the frac fluid-proppant two-phase movement velocity by using PIV/PTV technology, and analyzed the influence of different factors on the final sand bank morphology from the perspective of particle movement. At present, visual fracture simulators are commonly used to study proppant transport and placement processes. In the visual fracture simulation device, the fracture scale is relatively small and different from the actual scale in the field, so the experimental study of the proppant transport and placement process has certain limitations.

Compared with indoor physical experiments, numerical simulation can realize more complex working conditions because of its low cost, diverse model forms, and boundary conditions. Currently, the Eulerian–Eulerian method (TFM) and Eulerian–Lagrange method (CFD-DEM) are mainly used for the numerical calculation of fracturing fluid-proppant two-phase flow. Tsuji et al. [10] first combined CFD and DEM for the numerical simulation of a fluidized bed. Zhang et al. [11] investigated the two-phase flow law based on the CFD-DEM model for different fracture widths and angles, and pump discharge and fluid viscosity conditions. Tao Zhang et al. [12] use the Eulerian–Eulerian two-fluid model to study the flow of fracturing fluid and proppant in a flat plate fracture under the influence of different inlet velocity and position, proppant concentration, and other parameters, and the simulation results were compared with experiments with high compliance, which verified the validity of the model. Desheng Zhou et al. [13] studied the proppant transport law in the main fracture during large displacement by using a large visualization plate fracture, and established a corresponding numerical model based on the Eulerian–Eulerian method to simulate the pattern of the dune at different moments and analyzed the influence law of turbulence on proppant placement. Kong et al. [14] studied the flow of multiphase slurry containing proppant based on the Eulerian multiphase flow model, the support performance of different fluids and proppant on different types of fracture networks, and a sensitivity analysis. Based on the Eulerian two-fluid model, Lihua Hao [15] studied the settlement and transport behavior of proppant in complex fractures, and considered the effects of injection speed, injection location, location of branch, and other factors on the distribution morphology of dunes.

Based on the above research status, this study carried out research on proppant migration and placement in the main fracture of the shale reservoir based on a large-scale flat fracture device, found the law of proppant migration and placement in the main fracture under different influencing factors, and then extracted the characteristic parameters of proppant accumulation to quantitatively analyze the relationship between the influencing factors and the characteristic parameters.

2. Liquid–Solid Two-Phase Flow Mathematical Model

2.1. Governing Equations

Based on the Eulerian two-fluid (TFM) model, a solid–liquid two-phase flow model for proppant transport in fractures was developed. In the two-fluid model, the discrete particle phase and continuous fluid phase were treated as an imaginary continuum through space and time averaging. The following assumptions were made for the model: (i) the sand-carrying liquid flow is unsteady and incompressible, (ii) the proppant particles are spheres of equal diameter, (iii) the proppant is regarded as a proposed fluid, but also contains the basic properties of solid particles, and (iv) there is no mass transfer between phases.

In the governing equations of this study, the equations of mass conservation, momentum conservation, and particle temperature transport in the solid phase are given, which were obtained by the model evolution or particle dynamics theory (KTGF) of related studies [12,16,17].

The continuity equations for the liquid and solid phases, respectively, are

$$\frac{\partial }{\partial t}\left({\alpha }_l{\rho }_l\right)+\nabla \cdot \left({\alpha }_l{\rho }_l{v}_l\right)=0,$$

(1)

$$\frac{\partial }{\partial t}\left({\alpha }_{\mathrm{s}}{\rho }_{\mathrm{s}}\right)+\nabla \cdot \left({\alpha }_{\mathrm{s}}{\rho }_{\mathrm{s}}{v}_{\mathrm{s}}\right)=0,$$

(2)

where $t$—time, s; $\alpha$—volume fraction, dimensionless; $\rho$—density, kg/m³; $v$—velocity, m/s; and subscripts l, s represent liquid phase and solid phase, respectively.

The conservation of momentum equations for the liquid and solid phases, respectively, are:

$$\frac{\partial }{\partial t}\left({\alpha }_l{\rho }_l{v}_l\right)+\nabla \cdot \left({\alpha }_l{\rho }_l{v}_l{v}_l\right)=-{\alpha }_l\nabla p_l+\nabla \cdot {\tau }_l+{\alpha }_l{\rho }_{l}g+\beta \left(v_{\mathrm{s}}-v_l\right),$$

(3)

$$\frac{\partial }{\partial t}\left({\alpha }_s{\rho }_s{v}_s\right)+\nabla \cdot \left({\alpha }_s{\rho }_s{v}_s{v}_s\right)=-{\alpha }_s\nabla p_s+\nabla \cdot {\tau }_s+{\alpha }_s{\rho }_s\mathrm{g}+\beta \left(v_l-v_s\right),$$

(4)

where $p$—partial pressure, pa; $\tau$—shear stress tensor, pa; $\beta$—interphase momentum exchange coefficient, kg/(m³·s); ∇ is Hamiltonian differential operator; and gravitational acceleration g = 9.8 m/s².

The solid-phase particle temperature is proportional to the particle random pulsation kinetic energy, and the solid-phase transport equation is:

$$\begin{array}{c}\frac{3}{2}{\rho }_s\left[\frac{\partial }{\partial t}\left({\alpha }_s{\Theta }_s\right)+\nabla \cdot \left({\alpha }_s{v}_s{\Theta }_s\right)\right]=\nabla \cdot \left({\kappa }_s\nabla {\Theta }_s\right)+{\tau }_s:\nabla v_s-J_s+{\Pi }_{\Theta }\end{array},$$

(5)

where ${\Theta }_{\mathrm{s}}$—particle proposed temperature, m²/s²; ${\kappa }_{\mathrm{s}}$—particle energy conduction coefficient, kg/(m·s); $J_{\mathrm{s}}$—energy dissipation due to inelastic collision, kg/(m·s³); and ${\Pi }_{\Theta }$—energy dissipation due to fluid viscous drag, kg/(m·s³).

The k-ε model is used for the turbulence equations, and the equations for the turbulent kinetic energy k and the dissipation rate ε are as follows:

$$\begin{array}{c}\frac{\partial }{\partial t}\left({\alpha }_l{\rho }_{l}k\right)+\nabla \cdot \left({\alpha }_l{\rho }_l{v}_{l}k\right)=\nabla \cdot \left({\alpha }_l\frac{{\mu }_{\mathrm{t}}}{{\sigma }_k}\nabla k\right)+G_{k,l}+{\Pi }_k-{\alpha }_l{\rho }_l\epsilon \end{array},$$

(6)

$$\begin{array}{c}\frac{\partial }{\partial t}\left({\alpha }_l{\rho }_l\epsilon \right)+\nabla \cdot \left({\alpha }_l{\rho }_l{v}_l\epsilon \right)=\nabla \cdot \left(\frac{{\alpha }_l{\mu }_{\mathrm{t}}}{{\sigma }_{\epsilon }}\nabla \epsilon \right)+{\alpha }_l\frac{\epsilon }{k}\left(C_{1\epsilon }{G}_{k,l}-C_{2\epsilon }{\rho }_l\epsilon \right)+{\Pi }_{\epsilon }\end{array},$$

(7)

where $k$—turbulent energy of fluid phase, m²/s²; ${\mu }_{\mathrm{t}}$—turbulent viscosity coefficient, pa·s; ${\sigma }_k$—turbulent kinetic energy corresponding to Prandtl number, uncaused, take ${\sigma }_k$ = 1.0; $G_{k,l}$—turbulent kinetic energy generation term, kg/(m-s³); ${\Pi }_k$, ${\Pi }_{\epsilon }$—turbulent exchange term between liquid and solid phases, kg/(m-s³); $\epsilon$—turbulent dissipation rate, m²/s³; ${\sigma }_{\epsilon }$—turbulent dissipation rate corresponding to Prandtl number, uncaused, take ${\sigma }_{\epsilon }$—Prandtl number corresponding to the turbulent dissipation rate, uncaused, take ${\sigma }_{\epsilon }$ = 1.3; and $C_{1\epsilon }$, $C_{2\epsilon }$—empirical constants, uncaused, take $C_{1\epsilon }$ = 1.44, $C_{2\epsilon }$ = 1.92.

2.2. Constitutive Equation

The momentum exchange coefficient β between the liquid and solid phases is

$$\beta =\left\{\begin{array}{ll}\frac{3}{4}{C}_{\mathrm{D}}\frac{{\rho }_l{\alpha }_l{\alpha }_s\left|{\mathit{v}}_l-{\mathit{v}}_s\right|}{d_{\mathrm{s}}}{\alpha }_l^{-2.65}& {\alpha }_l\ge 0.8\\ \frac{150{\alpha }_s\left(1-{\alpha }_l\right){\mu }_l}{{\alpha }_l{d}_s^2}+\frac{1.75{\rho }_l{\alpha }_s\left|{\mathit{v}}_l-{\mathit{v}}_s\right|}{d_s}& {\alpha }_l<0.8\end{array}\right.,$$

(8)

for which

$$C_{\mathrm{D}}=\left\{\begin{array}{ll}\frac{24}{R{e}_s}\left[1+0.15{\left(R{e}_s\right)}^{0.687}\right]& R{e}_s<1000\\ 0.44& R{e}_s⩾1000\end{array}\right.,$$

(9)

$$R{e}_s=\frac{{\rho }_l{d}_s{\epsilon }_l\left|{\mathit{v}}_{\mathit{s}}-{\mathit{v}}_{\mathit{l}}\right|}{{\mu }_l},$$

(10)

where $C_{\mathrm{D}}$—interphase momentum exchange resistance coefficient, dimensionless; $d_s$—particle diameter, m; ${\mu }_l$—liquid phase viscosity, pa·s; and $R{e}_s$—particle Reynolds number defined by the relative slip velocity between particles, dimensionless [16].

The liquid and solid phase shear stress tensors are

$${\tau }_l=2{\alpha }_l{\mu }_l{S}_l,$$

(11)

$${\tau }_s=\left[\eta {\mu }_{\mathrm{b}}\nabla \cdot v_s-\left(p_s+p_{\mathrm{f}}\right)\right]I+2\left({\mu }_s+{\mu }_{\mathrm{f}}\right)S_s,$$

(12)

$$\eta =\frac{\left(1+e\right)}{2},$$

(13)

where $S_l$, $S_s$—liquid-phase, solid-phase variable tensor, s⁻¹; $p_s$—solid-phase pressure, pa; ${\mu }_{\mathrm{b}}$—solid-phase bulk viscosity coefficient, pa·s; ${\mu }_{\mathrm{s}}$—solid-phase shear viscosity coefficient, pa·s; ${\mu }_{\mathrm{f}}$—frictional viscosity coefficient, pa·s; $I$—second-order unit tensor; and $e$—regression coefficient of inter-particle collision, taken as 0.9.

The corresponding variable tensors for liquid and solid are

$$S_l=\frac{1}{2}\left[\nabla v_l+{\left(\nabla v_l\right)}^{\mathrm{T}}\right]-\frac{1}{3}\left(\nabla \cdot v_l\right)I,$$

(14)

$$S_s=\frac{1}{2}\left[\nabla v_s+{\left(\nabla v_s\right)}^{\mathrm{T}}\right]-\frac{1}{3}\left(\nabla \cdot v_s\right)I$$

(15)

The particle contact radial distribution function is

$$g_0=\frac{1-0.5{\alpha }_s}{{\left(1-{\alpha }_s\right)}^3}$$

(16)

The solid phase shear viscosity coefficients are

$$\begin{array}{c}{\mu }_{\mathrm{s}}=\left(\frac{2+c}{3}\right)\cdot \frac{3}{5}\eta {\mu }_{\mathrm{b}}+\left(\frac{2+c}{3}\right)\cdot \frac{{\mu }^{\ast }}{g_0\eta (2-\eta )}\left(1+\frac{8}{5}\eta {\alpha }_{\mathrm{s}}{g}_0\right)\left[1+\frac{8}{5}\eta (3\eta -2){\alpha }_s{g}_0\right]\end{array},$$

(17)

$${\mu }^{\ast }=\mu {\left[1+\frac{2\beta \mu }{{\left({\alpha }_s{\rho }_s\right)}^2{g}_0{\Theta }_s}\right]}^{-1},$$

(18)

$$\mu =\frac{5{\rho }_s{d}_s\sqrt{{\Theta }_s\pi }}{96},$$

(19)

$${\mu }_{\mathrm{b}}=\frac{256}{5\pi }\mu {\alpha }_{\mathrm{s}}^2{g}_0,$$

(20)

where $c$—solid phase viscosity coefficient, takes the value of 1.6; ${\mu }^{\ast }$—consider the influence of inter-particle fluid solid phase viscosity coefficient, pa·s; and $\mu$—sparse solid phase viscosity coefficient, pa·s.

The conduction coefficients of solid-phase pulsation energy are

$$\begin{array}{c}{\kappa }_{\mathrm{s}}=\left(1+\frac{12}{5}\eta {\alpha }_{\mathrm{s}}{g}_0\right)\left[1+\frac{12}{5}{\eta }^2\left(4\eta -3\right){\alpha }_{\mathrm{s}}{g}_0\right]\\ \left(\frac{{\kappa }^{\ast }}{g_0}\right)+\frac{64}{25\pi }(41-33\eta ){\eta }^2{\left({\alpha }_{\mathrm{s}}{g}_0\right)}^2\left(\frac{{\kappa }^{\ast }}{g_0}\right)\end{array},$$

(21)

$${\kappa }^{\ast }=\kappa {\left[1+\frac{6\beta \kappa }{5{\left({\alpha }_{\mathrm{s}}{\rho }_{\mathrm{s}}\right)}^2{g}_0{\mathsf{\Theta }}_{\mathrm{s}}}\right]}^{-1},$$

(22)

$$\kappa =\frac{75{\rho }_{\mathrm{s}}{d}_{\mathrm{s}}\sqrt{\pi {\mathsf{\Theta }}_{\mathrm{s}}}}{48\eta (41-33\eta )},$$

(23)

where ${\kappa }^{\ast }$—solid-phase energy transfer coefficient considering interparticle fluid interaction, kg/(m·s) and $\kappa$—sparse solid-phase energy transfer coefficient, kg/(m·s).

The solid phase friction pressure and viscosity coefficient are

$$\frac{p_{\mathrm{f}}}{p_{\mathrm{c}}}={\left(1-\frac{\nabla \cdot v_{\mathrm{s}}}{n\sqrt{2}\mathrm{s}\mathrm{i}\mathrm{n}\delta \sqrt{S_{\mathrm{s}}:S_{\mathrm{s}}+{\mathsf{\Theta }}_{\mathrm{s}}/d_{\mathrm{p}}^2}}\right)}^{n-1},$$

(24)

$${\mu }_{\mathrm{f}}=\&\frac{p_{\mathrm{f}}\mathrm{s}\mathrm{i}\mathrm{n}\delta }{\sqrt{2}\sqrt{{\mathit{S}}_{\mathrm{s}}:{\mathit{S}}_{\mathrm{s}}+{\Theta }_{\mathrm{s}}/d_{\mathrm{p}}^2}}\left[n-(n-1){\left(\frac{p_{\mathrm{f}}}{p_{\mathrm{c}}}\right)}^{\frac{1}{n-1}}\right],$$

(25)

where

$$p_{\mathrm{c}}=\left\{\begin{array}{ll}{10}^{25}{\left({\alpha }_{\mathrm{s}}-{\alpha }_{\mathrm{s}}^{max}\right)}^{10}& {\alpha }_{\mathrm{s}}>{\alpha }_{\mathrm{s}}^{max}\\ F_{\mathrm{r}}\frac{{\left({\alpha }_{\mathrm{s}}-{\alpha }_{\mathrm{s}}^{min}\right)}^{{\mathrm{r}}^{\prime }}}{{\left({\alpha }_{\mathrm{s}}^{max}-{\alpha }_{\mathrm{s}}\right)}^{{\mathrm{s}}^{\prime }}}& {\alpha }_{\mathrm{s}}^{max}⩾{\alpha }_{\mathrm{s}}>{\alpha }_{\mathrm{s}}^{min}\\ 0& {\alpha }_{\mathrm{s}}⩽{\alpha }_{\mathrm{s}}^{min}\end{array}\right.,$$

(26)

$$n=\left\{\begin{array}{ll}\frac{\sqrt{3}}{2}\sin \delta & \nabla \cdot v_{\mathrm{s}}⩾0\\ 1.03& \nabla \cdot v_{\mathrm{s}}<0\end{array}\right.,$$

(27)

where $p_{\mathrm{c}}$—critical solid-phase pressure, pa; $F_{\mathrm{r}}$—friction model coefficient, takes the value of 0.05, dimensionless; ${\mathrm{r}}^{\prime }$, ${\mathrm{s}}^{\prime }$—constant, take the values of 2 and 5, respectively; $\delta$—internal friction angle between solid phases, rad, takes the value of π/6; ${\alpha }_{\mathrm{s}}^{max}$—maximum accumulation concentration of particles, %, takes the value of 63%; and ${\alpha }_{\mathrm{s}}^{min}$—solid-phase volume fraction to generate critical pressure, %, takes the value of 50%.

The turbulent kinetic energy generation term is

$$G_{\mathrm{k},l}=\epsilon {\mu }_{\mathrm{t}}\left(\nabla v_1+\nabla v_1^{\mathrm{T}}\right):\nabla v_l$$

(28)

The empirical equations for the collisional dissipation of the solid-phase pulsation energy and the viscous damping term are

$$J_{\mathrm{s}}=\frac{48}{\sqrt{\pi }}\eta (1-\eta )\frac{{\rho }_{\mathrm{s}}{\alpha }_{\mathrm{s}}^2{g}_0}{d_{\mathrm{s}}}{\mathsf{\Theta }}_{\mathrm{s}}^{3/2},$$

(29)

$${\mathsf{\Pi }}_{\mathsf{\Theta }}=-3\beta {\mathsf{\Theta }}_{\mathrm{s}}+81\frac{{\alpha }_{\mathrm{s}}{\mu }_1^2{\left|v_1-v_{\mathrm{s}}\right|}^2}{g_0{d}_{\mathrm{s}}^3{\rho }_{\mathrm{s}}\sqrt{\pi {\mathsf{\Theta }}_{\mathrm{s}}}}$$

(30)

The empirical equation for the two-phase turbulence action term is

$${\Pi }_{\mathrm{k}}=\beta \left(3{\mathsf{\Theta }}_{\mathrm{s}}-2k\right),{\Pi }_{\epsilon }=0$$

(31)

2.3. Boundary Conditions

The boundary conditions include inlet and outlet as well as wall boundary conditions. The inlet boundary gives the velocity and phase fraction of the liquid and solid phases, and the outlet boundary specifies that the two-phase surface pressure values are zero. The liquid phase has a no-slip boundary condition at the solid wall, and the normal velocity at the wall is zero. The tangential velocity and particle temperature of the particle phase are then calculated according to the Johnson–Jackson model [18].

$$\begin{array}{c}\frac{v_{\mathrm{s}l}}{\left|v_{\mathrm{s}l}\right|}\cdot \left({\tau }_{\mathrm{k}}+{\tau }_{\mathrm{f}}\right)\cdot w+\frac{\varphi \pi {\rho }_{\mathrm{s}}{\alpha }_{\mathrm{s}}{g}_0\sqrt{{\mathsf{\Theta }}_{\mathrm{s}}}}{2\sqrt{3}{\alpha }_{\mathrm{s}}^{max}}{v}_{\mathrm{s}l}+\left(w\cdot {\tau }_{\mathrm{f}}\cdot w\right)\tan {\delta }_{\mathrm{W}}=0\end{array},$$

(32)

$$\begin{array}{c}{\kappa }_{\mathrm{s}}\frac{\partial {\Theta }_{\mathrm{s}}}{\partial x}=\frac{\varphi \pi \left|v_{\mathrm{s}\mathrm{l}}\right|{\rho }_{\mathrm{s}}{\alpha }_{\mathrm{s}}{g}_0\sqrt{{\Theta }_{\mathrm{s}}}}{2\sqrt{3}{\alpha }_{\mathrm{s}}^{max}}-\frac{\sqrt{3}\pi {\rho }_{\mathrm{s}}{\alpha }_{\mathrm{s}}{g}_0\left(1-e_{\mathrm{w}}^2\right)\sqrt{{\Theta }_{\mathrm{s}}}}{4{\alpha }_{\mathrm{s}}^{max}}{\Theta }_{\mathrm{s}}\end{array}$$

(33)

where $v_{\mathrm{s}l}$—slip velocity vector between solid phase and wall, m/s; ${\tau }_{\mathrm{k}}$,${\tau }_{\mathrm{f}}$—shear stress tensor generated by solid phase kinetic collision and friction at the wall, pa; $w$—normal vector inside the wall; $\varphi$—reflection coefficient, dimensionless, takes the value of 0.001; ${\delta }_{\mathrm{W}}$—wall friction angle, rad, takes the value of π/10; and $e_{\mathrm{w}}$—recovery coefficient of particle-wall collision, takes the value of 0.9.

3. Experimental and Numerical Model Validation

3.1. Geometric Modeling and Meshing

The main section of the experimental device is a large-scale flat, as shown in Figure 1. It is composed of five large visual flats with a width of 10 mm, a length of 2000 mm, a height of 600 mm, and a total length of 10 m. The model entrance consists of three holes with a diameter of 8 mm, located on the left side of the flat, and the exit is located on the top of the left side of the flat model, with a diameter of 15 mm.

In order to obtain more proppant accumulation patterns in large-scale shale fractures, and considering the workstation calculation capability, the height of the experimental device was kept constant and the length was increased by 5 m to establish a single fracture geometry model with a length of 15 m, a height of 0.6 m, and an adjustable width of 4–10 mm. As shown in Figure 2, three inlets of the same size with a height of 0.02 m and a width of the fracture width were set up at the front of the flat fracture, which were noted as the upper hole, middle hole, and lower hole. Three outlets of the same size and position were located at the back end of the fracture.

3.2. Experimental Parameter Settings

In order to ensure that the artificial fractures in the field have the same hydrodynamic characteristics as in the experimental flat, the field displacements were converted to the experimental displacements according to the Reynolds similarity principle, and the calculation formulas are as follows:

$$Q_E=\frac{Q_F}{2}\times \frac{H_E\times W_E}{H_F\times W_F}\times 1000,$$

(34)

where Q_E is experimental displacement, L/min; Q_F is site displacement, m³/min; W_E is the width of the flatbed unit, mm; H_E is the height of the flatbed unit, m; H_F is the height of the artificial fracture, m; and W_F is the width of the artificial fracture, mm.

The on-site fracturing construction displacement is located at 12–18 m³/min in 6–12 clusters of shot holes with double wings, the on-site fracture height is 10–30 m, and the experimental device has a height of 0.6 m, a length of 10 m, and a width of 10 mm, and the range of experimental displacements is obtained according to the above formula, as shown in

Table 1. Conversion of experimental displacement ranges.

Site Displacement (m3/min)	Height of Artificial Crack (m)	Height of Flatbed Unit (m)	Number of Perforation Clusters	Experimental Displacement (L/min)
12	30	0.6	12	10
18	10	0.6	6	90

.

As can be seen from the above table, the indoor experimental displacement is 10–90 L/min, and the pumping parameters need to be controlled within this range during the experiment.

In order to study the influence of other physical parameters on the proppant placement pattern, different physical parameters were set in this study, including proppant particle size, fluid viscosity, fracture width, injection position, etc. In the field construction, the viscosity of slickwater was 2–3 mPa∙s, the quartz sand proppant was the main one and the ceramic proppant was the auxiliary one, and the fracture width was unknown. In the experiment, the same ratio of slickwater was used as in the field, the proppant was 70/140 or 40/70, and the fracture width was 10 mm, and the specific values are shown in

Table 2. Experimental and simulation parameters.

Proppant Size	Displacement (L/min)	Fluid Viscosity (mPa∙s)	Width of Crack (mm)	Position of Injection
40/70, 70/140	70	2.5	10	Three-hole injection

.

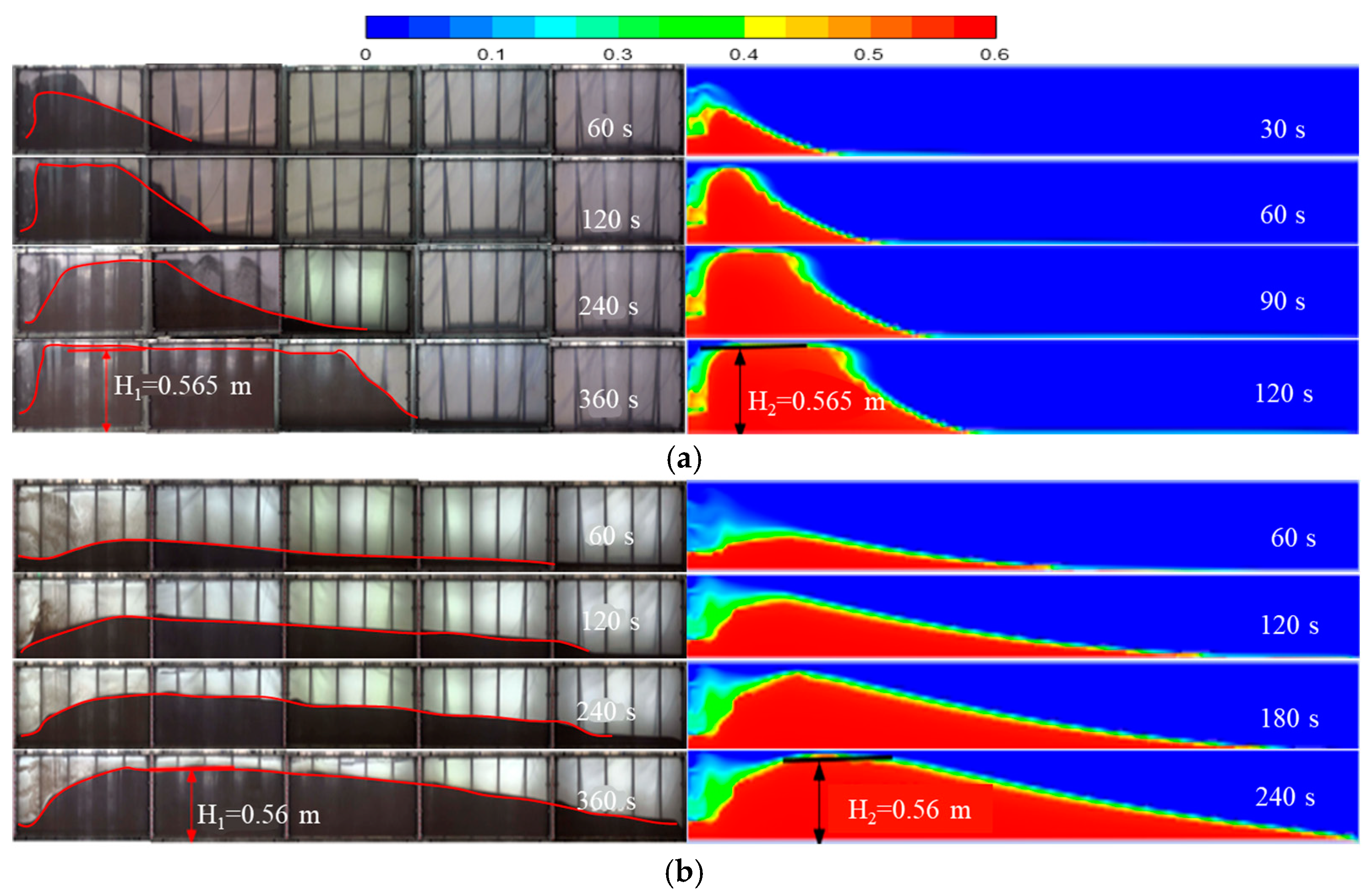
3.3. Numerical Model Validation

In order to verify the correctness of the numerical model of solid–liquid two-phase flow, the experimental results and numerical simulation results were compared and analyzed (Figure 3). The simulation parameters used in numerical model verification were consistent with the experimental parameters.

According to the experimental and numerical simulation of the dune formation process under the two particle sizes, it can be seen that the numerical simulation results are closer to the experimental results as a whole, the dune morphology is similar, and the equilibrium heights of the two are the same. It can be considered that the Eulerian–Eulerian two-phase flow numerical model established in this paper can more accurately describe the transportation and placement law of the proppant in the fracture.

4. Results

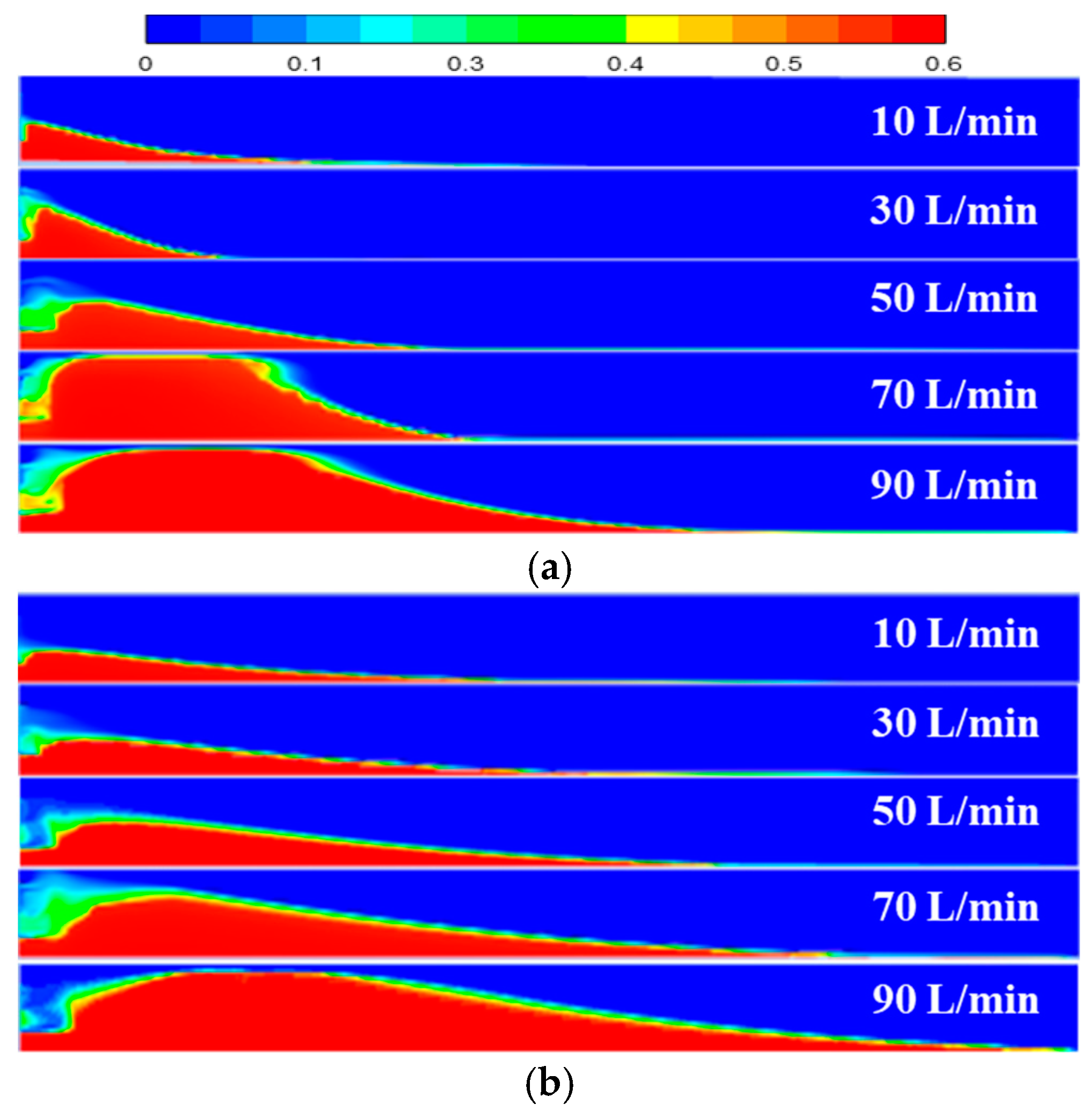
4.1. Effect of Displacement

The influence of displacement on proppant placement is mainly manifested in three aspects. (1) Proppant placement in the near-well area. With low-rate injection, proppant mainly settles near the well and migrates with difficulty to deep depths due to the low initial kinetic energy of proppant. During high-rate injection, the proppant settling near the well is eroded, convolved, and then re-carried by the fracturing fluid to the fracture depth. (2) Equilibrium height of the dune. The influence of displacement on the equilibrium height of the dune is mainly reflected in the time needed to reach the equilibrium height, and the proppant dune can reach the equilibrium height faster under larger displacement. (3) Horizontal transportation distance of proppant. The influence of displacement on the proppant horizontal migration distance is mainly reflected in the kinetic energy of the proppant particles. In general, the velocity of the proppant entering the fracture, the erosion of the proppant deposited at the entrance by the fluid, and the horizontal migration distance of the proppant are positively correlated with the flow rate, while the placement area near the well and the equilibrium height of the dune are negatively correlated with the flow rate (Figure 4).

Figure 5 demonstrates the comparison of the characteristic parameters of the two proppant grain sizes under different displacements. As shown in Figure 5a, the equilibrium height of the dune increases with the increase in the proppant particle size, and the equilibrium height of the 70/140 mesh proppant decreases from 0.575 m to 0.559 m, with a reduction of 2.7%, when the displacements are in the range of 10 L/min–90 L/min, and the equilibrium height of 40/70 mesh proppant decreases from 0.579 m to 0.563 m with a reduction of 2.8%. As can be seen from Figure 5b, with the increase in proppant particle size, the time for the dune to reach the equilibrium height decreases, and the time difference between the two to reach the equilibrium height is large at small displacement, and with the increase in displacement, the time for the two to reach the equilibrium height gradually decreases. It can be seen from Figure 5c that with the increase in proppant particle size, the angle of the back edge of the sand embankment increases, and the angle of the back edge of the sand embankment changes greatly under different displacement rates of 40/70 mesh proppant, while the angle of the back edge accumulation of 70/140 mesh proppant remains almost unchanged with the change in displacement rate. In addition, we notice in Figure 5c that the curve corresponding to the 40/70 mesh has a sudden change in position. This is because when the flow rate increases from 50 L/min to 70 L/min, more proppant passes over the top of the sand bank and settles to the lee side of the sand bank. As the flow rate continues to increase, more proppant migrates deeper into the fracture, causing the settlement profile angle to continue to decrease. From Figure 5d, it can be seen that in the same flow time, with the increase in proppant particle size, the dune area increases, and with a flow time of 120 s, the dune area of the 40/70 mesh proppant increases from 0.5795 m³ to 2.37 m³, with an increase of 308%, and the dune area of 70/140 mesh proppant increases from 0.1 m³ to 1.908 m³, with an increase of 180.8%.

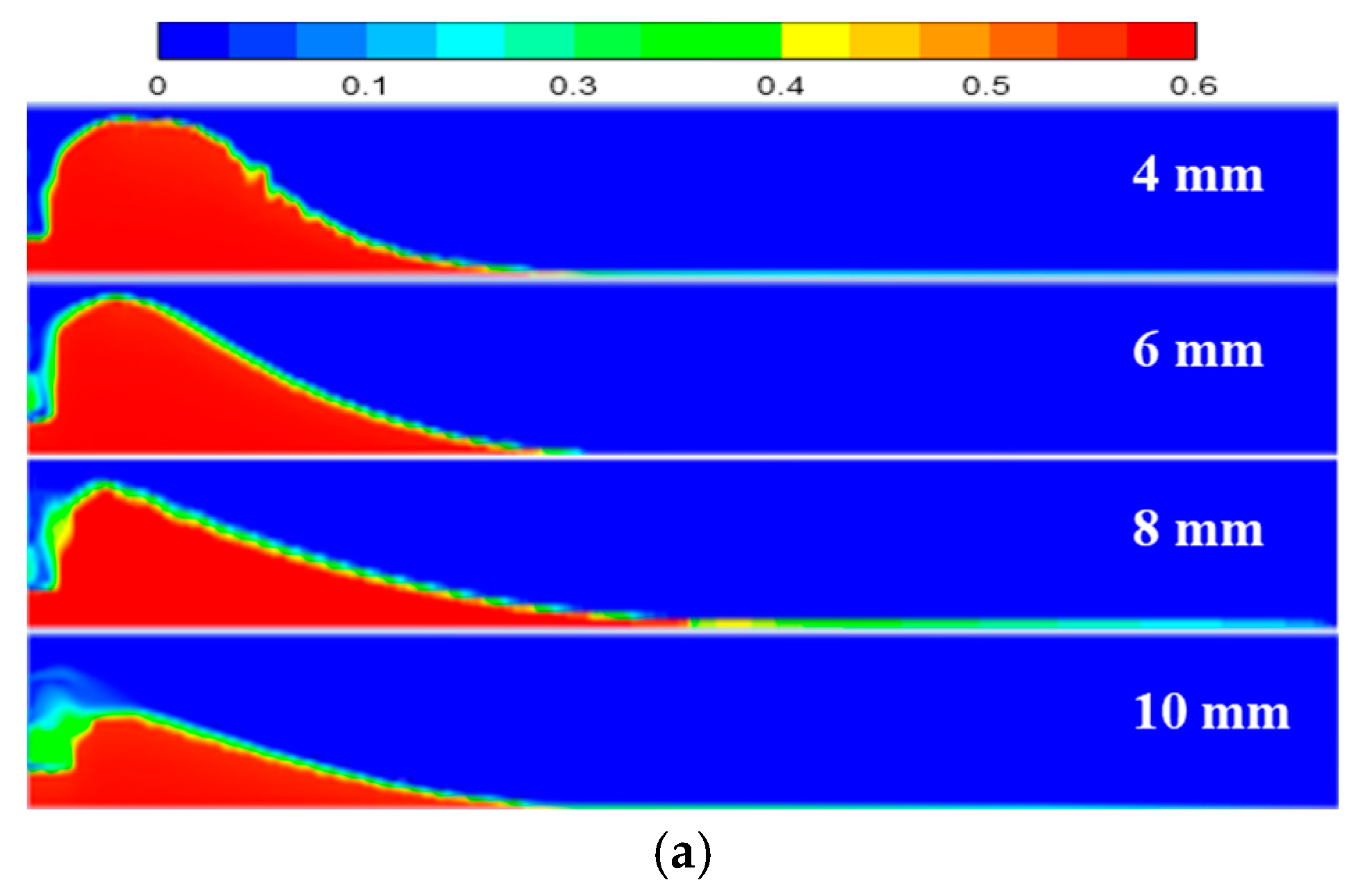
4.2. Effect of Viscosity

The viscosity has a great influence on the horizontal migration distance of proppant particles and the settling velocity of the proppant. Higher viscosity of the fracturing fluid, greater horizontal migration distance of the proppant, smaller sedimentation rate, and higher viscosity can promote the diffusion of the fracturing fluid polymer solution. The smaller the viscosity of fracturing fluid is, the larger the area of the dune will be. When the viscosity is low, the carrying capacity of the fracturing fluid is low, and the dune can grow rapidly to the equilibrium height. When the viscosity is high, the height of the dune in the main fracture increases slowly due to the larger carrying capacity of the fracturing fluid. In addition, fracturing fluid viscosity has a great influence on the degree of turbulence in the near-wellbore area. As shown in Figure 6b, when the proppant was carried with clean water, a pit appeared at the top of the embankments formed at 70/140 mesh. This is because the turbulence in the near-wellbore area is stronger when the sand is transported with low viscosity, and the resulting vortex can convolute the proppant at the top of the sand bank and carry it deeper into the fracture.

As can be seen from Figure 7a, under different viscosities, the equilibrium heights of the two kinds of particle have the same trend of change, and decrease with the increase in viscosity. Under the same viscosity, the equilibrium height of the dune of 40/70 mesh is greater than 70/140 mesh, and the height difference between the two increases with the increase in viscosity. When the viscosity is 1 mPa·s, the equilibrium height difference is 1.465 cm, and when the viscosity is 15 mPa·s, the equilibrium height difference is 2.568 cm. It can be seen from Figure 7b that the slope angle at the entrance of the dune decreases with the increase in viscosity. For the same viscosity, the inlet slope angle of the 40/70 mesh dune is larger than the 70/140 mesh, and the difference between the two decreases with the increase in viscosity. When the viscosity is 1 mPa·s, the difference between the two is 13 degrees, and when the viscosity is 15 mPa·s, the two are almost the same. As can be seen from Figure 7c, the subsidence slope angle of the dune also decreases with the increase in viscosity. With the same viscosity, the subsidence slope angle of the 40/70 mesh dune is larger than the 70/140 mesh. With the increase in viscosity, the subsidence profile angle of the two particle sizes of the dune gradually become closer.

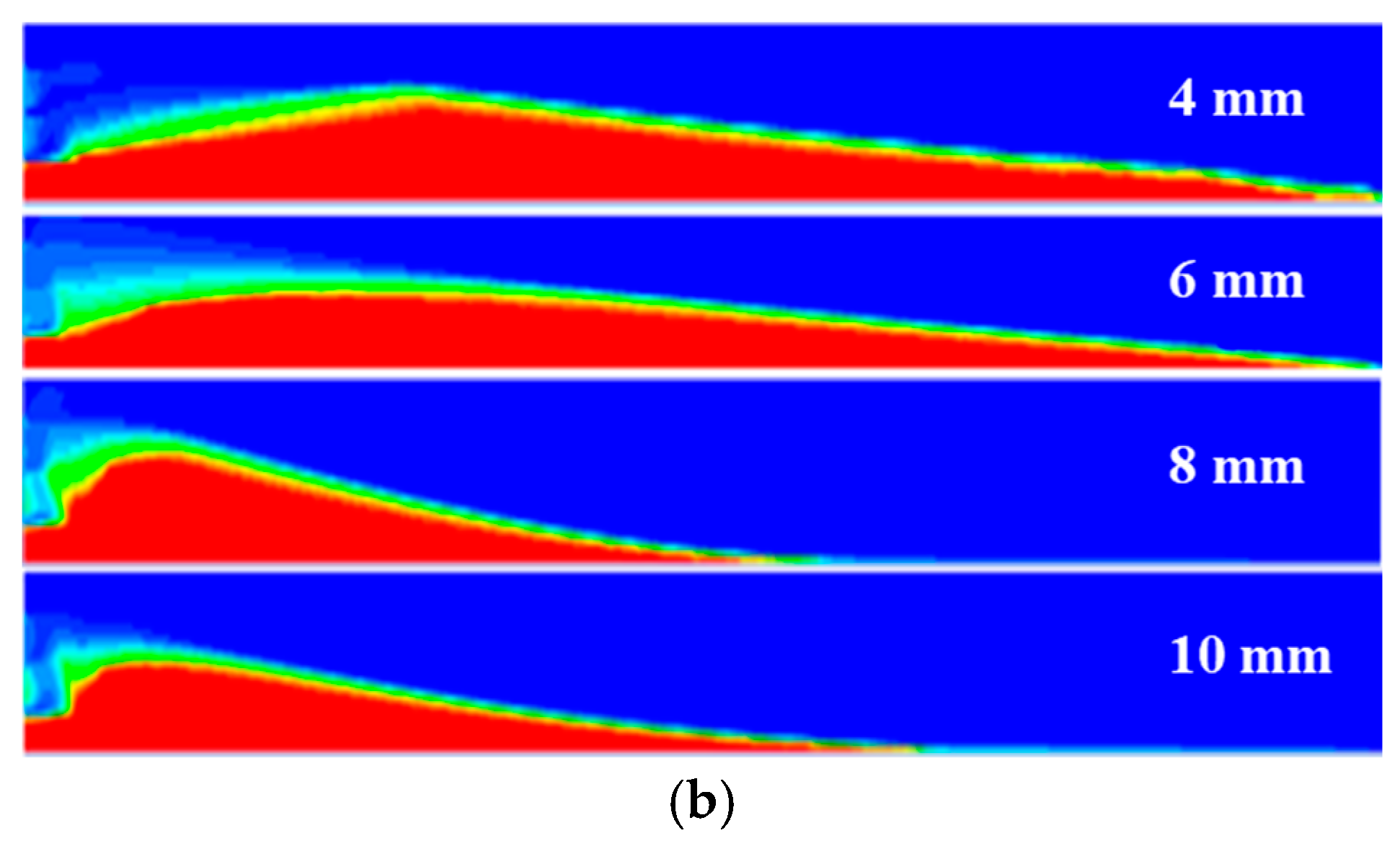
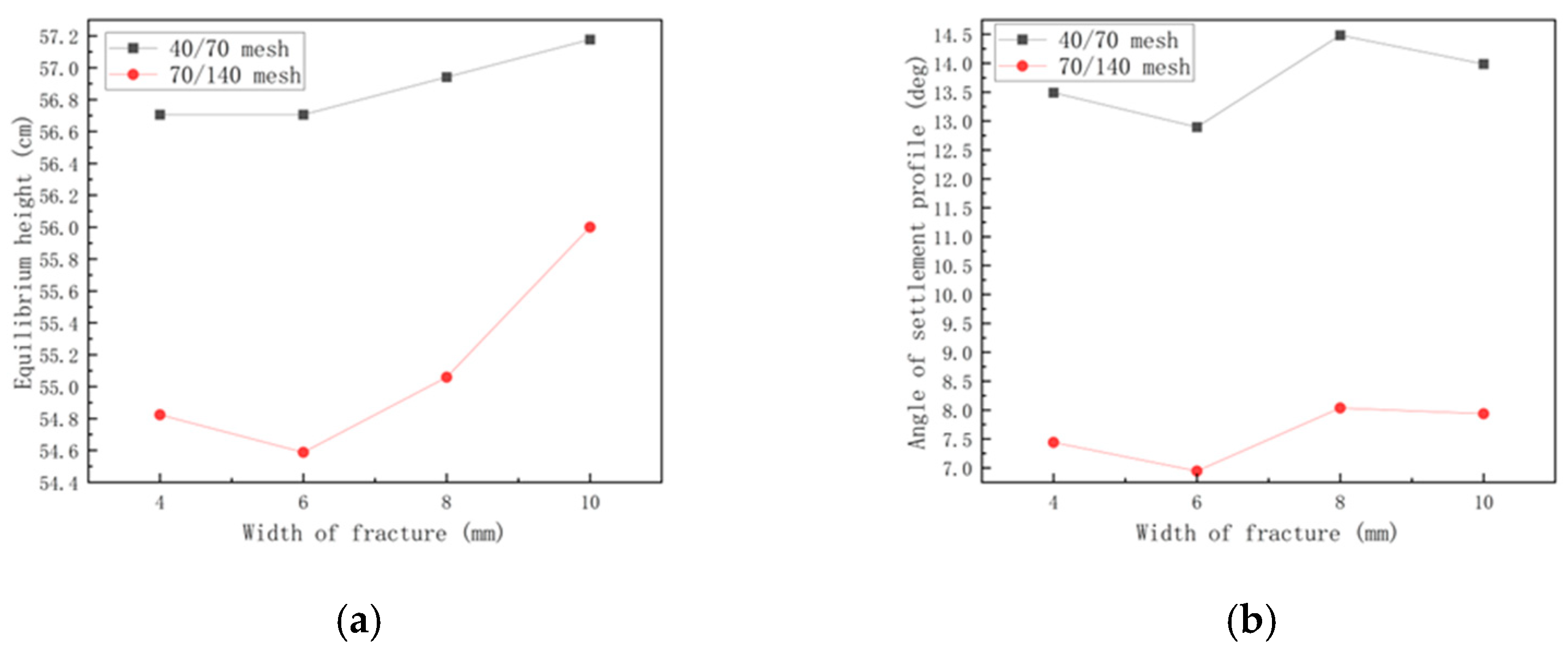
4.3. Effect of Fracture Width

Fracture width is an important factor affecting the settlement and final distribution of the proppant. When proppant particles settle in the fracture, the wall effect of the fracture will affect the settlement rate of the proppant particles and prevent their settlement. When proppant particles move in fractures, they will be affected by the wall effect. The smaller the crack width, the more obvious the wall effect. Therefore, the more the proppant particles are pulled by the wall, the lower the settling speed and horizontal migration speed of proppant particles. Figure 8 shows the placement of two particle sizes under different fracture widths. The smaller the fracture widths, the larger the dune height, and the height of the dune formed by the small particle is smaller than that of the large particle.

It can be seen from Figure 9a that under different fracture width conditions, the equilibrium height of the dune with the small-particle-size proppant is lower than that with the large-particle-size proppant. When the fracture width is 4 mm, the height difference between the two is 2.02 mm, and when the fracture width is 8 mm, the height difference between the two is only 0.53 mm, which indicates that with the increase in the fracture width, the balance height difference under different particle sizes decreases, but under the same particle size, the balance height difference between different fracture widths is small, indicating that the impact of the particle size on the balance height is greater than the impact of the fracture width on the balance height. It can be seen from Figure 9b that under different fracture width conditions, the angle of the back edge of the dune of the 40/70 mesh proppant is larger than that of the 70/140 mesh proppant, but the change trend of both is the same.

4.4. Effect of Shot Hole Location

In order to study the influence rule of different perforation positions on sand bank accumulation morphology, the 70/140 mesh was taken as an example, and the perforation positions were selected as upper hole, middle hole and lower hole respectively for simulation study. Other parameters were set as shown in

Table 3. Parameter settings.

Displacement (L/min)	Proppant Size (mesh)	Fluid Viscosity (mPa·s)	Width of Fracture (mm)
50	70/140	2.5	10

.

As shown in Figure 10, in the early stage of dune placement, a small dune is formed in the near-well region, and the higher the injection position, the closer the dune position is to the wellbore, and the farther the proppant transportation distance is, after the dune reaches the equilibrium height, the further down the injection position is, and the larger the unfilled area is in the near-well region. In order to quantitatively characterize the degree of unfilled near-well region, the trapezoidal area on the left side of the dune that is not filled by the proppant is selected to approximate the degree of unfilled near-well zone fracture S, and the expression is defined as follows:

$$S=\left(l+\frac{H-h}{2tan\alpha }\right)\times (H-h)$$

(35)

where l is the distance between the beginning growth point of the dune and the wellbore, cm; H is equilibrium height, cm; h is the height of the starting growth point of the dune, cm; and α is the inlet profile angle of the dune, deg.

Figure 11 quantifies the unfilled extent of the near-well area after the dune reaches the equilibrium height for three different injection locations. From the Figure 11, it can be seen that the unfilled extent of the near-well zone after the sand dike reaches the equilibrium height is the largest when the injection position is located in the lower hole, which is 0.713 m², about 8% of the entire single-seam lateral area, and the difference in the unfilled extent when injecting in the middle and upper holes is smaller, but the general trend is that the further the injection position is located in the lower hole for the single-hole injection, then the greater the ineffective filled area in the near-well zone is. The degree of unfilled area when injecting from the lower hole is about 11 times higher than that of the upper and middle holes, and the flow conductivity of the near-well zone is crucial for the final flow conductivity of the whole fracture, which shows that the use of the lower injection position for the operation should be avoided in the field as much as possible.

5. Conclusions

(1)

The laboratory experiment was in good agreement with the simulation results, indicating that the Euler two-fluid method can reflect the flow of proppant in the fracture well, and the numerical model established is effective and feasible.

(2)

The process of proppant accumulation in the fracture can be divided into three stages. The first stage is the gravity settlement stage, which forms a small sand bank at the bottom of the fracture; The second stage is the vertical growth stage, in which the proppant accumulates in the vertical direction and the height increases. The third stage is the horizontal growth stage, when the proppant settles to the length beyond the equilibrium height.

(3)

The displacement mainly affects the proppant settlement distance, equilibrium height and equilibrium time in the early stage. The larger the displacement, the smaller the equilibrium height, the faster the proppant accumulation, and the farther the migration distance, but the larger the unfilled area at the inlet. Fracturing fluid viscosity mainly affects the settling rate and migration distance of the proppant. The greater the viscosity, the slower the settling rate of the proppant, which is more conducive to sending the proppant to the remote well zone.

(4)

The smaller the proppant particle size is, the easier it is for it to be carried deeper into the fracture by the fluid, the smaller the equilibrium height, and the smoother the inlet angle and settlement slope angle. The width of the fracture has little effect on proppant accumulation, but when the fracture is narrow, the proppant is affected more by the wall surface, and the upper end of the accumulation body will show pits. The injection position only affects the accumulation near the well, but has little influence on the far end of the fracture and the equilibrium height.