Investigation on Electrostatical Breakup of Bio-Oil Droplets

Abstract

In electrostatic atomization, the input electrical energy causes breaking up of the droplet surface by utilizing a mutual repulsion of net charges accumulating on that surface. In this work a number of key parameters controlling the bio-oil droplet breakup process are identified and these correlations among the droplet size distribution, specific charges of droplets and externally applied electrical voltages are quantified. Theoretical considerations of the bag or strip breakup mechanism of biodiesel droplets experiencing electrostatic potential are compared to experimental outcomes. The theoretical analysis suggests the droplet breakup process is governed by the Rayleigh instability condition, which reveals the effects of droplets size, specific charge, surface tension force, and droplet velocities. Experiments confirm that the average droplet diameters decrease with increasing specific charges and this decreasing tendency is non-monotonic due to the motion of satellite drops in the non-uniform electrical field. The measured specific charges are found to be smaller than the theoretical values. And the energy transformation from the electrical energy to surface energy, in addition to the energy loss, Taylor instability breakup, non-excess polarization and some system errors, accounts for this discrepancy. The electrostatic force is the dominant factor controlling the mechanism of biodiesel breakup in electrostatic atomization.

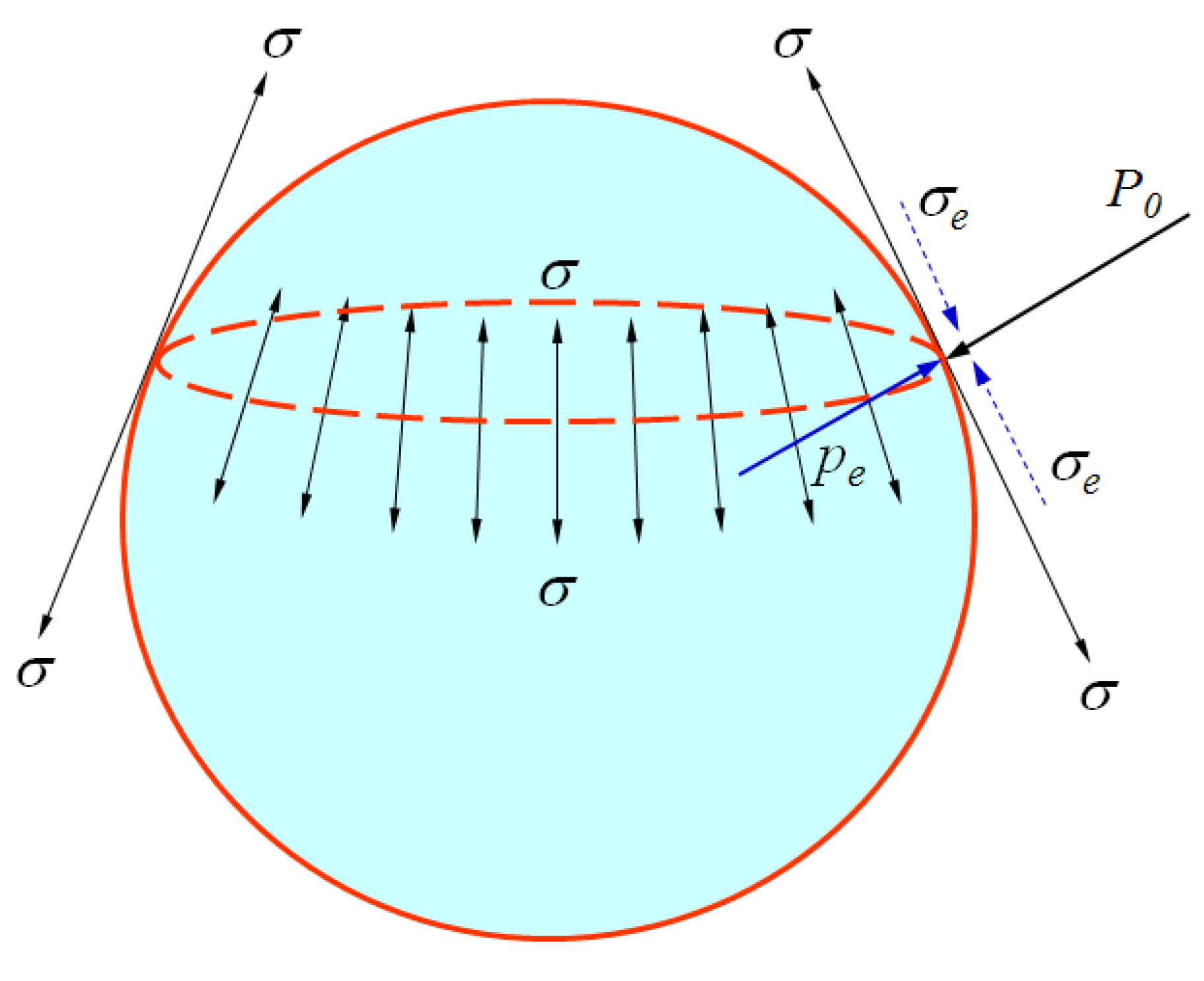
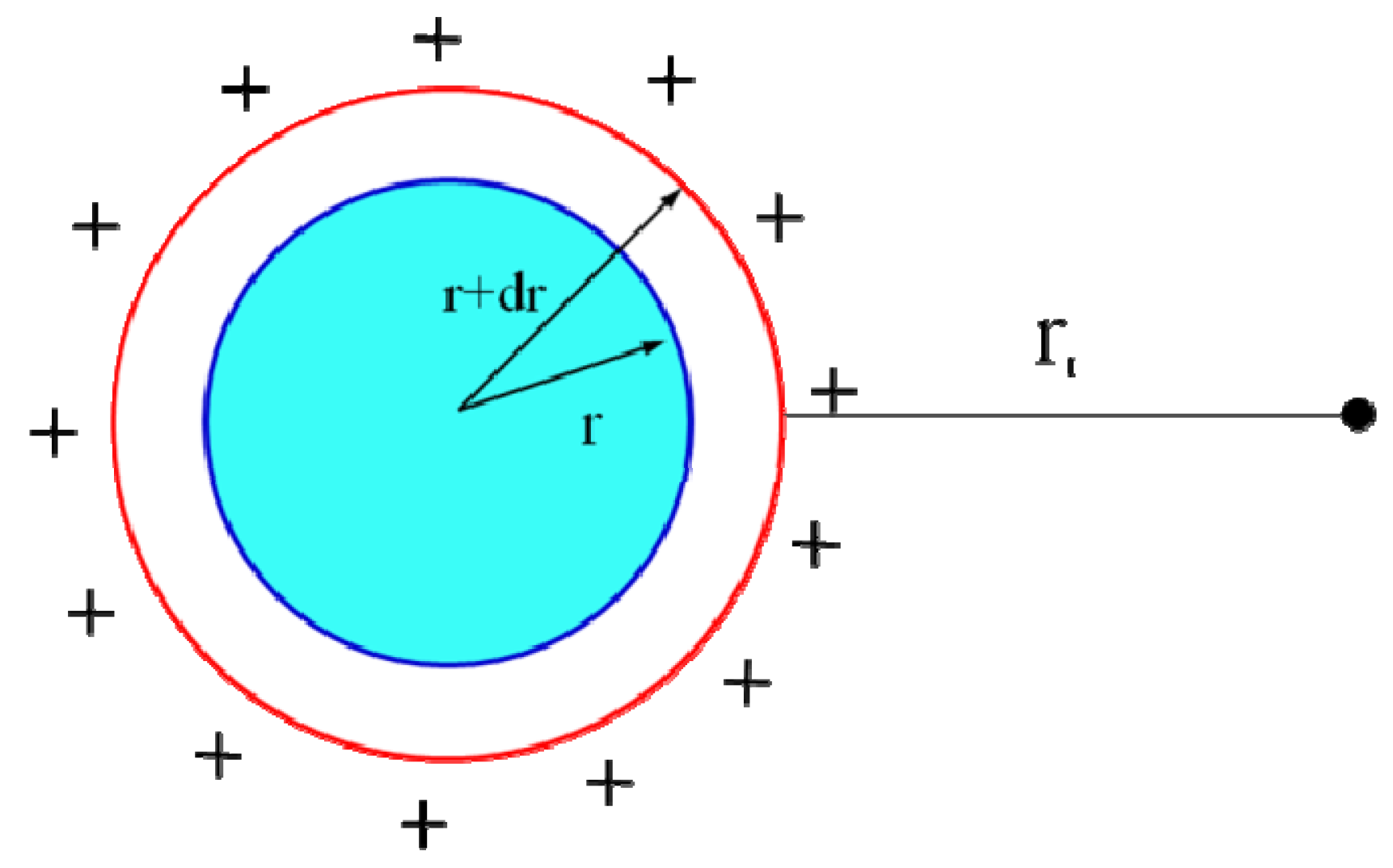
1. Introduction

Bio-oils derived from the pyrolysis of biomass or Fischer–Tropsch processes are considered as one of the major future renewable energy sources [1,2,3,4]. The study of the thermo-mechanical and physical properties of bio-oil, biodiesel, and other liquid bio-oils is therefore very important for obtaining the fundamental characteristics of bio-oil combustion. Due to their high viscosities and larger water contents, effective atomization of bio-oils has been however difficult and faces challenges in powering direct injection (DI) engines [5,6,7]. In order to increase the distribution of fine droplets over the entire reaction zone, the electrostatic atomization method is of great interest. In addition to its application in fuel atomization for gas turbines and internal combustion engines, electrostatic atomization also could be used in other spray systems, e.g., in pesticide processing, industrial painting, film preparation, and ink-jet painting. The implementation of electrostatic atomization can separate a bio-oil stream into fine droplets with a narrow size distribution. This process does not require a high air pressure like conventional atomization techniques do (e.g., 20 MPa for an indirect injection system and up to about 140 MPa for a DI one). When electrostatic force is utilized to break up a bulk liquid into fine and mono-dispersed droplets, the motion and trajectories of these droplets can be controlled by regulating the applied electrical voltage. Moreover, this process can be optimized with relative ease to achieve the desired heat and mass transfer rates. Since the droplets are highly charged in the electrical field, the Coulombic repulsion prevents their agglomeration and this results in a more uniform space distribution of droplet sizes.

In the past 30 years, fuel electrostatic atomization technologies have been developed for diesel, hydrocarbons, and ethanol [8,9,10,11,12,13]. Several researchers have extensively designed and tested several kinds of atomizers to comprehend the effects of parameters such as the nozzle geometry, electrode style, location relative to the grounded surface, orifice size, fuel viscosity, and other physical properties on the specific charge of the resulting spray [8,9,14,15,16,17]. However, electrostatic atomization of bio-oils, as one of the most important and best alternative bio-energy forms, has not been broadly investigated, and atomization of some vegetable and corn oils has been only studied in the rare literature on the topic [13,18]. The breakup mechanism of the electrostatic atomization for diesel, kerosene and hydrocarbons was thoroughly investigated in previous work [19,20,21,22,23,24,25,26]. Although the previous excellent work has determined the highest possible specific charge and the theoretical interpretation of the breakup mechanism(s) of hydrocarbons using the Rayleigh limit or other energy conservation methods for diesel and other hydrocarbons have been done, the current literature does not contain fundamental understanding of the electrostatic breakup mechanism of bio-oils in sprays.

In this work, a theoretical and experimental investigation on the breakup mechanism for biodiesel droplets under different critical instability conditions, which are the bag and strip breakup instability modes, was carried out. This paper aims to interpret the electrostatic breakup mechanism for a single droplet which possesses net charges on the whole surface or partial areas using the Rayleigh instability condition. The parameters controlling the droplet breakup process are identified and correlations among the droplet size distribution, droplets’ specific charges and applied electrostatic voltages are quantified. Experimental results are compared with the theoretical findings.

2. Theoretical Analysis

A basic requirement for atomizing bio-oils is to make their surface area unstable. The surface would then be ruptured into filaments which subsequently disintegrate the surface into many droplets. In electrostatic atomization, the energy causing the surface to disrupt arises from the mutual repulsion of net charges which are accumulated on the whole or partial surface of droplets. A localized electrostatic stress is created and this tends to expand the surface area. This stress is opposed by the surface tension force which tends to contract or minimize the droplet surface area and the forces acting on a droplet are illustrated in Figure 1, where σ is the surface tension, p₀ the additional surface pressure due to the surface tension force, p_e the internal pressure due to charges on the droplets, that could be converted into electrostatic stress σ_E along the droplets’ surface. When the electrostatic stress exceeds the surface tension force, the surface becomes unstable and atomization may occur. If the surface charges keep accumulating and the electrostatic stress remains larger than the critical value, a continuous sustained atomization process will occur.

Figure 1. Forces on a charged droplet.

Figure 1. Forces on a charged droplet.

2.1. The Breakup Mechanism of Bio-Oils Droplets

The instability condition could be derived from energy analysis for a single droplet suspended in a surrounding medium. In Figure 2, assuming that the radius of droplet is r, and there is surface charge q on the droplet’s surface, then the intensity of the electrical field at any point in space should be expressed by:

$$E_i=\frac{q}{4\pi {\epsilon }_0{r}_i^2}$$

(1)

where ε₀ the permittivity of vacuum, r_i the distance from the centre of a droplet to any point in space, E_i the intensity of field induced by the charges on the droplet. So, the electrical potential and energy on the droplets surface should be derived, respectively:

$$U_S={\displaystyle {\int }_{-\infty }^r\frac{q}{4\pi {\epsilon }_0{r}_i^2}d{r}_i=}\frac{q}{4\pi {\epsilon }_{0}r}$$

(2)

$$W_E={\displaystyle {\int }_0^q\frac{q}{4\pi {\epsilon }_{0}r}dq=}\frac{q^2}{8\pi {\epsilon }_{0}r}$$

(3)

The total energy on the droplets surface should be expressed as:

$$W_{total}=\frac{q^2}{8\pi {\epsilon }_{0}r}+\sigma \cdot 4\pi r^2$$

(4)

where W_total is the total energy which a droplet holds, the first term on the right hand side of this equation is the electrical energy and the second term is the surface energy. According to the principle of virtual work, if we take the derivative of the total energy with respect to the radius and set it equal to zero for the condition of equilibrium:

$$\frac{d{W}_{total}}{dr}=-\frac{q^2}{8\pi {\epsilon }_0{r}^2}+\sigma \cdot 8\pi r=0$$

(5)

then the balance equation named the Rayleigh instability condition (or Rayleigh limit) between surface charges and surface tension can be obtained [27]. In fact, some literature has pointed out these individually charged droplets usually break up at a sub-Rayleigh limit [12,21], so the Rayleigh instability could be revised as the following equation:

$$q=\eta \cdot 8\pi {\left({\epsilon }_0\sigma r^3\right)}^{1/2}$$

(6)

where η is the Rayleigh limit coefficient (η ≤ 1.0), σ the liquid (bio-oil) surface tension, and r the original radius of the bio-oil droplet.

Figure 2. A single droplet holding charges and inducing an electrical field.

Figure 2. A single droplet holding charges and inducing an electrical field.

For the spherical droplet in Figure 1, we note that the surface tension force σ and electrostatic force σ_E oppose each other. When the droplet holds a net charge on the whole surface or partial surface, clearly the net force which is defined as the difference between the restorative (positive) force of surface tension and the disruptive (negative) force of electrical stress of electrostatic surface charge could be written as:

$${\sigma }^{\prime }=\sigma -q^2/64{\eta }^2{\pi }^2{\epsilon }_0{r}^3$$

(7)

where σ and σ' are the bio-oil surface tension before and after charging, respectively, and q the amount of surface charges of the bio-oil droplet. If there are no charges on the droplet, it is clear that σ = σ'. While there is a Rayleigh limit charge on the droplet surface and σ' is equal to zero, the droplet will be disrupted at least into two drops.

The breakup of bio-oil droplets is determined by many other dimensionless numbers as well, such as the We number (the ratio of inertial force to the droplet surface tension), Re number (the ratio of inertial force to viscosity force), and k (the mass density ratio of gas to bio-oil). These dimensionless numbers could be described as:

$$\text{We}={\rho }_{g}r{v}^2/\sigma$$

(8)

$$\mathrm{Re}={vd/\upsilon }_g$$

(9)

$$k={\rho }_g/{\rho }_l$$

(10)

where v is the droplets velocity, υ_g the air viscosity that varies with temperature, ρ_g the gas mass density that also varies with temperature, and ρ_l the bio-oil’s mass density. The surface tension of bio-oil droplets is similar to that of diesel at the normal temperature for both experimental and theoretical investigations, as discussed later. As shown in the theoretical consideration, the biodiesel surface area decreases more slowly with temperature and is nearly an order of magnitude lower than diesel at a temperature close to the boiling point of diesel. The surface tension of bio-oils has a linear correlation with temperature, like water, as shown in Equation (11):

$${\sigma }_T={\sigma }_0-\alpha T$$

(11)

where σ₀ is a constant number and α the constant of temperature coefficient. In this work, the bag and strip break-up processes were considered to describe a droplet breakup ability when the droplet holding some net charges on the droplet surface. In the Reitz and Diwakar secondary atomization mode, the stability criteria for bag and strip breakup modes occur when:

$$\text{bag}:\text{ We}=\frac{{\rho }_g{v}^{2}r}{{\sigma }^{\prime }}>B$$

(12)

$$\text{and strip}:\frac{\text{We}}{\sqrt{\mathrm{Re}}}=\frac{\frac{{\rho }_g{v}^{2}r}{{\sigma }^{\prime }}}{\sqrt{\frac{2vr}{{\upsilon }_g}}}=\frac{\sqrt{2}}{2}\frac{{\rho }_g{v}^{3/2}{r}^{1/2}{\upsilon }_g^{1/2}}{{\sigma }^{\prime }}>S$$

(13)

respectively, where B and S are constant and vary in the literature. In this paper their values are set to 8 and 0.5 respectively [28]. When a droplet breaks up into two smaller droplets, the critical condition Equations (12) and (13) would be used to predict the droplet’s specific charge, and therefore the critical charges could be described as:

$$\text{bag}:{\beta }_c=\frac{6\eta \sqrt{\epsilon \left[({\sigma }_0-\alpha t)-{\rho }_{g}r{v}^2/8\right]}}{{\rho }_l{r}^{3/2}}$$

(14)

$$\text{and strip}:{\beta }_c=\frac{6\eta \sqrt{\epsilon \left[({\sigma }_0-\alpha t)-\sqrt{2}{\rho }_g{v}^{3/2}{r}^{1/2}{\upsilon }_g^{1/2}\right]}}{{\rho }_l{r}^{3/2}}$$

(15)

where ε the permittivity of air, and β_c the critical specific charge.

2.2. The Rayleigh Limit Coefficient

In our work, the disintegration of an electrically charged droplet into two drops is assumed. In 1964, Ryce and Wyman used the minimum energy method originated by Vonnegut and Neubauer to analyze the energy variation before and after the breakup of droplets [19,21]. In their surface-charged droplets breakup analysis they assumed: (a) that two spherical drops for the electrical interaction to be negligible in the final state; (b) that the division takes place so as to make the surface energy and electrical energy of electrical energy of final state reach a minimum; (c) that there is a possibility of division with an electrical charge less than that given by the Rayleigh instability conditions; (d) that the permittivity of the surrounding air is uniform. According to their work, both droplets are at the same electrical potential after the breakup, so when the original droplet divides into two drops of radius r and ξr, and they must hold the charges of q and ξq [21]. Considering the conservation of volume and charge R³ = (1 + ξ³)r³, Q = (1 + ξ)q and the assumption of Equation (6), the final energy including these surface and electrical energies is expressed as:

$$W_{total}=4\pi \sigma R^2\left[\frac{\left(1+{\xi }^2\right)}{\sqrt[3]{{\left(1+{\xi }^3\right)}^2}}+2{\eta }^2\frac{\sqrt[3]{\left(1+{\xi }^3\right)}}{\left(1+\xi \right)}\right]$$

(16)

If we take the derivative of the total energy with the ξ and set it equal to zero for the condition of equilibrium, the condition for the system to be at minimum energy after breakup is found:

$$\frac{d{W}_{total}}{d\xi }=8\pi \sigma R^2\frac{\xi -1}{{\left(1+{\xi }^3\right)}^{5/3}}\left[{\eta }^2{\xi }^2-\left({\eta }^2+1\right)\xi +{\eta }^2\right]$$

(17)

For a droplet breakup, we assume that 0 < ξ ≤ 1.0. When $\frac{d{W}_{total}}{d\xi }=0$, the solution of Equation (17) is solved as:

$$\xi =\frac{1}{2}\left\{\left(1+\frac{1}{{\eta }^2}\right)-{\left[\left(\frac{1}{{\eta }^2}+3\right)\left(\frac{1}{{\eta }^2}-1\right)\right]}^{0.5}\right\}$$

(18)

If we take the second derivative of the total energy with the ξ, using the equation of η²ξ² − (η² + 1)ξ + η² = 0, and we get:

$$\frac{d^2{W}_{total}}{d{\xi }^2}=8\pi \sigma R^2\frac{\left(\xi -1\right)\left(2{\eta }^2\xi -{\eta }^2-1\right)}{{\left(1+{\xi }^3\right)}^{5/3}}$$

(19)

For the symmetrical breakup of a droplet, ξ = 1.0, and this result indicates that the symmetrical breakup only happens under the Rayleigh instability condition, i.e., η = 1.0. For an asymmetrical breakup of a droplet, 0 < ξ < 1.0, this solution will cause the energy to be a minimum and we can get the ratio of total energies before and after breakup of a droplet:

$$\omega =\frac{W_{final}}{W_{original}}={\left(1+2{\eta }^2\right)}^{-1}\times \left[\frac{1+{\xi }^2}{{\left(1+{\xi }^3\right)}^{2/3}}+2{\eta }^2\frac{{\left(1+{\xi }^3\right)}^{1/3}}{1+\xi }\right]$$

(20)

Figure 3 shows the ratio of energies after and before breakup of a droplet for different values of ξ and η² [21]. From these droplet energy ratio results, the total energy after breakup is equal to the total energy before breakup, when η² = 0.351 [21]. When η² < 0.351, it is impossible that the energy after breakup is higher than the energy before breakup, unless the droplets could get some additional energy from the aerodynamic force, i.e., through dispersing the droplets. On the other hand, when η² > 0.351, the total energy will reduce and it could satisfy the droplets breakup process which is only caused by the electrostatic force. In an ideal situation, when η² = 0.351 is considered as the critical value of Rayleigh limit coefficients, so found in our work, the Rayleigh limit coefficient η is equal to 0.592. This value of η is in agreement with the data given by Shrimpton who pointed out that these individually charged droplets usually break up at between 70% and 80% of the Rayleigh limit value, while the charged droplets within a spray plume can break up at 55% value of this limit [12].

Figure 3. Energy variation with η² and ξ.

Figure 3. Energy variation with η² and ξ.

3. Analysis of the Critical Specific Charges on the Droplet

When the specific charge of a droplet exceeds the critical value, atomization will certainly happen. Generally speaking, the specific charges are used to represent the atomization capacity of the droplets. In the model of Equations (14) and (15), which are derived from the Rayleigh instability condition, these factors which can determine the atomization process in an externally applied electrostatic field are identified as the amount of surface charges or the specific charges, original droplet size, bio-oil surface tension, surrounding medium gas density, temperature and droplet velocity. In this paper, for biodiesel, the critical specific charges were obtained from different initial droplet sizes, temperatures, and for standing-still and moving droplets by adopting Equations (14) and (15). The other parameters like some calculated constants and liquid properties for biodiesel during atomization shown in Table 1 were used [29]. The gas mass density, viscosity and biodiesel density were calculated by considering their temperature dependences [30].

Table 1. Calculated constants and liquid properties for biodiesel.

Density (kg/m3)	Surface tension (N/m)	Critical temperature (K)	Permittivity of air (C2/N∙m2)	Conductivity (s/m)
880.20	0.02635	780.00	8.85 × 10−12	4.06 × 10−10

Table 1. Calculated constants and liquid properties for biodiesel.

Density (kg/m3)	Surface tension (N/m)	Critical temperature (K)	Permittivity of air (C2/N∙m2)	Conductivity (s/m)
880.20	0.02635	780.00	8.85 × 10−12	4.06 × 10−10

$${\rho }_g=0.0034851p/T$$

(21)

$${\rho }_l={\rho }_0\times {0.2370288}^{-\varphi }\left(\text{kg}/{\text{m}}^3\right)$$

(22)

$$\phi ={(1-T/T_C)}^{2/7}-{(1-T_0/T_C)}^{2/7}$$

(23)

$${\upsilon }_g=\frac{{\mu }_g}{{\rho }_g}=\frac{1}{{\rho }_g}\left[17040+56.02\left(T-273.15\right)-0.1189{\left(T-273.15\right)}^2\right]\times {10}^{-9}$$

(24)

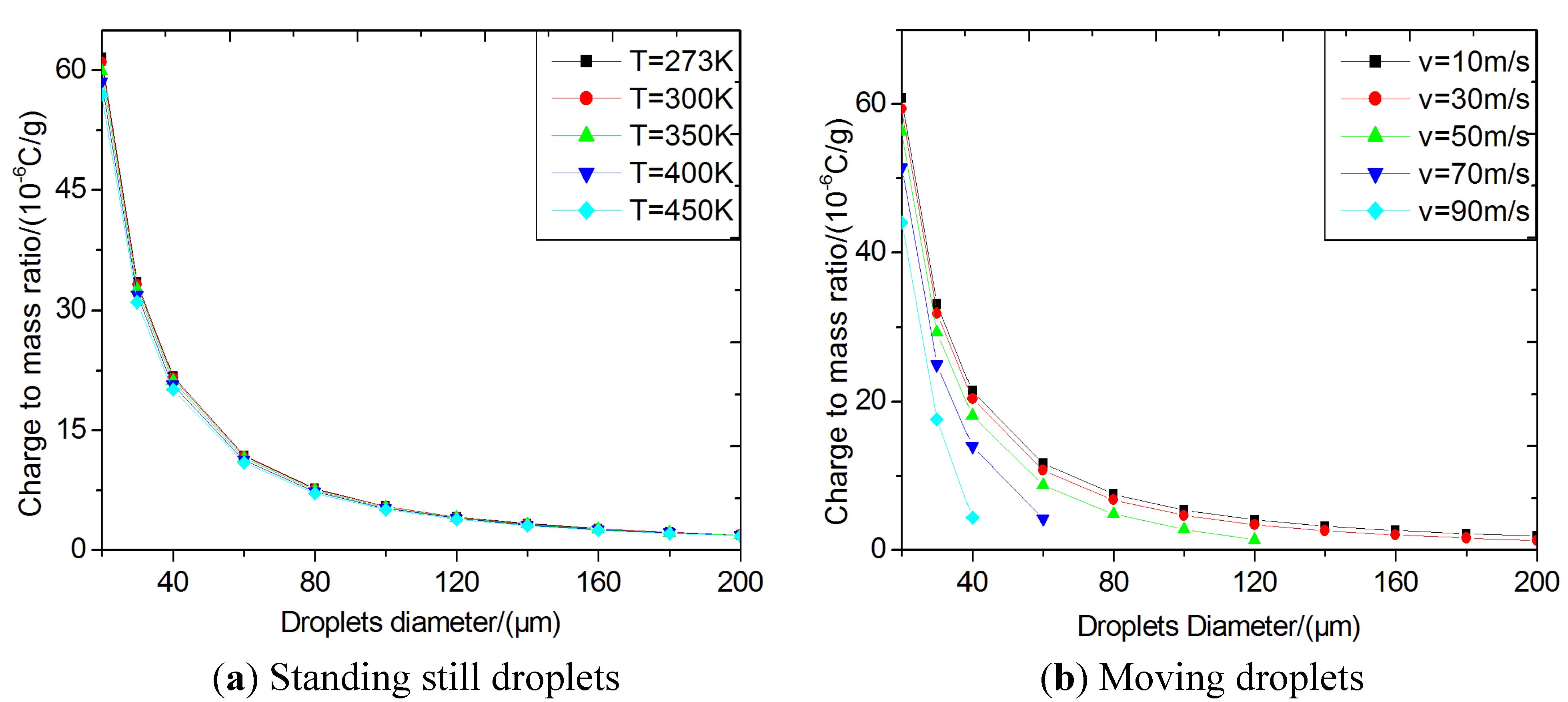
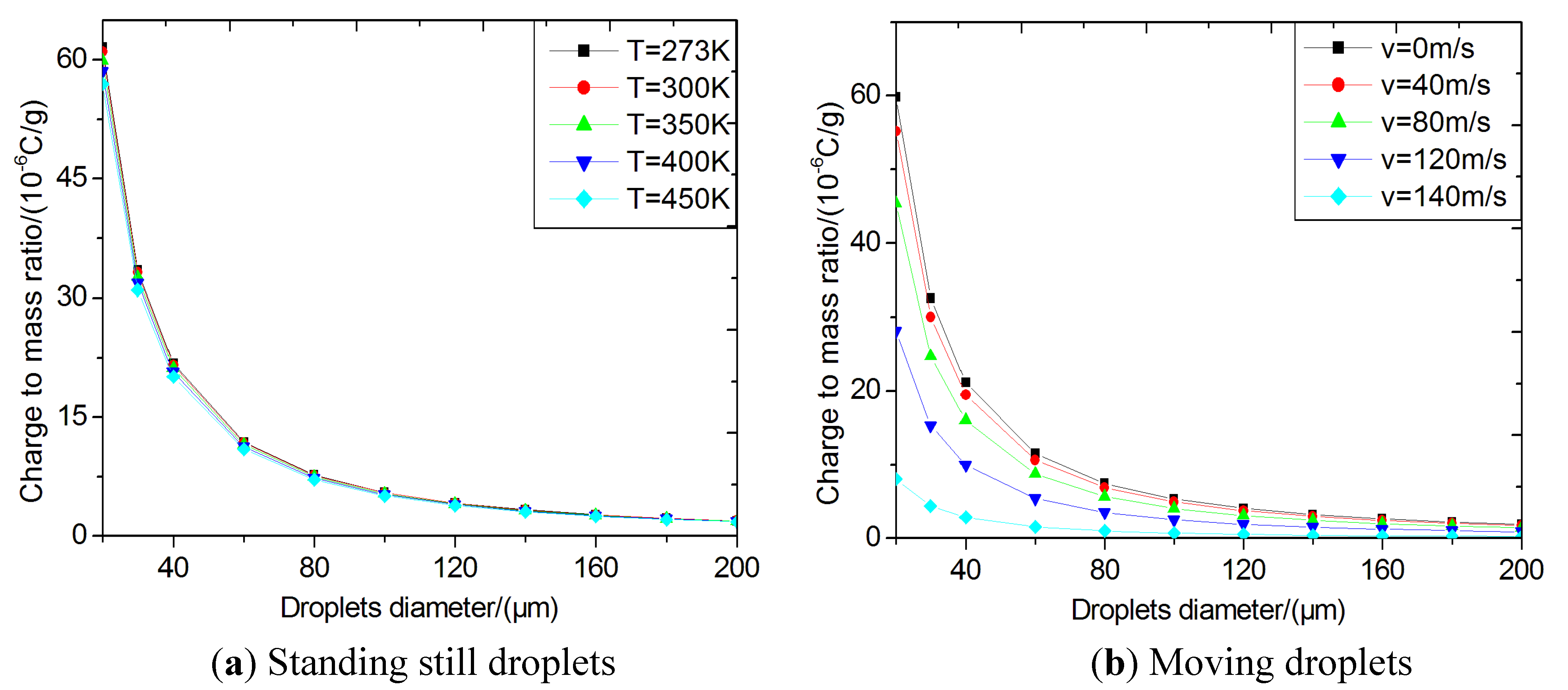
where p is the international normal atmosphere and set to 101325 Pa, T the absolute temperature, Ф the coefficient of temperature, and T₀ = 273.15 K. The specific charge was calculated for different droplet sizes for various temperatures and droplet velocities. The results are shown in Figure 4 and Figure 5, using the stability criteria for bag and strip break-up modes, respectively. Figure 4(a) shows the specific charges of the standing-still droplets with different sizes and varying temperatures. The critical specific charges of droplets decrease with increasing droplet size and temperature and the temperature dependence becomes insignificant when the droplet size become larger. Figure 4(b) shows the specific charges of moving droplets at T = 300 K. The critical specific charges decrease with increasing the droplet velocity for all droplet diameters, indicating that the aerodynamic force is another important factor influencing the breakup process.

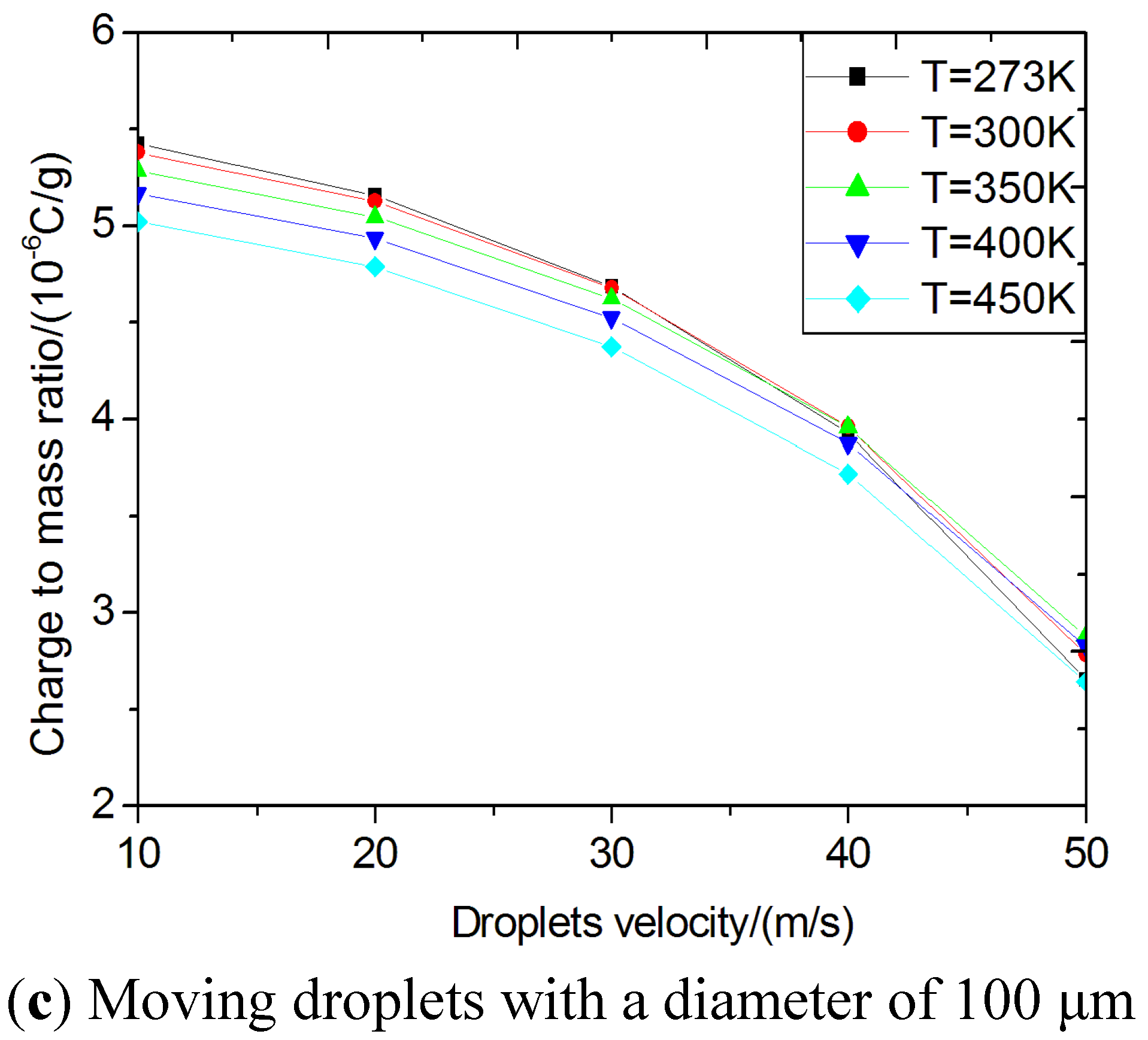
Figure 4. Critical specific charges using the stability criteria for bag break-up mode. (a) standing still droplets; (b) moving droplets; (c) moving droplets with a diameter of 100 μm.

Figure 4. Critical specific charges using the stability criteria for bag break-up mode. (a) standing still droplets; (b) moving droplets; (c) moving droplets with a diameter of 100 μm.

Figure 4(c) shows the calculated critical specific charges of moving droplets at different temperatures for a droplet of 100 μm in diameter. In general, smaller sized droplets are difficult to break up due to their higher critical specific charges corresponding to the Rayleigh instability condition. In this paper, the Laplace pressure (surface additional pressure) has been considered. Similarly, a lower velocity or temperature will make atomization more difficult. As shown in Figure 4, the calculated critical specific charges of normal biodiesel droplets in DI engines are on the order of magnitude of 10⁻⁶ C/g and 10⁻⁷ C/g for bigger drops. Figure 5(a) shows the specific charges of the standing-still droplets with different sizes and for varying temperatures and is the same with Figure 4(a).

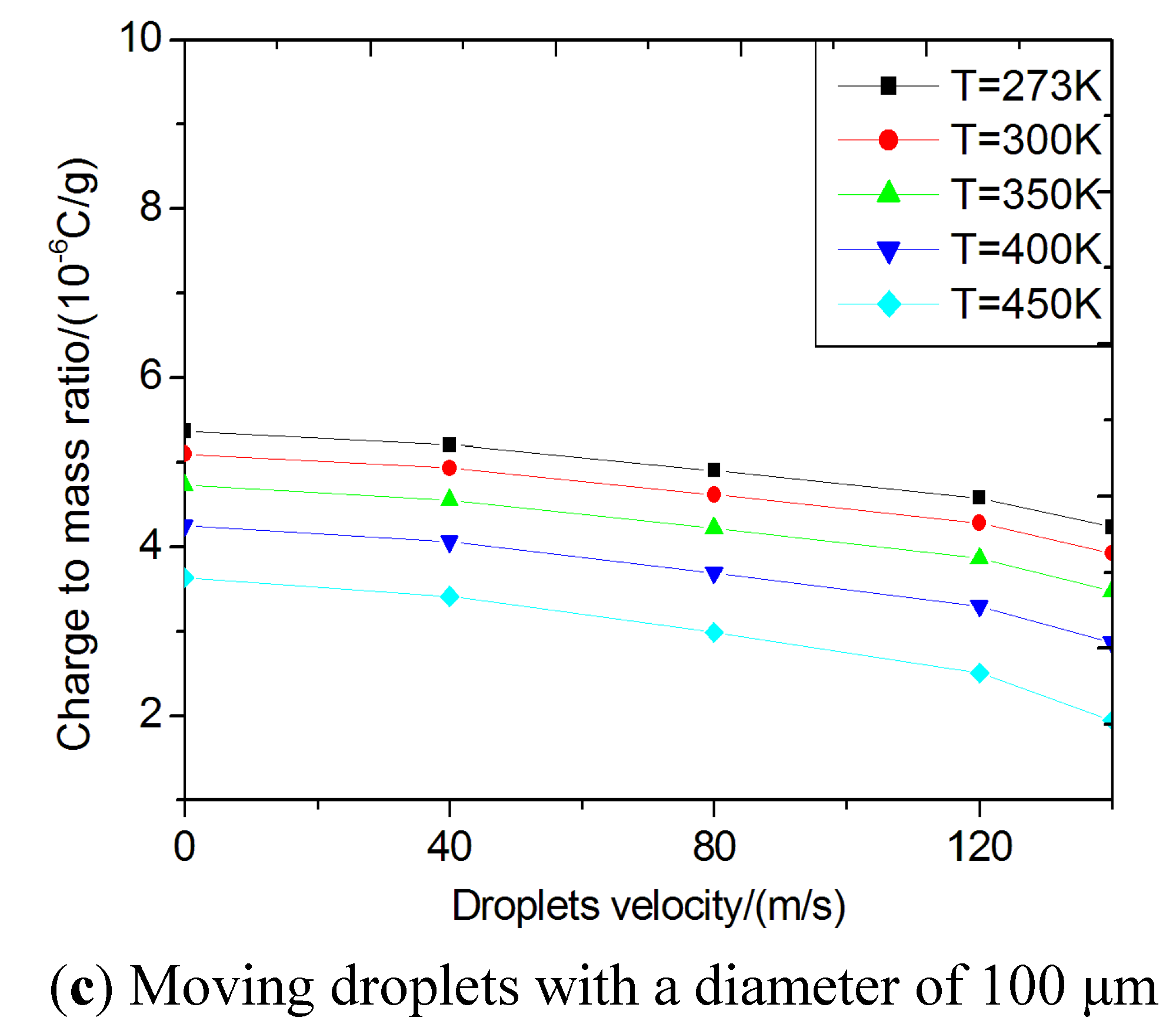
Figure 5. Critical specific charges using the stability criteria for strip break-up mode. (a) standing still droplets; (b) moving droplets; (c) moving droplets with a diameter of 100 μm.

Figure 5. Critical specific charges using the stability criteria for strip break-up mode. (a) standing still droplets; (b) moving droplets; (c) moving droplets with a diameter of 100 μm.

The critical specific charges of droplets usually decrease with increasing the droplet size and temperature. The effect of temperature on the critical specific charge is very small for all the droplets, as shown in Figure 5(a). Figure 5(b) shows the specific charges of moving droplets at T = 300 K. The critical specific charges decrease with increasing the droplet velocity for all droplets, indicating that the aerodynamic force is another factor affecting the breakup process, but in strip breakup mode the effect of aerodynamic force on the droplets’ breakup is smaller than in the bag breakup model. Figure 5(c) shows the critical specific charges of moving droplets at different temperatures for a droplet of 100 μm in diameter. In strip breakup mode the effect of temperature on the droplet breakup is larger than in the bag breakup model. In general, smaller sized droplets are difficult to break up due to their need for higher critical specific charges corresponding to the Rayleigh instability condition. In the strip breakup mode, the calculated critical specific charges of biodiesel droplets are also on the order of magnitude of 10⁻⁶ C/g for smaller drops and 10⁻⁷ C/g for larger ones. The critical specific charges are on the same order of magnitude as for the bag mode. Comparing the two different breakup modes, we found the bag breakup model just considered the effect of We number for droplet breakup, while the strip breakup mode took both the We and Re numbers into account.

In this paper, the effect of evaporation on droplet size was not taken into account, because in the real combustion process in powering DI energies, the lifetime of unstable drops is usually very short relative to their evaporation and momentum time scales, corresponding to both bag and strip breakup modes. In the breakup theory of the Reitz and Diwakar secondary atomization mode, the lifetimes of unstable drops are:

$$t_{bag}=B_t\sqrt{\frac{{\rho }_l{r}^3}{{\sigma }^{*}}}$$

(25)

$$\text{and }{t}_{strip}=S_t\frac{r}{v_d}\sqrt{\frac{{\rho }_l}{{\rho }_g}}$$

(26)

respectively, where B_t = π and S_t = 1.0, corresponding to the bag and strip breakup modes, respectively [28].

Figure 6 shows the lifetime of unstable droplets in internal combustion engines. It is clearly found that the lifetime of unstable droplets is less than 0.5 ms for both droplet breakup modes. For the bag breakup mode, for the droplet diameters which could be formed in powering real DI engines, the lifetime is increasing with varying droplet diameters and the effect of temperature on lifetime is unobvious. For the strip breakup mode, the lifetimes of unstable droplets is less than 0.25 ms, when the droplet velocity is 10.0 m/s; while it is less than 0.025 ms, when the droplet velocity is 100 m/s. It is noted that the breakup timescales are much shorter than their momentum and evaporation timescales for the drops themselves, so the effect of evaporation could be ignored in this paper.

Figure 6. The lifetimes of unstable drops for two breakup mode: (a) bag breakup mode; (b) strip breakup mode.

Figure 6. The lifetimes of unstable drops for two breakup mode: (a) bag breakup mode; (b) strip breakup mode.

4. Experimental Investigations of Biodiesel Droplet Breakup

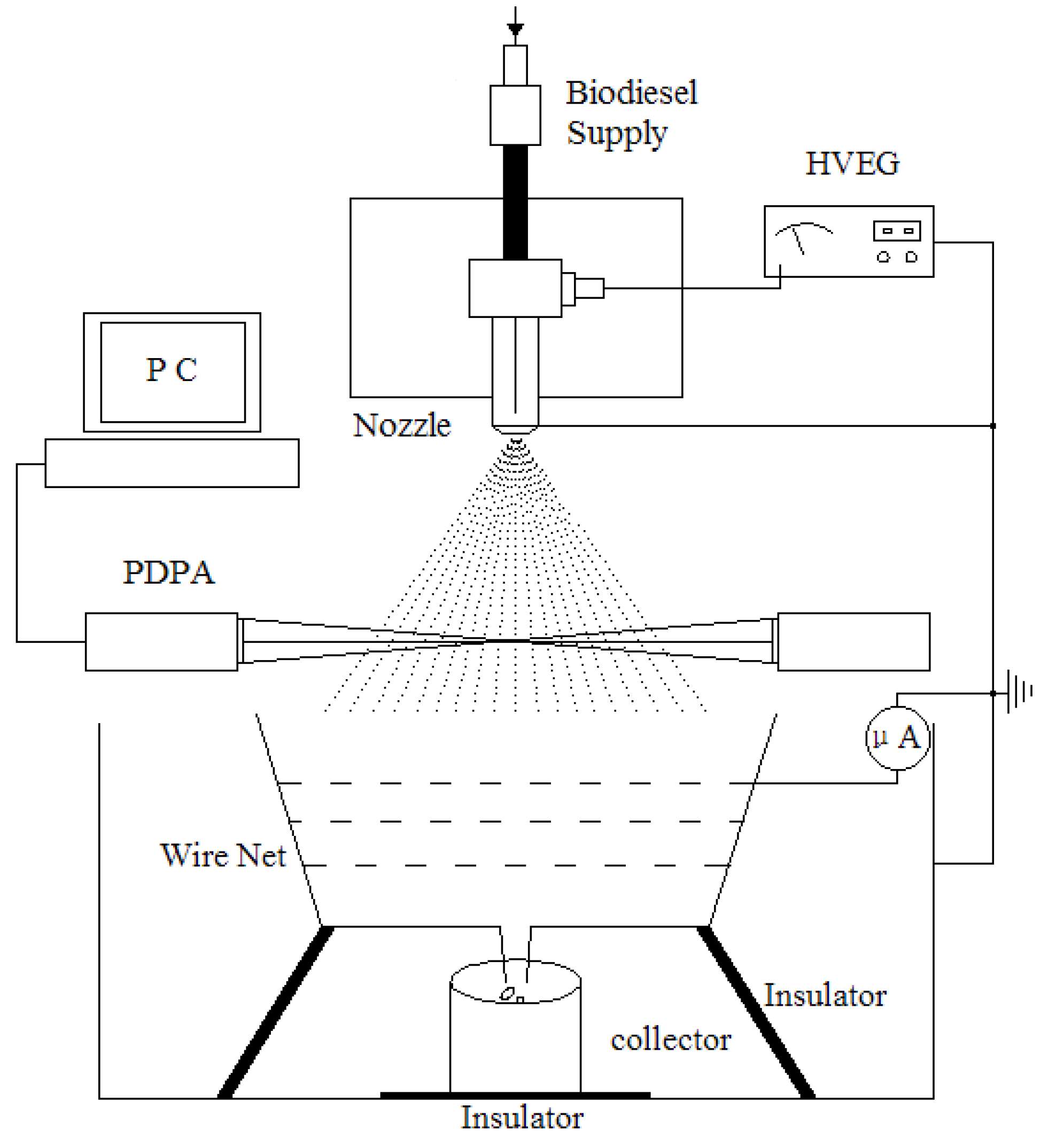
In order to validate the theoretically derived breakup modes shown as Equations (14) and (15), the droplet size and specific charges during the processes of electrostatic atomization were measured. Two data sets were simultaneously characterized using PDPA (Phase Doppler Particle Analyzer) measurements. The design of the atomization nozzle is shown in Figure 7. Figure 8 shows the experimental apparatus for PDPA and specific charge (using the Faraday cage principle) measurements. The measurement parameters can be found in Table 2. In this work, in order to detect the average droplet diameter distribution by varying the electrostatic high voltages, PDPA systems were used to measure the droplet sizes online. The measurement point lies in the center line and the distance between the nozzle and measurement point is set to 180 mm. In this study, we do not obtain the size distribution in space due to the narrow width of the jet spray and not getting enough number drops in the margin of jet spray in this situation. The drop size is just used to interpret the electrostatic breakup in the secondary atomization. Under these experimental conditions, the pressure of 0.25 MPa seems quite low compared to that from modern diesel engine injection systems. But in this paper, the purpose of this experiment is to discuss the effects of the electrostatic force on droplet breakup, so we artificially make the pressure of the air-compressor equal to 0.25 Mpa, which could atomize the liquid. The average specific charge was measured by the Faraday cage principle (as in Figure 8). This equipment is composed of a conducting material, wire net, collector, insulator and exact ammeter. The equipment cage is linked with the ground by a wire. When the biodiesel drops enter the cage, they can be captured by the wire net, and the charges on these droplets will transfer to the ground to produce a tiny electric current. The specific charge could then be obtained [31].

Table 2. Experimental conditions for characterizing the electrostatic atomization of biodiesel.

Room temperature (K)	Relative humidity (%)	Nozzle pressure (MPa)	Needle diameter (mm)	Nozzle aperture (mm)
298.15	72.2	0.25	2.5 mm	1.0 mm

Table 2. Experimental conditions for characterizing the electrostatic atomization of biodiesel.

Room temperature (K)	Relative humidity (%)	Nozzle pressure (MPa)	Needle diameter (mm)	Nozzle aperture (mm)
298.15	72.2	0.25	2.5 mm	1.0 mm

Figure 7. Schematic of the atomizer nozzle.

Figure 7. Schematic of the atomizer nozzle.

Figure 8. Electrodes, PDPA and the Faraday cage.

Figure 8. Electrodes, PDPA and the Faraday cage.

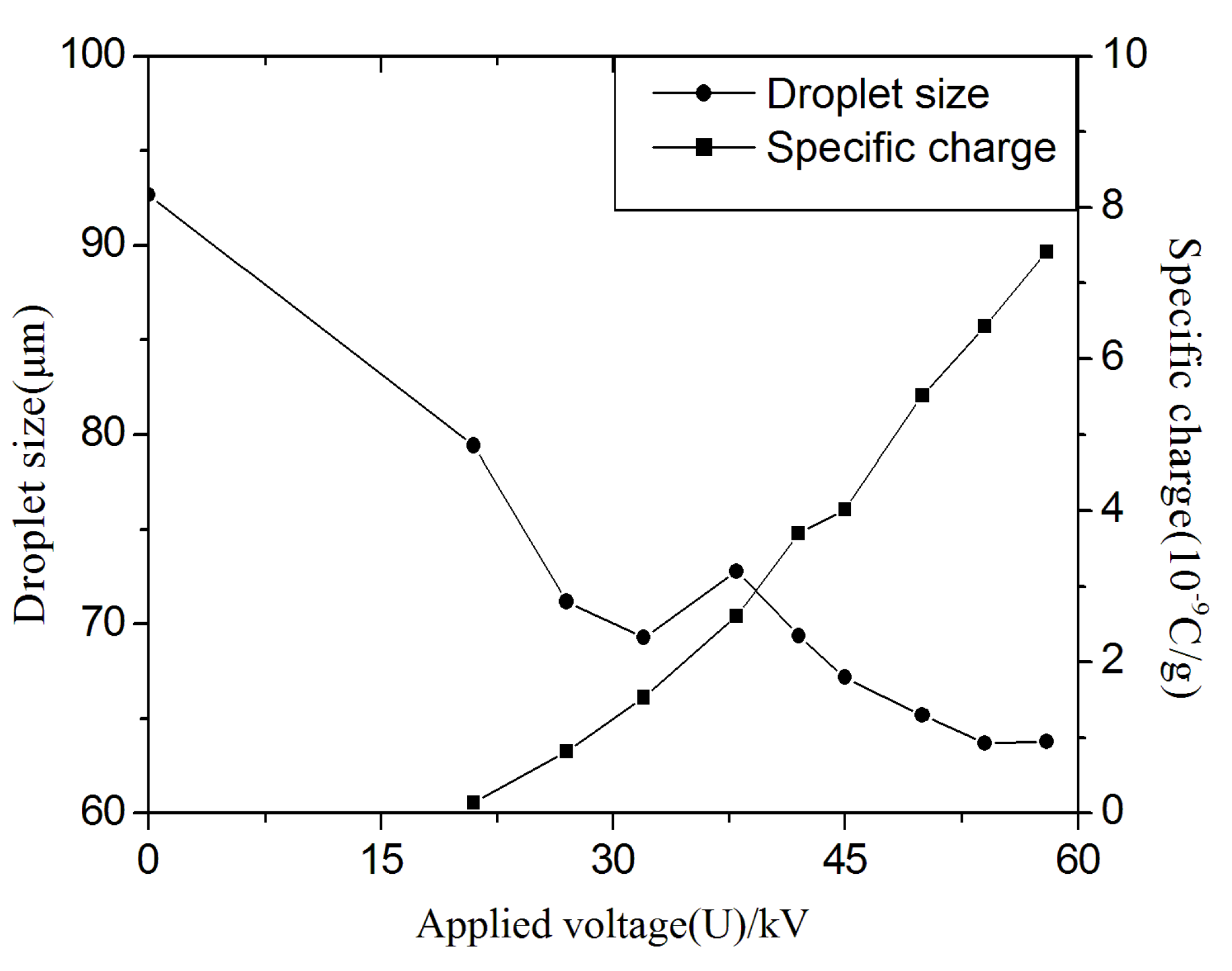
Figure 9 shows the measured correlations among the droplet size, applied voltage and specific charges for biodiesel. As a whole, it was found that by increasing the applied voltage, the droplet size decreases while the droplet specific surface charges increase. Recalling the previously derived breakup mechanism, when the surface tension of the droplet cannot balance the electrostatic stress, the droplet breaks up into much finer droplets. The critical specific surface charges calculated for biodiesel are on the order of magnitude of 10⁻⁷ and 10⁻⁶ C/g for different normal original droplet sizes with bag and strip breakup modes, respectively, while the measurements shown in Figure 9 are on order of magnitude of 10⁻⁹ C/g and 10⁻⁸ C/g if the voltage is high enough. This would argue against the validity of the Rayleigh instability conditions in describing biodiesel breakup. There exist several explanations for the discrepancy between experimental and theoretical results. The specific charges were measured on droplets after they disintegrated. In electrostatic atomization, droplets formed from secondary breakup will acquire much more surface tension energy and this energy comes from the electrical energy which the original droplet held. The electrical energy will be reduced because of the increasing surface and total energy loss due to discharge towards the surrounding media. In a non-uniform electrical field, the droplets will be polarized and hold negative and positive charges on the opposite poles. Consequently, on the pole area, the surface charge density is higher than on the droplets’ equator area. The surface tension may be less than the electrostatic stress, because the specific charge on this area may higher than the critical charge or measured value. A droplet may be disintegrated into two or more finer drops beginning from one of the pole areas. On the other hand, the shape of the droplet tends to deform into a flat and long ellipsoid due to the polarization force which is generated by a non-superfluous (non-excess) polarization phenomenon. This process is known as the Taylor instability condition. The simplified model derived from the Rayleigh instability condition did not take this Taylor effect into account. Note that the Taylor effect becomes much more significant when the external electrical field becomes stronger and in the theoretical analysis the external field was not considered. When the length of the semi-major axis of the ellipsoid is longer than 1.9 times that of the semi-minor axis, the droplet breakup would happen. Finally, some parameters may be arguable for theoretical calculations and experimental errors exist because the liquid biodiesel has a very low electrical conductivity and the total surface charges collected by the cage could be significantly different from the theoretical values.

Figure 9. Correlations among the droplets size, applied voltage and specific surface charges.

Figure 9. Correlations among the droplets size, applied voltage and specific surface charges.

From the experimental results in Figure 9, it is noted that although the droplet size variation is decreasing overall, the decrease tendency of the droplets’ size is non-monotonic. It is clearly found that the drop size at an applied voltage of 38 kV has a peak value not seen at other applied voltages. This special phenomenon will usually happen during the electrostatic atomization process. In fact, when the applied voltage is lower than 20 kV, the droplets have no net charge and the droplets’ sizes decrease with increasing voltage, and the jet from the nozzle could disintegrate into smaller droplets than in an uncharged situation, due to the existing external electrical field which could increase the disturbance or instability of the jet spray. The electrostatic force increases the disturbance on the jet flow, while on the contrary, uncharged atomization excludes the disturbance caused by electrostatic effects. It is well known that electrostatic atomization will produce much finer drops. When the applied voltage is lower than 32 kV, the very tiny drops are restricted in the main jet flow because the polarization force is not enough to dramatically change the drop motion. When the voltages further increase, many more satellite drops will be produced. The very tiny droplets could be pulled out from the main jet flow area due to the existence of a non-uniform field and flow entrainment, so the number of tiny drops would dramatically decrease in the main jet spray area, and the average size of droplets measured at the same point will increase with an increased applied voltage. When the applied voltage is higher than 38 kV, the droplets will produce secondary atomization due to the Taylor and Rayleigh instability conditions, so in the measurement area, the larger droplets will go on disrupting into smaller drops to maintain the requirements of stable state and the average size of drops will further decrease with increasing applied voltage.

5. Conclusions

These analyses of a few key factors which control the breakup process of biodiesel droplet for the instability criteria for the bag and strip breakup modes were carried out by means of the Rayleigh instability condition. These factors were identified as the original diameter of droplets, applied voltage, specific charge, surface tension force, droplet velocities, and electrical properties of biodiesel such as its dielectric constant and electrical conductivity. The critical specific surface charge was calculated using the Rayleigh instability condition and found being on the order of magnitude of 10⁻⁶–10⁻⁷ C/g for different original droplet sizes for both the bag and strip breakup modes. In order to validate this data, the droplet size and specific charges were measured simultaneously using a PDPA measurement system and the Faraday cage principle, respectively. The measured specific surface charge was on the order of magnitude of 10⁻⁹ C/g which is much smaller than the calculated value. The average droplets diameter is generally decreasing with increasing the voltage, and this decreasing tendency is not monotonic due to produced satellite drops which were dramatically affected by the externally applied non-uniform field and flow entrainment. Some factors such as the energy transformation from the electrical energy to the surface energy, energy loss, Taylor instability breakup mode, non-excess polarization, and system errors were proposed to account for these discrepancies.