Three-Phase Primary Control for Unbalance Sharing between Distributed Generation Units in a Microgrid

Abstract

For islanded microgrids, droop-based control concepts have been developed both in single and three-phase variants. The three-phase controllers often assume a balanced network; hence, unbalance sharing and/or mitigation remains a challenging issue. Therefore, in this paper, unbalance is considered in a three-phase islanded microgrid in which the distributed generation (DG) units are operated by the voltage-based droop (VBD) control. For this purpose, the VBD control, which has been developed for single-phase systems, is extended for a three-phase application and an additional control loop is added for unbalance mitigation and sharing. The method is based on an unbalance mitigation scheme by DG units in grid-connected systems, which is altered for usage in grid-forming DG units with droop control. The reaction of the DG units to unbalance is determined by the main parameter of the additional control loop, viz., the distortion damping resistance, $R_d$. The effect of $R_d$ on the unbalance mitigation is studied in this paper, i.e., dependent on $R_d$, the DG units can be resistive for unbalance (RU) or they can contribute in the weakest phase (CW). The paper shows that the RU method decreases the line losses in the system and achieves better power equalization between the DG unit’s phases. However, it leads to a larger voltage unbalance near the loads. The CW method leads to a more uneven power between the DG unit’s phases and larger line losses, but a better voltage quality near the load. However, it can negatively affect the stability of the system. In microgrids with multiple DG units, the distortion damping resistance is set such that the unbalanced load can be shared between multiple DG units in an actively controlled manner rather than being determined by the microgrid configuration solely. The unit with the lowest distortion damping resistance provides relatively more of the unbalanced currents.

1. Introduction

Microgrids can become incubators of smart grid technologies. These new technologies can be integrated faster and at a lower cost in microgrids than in the overall electric power system [1], and they can be specifically selected to meet the specific needs of the local microgrid users. The smart grid is expected to emerge as a plug-and-play integration of smart grid-connected microgrids [2]. Islanded microgrids can effectively electrify off-grid areas or “keep the lights on” in times of crisis. Their small-scale, often low-load factor (ratio of average and peak power), large share of variable power sources and the lack of a significant amount of inertia can make islanded microgrid control rather challenging. However, as islanded microgrids can be regarded as small pilot versions of the future electric power system, microgrid control is an actual topic [3]. In [3], an overview of microgrid controllers is provided. A promising control strategy is the droop control, which mimics the conventional control of the synchronous generators in the transmission system [4,5]. A specific variant of droop control is the active power/grid voltage (P/V) droop controller, based on the predominantly resistive lines in low-voltage microgrids. Based on the P/V droop control and further taking into account the large share of renewable energy sources, the voltage-based droop (VBD) control concept has been presented in [6]. In VBD control, constant-power bands are used to allow for an active participation of the renewables in the primary microgrid control during critical instants, such as a very low load burden. In previous papers, single-phase microgrids have been considered. In this paper, the VBD controller is extended for three-phase application, keeping its intrinsic advantages, such as maximizing the renewable energy capture and taking into account the specific nature of the low-voltage islanded microgrids, e.g., the low inertia and the predominantly resistive line parameters.

For distributed generation (DG) units in three-phase grid-connected systems, two control strategies are frequently being used in practice. First, the single-phase sinusoidal control strategy is used in the case that the three-phase DG unit consists of three single-phase inverters with a common DC-bus. Second, a three-phase control strategy with positive-sequence control can be used. These controllers do not deteriorate the voltage unbalance, but will not improve it either [7]. Unbalance can be caused, e.g., by asymmetrical loads, small single-phase DG units or an asymmetrical impedance of the system. The unbalance can be quantified by means of an unbalance factor, e.g., the voltage unbalance factor (VUF). International standards, such as EN-50160, pose limits for the VUF, as unbalance may lead to adverse effects. They may evoke additional losses in the electric power system [7]. Furthermore, the negative sequence components lead to inversely rotating fields, which are hazardous for rotating machines. Further, the capacity of the grid assets is reduced, as the capacity of the transformers or network lines is based on the maximum current. Compensation of unbalance is usually done by installing dedicated unbalance mitigation devices, such as active power filters injecting negative sequence voltages or currents [8]. The power quality of the system can also be improved by adding active power filtering functions in the control strategies of DG units [9].

Like in grid-connected networks, care should be taken to unbalance in islanded microgrids. Many of the three-phase controllers operate in the $\alpha \beta$ reference system, where proportional resonant controllers can be used and the values are transformed back to the stationary reference frame [10], generally without taking into account unbalance. In extension, inverter-based three-phase DG units can provide unbalance suppression by using a coordinated algorithm [11,12]. In [13,14], the DG units inject a negative sequence current by which the negative sequence conductance is controlled in order to reduce the voltage unbalance. The method is implemented in the synchronous $dq$ reference frame. The conductance defined in [14] is determined by a droop characteristic using the negative sequence reactive power. In this way, the compensation effort is shared between the DG units without inter-unit communication. A cascaded control loop is used, and the compensation term is injected at the input of the inner current control loop, which equals the output of the outer voltage control loop. It is, thus, considered as a disturbance for the voltage controller, leading to a trade-off between voltage regulation adequacy and unbalance compensation efficiency [15]. The voltage unbalance compensation can also be included directly at the input of the voltage control loop, such as the method in [15] for unbalance compensation, reducing the negative sequence voltage, which is implemented in the stationary $\alpha \beta$ reference frame. Compensation of the negative sequence current of unbalanced loads while focusing on minimal negative sequence currents in the lines is in the scope of [16]. The negative sequence current is shared among the DG units by adjusting the negative sequence output impedance.

In [17], a communication-based controller is added to the droop controller for improving the voltage quality of a critical load, i.e., compensation of the voltage unbalance and the harmonics. This compensation effort is shared among the DG units according to their rated powers.

This paper has two main aspects. First, the VBD control is extended for three-phase application, and an additional control loop, characterized by the distortion damping resistance, $R_d$, is included for taking into account the unbalance in the system. Next, the effect of the value of $R_d$ is studied. For different $R_d$, the sharing of unbalance between the DG units and unbalance mitigation are considered. Unbalance mitigation can either relate to voltage unbalance near the loads, which leads to adverse effects in load equipment and more heating and losses in the loads, as well as to current unbalance in the lines, which evokes increased line losses. The additional control loop in the VBD control is based on a similar strategy for grid-connected, i.e., grid-following, DG units described in Section 2. In Section 3, first, the three-phase VBD control, operating in the stationary abc reference frame, is presented. Next, the method for unbalance mitigation in grid-following units (Section 2) is altered for application in the grid-forming DG units and added to the VBD control as an additional control loop. The effect of the value of distortion damping resistance is discussed in Section 4. In Section 5, several case studies to verify the adequacy of the controllers and the effect of the value of the distortion damping resistance are presented.

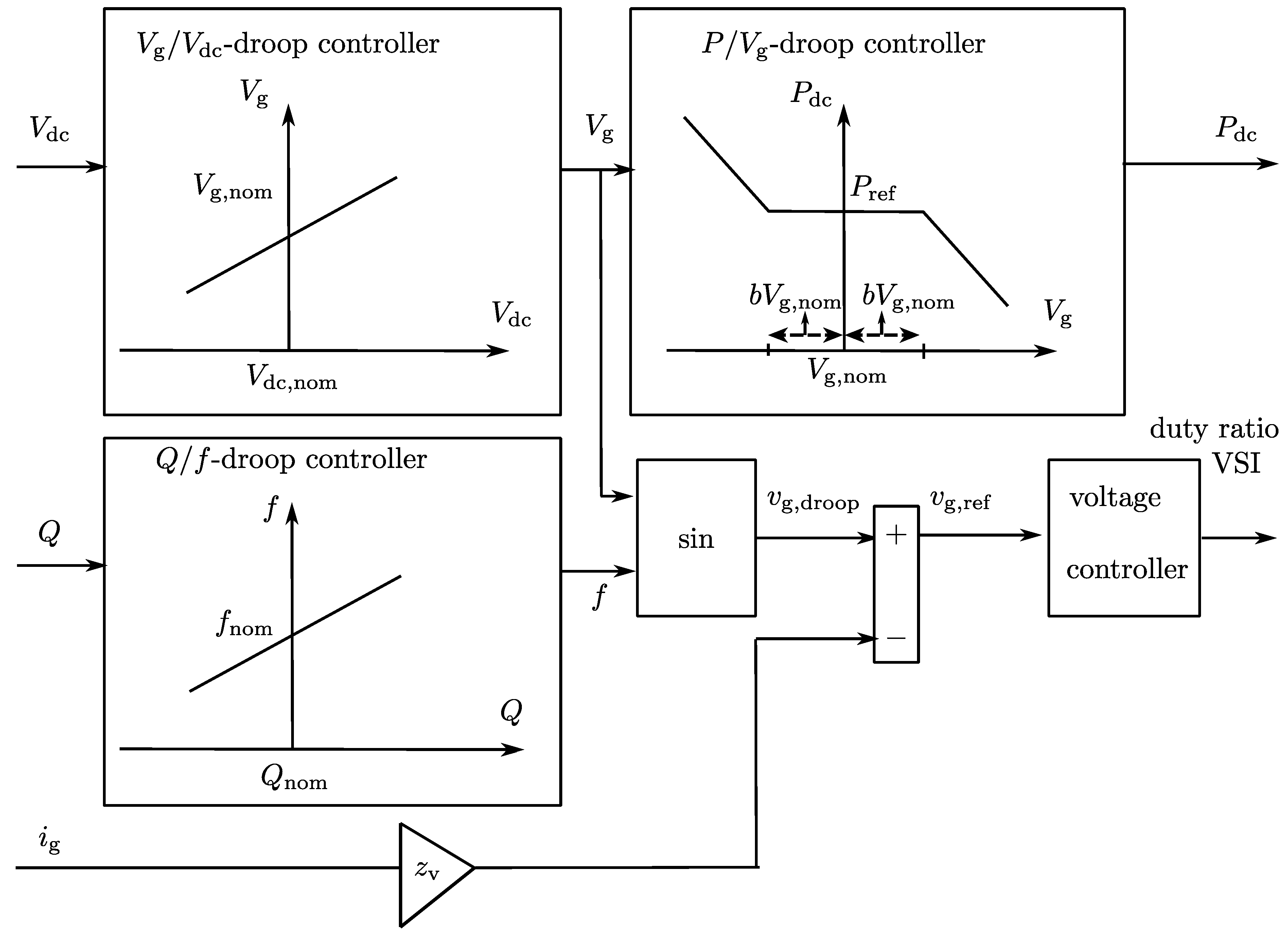
2. Single Phase PR-SHI Method in Grid-Connected Microgrids

DG units are mostly converter-connected to the distribution network. This offers the opportunity for the DG units to provide ancillary services to the electric power system, such as power quality improvement. In [9], the power quality is improved by adding active power filtering functions to the DG units’ control. This control strategy is called the Programmable Resistance Shunt Harmonic Impedance method (the PR-SHI method) and is used in single-phase DG units. The amount of voltage waveform improvement that can be obtained by one unit is limited with this approach, but the total improvement can be significant, because of the large number of DG units [9]. The PR-SHI method determines the inverter’s reference current in order to achieve a controlled resistive behavior towards voltage disturbances. This reference injected current, $i_{\mathrm{L}}^{✶}$(t), is constituted of two components:

$$i_{\mathrm{L}}^{✶}=g_1{V}_{\mathrm{g},\text{nom}}sin{\theta }_{\text{PLL}}+g_{\mathrm{d}}(v_{\mathrm{g}}-V_{\mathrm{g},\text{nom}}sin{\theta }_{\text{PLL}})$$

(1)

with $V_{\mathrm{g},\text{nom}}$ the nominal amplitude of the grid voltage, $v_{\mathrm{g}}$, $g_1$ the fundamental conductance (${\Omega }^{-1}$) and $g_d$ the distortion damping conductance (${\Omega }^{-1}$). The phase angle, ${\theta }_{\text{PLL}}$, of the sinusoidal reference signal is locked to the phase of the fundamental component of the main’s voltage by using a phase-locked loop (PLL). The first component in Equation (1) represents the fundamental component to inject a predefined amount of power in the network, e.g., the maximum power point of the primary energy source. The conductance, $g_1$, is adapted by the DC-link voltage controller to obtain a constant DC-link voltage, $V_{\text{dc}}$, enforcing that the generated DC-power is equal to the AC power delivered to the electrical network. The second term reacts on every deviation of $v_{\mathrm{g}}$ from its nominal value, $V_{\mathrm{g},\text{nom}}sin{\theta }_{\text{PLL}}$. Hence, this term is proportional with the voltage distortion in order to obtain a resistive behavior towards voltage harmonics and other voltage distortions, such as dips [18]. The control strategy is summarized in Figure 1.

Figure 1. The Programmable Resistance Shunt Harmonic Impedance (PR-SHI) method for grid-connected distributed generation (DG) units.

Figure 1. The Programmable Resistance Shunt Harmonic Impedance (PR-SHI) method for grid-connected distributed generation (DG) units.

The PR-SHI control strategy allows the setting of the distortion damping input conductance ($g_d^{-1}$) independently of the fundamental input impedance and, thus, independently of the power level of the converter [18,19]. Hence, the converter is able to maintain its damping potential over a wide range of power levels. This PR-SHI method is promising, because it may swiftly extract the distorted voltage, and also, the two components in the injected current are easy both to interpret and to implement in practice. The benefits of this control strategy have been discussed in [18,20,21]. This method is extended for a three-phase application in [7]. Damping the harmonic distortion and voltage dips in single-phase systems and unbalance mitigation in three-phase applications have been considered.

In conclusion, the factor, $g_{\mathrm{d}}$, damps the deviation of the terminal grid voltage from its ideal value, i.e., due to harmonics and voltage dips. The main advantages of this method are the simplicity of implementation and the low computational burden. In this paper, this idea is reformed for unbalance mitigation in islanded microgrids.

3. Extension of VBD Control to Three-Phase Control, Including Unbalance Mitigation/Sharing Control Loop

Current-controlled (i.e., grid-following) three-phase inverters with positive sequence control form an open circuit for unbalance in the three-phase system. The grid-forming (i.e., voltage-controlled) inverters in islanded systems with positive sequence control, on the other hand, form a short-circuit for unbalance in the three-phase system. Hence, the converter that is electrically closest to the source of unbalance will be burdened with most of the unbalanced current. By implementing a programmable resistive behavior for unbalance, similar to the PR-SHI method, the unbalance in islanded networks can be dealt with in a controlled manner. Two methods for this are discussed in this paper, namely a method making the converter resistive for unbalance (RU) versus a method that contributes in the weakest phase (CW). These are both included in the conventional voltage-based droop (VBD) control method, i.e., the Conventional Method (CM).

3.1. Extension to Three-Phase Systems

The VBD control method was originally developed for single-phase systems [6] and extended here for its three-phase application. The $V_{\mathrm{g}}$/$V_{\text{dc}}$ droop controller determines the terminal voltage amplitude, $V_{\mathrm{g}}$, of the DG unit based on a measurement of the DC-link voltage, $V_{\text{dc}}$. The Q/f droop controller determines the phase angle of phase a (${\theta }_a$) based on a measurement of the reactive power output of the unit. In the CM, the phase angles of the other phases are determined by phase-shifting this voltage with $2\pi /3$; hence, the CM does not take into account the unbalance in the microgrid. The three phases inject a voltage with the same amplitude, $V_{\mathrm{g}}$. In this way, a direct voltage component is generated. Together, these digital controllers determine the reference voltage $v_{\text{droop},i,k}^{✶}=V_{\mathrm{g},k}sin\left({\theta }_{i,k}\right)$ (k is the discrete time instance and phase $i=a,b,c$). Discrete values are utilized because pulse width modulation with sampling period $T_{\mathrm{s}}$ is used in the converter:

$$v_{\text{droop},i,k}^{✶}=V_{\mathrm{g},k}sin({\theta }_{i,k-1}+2\pi f_k{T}_{\mathrm{s}})$$

(2)

with $f_k$ the frequency at discrete time instant k, which is determined by the Q/f droop controller. Hence, the grid-forming VBD control determines the reference value, $v_{\text{ref}}^{✶}$, of the output voltage of the DG unit. In the Conventional Method, $v_{\text{ref},i}^{✶}=v_{\text{droop},i}^{✶}$. From the measurement of $V_{\text{dc}}$, the $V_{\mathrm{g}}$/$V_{\text{dc}}$ droop controller determines the reference amplitude of the grid voltage, $V_{\mathrm{g}}$. In an unbalanced grid, the output currents of the DG unit can be unbalanced; the voltage is balanced with the CM , because it is a controlled value in the grid-forming DG units.

Figure 2 shows the VBD control strategy, including a virtual output impedance loop. A resistive output impedance $z_v=R_v$ is chosen, as this provides more damping in the system [22] and complies with the power control strategies of the loads and generators:

$$v_{\text{ref},i,k}^{✶}=v_{\text{droop},i,k}^{✶}-R_{\mathrm{v}}{i}_{\mathrm{g},i,k}$$

(3)

with $v_{\text{ref},i,k}^{✶}$ the reference voltage for the voltage controller, $v_{\text{droop},i,k}^{✶}$ the voltage obtained by the VBD controller and $i_{\mathrm{g},i,k}$ the grid current delivered by the DG unit in phase i. The VBD controller also determines the input power, $P_{\text{dc}}$, of the unit by means of a $P_{\text{dc}}$/$V_{\mathrm{g}}$ droop controller. A constant-power band with width $2b{V}_{\mathrm{g},\text{nom}}$ is included in the latter controller. By determining the value of b according to the characteristics of the energy source, the priority of active power injection is automatically set between different DG units. Less dispatchable DG units (e.g., combined heat and power (CHP) units) have a larger constant power band than dispatchable units (e.g., diesel generators).

Figure 2. Voltage-based droop (VBD) controller and virtual impedance loop.

Figure 2. Voltage-based droop (VBD) controller and virtual impedance loop.

3.2. Addition of the Voltage Unbalance Control Loop

In the RU and CW method, an additional control loop is included, such that the DG units have a resistive behavior towards current distortions:

$$v_{\text{ref},i}^{✶}=v_{\text{droop},i}^{✶}-R_{\mathrm{v}}{i}_{\mathrm{g},i}-R_{\mathrm{d}}(i_{\mathrm{g},i}-i_{\text{balanced},i})$$

(4)

with $i_{\text{balanced},i}$ the ideal grid current as defined below and $R_d$ the distortion damping resistance. The theoretically balanced grid current provided by the DG unit equals:

$$i_{\text{balanced},\mathrm{a}}=\frac{\sqrt{2}}{3}\frac{\sqrt{Q^2+P^2}}{V_{\mathrm{g}}/\sqrt{2}}sin(arctan\frac{Q}{P_{\text{dc}}}+{\theta }_{\mathrm{a}})$$

(5)

with ${\theta }_{\mathrm{a}}$ the phase angle of the voltage reference determined by the Q/f droop controller; Q and P are the measured total reactive and active power outputs of the DG unit; $P_{\text{dc}}$ is the output variable of the $P_{\text{dc}}$/$V_{\mathrm{g}}$ droop controller, in steady state, $P_{\text{dc}}=P$. The balanced current of phase b is determined analogously:

$$i_{\text{balanced},\mathrm{b}}=\frac{\sqrt{2}}{3}\frac{\sqrt{Q^2+P^2}}{V_{\mathrm{g}}/\sqrt{2}}sin(arctan\frac{Q}{P_{\text{dc}}}+{\theta }_{\mathrm{b}})$$

(6)

with ${\theta }_{\mathrm{b}}={\theta }_{\mathrm{a}}-\frac{2\pi }{3}$ and similarly for ${\theta }_{\mathrm{c}}$. In the CM $R_{\mathrm{d}}=0\Omega$, in the RU method $R_{\mathrm{d}}>0\Omega$ and in the CW method $R_{\mathrm{d}}<0\Omega$. Equation (4) is the grid-forming variant of the PR-SHI method, which provides a resistive behavior of the grid-following unit towards voltage distortions. With grid-forming controllers, action towards current distortions can only be taken in a straightforward manner, because the units are voltage-controlled.

4. Value of the Distortion Damping Resistance, $R_d$: Qualitative Study

In this section, the effect of choosing a positive versus negative value of $R_d$ on the unbalance mitigation, the power sharing between phases in a DG unit and the line losses in the microgrid is discussed in a qualitative manner. In Section 5, this will further be quantitatively verified by means of simulations.

In this paragraph, the voltage unbalance factors of the different methods, i.e., CM, RU and CW methods, will be compared. The voltage unbalance factor (VUF) equals:

$$\text{VUF}=V_2/V_1$$

(7)

with $V_2$ the inverse and $V_1$ the direct component of the three-phase signal, V (consisting of the $V_a$, $V_b$ and $V_c$ components):

$$\left[\begin{array}{c}{V}_0\\ V_1\\ V_2\end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc}1& 1& 1\\ 1& a& a^2\\ 1& a^2& a\end{array}\right]\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\end{array}\right]$$

(8)

The current unbalance factor (CUF) is calculated analogously, with I the current:

$$\text{CUF}=I_2/I_1$$

(9)

4.1. Islanded Microgrid: One DG Unit

The difference between the RU ($R_d>0$) and CW method ($R_d<0$) is discussed in this section.

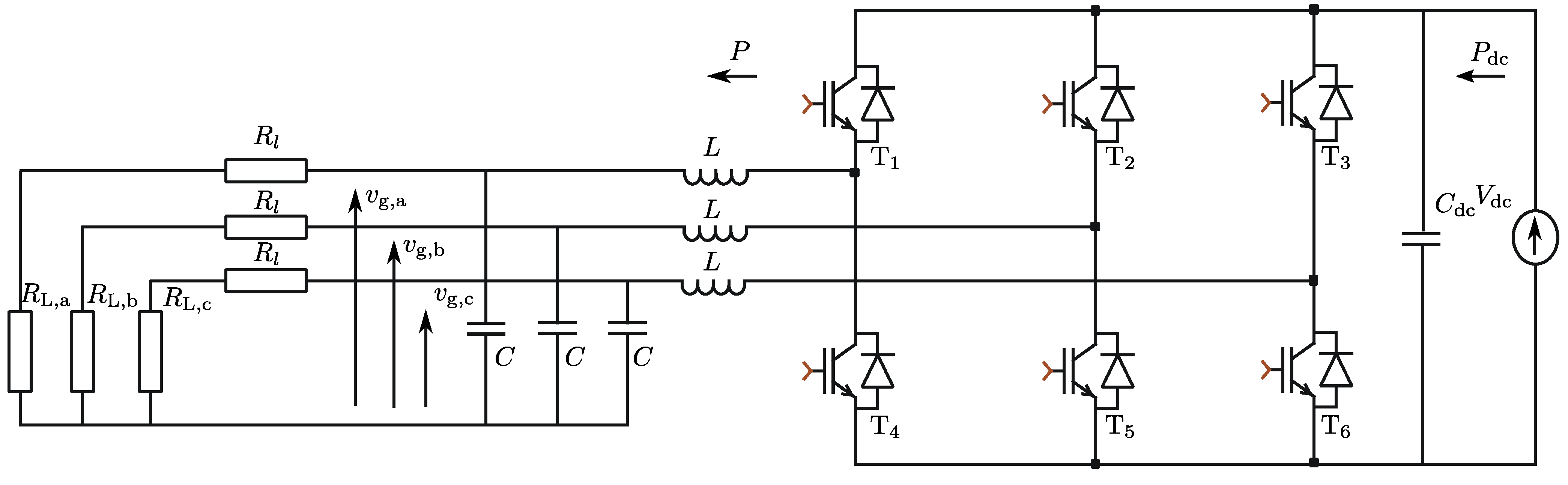
For this purpose, one DG unit and an unbalanced load with a larger load in phase a than in the phases, b and c, are considered in an islanded microgrid depicted in Figure 3 ($R_{\mathrm{L},\mathrm{a}}<R_{\mathrm{L},\mathrm{b}/\mathrm{c}}$). The three-phase DG unit utilizes VBD control with $b=8$% and $R_{\mathrm{v}}=0\Omega$, including a distortion damping with factor $R_d$, to determine the reference voltage.

Figure 3. Islanded microgrid with three-phase inverter.

Figure 3. Islanded microgrid with three-phase inverter.

With the conventional VBD control method (CM), the three reference voltages have an equal amplitude and a 120-degree phase shift in case $R_{\mathrm{v}}=0\Omega$. Hence, in the considered network, the current, $i_a$, will be higher than $i_b$ and $i_c$.

In the CW variant, the current, $i_a$, will be even larger, because of the additional contribution in the weakest phase, a. In this case, the VUF at the load terminals will, thus, be lower than in the CM case (higher $i_a$ combined with lower $R_a$). This lower unbalance factor is beneficial for, e.g., induction machines. However, for the same amount of delivered active power, the line losses will be significantly larger as the current unbalance factor, CUF, of the current in the lines is higher. The VUF at the DG unit terminals will be higher than in the CM case. In summary, the CW variant is beneficial for the VUF near the loads. It is disadvantageous for the VUF of the DG unit’s terminal voltage and the CUF, hence for line losses in the microgrid. Furthermore, the loading is more unevenly spread over the three phases of the DG unit than in the CM.

In the RU variant, the current, $i_a$, will be lower than in the CM. Hence, the loading of the DG unit will be more evenly shared between its three phases. Subsequently, the DG unit can inject more power in the grid without increasing the ratings of its inverter. The RU variant is good for the CUF in the lines, hence for the line losses. However, the VUF near the load will be higher than in the CM and CW case.

On overview of the advantages and disadvantages of the three methods is given in Table 1. The choice between RU and CW is dependent on the objectives in the case that a single DG unit is considered. Note that the RU method adds damping to the system (resistive behavior), while for the CW method, careful attention should be paid to the microgrid stability. For this, root locus analysis is often used, such as [23].

Table 1. Islanded microgrid, one DG unit. RU, resistive for unbalance; CW, contribution in the weakest phase; CM, Conventional Method.

Parameter	RU method	CW method	CM
Current unbalance, line losses	+	−	0
Voltage unbalance of load	−	+	0
Equalization of power in phases of DG	+	−	0
Voltage unbalance of DG units	−	−	+

Table 1. Islanded microgrid, one DG unit. RU, resistive for unbalance; CW, contribution in the weakest phase; CM, Conventional Method.

Parameter	RU method	CW method	CM
Current unbalance, line losses	+	−	0
Voltage unbalance of load	−	+	0
Equalization of power in phases of DG	+	−	0
Voltage unbalance of DG units	−	−	+

4.2. Grid-Connected Microgrid, One DG Unit

In the grid-connected case with the grid-forming control strategy of the DG unit (which has the advantage that the same controller can be used both in grid-connected and islanded mode), the CW method supports the weakest phase. Subsequently, the utility network can provide a more balanced current. This is beneficial for the utility network, as the unbalance remains local, inside the microgrid (Table 2). The RU method achieves a more balanced current in the section between the DG unit and the load. However, as the VUF at the DG unit’s and load’s terminal voltages are higher, the utility needs to deliver a more unbalanced current. The effect on the losses in the microgrid depends, thus, on the configuration.

Table 2. Grid-connected microgrid, one DG unit.

Parameter	RU method	CW method	CM
Current unbalance of utility grid current	−	+	0
Voltage unbalance of load	−	+	0
Equalization of power in phases of DG	+	−	0

Table 2. Grid-connected microgrid, one DG unit.

Parameter	RU method	CW method	CM
Current unbalance of utility grid current	−	+	0
Voltage unbalance of load	−	+	0
Equalization of power in phases of DG	+	−	0

4.3. Islanded Microgrid: Unbalance Sharing

For analysis of the sharing of unbalance between multiple DG units, a simple islanded microgrid consisting of two DG units and an unbalanced load is considered. In the CM, both DG units deliver a balanced voltage; hence, most of the unbalanced current needs to be provided by the DG unit that is electrically closest to the unbalanced load. Hence, this unbalance sharing is not actively controlled. By properly setting the parameter, $R_d$, the sharing between the DG units can be altered. The unit with the lower $R_d$ will be burdened with most of the unbalance. The effect on the CUF and the VUF depends on the configuration of the microgrid and the chosen $R_d$ values.

For comparing the three methods, Table 1 remains valid. By lowering the $R_d$ of one DG unit, this unit will contribute more in feeding the unbalance, compared to the DG unit with high $R_d$, which will deliver less of the unbalance.

4.4. Discussion

In grid-connected mode, the CW variant is generally most beneficial from the utilities point of view. In the islanded mode with one grid-forming DG unit, the choice between the CW and RU methods depends on the goals set. Generally, the unbalance factor near the loads is most important, leading to the CW variant as the best option. However, the RU variant achieves less line losses and a more even power sharing between the three phases of the DG unit, leading to less overrating of this unit. As will be shown further, the RU variant, providing a positive resistance, includes additional damping in the system. Therefore, in the case that multiple DG units in islanded microgrids are considered, the RU method is generally most effective for this stability reason. Both the RU and CW methods enable actively influencing of the unbalance sharing between different DG units.

5. Value of the Distortion Damping Resistance, $R_d$: Simulation Study

In the previous section, a qualitative comparison between the three methods, $R_d=0\Omega$, $R_d>0\Omega$ and $R_d<0\Omega$, is given. When tuning the exact value of $R_d$, one should take into account the line resistance of the grid (here, low-voltage, thus mainly resistive, microgrids are considered). Generally, a good value of $R_d$ is one in the same order of magnitude as the line resistance in the case of urban grids. In the case of rural grids, the effect of the unbalance sharing is sufficiently clear if the value of $R_d$ is in the same order of magnitude as the virtual resistance, $R_{\mathrm{v}}$, which generally is approximately equal to a few times the value of the line resistance, $R_{\mathrm{l}}$. Generally, no $R_{\mathrm{v}}$ is required if $R_{\mathrm{l}}>1\Omega$ (rural grids), while the control loop with $R_v$ is included when $R_{\mathrm{l}}<1\Omega$ (urban grids). In the case multiple DG units are considered and the contribution of the provision of unbalance is to be determined, it is more important to take into account all DG units for tuning the values of $R_d$.

In this section, the three theoretical cases described above are analyzed. First, an islanded microgrid with one DG unit is considered (see Section 4.1). The CM, CW and RU methods are compared. Next, a grid-connected microgrid is briefly discussed (see Section 4.2). Third, the unbalance sharing between multiple DG units in islanded mode is considered (see Section 4.3). Finally, a dynamic simulation is included.

5.1. Islanded Microgrid, One DG Unit

In this case, the islanded microgrid of Figure 3 as described above is considered. Purely resistive line parameters, $R_{\mathrm{l}}$, are assumed, as low-voltage networks are studied [5,24]. In purely resistive networks, the active power is linked with the grid voltage, while in inductive networks, a well-known reactive power/grid voltage linkage exists. Generally, the R/X (the resistive versus inductive part of the line impedance) value in low-voltage microgrids is sufficiently high, such that the voltage is predominantly linked with the active power. In [25], it is concluded that the effect of a realistic $R/X$ on the VBD control is limited, even more so when including virtual resistance in the microgrid lines, as the real R/X seen by the DG units becomes [($R+R_v)/X$]. For these reasons, this is not considered in this paper; purely line resistances are assumed, i.e., $R+R_v$ is sufficiently larger than X. The load is a grounded star-connection of $20\Omega$ in phase a and $400\Omega$ in phases b and c. The nominal power of the DG unit equals 2.5 kW; the unit has a constant-power band b of 8%, representing a slightly dispatchable DG unit. Small-scale microgrids are often burdened with even more unbalance problems compared to the conventional networks, because the small amount of single phase loads balance each other out only a little bit when there are a small number of loads. Hence, in the simulations, the unbalance is exaggerated, such that the unbalance mitigation becomes stringent. First, a rural network is considered, generally characterized by long lines. This allows for applying the VBD control without virtual resistance. The advantage of the latter is that the separate effect of $R_v$ and $R_d$ can be studied. Next, a more urban low-voltage microgrid is considered, where also virtual resistance is included. The separated effect of virtual and damping resistances becomes less clear, but the same conclusions are valid.

5.1.1. Without $R_v$

Table 3 shows the simulation results for the case of a relatively large line resistance $R_l$, i.e., a rural network, and, hence, without virtual resistance $R_v$. All three methods obtain a stable microgrid operation. As the voltage is close to the nominal voltage (in the $\pm 8$% voltage band), the delivered power of the DG unit equals 2.5 kW in all three cases. In the Conventional Method (CM), the DG unit, which is grid-forming, and, thus, voltage-controlled, generates a balanced output voltage. Hence, the VUF($v_{\mathrm{g}}$) is equal to zero zero. Therefore, the line current is largely unbalanced, acquiring a large CUF($i_{\mathrm{g}}$).

Table 3. One DG unit: CM (Conventional Method) versus RU versus the CW variant ($R_l=3\Omega$ and $R_v=0\Omega$). VUF, voltage unbalance factor; CUF, current unbalance factor.

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	2244	2299	2186
$P_b$,$P_c$ (W)	128	101	157
$V_{\mathrm{g},\mathrm{a}}$ (V)	227.2	229.9	224.2
$V_{\mathrm{g},\mathrm{b}}$,$V_{\mathrm{g},\mathrm{c}}$ (V)	227.2	201.4	251.6
VUF($v_{\mathrm{g}}$)	0	0.0450	0.0376
CUF($i_{\mathrm{g}}$)	0.8463	0.8636	0.8297
VUF($v_{\mathrm{L}}$)	0.0431	0	0.0788
losses (W)	295	301	287

Table 3. One DG unit: CM (Conventional Method) versus RU versus the CW variant ($R_l=3\Omega$ and $R_v=0\Omega$). VUF, voltage unbalance factor; CUF, current unbalance factor.

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	2244	2299	2186
$P_b$,$P_c$ (W)	128	101	157
$V_{\mathrm{g},\mathrm{a}}$ (V)	227.2	229.9	224.2
$V_{\mathrm{g},\mathrm{b}}$,$V_{\mathrm{g},\mathrm{c}}$ (V)	227.2	201.4	251.6
VUF($v_{\mathrm{g}}$)	0	0.0450	0.0376
CUF($i_{\mathrm{g}}$)	0.8463	0.8636	0.8297
VUF($v_{\mathrm{L}}$)	0.0431	0	0.0788
losses (W)	295	301	287

The RU method shows a resistive behavior towards unbalanced currents; hence, it generates some unbalance in the terminal voltage of the DG units (VUF$\left(v_{\mathrm{g}}\right)>0$) to counteract the unbalance in the line currents CUF($i_{\mathrm{g}}$). Consequently, the line losses are lower. Furthermore, the 2.5 kW output power is more evenly spread among the three phases of the DG unit, which is beneficial, first for the inverter losses, which depend on the current amplitude, and second, from a planning perspective, as the same amount of power can be delivered with a lower rating of the DG unit. A disadvantage is that the voltage unbalance near the load, thus the VUF($v_{\mathrm{L}}$), has increased.

The CW method lowers the VUF of the load, with the cost of increased unbalance in the line currents and, subsequently, larger line losses. Furthermore, the power is less evenly spread between the three phases of the DG unit, as illustrated in Table 3.

5.1.2. With $R_v$

In Table 4, resistive virtual impedance is added to the system to provide more damping when facing a lower line resistance, e.g., in urban microgrids with lower line resistance. The primary effect of adding $R_{\mathrm{v}}\ne 0$ is that also in the CM, the VUF($v_{\mathrm{g}}$) becomes a nonzero value. The table again shows that the CW method supports the weakest phase, which increases the unbalance in the output power of the DG unit. The VUF of the load is better in the CW method than in the RU case, but at the expense of more line losses.

Table 4. One DG unit: CM(Conventional Method) versus RU versus the CW variant ($R_l=0.3\Omega$ and $R_v=1.5\Omega$).

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	2240	2299	2178
$P_b$,$P_c$ (W)	130	101	161
VUF($v_{\mathrm{g}}$)	0.0223	0.0246	0.0609
CUF($i_{\mathrm{g}}$)	0.8532	0.8708	0.8369
VUF($v_{\mathrm{L}}$)	0.0268	0.0198	0.0653
losses (W)	33.3	34.1	32.4

Table 4. One DG unit: CM(Conventional Method) versus RU versus the CW variant ($R_l=0.3\Omega$ and $R_v=1.5\Omega$).

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	2240	2299	2178
$P_b$,$P_c$ (W)	130	101	161
VUF($v_{\mathrm{g}}$)	0.0223	0.0246	0.0609
CUF($i_{\mathrm{g}}$)	0.8532	0.8708	0.8369
VUF($v_{\mathrm{L}}$)	0.0268	0.0198	0.0653
losses (W)	33.3	34.1	32.4

The effect of including a resistive virtual output impedance, $R_v$, in the VBD control is that it provides additional damping in order to acquire a stable system operation despite the low line resistances. Such low $R_l$ indeed implies that a low voltage change could lead to a relatively large variation in the power flow, which makes the system difficult to stabilize.

5.1.3. Discussion

In this paragraph, the theoretical statements of Section 4.1 are validated. Without additional control loops, the conventional VBD control method, i.e., CM, can achieve a stable three-phase microgrid operation, but the unbalance cannot be actively handled. A positive distortion damping resistance, $R_d$, in the RU method emulates a resistive behavior of the DG unit towards unbalance, lower current imbalance in the lines and, hence, lower line losses. Furthermore, the RU method spreads the output power more evenly over the three phases of the DG unit, at the expense of the larger VUF of the load. A negative $R_d$ in the CW method better mitigates the voltage unbalance of the loads, at the expense of larger line losses and the output power of the DG unit being more unevenly spread between the three phases, which was also expected in Section 4.1; see Table 1.

5.2. Grid-Connected Microgrid, One DG Unit

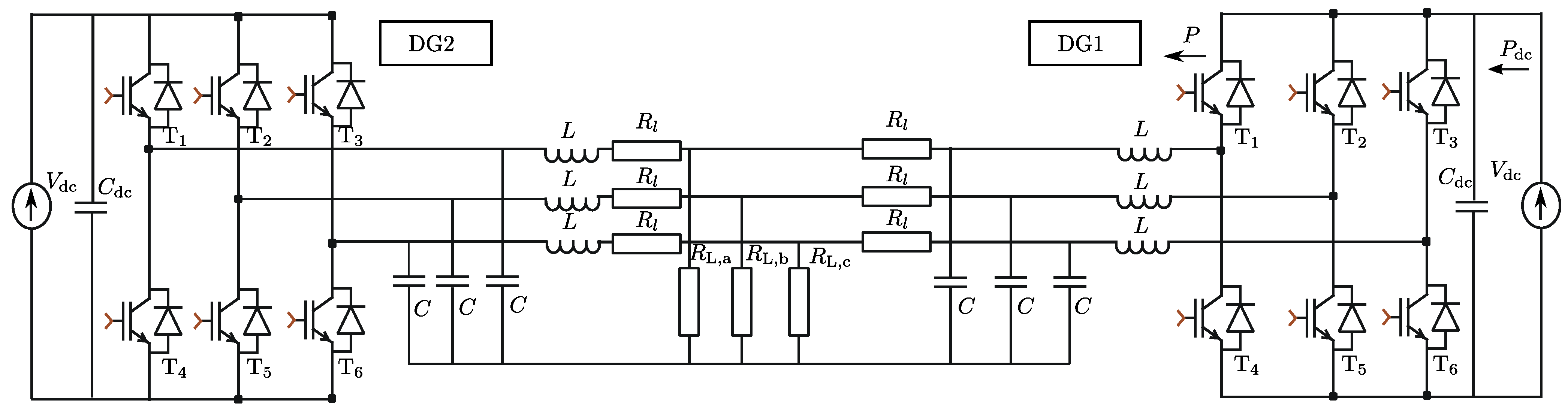
In this section, following Section 4.2, a grid-connected microgrid is studied. From a theoretical point of view, the goals of the unbalance mitigation scheme is to mitigate the unbalance seen by the utility grid, as opposed to the case in Section 4.1 and Section 5.1. The here-considered microgrid consists of the same grid as previously, with the load connected to a three-phase utility grid. The grid is modeled as a strong three-phase balanced voltage source generating a 50 Hz phase voltage of 230 V rms. The microgrid topology is depicted in Figure 4, but with the three-phase grid as described above instead of DG2. The DG unit’s nominal power equals 2.5 kW, and it has a constant-power band of 8%. The advantage of using the VBD control strategy, RU, CW and CM, is that the microgrid can be controlled with the same control strategy in islanded and grid-connected mode [26].

Figure 4. Islanded microgrid with two three-phase inverters.

Figure 4. Islanded microgrid with two three-phase inverters.

Table 5 shows that the CW method supports the grid, which has to deliver less of the unbalanced power as the DG units inject more power in the phase with the largest load. Subsequently, lower line losses are obtained in the line segment between the utility and the load. The load voltage is better balanced at the expense of higher CUF in the grid current injected by the DG unit, hence larger line losses in the section between load and DG unit.

Table 5. Grid-connected microgrid and one DG unit: CM(Conventional Method) versus RU versus the CW variant (Rural: $R_l=3\Omega$; $R_{\text{grid}}=2\Omega$; $R_v=0\Omega$).

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	1500	2695	1224
$P_b$, $P_c$ (W)	500	−98	638
VUF($v_{\mathrm{g}}$)	0	0.0456	0.0108
CUF($i_{\mathrm{g}}$) - DG unit	0.3996	1.1355	0.2461
CUF($i_{\mathrm{n}}$) - grid	0.7894	0.6357	0.8675
VUF($v_{\mathrm{L}}$)	0.0183	0	0.0226
losses (W) L to DG	144	326	124
losses (W) U to L	27.3	3.1	41.1

Table 5. Grid-connected microgrid and one DG unit: CM(Conventional Method) versus RU versus the CW variant (Rural: $R_l=3\Omega$; $R_{\text{grid}}=2\Omega$; $R_v=0\Omega$).

Parameter method	$R_d=0$ (CM)	$R_d=-3\Omega$ (CW)	$R_d=3\Omega$ (RU)
$P_a$ (W)	1500	2695	1224
$P_b$, $P_c$ (W)	500	−98	638
VUF($v_{\mathrm{g}}$)	0	0.0456	0.0108
CUF($i_{\mathrm{g}}$) - DG unit	0.3996	1.1355	0.2461
CUF($i_{\mathrm{n}}$) - grid	0.7894	0.6357	0.8675
VUF($v_{\mathrm{L}}$)	0.0183	0	0.0226
losses (W) L to DG	144	326	124
losses (W) U to L	27.3	3.1	41.1

The adverse VUF of the load is a cost to be paid with positive $R_d$ for lowering the line losses in the segment between the DG unit and the load and improving the DG unit’s operation (more even distribution of output power between phases). In the RU method, the unbalanced currents are, to a large extent, delivered by the utility network (CUF($i_{\mathrm{n}}$)). In the CW method, these are provided by the DG unit inside the microgrid. From the utilities point of view, this is a significant benefit, as the microgrid can be regarded as a controllable entity mitigating current unbalance. Vice versa, the adverse CUF of the DG units output currents (CUF($i_{\mathrm{g}}$)) and increased ratings is a cost to be paid with negative $R_d$ for improving the voltage unbalance near the loads and mitigating the unbalance of the utility.

5.3. Islanded Microgrid, Unbalance Sharing

In this paragraph, the unbalance sharing between multiple DG units in an islanded microgrid is considered. First, a symmetrical microgrid is considered. The CM, CW and RU methods are compared in Table 6 and Table 7. Only two DG units are considered, but the conclusions can be extrapolated for multiple units. Second, it is shown that by choosing a proper distortion damping resistance, $R_d$, the unbalance sharing between DG units can be actively controlled in Table 8. Third, an asymmetrical microgrid is studied in Table 9 to Table 10 in order to illustrate that with the CM, the microgrid configuration determines the unbalance sharing, whereas the CW and RU methods achieve an active control of this. Fourth, in Table 11, DG units of different ratings are included, showing that a proper setting of $R_d$ according to the units’ ratings allows for a better sharing of the unbalance.

For analyzing the unbalance sharing, an islanded microgrid consisting of two DG units and an unbalanced load, as depicted in Figure 4, is considered. The load has 10 Ω in phase a and 400 Ω in phases b and c. Both DG units have a constant-power band of 8% and have equal ratings $P_{\text{dc},\text{nom}}=2500$ W, except when explicitly stated otherwise. The line impedances between the DG units and the load are sufficiently large, such that the effects of $R_v$ and $R_d$ can be separated. An analysis of a microgrid with smaller line impedances is given in Table 4.

5.3.1. Symmetrical Microgrid: Comparison CW and RU Method

In the first case, a symmetrical line configuration is considered, i.e., $R_{\mathrm{l},1}=R_{\mathrm{l},2}$. Furthermore, the DG units are symmetrical, i.e., equal ratings and equal parameters. The two DG units give equal results; hence, the tables only show the results of one unit.

Table 6 compares the CM, CW and RU methods in this symmetrical microgrid. The RU method clearly achieves lower line losses and a better balancing of the output current between the three phases compared with the CM. However, the VUF of the load is worse. The CW method proves to be unstable in this case, as a negative $R_d$ lowers the damping of the system.

Table 6. Islanded microgrid with two DG units: CM versus RU versus the CW variant ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_d=0$	$R_d=3\Omega$	$R_d=-3\Omega$
	DG 1 and 2	DG 1 and 2	unstable
$P_a$ (W)	2364	2282	-
$P_b$, $P_c$ (W)	68	84	-
$V_{\mathrm{g},\mathrm{a}}$ (V)	233.1	229.1	-
$V_{\mathrm{g},\mathrm{b}}$, $V_{\mathrm{g},\mathrm{c}}$ (V)	233.1	258.0	-
VUF($v_{\mathrm{g}}$)	0	0.0388	-
CUF($i_{\mathrm{g}}$)	0.9124	0.9063	-
VUF($v_{\mathrm{L}}$)	0.0443	0.0811	-
losses (W)	310.3	298.8	-

Table 6. Islanded microgrid with two DG units: CM versus RU versus the CW variant ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_d=0$	$R_d=3\Omega$	$R_d=-3\Omega$
	DG 1 and 2	DG 1 and 2	unstable
$P_a$ (W)	2364	2282	-
$P_b$, $P_c$ (W)	68	84	-
$V_{\mathrm{g},\mathrm{a}}$ (V)	233.1	229.1	-
$V_{\mathrm{g},\mathrm{b}}$, $V_{\mathrm{g},\mathrm{c}}$ (V)	233.1	258.0	-
VUF($v_{\mathrm{g}}$)	0	0.0388	-
CUF($i_{\mathrm{g}}$)	0.9124	0.9063	-
VUF($v_{\mathrm{L}}$)	0.0443	0.0811	-
losses (W)	310.3	298.8	-

In Table 7, exactly the same configuration is considered, but with a lower $R_d$. Clearly, the RU method with low $R_d$ achieves less of the valued benefits compared to having a large $R_d$, i.e., line loss reduction and equalizing of the DG unit’s output power between the phases. However, the VUF at the load terminals is better. The choice of $R_d$ hence provides a trade-off between unbalance in the grid currents and in the load voltage. The CW method is stable in this case. It achieves a better voltage unbalance mitigation of the load with the cost of increased line losses.

Table 7. Islanded microgrid with two DG units: RU versus the CW variant ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_d=1\Omega$	$R_d=-1\Omega$
	DG 1 and 2	DG 1 and 2
$P_a$ (W)	2353	2373
$P_b$, $P_c$ (W)	74	64
$V_{\mathrm{g},\mathrm{a}}$ (V)	232.6	233.6
$V_{\mathrm{g},\mathrm{b}}$, $V_{\mathrm{g},\mathrm{c}}$ (V)	242.4	223.7
VUF($v_{\mathrm{g}}$)	0.0137	0.0145
CUF($i_{\mathrm{g}}$)	0.9103	0.9095
VUF($v_{\mathrm{L}}$)	0.0573	0.0304
losses (W)	308.7	313.2

Table 7. Islanded microgrid with two DG units: RU versus the CW variant ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_d=1\Omega$	$R_d=-1\Omega$
	DG 1 and 2	DG 1 and 2
$P_a$ (W)	2353	2373
$P_b$, $P_c$ (W)	74	64
$V_{\mathrm{g},\mathrm{a}}$ (V)	232.6	233.6
$V_{\mathrm{g},\mathrm{b}}$, $V_{\mathrm{g},\mathrm{c}}$ (V)	242.4	223.7
VUF($v_{\mathrm{g}}$)	0.0137	0.0145
CUF($i_{\mathrm{g}}$)	0.9103	0.9095
VUF($v_{\mathrm{L}}$)	0.0573	0.0304
losses (W)	308.7	313.2

5.3.2. Symmetrical Microgrid Configuration: Affecting Unbalance Sharing by Setting Different $R_d$

In this section, the effect of setting different $R_d$ in the DG units in order to affect their contribution in the unbalance sharing is studied.

Table 8 shows the case where the $R_{\mathrm{d}}$ of the two DG units differs, again with $b=8$%. The first DG unit does not incorporate the resistive behavior, and hence, $R_{d,DG1}=0\Omega$. The second DG unit utilizes the RU or CW method. The DG unit with the lowest $R_d$ will be burdened with most of the unbalance. In this way, the unbalance sharing can be affected by the control strategy. The choice between positive and negative $R_d$ values for all DG units is the same as for the case with one DG unit, taking into account the lower damping of the system with negative $R_d$.

Table 8. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{d}}$ ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_{d,DG1}=0\Omega$		$R_{d,DG1}=0\Omega$
	$R_{d,DG2}=3\Omega$		$R_{d,DG1}=-3\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	2898	1794	854	3889
$P_b$, $P_c$ (W)	−201	355	852	−663
VUF($v_{\mathrm{g}}$)	0	0.0273	0	0.0934
CUF($i_{\mathrm{g}}$)	1.2361	0.5970	0.0286	2.1655
VUF($v_{\mathrm{L}}$)	0.0573		0.0019
losses (W) L to DG	450.4	203.9	151.6	829.4

Table 8. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{d}}$ ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_{d,DG1}=0\Omega$		$R_{d,DG1}=0\Omega$
	$R_{d,DG2}=3\Omega$		$R_{d,DG1}=-3\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	2898	1794	854	3889
$P_b$, $P_c$ (W)	−201	355	852	−663
VUF($v_{\mathrm{g}}$)	0	0.0273	0	0.0934
CUF($i_{\mathrm{g}}$)	1.2361	0.5970	0.0286	2.1655
VUF($v_{\mathrm{L}}$)	0.0573		0.0019
losses (W) L to DG	450.4	203.9	151.6	829.4

In the RU method of the second DG unit, this unit clearly bares less of the unbalance. In the CW method, this unit bares more of the unbalance and, like in the case of one DG unit, the VUF of the load has improved with the cost of increased line losses. The unbalance sharing can, thus, effectively be controlled by choosing a proper value of $R_d$.

5.3.3. Asymmetrical Microgrid Configuration: Comparison of the CW and RU Methods

In this section, it is illustrated that the line impedance determines the unbalance sharing in the CM, whereas with the CW and RU methods, this sharing can be managed by the control strategy. In this case, the line resistances near the two DG units are different. The results are depicted in Table 9 and Table 10. A resistive virtual impedance is included to add damping in the face of the lower line resistance $R_l=0.3\Omega$.

Table 9. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{l}}$, part 1 ($R_{\mathrm{l},1}=0.3\Omega$; $R_{\mathrm{l},2}=3\Omega$; $R_v=3\Omega$).

Parameter	$R_d=0\Omega$		$R_d=3\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	2620	1806	2,151	1,734
$P_b$, $P_c$ (W)	−60	215	52	117
VUF($v_{\mathrm{g}}$)	0.0574	0.0290	0.0913	0.0619
CUF($i_{\mathrm{g}}$)	1.0574	0.7289	0.9463	0.8475
VUF($v_{\mathrm{L}}$)	0.0605		0.0943
losses (W) L to DG	47.5	192.8	36.8	196.1

Table 9. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{l}}$, part 1 ($R_{\mathrm{l},1}=0.3\Omega$; $R_{\mathrm{l},2}=3\Omega$; $R_v=3\Omega$).

Parameter	$R_d=0\Omega$		$R_d=3\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	2620	1806	2,151	1,734
$P_b$, $P_c$ (W)	−60	215	52	117
VUF($v_{\mathrm{g}}$)	0.0574	0.0290	0.0913	0.0619
CUF($i_{\mathrm{g}}$)	1.0574	0.7289	0.9463	0.8475
VUF($v_{\mathrm{L}}$)	0.0605		0.0943
losses (W) L to DG	47.5	192.8	36.8	196.1

Table 10. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{l}}$, part 2 ($R_{\mathrm{l},1}=0.3\Omega$; $R_{\mathrm{l},2}=3\Omega$; $R_v=3\Omega$).

Parameter	$R_d=-3\Omega$
	DG 1	DG 2
$P_a$ (W)	3577	1125
$P_b$, $P_c$ (W)	−539	688
VUF($v_{\mathrm{g}}$)	0.0016	0
CUF($i_{\mathrm{g}}$)	1.6299	0.1751
VUF($v_{\mathrm{L}}$)	0.0089
losses (W) L to DG	84.6	130.0

Table 10. Islanded microgrid: power sharing between two DG units with different $R_{\mathrm{l}}$, part 2 ($R_{\mathrm{l},1}=0.3\Omega$; $R_{\mathrm{l},2}=3\Omega$; $R_v=3\Omega$).

Parameter	$R_d=-3\Omega$
	DG 1	DG 2
$P_a$ (W)	3577	1125
$P_b$, $P_c$ (W)	−539	688
VUF($v_{\mathrm{g}}$)	0.0016	0
CUF($i_{\mathrm{g}}$)	1.6299	0.1751
VUF($v_{\mathrm{L}}$)	0.0089
losses (W) L to DG	84.6	130.0

Table 9 shows that with $R_d=0\Omega$, with the CM, the unit that is electrically closest to the load (here, DG 1) bares significantly more of the unbalance. This sharing is thus not actively controlled, but is determined by the microgrid configuration. The VUF of the DG units’ terminal voltage is not zero, because $R_v$ has a nonzero value. With the RU method, the unbalance is more evenly shared between the two DG units. The CW method in Table 10 leads to a worse sharing of unbalance, i.e., DG 1 bares even more of the unbalance, but a better VUF of the load voltage.

5.3.4. Symmetrical Microgrid Configuration: Different Ratings of DG Units

In this section, it is shown that the unbalance sharing can be controlled to be according to the ratings of the DG units.

In this case, the nominal power of the DG units equals 1.6 and 3.2 kW, respectively. The results are given in Table 11. Despite the different ratings, the DG units with CM are evenly burdened with the unbalance, because of the symmetric microgrid configuration. The inverse components of the delivered grid currents of the two DG units are about equal, as:

$$\begin{array}{cc}\hfill \text{CUF}\left(i_{\mathrm{l},\text{DG}1}\right)/\text{CUF}\left(i_{\mathrm{l},\text{DG}2}\right)& \approx 2=P_{\text{nom},\text{DG}2}/P_{\text{nom},\text{DG}1}\hfill \end{array}$$

(10)

Table 11. Islanded microgrid: power sharing between two DG units with different ratings ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_{d,DG1}=0\Omega$		$R_{d,DG1}=2\Omega$
	$R_{d,DG2}=0\Omega$		$R_{d,DG1}=1\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	1975	2549	1795	2707
$P_b$, $P_c$ (W)	−186	324	−97	245
VUF($v_{\mathrm{g}}$)	0	0	0.0243	0.0148
CUF($i_{\mathrm{g}}$)	1.3296	0.6936	1.1573	0.7764
VUF($v_{\mathrm{L}}$)	0.0443		0.0628
losses (W) L to DG	237.6	377.8	198.9	413.9

Table 11. Islanded microgrid: power sharing between two DG units with different ratings ($R_l=3\Omega$; $R_v=0\Omega$).

Parameter	$R_{d,DG1}=0\Omega$		$R_{d,DG1}=2\Omega$
	$R_{d,DG2}=0\Omega$		$R_{d,DG1}=1\Omega$
	DG 1	DG 2	DG 1	DG 2
$P_a$ (W)	1975	2549	1795	2707
$P_b$, $P_c$ (W)	−186	324	−97	245
VUF($v_{\mathrm{g}}$)	0	0	0.0243	0.0148
CUF($i_{\mathrm{g}}$)	1.3296	0.6936	1.1573	0.7764
VUF($v_{\mathrm{L}}$)	0.0443		0.0628
losses (W) L to DG	237.6	377.8	198.9	413.9

In the second column of Table 11, the parameter, $R_d$, is set differently for the DG units. This illustrates that the setting of $R_d$ can induce an unbalance sharing, which can be actively affected by the control strategy.

5.4. Dynamic Simulation

A dynamic simulation with varying load, DG output and distortion damping resistance, $R_d$, is included. The microgrid configuration is depicted in Figure 4.

Both DG units are rated at 3.5 kW and have a constant-power band of 8%. From $0<t<0.8$ s, $R_d=3\Omega$ for both units, and the load is balanced and equal to $20\Omega$ in each phase. At $t=0.8$ s, the load becomes unbalanced, as in phase a, an additional $20\Omega$ load turns on in parallel with the first one. At $t=1.6$ s, the output of DG 1 increases with 1 kW. From $t=2.4$ s on, the $R_d$ of DG 1 becomes zero, and at $t=3.2$ s, the output of DG 1 drops again to its nominal value. 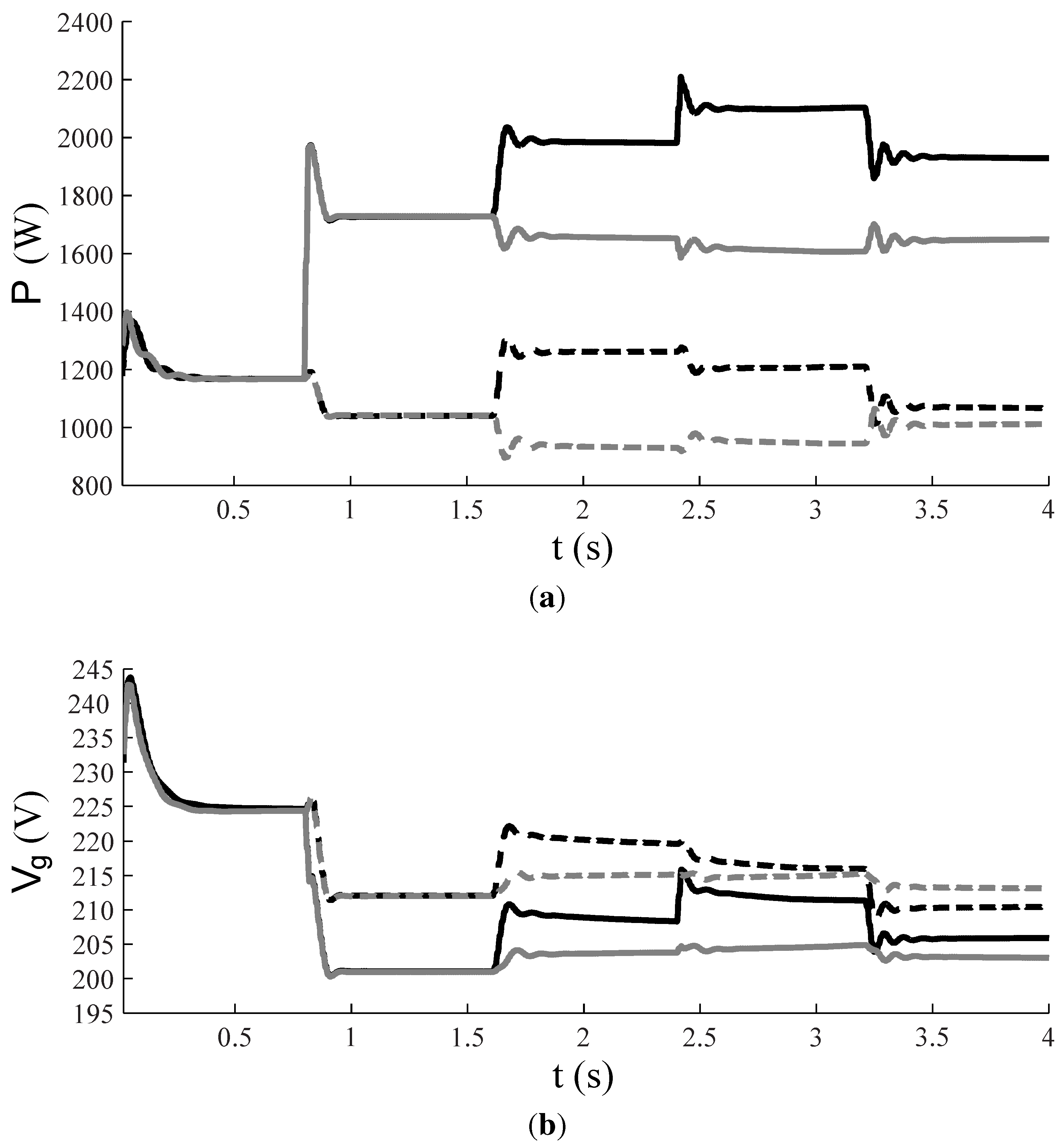Figure 5 shows the obtained results.

Figure 5. Dynamic simulation: (a) Output power P; (b) Terminal voltage $V_{\mathrm{g}}$. (— = DG 1/ phase a; - - -= DG 1/phases b and c; — (gray)= DG 2/phase a, - - - (gray)= DG 2 /phases b and c).

Figure 5. Dynamic simulation: (a) Output power P; (b) Terminal voltage $V_{\mathrm{g}}$. (— = DG 1/ phase a; - - -= DG 1/phases b and c; — (gray)= DG 2/phase a, - - - (gray)= DG 2 /phases b and c).

In conclusion, a stable three-phase microgrid operation is shown despite the large unbalance in the system. Relatively small transients are obtained despite the large variations in the small-scale islanded microgrid. After the $R_d$ decrease (after 2.4 s) in DG 1, this unit is clearly more burdened with the delivery of unbalanced currents. Hence, by tuning the distortion damping resistance, the contribution of each DG unit in the unbalance sharing can be affected.

Previously, the assumption of purely resistive lines was made. In Figure 6, the results are shown for the same case as above, but with additional inductance in the lines, such that R/X = 1 (which is unrealistically low in a low-voltage microgrid). Still, a stable microgrid operation is obtained. The transients take slightly less time as the total line impedance becomes $\sqrt{2}$ times the previous line resistance. However, the settling time of voltage in Figure 6b is slightly longer. As assumed above, it is shown here that the effect of not purely resistive lines on the VBD control operation and the unbalance is limited.

Figure 6. Dynamic simulation with inductance in the lines: (a) Output power P; (b) Terminal voltage $V_{\mathrm{g}}$. (— = DG 1/ phase a; - - -= DG 1/phases b and c; — (gray)= DG 2/phase a; - - - (gray)= DG 2 /phases b and c).

Figure 6. Dynamic simulation with inductance in the lines: (a) Output power P; (b) Terminal voltage $V_{\mathrm{g}}$. (— = DG 1/ phase a; - - -= DG 1/phases b and c; — (gray)= DG 2/phase a; - - - (gray)= DG 2 /phases b and c).

5.5. Discussion

When considering only one DG unit with distortion damping resistance, the CW method is generally most beneficial, but one should pay attention to this, as it provides less damping in the system. For achieving actively controlled unbalance sharing between multiple DG units, the RU method is generally most beneficial, mainly because of its damping effect. The unit with the smallest $R_d$ contributes most to the unbalance sharing.

6. Conclusions

In this paper, the VBD control is modified for application in three-phase networks. This controller achieves a stable three-phase islanded microgrid operation and has the same benefits as its single-phase variant. An additional control loop is added, with the distortion damping resistance as characterizing parameter, in order to actively control the effect of the DG units on the unbalance in the microgrid. A comparison is made between positive and negative values of this resistance. It is shown that the value of the distortion damping resistance can affect the voltage unbalance factor at the load and the line losses in the microgrid. A trade-off between these two parameters should be made. By properly setting the distortion damping resistance, e.g., according to the ratings of the DG units, the unbalance sharing between the DG units can be actively controlled.