Evaluation of Power Generation Efficiency of Cascade Hydropower Plants: A Case Study
Abstract
:1. Introduction
2. The Three Gorges and Gezhouba Cascade Complex
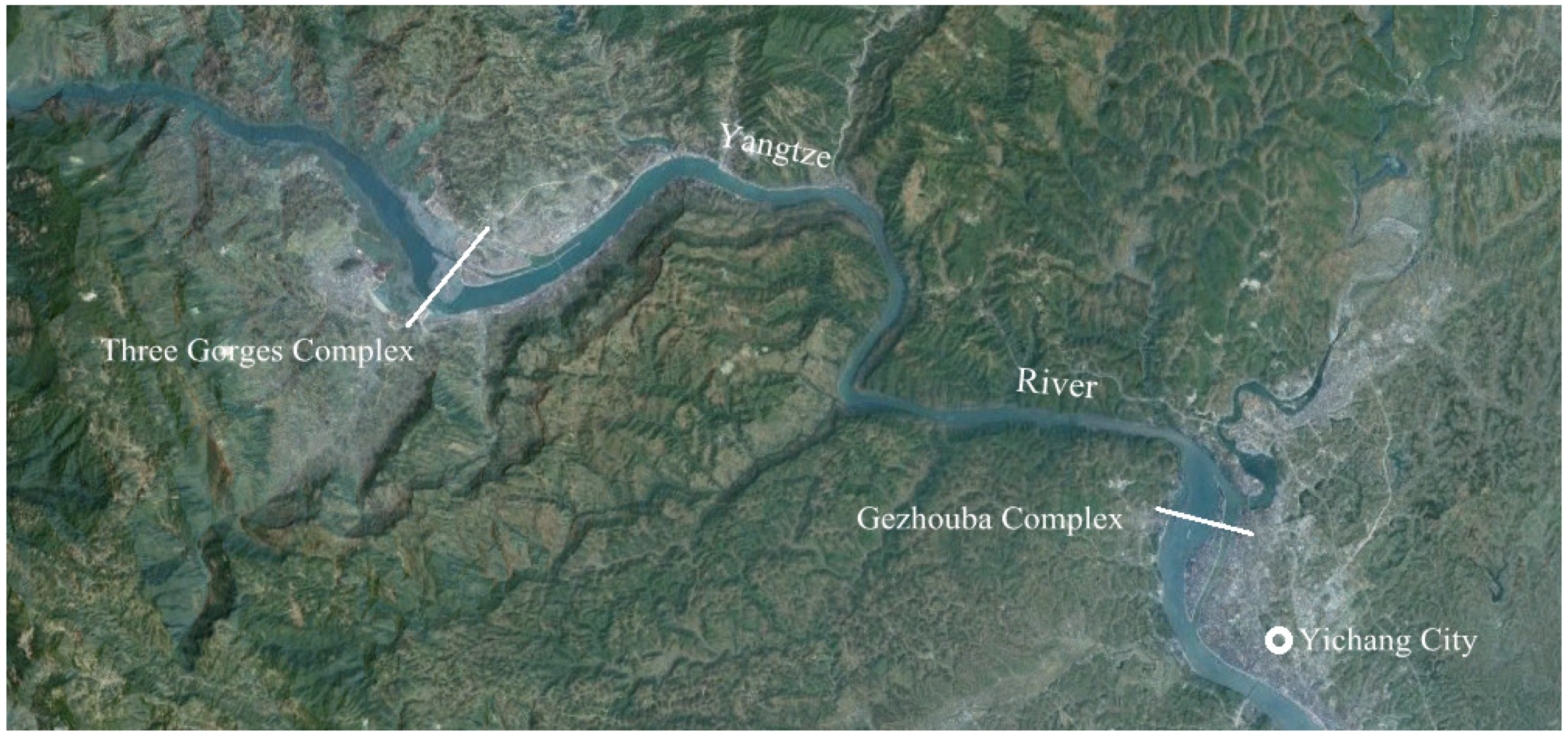
| Parameter | Unit | TGP | Gezhouba |
|---|---|---|---|
| Total storage | billion m3 | 39.3 | 1.58 |
| Flood control storage | billion m3 | 22.15 | - |
| Crest level | m | 185 | 70 |
| Normal pool level (NPL) | m | 175 | 66 |
| Flood control level (FCL) | m | 145.0 | - |
| Installed capacity | MW | 22,500 | 2,715 |
| Annual output | TWh | 88.2 | 15.7 |
| Reservoir regulation | - | Seasonal | Daily |
3. Methodology for the Evaluation of Power Generation Benefits
3.1. Integrated Evaluation Model
3.1.1. Potential Hydropower Output
3.1.2. Potential Increasing Percentage of Power Output
3.2. Sensitivity Analysis
3.2.1. Impact of Hydrological Forecast Quality
3.2.2. Impact of Flood Control
4. Results and Discussion
4.1. Integrated Evaluation of Power Generation Benefits for Joint Operation of the Three Gorges and Gezhouba Cascade Complex
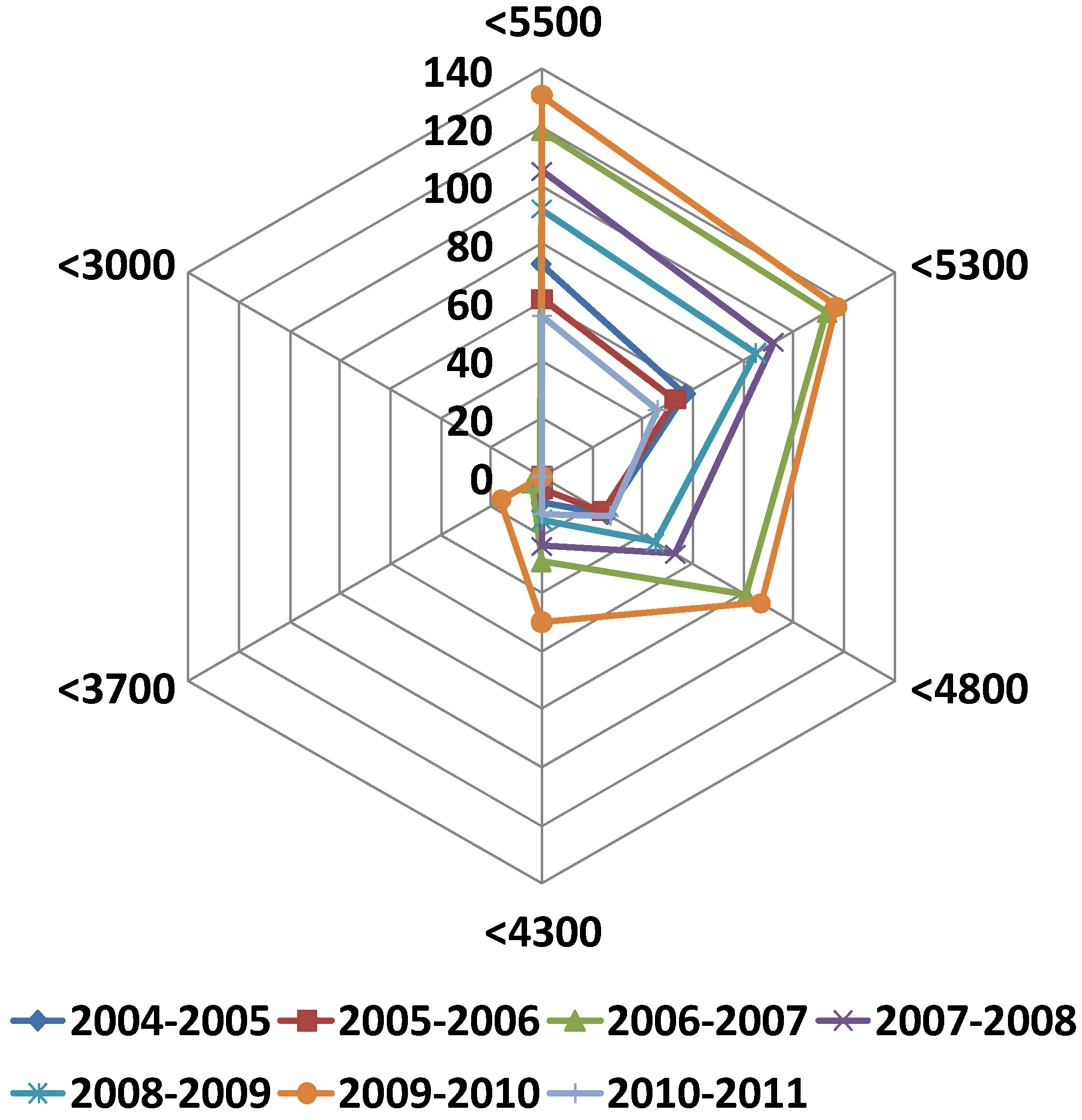
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|
| Three Gorges | Actual power output | 39.16 | 49.09 | 49.62 | 61.31 | 80.31 | 79.55 | 83.94 |
| Simulated max. power output | 42.40 | 54.98 | 54.70 | 64.55 | 86.65 | 84.64 | 87.73 | |
| Gezhouba | Actual power output | 17.01 | 16.25 | 14.53 | 15.46 | 17.05 | 16.15 | 16.10 |
| Simulated max. power output | 15.03 | 14.42 | 14.66 | 14.20 | 16.61 | 15.48 | 15.85 | |
| Cascade | Actual power output | 56.17 | 65.34 | 64.16 | 76.77 | 97.36 | 95.70 | 100.04 |
| Simulated max. power output | 57.43 | 69.40 | 69.36 | 78.75 | 103.26 | 100.13 | 103.59 | |
| Potential hydropower output | 1.27 | 4.06 | 5.21 | 1.98 | 5.90 | 4.43 | 3.55 | |
| Potential increasing percentage (δ) | 3.23% | 8.27% | 10.49% | 3.22% | 7.35% | 5.57% | 4.23% | |
4.2. Analysis of Influencing Factors
4.2.1. Impact of Hydrological Forecast Quality
| Year | Forecast time of 1-day | Forecast time of 2-day | Forecast time of 3-day | Forecast time of 4-day |
|---|---|---|---|---|
| 2004 | 0.94 | 0.90 | 0.84 | 0.80 |
| 2005 | 0.94 | 0.91 | 0.85 | 0.80 |
| 2006 | 0.94 | 0.91 | 0.85 | 0.82 |
| 2007 | 0.94 | 0.91 | 0.85 | 0.82 |
| 2008 | 0.94 | 0.92 | 0.86 | 0.82 |
| 2009 | 0.92 | 0.90 | 0.84 | 0.80 |
| 2010 | 0.95 | 0.92 | 0.86 | 0.83 |
| Average | 0.94 | 0.91 | 0.85 | 0.81 |
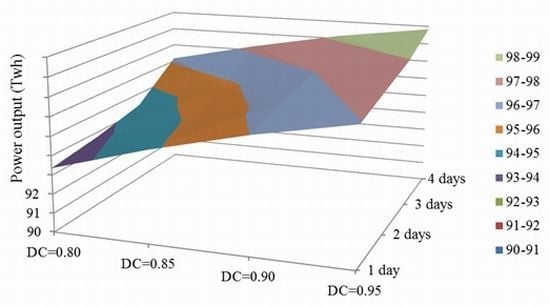
| Forecast time | DC = 0.80 | DC = 0.85 | DC = 0.90 | DC = 0.95 |
|---|---|---|---|---|
| 1-day | 93.37 | 94.80 | 96.00 | 96.96 |
| 2-day | 93.76 | 95.09 | 96.49 | 97.46 |
| 3-day | 94.33 | 95.77 | 96.98 | 97.95 |
| 4-day | 96.16 | 97.23 | 98.16 | 98.84 |
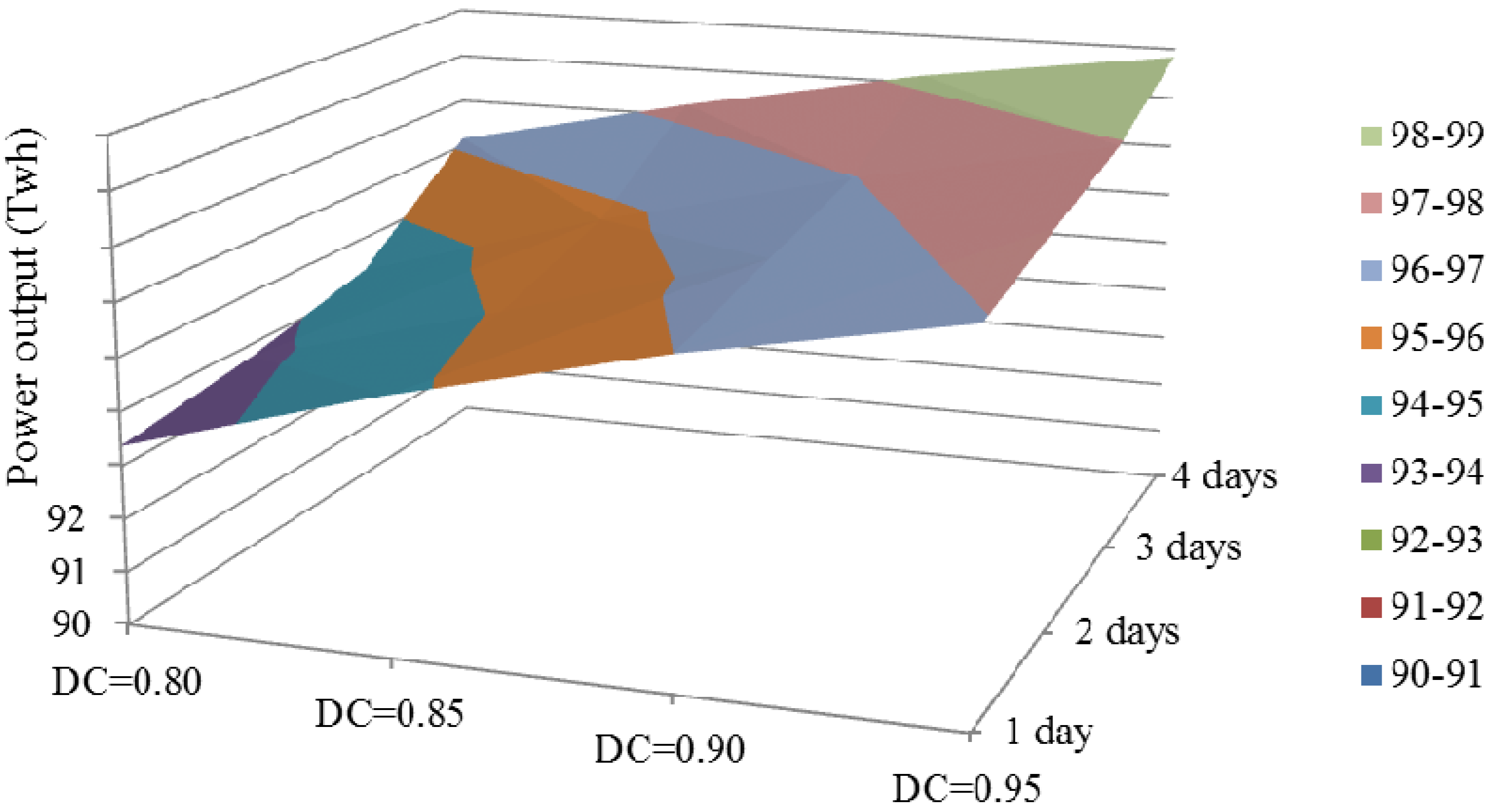
4.2.2. Impact of Flood Control Level
| FCL (m) | 2009 | 2010 | Typical wet year (1931) | Typical normal year (1906) | Typical dry year (1928) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SPO | δ | SPO | δ | SPO | δ | SPO | δ | SPO | δ | |
| 145* | 99.2 | - | 102.6 | - | 101.4 | - | 97.7 | - | 93.1 | - |
| 150 | 101.4 | 2.2% | 104.3 | 1.6% | 104.8 | 3.3% | 101.4 | 3.8% | 95.7 | 2.8% |
| 155 | 104.1 | 4.9% | 105.3 | 2.6% | 106.8 | 5.3% | 103.6 | 6.0% | 98.5 | 5.8% |
| 160 | 105.4 | 6.2% | 106.0 | 3.3% | 107.1 | 5.6% | 105.2 | 7.6% | 101.3 | 8.8% |
| 165 | 106.1 | 6.9% | 106.6 | 3.8% | 107.5 | 5.9% | 105.2 | 7.6% | 103.5 | 11.2% |
5. Conclusions
Acknowledgments
References
- Simonovic, S.P. Reservoir systems analysis: Closing gap between theory and practice. J. Water Resour. Plan. Manag. 1992, 3, 262–280. [Google Scholar] [CrossRef]
- Lenzen, M. Current state of development of electricity-generating technologies: A literature review. Energies 2010, 3, 462–591. [Google Scholar] [CrossRef]
- Yeh, W. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multi-reservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Stein, S.M.; Martin, B.; Stout, S.R. Evaluating Reservoir Operations in the Muskingum Basin. In Proceedings of the World Environmental and Water Resources Congress, Ahupua’a, HI, USA, 13–16 May 2008; pp. 1–10.
- Dai, H.C.; Dong, Q.J.; Cao, G.J. Status and progress of operation techniques integration on cascade project of Three Gorges and Gezhouba [in Chinese]. J. Sichuan Univ. Eng. Sci. Ed. 2009, 4, 1–7. [Google Scholar]
- Cao, G.J.; Cai, Z.G. The preliminary study on evaluation methods and its improvement of economical operation of hydropower station [in Chinese]. J. China Three Gorges Constr. 2008, 11, 16–23. [Google Scholar]
- Lu, Y.M.; Cao, G.J. Yangtze Three Gorges Project—Technology; [in Chinese]; China Water Conservancy and Hydropower Press: Beijing, China, 2009. [Google Scholar]
- Cai, Z.G.; Cao, G.J.; Zheng, Y. A new approach to assess the power-generating management for cascade hydropower plants [in Chinese]. J. Hydroelectr. Eng. 2011, 2, 15–19. [Google Scholar]
- Teasley, R.L.; McKinney, D.C. Calculating the benefits of transboundary river basin cooperation: Syr Darya Basin. J. Water Resour. Plan. Manag. 2011, 6, 481–490. [Google Scholar] [CrossRef]
- Liu, J.; Zuo, J.; Sun, Z.; Zillante, G.; Chen, X. Sustainability in hydropower development—A case study. Renew. Sustain. Energy Rev. 2013, 19, 230–237. [Google Scholar] [CrossRef]
- Zhang, Y.C. Principles Operation of Hydropower Stations; [in Chinese]; Huazhong University of Science and Technology Press: Wuhan, China, 1998. [Google Scholar]
- Spendley, W.; Hext, G.R.; Himsworth, F.R. Sequential application of simplex designs in optimization and evolutionary operation. Technometrics 1962, 4, 441–461. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Howsan, H.R.; Sancho, N.G.F. A new algorithm for the solution of multistate dynamic programming problems. Math. Program. 1975, 8, 104–116. [Google Scholar] [CrossRef]
- Turgeon, A. Optimal short-term hydro scheduling from the principle of progressive optimality. J. Water Resour. Res. 1981, 17, 481–486. [Google Scholar] [CrossRef]
- Guo, S.L.; Chen, J.H.; Li, Y.; Liu, P.; Li, T.Y. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang Cascade Reservoirs. Energies 2011, 4, 1036–1050. [Google Scholar] [CrossRef]
- The Ministry of Water Resources Conservancy Information Center (MWRCIC). Standard for Hydrological Information and Hydrological Forecasting (Chinese, SL250-2000); [in Chinese]; China Water Conservancy and Hydropower Press: Beijing, China, 2000; pp. 18–19. [Google Scholar]
- Zhao, Y.F.; Liu, Z.W.; Zhang, J.S. Discussion on dynamic limited flood water level control of Three Gorges Reservoir [in Chinese]. Hydropower Autom. Dam Monit. 2007, 1, 1–10. [Google Scholar]
- Liu, P.; Guo, S.L.; Wang, C.J.; Zhou, F. Optimization of limited water level in flood season and impounding scheme for reservoir in Three Gorges Project [in Chinese]. J. Hydraulic Eng. 2004, 7, 11–20. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zheng, Y.; Fu, X.; Wei, J. Evaluation of Power Generation Efficiency of Cascade Hydropower Plants: A Case Study. Energies 2013, 6, 1165-1177. https://doi.org/10.3390/en6021165
Zheng Y, Fu X, Wei J. Evaluation of Power Generation Efficiency of Cascade Hydropower Plants: A Case Study. Energies. 2013; 6(2):1165-1177. https://doi.org/10.3390/en6021165
Chicago/Turabian StyleZheng, Ying, Xudong Fu, and Jiahua Wei. 2013. "Evaluation of Power Generation Efficiency of Cascade Hydropower Plants: A Case Study" Energies 6, no. 2: 1165-1177. https://doi.org/10.3390/en6021165
APA StyleZheng, Y., Fu, X., & Wei, J. (2013). Evaluation of Power Generation Efficiency of Cascade Hydropower Plants: A Case Study. Energies, 6(2), 1165-1177. https://doi.org/10.3390/en6021165