Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor
Abstract
:1. Introduction
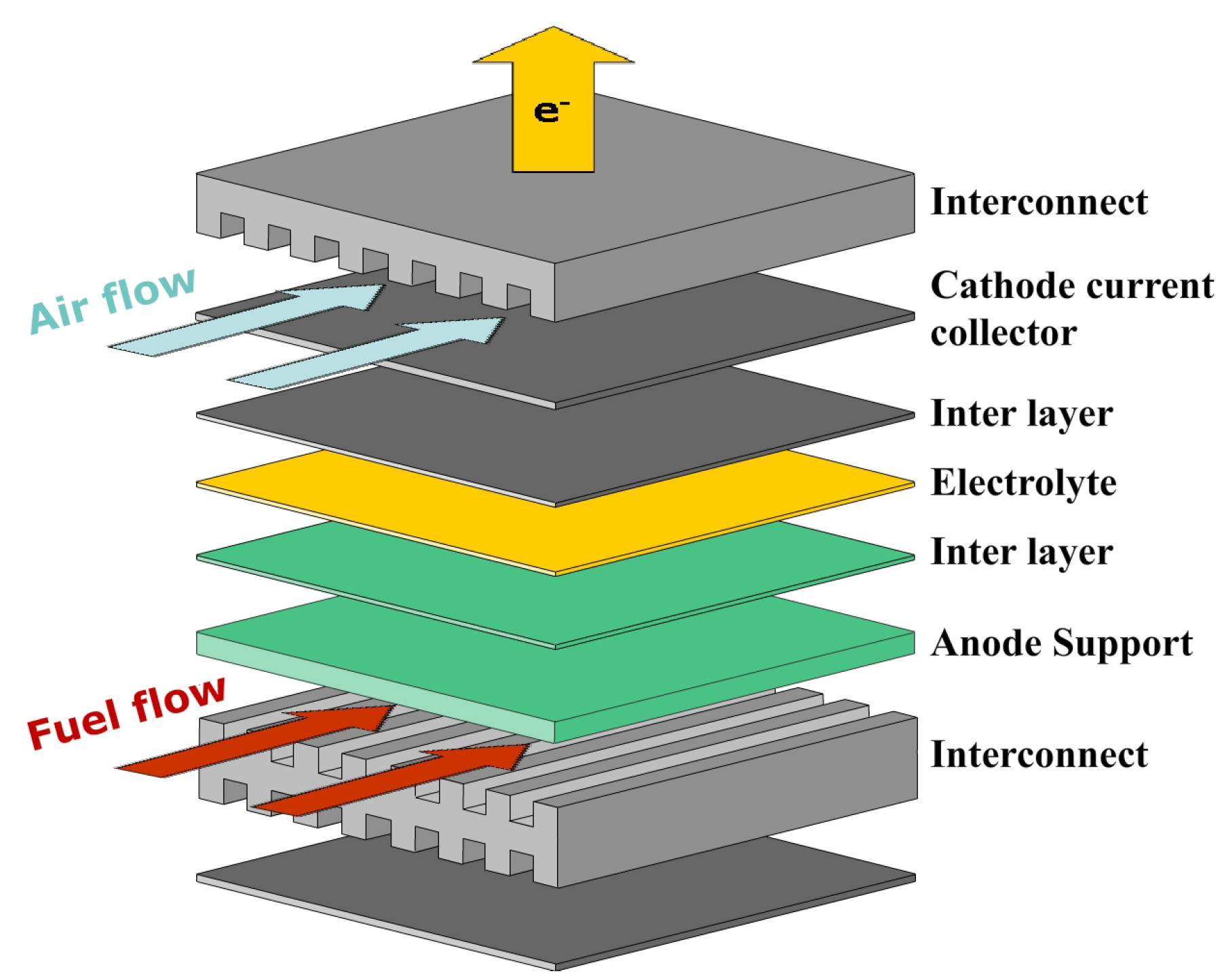
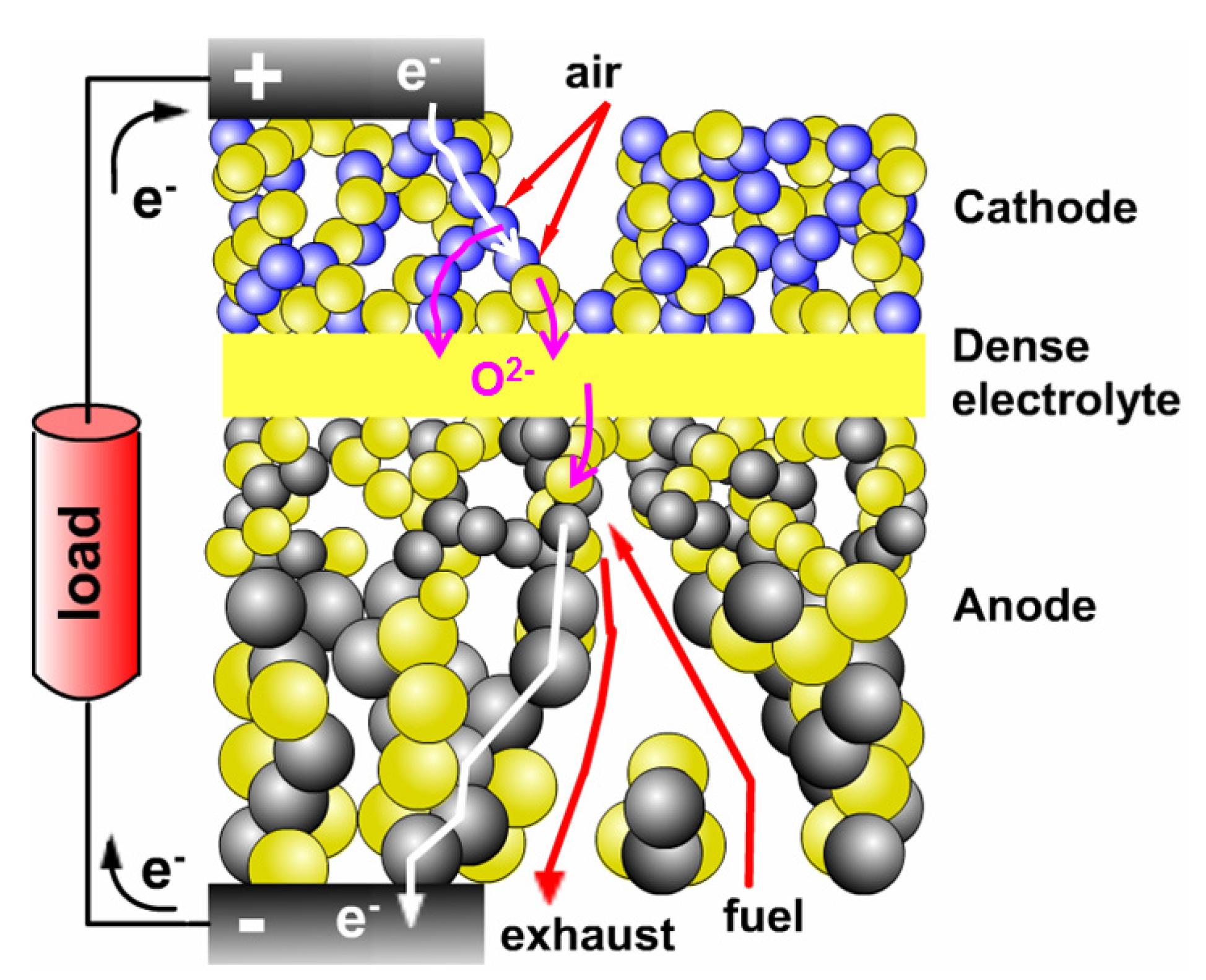
2. Schematic Diagram of a Single Cell: LSCF + YSZ/YSZ/Ni + YSZ
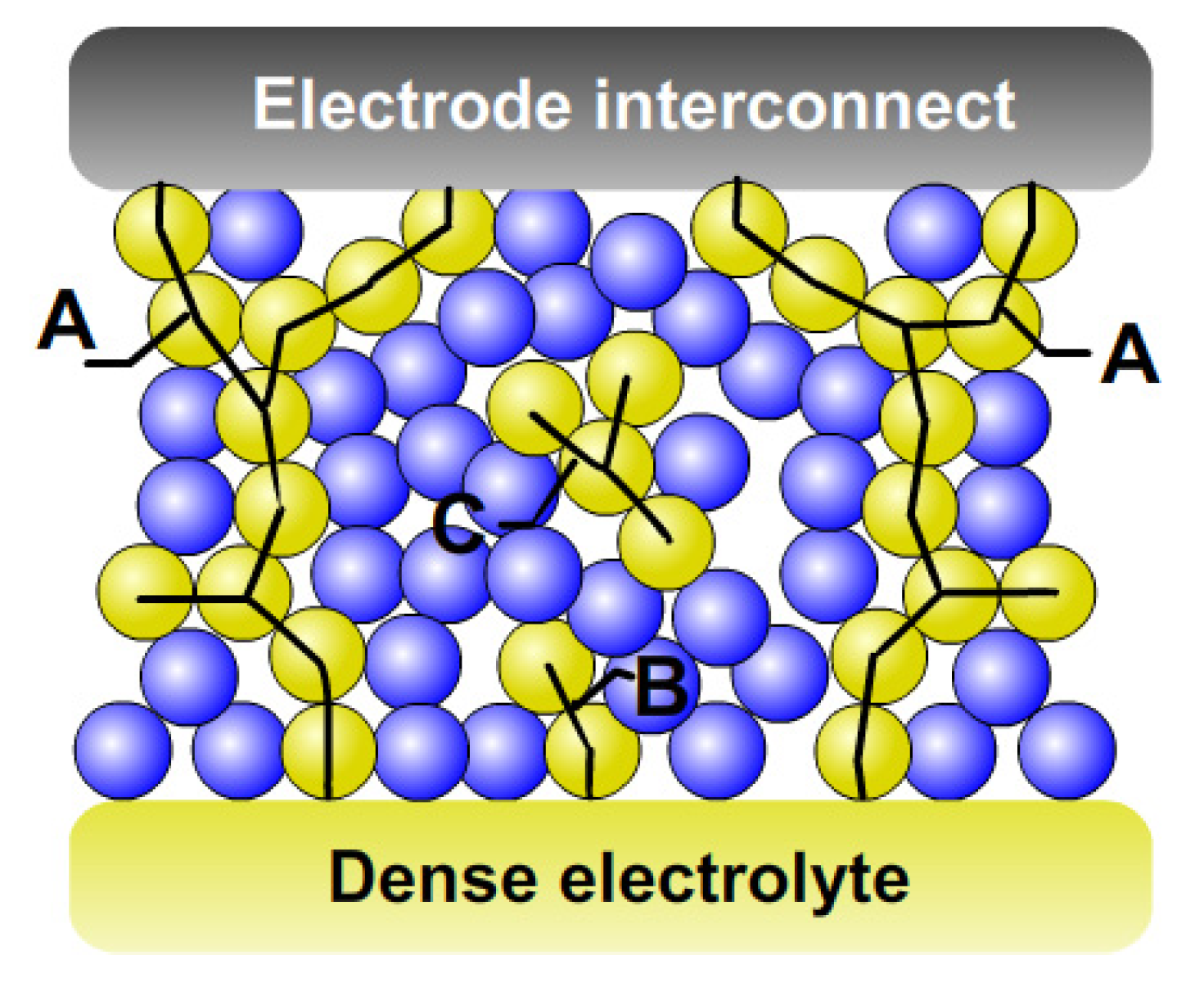
3. Percolation Theory for a Composite Electrode
- (i)
- Coordination number theory: the coordination numbers of the particles are generally considered to be valid parameters that characterize the microstructure of a composite electrode. Generally, these numbers can be evaluated as a function of the specific material parameters, such as the volume composition of each particle type and the relevant particle size distribution.
- (ii)
- Micro-model: For a specific composite electrode, the effective electrode properties, such as the electric conductivity, mechanic stress, thermal expansion coefficient and electrochemical reaction sites should significantly rely on the coordination numbers, which represent the connecting condition among the particles within the composite electrode. The relation between these properties and the coordination numbers can be described by a specific expression in the micro-model.
3.1. Coordination Number Theory
3.2. Binary Mixture Properties
3.2.1. Probability of Each Particle Belonging to the Percolated Ion and Electron Conducting Paths
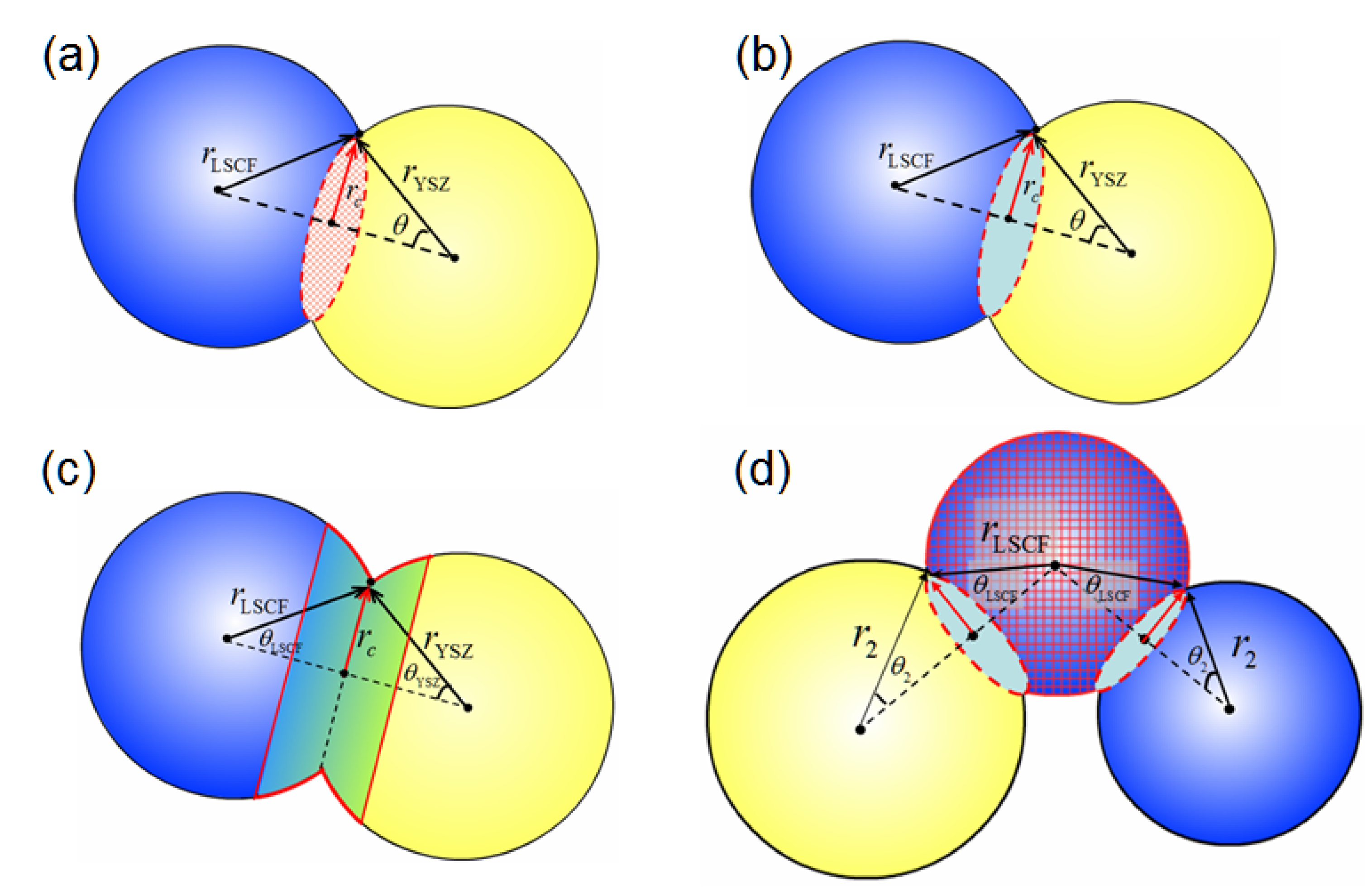
3.2.2. Electrochemical Reaction Sites per Unit Volume
3.2.3. Electrochemical Reaction Sites at the Dense Electrolyte Surface
3.2.4. The Effective Electric Conductivity
3.2.5. Modified Expression for the Effective inter-Particle Conductivity
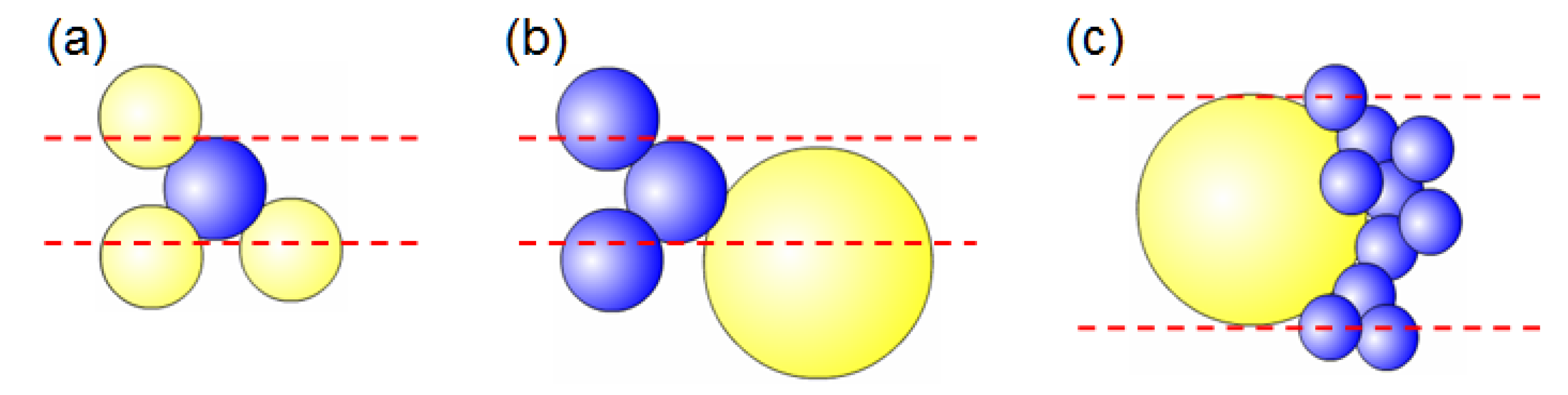
3.2.6. The Hydraulic Radius of the Porous Cathode Structure
3.3. LSCF + YSZ Composite Cathode with Poly-Dispersed Particle Sizes
| Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 6.77% | 9.53% | 12.2% | 14.1% | 14.8% | 14.1% | 12.2% | 9.53% | 6.77% |
4. Results and Discussion
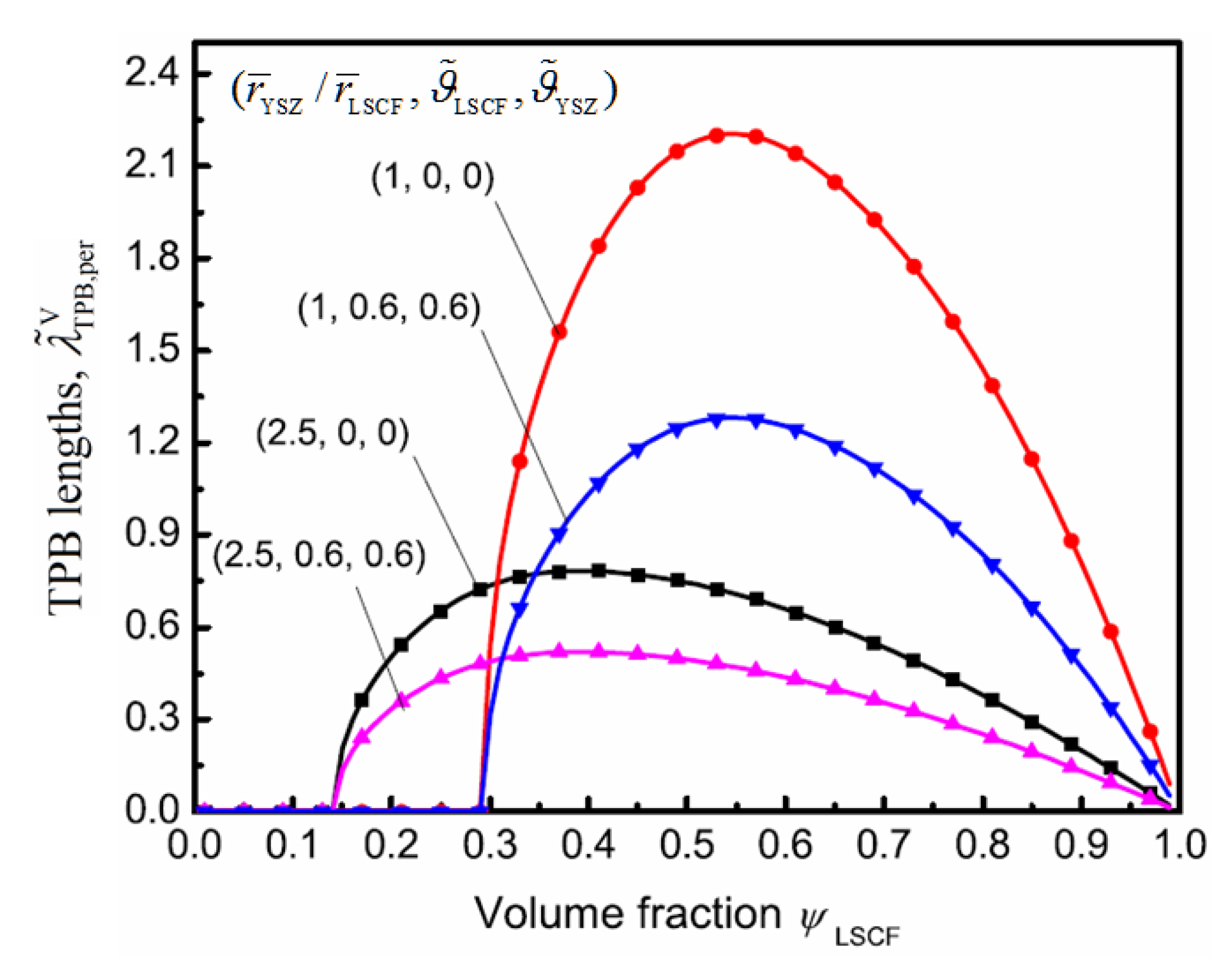
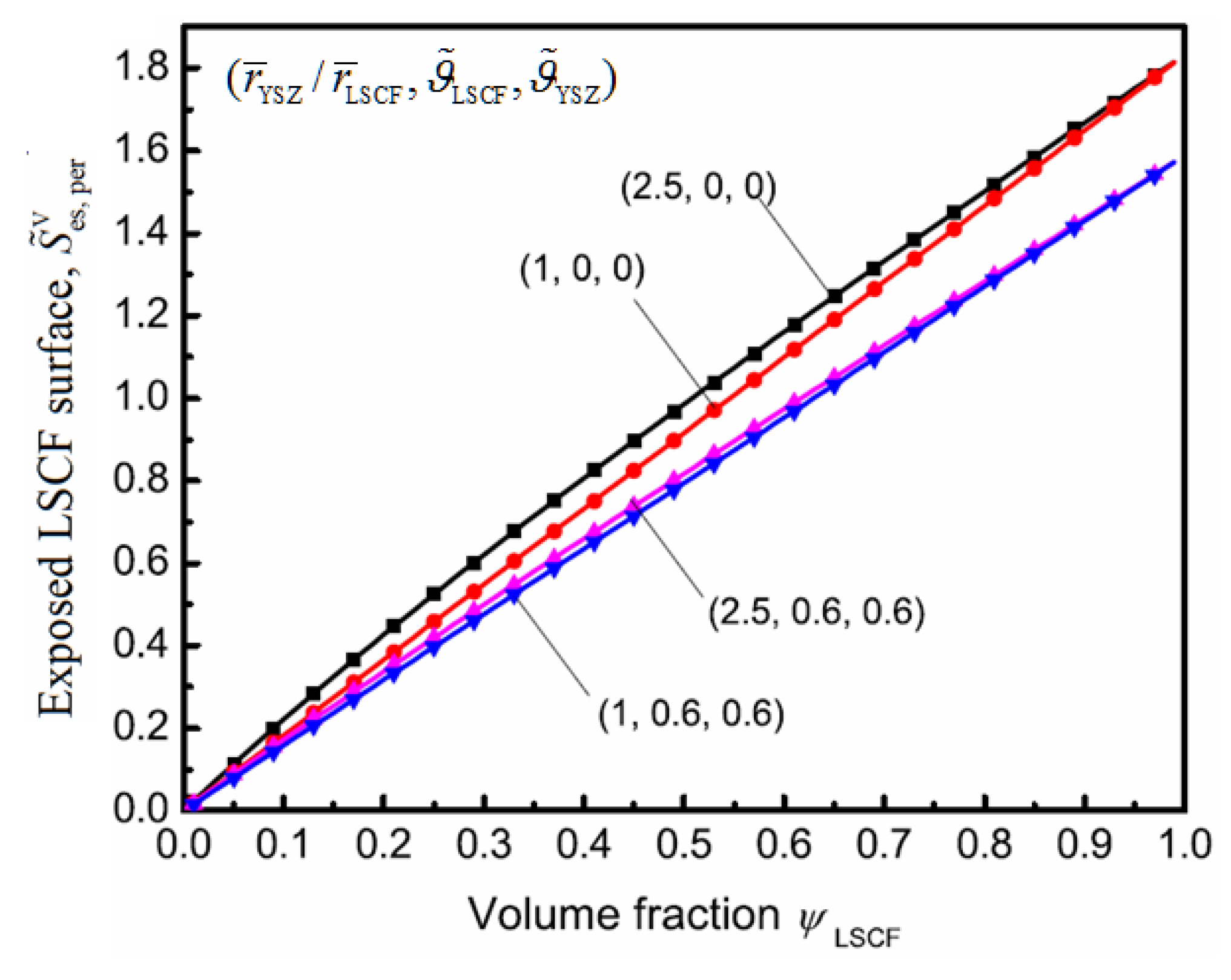
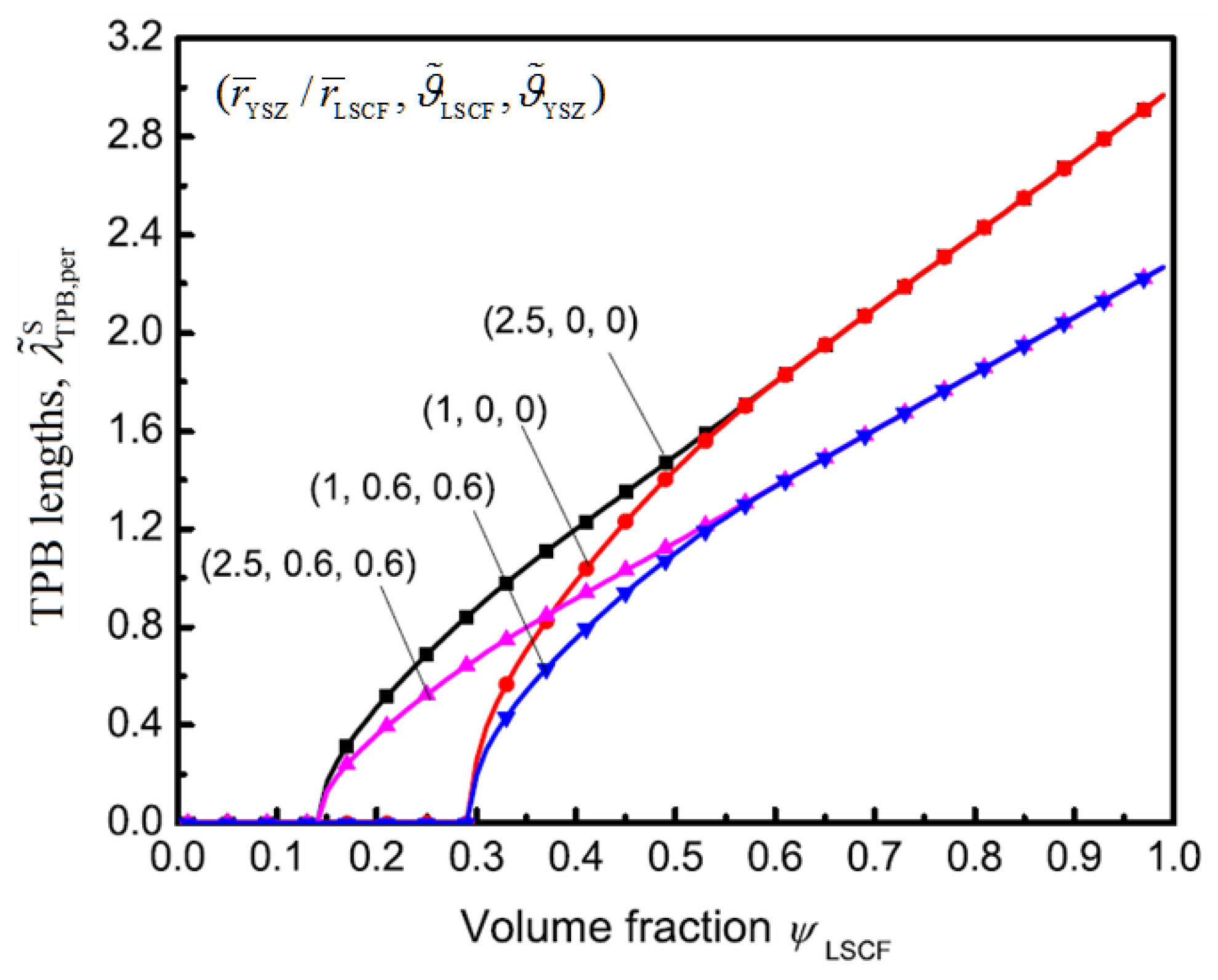
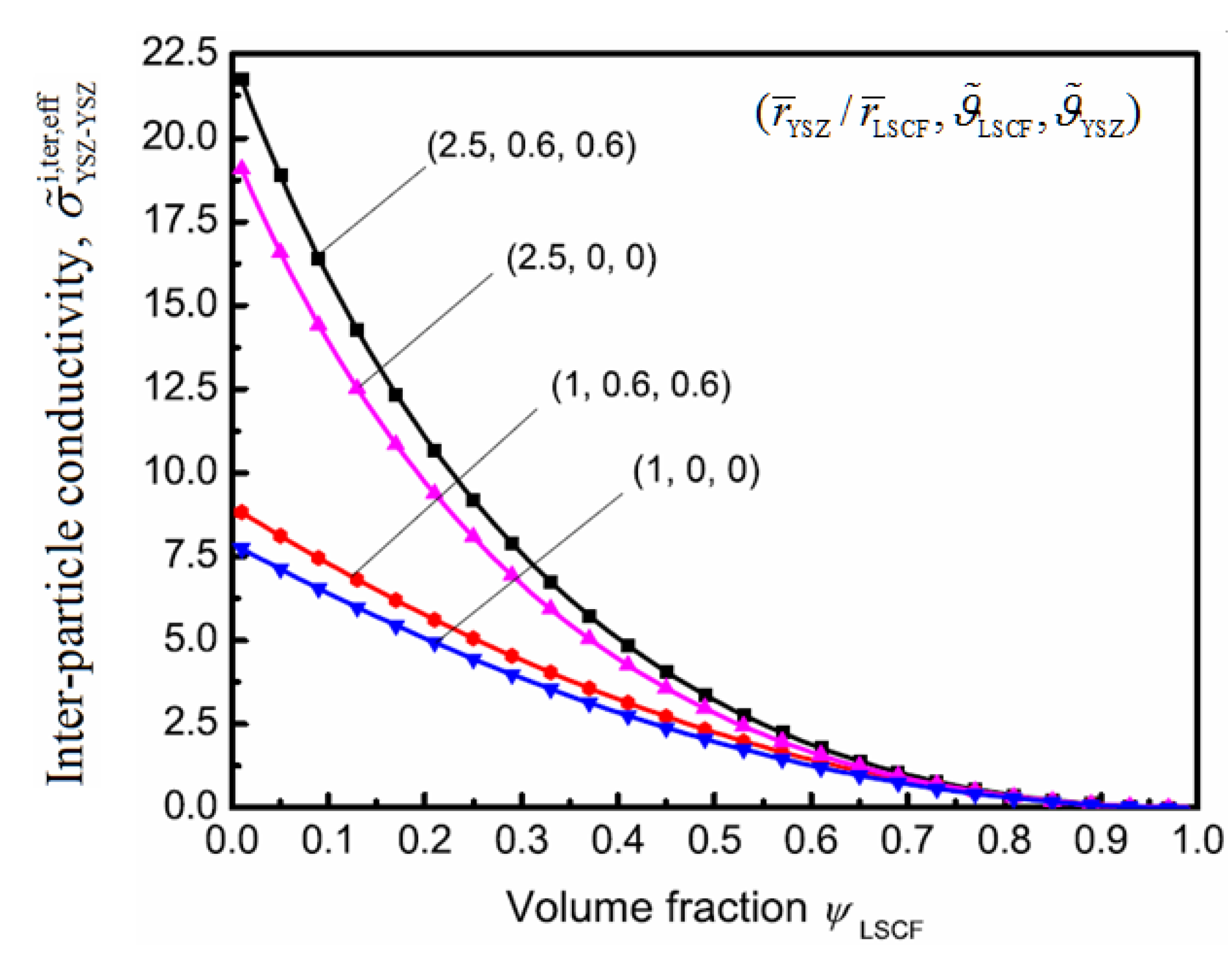
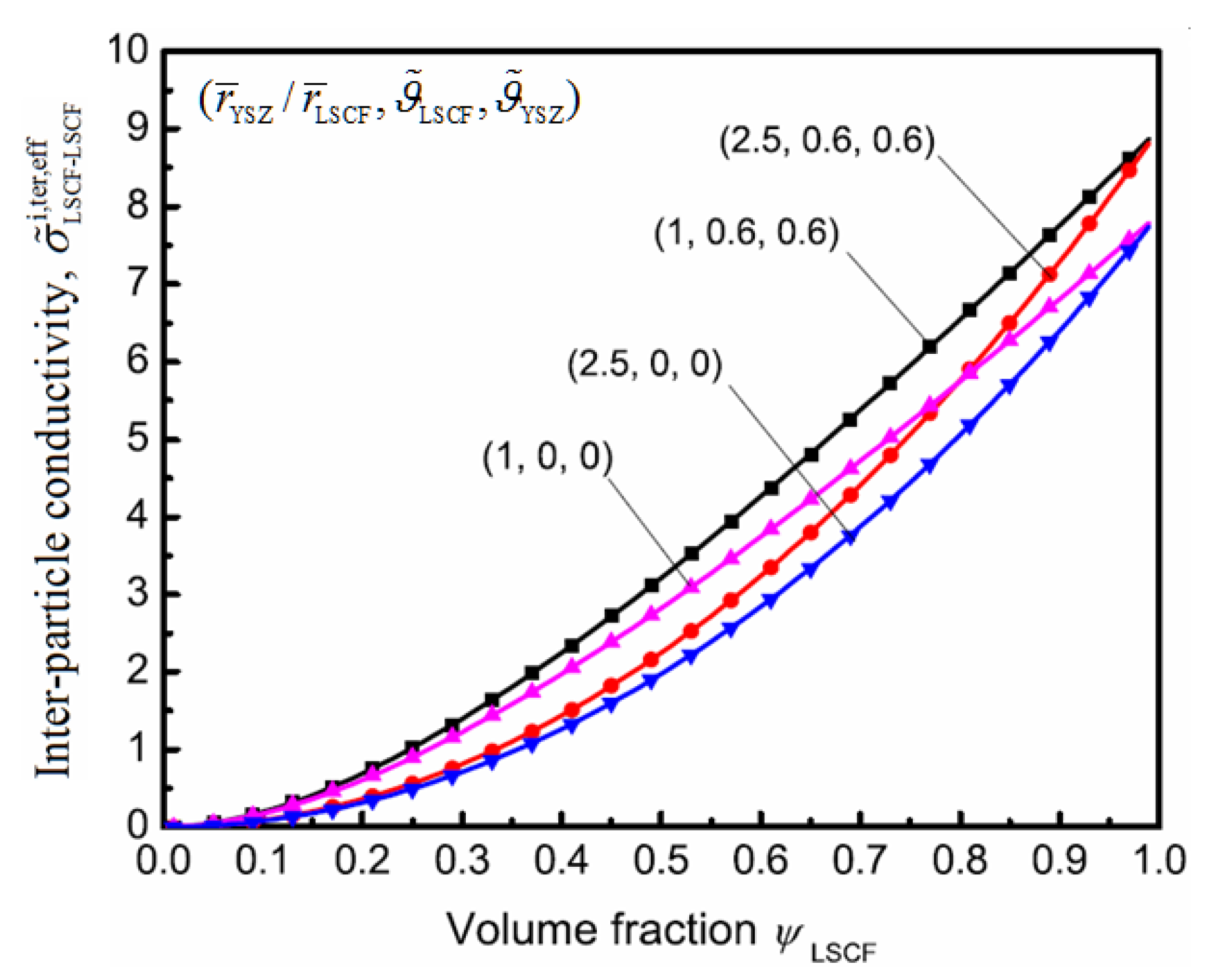
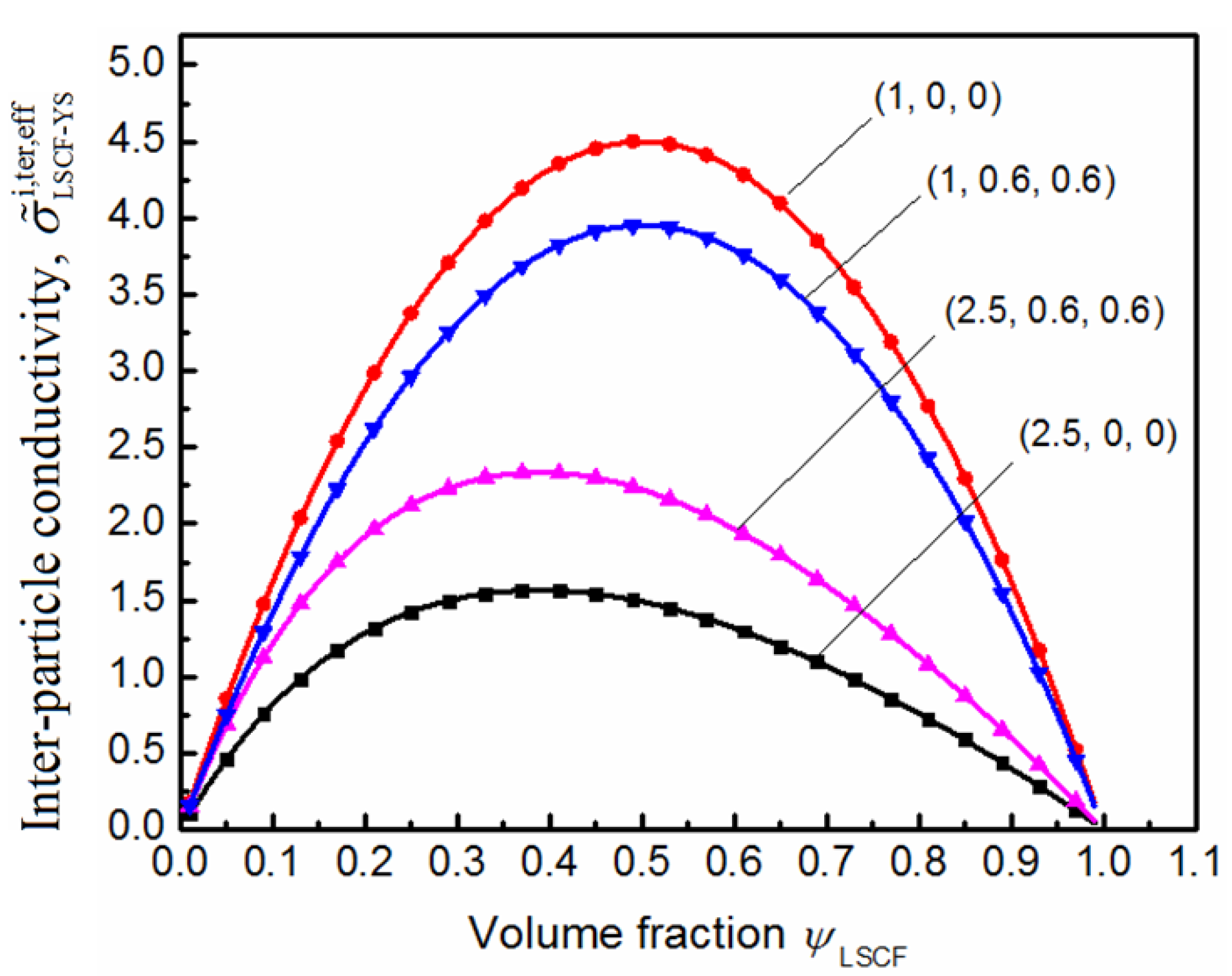
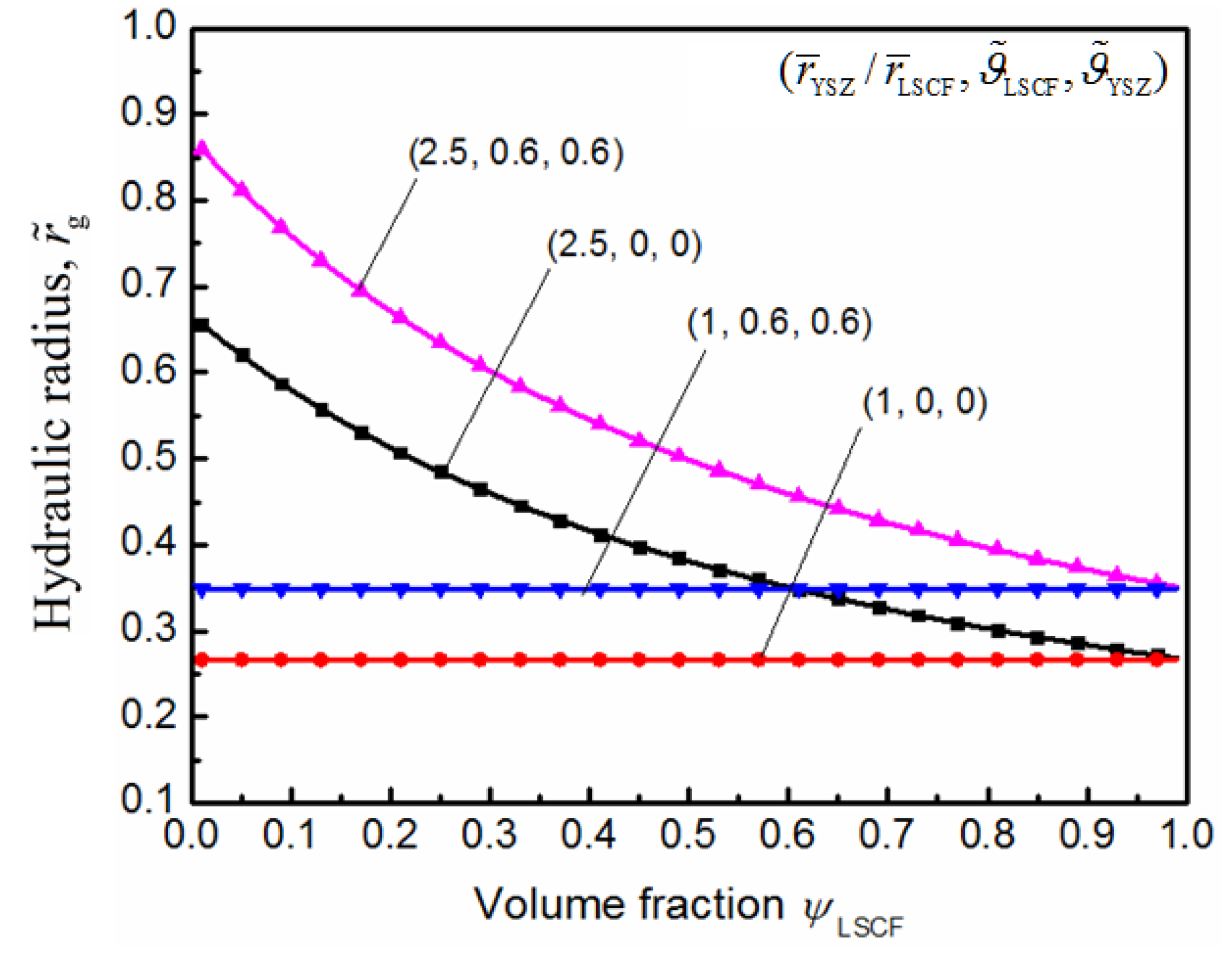
5. Conclusions
Acknowledgments
Nomenclature
surface area per contact between two YSZ particles | |
probability density of the normal distribution particle size | |
| L | thickness of the composite cathode |
total thickness of the YSZ particle interfaces along the ion conducting path | |
| M | particle size types of the multi-component mixture |
number of k particles per unit volume within the entire composite electrode | |
number of k particles per unit dense electrolyte surface | |
probability of the mat particle belonging to the percolated cluster A | |
probability of the mat particle belonging to the percolated ion conducting path | |
probability of the mat particle belonging to the percolated electron conducting path | |
normalized probability of the non-dimensional radius | |
radii of the different particle sizes with number index k | |
mean radius of the mat phase material | |
radius of the k particle | |
neck radius between the contact particles | |
hydraulic radius of the composite cathode structure | |
| S | geometric cross-sectional area of the composite cathode |
effective contact surface area among the YSZ particles per particle layer | |
exposed surface sites of the percolated LSCF particles per unit volume | |
average coordination number of all the particles | |
average number of contacts between a k type particle and all of its neighboring particles | |
number of contacts between the k particle and all of its neighboring particles | |
average coordination number of all of the mat phase particles |
Greek Letters
inter-particle interface thickness | |
standard deviation of the normal distribution particle size | |
contact angle | |
porosity of the composite electrode | |
solid volume fraction of the k particles | |
relative volume fraction of the matk particles in the whole mat phase material | |
electrochemical reaction site per contact between LSCF and YSZ particles | |
electrochemical reaction site per connect between a k particle and the dense electrolyte | |
TPB electrochemical reaction site per unit volume | |
TPB electrochemical reaction site per unit electrolyte surface area | |
net ionic conductivity of the composite cathode | |
effective intra-particle ion conductivity of mat phase material | |
intrinsic inter-particle ion conductivity at the mat- mat interfaces | |
effective inter-particle ion conductivity at the mat- mat interfaces |
Subscript
| ~ | non-dimensional item |
References
- Yokoo, M.; Tabata, Y.; Yoshida, Y.; Hayashi, K.; Nozaki, Y.; Nozawa, K.; Arai, H. Restoration of solid oxide fuel cell stacks after failure of partial cells. J. Power Sources 2009, 190, 252–257. [Google Scholar] [CrossRef]
- Marquez, A.I.; Ohrn, T.R.; Trembly, J.P.; Ingram, D.C.; Bayless, D.J. Effects of coal syngas and H2S on the performance of solid oxide fuel cells: Part 2. Stack tests. J. Power Sources 2007, 164, 659–667. [Google Scholar] [CrossRef]
- Zhao, F.; Virkar, A.V. Dependence of polarization in anode-supported solid oxide fuel cells on various cell parameters. J. Power Sources 2005, 141, 79–95. [Google Scholar] [CrossRef]
- Chen, J.; Liang, F.; Yan, D.; Pu, J.; Chi, B.; Jiang, S.P.; Jian, L. Performance of large-scale anode-supported solid oxide fuel cells with impregnated La0.6Sr0.4Co0.2Fe0.8O3−δ + Y2O3 stabilized ZrO2 composite cathodes. J. Power Sources 2010, 195, 5201–5205. [Google Scholar] [CrossRef]
- Iwai, H.; Shikazono, N.; Matsui, T.; Teshima, H.; Kishimoto, M.; Kishida, R.; Hayashi, D.; Matsuzaki, K.; Kanno, D.; Saito, M.; et al. Quantification of SOFC anode microstructure based on dual beam FIB-SEM technique. J. Power Sources 2010, 195, 955–961. [Google Scholar] [CrossRef]
- Wilson, J.R.; Kobsiriphat, W.; Mendoza, R.; Chen, H.Y.; Hiller, J.M.; Miller, D.J.; Thornton, K.; Voorhees, P.W.; Adler, S.B.; Barnett, S.A. Three-dimensional reconstruction of a solid-oxide fuel-cell anode. Nat. Mater. 2006, 5, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Schneider, L.C.R.; Martin, C.L.; Bultel, Y.; Dessemond, L.; Bouvard, D. Percolation effects in functionally graded SOFC electrodes. Electrochim. Acta 2007, 52, 3190–3198. [Google Scholar] [CrossRef]
- Ali, A.; Wen, X.; Nandakumar, K.; Luo, B.J.; Chuang, K.T. Geometrical modeling of microstructure of solid oxide fuel cell composite electrodes. J. Power Sources 2008, 185, 961–966. [Google Scholar] [CrossRef]
- Kenney, B.; Valdmanis, M.; Baker, C.; Pharoah, J.G.; Karan, K. Computation of TPB length, surface area and pore size from numerical reconstruction of composite solid oxide fuel cell electrodes. J. Power Sources 2009, 189, 1051–1059. [Google Scholar] [CrossRef]
- Chan, S.H.; Chen, X.J.; Khor, K.A. Cathode micromodel of solid oxide fuel cell. J. Electrochem. Soc. 2004, 151, A164–A172. [Google Scholar] [CrossRef]
- Chen, D.; Lin, Z.; Zhu, H.; Kee, R.J. Percolation theory to predict effective properties of solid oxide fuel-cell composite electrodes. J. Power Sources 2009, 191, 240–252. [Google Scholar] [CrossRef]
- Costamagna, P.; Costa, P.; Antonucci, V. Micro-modelling of solid oxide fuel cell electrodes. Electrochim. Acta 1998, 43, 375–394. [Google Scholar] [CrossRef]
- Yoon, J.; Araujo, R.; Grunbaum, N.; Baque, L.; Serquis, A.; Caneiro, A.; Zhang, X.H.; Wang, H.Y. Nanostructured cathode thin films with vertically-aligned nanopores for thin film SOFC and their characteristics. Appl. Surf. Sci. 2007, 254, 266–269. [Google Scholar] [CrossRef]
- Song, H.S.; Lee, S.; Hyun, S.H.; Kim, J.; Moon, J. Compositional influence of LSM-YSZ composite cathodes on improved performance and durability of solid oxide fuel cells. J. Power Sources 2009, 187, 25–31. [Google Scholar] [CrossRef]
- Suzuki, M.; Oshima, T. Estimation of the co-ordination number in a multi-component mixture of spheres. Powder Technol. 1983, 35, 159–166. [Google Scholar] [CrossRef]
- Bouvard, D.; Lange, F.F. Relation between percolation and particle coordination in binary powder mixtures. Acta Metall. Mater. 1991, 39, 3083–3090. [Google Scholar] [CrossRef]
- Chen, D.; Lu, L.; Li, J.; Yu, Z.; Kong, W.; Zhu, H. Percolation micro-model to predict the effective properties of the composite electrode with poly-dispersed particle sizes. J. Power Sources 2011, 196, 3178–3185. [Google Scholar] [CrossRef]
- Bertei, A.; Nicolella, C. Percolation theory in SOFC composite electrodes: Effects of porosity and particle size distribution on effective properties. J. Power Sources 2011, 196, 9429–9436. [Google Scholar] [CrossRef]
- Hussain, M.M.; Li, X.; Dincer, I. A numerical investigation of modeling an SOFC electrode as two finite layers. Int. J. Hydrogen Energy 2009, 34, 3134–3144. [Google Scholar] [CrossRef]
- Jeon, D.H.; Nam, J.H.; Kim, C.J. Microstructural optimization of anode-supported solid oxide fuel cells by a comprehensive microscale model. J. Electrochem. Soc. 2006, 153, A406–A417. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Kee, R.J. Modeling distributed charge-transfer processes in SOFC membrane electrode assemblies. J. Electrochem. Soc. 2008, 155, B715–B729. [Google Scholar] [CrossRef]
- Völker, B.; McMeeking, R.M. Impact of particle size ratio and volume fraction on effective material parameters and performance in solid oxide fuel cell electrodes. J. Power Sources 2012, 215, 199–215. [Google Scholar] [CrossRef]
- Zhang, C.; Grass, M.; McDaniel, A.; DeCaluwe, S.; El Gabaly, F.; Liu, Z.; McCarty, K.; Farrow, R.; Linne, M.; Hussain, Z. Measuring fundamental properties in operating solid oxide electrochemical cells by using in situ X-ray photoelectron spectroscopy. Nat. Mater. 2010, 9, 944–949. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Wang, S.; Blinn, K.; Liu, M.; Liu, Z.; Cheng, Z. Enhanced Sulfur and Coking Tolerance of a Mixed Ion Conductor for SOFCs: BaZr0.1Ce0.7Y0.2−xYbxO3−δ. Science 2009, 326, 126–129. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.-F.; Wang, S.R.; Wang, Z.R.; Hu, Q.; Sun, X.F.; Wen, T.L.; Wen, Z.Y. Use of La0.75Sr0.25Cr0.5Mn0.5O3 materials in composite anodes for direct ethanol solid oxide fuel cells. J. Power Sources 2008, 183, 512–517. [Google Scholar] [CrossRef]
- Chen, J.; Liang, F.; Yan, D.; Pu, J.; Chi, B.; Jiang, S.P.; Jian, L. Performance of large-scale anode-supported solid oxide fuel cells with impregnated La0.6Sr0.4Co0.2Fe0.8O3−δ + Y2O3 stabilized ZrO2 composite cathodes. J. Power Sources 2010, 195, 5201–5205. [Google Scholar] [CrossRef]
- Ruiz-Morales, J.C.; Canales-Vazquez, J.; Marrero-Lopez, D.; Irvine, J.T.S.; Nunez, P. Improvement of the electrochemical properties of novel solid oxide fuel cell anodes, La0.75Sr0.25Cr0.5Mn0.5O3−δ and La4Sr8Ti11Mn0.5Ga0.5O37.5−δ, using Cu-YSZ-based cermets. Electrochim. Acta 2007, 52, 7217–7225. [Google Scholar] [CrossRef]
- Lu, L.; Chen, D.; Zhao, G.; Ren, X.; Guo, G. Temperature and Excitation wavelength dependence of surface-plasmon-mediated emission from CdSe nanocrystals. J. Phys. Chem. C 2010, 114, 18435–18438. [Google Scholar] [CrossRef]
- Kee, R.J.; Zhu, H.; Goodwin, D.G. Modeling electrochemistry and solid-oxide fuel cells: II. Research challenges. J. Combust. Soc. Jpn. 2005, 47, 276–289. [Google Scholar]
- Suzuki, M.; Oshima, T. Co-ordination number of a multi-component randomly packed bed of spheres with size distribution. Powder Technol. 1985, 44, 213–218. [Google Scholar] [CrossRef]
- Bertei, A.; Nicolella, C. A comparative study and an extended theory of percolation for random packings of rigid spheres. Powder Technol. 2011, 213, 100–108. [Google Scholar] [CrossRef]
- Chen, D.; Bi, W.; Kong, W.; Lin, Z. Combined micro-scale and macro-scale modeling of the composite electrode of a solid oxide fuel cell. J. Power Sources 2010, 195, 6598–6610. [Google Scholar] [CrossRef]
- Bessler, W.G.; Warnatz, J.; Goodwin, D.G. The influence of equilibrium potential on the hydrogen oxidation kinetics of SOFC anodes. Solid State Ion. 2007, 177, 3371–3383. [Google Scholar] [CrossRef]
- Wang, D.Y.; Nowick, A.S. Diffusion‐controlled polarization of Pt, Ag, and Au electrodes with doped ceria electrolyte. J. Electrochem. Soc. 1981, 128, 55–63. [Google Scholar] [CrossRef]
- Chen, X.J.; Khor, K.A.; Chan, S.H.; Yu, L.G. Influence of microstructure on the ionic conductivity of yttria-stabilized zirconia electrolyte. Mater. Sci. Eng. A 2002, 335, 246–252. [Google Scholar] [CrossRef]
- Park, H.J.; Kwak, C.; Lee, S.M. Mixed conduction behavior in nanostructured lanthanum gallate. Electrochem. Commun. 2009, 11, 962–964. [Google Scholar] [CrossRef]
- M.J. Verkerk, B.J.M.a.A.J.B. Effect of grain boundaries on the conductivity of high-purity ZrO2-Y2O3 ceramics. Solid State Ion. 1982, 6, 159–170. [Google Scholar]
- Suwanwarangkul, R.; Croiset, E.; Entchev, E.; Charojrochkul, S.; Pritzker, M.D.; Fowler, M.W.; Douglas, P.L.; Chewathanakup, S.; Mahaudom, H. Experimental and modeling study of solid oxide fuel cell operating with syngas fuel. J. Power Sources 2006, 161, 308–322. [Google Scholar] [CrossRef]
- Bertei, A.; Choi, H.W.; Pharoah, J.G.; Nicolella, C. Percolating behavior of sintered random packings of spheres. Powder Technol. 2012, 231, 44–53. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, D.; He, H.; Zhang, D.; Wang, H.; Ni, M. Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor. Energies 2013, 6, 1632-1656. https://doi.org/10.3390/en6031632
Chen D, He H, Zhang D, Wang H, Ni M. Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor. Energies. 2013; 6(3):1632-1656. https://doi.org/10.3390/en6031632
Chicago/Turabian StyleChen, Daifen, Huanhuan He, Donghui Zhang, Hanzhi Wang, and Meng Ni. 2013. "Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor" Energies 6, no. 3: 1632-1656. https://doi.org/10.3390/en6031632
APA StyleChen, D., He, H., Zhang, D., Wang, H., & Ni, M. (2013). Percolation Theory in Solid Oxide Fuel Cell Composite Electrodes with a Mixed Electronic and Ionic Conductor. Energies, 6(3), 1632-1656. https://doi.org/10.3390/en6031632





