Metaheuristic Algorithms Applied to Bioenergy Supply Chain Problems: Theory, Review, Challenges, and Future

Abstract

Bioenergy is a new source of energy that accounts for a substantial portion of the renewable energy production in many countries. The production of bioenergy is expected to increase due to its unique advantages, such as no harmful emissions and abundance. Supply-related problems are the main obstacles precluding the increase of use of biomass (which is bulky and has low energy density) to produce bioenergy. To overcome this challenge, large-scale optimization models are needed to be solved to enable decision makers to plan, design, and manage bioenergy supply chains. Therefore, the use of effective optimization approaches is of great importance. The traditional mathematical methods (such as linear, integer, and mixed-integer programming) frequently fail to find optimal solutions for non-convex and/or large-scale models whereas metaheuristics are efficient approaches for finding near-optimal solutions that use less computational resources. This paper presents a comprehensive review by studying and analyzing the application of metaheuristics to solve bioenergy supply chain models as well as the exclusive challenges of the mathematical problems applied in the bioenergy supply chain field. The reviewed metaheuristics include: (1) population approaches, such as ant colony optimization (ACO), the genetic algorithm (GA), particle swarm optimization (PSO), and bee colony algorithm (BCA); and (2) trajectory approaches, such as the tabu search (TS) and simulated annealing (SA). Based on the outcomes of this literature review, the integrated design and planning of bioenergy supply chains problem has been solved primarily by implementing the GA. The production process optimization was addressed primarily by using both the GA and PSO. The supply chain network design problem was treated by utilizing the GA and ACO. The truck and task scheduling problem was solved using the SA and the TS, where the trajectory-based methods proved to outperform the population-based methods.

1. Introduction

Bioenergy is a crucial renewable source of energy that provides benefits, in terms of the economical and the environmental perspectives, by diminishing the dependence on oil as a source of energy [1]. Although the production of bioenergy (defined as the biomass exploitation for the production of energy and bio-based chemical products) is expected to increase in the near future [2,3,4], logistics costs are a major obstacle in the enhancement of the bioenergy production [5], primarily because biomass is bulky, has low energy density, and its availability is seasonal.

Mathematical optimization of logistics problems within the bioenergy industry includes complex constraints related to transportation, feedstock supply sources, operational and logistics costs and power plant location and capacity. Mathematical optimization involves maximizing or minimizing an objective function by selecting input values from a set of data, while meeting a set of constraints. In bioenergy, the aim of optimization algorithms is primarily to obtain a solution that maximizes profits, minimizes emissions and/or minimizes costs. Moreover, some solution procedures optimize multiple-objectives using multi-criteria optimization. An extensive range of classical optimization methods have been utilized to address bioenergy supply chain problems. Linear programming (LP) models have been used primarily to minimize overall costs; the common limitation of LP models is that they over-simplify the problem to only linear deterministic equations. Mixed integer linear programming (MILP) models have been used primarily to design supply chain networks, where decision variables can be continuous and/or integer. A few non-linear programming (NLP) and dynamic programming models have been proposed to capture the uncertainty prevalent in real-life problems. Moreover, deterministic multi-criteria programming models can optimize two conflicting objectives by providing a Pareto front with non-dominated feasible solutions. Classical optimization approaches are based upon gradient methods to obtain the optimal solution of convex, continuous, and differentiable functions. However, classical optimization algorithms cannot easily provide a global solution for large-scale stochastic non-convex non-linear problems with multiple objective functions and constraints. To address this problem, metaheuristics, which are higher-level strategies that guide and modify other heuristics (experience-based techniques for problem solving) to produce solutions beyond local optimal solutions and obtain a near-optimal solution for large-scale complex problems [6,7,8], can be employed. In comparison, metaheuristics are more effective than classical optimization methods to obtain near-optimal solutions for hard problems (e.g., NP-hard, non-deterministic polynomial-time hard problems) [9]. In the literature, noteworthy uses of metaheuristics include ant colony optimization (ACO), the genetic algorithm (GA), particle swarm optimization (PSO), bee colony algorithm (BCA), tabu search (TS), and simulated annealing (SA). Baños et al. [10] provided an outline of computational optimization methods utilized for renewable and sustainable energy including solar energy, hydropower, wind power, geothermal energy, bioenergy, and hybrid systems. Kurka and Blackwood [11] selected and reviewed the Multi-Criteria Analysis (MCA) method for decision making in renewable energy. Both of these reviews did not present a detailed analysis of a specific source of energy and offered a general trend of optimization techniques applied to a wide variety of renewable energy sources. While these reviews are of value and cover different aspects of the renewable energy literature, they do not present a focalized and detailed review for a specific source of renewable energy (for instance, bioenergy). De Meyer et al. [12] presented a review on bioenergy and the use of classical mathematical programming approaches and MCA. The delivery of biomass to meet the national goals (in the case of the U.S., the first renewable fuel volume mandate was established by the renewable fuel standards (RFS) program [13]) requires major changes in the supply chain (SC) infrastructure and management to reduce the biomass delivery cost and to improve its quality, consequently enabling an economically feasible and reliable bioenergy industry. One of the main challenges in the bioenergy field is the design of sustainable biomass supply chains that can be economically scaled up and provide tangible benefits from biomass utilization [14]. Hence, there is a need for sophisticated mathematical models and advanced optimization techniques to enhance the bioenergy supply chains by integrating uncertainty and risk. The majority of the models developed in the bioenergy supply chain are deterministic models based on linear and mixed integer programming. A recent area of inquiry is the development of stochastic and hybrid models and algorithms. Therefore, of particular interest is the application of metaheuristic algorithms to solve large-scale stochastic bioenergy supply chain problems. Indeed, while metaheuristics have been employed to solve challenging problems in several fields of research, the application of metaheuristics in the bioenergy supply chain field is new and limited. In response to this need, this review contributes substantially to the body of literature by providing:

• A complete overview of the theory and applications of metaheuristics employed to solve complex bioenergy supply chain models and,
• An outline of challenges, issues, and future research in the modeling and optimization of bioenergy supply chains.

The structure of this paper is as follows: Section 2 presents an introduction of the bioenergy supply chain optimization. Section 3 reviews selected metaheuristic algorithms. The classification of the problems in bioenergy supply chain optimization and solution procedures are presented in Section 4. The results of the literature review are presented in Section 5. Finally, Section 6 provides concluding remarks and outlines future research.

2. Bioenergy Supply Chain Taxonomy

Supply chain management refers to the coordination of the flow of materials and information involving the movement and storage of raw materials, work-in-process inventory and finished products from origin to consumption [15]. To achieve an optimal design for efficient supply chain management, supply chain modeling develops mathematical models to optimize resources. Numerous works are available on supply chain modeling and design, especially for the manufacturing sector; however, the nascent bioenergy industry faces unique challenges in terms of logistics and, thus, existing supply chain models cannot be directly implemented in the bioenergy area. In this paper, biomass includes all plant-derived materials utilized for energy production. The biomass resources include agricultural and forestry residues, industrial process residues, urban solid waste, and urban wood trash [16]. Bioenergy supply chains are subject to biomass availability and seasonality as well as uncertainty due to weather conditions and variations in biomass quality across harvesting periods; contrary, manufacturing supply chains are driven by demand uncertainty. Besides biomass availability and quality uncertainty, the biomass supply deteriorates and loosens dry matter with time, has a low energy density and poor flow properties, therefore, it is expensive to transport. These properties justify the necessity of re-thinking modeling frameworks.

Sharma et al. [17] presented a comprehensive review of mathematical programming models developed for biomass supply chain design as well as the key challenges faced by the bioenergy industry and adapted the classification taxonomies proposed by [18,19] for the classification of bioenergy supply chain models. Following, a brief discussion on these different conceptual models is presented to properly situate the present review. The taxonomy consists of decision levels, supply chain structure, modeling approach, quantitative performance measures, entities, biomass types, and end-products.

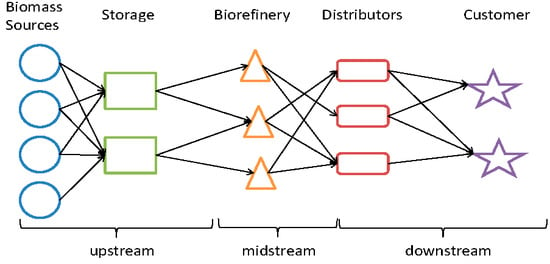
The first classification refers to the decision level and includes the operational timeframe, which refers to hourly and weekly decisions such as vehicle routing and scheduling; the tactical timeframe, which involves monthly decisions such as acres harvested in a time period, biomass inventory/storage policies, biomass processed and transported in a time period; and the strategic timeframe, which comprises multi-annual decisions including supply chain network design, selection/sourcing of biomass type(s) (usually multiple biomass types are needed as shown in [20]), selection of mode of transportation, sustainability issues and location/capacity planning of biomass processing, storage, pretreatment site(s). In addition, upstream, midstream, and downstream are the three primary supply chain levels of supply chain modeling. More precisely, the upstream level includes decisions related to farms, biomass storage facilities and the distribution of biomass to biorefineries; the midstream level includes decisions related to biorefineries location and the conversion process; and the downstream level includes decision regarding the distribution of final product (biofuel or electricity) to the final customer. A generic bioenergy supply chain is illustrated in Figure 1.

Figure 1. Schematic diagram of a generic bioenergy supply chain.

Figure 1. Schematic diagram of a generic bioenergy supply chain.

The supply chain structure, defined as the connections of the entities and links among the entities that represent information and material flows, is divided by into [21]: convergent, divergent, conjoined, and general network. Convergent structure is usually associated with assembly-like processes, such as the aircraft industry, where many suppliers are needed to assemble the final product. The divergent structure is the opposite of the convergent structure, where a particular node has one predecessor but several successors (i.e., arborescent structure). Some mineral extraction processes follow this structure. The conjoined structure combines both the convergent and the divergent structures. Finally, the network structure is not convergent, divergent or conjoined. This flexible structure is characteristic of manufacturing companies such as automobile and electronics.

Supply chains can be classified by their mathematical modeling approach. The classification used by Sharma et al. [17] which is taken from [19,22,23] is discussed as follows. The main mathematical modeling approaches used in supply chain are: deterministic, stochastic, hybrid, and IT-driven models. Deterministic models are widely used and these models assume that all parameters and known and fixed in a time period. Deterministic models can be further divided into: single- and multi- objective optimization. Both single- or multi- objective optimization models can be broken into linear, mixed-integer, integer, nonlinear, mixed-integer nonlinear, and integer nonlinear programming. Stochastic (or probabilistic) models involve uncertainty in the input parameters, which follow a probabilistic distribution. Hybrid models combine both deterministic and stochastic models and also include simulation techniques. Metaheuristic optimization techniques (the focus of this review) have proved to be efficient solution procedures for solving stochastic and hybrid models. Finally, IT-driven models integrate real-time application software to enhance coordination, communication, and visualization throughout the supply chain.

In supply chain modeling and optimization, quantitative performance measures are the objective function to be minimized or maximized. Qualitative performance measures are not generally used in bioenergy supply chains [17]. Sharma et al. [17] categorizes the quantitative performance measures in bioenergy supply chains as: cost minimization, profit maximization, inventory investment minimization, net present worth maximization, and return on investment maximization.

Lastly, the modeling of bioenergy supply chains will vary depending on the number and type of entities, type of biomass and end-products as stated by [17]. The main entities in a bioenergy supply chain are: biomass source site(s), storage site(s), collection site(s), pre-processing facilities, biorefineries, distribution site(s), and customer(s). The type of biomass such as: oil crops, sugar and starch, lignocellulosic, agriculture residues, woody biomass, municipal solid waste, microalgae, and wet biomass. The end-products are usually biofuels for transportation (biodiesel, bioethanol, and hydrocarbon/bio-oil), bio-electricity, and bio-heating.

The taxonomy used in this review is based on the specific decision taken at different decision levels, that is, integrated supply chain planning, bioconversion and production process optimization, supply chain network design, scheduling problems, and facility location (refer to Section 4). The common thrust is the application of metaheuristics and hybrid techniques to solve these decisions in bioenergy supply chain decisions. Several supply chain structures, modeling approaches, and performance measures were used by the works reviewed in this review.

3. Review Methodology

Forty three original publications have been revised in this review including journal articles, dissertations, and conference proceedings. To further illustrate the trends in the field of metaheuristic applied to solve bioenergy supply chain problems, the Web of Science (WoS) database was used to determine journal and authors’ information for all of the articles included in this review. WoS includes the information of articles, journals, impact factors, authors’ institution, and the location of institutions.

When comparing journals, one of the most important aspects is the impact factor of the journal. Impact factor is a measure of the average citations which a journal has over a certain span of time [24]. In this case, the considered impact factor was the five-year average impact factor, which is available in the Thomson Reuters’ Journal Citation Report (JCR).

For the author analysis, the most important aspect is the authors’ h-index, which was first proposed by Hirsch [25]. The h-index aims to measure an author’s overall productivity and impact. It is linked to the authors’ number of citations [25]. Comparing the contributing authors’ h-index will help to assess the authors tenured and scholarly productivity in the field of metaheuristics applied to bioenergy. The assumptions used to gather data from the WoS were as follows:

(1)

Only journal articles were considered for the study since the impact factor was readily available for them. Conference proceedings and book chapters were not considered.

(2)

Of the remaining journal articles, four papers were published in the journals not indexed in WoS. The information of the institutions and country were available and included in the study but the impact factor, the number of citations, and the h-index of the authors were not.

(3)

Several articles have multiple authors from different institutions in different countries. Articles having authors from two different institutions and/or countries were treated as an individual entity during the analysis.

(4)

The impact factor used to compare journals was the 5-year average (2007–2011).

It is noteworthy that the WoS has some limitations. For instance, the h-index for an author might not be accurately portrayed. Despite WoS’s large database of journals, there are still some reputable journals which are not included in WoS. Consequently, citations to authors’ work published in journals not included in WoS are not considered in this analysis. Thus, the author’s total citations would not be reflected accurately and the h-index values could be deflated. Another limitation is that the process of calculating an author’s h-index is mechanical in nature. It is important to isolate all the articles associated with the author before generating a citation report. Sometimes, not all the author’s articles appear in the search and it is crucial to try different name searches to ensure all the author’s articles are accounted to calculate the h-index.

One of the important observations in this study is that performing comparisons of articles based on the number of citations would not be a standardized measure. Indeed, as Figure 2 illustrates, the impact of a paper from five years ago by the number of citations it received is a good measure; however, it is difficult to gauge the impact of recent publications of about three years ago since the paper is too recent to receive enough citations. Moreover, this is a recent area of inquiry and the number of articles has increased in the last years.

Based on the publications and their information on WoS, it was found that authors from twenty three countries have contributed to this topic. Furthermore, fifty one institutions have published in this area, and out of which, the top countries in terms of number of institutions are shown in Figure 3. When considering the countries ranking by the number of journal articles they have contributed to, United States and Spain tie on five articles each as shown in Table 1. Table 2 shows that Asian and European institutions have contributed significantly in this area.

Figure 2. Total article citations and number of citations over the years.

Figure 2. Total article citations and number of citations over the years.

Figure 3. Number of institutions by countries.

Figure 3. Number of institutions by countries.

Table 1. Top six countries by the number of journal articles.

Country	No. of articles
United States	5
Spain	5
Japan	4
India	3
Greece	3
Italy	3

Table 1. Top six countries by the number of journal articles.

Country	No. of articles
United States	5
Spain	5
Japan	4
India	3
Greece	3
Italy	3

Table 2. The distribution of institutions by continent.

Continent	Institutions	% of institutions
Asia	17	33.3%
Europe	16	31.4%
Americas	10	19.6%
Africa	3	5.9%
Australasia	5	9.8%

Table 2. The distribution of institutions by continent.

Continent	Institutions	% of institutions
Asia	17	33.3%
Europe	16	31.4%
Americas	10	19.6%
Africa	3	5.9%
Australasia	5	9.8%

Out of the fifty one institutions that have contributed, Table 3 shows the top ten institutions in terms of contributions to the topic. Overall, diversity in the institutions contributing to this area is observed.

Table 3. Top ten institutions by contributions.

Name of institutions	No. of publications
University of Jaen, Spain	5
Tokyo Institute of Technology, Japan	3
Dalian University of Technology, China	2
Helwan University, Egypt	2
National Technical University of Athens, Greece	2
Norwegian School Economics & Business Administration, Norway	2
Oregon State University, United States	2
The Forestry Research Institute of Sweden, Sweden	2
University of Aarhus, Denmark	2
University of Turin, Italy	2

Table 3. Top ten institutions by contributions.

Name of institutions	No. of publications
University of Jaen, Spain	5
Tokyo Institute of Technology, Japan	3
Dalian University of Technology, China	2
Helwan University, Egypt	2
National Technical University of Athens, Greece	2
Norwegian School Economics & Business Administration, Norway	2
Oregon State University, United States	2
The Forestry Research Institute of Sweden, Sweden	2
University of Aarhus, Denmark	2
University of Turin, Italy	2

There are thirty one distinct journals in this review and twenty seven of them are recognized by the Thomson Reuter’s databases. Out of twenty seven, Table 4 lists the top six journals in terms of the number of contributions published in this area as well as their impact factors. It can be observed that several articles in the review have been published in high impact journals and have the potential to get more citations in the near future.

From the articles recognized by the WoS database, there are ninety six authors and thirty authors of them are distinct first authors. The most productive first authors in this field are P. Reche López (University of Jaen) with four articles, Nasser Ayoub (Tokyo Institute of Technology) with three papers and Anthanasios A. Rentizelas (National Technical University of Athens) with two manuscripts.

Table 4. Top six journals in terms of publications.

Journal Name	No of Publications	Impact Factor
Biomass and Bioenergy	3	3.931
Computers and Electronics in Agriculture	3	1.998
Energy Conversion and Management	3	3.075
Applied Energy	2	4.783
Computers & Chemical Engineering	2	2.367
Renewable Energy	2	3.456

Table 4. Top six journals in terms of publications.

Journal Name	No of Publications	Impact Factor
Biomass and Bioenergy	3	3.931
Computers and Electronics in Agriculture	3	1.998
Energy Conversion and Management	3	3.075
Applied Energy	2	4.783
Computers & Chemical Engineering	2	2.367
Renewable Energy	2	3.456

When considering all the ninety six authors who have contributed to this field, the top ten scholars are listed in Table 5. It can be observed that several productive scholars have contributed to the field of metaheuristics applied to bioenergy supply chain problems.

Table 5. Top ten scholars’ contributions.

Author	h-Index	Relevant Publications	Total Publications	Institution
Xiao Dong Chen	30	1	213	University of Aukland
Sing Kiong Nguang	25	1	108	University of Aukland
Pragasen Pillay	21	1	101	Concordia University
Taher Niknam	21	1	116	Shiraz University of Technology
Francisco Jurado	18	5	80	University of Jaén
Brigitte Jaumard	17	1	92	Concordia University
Zhilong Xiu	17	2	43	Dalian University of Technology
Ralf Seppelt	16	1	41	The Helmholtz Centre for Environmental Research
John Sessions	14	1	57	Oregon State University
Jens Schrader	14	1	50	Karl Winnacker Institute

Table 5. Top ten scholars’ contributions.

Author	h-Index	Relevant Publications	Total Publications	Institution
Xiao Dong Chen	30	1	213	University of Aukland
Sing Kiong Nguang	25	1	108	University of Aukland
Pragasen Pillay	21	1	101	Concordia University
Taher Niknam	21	1	116	Shiraz University of Technology
Francisco Jurado	18	5	80	University of Jaén
Brigitte Jaumard	17	1	92	Concordia University
Zhilong Xiu	17	2	43	Dalian University of Technology
Ralf Seppelt	16	1	41	The Helmholtz Centre for Environmental Research
John Sessions	14	1	57	Oregon State University
Jens Schrader	14	1	50	Karl Winnacker Institute

4. Review of Metaheuristics

Metaheuristics are solution procedures that orchestrate local improvement algorithms and higher-level strategies to create a method capable of escaping local optima and performing an efficient search of large and complex (nonlinear/non-convex) solution spaces [26]. Metaheuristics usually provide good solution to optimization problems with imperfect information and/or limited computation capacity. Although metaheuristics can be employed for a large variety of research areas, ad hoc heuristics are frequently applied for a particular type of problem. Two classifications of metaheuristic algorithms are as follows: (1) population approaches, such as ant colony optimization, the genetic algorithm, particle swarm optimization, and bee colony algorithm; and (2) trajectory approaches, such as the tabu search, and simulated annealing. This paper reviews and studies the metaheuristic algorithms that have been employed for the bioenergy supply chain.

4.1. Ant Colony Optimization (ACO) Algorithm

Ant colony optimization (ACO), introduced by Dorigo [27] in 1992, is based on the behavior of ants searching for a trail between their colony and a source of food to seek an optimal path. ACO aimed to solve the traveling salesman problem (TSP). Although sound results were achieved, ACO did not perform better than other algorithms utilized to solve the TSP. Nonetheless, ACO has obtained world class performance when applied to solve manufacturing and logistics problems such as scheduling [28], sequential ordering [29], assembly line balancing [30], and probabilistic TSP [31], among others. In the structure of ACO, first, ants will seek areas near the nest aimlessly, and then, they spread out farther to find food. While ants search for food, they leave a chemical substance called a pheromone, which can be discovered by other members of their nest. After finding food and evaluating its quality and quantity, the ant will leave a sufficient amount of pheromone to help the rest of colony to track the food source. In technical terms, artificial ants of ACO are stochastic solution construction techniques using pheromone trails based upon previous search knowledge to suggest candidate solutions for the problem [32]. The performance of the ACO is enriched by increasing the diversity via transferring knowledge from previous environments to the pheromone trails using immigrant schemes [33]. The pseudo code of ACO is presented in Algorithm 1 [26].

Algorithm 1 Ant colony optimization [26]

procedure ACO algorithm for combinatorial optimization problems Initialization while (termination condition is not satisfied) do Construct Ant Solutions Apply Local Search  % optional Update Pheromones end

end

4.2. Genetic Algorithm (GA)

The genetic algorithm (GA), which was introduced by John H. Holland [34] in 1975, is an adaptive metaheuristic emulating the process of natural selection and evolution. Holland’s influential book Adaptation in Natural and Artificial Systems was seminal and created a new area of scientific inquiry. In addition, Holland’s PhD student, Ken De Jong, made a valuable contribution by presenting the use of GA in optimization in his dissertation work completed in 1975 [35]. The first conference on this new field was held in 1985. Subsequently, David Goldberg, another PhD student of Holland, wrote a first-winning award dissertation where a gas pipeline optimization problem was addressed and also wrote a seminal book entitled Genetic Algorithms in Search, Optimization, and Machine Learning [36].

Genes in the GA are the design variables, and the chromosome represents a potential solution. The possible solutions are saved after each iteration. By computing the fitness value (which is determined through an evaluation of the population’s individuals), two individuals are selected and are modified through genetic operators, including crossover and mutation, to create a new generation of individuals. The general pseudo code of the GA is illustrated in Algorithm 2 [26]. GA has become a popular solution procedure to solve combinatorial problems, with application to numerous fields, because it is problem independent. The application of GA to address multi-objective problems is also remarkable. A notable improvement on the performance of the multi-objective genetic algorithm is the use of a new constraint handling technique, providing solutions close to the real Pareto front, where closeness, diversity, and feasibility are considered the three objectives in a multi-objective sub-problem [37].

4.3. Particle Swarm Optimization (PSO)

Particle swarm optimization (PSO) is a swarm-based optimization algorithm introduced by Kennedy and Eberhart in 1995 [38]. Indeed, PSO was inspired by the flying of a bird flock as the birds utilize different paths to arrive at the same destination. There are different stages to the PSO. Beginning with particles representation, in which particles represent the possible solutions. Also, swarm based PSO uses a bundle of particles in order to search for best solutions. Then, it follows into the particles’ and swarms’ best experience in which the algorithm collects each particle’s best location and velocities. Then follows down to the particle movement, where the particles move until the stopping criterion is met, which is either an acceptable optimal solution or a given number of iterations [39]. Algorithm 3 shows the PSO pseudocode.

Algorithm 2 The general pseudo code of the genetic algorithm [26]

Choose an initial population of chromosomes:

while termination condition is not satisfied do

repeat

if crossover condition is satisfied then choose parent chromosomes; select crossover parameters; perform crossover; if mutation condition is satisfied then select mutation points; perform mutation; evaluate fitness of offspring;

until sufficient offspring is generated;

choose new population;

end while

Algorithm 3 Particle swarm optimization [39]

Initialize the particles with random positions and velocities. Until a termination criterion is satisfied (e.g., a given number of fitness evaluations have been executed, observed fitness stagnates, or a fitness threshold is satisfied), repeat: For each particle with position $\overrightarrow{x}$ and velocity $\overrightarrow{v}$. do: Update the particle's velocity using the following equation: $\overrightarrow{v}\leftarrow \omega \overrightarrow{v}+{\varnothing }_p{r}_p\left(\overrightarrow{p}-\overrightarrow{x}\right)+{\varnothing }_g{r}_g\left(\overrightarrow{g}-\overrightarrow{x}\right)$ where the user-defined behavioral parameter $\omega ϵℝ$ is named the inertia weight and controls the amount of recurrence in the particle’s velocity. The particle’s previous best position is $\overrightarrow{p}$, and $\overrightarrow{g}$ is the swarm’s previous best position through which the particles communicate implicitly with each other. These are wghted by the stochastic variables $r_p, r_g\sim U(0,1)$ and the user-defined behavioral parameters ${\varnothing }_p, {\varnothing }_gϵℝ$ Enforce velocity boundaries Move the particle to its new position using $\overrightarrow{x} \leftarrow \overrightarrow{x}+\overrightarrow{v}$ Enforce search-space boundaries on the particle’s position by moving it back to the boundary value if it has been exceeded. If ($f(\overrightarrow{x})<f(\overrightarrow{p}))$) then update the particle’s best known position:     $\overrightarrow{p} \leftarrow \overrightarrow{x}$ And similarly for the entire swarm's best known position $\overrightarrow{g}$.

4.4. Bee Colony Algorithm (BCA)

The bee colony algorithm (BCA) is an optimization algorithm inspired by the intelligent behavior of honey bees and was introduced by Karaboga in 2005 [40]. BCA is based on the bees’ logic for finding food. There are three classifications for bees: employee, onlooker, and scout. First, the employee bees seek food, and when these bees find food, they return to the hive. Then, onlooker bees can track a high quality source of food. When the collection is terminated, the employee bee joins the scout bees that are constantly seeking for food. In this respect, the onlooker and employee bee are modeled as the exploitation method while the scout bees are modeled as the exploration technique. The BCA’s pitfall is that it is good for exploration but it lacks the exploitation factor. In other words, it suffers from being trapped in local optimal solutions because its functions for searching for new solutions are based on previous ones. The capabilities of the bee colony can be enhanced using a hybrid representation and a combination of forward decoding and backward decoding methods as in [41]. A general pseudo code of the bee colony algorithm is presented in Algorithm 4 [42].

Algorithm 4 General bee colony algorithm [42]

B—The number of bees in the hive;

NC—The number of constructive moves during one forward pass.

At the start of the search, all the bees are in the hive. The pseudo-code of the BCO algorithm follows: (1) Initialization: an empty solution is given to each bee; (2) For each bee: // (the forward pass) (a) Set k = 1; //(count constructive moves in the forward pass) (b) Evaluate all possible constructive moves; (c) Select one move utilizing the roulette wheel; (d) k = k + 1; If k ≤ NC Go to step (b). (3) All bees are back to the hive; // (backward pass starts) (4) Evaluate (partial) objective function value for each bee; (5) Each bee decides randomly whether to continue its own search and become a recruiter, or a follower; (6) For each follower, select a new solution from recruiters by the roulette wheel; (7) If solutions are not completed Go to step 2; (8) Evaluate all solutions and find the best one; (9) If the stopping criteria is not satisfied Go to step 2; (10) Output (i.e., the best found solution).

Step (2) and (4) are problem dependent and should be resolved in each BCO algorithm implementation. However, there are formulae stating steps, (5) loyalty decisions, and (6) recruiting process.

4.5. Tabu Search

The tabu search (TS) introduced by Glover in 1986 is a metaheuristic approach to address combinatorial optimization problems [43]. More precisely, TS is an extension of classical local search methods, in fact, it can be interpreted as the combination of local search with short-term memories. Two basic elements of TS are the definition of its search space and its neighborhood structure. The search space is defined as the space of all possible solutions that can be visited during the search. Regarding the neighborhood structure, at each iteration of the algorithm, the local transformation that can be applied to the current solution, define a set of neighboring solutions in the search space, that is, the neighborhood of current solution. Indeed, the neighborhood of the current solution is a subset of the search space of all the solutions obtained by employing a single local transformation to the present solution.

Tabus are used to prevent cycling (doing non-improving moves) when moving away from local optima. Tabus are implemented to prevent the search from back-tracking its steps. Therefore, tabus mean forbidden moves that reverse the effect of recent moves. However, it is possible to back-track if the solution obtained results better than any found so far (by using the aspiration criteria). The tabu list (or restrictive list) contains tabus and it is stored in a short-term memory of the search. The tabu list causes the restriction of certain moves. Multiple tabu lists can be used simultaneously. Some modifications to the basic tabu list are: variable tabu list length during the search [44,45,46,47,48] and tabu tenure [49] of each move within some number of iterations. As mentioned before, the tabu list may prevent the algorithm from making attractive moves. Thus, it is necessary to implement algorithmic devices that allow cancelling tabus. These are called aspiration criteria. A flow chart of a TS is presented in Algorithm 5 [26]. For instance, one recent improvement of the traditional is the implementation of a guided perturbation mechanism [50]. Gendreau and Potvin [26] provided a tutorial and template for the tabu search application.

Algorithm 5 Tabu search [26]

Notation

S, the current solution, S∗, the best-known solution, f ∗, the value of S∗, N(S), the neighborhood of S, $\tilde{N} (S)$, the admissible subset of N(S) (i.e., non-tabu or allowed by aspiration), T, the tabu list.

Initialization

Choose (construct) an initial solution S0.

Set S ← S0, f∗ ← f (S0), S∗ ← S0, T ← ∅.

Search

While termination criterion not satisfied do select S in $argmi{n}_{S’\in \tilde{N} (S)}$ [f(S’)]; if f (S) < f∗, then set f∗ ← f (S), S∗ ← S; record tabu for the current move in T (delete oldest entry if necessary).

4.6. Simulated Annealing (SA)

Simulated annealing (SA) is an adaptation of the Metropolis-Hastings algorithm published in a paper by Metropolis et al. [51] in 1953 and it is a metaheuristic algorithm inspired by annealing in metallurgy that aims to find the global optimum in a large search space. SA is frequently utilized when the search space is discrete and can also be used for continuous and multi-objective optimization problems (known as MOSA). The unique advantages of SA are its ability to escape from local optima, straightforward implementation, and rapid convergence. The origin of SA is the physical annealing process, which is a technique for heating and controlled cooling of a solid and achieving low energy states of a solid in a heat bath [52]. The comparison between the physical process and a combinatorial optimization problem illustrates that solutions in a combinatorial problem are analogous to the states of a physical system, and the value of a solution is similar to the energy of a state [52]. First, SA begins with an initial feasible solution accompanied by assessment and perturbation functions and then proceeds to performing a random search of the state space. SA improves its search strategy by introducing the Metropolis algorithm and a cooling ratio. First, after comparing the present and new generated solutions at each iteration, better solutions are always accepted, while inferior (substandard) solutions are accepted with a probability determined by the Metropolis criteria to allow the algorithm to perform hill-climbing moves and explore more of the possible space of solutions. The criterion is based on the following formula, $e^{-\Delta D/T}>R\left(0,1\right)$, where ΔD is the change of the output value of the objective function, T is the system’s temperature and R(0,1) is a random number in the interval [0,1]. Because of the Metropolis criterion, SA has the ability to escape from local optima. However, as the temperature of the system (T) decreases, transition moves to feasible solutions with lower quality occur less frequently. The second strategy is to lower the temperature according to a cooling ratio; by lowering the temperature, SA will reject inferior solutions and will focus in conducting a local search. The performance of simulated annealing can be enhanced via coupling it with a dynamically restricted search space strategy to accomplish the global optimization of the energy management [53].

The pseudo code of the simulated annealing is shown in Algorithm 6 [26]. Literature reviews of the theoretical development and applications of simulated annealing can be found in references [54,55,56,57,58,59]. The following books are also appropriate for interested readers: Aarts and Korst [52] and Van Laarhoven [60].

Algorithm 6 Simulated annealing [26]

Choose an initial solution ω ϵ Ω

Choose the temperature change counter k = 0

Choose a temperature cooling schedule, tk

Choose an initial temperature T = t0 ≥ 0

Choose a repetition schedule, Mk, which defines the number of iterations executed at each temperature, tk

Repeat

Set repetition counter m = 0

Repeat

Generate a solution ${\omega }^{\text{'}}ϵN\left(\omega \right)$

Calculate ${\Delta }_{\omega ,{\omega }^{\text{'}}}=f\left({\omega }^{\text{'}}\right)-f\left(\omega \right)$

If ${\Delta }_{\omega ,{\omega }^{\text{'}}}\le 0$, then $\omega \leftarrow {\omega }^{\text{'}}$

If ${\Delta }_{\omega ,{\omega }^{\text{'}}}>0$, then $\omega \leftarrow {\omega }^{\text{'}}$ with probability $\exp \left(-{\Delta }_{\omega ,{\omega }^{\text{'}}}/t_k\right)$

$m\leftarrow m+1$

Until $m=M_k$

k ← k + 1

Until stopping criterion is satisfied

4.7. Hybrid Metaheuristics

Because of the advantages of using two or more optimization algorithms simultaneously, there is an increasing tendency to utilize hybrid optimization algorithms [26]. More precisely, the hybrid algorithms can be a hybrid of two or more metaheuristics or can be a hybrid of metaheuristics and traditional mathematical optimization approaches. Furthermore, multistep approaches and nested methods have been suggested in the literature. By using the advantages of the individual methods, most of hybrid algorithms operate better than their pure counterparts [26].

5. Review of Metaheuristics Applied to Solve Bioenergy Supply Chain Problems

The objective of this paper is to review the application of metaheuristics in bioenergy supply chains. This research was carried out via utilizing scholar databases such as Wiley Online Library, Science Direct, Scopus, IEEE, EBSCO Host, ProQuest, Google Scholar, among others. Only academic publications (i.e., journal articles, dissertations/thesis, and conference proceedings) were included.

This paper focuses on the aforementioned described metaheuristics. In addition, hybrid methods, multi-step, and nested methods are discussed. Depending on the aspect of the supply chain to which the metaheuristics are applied, the research publications are classified into several categories in this paper. In the category of “integrated supply chain planning”, combined solutions for strategic supply chain planning and investment are presented. Indeed, several different decisions such as distribution routes, facility location, the size of production, supply resources, production, and technology are included in this area. Some of these decisions are associated with each other, for example, national route databases and geographic information systems (GIS) are coupled in the optimization problem.

The category of “Bioconversion and Production Process Optimization” involves papers primarily concerning both tactical and operational decisions related to the optimization of conversion process’ parameters (midstream supply chain) including yield, energy requirements, and capacity planning, among others. Proposing solution methods to design the best route of transportation from a network are presented in the category of “supply chain network design”, which includes both strategic and tactical decisions. The operational decisions, focused on scheduling trucks for the distribution of biomass/biofuel and task scheduling, are discussed in the section “scheduling problems”. The category of “facility location” includes the strategic decision of finding the best location for biorefineries.

5.1. Integrated Supply Chain Planning

To design the bioenergy production from biomass, many notable factors should be considered including transportation, the conversion process, biomass suppliers, electricity suppliers, costs, environmental impacts, and social concerns. In this respect, some of the decision variables concerning the design of supply chains involve location, size, and distribution routes. Table 6 summarizes the reviewed articles.

5.2. Bioconversion and Production Process Optimization

Bioconversion science is the conversion of organic materials, such as plant or animal waste, into energy sources or usable materials using biological processes such as microorganisms, enzymes or Detritivores. Bioenergy process optimization consists of finding appropriate process parameters to improve the bioenergy yield and/or minimize energy and water requirements. Due to the conflicting objective function, multi-objective metaheuristics are often developed. The bioconversion process usually involves chemical reactions following nonlinear relationships making the use of metaheuristics and hybrid heuristics a widely used technique to optimize conversion processes. Table 7 presents a summary of the reviewed works according to the bioconversion and production process optimization category.

Table 6. Reviewed articles in the integrated supply chain planning category.

Ref.	Metaheuristic(s)	Application and Relevant Findings
[61]	GA	Two-level general Bioenergy Decision System (gBEDS) for bioenergy production planning and implementation is developed. The gBEDS includes the basic bioenergy information and the detailed decision information. Basic bioenergy information involves the geographical information system (GIS), biomass materials, biomass logistic, and conversion databases. The detailed decision information consists of the parameters’ default values database and the decision variables database obtained through optimization and simulation. A simulation based on the unit process definition and the GA are performed to decide the biomass storage places and define the location of storage and bioenergy conversion plants.
[62]	GA	The gBEDS [61] is extended by considering supply chains that simultaneously use the different nature and sources of bio-resources utilized in the bioenergy production instead of a single type of biomass previously considered. To optimize costs, energy utilization, emissions, or labor individually, an optimization model using the GA for designing and assessing the integrated bioenergy production supply chain is implemented. This optimization problem is an order-based problem because the solution is specified in the form of an arrangement of unit process models. Finding the best combination of unit processes that meet constraints is a difficult-to-solve combinatorial problem (GA have proven to be a successful algorithm for solving combinatorial problems). Finally, the experiments illustrate that this system can ascertain many combinations of unit processes in a remarkable running time of 65 s for the small-size problem consisting of 16 unit processes in the supply chain and a running time of 170 s for the large-size problem including 43 unit processes.
[63]	GA	GA is used to determine the optimal number, location, and capacity of a biomass combined heat and power facility in Sardinia (Italy) by maximizing the economic benefit of private investors. This optimization procedure is based upon a grid subdivision of the territory and is integrated with a GIS to collect all pertinent spatial or geographical data. The objective function is the profitability, which involves three main terms: (1) the cost of building and the operation of the biomass combined heat and power facility; (2) the revenue derived from the sales of electrical energy and the other products gained during the process; and (3) the cost for the disposal of the biomass available but not utilized.
[64]	PSO	A biomass supply chain optimization model with a nonlinear objective function is presented. In this problem, the continuous and binary decision variables are the annual biomass quantity harvested and the presence of the technology in a known location, respectively. In a previous work, the author developed a PSO which improves the performance of standard discrete PSO. To preclude premature convergence, the random regeneration of many birds that tended to hit the best birds, is utilized. The inclusion of this procedure into the discrete PSO showed increased diversity, improved convergence and higher solution quality. The model is used for the community of Val Bormida, Italy.
[5]	Hybrid: GA and sequential quadratic programing (SQP)	A decision support system for multi-biomass energy conversion to help investors evaluate an investment in regional current multi-biomass exploitation for tri-generation applications, that is electricity, heating, and cooling is developed. The use of a multi-biomass supply chain provides considerable potential for cost reduction by spreading capital costs and diminishing warehousing requirements in the case of seasonal biomass. To optimize the entire bioenergy system, first, GA is employed to define a good solution to the problem. This solution is used as the starting point of the second optimization method (SQP) which aims to enhance further the solution found at the first step. Although GA performs appropriately in finding a solution near the global optimum, GA converges very slowly after a particular point. In this respect, GA cannot perform properly in the case of a local search. However, SQP is appropriate for a local search. Therefore, a hybrid algorithm (combining GA and SQP) is employed. The results show insights for potential investors concerning the sensitivity to investment parameters.
[65]	Hybrid: GA and sequential quadratic programing (SQP)	The same hybrid method used [5] is implemented to optimize the facility location, biomass supply and inventory, and operational parameters of a biomass tri-generation plant providing particular energy needs in Greece. The decision variables of this paper involve the exact location of the power plant, which is the longitude and latitude of the facility location, thermal capacity, initial annual biomass inventory, and monthly biomass inventory. The objective function of this problem is to maximize the net present value of the investment for the project’s lifetime. Results show the superior performance of the hybrid algorithm compared with each single algorithm. When considering objective function values over 98 percent of the real optimum solution, the hybrid approach passed the indicated threshold in 87 percent of the cases, SQP in 54 percent, and GA in 40 percent.
[66]	Hybrid: GA, Monte Carlo (MC) simulation and mixed integer linear programming (MILP)	Strategic planning of bioethanol supply chains under uncertainty in the demand of the sugar cane industry is studied. A two-level optimization algorithm is used, including an outer loop, which is a GA, and an inner loop, which is a MC simulation over a MILP deterministic supply chain model. The optimization algorithm involves two stages of variables. The first-stage variables are proposed by GA and include supply chain design decision, initial capacities, capacity expansions over the time horizon, and the number of production, storage, and transportation units. Then, an MILP optimization model is used to evaluate the second-stage variables, including the amount of products to be produced and stored and the flows of materials shipped among the supply chain entities and product trades. The objective function of the inner loop is the net present value. Finally, the net present value (NPV) gained at each iteration is inserted into GA to input new values for the first stage variables regarding the objective function of the outer loop as the expected value of customer satisfaction (CSat). Thus, this approach combines two objective functions, NPV and CSat and handles 70 uncertain parameters. This model provides the investment strategy for the near-optimal SC configuration.
[67]	Hybrid: GA with embedded Lagrangian relaxation and traffic assignment algorithms	An integrated mathematical model for the biofuel supply chain design by ascertaining the near-optimal number and position of biorefinery facilities, near-optimal routing of biomass and biofuel transportation, and feasible highway/railroad capacity expansion is presented. A GA with embedded Lagrangian relaxation and traffic assignment algorithms is implemented. A practical case study for the state of Illinois is presented. The objective function of this study is to minimize the total cost for biorefinery construction, transportation infrastructure development, and transportation delay for both biofuel/biomass transportation and public travel under traffic jam. The proposed GA randomly conducts chromosome operations (selection of links); thus, this approach is not exploiting the underlying network structure. The authors state as future work addressing the possible correlation of sequential links by developing chromosome operations that selects blocks of links.
[68]	TS	The problem of the plant design and the location-transportation design of biomass, which includes the biomass-producing regions, the amounts of biomass for transportation, the location of the plant, and generating the best combination of technologies for converting biomass into specific products is studied. TS is used to determine the plant location based upon defined binary variables to maximize the profit with given demands and product prices. TS is set up by a maximum of 500 iterations and a tabu list of 50 solutions. The results demonstrate the proper performance of the TS procedure and the possibility of integrating the logistics and process synthesis in a combined approach.

Table 6. Reviewed articles in the integrated supply chain planning category.

Ref.	Metaheuristic(s)	Application and Relevant Findings
[61]	GA	Two-level general Bioenergy Decision System (gBEDS) for bioenergy production planning and implementation is developed. The gBEDS includes the basic bioenergy information and the detailed decision information. Basic bioenergy information involves the geographical information system (GIS), biomass materials, biomass logistic, and conversion databases. The detailed decision information consists of the parameters’ default values database and the decision variables database obtained through optimization and simulation. A simulation based on the unit process definition and the GA are performed to decide the biomass storage places and define the location of storage and bioenergy conversion plants.
[62]	GA	The gBEDS [61] is extended by considering supply chains that simultaneously use the different nature and sources of bio-resources utilized in the bioenergy production instead of a single type of biomass previously considered. To optimize costs, energy utilization, emissions, or labor individually, an optimization model using the GA for designing and assessing the integrated bioenergy production supply chain is implemented. This optimization problem is an order-based problem because the solution is specified in the form of an arrangement of unit process models. Finding the best combination of unit processes that meet constraints is a difficult-to-solve combinatorial problem (GA have proven to be a successful algorithm for solving combinatorial problems). Finally, the experiments illustrate that this system can ascertain many combinations of unit processes in a remarkable running time of 65 s for the small-size problem consisting of 16 unit processes in the supply chain and a running time of 170 s for the large-size problem including 43 unit processes.
[63]	GA	GA is used to determine the optimal number, location, and capacity of a biomass combined heat and power facility in Sardinia (Italy) by maximizing the economic benefit of private investors. This optimization procedure is based upon a grid subdivision of the territory and is integrated with a GIS to collect all pertinent spatial or geographical data. The objective function is the profitability, which involves three main terms: (1) the cost of building and the operation of the biomass combined heat and power facility; (2) the revenue derived from the sales of electrical energy and the other products gained during the process; and (3) the cost for the disposal of the biomass available but not utilized.
[64]	PSO	A biomass supply chain optimization model with a nonlinear objective function is presented. In this problem, the continuous and binary decision variables are the annual biomass quantity harvested and the presence of the technology in a known location, respectively. In a previous work, the author developed a PSO which improves the performance of standard discrete PSO. To preclude premature convergence, the random regeneration of many birds that tended to hit the best birds, is utilized. The inclusion of this procedure into the discrete PSO showed increased diversity, improved convergence and higher solution quality. The model is used for the community of Val Bormida, Italy.
[5]	Hybrid: GA and sequential quadratic programing (SQP)	A decision support system for multi-biomass energy conversion to help investors evaluate an investment in regional current multi-biomass exploitation for tri-generation applications, that is electricity, heating, and cooling is developed. The use of a multi-biomass supply chain provides considerable potential for cost reduction by spreading capital costs and diminishing warehousing requirements in the case of seasonal biomass. To optimize the entire bioenergy system, first, GA is employed to define a good solution to the problem. This solution is used as the starting point of the second optimization method (SQP) which aims to enhance further the solution found at the first step. Although GA performs appropriately in finding a solution near the global optimum, GA converges very slowly after a particular point. In this respect, GA cannot perform properly in the case of a local search. However, SQP is appropriate for a local search. Therefore, a hybrid algorithm (combining GA and SQP) is employed. The results show insights for potential investors concerning the sensitivity to investment parameters.
[65]	Hybrid: GA and sequential quadratic programing (SQP)	The same hybrid method used [5] is implemented to optimize the facility location, biomass supply and inventory, and operational parameters of a biomass tri-generation plant providing particular energy needs in Greece. The decision variables of this paper involve the exact location of the power plant, which is the longitude and latitude of the facility location, thermal capacity, initial annual biomass inventory, and monthly biomass inventory. The objective function of this problem is to maximize the net present value of the investment for the project’s lifetime. Results show the superior performance of the hybrid algorithm compared with each single algorithm. When considering objective function values over 98 percent of the real optimum solution, the hybrid approach passed the indicated threshold in 87 percent of the cases, SQP in 54 percent, and GA in 40 percent.
[66]	Hybrid: GA, Monte Carlo (MC) simulation and mixed integer linear programming (MILP)	Strategic planning of bioethanol supply chains under uncertainty in the demand of the sugar cane industry is studied. A two-level optimization algorithm is used, including an outer loop, which is a GA, and an inner loop, which is a MC simulation over a MILP deterministic supply chain model. The optimization algorithm involves two stages of variables. The first-stage variables are proposed by GA and include supply chain design decision, initial capacities, capacity expansions over the time horizon, and the number of production, storage, and transportation units. Then, an MILP optimization model is used to evaluate the second-stage variables, including the amount of products to be produced and stored and the flows of materials shipped among the supply chain entities and product trades. The objective function of the inner loop is the net present value. Finally, the net present value (NPV) gained at each iteration is inserted into GA to input new values for the first stage variables regarding the objective function of the outer loop as the expected value of customer satisfaction (CSat). Thus, this approach combines two objective functions, NPV and CSat and handles 70 uncertain parameters. This model provides the investment strategy for the near-optimal SC configuration.
[67]	Hybrid: GA with embedded Lagrangian relaxation and traffic assignment algorithms	An integrated mathematical model for the biofuel supply chain design by ascertaining the near-optimal number and position of biorefinery facilities, near-optimal routing of biomass and biofuel transportation, and feasible highway/railroad capacity expansion is presented. A GA with embedded Lagrangian relaxation and traffic assignment algorithms is implemented. A practical case study for the state of Illinois is presented. The objective function of this study is to minimize the total cost for biorefinery construction, transportation infrastructure development, and transportation delay for both biofuel/biomass transportation and public travel under traffic jam. The proposed GA randomly conducts chromosome operations (selection of links); thus, this approach is not exploiting the underlying network structure. The authors state as future work addressing the possible correlation of sequential links by developing chromosome operations that selects blocks of links.
[68]	TS	The problem of the plant design and the location-transportation design of biomass, which includes the biomass-producing regions, the amounts of biomass for transportation, the location of the plant, and generating the best combination of technologies for converting biomass into specific products is studied. TS is used to determine the plant location based upon defined binary variables to maximize the profit with given demands and product prices. TS is set up by a maximum of 500 iterations and a tabu list of 50 solutions. The results demonstrate the proper performance of the TS procedure and the possibility of integrating the logistics and process synthesis in a combined approach.

Table 7. Reviewed articles in the bioconversion and production process optimization category.

Ref.	Method	Application and Relevant Findings
[69]	GA	GA combined with an extended recurrent neural network model is proposed to augment the final biomass quality for the fed-batch fermentation process. To provide meaningful information for the biomass prediction, the nonlinear relationship between the biomass product and the manipulated feed rate is described by two recurrent neural sub-models. In this work, a population size of 150 is selected for GA. Regarding procedure’s parameters, 2000 generations are required to gain a smooth profile for the mathematical model and 2500 generations are required to obtain a smooth profile for the neural network model. The final biomass quantity that results from the optimal feed rate profile reaches 99.8% of the real optimal value obtained using the mechanistic model.
[70]	Multi-objective: MOGA II	MOGA II is implemented to design the parameters of the industrial biodiesel production process, including conversion and biodiesel purification, to maximize the purity of some crucial compounds and to minimize the energy requirements in the process. The results indicate that one point of the Pareto front guarantees the lowest specific energy consumption, while all the obtained optimal configurations meet the requirements of EN 14214 in terms of the biodiesel quality.
[71]	Hybrid: artificial neural network (ANN) coupled with GA	A model and solution procedure is proposed to optimize the biogas production process on mixed substrates of saw dust, cow dung, banana stem, rice bran, and paper waste using an Artificial Neural Network (ANN) coupled with GA. Twenty five semi-pilot biogas fermentations runs were used to train the ANN, which serves as the fitness function in the GA optimization. A recipe for an optimum biogas production is obtained, which provides an increase of 8.64% in biogas production and an accelerated biogas fermentation (the solution started the fermentation on the 3rd day vs. the 8th day in the non-optimized scenario).
[72]	GA	GA is proposed to optimize the fermentation parameters for maximum yield of ethanol produced from renewable biomass. The regression equation obtained after regression analysis is utilized as a fitness function of the GA. The population size of 20, the 100 generations, the uniform selection function, the adaptive feasible mutation function, and the arithmetic crossover function are the selected parameters of the genetic algorithm. The results indicate that the maximum experimental ethanol yield gained is 58.4 g/L, which confirms the results of the predictions of the proposed model (i.e., a maximum ethanol yield of 59.59 g/L at 32 °C).
[73]	GA	GA is used to design the reaction variables of karanja biodiesel. A regression model obtained from the response surface methodology is used in the GA’s fitness function. Moreover, the GA’s parameters are the population size, crossover function, elite count, crossover fraction, mutation fraction, and number of generations, which are equal to 5000, 2 points, 1, 0.9, 0.01, and 20, respectively. The results illustrate a 25 percent enhancement in the average biodiesel yield. Moreover, the obtained qualities of karanja biodiesel are closer to the American Society for Testing & Materials (ASTM) standard of biodiesel.
[74]	Multi-objective: Non-dominated Sorting Genetic Algorithm-II (NSGA II)	NSGA II is proposed to address the problem of bioenergy crop production based on rape seed, food crop production, and water quality in the Parthe catchment in Central Germany. The four objective functions in this problem involve the bioenergy yield, food yield, average nitrate concentration, and low flow. The simulation ran with a population size of 360 individuals and ceased after 200 generations. Results indicate that the same level of bioenergy crop production can be achieved at different costs with respect to the other objectives. The main contribution of the algorithm is the quantification of the functional trade-offs for the feasible range of all objectives.
[75]	GA	GA selects an appropriate set of features for the estimation of forest biomass variables in two areas in Southern Finland. The biomass variables were obtained based upon tree-level field measurements with biomass models used for spruce, pine, and birch. The objective of the optimization algorithm was to minimize the root mean square error of the total biomass or stem value. In this algorithm, the size of the population was 300 strings, and the number of generations was 30.
[14]	Hybrid: Differential evolution and SA	An iterative approach integrating the Net Present Value with detailed mechanistic modeling, simulation, and process optimization is studied. This framework finds a suitable capacity plan and operating conditions for the process. Two metaheuristic algorithms, differential evolution and SA, are implemented to optimize the process conditions, including the temperature (hydrolysis), raw material loading (enzymes for hydrolysis), and flow rates (sugar allocation), for the efficiency of the selected biorefining process. The general configuration of the proposed iterative decision support method is classified into three types: strategic optimization, process simulation, and operational level optimization. A hypothetical case study of the lignocellulosic biorefinery is used to produce bioelectricity, bioethanol, and bio-succinic acid from switchgrass. The results reveal a deviation in optimal process yield and production capacities from initial literature estimates, which highlights the impact of using a multi-stage framework when designing the production system.
[76]	TS	TS is implemented to maximize revenue from biomass waste to energy conversion system for a sample farm with a herd size of 500. The objective function of this problem includes the capital cost, monthly cost of backup propane, value of incentives given monthly for the generation of renewable energy, and monthly cost of electricity obtained or sold to the grid. Due to the use of TS, optimal utilization of the installed generation capacity results in 48% more cost savings for the sample farm.
[77]	GA	GA is used to enhance the bioconversion of L-phenylalanine to 2-phenylethanol by designing different nutrients and temperatures. In the algorithm, the probability of the occurrence of crossover is set at 95%, and the mutation rate is set at 1%. In addition, the maximum number of individuals in one generation is 40. For a maximum concentration of 4 g/L for 2-phenylethanol in the organic phase, the product concentration is enhanced by 32% compared with the non-optimized medium. The results of this study demonstrate that product yields of enzyme and whole-cell bio-catalysis can be considerably enhanced not only by the enzyme but also by medium engineering employing a GA.
[78]	GA and ACO	To determine the optimal parameters of an E. coli fed-batch cultivation process model in terms of the biomass growth and substrate utilization, the GA and ACO are implemented and compared. The adjustment of the parameters of the optimization algorithms is performed through several pre-tests. In GA, the crossover rate is 0.7, the mutation rate is 0.5, the number of individuals is 200, and the number of generations is 200. In ACO, the number of ants is 20, the initial pheromone is 0.5, and the evaporation is 0.1. The results indicate that both ACO and GA perform adequately for this parameter optimization problem.
[79]	PSO	The problem of an impulsive dynamical system of glycerol bioconversion to 1,3-propanediol driven by a vector-valued measure in fed-batch fermentation is solve by a PSO. The objective function involves the concentration of biomass, glycerol, 1,3-propanediol, acetic acid, and ethanol. In this algorithm, the number of particles, maximum evolution generation, initial weight of inertia, and final weight of inertia are 20, 2000, 0.9, and 0.4, respectively. This study demonstrates the effectiveness of the variant from the classical PSO to address the problem of glycerol bioconversion to 1,3-propanediol in fed-batch fermentation.
[80]	PSO	Parallel PSO is used to gain the optimal pathway and the optimal parameter for the 14-dimensional nonlinear hybrid dynamical system of the bioconversion of glycerol to 1,3-propanediol. The robustness of the metabolic system is considered as the performance index in the study. To find global optimal solutions, a dynamic inertia weight is considered by the minimum inertia weight of 0.4 and the maximum inertia weight of 0.9. Moreover, the number of sub-processes is 30, the maximum iteration is 300, the cognitive scaling parameter is 2, and the social scaling parameter is 2. The results illustrate the feasibility of passing of 1,3-propanediol from the cell membrane by active transportation coupled with passive diffusion.
[81]	Hybrid: PSO and the Nelder-Mead simplex search method	This hybrid method estimate distribution state variables in the presence of renewable energy resources (biomass sources, geothermal sources, water, wind, and the sun). The objective function of the study involves the active power of renewable energy resources and loads. The comparison of the hybrid algorithm with ACO, GA, PSO, honey bee mating optimization, and neural networks shows that the proposed method can estimate the conditions of the target system more accurately than other algorithms for locating the best-practice optimum solutions of complex distribution state estimation problems.

Table 7. Reviewed articles in the bioconversion and production process optimization category.

Ref.	Method	Application and Relevant Findings
[69]	GA	GA combined with an extended recurrent neural network model is proposed to augment the final biomass quality for the fed-batch fermentation process. To provide meaningful information for the biomass prediction, the nonlinear relationship between the biomass product and the manipulated feed rate is described by two recurrent neural sub-models. In this work, a population size of 150 is selected for GA. Regarding procedure’s parameters, 2000 generations are required to gain a smooth profile for the mathematical model and 2500 generations are required to obtain a smooth profile for the neural network model. The final biomass quantity that results from the optimal feed rate profile reaches 99.8% of the real optimal value obtained using the mechanistic model.
[70]	Multi-objective: MOGA II	MOGA II is implemented to design the parameters of the industrial biodiesel production process, including conversion and biodiesel purification, to maximize the purity of some crucial compounds and to minimize the energy requirements in the process. The results indicate that one point of the Pareto front guarantees the lowest specific energy consumption, while all the obtained optimal configurations meet the requirements of EN 14214 in terms of the biodiesel quality.
[71]	Hybrid: artificial neural network (ANN) coupled with GA	A model and solution procedure is proposed to optimize the biogas production process on mixed substrates of saw dust, cow dung, banana stem, rice bran, and paper waste using an Artificial Neural Network (ANN) coupled with GA. Twenty five semi-pilot biogas fermentations runs were used to train the ANN, which serves as the fitness function in the GA optimization. A recipe for an optimum biogas production is obtained, which provides an increase of 8.64% in biogas production and an accelerated biogas fermentation (the solution started the fermentation on the 3rd day vs. the 8th day in the non-optimized scenario).
[72]	GA	GA is proposed to optimize the fermentation parameters for maximum yield of ethanol produced from renewable biomass. The regression equation obtained after regression analysis is utilized as a fitness function of the GA. The population size of 20, the 100 generations, the uniform selection function, the adaptive feasible mutation function, and the arithmetic crossover function are the selected parameters of the genetic algorithm. The results indicate that the maximum experimental ethanol yield gained is 58.4 g/L, which confirms the results of the predictions of the proposed model (i.e., a maximum ethanol yield of 59.59 g/L at 32 °C).
[73]	GA	GA is used to design the reaction variables of karanja biodiesel. A regression model obtained from the response surface methodology is used in the GA’s fitness function. Moreover, the GA’s parameters are the population size, crossover function, elite count, crossover fraction, mutation fraction, and number of generations, which are equal to 5000, 2 points, 1, 0.9, 0.01, and 20, respectively. The results illustrate a 25 percent enhancement in the average biodiesel yield. Moreover, the obtained qualities of karanja biodiesel are closer to the American Society for Testing & Materials (ASTM) standard of biodiesel.
[74]	Multi-objective: Non-dominated Sorting Genetic Algorithm-II (NSGA II)	NSGA II is proposed to address the problem of bioenergy crop production based on rape seed, food crop production, and water quality in the Parthe catchment in Central Germany. The four objective functions in this problem involve the bioenergy yield, food yield, average nitrate concentration, and low flow. The simulation ran with a population size of 360 individuals and ceased after 200 generations. Results indicate that the same level of bioenergy crop production can be achieved at different costs with respect to the other objectives. The main contribution of the algorithm is the quantification of the functional trade-offs for the feasible range of all objectives.
[75]	GA	GA selects an appropriate set of features for the estimation of forest biomass variables in two areas in Southern Finland. The biomass variables were obtained based upon tree-level field measurements with biomass models used for spruce, pine, and birch. The objective of the optimization algorithm was to minimize the root mean square error of the total biomass or stem value. In this algorithm, the size of the population was 300 strings, and the number of generations was 30.
[14]	Hybrid: Differential evolution and SA	An iterative approach integrating the Net Present Value with detailed mechanistic modeling, simulation, and process optimization is studied. This framework finds a suitable capacity plan and operating conditions for the process. Two metaheuristic algorithms, differential evolution and SA, are implemented to optimize the process conditions, including the temperature (hydrolysis), raw material loading (enzymes for hydrolysis), and flow rates (sugar allocation), for the efficiency of the selected biorefining process. The general configuration of the proposed iterative decision support method is classified into three types: strategic optimization, process simulation, and operational level optimization. A hypothetical case study of the lignocellulosic biorefinery is used to produce bioelectricity, bioethanol, and bio-succinic acid from switchgrass. The results reveal a deviation in optimal process yield and production capacities from initial literature estimates, which highlights the impact of using a multi-stage framework when designing the production system.
[76]	TS	TS is implemented to maximize revenue from biomass waste to energy conversion system for a sample farm with a herd size of 500. The objective function of this problem includes the capital cost, monthly cost of backup propane, value of incentives given monthly for the generation of renewable energy, and monthly cost of electricity obtained or sold to the grid. Due to the use of TS, optimal utilization of the installed generation capacity results in 48% more cost savings for the sample farm.
[77]	GA	GA is used to enhance the bioconversion of L-phenylalanine to 2-phenylethanol by designing different nutrients and temperatures. In the algorithm, the probability of the occurrence of crossover is set at 95%, and the mutation rate is set at 1%. In addition, the maximum number of individuals in one generation is 40. For a maximum concentration of 4 g/L for 2-phenylethanol in the organic phase, the product concentration is enhanced by 32% compared with the non-optimized medium. The results of this study demonstrate that product yields of enzyme and whole-cell bio-catalysis can be considerably enhanced not only by the enzyme but also by medium engineering employing a GA.
[78]	GA and ACO	To determine the optimal parameters of an E. coli fed-batch cultivation process model in terms of the biomass growth and substrate utilization, the GA and ACO are implemented and compared. The adjustment of the parameters of the optimization algorithms is performed through several pre-tests. In GA, the crossover rate is 0.7, the mutation rate is 0.5, the number of individuals is 200, and the number of generations is 200. In ACO, the number of ants is 20, the initial pheromone is 0.5, and the evaporation is 0.1. The results indicate that both ACO and GA perform adequately for this parameter optimization problem.
[79]	PSO	The problem of an impulsive dynamical system of glycerol bioconversion to 1,3-propanediol driven by a vector-valued measure in fed-batch fermentation is solve by a PSO. The objective function involves the concentration of biomass, glycerol, 1,3-propanediol, acetic acid, and ethanol. In this algorithm, the number of particles, maximum evolution generation, initial weight of inertia, and final weight of inertia are 20, 2000, 0.9, and 0.4, respectively. This study demonstrates the effectiveness of the variant from the classical PSO to address the problem of glycerol bioconversion to 1,3-propanediol in fed-batch fermentation.
[80]	PSO	Parallel PSO is used to gain the optimal pathway and the optimal parameter for the 14-dimensional nonlinear hybrid dynamical system of the bioconversion of glycerol to 1,3-propanediol. The robustness of the metabolic system is considered as the performance index in the study. To find global optimal solutions, a dynamic inertia weight is considered by the minimum inertia weight of 0.4 and the maximum inertia weight of 0.9. Moreover, the number of sub-processes is 30, the maximum iteration is 300, the cognitive scaling parameter is 2, and the social scaling parameter is 2. The results illustrate the feasibility of passing of 1,3-propanediol from the cell membrane by active transportation coupled with passive diffusion.
[81]	Hybrid: PSO and the Nelder-Mead simplex search method	This hybrid method estimate distribution state variables in the presence of renewable energy resources (biomass sources, geothermal sources, water, wind, and the sun). The objective function of the study involves the active power of renewable energy resources and loads. The comparison of the hybrid algorithm with ACO, GA, PSO, honey bee mating optimization, and neural networks shows that the proposed method can estimate the conditions of the target system more accurately than other algorithms for locating the best-practice optimum solutions of complex distribution state estimation problems.

5.3. Supply Chain Network Design (SCND)

The design of the routes and transportation modes as well as the costs associated with them are considered as important Supply Chain Network Design (SCND) factors that can have a significant effect on the final price and competitiveness of bioenergy vs. petroleum-based products. Traditionally, first-generation biorefineries were located in the middle of the farms and received shipments from suppliers located within a 50-miles radius. The reason for this practice was the minimization of in-bound transportation costs. The biomass was typically delivered using trucks due to the short distance and the low volumes transported. As the industry is moving from local to large-scale supply chains to satisfy nation-wide demand for bioenergy, novel supply chain network design models and optimization algorithms are necessary to ensure the cost-efficient production of bioenergy. Table 8 presents the metaheuristics and models developed in the SCND class.

Table 8. Reviewed articles in the supply chain network design category.

Ref.	Method	Application and Relevant Findings
[82]	ACO	ACO and an unified modeling language is developed to optimize the supply chain route regarding the objective function of cost analysis in the route design for the transportation of raw biomass and the products of the bioenergy industry. Furthermore, the unified modeling language, which is an approach for analysis and software design, is utilized for the depiction of the complicated system using activity diagrams, class diagrams, case diagrams, state chart diagrams, sequence diagrams, and collaboration diagrams.
[83]	GA	GA is developed to optimize a combinatorial problem regarding three optimization criteria, which are bioenergy unit network (BUN) cost minimization, BUN emission minimization, and BUN energy consumption minimization, to determine the different economic and environmental burdens of the established biomass utilization networks. Their results show that GA is an effective algorithm to address the combinatorial problems of unit process models in the biomass utilization networks.
[84]	GA	A demand-driven processing optimization pattern to address seasonal variations in biomass supply and use of new utilization approaches is proposed. To guarantee flexibility in the biomass network design, a hierarchical method involving three steps is utilized. The first step is the design of the supply/demand processes in the local region. The second step involves defining the demands, requisites, and preferences of local administrators. The network design and optimization are performed in the third step. A case study is performed in the northern part of Japan, and the results illustrate the great potential of the solution approach.
[85]	Multi-objective ACO	A supply path problem in the palm-oil-based bioenergy supply chain using multi-objective fuzzy ACO is presented. Five echelons of the supply chain are the farmers, collectors, factories, bioenergy factories, and end customers. The research framework of this study involves seven steps: (1) defining the partners of the supply chain; (2) developing the supply network; (3) recognizing the measurement variables; (4) implementing a fuzzy logic method for obtaining three variables: transportation cost, value added, and performance of human resources; (5–6) measuring supply chain element and supply chain overall performance, and, finally; (7) searching for an intelligent supply chain based on ACO.

Table 8. Reviewed articles in the supply chain network design category.

Ref.	Method	Application and Relevant Findings
[82]	ACO	ACO and an unified modeling language is developed to optimize the supply chain route regarding the objective function of cost analysis in the route design for the transportation of raw biomass and the products of the bioenergy industry. Furthermore, the unified modeling language, which is an approach for analysis and software design, is utilized for the depiction of the complicated system using activity diagrams, class diagrams, case diagrams, state chart diagrams, sequence diagrams, and collaboration diagrams.
[83]	GA	GA is developed to optimize a combinatorial problem regarding three optimization criteria, which are bioenergy unit network (BUN) cost minimization, BUN emission minimization, and BUN energy consumption minimization, to determine the different economic and environmental burdens of the established biomass utilization networks. Their results show that GA is an effective algorithm to address the combinatorial problems of unit process models in the biomass utilization networks.
[84]	GA	A demand-driven processing optimization pattern to address seasonal variations in biomass supply and use of new utilization approaches is proposed. To guarantee flexibility in the biomass network design, a hierarchical method involving three steps is utilized. The first step is the design of the supply/demand processes in the local region. The second step involves defining the demands, requisites, and preferences of local administrators. The network design and optimization are performed in the third step. A case study is performed in the northern part of Japan, and the results illustrate the great potential of the solution approach.
[85]	Multi-objective ACO	A supply path problem in the palm-oil-based bioenergy supply chain using multi-objective fuzzy ACO is presented. Five echelons of the supply chain are the farmers, collectors, factories, bioenergy factories, and end customers. The research framework of this study involves seven steps: (1) defining the partners of the supply chain; (2) developing the supply network; (3) recognizing the measurement variables; (4) implementing a fuzzy logic method for obtaining three variables: transportation cost, value added, and performance of human resources; (5–6) measuring supply chain element and supply chain overall performance, and, finally; (7) searching for an intelligent supply chain based on ACO.

5.4. Scheduling Problems

The bioenergy industry faces unique challenges in terms of reduction of logistic costs (biomass has a low density and poor flow properties), travel time (biomass degrades over time), and waiting time. These factors are usually subject to many constraints, such as truck capacities, machinery availability, sparse and seasonal biomass supply, route limitations, and available transportation modes, among others. Minimizing logistic costs, travel time, and waiting time while satisfying constraints is a challenging scheduling problem. Moreover, the task scheduling is a prominent problem included in this category. To address these problems, heuristic optimization algorithms applied to both truck and task scheduling problems have been developed. Table 9 discusses the metaheuristics, models, and main findings in the bioenergy SCND.

Table 9. Reviewed articles in the scheduling category.

Ref.	Method	Application and Relevant Findings
[86]	SA	A model to enhance the economic feasibility of employing woody biomass to produce energy by diminishing the transportation costs is proposed. SA is implemented to address the truck scheduling problem for the transportation of woody biomass. The objective function of the study involves coping with the demand for different products and minimizing transportation costs and total labor hours. To evaluate the performance of the algorithm, a real case study including the scheduling of 50 loads is solved with satisfactory results.
[87]	SA	The transportation of woodchips for in-field chipping operations, where many operational factors affect their efficacy is studied. An adapted version of SA is proposed to minimize the objective functions of transportation costs, which involve fixed costs, travel times, and waiting times, while reaching a minimum level of utilization through the chippers determined by the operator. The truck payload and chipper utilization are two notable factors in this study, representing 52% and 29% of the obtained total cost savings, respectively. The algorithm is tested for a range of different scenarios for a case study in western Oregon.
[88]	Hybrid: TS and linear programming	A routing planning problem to decide the daily routes of logging trucks in forestry is developed. A two-step approach is proposed. In the first step, a LP problem to find a destination of flow from supply points to demand points (i.e., constructing transport nodes) is solved. In the second step, basic and extended TS are used to combine transport nodes (customers) into routes. The main idea of the proposed procedure is to decompose the problem into a standard vehicle routing problem with time windows. The model does not include queuing at nodes, which is indicated as potential future work. The method is tested in a case study involving major forest companies in Sweden.
[89]	Hybrid: TS and linear programming	A decision support system called RuttOpt to schedule logging trucks in the Swedish forest industry is proposed. The RuttOpt tool was built for the forest and hauling industries; however, it can be used by the biofuel industry for the transportation of woody material. This tool involves three modules. The first module is the road database. The second module is a two-phase optimization algorithm based upon a TS and linear programming proposed in a previous work [88]. The third module includes a database that saves all relevant information. Based on four case studies ranging from 10 to 110 trucks and a planning horizon ranging from 1 to 5 days, the results illustrate that the system can be utilized to address large systems with potential savings in the range of 5%–30%. Regarding solution time, for instance, a case with 12 trucks, 8 transporters, 22 demand nodes, 167 supply nodes, and a planning horizon of 3 days requires 10 min. For cases with 110 trucks and a planning horizon of 5 days, the authors used 100 min as solution time.
[90]	Hybrid: SA, GA, and hybrid Petri nets	A resource assignment and scheduling model is optimized via a two-phase metaheuristic based upon a SA, GA, and hybrid Petri nets. SA is used to optimize the resource assignment, and GA is utilized to search the priority lists and produce the schedule based upon the hybrid Petri nets. The hybrid net is a graphical and mathematical modeling device used for simulating the simultaneous, parallel, and stochastic activities of the system. The two-phase metaheuristic algorithm starts with a typical SA under a constraint, guaranteeing that at least one resource, such as machinery and labor, is used to perform work. Afterwards, the length of the chromosome in GA can be specified. The results demonstrate that the formulated plan has a large ratio of resource utilization in sugarcane production.
[91]	SA	The truck scheduling problem for woody biomass transportation for multiple distribution sites in western Oregon is studied. The problem is confined to transporting by-products such as hog fuel, chips, saw dust or shavings from sawmills to conversion plants or harbors for export. The goal is to satisfy the demand for different products at each destination while minimizing transportation costs, and the total working time subject to constraints on routes, working time, and predetermined order requirements. By testing different sets of parameters, the best result is obtained for an initial temperature of 10, a final temperature of 0.01, a cooling rate of 0.975, and iterations at each temperature of 1000. The results of the near-optimal truck-route-scheduling model show an 18% decrease in total transportation cost and a 15% decrease in total travel time compared with the actual schedule.
[92]	TS	A planning method to arrange sequential tasks concerning biomass harvesting and handling operations performed by machinery teams is considered. The method finds the field of operation for each machine, the sequence and time, the total operational cost of the optimized schedule, and accessible agricultural tools. The capability to evaluate the relationship and trade-off between cost and time for each feasible derived machinery combination in the available machinery fleet is provided for the decision maker. This work [92] is an extension of Bochtis et al.’s work [93] where the task scheduling problem combining multiple machinery systems and regarding the operational time and cost is developed to reach an optimal schedule with a reduction of 9.8% in the total time by using an exhaustive enumeration of a small problem (four jobs and two machine types). Orfanou et al. [92] observed that the greedy strategy and TS proposed by Basnet et al. [94] to solve large harvesting scheduling problems for multiple farms could be adapted to address their problem.
[94]	TS	A harvesting problem involving a commercial contracting company that travels from farm-to-farm harvesting crops is presented. The model considers the sequence in which the farms are visited and the inter-farm travel times. The duration of each operation depends on the combination of constrained resources allocated to it (i.e., equipment and worker allocation, minimum and maximum time lags on starting and ending time completion). A greedy heuristic and TS are developed. A comparison among a commercial integer programming code, the greedy heuristic, and the TS is executed. The TS outperforms the greedy heuristic and for a large problem (20 farms and 5 operations), it requires 26 s. The commercial solver obtains solutions for up to 6 farms and 3 operations.
[95]	ACO	ACO is proposed to schedule multiple biomass operations for a road network to recognize the amalgamation of optimal vehicle choices and road modifications to efficiently transport non-conventional products. Although the stopping criterion of 1000 iterations is considered for the optimization algorithm, the algorithm converges to its solution in 282 iterations. The results represent a 27% reduction in total transportation costs. Transportation costs equal the sum of the modification costs and the round-trip variable costs multiplied by the volume of each harvest unit. Thus, it is cost-effective to modify the network to allow larger vehicle access. However, modifying the transportation network is not always the economical option for the single harvest unit case.

Table 9. Reviewed articles in the scheduling category.

Ref.	Method	Application and Relevant Findings
[86]	SA	A model to enhance the economic feasibility of employing woody biomass to produce energy by diminishing the transportation costs is proposed. SA is implemented to address the truck scheduling problem for the transportation of woody biomass. The objective function of the study involves coping with the demand for different products and minimizing transportation costs and total labor hours. To evaluate the performance of the algorithm, a real case study including the scheduling of 50 loads is solved with satisfactory results.
[87]	SA	The transportation of woodchips for in-field chipping operations, where many operational factors affect their efficacy is studied. An adapted version of SA is proposed to minimize the objective functions of transportation costs, which involve fixed costs, travel times, and waiting times, while reaching a minimum level of utilization through the chippers determined by the operator. The truck payload and chipper utilization are two notable factors in this study, representing 52% and 29% of the obtained total cost savings, respectively. The algorithm is tested for a range of different scenarios for a case study in western Oregon.
[88]	Hybrid: TS and linear programming	A routing planning problem to decide the daily routes of logging trucks in forestry is developed. A two-step approach is proposed. In the first step, a LP problem to find a destination of flow from supply points to demand points (i.e., constructing transport nodes) is solved. In the second step, basic and extended TS are used to combine transport nodes (customers) into routes. The main idea of the proposed procedure is to decompose the problem into a standard vehicle routing problem with time windows. The model does not include queuing at nodes, which is indicated as potential future work. The method is tested in a case study involving major forest companies in Sweden.
[89]	Hybrid: TS and linear programming	A decision support system called RuttOpt to schedule logging trucks in the Swedish forest industry is proposed. The RuttOpt tool was built for the forest and hauling industries; however, it can be used by the biofuel industry for the transportation of woody material. This tool involves three modules. The first module is the road database. The second module is a two-phase optimization algorithm based upon a TS and linear programming proposed in a previous work [88]. The third module includes a database that saves all relevant information. Based on four case studies ranging from 10 to 110 trucks and a planning horizon ranging from 1 to 5 days, the results illustrate that the system can be utilized to address large systems with potential savings in the range of 5%–30%. Regarding solution time, for instance, a case with 12 trucks, 8 transporters, 22 demand nodes, 167 supply nodes, and a planning horizon of 3 days requires 10 min. For cases with 110 trucks and a planning horizon of 5 days, the authors used 100 min as solution time.
[90]	Hybrid: SA, GA, and hybrid Petri nets	A resource assignment and scheduling model is optimized via a two-phase metaheuristic based upon a SA, GA, and hybrid Petri nets. SA is used to optimize the resource assignment, and GA is utilized to search the priority lists and produce the schedule based upon the hybrid Petri nets. The hybrid net is a graphical and mathematical modeling device used for simulating the simultaneous, parallel, and stochastic activities of the system. The two-phase metaheuristic algorithm starts with a typical SA under a constraint, guaranteeing that at least one resource, such as machinery and labor, is used to perform work. Afterwards, the length of the chromosome in GA can be specified. The results demonstrate that the formulated plan has a large ratio of resource utilization in sugarcane production.
[91]	SA	The truck scheduling problem for woody biomass transportation for multiple distribution sites in western Oregon is studied. The problem is confined to transporting by-products such as hog fuel, chips, saw dust or shavings from sawmills to conversion plants or harbors for export. The goal is to satisfy the demand for different products at each destination while minimizing transportation costs, and the total working time subject to constraints on routes, working time, and predetermined order requirements. By testing different sets of parameters, the best result is obtained for an initial temperature of 10, a final temperature of 0.01, a cooling rate of 0.975, and iterations at each temperature of 1000. The results of the near-optimal truck-route-scheduling model show an 18% decrease in total transportation cost and a 15% decrease in total travel time compared with the actual schedule.
[92]	TS	A planning method to arrange sequential tasks concerning biomass harvesting and handling operations performed by machinery teams is considered. The method finds the field of operation for each machine, the sequence and time, the total operational cost of the optimized schedule, and accessible agricultural tools. The capability to evaluate the relationship and trade-off between cost and time for each feasible derived machinery combination in the available machinery fleet is provided for the decision maker. This work [92] is an extension of Bochtis et al.’s work [93] where the task scheduling problem combining multiple machinery systems and regarding the operational time and cost is developed to reach an optimal schedule with a reduction of 9.8% in the total time by using an exhaustive enumeration of a small problem (four jobs and two machine types). Orfanou et al. [92] observed that the greedy strategy and TS proposed by Basnet et al. [94] to solve large harvesting scheduling problems for multiple farms could be adapted to address their problem.
[94]	TS	A harvesting problem involving a commercial contracting company that travels from farm-to-farm harvesting crops is presented. The model considers the sequence in which the farms are visited and the inter-farm travel times. The duration of each operation depends on the combination of constrained resources allocated to it (i.e., equipment and worker allocation, minimum and maximum time lags on starting and ending time completion). A greedy heuristic and TS are developed. A comparison among a commercial integer programming code, the greedy heuristic, and the TS is executed. The TS outperforms the greedy heuristic and for a large problem (20 farms and 5 operations), it requires 26 s. The commercial solver obtains solutions for up to 6 farms and 3 operations.
[95]	ACO	ACO is proposed to schedule multiple biomass operations for a road network to recognize the amalgamation of optimal vehicle choices and road modifications to efficiently transport non-conventional products. Although the stopping criterion of 1000 iterations is considered for the optimization algorithm, the algorithm converges to its solution in 282 iterations. The results represent a 27% reduction in total transportation costs. Transportation costs equal the sum of the modification costs and the round-trip variable costs multiplied by the volume of each harvest unit. Thus, it is cost-effective to modify the network to allow larger vehicle access. However, modifying the transportation network is not always the economical option for the single harvest unit case.

5.5. Facility Location

With its significant effect on time and costs, the facility location (which involves the locations of entities for supply, distribution, and conversion) is considered as a crucial aspect in the design of the manufacturing system. Finding optimal places can sometimes be challenging when there are several restrictions such as avoiding placing hazardous conditions near people or selecting places far from competitors. To address this problem, heuristic optimization algorithms are suitable approaches to find proper places while minimizing transportation costs. Table 10 presents the works reviewed regarding facility location models.

Table 10. Reviewed articles in the facility location category.

Ref.	Method	Application and Relevant Findings
[96]	PSO	The optimal location of biomass-based power plants and the supply area of the biomass plant are addressed using a binary where the initial probability is an exponentially diminishing function. The following variables are considered: the cost of transportation, local distribution, and distance to the current electric lines. Furthermore, the productivity index is the fitness function defined as the ratio between the net present value and the initial investment. The results illustrate that the proposed PSO provides high-quality solutions in less computation time (the time needed by PSO is 170 times lower than the time required for an exhaustive search).
[97]	PSO	The binary PSO algorithm is used to gain the optimal location of biomass-fuelled systems for distributed power generation. Forest residues are the biomass source considered, and the profitability index is the fitness function to be optimized. The solutions are coded using 20 bits. The comparison of the binary PSO algorithm with GA illustrates the better performance of PSO for a similar computational cost. The proposed algorithm shows rapid convergence and a computational cost 1370 times lower than that the time needed for the exhaustive search.
[98]	PSO	Once again, the binary PSO-based approach is implemented to find the optimal location for the biomass plants and the supply area for the biomass plants. In this problem, the ratio between the net present value and the initial investment is regarded as the fitness function for the binary optimization algorithm.
[99]	SA, TS, PSO, and GA independently	This work presents different methods including SA and the TS as two prominent trajectory approaches as well as PSO and GA as two popular population-based algorithms to find the optimal location and supply area of biomass-fueled power plants. Moreover, a modified binary PSO algorithm is proposed, in which an inertia weight factor is used, similar to the classical continuous method. The results demonstrate that the proposed binary PSO performs better than other PSO binary algorithms and GA. Based upon the computational experimentation, the researchers conclude that the population-based approaches outperform the trajectory approaches for this problem.
[100]	GA	GA is employed to address a p-median problem representing a hierarchical location-allocation problem to optimize the supply location, conversion facility locations, domestic and commercial energy demands, and energy flows. The GA utilizes a binary encoding of the decision variables, which denote the candidate supply locations and candidate conversion locations.
[101]	GA and PSO	Binary PSO and GA are utilized to find the optimal location, biomass supply area, and power plant size in a typical region in Iran. The profitability index is selected as the objective function, where an investment is considered profitable if the profitability index is greater than zero. The constraints of the problem are as follows: (1) the electric power produced by the plant is limited; and (2) the plant must be supplied through optimized parcels. By comparing GA with binary PSO, the experiment demonstrates that GA converges more rapidly with the advantage of a lower CPU time.
[102]	Binary honey bee foraging (BHBF), GA, PSO	Olive tree pruning residues (common in Mediterranean countries) are currently underutilized and farmers usually burn the residues in an uncontrolled manner. A novel tool based upon binary honey bee foraging (BHBF) is proposed to determine the optimal location, biomass supply area, and power plant size that provide the best productivity for investors. The profitability index is selected as the fitness function. To evaluate the performance of BHBF, this algorithm is compared with a binary PSO algorithm and GA. Guided by the results of the work of Reche-Lopez et al. [99], in which the population-based algorithms (binary PSO and GA) show superior performance compared with the trajectory-based algorithms (SA and TS), This work demonstrates that BHBF benefits from a higher value of profitability index with less standard deviation, and its convergence occurs in fewer iterations compared with GA and binary PSO.
[103]	Multi-objective: NSGA II	A model of the facility location problem in which the total cost of the supply chain and the total cost of echelon are conflicting objective functions is optimized via NSGA II. In this work, the effect of population size and the number of generations on the quality of the solutions is investigated. The results show that one of the minimum solutions is obtained for a population size of 300 and 164 generations. Increasing the population size to 300 increases the search space and the number of non-dominated solutions to 285. Moreover, the deviation in results decreases as the number of generations increase and the solutions are concentrated toward a particular portion of the Pareto graph.

Table 10. Reviewed articles in the facility location category.

Ref.	Method	Application and Relevant Findings
[96]	PSO	The optimal location of biomass-based power plants and the supply area of the biomass plant are addressed using a binary where the initial probability is an exponentially diminishing function. The following variables are considered: the cost of transportation, local distribution, and distance to the current electric lines. Furthermore, the productivity index is the fitness function defined as the ratio between the net present value and the initial investment. The results illustrate that the proposed PSO provides high-quality solutions in less computation time (the time needed by PSO is 170 times lower than the time required for an exhaustive search).
[97]	PSO	The binary PSO algorithm is used to gain the optimal location of biomass-fuelled systems for distributed power generation. Forest residues are the biomass source considered, and the profitability index is the fitness function to be optimized. The solutions are coded using 20 bits. The comparison of the binary PSO algorithm with GA illustrates the better performance of PSO for a similar computational cost. The proposed algorithm shows rapid convergence and a computational cost 1370 times lower than that the time needed for the exhaustive search.
[98]	PSO	Once again, the binary PSO-based approach is implemented to find the optimal location for the biomass plants and the supply area for the biomass plants. In this problem, the ratio between the net present value and the initial investment is regarded as the fitness function for the binary optimization algorithm.
[99]	SA, TS, PSO, and GA independently	This work presents different methods including SA and the TS as two prominent trajectory approaches as well as PSO and GA as two popular population-based algorithms to find the optimal location and supply area of biomass-fueled power plants. Moreover, a modified binary PSO algorithm is proposed, in which an inertia weight factor is used, similar to the classical continuous method. The results demonstrate that the proposed binary PSO performs better than other PSO binary algorithms and GA. Based upon the computational experimentation, the researchers conclude that the population-based approaches outperform the trajectory approaches for this problem.
[100]	GA	GA is employed to address a p-median problem representing a hierarchical location-allocation problem to optimize the supply location, conversion facility locations, domestic and commercial energy demands, and energy flows. The GA utilizes a binary encoding of the decision variables, which denote the candidate supply locations and candidate conversion locations.
[101]	GA and PSO	Binary PSO and GA are utilized to find the optimal location, biomass supply area, and power plant size in a typical region in Iran. The profitability index is selected as the objective function, where an investment is considered profitable if the profitability index is greater than zero. The constraints of the problem are as follows: (1) the electric power produced by the plant is limited; and (2) the plant must be supplied through optimized parcels. By comparing GA with binary PSO, the experiment demonstrates that GA converges more rapidly with the advantage of a lower CPU time.
[102]	Binary honey bee foraging (BHBF), GA, PSO	Olive tree pruning residues (common in Mediterranean countries) are currently underutilized and farmers usually burn the residues in an uncontrolled manner. A novel tool based upon binary honey bee foraging (BHBF) is proposed to determine the optimal location, biomass supply area, and power plant size that provide the best productivity for investors. The profitability index is selected as the fitness function. To evaluate the performance of BHBF, this algorithm is compared with a binary PSO algorithm and GA. Guided by the results of the work of Reche-Lopez et al. [99], in which the population-based algorithms (binary PSO and GA) show superior performance compared with the trajectory-based algorithms (SA and TS), This work demonstrates that BHBF benefits from a higher value of profitability index with less standard deviation, and its convergence occurs in fewer iterations compared with GA and binary PSO.
[103]	Multi-objective: NSGA II	A model of the facility location problem in which the total cost of the supply chain and the total cost of echelon are conflicting objective functions is optimized via NSGA II. In this work, the effect of population size and the number of generations on the quality of the solutions is investigated. The results show that one of the minimum solutions is obtained for a population size of 300 and 164 generations. Increasing the population size to 300 increases the search space and the number of non-dominated solutions to 285. Moreover, the deviation in results decreases as the number of generations increase and the solutions are concentrated toward a particular portion of the Pareto graph.

6. Discussion

Due to their unique advantages in solving large-scale, multi-objective problems and/or non-differentiable, non-continuous, and non-linear functions with less computational resources than classical optimization methods, metaheuristic and hybrid approaches have been employed to address bioenergy supply chain problems. To this end, the application of metaheuristics in literature was divided into the following sub-topics: integrated supply chain planning, bioconversion and production process optimization, supply chain network design, scheduling problems, and facility location. Forty three original publications have been revised in this review including journal articles, dissertations, and conference proceedings. Figure 4 shows the distribution of papers among the sub-topics. It can be observed that bioconversion and production process optimization accounts for 30% of the research efforts closely followed by scheduling problems and integrated supply chain planning papers.

Figure 4. Publications distribution by topic.

Figure 4. Publications distribution by topic.

Figure 5 shows the implementations of metaheuristics (differentiating among pure metaheuristics, hybrid, and multi-objective methods) by the proposed categories; it can be observed that “bioconversion and production process optimization” presents a variety of implementations as well as “facility location”.

Regarding the most applied algorithms, the GA, hybrids containing GA, and multi-objective GA have been the most utilized methods implemented in fifteen, six and three articles, respectively. The PSO and hybrid PSO are used in nine and one manuscripts, respectively. The less utilized metaheuristics are BHBF with only one application and ACO with three papers addressing a single-objective problem and one paper solving a multi-objective problem. Figure 5 also shows that 8% of the metaheuristics correspond to multi-objective algorithms and 18% correspond to hybrid optimization methods. The trajectory-based metaheuristics account for 24% of the implementation being the population-based metaheuristics the most utilized algorithms.

Figure 5. Metaheuristics by category.

Figure 5. Metaheuristics by category.

7. Conclusions and Future Work

This review summarized the latest research regarding the development of metaheuristics including population-based algorithms: ACO, GA, PSO, and BCA as well as two trajectory-based methods: TS and SA for solving bioenergy supply chain problems and provided insights for researchers and practitioners. More precisely, this review illustrates that bioconversion and production process optimization, scheduling, and integrated supply chain planning are remarkable areas of inquiry and application of metaheuristics. Based on this literature review, the integrated design and planning of bioenergy supply chains was solved primarily by implementing the GA and hybrid GA (e.g., GA combined with sequential quadratic programming, mixed integer linear programming, and Lagrangian relaxation); the production process optimization was addressed primarily by using the GA (in its pure, hybrid, and multi-objective version) and PSO (both in pure and hybrid form); the supply chain network design problem was tackled by utilizing GA and ACO; the facility location problem mainly used PSO and GA (including NSGAII); the truck and task scheduling problem was primarily solved by SA and TS.

The reviewed works showed that trajectory-based metaheuristics have been utilized repeatedly and successfully for addressing scheduling problems in the bioenergy industry. On the other hand, the population-based methods, specifically, GA and PSO have been widely employed with successful results for solving facility location, SCND, process production, and integrated supply chain planning problems. Noteworthy, in only one work [102], BCA optimization was reported to perform better than the GA and PSO. Multi-objective optimization was applied to solve production process optimization, supply chain network design, and facility location problems.

Based on the review, it is expected to see more population-based applications because these metaheuristics have proven to outperform trajectory-based algorithms for the majority of the bioenergy supply chain decisions (the exception being scheduling problems). Moreover, hybrids are gaining popularity because they allow exploiting the strengths of different algorithms used to address different decisions at different stages of the solution procedure.

With respect to multi-objective optimization, in biofuels process optimization, the work presented in [70] aimed to maximize the purity of compounds while minimizing the energy requirements. The model presented in [74] addressed four different objectives: bioenergy yield, food yield, average nitrate concentration, and low flow related to bioenergy and food production as well as water quality. In the supply chain network design topic finding the best path is usually associated to minimize the distance or transportation cost; however, a hybrid multi-objective approach is presented in [85] to also consider other performance measures such as the quality of involved companies, quality of delivered product, and other value resulted by quality measurement.

Future research on implementing metaheuristics for bioenergy supply chain problems involves creating novel computational optimization algorithms with provable bounds that provide near-optimal solutions with less computational resources to enhance the feasibility and quality of biomass production and transportation while minimizing total cost. To this end, integrated bioenergy supply chain models need the application of several tools in association with metaheuristics to gain practical near-optimal solutions. Some of these tools include GIS databases, route databases, transit databases, data mining, fuzzy logic, simulation-based optimization approaches, and Monte Carlo simulation, among others. Thus, the hybrid and hierarchical methods are potential fruitful areas of inquiry.

Another area of future research is the development of models that take into account uncertainties and/or fuzziness as well as multiple conflicting objectives to further advance toward modeling real-life problems including all of their intricacies. Metaheuristics will play an important role as suitable solution procedures for these models. To add orderliness to this nascent area of research, the development of library with instances should be pursued so that the metaheuristic with best performance by type of problem can be elucidated. Several of the reviewed works do not present a comprehensive comparison of metaheuristics over diverse instances with different sizes; thus, designed computational experiments instead of specific case studies are needed to advance our understanding of the metaheuristics with best performance per problem type.

Since the intricacy added due to the stochastic hybrid and hierarchical models is significant, there are some cases in which the application of metaheuristics does not provide an appropriate solution in a reasonable amount of run time (usually minutes for operational decisions and hours for tactical and strategic decisions). Hence, parallel processing and high performance computing (HPC) might become an efficient approach to address the computational time challenge. The role of cloud computing when implementing and solving large-scale bioenergy problems is an interesting future line of research. Hence, it is expected to see more research contributions in the area of parallel processing, HPC, and cloud computing applied to bioenergy logistic systems.