Transient Oscillations Analysis and Modified Control Strategy for Seamless Mode Transfer in Micro-Grids: A Wind-PV-ES Hybrid System Case Study
Abstract
:1. Introduction
- (i)
- To the best of the authors’ knowledge, there is no work exploring on the underlying reasons for transient oscillations occurrence during mode transfer. The underlying reason for such transient oscillations is discovered in the Wind-PV-ES hybrid system case study.
- (ii)
- A modified control strategy for seamless mode transfer is designed and implemented, whereby an improved PQ control method is designed by which the output of the PQ controller always synchronously tracks the output of the V/f controller for micro-grid switches from islanded mode to grid-connected, and a dq rotating coordinate synchronization based V/f control method is proposed for transition from grid-connected mode to islanded mode.
2. Control Strategies for Micro-Grid

2.1. Operation Modes of Micro-Grids

2.2. Droop Based V/f Control Method

2.3. PQ Control Method

3. Analysis of Transient Oscillations: Case Study
3.1. Transient Oscillations in a Grid-Connecting Process


3.2. Transient Oscillations in a Islanding Process


4. Modified Control Strategy for Seamless Mode Transfer
4.1. Improved Pre-Synchronous Controller

4.2. Status Tracking Based PQ Control Method



4.3. dq Rotating Coordinate Synchronization Based V/f Control Method



5. Experiments and Analysis
5.1. Light Intensity and Wind Speed Changing in Islanded Mode


5.2. Load Switching in Grid-Connected Mode


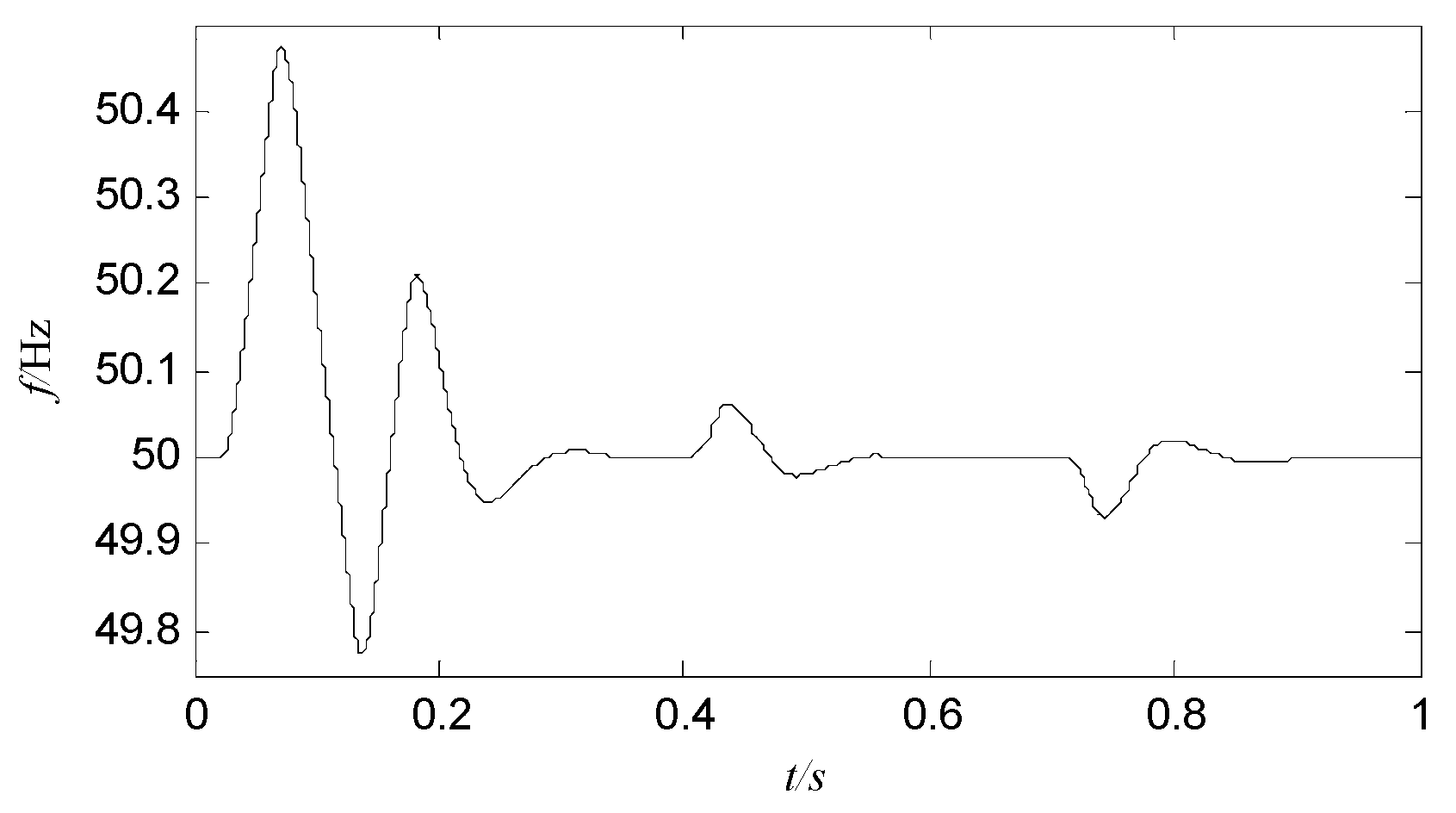
5.3. Grid-Connected/Islanding Smooth Switching




6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. A Control Architecture to Coordinate Renewable Energy Sources and Energy Storage Systems in Islanded Microgrids. IEEE Trans. Smart Grid 2015, 6, 1156–1166. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids-A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Lu, Z.X.; Wang, C.X.; Min, Y. Overview on microgrid research. Autom. Electron. Power Syst. 2007, 31, 100–107. [Google Scholar]
- Liu, Y.H.; Zhang, N.; Zhang, X. Research on grid-connected/islanding smooth switching of micro-grid based on energy storage. In Proceedings of the IEEE International Conference on Power System Technology, Auckland, New Zealand, 30 October–2 November 2012; pp. 1–5.
- Zhao, D.M.; Zhang, N.; Liu, Y.H. Micro-grid connected/islanding operation based on wind and PV hybrid power system. In Proceedings of the IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Tianjin, China, 21–24 May 2012; pp. 1–6.
- Zhang, Z.; Chen, W.; Zhang, Z. A new seamless transfer control strategy of the microgrid. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Wang, C.; Che, Y. A small-scale microgrid system with flexible modes of operation. Autom. Electron. Power Syst. 2009, 33, 89–92. [Google Scholar]
- Huang, W.; Lu, M.; Zhang, L. Survey on microgrid control strategies. Energy Procedia 2011, 12, 206–212. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F. Coordinated Vf and PQ control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Fang, L.; Chen, J.; Chen, X.; Gong, C.; Fan, Y. Analysis and control of smooth transferring for micro-grid with droop control. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013; pp. 1–5.
- Vandoorn, T.L.; Meersman, B.; de Kooning, J.D.; Vandevelde, L. Transition from islanded to grid-connected mode of microgrids with voltage-based droop control. IEEE Trans. Power Syst. 2013, 28, 2545–2553. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Zhuo, F.; Zhu, Y.; Hao, Y. System operation and energy management of a renewable energy-based DC micro-grid for high penetration depth application. IEEE Trans. Smart Grid 2015, 6, 1147–1155. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Meegahapola, L.G.; Robinson, D.; Agalgaonkar, A.P.; Perera, S.; Ciufo, P. Microgrids of commercial buildings: Strategies to manage mode transfer from grid connected to islanded mode. IEEE Trans. Sust. Energy 2014, 5, 1337–1347. [Google Scholar] [CrossRef]
- Mohamed, Y.A.R.I.; Radwan, A. Hierarchical control system for robust microgrid operation and seamless mode transfer in active distribution systems. IEEE Trans. Smart Grid 2011, 2, 352–362. [Google Scholar] [CrossRef]
- Hwang, T.S.; Park, S.Y. A seamless control strategy of a distributed generation inverter for the critical load safety under strict grid disturbances. IEEE Trans. Power Electron. 2013, 28, 4780–4790. [Google Scholar] [CrossRef]
- Ashabani, S.M.; Mohamed, Y.A.R. A flexible control strategy for grid-connected and islanded microgrids with enhanced stability using nonlinear microgrid stabilizer. IEEE Trans. Smart Grid 2012, 3, 1291–1301. [Google Scholar] [CrossRef]
- Ashabani, S.M.; Mohamed, Y.A.R. General interface for power management of micro-grids using nonlinear cooperative droop control. IEEE Trans. Power Syst. 2013, 28, 2929–2941. [Google Scholar] [CrossRef]
- Ashabani, S.M.; Mohamed, Y.A.R. Integrating VSCs to weak grids by nonlinear power damping controller with self-synchronization capability. IEEE Trans. Power Syst. 2014, 29, 805–814. [Google Scholar] [CrossRef]
- Ashabani, M.; Freijedo Fernandez, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters with Auto-Synchronization and Emulated Inertia Capability. Available online: http://vbn.aau.dk/ws/files/217421230/converter_corrections_last_version.pdf (accessed on 3 December 2015).
- Jiang, J.; Duan, S.; Chen, Z. Research on control strategy for three-phase double mode inverter. Trans. China Electrotech. Soc. 2012, 27, 52–58. [Google Scholar]
- Yang, Z.L.; Wu, C.S.; Wang, H. Design of three-phase inverter system with double mode of grid-connection and stand-alone. Power Electron. 2010, 44, 14–16. [Google Scholar]
- Integration of Distributed Energy Resources: The CERTS Microgrid Concept. Available online: http://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0ahUKEwj3wviswb7JAhXIpJQKHaiBAqcQFggfMAA&url=http%3A%2F%2Fbnrg.eecs.berkeley.edu%2F~randy%2FCourses%2FCS294.F09%2FMicroGrid.pdf&usg=AFQjCNHMSY1rAeFXm1z9Mrh6EGUjyyVDhg&cad=rja (accessed on 3 December 2015).
- Huang, P.H.; Liu, P.C.; Xiao, W.; Moursi, E.; Shawky, M. A novel droop-based average voltage sharing control strategy for DC microgrids. IEEE Trans. Smart Grid 2015, 6, 1096–1106. [Google Scholar] [CrossRef]
- Pan, Y.; Li, P.Q.; Li, X.R.; Lei, B. Strategy of research and application for the microgrid coordinated control. In Proceedings of the IEEE Advanced Power System Automation and Protection (APAP), Beijing, China, 16–20 October 2011; pp. 873–878.
- Gao, D.K.; Jiang, J.G.; Zhang, Y.H. Design of microgrid control strategy using voltage amplitude and phase angle droop control. Autom. Electron. Power Syst. 2012, 36, 29–34. [Google Scholar]
- Wang, Z.; Zhu, S.; Zhou, S. Controller design for inverter-based distributed generation. Autom. Electron. Power Syst. 2004, 28, 61–66. [Google Scholar]
- Huang, W.; Zhang, J.H.; Wu, Z.P.; Niu, M. Dynamic modelling and simulation of a Micro-turbine generation system in the microgrid. In Proceedings of the IEEE Sustainable Energy Technologies (ICSET), Singapore, 24–27 November 2008; pp. 345–350.
- Huang, X.; Jin, X.M. A voltage and frequency droop control method for microsources. Trans. China Electrotech. Soc. 2012, 27, 29–36. [Google Scholar]
- Kim, J.Y.; Kim, S.K.; Jeon, J.H. Coordinated state-of-charge control strategy for microgrid during islanded operation. In Proceedings of the 3rd IEEE International Symposium on Power Electronics for Distributed Generation systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 133–139.
- Zeng, Z.; Zhao, R.; Yang, H.; Tang, S. Policies and demonstrations of micro-grids in China: A review. Renew. Sust. Energy Rev. 2014, 29, 701–718. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Li, C.H.; Zhu, X.J. Dynamic modeling and simulation of hybrid energy storage-based photovoltaic microgrid. Power Syst. Technol. 2013, 37, 39–46. [Google Scholar]
- Wang, C.; Nehrir, M.H.; Gao, H. Control of PEM fuel cell distributed generation systems. IEEE Trans. Energy Convers. 2006, 21, 586–595. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Castilla, M.; de Vicuňa, L.G. Control strategy for flexible microgrid based on parallel line-interactive UPS systems. IEEE Trans. Ind. Electron. 2009, 56, 726–736. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Z.Z.; Chai, J.Y.; You, R.; Gan, S. Analysis of Grid-connecting Pre-synchronized Process for Synchronously Controlled Inverter Power Source. Autom. Electron. Power Syst. 2015, 39, 152–158. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Yue, D.; O’Grady, M.J.; O’Hare, G.M.P. Transient Oscillations Analysis and Modified Control Strategy for Seamless Mode Transfer in Micro-Grids: A Wind-PV-ES Hybrid System Case Study. Energies 2015, 8, 13758-13777. https://doi.org/10.3390/en81212396
Zhang T, Yue D, O’Grady MJ, O’Hare GMP. Transient Oscillations Analysis and Modified Control Strategy for Seamless Mode Transfer in Micro-Grids: A Wind-PV-ES Hybrid System Case Study. Energies. 2015; 8(12):13758-13777. https://doi.org/10.3390/en81212396
Chicago/Turabian StyleZhang, Tengfei, Dong Yue, Michael J. O’Grady, and Gregory M. P. O’Hare. 2015. "Transient Oscillations Analysis and Modified Control Strategy for Seamless Mode Transfer in Micro-Grids: A Wind-PV-ES Hybrid System Case Study" Energies 8, no. 12: 13758-13777. https://doi.org/10.3390/en81212396
APA StyleZhang, T., Yue, D., O’Grady, M. J., & O’Hare, G. M. P. (2015). Transient Oscillations Analysis and Modified Control Strategy for Seamless Mode Transfer in Micro-Grids: A Wind-PV-ES Hybrid System Case Study. Energies, 8(12), 13758-13777. https://doi.org/10.3390/en81212396







