Optimal Design of an Axial-Flux Permanent-Magnet Middle Motor Integrated in a Cycloidal Reducer for a Pedal Electric Cycle
Abstract
:1. Introduction
2. Specifications of the Pedelec Middle Motor


| Bicycle | |
|---|---|
| Type | Roadster |
| Wheel size | 26 inches |
| Power assist ratio | 1 |
| Bicycle weight | 20 kg |
| Rider’s height | 175 cm |
| Rider’s weight | 80 kg |
| Air temperature | 24 °C |
| Max. riding slope | 25% |
| Max. speed on level road | 25 km/h |
| Middle Motor | |
| Max. motor torque (Tmax) | 1.4 Nm |
| Min. motor power (Pmin) | 250 W |
| Battery voltage (VDC) | 36 V |
| Max. DC current (IDC-max) | <14 A |
| Winging type | Y-connection |
| Modulation type | SVPWM |
| Gear ratio | 35 |
| Motor axial length | <40 mm |

3. Optimal Design of the AFPM Motor

3.1. Preliminary Design (0-D)
| Coil | Coil Angle (Degree) | Slots of Phase A | Slots of Phase B | Slots of Phase C | |||
|---|---|---|---|---|---|---|---|
| in | out | in | out | in | out | ||
| 1 | 0 | 1 | 2 | 5 | 6 | 9 | 10 |
| 2 | 30 | 3 | 2 | 7 | 6 | 11 | 10 |
| 3 | 0 | 8 | 7 | 12 | 11 | 4 | 3 |
| 4 | 30 | 7 | 9 | 12 | 1 | 4 | 5 |
3.2. Sensitivity Analysis (1-D)


3.3. Multi-Objective Optimal Design (1-D)
| 10:1:1 | 5:5:1 | 5:1:5 | |||
| Design Variable | Initial | Range | |||
| Motor inner radius (mm) | 14.5 | 14.5–15.5 | 14.5 | 14.55 | 14.5 |
| Magnet thickness (mm) | 4 | 3.8–4.2 | 3.83 | 4.122 | 3.99 |
| Slot opening (mm) | 5.6 | 5.5–5.8 | 5.6 | 5.8 | 5.6 |
| Performance | |||||
| Torque (Nm) | 1.619 | 1.625 | 1.63 | ||
| Torque ripple (%) | 1.499 | 1.250 | 1.57 | ||
| Torque density (Nm/kg) | 3.833 | 3.856 | 3.84 | ||
| Other Design Variables | |||||
| Slot/pole number | 12/14 | ||||
| back iron thickness (mm) | 3 | ||||
| Nominal DC bus voltage (V) | 36 | ||||
| # of turns/coils per phase | 21/4 | ||||
| Air-gap length (mm) | 0.5 | ||||
| Max. phase current, A at 36 V | 14 | ||||
| Stator outer diameter (mm) | 62 | ||||
| Stator inner diameter (mm) | 31 | ||||
| Air gap length (mm) | 0.5 | ||||
4. Finite Element Analysis (3-D)
4.1. Electromagnetic Analysis

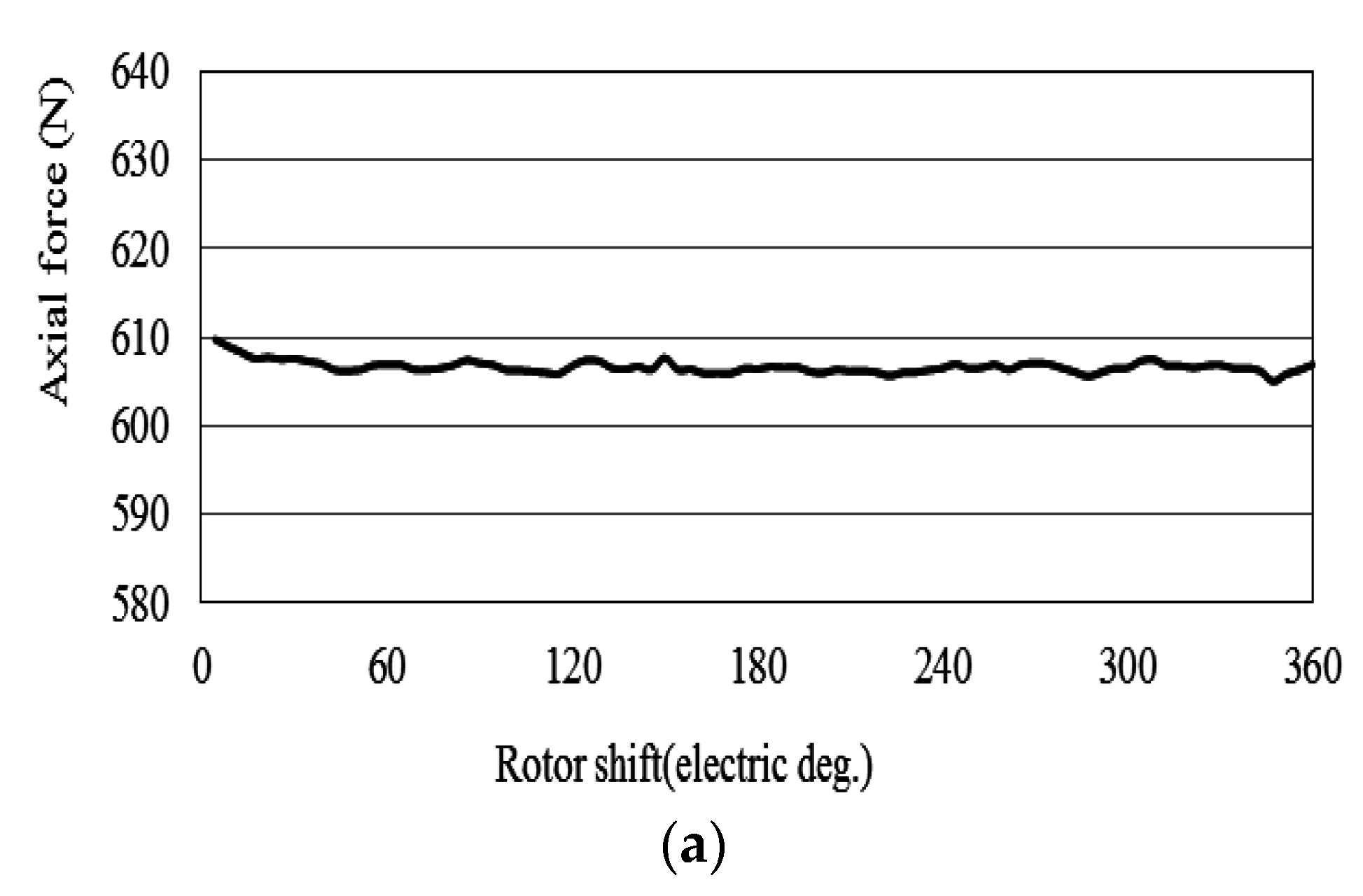

4.2. Estimation of Torque versus Speed (TN) Curve

4.3. Efficiency Analysis and Driving Performance

4.4. Thermal Analysis
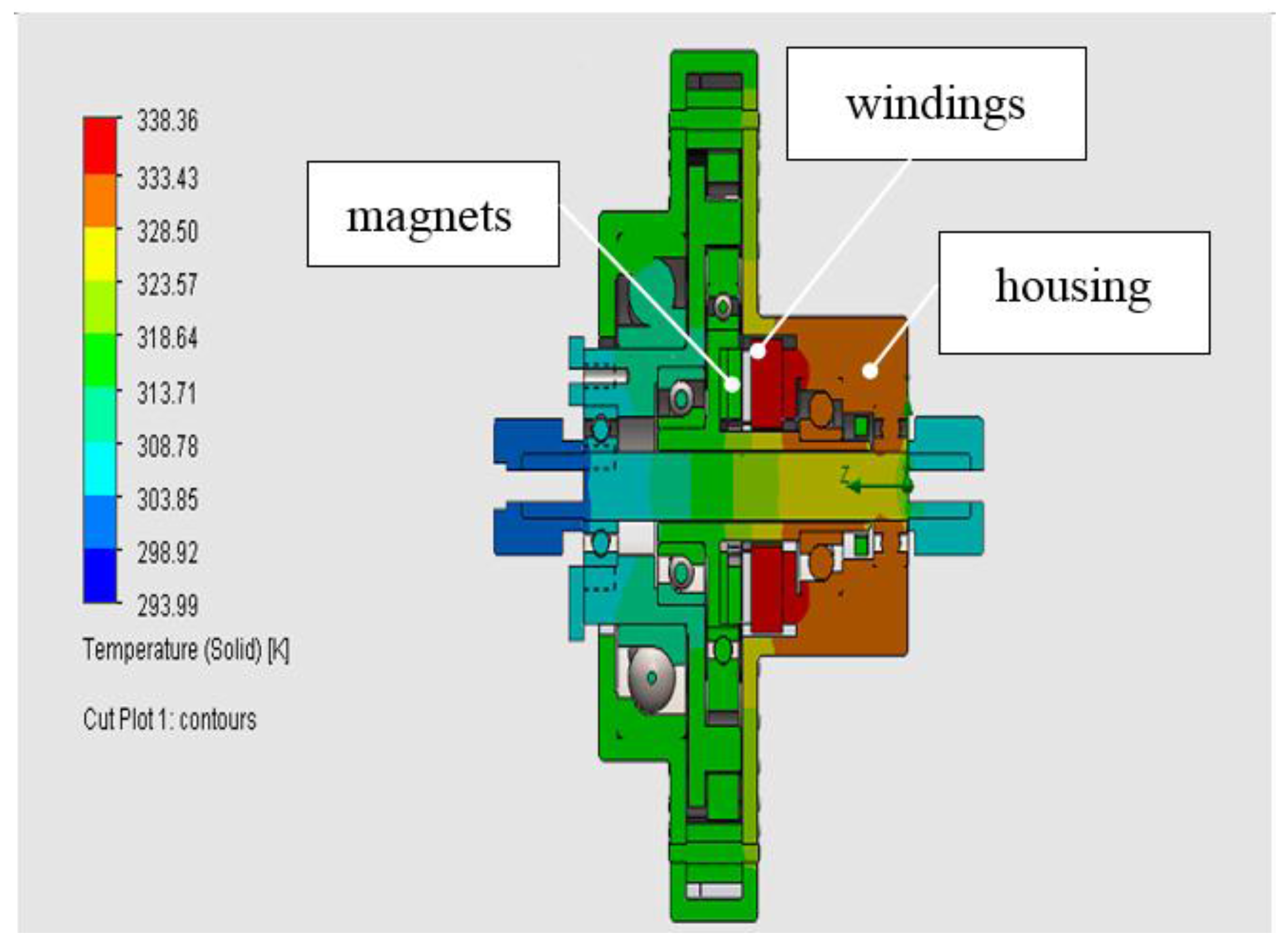
5. Prototype and Experiments
5.1. Prototype Manufacturing


5.2. Motor Performance

6. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Rose, G. E-bikes and urban transportation: Emerging issues and unresolved questions. Transportation 2012, 39, 81–96. [Google Scholar] [CrossRef]
- Johnson, M.; Rose, G. Electric bikes—Cycling in the new world city: An investigation of Australian electric bicycle owners and the decision making process for purchase. In Proceedings of the 36th Australasian Transport Research Forum, Brisbane, Australia, 2–4 October 2013; pp. 1–10.
- Mcleod, K. Electric Bicycle: Public Perceptions & Policy; The League of American Bicyclists: Newport, RI, USA, 2015. [Google Scholar]
- Yang, Y.P.; Ding, F.X. Driving-scenario oriented design of an axial-flux permanent-magnet synchronous motor for a pedal electric cycle. IET Electr. Power App. 2015, 9, 420–428. [Google Scholar] [CrossRef]
- Muetze, A.; Tan, Y.C. Electric bicycles—A performance evaluation. IEEE Ind. Appl. Mag. 2007, 13, 12–21. [Google Scholar] [CrossRef]
- 17 Factory Mid Drive Electric Bikes. Available online: https://www.electricbike.com/2014-mid-drive/ (accessed on 21 January 2014).
- Turner, J.R. Electric Bicycle and Methods. U.S. Patent 6,629,574, 17 August 2001. [Google Scholar]
- Li, P.; Tu, Q. Middle Electric Motor Drive Unit for Electric Bicycle. U.S. Patent 8,205,705, 26 June 2012. [Google Scholar]
- Li, K.M.; Wang, W.S.; Li, B.; Zhu, Q. Electric Power-Assisted Bicycle. U.S. Patent 6,152,249, 25 November 1998. [Google Scholar]
- Hanselman, D.C. Brushless Permanent-Magnet Motor Design, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Permanent-magnet brushless machines with unequal tooth widths and similar slot and pole numbers. IEEE Trans. Ind. Appl. 2005, 41, 584–590. [Google Scholar] [CrossRef]
- Yang, Y.P.; Chuang, D.S. Optimal design and control of a wheel motor for electric passenger cars. IEEE Trans. Magn. 2007, 43, 51–61. [Google Scholar] [CrossRef]
- Qi, G.; Chen, J.T.; Zhu, Z.Q.; Howe, D.; Zhou, L.B.; Gu, C.L. Influence of skew and cross-coupling on flux-weakening performance of permanent-magnet brushless AC machines. IEEE Trans. Magn. 2009, 45, 2110–2117. [Google Scholar] [CrossRef]
- Chen, Y.; Pillay, P. An improved formula for lamination core loss calculations in machines operating with high frequency and high flux density excitation. In Proceedings of the 37th IAS Conference Record of the Industry Applications, Pittsburgh, PA, USA, 13–18 October 2002; pp. 759–766.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.-P.; Jiang, J.-M. Optimal Design of an Axial-Flux Permanent-Magnet Middle Motor Integrated in a Cycloidal Reducer for a Pedal Electric Cycle. Energies 2015, 8, 14151-14167. https://doi.org/10.3390/en81212421
Yang Y-P, Jiang J-M. Optimal Design of an Axial-Flux Permanent-Magnet Middle Motor Integrated in a Cycloidal Reducer for a Pedal Electric Cycle. Energies. 2015; 8(12):14151-14167. https://doi.org/10.3390/en81212421
Chicago/Turabian StyleYang, Yee-Pien, and Jia-Ming Jiang. 2015. "Optimal Design of an Axial-Flux Permanent-Magnet Middle Motor Integrated in a Cycloidal Reducer for a Pedal Electric Cycle" Energies 8, no. 12: 14151-14167. https://doi.org/10.3390/en81212421
APA StyleYang, Y.-P., & Jiang, J.-M. (2015). Optimal Design of an Axial-Flux Permanent-Magnet Middle Motor Integrated in a Cycloidal Reducer for a Pedal Electric Cycle. Energies, 8(12), 14151-14167. https://doi.org/10.3390/en81212421





