A Cell-in-the-Loop Approach to Systems Modelling and Simulation of Energy Storage Systems
Abstract
:1. Introduction
2. Cell Type
3. Cell Model Developments and Off-Line Simulation
3.1. Model Structure

3.2. Parameter Estimation


3.3. Off-Line Simulation and Model Validation

4. Hardware-in-the-Loop Simulation Environment and Real-Time Validation
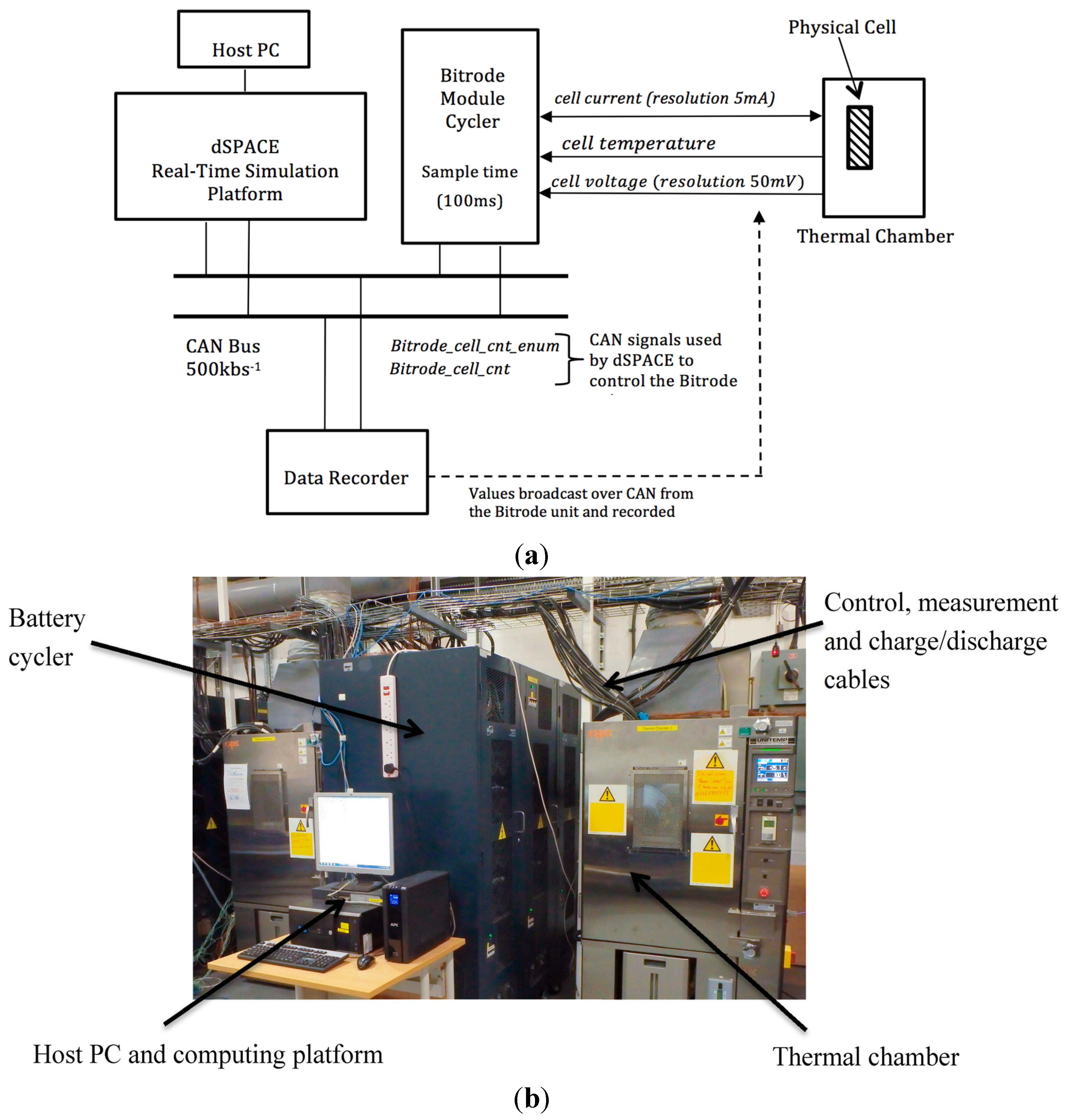


5. Case Study: Defining the State of Charge (SOC) for a Series Connection of 18650 Cells


6. Discussion
6.1. Application
6.2. Further Work
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, B.; Yufit, V.; Marinescu, M.; Offer, G.J.; Martinez-Botas, R.F.; Brandon, N.P. Coupled thermal–electrochemical modelling of uneven heat generation in lithium-ion battery packs. J. Power Sources 2013, 243, 544–554. [Google Scholar] [CrossRef]
- Thanheiser, A.; Kohler, T.P.; Bertram, C.; Herzog, H.G. Battery emulation considering thermal behavior. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicargo, IL, USA, 6–9 September 2011; pp. 1–5.
- Marinescu, M.; Wu, B.; von Srbik, M.; Yufit, V.; Offer, G.J. The effect of thermal gradients on the performance of battery packs in automotive applications. In Proceedings of the IET Hybrid Electric Vehicle Conference (HEVC), London, UK, 6–7 November 2013.
- Gogoana, R.; Pinson, M.B.; Bazant, M.Z.; Sarma, S.E. Internal resistance matching for parallel-connected lithium-ion cells and impacts on battery pack cycle life. J. Power Sources 2014, 252, 8–13. [Google Scholar] [CrossRef]
- Wu, J.; Member, S.; Wang, J.; Li, K. Large-scale energy storage system design and optimization for emerging electric-drive vehicles. IEEE Trans. Comput. Aided Des. Integr. Cicuits Syst. 2013, 32, 325–338. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 186, 500–507. [Google Scholar] [CrossRef]
- Kenney, B.; Darcovich, K.; MacNeil, D.D.; Davidson, I.J. Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules. J. Power Sources 2012, 213, 391–401. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Quantifying cell-to-cell variations in lithium ion batteries. Int. J. Electrochem. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Lotfi, N.; Fajri, P.; Novosad, S.; Savage, J.; Landers, R.; Ferdowsi, M. Development of an experimental testbed for research in lithium-ion battery management systems. Energies 2013, 6, 5231–5258. [Google Scholar] [CrossRef]
- Molitor, C.; Member, S.; Benigni, A.; Helmedag, A.; Chen, K.; Calì, D.; Jahangiri, P.; Müller, D.; Monti, A.; Member, S. Multiphysics test bed for renewable energy systems in smart homes. IEEE Trans. Ind. Electron. 2013, 60, 1235–1248. [Google Scholar] [CrossRef]
- Guo, F.; Member, S.; Inoa, E.; Choi, W.; Wang, J. Study on global optimization and control strategy development for a PHEV charging facility. IEEE Trans. Veh. Technol. 2012, 61, 2431–2441. [Google Scholar] [CrossRef]
- Allen, J. Simulation and test systems for validation of electric drive and battery management systems. SAE Tech. Paper 2012. [Google Scholar] [CrossRef]
- Bazargan, D.; Filizadeh, S.; Bistyak, G. Battery Characterization for Vehicular Applications using hardware-in-loop real-time simulation. In Proceedings of the 23rd International Conference on Electric Power and Energy Conversion Systems, Instabul, Turkey, 2–4 October 2013; pp. 1–6.
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Online estimation of peak power capability of Li-ion batteries in electric vehicles by a hardware-in-loop approach. Energies 2012, 5, 1455–1469. [Google Scholar] [CrossRef]
- He, Y.; Liu, W.; Koch, B.J. Battery algorithm verification and development using hardware-in-the-loop testing. J. Power Sources 2010, 195, 2969–2974. [Google Scholar] [CrossRef]
- He, Y.; Liu, W.; Koch, B.J. Power capability testing of a lithium-ion battery using hardware in the loop. SAE Tech. Paper 2010. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhao, K.; Liu, Z. Energy management strategy research on a hybrid power system by hardware-in-loop experiments. Appl. Energy 2013, 112, 1311–1317. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, X.; Wei, X.; Sun, Z.; Wang, J.; Hu, F. Cell-BMS validation with a hardware-in-the-loop simulation of lithium-ion battery cells for electric vehicles. Int. J. Electr. Power Energy Syst. 2013, 52, 174–184. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stan, A.I.; Teodorescu, R. Accelerated lifetime testing methodology for lifetime estimation of Lithium-ion batteries used in augmented wind power plants. IEEE Trans. Ind. Appl. 2014, 50, 4006–4017. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Hegazy, O.; Mulder, G.; Timmermans, J.M.; Coosemans, T.; Van den Bossche, P.; Van Mierlo, J. Standardization work for BEV and HEV applications: Critical appraisal of recent traction battery documents. Energies 2012, 5, 138–156. [Google Scholar] [CrossRef]
- Fernández, I.J.; Calvillo, C.F.; Sánchez-Miralles, A.; Boal, J. Capacity fade and aging models for electric batteries and optimal charging strategy for electric vehicles. Energy 2013, 60, 35–43. [Google Scholar] [CrossRef]
- Bizeray, A.; Duncan, S.R.; Howey, D.A. Advanced battery management systems using fast electrochemical modelling. In Proceedings of the IET Hybrid Electric Vehicle Conference (HEVC), London, UK, 6–7 November 2013; pp. 1–6.
- Birkl, C.R.; Howey, D.A. Model identification and parameter estimation for LiFePO4. In Proceedings of the IET Hybrid Electric Vehicle Conference 2013 (2013 HEVC), London, UK, 6–7 November 2013; pp. 1–6.
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Christensen, J.; Ahmed, J. Modelling, Estimation and control challenges for lithium-ion batteries. In Proceedings of the 2010 American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 1997–2002.
- Hariharan, K.S. A coupled nonlinear equivalent circuit—Thermal model for lithium ion cells. J. Power Sources 2013, 227, 171–176. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical model based observer design for a lithium-ion battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Speltino, C.; Domenico, D.; Fiengo, G.; Stefanopoulou, A. Comparison of reduced order lithium-ion battery models for control applications. In Proceedings of the 48th IEEE Conference on Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 3276–3281.
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Dey, S.; Ayalew, B.; Pisu, P. Nonlinear robust observers for state-of-charge estimation of lithium-ion cells based on a reduced electrochemical model. IEEE Trans. Control Syst. Technol. 2015. [Google Scholar] [CrossRef]
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and simulation of lithium-ion batteries from a systems engineering perspective. J. Electrochem. Soc. 2012, 159, 31–45. [Google Scholar] [CrossRef]
- Collet, A.; Crébier, J.; Chureau, A. Multi-cell battery emulator for advanced battery management system benchmarking. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics (ISIE), Gdansk, Poland, 27–30 June 2011; pp. 1093–1099.
- Antaloae, C.; Marco, J.; Assadian, F. A Novel method for the parameterization of a Li-ion cell model for EV/HEV control applications. IEEE Trans. Veh. Technol. 2012, 61, 3881–3892. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Marco, J.; Vaughan, N.D. The control-oriented design and simulation of a high voltage bus management strategy for use within hybrid electric vehicles. Int. J. Veh. Syst. Model. Test. 2007, 2, 345–368. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 3: State and Parameter Estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 2: Modelling and Identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 1: Backgrounds. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Improved extended Kalman filter for state of charge estimation of battery pack. J. Power Sources 2014, 255, 368–376. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Truchot, C.; Dubarry, M.; Liaw, B.Y. State-of-charge estimation and uncertainty for lithium-ion battery strings. Appl. Energy 2014, 119, 218–227. [Google Scholar] [CrossRef]
- Bruen, T.; Marco, J.; Gama, M. Current Variation in Parallelized Energy Storage Systems. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference, Coimbra, Portugal, 27–30 October 2014.
- Yang, C.P.; Ball, R.; Mcgordon, A.; Dhadyalla, G. Simulation methodologies to support novel fuse design for energy storage systems using COMSOL. In Proceedings of the IET Hybrid Electric Vehicle Conference 2013 (HEVC 2013), London, UK, 6–7 Novenmber 2013; pp. 1–5.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marco, J.; Kumari, N.; Widanage, W.D.; Jones, P. A Cell-in-the-Loop Approach to Systems Modelling and Simulation of Energy Storage Systems. Energies 2015, 8, 8244-8262. https://doi.org/10.3390/en8088244
Marco J, Kumari N, Widanage WD, Jones P. A Cell-in-the-Loop Approach to Systems Modelling and Simulation of Energy Storage Systems. Energies. 2015; 8(8):8244-8262. https://doi.org/10.3390/en8088244
Chicago/Turabian StyleMarco, James, Neelu Kumari, W. Dhammika Widanage, and Peter Jones. 2015. "A Cell-in-the-Loop Approach to Systems Modelling and Simulation of Energy Storage Systems" Energies 8, no. 8: 8244-8262. https://doi.org/10.3390/en8088244
APA StyleMarco, J., Kumari, N., Widanage, W. D., & Jones, P. (2015). A Cell-in-the-Loop Approach to Systems Modelling and Simulation of Energy Storage Systems. Energies, 8(8), 8244-8262. https://doi.org/10.3390/en8088244







