Model-Free Coordinated Control for MHTGR-Based Nuclear Steam Supply Systems

Abstract

The modular high temperature gas-cooled reactor (MHTGR) is a typical small modular reactor (SMR) that offers simpler, standardized and safer modular design by being factory built, requiring smaller initial capital investment, and having a shorter construction period. Thanks to its small size, the MHTGRs could be beneficial in providing electric power to remote areas that are deficient in transmission or distribution and in generating local power for large population centers. Based on the multi-modular operation scheme, the inherent safety feature of the MHTGRs can be applicable to large nuclear plants of any desired power rating. The MHTGR-based nuclear steam supplying system (NSSS) is constituted by an MHTGR, a side-by-side arranged helical-coil once-through steam generator (OTSG) and some connecting pipes. Due to the side-by-side arrangement, there is a tight coupling effect between the MHTGR and OTSG. Moreover, there always exists the parameter perturbation of the NSSSs. Thus, it is meaningful to study the model-free coordinated control of MHTGR-based NSSSs for safe, stable, robust and efficient operation. In this paper, a new model-free coordinated control strategy that regulates the nuclear power, MHTGR outlet helium temperature and OTSG outlet overheated steam temperature by properly adjusting the control rod position, helium flowrate and feed-water flowrate is established for the MHTGR-based NSSSs. Sufficient conditions for the globally asymptotic closed-loop stability is given. Finally, numerical simulation results in the cases of large range power decrease and increase illustrate the satisfactory performance of this newly-developed model-free coordinated NSSS control law.

1. Introduction

Small modular reactors (SMRs) are those nuclear fission reactors with electrical output power less than 300 MWe, and could be beneficial in providing electricity to the areas without transmission or distribution infrastructure in generating local power for a large population center and in being viable for specific applications such as heat sources for industrial complexes [1,2]. Due to the low power density and large heat capacity, some SMRs even have the inherent safety feature which is the most advanced feature of these SMR-based plants relative to those conventional nuclear plants and also prevents these SMRs from the hazards of core-melting, radiological release and loss of coolant accident (LOCA) [3,4]. Due to the ability of offering simpler, safer and standardized modular design by factory-building, less initial capital investment, and shorter construction period, SMRs have been viewed by International Atomic Energy Agency (IAEA) as a developing trend of nuclear energy. Through adopting multi-modular scheme, i.e., multi-SMRs providing steam for one turbine/generator set, the inherent safety feature can be applicable to the large power plants of any desired power ratings. It is well known that the modular high temperature gas-cooled reactor (MHTGR, such as the HTR (High Temperature Reactor)-Module designed in Germany [5]), which uses helium as coolant and graphite as both moderator and structural materials, is a typical SMR with a strong inherent safety feature [6,7]. An MHTGR-based nuclear steam supplying system (NSSS) module composed of a one-zone pebble-bed MHTGR, a helical-coil once-through steam generator (OTSG) arranged side-by-side with the MHTGR and some connecting pipes is shown in Figure 1, which is one module of the under-constructed two-modular plant HTR-PM (Pebble-Bed Module) designed by Institute of Nuclear and New Energy Technology in Tsinghua University [8].

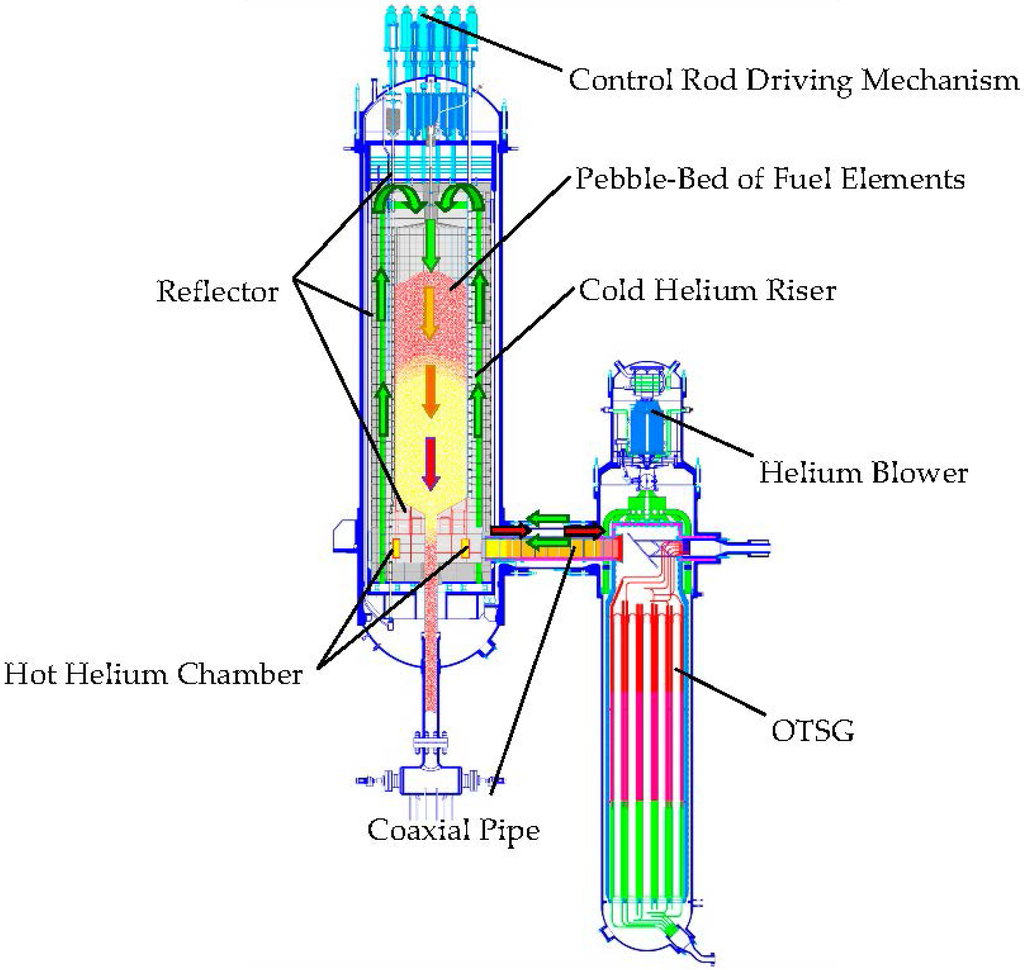
Figure 1. Schematic view of a modular high temperature gas-cooled reactor (MHTGR)-based nuclear steam supplying system (NSSS) module.

Figure 1. Schematic view of a modular high temperature gas-cooled reactor (MHTGR)-based nuclear steam supplying system (NSSS) module.

It is very clear that both the MHTGR and OTSG are complex nonlinear dynamic systems, and their dynamics are tightly coupled with each other. To improve both the steady and transient performance, it is necessary to develop coordinated control methods for the NSSS composed of the MHTGR and OTSG by considering the nonlinear dynamics. There are still very few results in the coordinated control of the reactor and steam generator. However, there have been some promising results in nonlinear control design methods for the reactors or the steam generators (SGs), which are helpful for developing coordinated control strategies. The sliding mode control (SMC) method is an effective approach to realize nonlinear control design for nuclear reactors. Shtessel gave a nonlinear power-level controller for space reactor TOPAZ II through the SMC method [9]. Due to the intrinsic chattering effect of the SMC, the recursive sliding mode control (RSMC) method was introduced by Huang, Edwards and Lee to solve the chattering problem and to improve the robustness. Based on the RSMC method, a fuzzy-adapted nonlinear power-level control law was designed for the advanced boiling water reactors (ABWR) [10]. The physics-based control (PBC) method is also an effective way to design nonlinear reactor control laws by retaining or strengthening stable subdynamics and by cancelling or suppressing unstable subdynamics, which has been applied to the load-following control design for the PWRs (Pressurized Water Reactors) [11,12,13] and MHTGRs [14,15] recently. From the aspect of SG controller design, some advanced control approaches such as the model predictive control (MPC) [16], neurofuzzy [17] and feedback-dissipation [18] methods have all been applied to improve the regulation performance of SGs.

Although the above control strategies can provide large-scale closed-loop stability for the nuclear reactors or steam generators. However, these control laws have the drawback of heavy model-reliance. Some control laws needs the state prediction or observation directly based upon the reactor or SG models [9,10,11,12,14,15,16,17], and the control parameters also vary with the reactor or SG physical and thermal-hydraulic parameters [9,10,11,12,13,14,15,16,17,18], which leads to the difficulty in practically tuning and implementation. Therefore, it is necessary to develop model-free control methods to relieve the heavy model reliance of the designed control strategies. In the early 2000s, by applying the stable adaptive fuzzy control theory presented in [19], Marseguerra and Zio gave a model-free reactor control [20]. However, the fuzzy system of this model-free controller should be either suggested by experienced operators or trained online by measurement data, which is expensive especially for the newly-built reactors. Moreover, the fuzzy adaptive nonlinear control approach given in [19] is only suitable to those nonlinear systems in Brunovsky normalized form, which lose the prior knowledge about the structure of the plant dynamics given by both neutron kinetics and thermal-hydraulics. Thus, it is necessary and meaningful to study the model-free NSSS coordinated control design approach based on the inherent physical structure of the reactor and SG dynamics, which is not only for the freedom from the expression of dynamic model but also for insensitivity to the physical and thermal-hydraulic parameters. Actually, using inherent dynamical structure given by the energy or ectropy is a crucial way to design model-free control laws. For example, based upon the energy method, Rigatos gave a model-free controller of flexible-link robots [21], which is free from the dynamic model, and is also insensitive to the robot parameters. Thus, a physics-based control design method may also be an effective way to realize model-free coordinated control for MHTGR-based NSSSs.

Motivated by the necessity of developing model-free coordinated control method for NSSSs, a model-free coordinated controller of the NSSS composed of one MHTGR and one OTSG are proposed through the physics-based approach in this paper. This NSSS coordinated control law has three key features: (a) there is no representation of any dynamic models for generating control input, state-observation or prediction; (b) the controller parameters are insensitive to the NSSS physical or thermal-hydraulic parameters; and (c) the closed-loop is globally asymptotically stable. Numerical simulation results in the cases of large range power increase and decrease illustrate the satisfactory regulating performance of this NSSS coordinated controller.

2. Modeling and Problem Formulation

In this section, the state-space model of the MHTGR-based NSSS for coordinate control design is firstly given, and then the theoretic problem to be solved in the following sections is formed.

From Figure 1, the MHTGR and OTSG in one NSSS are arranged side by side, and are connected with each other by a horizontal coaxial hot/cold gas duct. The cold helium enters the blower that mounted on the upper part of the OTSG, and is pressurized before flowing into the cold gas duct. It enters the channels inside the reflector from bottom to top for cooling the reflector, and then passes through the pebble-bed from top to bottom where it is heated to a very high temperature. The hot helium leaves the hot chamber inside the bottom reflector, and then flows into the OTSG primary side where it is cooled to be the cold helium by transferring its heat to the secondary water/steam flow. By adopting the point kinetics with one equivalent delayed neutron group and by considering the temperature feedback effect of the reactor core composed of the pebble-bed and reflector, the dynamic model for coordinated control design is:

$$\{\begin{array}{l}\mathrm{\Lambda }{\dot{n}}_{\mathrm{r}}=\left({\mathsf{\rho }}_{\mathrm{r}}-\mathsf{\beta }\right)n_{\mathrm{r}}+\mathsf{\beta }{c}_{\mathrm{r}}+{\mathsf{\alpha }}_{\mathrm{R}}{n}_{\mathrm{r}}\left(T_{\mathrm{R}}-T_{\mathrm{R},\mathrm{m}}\right),\\ {\dot{c}}_{\mathrm{r}}=\lambda \left(n_{\mathrm{r}}-c_{\mathrm{r}}\right),\\ {\mathsf{\mu }}_{\mathrm{R}}{\dot{T}}_{\mathrm{R}}=-{\mathrm{\Omega }}_{\mathrm{P}}\left(T_{\mathrm{R}}-T_{\mathrm{H}}\right)+P_0{n}_{\mathrm{r}},\\ {\mathsf{\mu }}_{\mathrm{H}}{\dot{T}}_{\mathrm{H}}={\mathrm{\Omega }}_{\mathrm{P}}\left(T_{\mathrm{R}}-T_{\mathrm{H}}\right)-{\mathrm{\Omega }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right),\\ {\mathsf{\mu }}_{\mathrm{S}}{\dot{T}}_{\mathrm{S}}={\mathrm{\Omega }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)-2M_{\mathrm{S}}\left(T_{\mathrm{S}}-T_{\mathrm{Sin}}\right),\\ {\dot{\mathsf{\rho }}}_{\mathrm{r}}=G_{\mathrm{r}}{v}_{\mathrm{r}},\end{array}$$

(1)

where the meaning of the variables are given in Nomenclature. Here, it is worthy to be noted that α_R is guaranteed to be negative by the physical design.

Define deviations of n_r, c_r, T_R, T_H, T_S, T_Sin and ρ_r from their equilibrium values, i.e., n_r0, c_r0, T_R0, T_H0, T_S0, T_Sin0 and ρ_r0, respectively, as δn_r = n_r − n_r0, δc_r = c_r − c_r0, δT_R = T_R − T_R0, δT_H = T_H − T_H0, δT_S = T_S − T_S0, δT_Sin = T_Sin − T_Sin0, δρ_r = ρ_r − ρ_r0. Since T_Sin is usually given by the environment, assume that:

$$\mathsf{\delta }{T}_{\mathrm{Sin}}\equiv 0$$

(2)

Because the helium flowrate can be adjusted by changing the main blower speed, it is not a loss of generality to assume that:

$$\mathsf{\delta }{\mathrm{\Omega }}_{\mathrm{S}}={\mathrm{\Omega }}_{\mathrm{S}}-{\mathrm{\Omega }}_{\mathrm{S}0}={\mathsf{\kappa }}_{\mathrm{S}}\mathsf{\delta }{W}_{\mathrm{P}}$$

(3)

where Ω_S0 is the steady value of Ω_S, and δW_P is the variation of the primary helium flowrate relative to its steady value, and κ_S is a positive scalar.

Moreover, the feedwater flowrate can also be adjusted, and thus we assume that:

$$\mathsf{\delta }{M}_{\mathrm{S}}=M_{\mathrm{S}}-M_{\mathrm{S}0}=C_{\mathrm{S}}\mathsf{\delta }{W}_{\mathrm{S}}$$

(4)

where M_S0 is the steady value of M_S, δW_S is the error of the feedwater flowrate relative to its steady value, and C_S is a positive scalar denoting the heat capacity of secondary coolant.

Define:

$$x={\left[\begin{array}{ccccc}{x}_1& x_2& x_3& x_4& x_5\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{ccccc}\mathsf{\delta }{n}_{\mathrm{r}}& \mathsf{\delta }{c}_{\mathrm{r}}& \mathsf{\delta }{T}_{\mathrm{R}}& \mathsf{\delta }{T}_{\mathrm{H}}& \mathsf{\delta }{T}_{\mathrm{S}}\end{array}\right]}^{\mathrm{T}}$$

(5)

$$\mathsf{\xi }=\mathsf{\delta }{z}_{\mathrm{r}}=G_{\mathrm{r}}^{-1}\mathsf{\delta }{\mathsf{\rho }}_{\mathrm{r}}$$

(6)

$$u={\left[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{ccc}{v}_{\mathrm{r}}& \mathsf{\delta }{W}_{\mathrm{P}}& \mathsf{\delta }{W}_{\mathrm{S}}\end{array}\right]}^{\mathrm{T}}$$

(7)

and

$$y={\left[\begin{array}{ccc}{x}_1& x_4& x_5\end{array}\right]}^{\mathrm{T}}$$

(8)

where x is called the NSSS state-vector, u is called the control input, y is the output that can be obtained by measurement, and δz_r is the total displacement of the control rods.

Then, nonlinear state-space model for coordinated control design can be written as:

$$\{\begin{array}{c}\dot{x}=f\left(x\right)+g_1\left(x\right)\mathsf{\xi }+g_2\left(x\right)u_2+g_3\left(x\right)u_3,\hfill \\ \dot{\mathsf{\xi }}=u_1,\hfill \\ y=h\left(x\right),\hfill \end{array}$$

(9)

where

$$f\left(x\right)=\left[\begin{array}{c}-{\mathrm{\Lambda }}^{-1}\mathsf{\beta }\left(x_1-x_2\right)+{\mathrm{\Lambda }}^{-1}{\mathsf{\alpha }}_{\mathrm{R}}\left(n_{\mathrm{r}0}+x_1\right)x_3\\ \lambda \left(x_1-x_2\right)\\ {\mathsf{\mu }}_{\mathrm{R}}^{-1}{P}_0{x}_1-{\mathsf{\mu }}_{\mathrm{R}}^{-1}{\mathrm{\Omega }}_{\mathrm{P}}\left(x_3-x_4\right)\\ {\mathsf{\mu }}_{\mathrm{H}}^{-1}{\mathrm{\Omega }}_{\mathrm{P}}\left(x_3-x_4\right)-{\mathsf{\mu }}_{\mathrm{H}}^{-1}{\mathrm{\Omega }}_{\mathrm{S}0}\left(x_4-x_5\right)\\ {\mathsf{\mu }}_{\mathrm{S}}^{-1}{\mathrm{\Omega }}_{\mathrm{S}0}\left(x_4-x_5\right)-2{\mathsf{\mu }}_{\mathrm{S}}^{-1}{M}_{\mathrm{S}0}{x}_5\end{array}\right]$$

(10)

$$g_1\left(x\right)={\left[\begin{array}{cc}{\mathrm{\Lambda }}^{-1}{G}_{\mathrm{r}}\left(n_{\mathrm{r}0}+x_1\right)& O_{1\times 4}\end{array}\right]}^{\mathrm{T}}$$

(11)

$$g_2\left(x\right)={\left[\begin{array}{ccc}{O}_{1\times 3}& -{\mathsf{\mu }}_{\mathrm{H}}^{-1}{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)& {\mathsf{\mu }}_{\mathrm{S}}^{-1}{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)\end{array}\right]}^{\mathrm{T}}$$

(12)

$$g_3\left(x\right)={\left[\begin{array}{cc}{O}_{1\times 4}& -2{\mathsf{\mu }}_{\mathrm{S}}^{-1}{C}_{\mathrm{S}}{T}_{\mathrm{S}}\end{array}\right]}^{\mathrm{T}}$$

(13)

and

$$h\left(x\right)={\left[\begin{array}{ccc}{x}_1& x_4& x_5\end{array}\right]}^{\mathrm{T}}$$

(14)

From the MHTGR-based NSSS state-space model Equation (9), the theoretic problem to be solved in the next sections is summarized as:

Problem 1. How can a model-free control input u defined by:

$$u={\left[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}\right]}^{\mathrm{T}}$$

(15)

for nonlinear system Equation (9) be designed so that the closed-loop is globally asymptotically stable?

3. Model-Free Coordinated Control Design

The following Theorem 1, which is the main result of this paper, summarizes the design of model-free coordinated control input u for the MHTGR-based NSSS. The corresponding design process can be seen in the proof Theorem 1.

Theorem 1. Consider nonlinear system Equation (9). The coordinated control given by:

$$u_1=-\left(k_{\mathrm{p}11}{x}_1+k_{\mathrm{d}11}{\dot{x}}_1+k_{\mathrm{p}14}{x}_4+k_{\mathrm{d}14}{\dot{x}}_4+k_{\mathrm{p}15}{x}_5+k_{\mathrm{d}15}{\dot{x}}_5\right)$$

(16)

$$u_2=\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)}\left(k_{\mathrm{p}24}{x}_4-k_{\mathrm{p}25}{x}_5\right)$$

(17)

and

$$u_3=\frac{M_{\mathrm{S}0}}{C_{\mathrm{S}}{T}_{\mathrm{S}}}{k}_{\mathrm{p}35}{x}_5$$

(18)

where feedback gains k_p11, k_d11, k_p14, k_d14, k_p15, k_d15, k_p24, k_p25 and k_p35 are all positive constants satisfying:

$$k_{\mathrm{d}14}=\left(1-{\mathsf{\eta }}_1\right)\left({\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2\right)\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|{\mathsf{\mu }}_{\mathrm{H}}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}$$

(19)

$$k_{\mathrm{d}15}=\left(1-{\mathsf{\eta }}_2\right)\left[{\mathsf{\gamma }}_1+\frac{{\mathrm{\Omega }}_{\mathrm{S}0}\left(1+k_{\mathrm{p}25}\right)}{{\mathrm{\Omega }}_{\mathrm{S}0}\left(1+k_{\mathrm{p}25}\right)+2M_{\mathrm{S}0}\left(1+k_{\mathrm{p}35}\right)}{\mathsf{\gamma }}_2\right]\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|{\mathsf{\mu }}_{\mathrm{S}}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}$$

(20)

$$k_{\mathrm{p}14}={\mathsf{\gamma }}_2\left(1+k_{\mathrm{p}24}\right)\frac{2M_{\mathrm{S}0}\left(1+k_{\mathrm{p}35}\right)}{{\mathrm{\Omega }}_{\mathrm{S}0}\left(1+k_{\mathrm{p}25}\right)+2M_{\mathrm{S}0}\left(1+k_{\mathrm{p}35}\right)}\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|{\mathrm{\Omega }}_{\mathrm{S}0}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}$$

(21)

and

$$k_{\mathrm{p}15}={\mathsf{\gamma }}_1\left(1+k_{\mathrm{p}35}\right)\frac{2\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|M_{\mathrm{S}0}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}$$

(22)

respectively, and γ_i and η_i (i = 1, 2) are all given positive constants with 0 < η_i < 1. Then, the closed-loop system formed by Equations (9) and (16)–(18) is globally asymptotically stable if:

$$k_{\mathrm{d}11}>\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|P_0}{G_{\mathrm{r}}{\mathrm{\Omega }}_{\mathrm{P}}}{\left({\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2\right)}^2\left[1+\frac{{\mathsf{\eta }}_1{\mathsf{\mu }}_{\mathrm{H}}}{4{\mathsf{\mu }}_{\mathrm{R}}}+\frac{{\mathsf{\eta }}_2{\mathsf{\mu }}_{\mathrm{S}}\left(1+k_{\mathrm{p}24}\right)}{4{\mathsf{\mu }}_{\mathrm{R}}\left(1+k_{\mathrm{p}25}\right)}\right]$$

(23)

$$k_{\mathrm{p}24}>\frac{2{\mathrm{\Omega }}_{\mathrm{P}}}{{\mathrm{\Omega }}_{\mathrm{S}0}}\left(1+{\mathsf{\eta }}_1\frac{{\mathsf{\mu }}_{\mathrm{H}}}{{\mathsf{\mu }}_{\mathrm{R}}}\right)-1$$

(24)

and

$$k_{\mathrm{p}35}>\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{2M_{\mathrm{S}0}}\left(1+k_{\mathrm{p}25}+{\mathsf{\eta }}_2\frac{{\mathrm{\Omega }}_{\mathrm{P}}{\mathsf{\mu }}_{\mathrm{S}}}{{\mathrm{\Omega }}_{\mathrm{S}0}{\mathsf{\mu }}_{\mathrm{R}}}\right)-1$$

(25)

Proof: See Appendix.

Remark 1. Define

$${\mathsf{\kappa }}_{\mathrm{p}24}=\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)}{k}_{\mathrm{p}24}$$

(26)

$${\mathsf{\kappa }}_{\mathrm{p}25}=\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)}{k}_{\mathrm{p}25}$$

(27)

and

$${\mathsf{\kappa }}_{\mathrm{p}35}=\frac{M_{\mathrm{S}0}}{C_{\mathrm{S}}{T}_{\mathrm{S}}}{k}_{\mathrm{p}35}$$

(28)

From Equations (26)–(28), as well as inequalities Equations (24) and (25), we can easily obtain that both

$${\mathsf{\kappa }}_{\mathrm{p}24}>\left[\frac{2{\mathrm{\Omega }}_{\mathrm{P}}}{{\mathrm{\Omega }}_{\mathrm{S}0}}\left(1+{\mathsf{\eta }}_1\frac{{\mathsf{\mu }}_{\mathrm{H}}}{{\mathsf{\mu }}_{\mathrm{R}}}\right)-1\right]\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)}$$

(29)

and

$${\mathsf{\kappa }}_{\mathrm{p}35}>\left\{\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{2M_{\mathrm{S}0}}\left[1+\frac{{\mathsf{\kappa }}_{\mathrm{S}}}{{\mathrm{\Omega }}_{\mathrm{S}0}}{\mathsf{\kappa }}_{\mathrm{p}25}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)+{\mathsf{\eta }}_2\frac{{\mathrm{\Omega }}_{\mathrm{P}}{\mathsf{\mu }}_{\mathrm{S}}}{{\mathrm{\Omega }}_{\mathrm{S}0}{\mathsf{\mu }}_{\mathrm{R}}}\right]-1\right\}\frac{{\mathrm{\Omega }}_{\mathrm{S}0}}{{\mathsf{\kappa }}_{\mathrm{S}}\left(T_{\mathrm{H}}-T_{\mathrm{S}}\right)}$$

(30)

should be satisfied for guaranteeing globally asymptotic closed-loop stability. Moreover, control input u₂ and u₃ can be certainly rewritten as:

$$u_2={\mathsf{\kappa }}_{\mathrm{p}24}{x}_4-{\mathsf{\kappa }}_{\mathrm{p}25}{x}_5$$

(31)

and

$$u_3={\mathsf{\kappa }}_{\mathrm{p}35}{x}_5$$

(32)

respectively.

Remark 2. Since γ_i (i = 1, 2) are arbitrarily given positive constants, from Equations (21) and (22), it is clear that feedback gains k_p14 and k_p15 can be arbitrary positive values. Moreover, since η_i (i = 1, 2) are arbitrary given constants satisfying 0 < η_i < 1, from Equations (19) and (20), feedback gains k_d14 and k_d15 can be arbitrarily in the sets

$${\Pi }_{\mathrm{d}14}=\left\{\begin{array}{cc}\mathsf{\theta }\in \mathrm{R}|& 0<\mathsf{\theta }<\left({\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2\right)\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|{\mathsf{\mu }}_{\mathrm{H}}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}\end{array}\right\}$$

(33)

and

$${\Pi }_{\mathrm{d}15}=\left\{\begin{array}{cc}\mathsf{\theta }\in \mathrm{R}|& 0<\mathsf{\theta }<\left[{\mathsf{\gamma }}_1+\frac{{\mathrm{\Omega }}_{\mathrm{S}0}\left(1+k_{\mathrm{p}25}\right)}{{\mathrm{\Omega }}_{\mathrm{S}0}\left(1+k_{\mathrm{p}25}\right)+2M_{\mathrm{S}0}\left(1+k_{\mathrm{p}35}\right)}{\mathsf{\gamma }}_2\right]\frac{\left|{\mathsf{\alpha }}_{\mathrm{R}}\right|{\mathsf{\mu }}_{\mathrm{S}}}{G_{\mathrm{r}}{\mathsf{\mu }}_{\mathrm{R}}}\end{array}\right\}$$

(34)

respectively. If constants γ_i and η_i (i = 1, 2) are given, then the values of feedback gains k_p14, k_p15, k_d14 and k_d15 are given. From Theorem 1, we can see that the globally asymptotic closed-loop stability can be guaranteed if inequalities Equations (23)–(25) are all well satisfied. Therefore, from Equations (19)–(22) as well as inequalities Equations (23), (29) and (30), the values of feedback gains k_d11, k_d14, k_d15, k_p11, k_p14, k_p15, κ_p24, κ_p25, κ_p35 are all not directly determined by the NSSS physical and thermal parameters. Actually, the values of feedback gains k_p11, k_p14, k_p15 and κ_p35 can be arbitrarily given, and the values of feedback gains k_d11, k_d14, k_d15, κ_p24 and κ_p25 can be chosen in the scopes determined by Equations (33), (34), (23), (29) and (30). Moreover, from the expressions of this newly-built coordinated control law composed of Equations (16), (31) and (32), there is no expressions about the dynamic model in this controller utilized for either state-prediction or control input generation. From the above discussion, MHTGR-based NSSS coordinated control given by Equations (16), (31) and (32) is model-free, which leads to easy implementation and tuning.

4. Simulation Results with Discussion

To show the feasibility and performance of the newly-built nonlinear adaptive coordinated control strategy given in Theorem 1, it is applied to the regulation of an NSSS of HTR-PM plant in this section.

The dynamic model of the MHTGR that is used for numerical simulation is the nodal model given in [22]. The OTSG model adopted the moving boundary model given in [23]. The code was developed based on VC++ [24], and this simulation was done by using this software. Actually, both the space-dependent reactor models given in [22,23] and point model Equation (1) can describe the NSSS dynamics. The former one gives a more detailed description and is more suitable for verification, and the later model is much simpler and is more suitable for control law design. The dynamic model of the second-loop system gives the feedwater temperature and pressure for the dynamic model of the NSSS. In the numerical verification, the simulation software adopts the software given in [24] which contains the dynamics models of the NSSS as well as the secondary-loop. Moreover, from the above Theorem 1 and Comment 1, the NSSS coordinated control law can be written as Equations (16)–(18), and can also take the form as Equations (16), (31) and (32). If the first form is adopted, then control gains k_p24 and k_p35 should satisfy inequalities Equations (24) and (25). Moreover, if the second form is adopted, then control gains κ_p24 and κ_p35 should satisfy inequalities Equations (29) and (30). Here, the second form is adopted, and control gains are chosen as k_d11 = 2.0, k_p11 = 0.2, k_d14 = 0.5, k_p14 = 0.05, k_d15 = 0.02, k_p15 = 0.001, κ_p24 = 0.5, κ_p25 = 0.05 and κ_p35 = 0.3 so that Equations (23), (29), (30), (33) and (34) are satisfied.

To illustrate the coordinate control performance, the following two case studies are done:

• Case A: Power-demand decreases from 100% to 50% RFP (Reactor Full Power) linearly in 10 min.
• Case B: Power-demand increases from 50% to 100% RFP linearly in 10 min.

Both cases A and B represent hard operations of the NHR. Dynamic responses of the relative nuclear power n_r, reactor outlet helium temperature T_cout and OTSG outlet steam temperature T_s as well as the control rod speed v_r, helium flowrate G_p and feedwater flowrate G_s generated by the newly-built coordinated controller in the above two cases are shown in Figure 2 and Figure 3, respectively. Here, the power-demand decrease starts at the 1000 s, and the power-demand increase starts at the 2000 s. The difference in the start-time of power-demand variation does not affect the verification result. Since the OTSG outlet steam temperature is constant (571 °C), and since the feed-water temperature of the OTSG is different at different power-levels, it is very clear that the feedwater flowrate in a 50% reactor full power-level (RFP) is not the 50% flowrate at 100% RFP.

Since the power-demand changes, the errors between the actual and referenced values of the relative nuclear power, reactor outlet helium temperature and OTSG outlet steam temperature become larger. These three errors make coordinated control law to drive the control rods, primary helium blower and feedwater pump to suppress these error signals. The system enters into a steady state when the supplied and demanded power balances with each other. From Figure 2 and Figure 3, it is clear that closed-loop stability can be well guaranteed by properly choosing the feedback gains k_d11, k_d14, k_d15, k_p11, k_p14, k_p15, κ_p24, κ_p25 and κ_p35 so that feedback gains k_d14 and k_d15 are in the sets given by Equations (33) and (34), and inequalities Equations (23), (29) and (30) are satisfied. Thus, it is very clear that the numerical phenomena in this simulation fit well with the theoretic results. Finally, this newly-built model-free coordinated control for MHTGR-based NSSSs proposed in this paper has a simple form and can be easily implemented in the practical engineering.

Due to the HTR-PM plant still being under construction, we cannot verify the result in this paper by some real operating data in this stage. However, the obtained control parameters, i.e., controller structures given by Equations (16), (31) and (32) as well as control gain scopes given by Equations (23), (29), (30), (33) and (34) have deep implications to the future realization of controlling the real HTR-PM nuclear system. Here, the implication lies in the following two aspects:

(1)

Since the coordinated control law given by Equations (16), (31) and (32) has been proven to have the globally asymptotically stabilization performance, the coordinated control law of the real HTR-PM NSSS module should take the same form as Equations (16), (31) and (32) in the engineering.

(2)

The control gains in the practical engineering should be chosen to satisfy conditions Equations (23), (29), (30), (33) and (34) generally. However, due to the mismatch between the real and designed NSSS parameters as well as that between the dynamic features of the real and designed actuators (such as the control rods, helium bowers and feedwater pumps), some experiments or tests should be given practically to verify that the overshoots and transition periods of the real response of key process variables meets the engineering requirements.

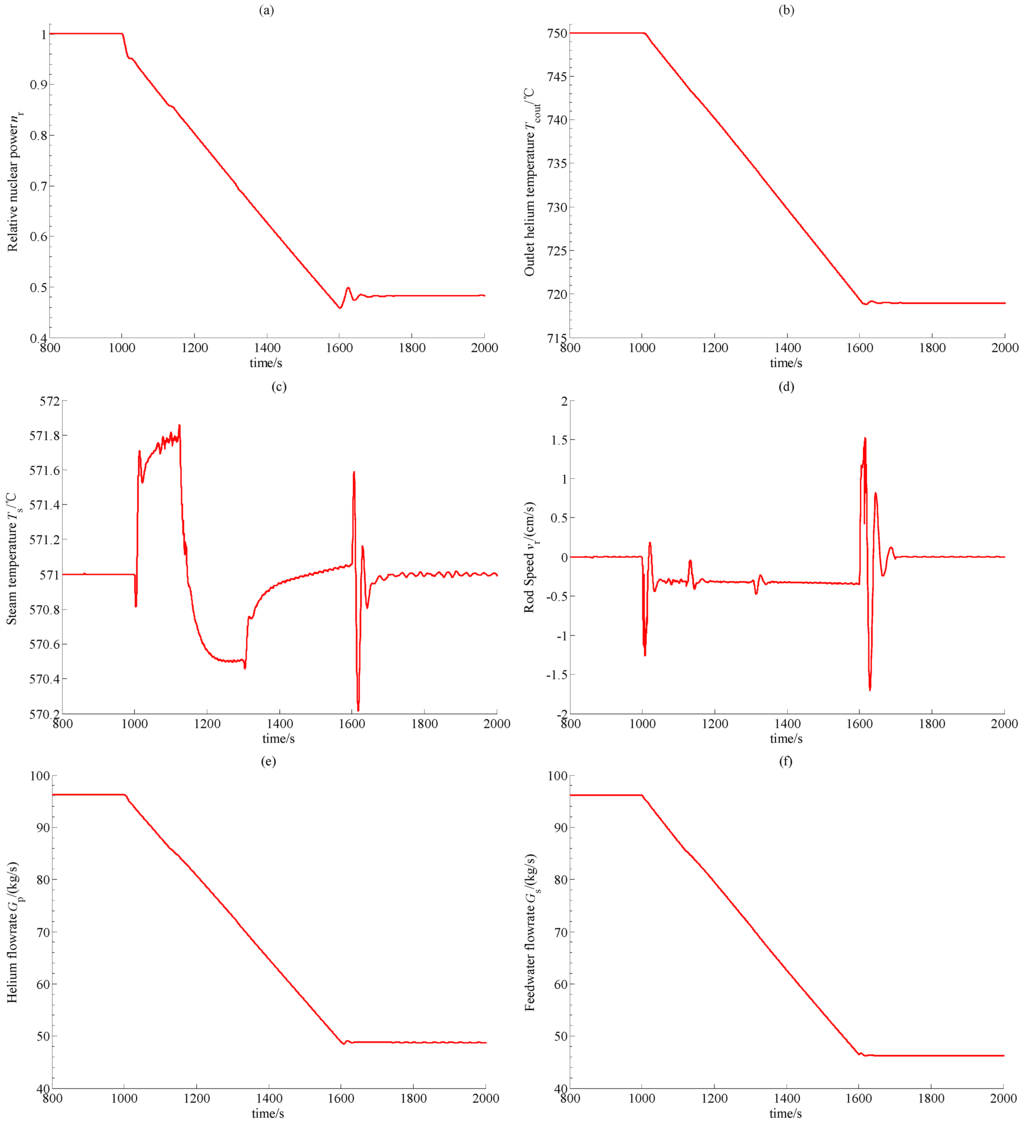
Figure 2. Simulation results in Case A: (a) Relative nuclear power; (b) Outlet helium temperature; (c) steam temperature; (d) Control rod speed signal; (e) Primary helium flowrate; (f) Feedwater flowrate.

Figure 2. Simulation results in Case A: (a) Relative nuclear power; (b) Outlet helium temperature; (c) steam temperature; (d) Control rod speed signal; (e) Primary helium flowrate; (f) Feedwater flowrate.

Furthermore, the parameters of the NSSS models for control design and simulation are given by physical and thermal-hydraulic design. It was verified that the model and software given in [22,23,24] can provide credible dynamical simulation for the HTR-PM plant. The theoretical and simulation results in this paper show at least that the coordinated control law determined by Equations (16), (31) and (32) can be implemented in the practical engineering. Verifying the results in this paper by the operating data of the HTR-PM plant will be very meaningful work in the future.

Figure 3. Simulation results in Case B: (a) Relative nuclear power; (b) Outlet helium temperature; (c) steam temperature; (d) Control rod speed signal; (e) Primary helium flowrate; and (f) Feedwater flowrate.

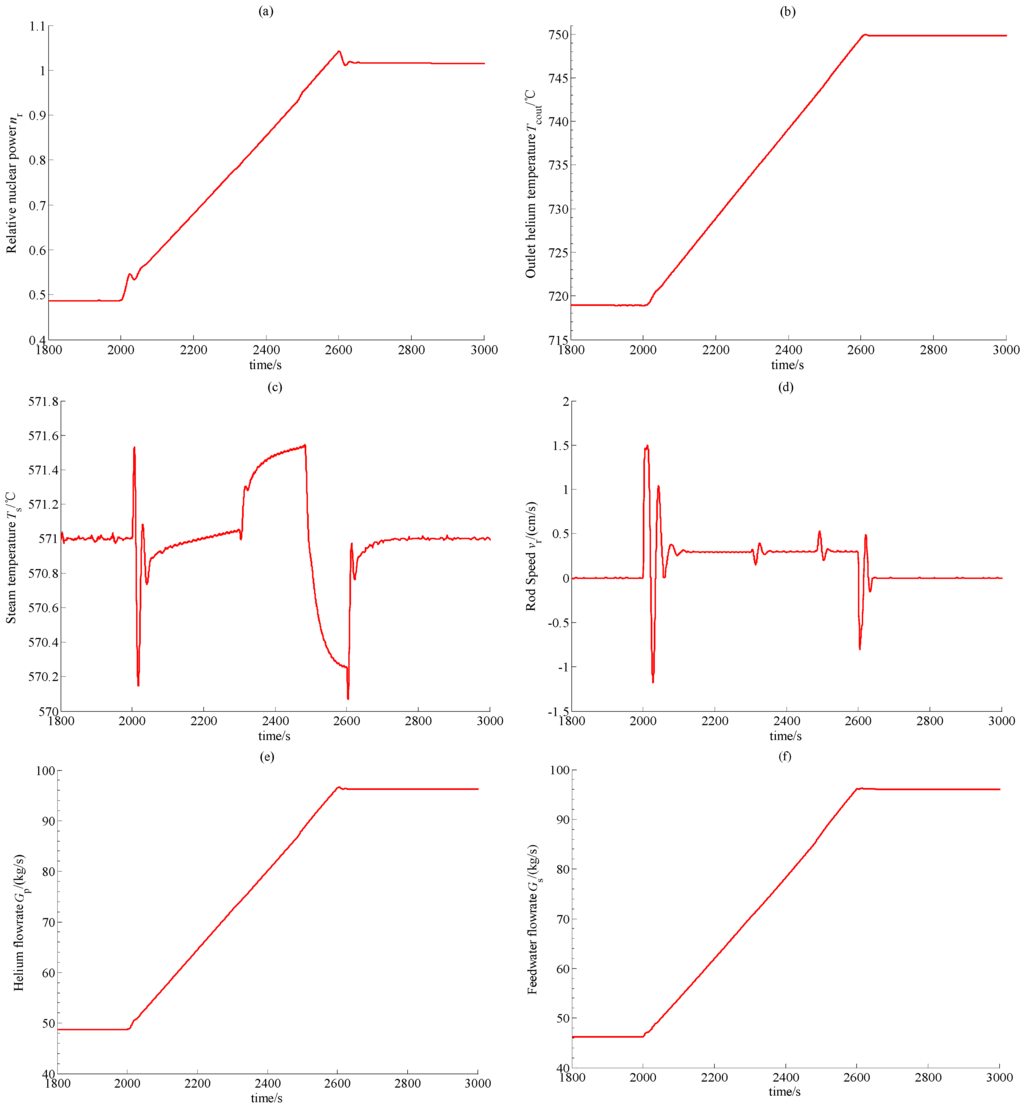
Figure 3. Simulation results in Case B: (a) Relative nuclear power; (b) Outlet helium temperature; (c) steam temperature; (d) Control rod speed signal; (e) Primary helium flowrate; and (f) Feedwater flowrate.

5. Conclusions

Due to the simpler, standardized, and safer modular design, SMRs have the virtues of being factory built, requiring smaller initial capital investment, and having shorter construction time. Because of its persistency of power supply, SMRs can be incorporated with new energy resources to build micro-grids and can also be used to build large-scale nuclear plants by the multi-modular scheme. Coordinated control of SMR-based NSSSs is meaningful to realize the load-following function of SMR-based nuclear plants. However, until now, there has still been very little work in the field of NSSS coordinated control. MHTGR is a typical SMR having the inherent safety features and economic competitive power, and has also been seen as a candidate for a next generation nuclear reactor. Coordinated control of MHTGR-based NSSSs is quite important in providing the stable and efficient operation for the MHTGR-based nuclear energy systems. In this paper, by considering the exterior disturbances, a model-free coordinated control law for the MHTGR-based NSSS is proposed, which does not contain any expressions of the NSSS dynamic model and is insensitive to the physical or thermal parameters. The sufficient conditions for guaranteeing globally asymptotic closed-loop stability are given. Numerical simulation results show the satisfactory regulation performance of this newly-built model-free coordinated controller. Due to its simplicity, this control law can be very easily implemented in those digital control system platforms.

Moreover, the MHTGR-based NSSS is quite different from the PWR-based NSSS. As stated in Section 1 of this paper, the MHTGR-based NSSS consists of a modular high temperature gas-cooled reactor (MHTGR), a helical-coil once-through steam-generator (OTSG), primary helium blower and some connecting pipes. However, the PWR-based NSSS usually consists of a pressurized water reactor (PWR), a U-tube steam-generator (UTSG), primary feed-water pump and some pipes. The main difference of the dynamics of the MHTGR and that of the PWR is determined by the reactivity effect of the coolant. For the MHTGR, the coolant is helium, which is transparent to the fission reaction and has NO reactivity feedback effect on the neutron kinetics. For the PWR, the coolant is the pressurized water, which is also utilized as the moderator and does have reactivity feedback effect on the neutron kinetics. The difference in the reactor dynamics is only the first difference between the MHTGR and PWR based NSSSs. The second difference is that the MHTGR-based NSSS adopts the helical-coil OTSG, and the PWR-based NSSS adopts the UTSG. Since natural circulation in the UTSG exists, its dynamic behavior is quite different from that of the OTSG. Therefore, the dynamic behavior of the PWR-based NSSS cannot be described by model Equation (1) in this paper, and the coordinated control proposed in this paper for the MHTGR-based NSSS cannot be directly applied to the other types of NSSSs such as the PWR-based NSSS. However, the key idea of control design approach in this paper, i.e., the physics-based control design approach is helpful to realize the coordinated control laws for other types of NSSSs.