1. Introduction
Due to economic development and population growth in the past decades, the global consumption of energy has increased significantly. The air conditioning sector consumes approximately one third of the primary energy and 50% of building energy consumption comprises air conditioning load [
1]. The low exergetic efficiencies of conventional air conditioning systems, negative environmental impacts, and depleting nature of fossil fuels enforce the need for alternative air conditioning techniques which can effectively employ renewable and low grade thermal energy sources.
Although conventional air conditioning systems can effectively control the sensible loads of the conditioned space these systems are inefficient to control the latent load. The conventional systems control the humidity of indoor air by condensation processes in which the temperature of the cooling coil must be lower than the dew point temperature of the air. Often, the air is overcooled after moisture removal from the air and needs to be reheated before supplying it to the conditioned space. The overcooling and reheating of process air makes the conventional air conditioning systems energy inefficient [
2]. Moreover, this process of condensation may result in the growth of mold and bacteria because of the wet surfaces of cooling coils which leads to poor indoor air quality and undesirable health issues within the conditioned space [
3,
4]. Since, in hot and humid climatic conditions latent load is more dominant, these conventional systems are inefficient and the need arises for alternative and efficient air conditioning systems to effectively handle the latent load [
5,
6,
7].
Among the various techniques actively pursued currently, desiccant cooling is a promising choice [
8,
9,
10]. Desiccant air conditioning techniques have been proved to be promising energy efficient cooling systems which can improve the health and productivity of the occupants by maintaining acceptable indoor air quality [
11,
12].
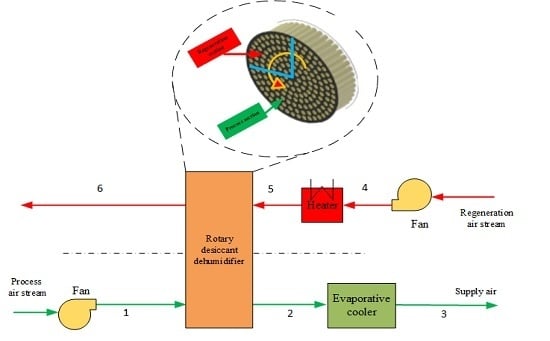
In this paper a rotary type liquid desiccant cooling system has been investigated. The purpose of the this investigation was to analyze the performance of a liquid desiccant cooling system with a rotary dehumidifier using a low cost and easily available liquid desiccant material (CaCl2) system. CaCl2 has a regeneration temperature of about 50–85 °C which makes the use of low grade thermal energy, like solar, more feasible. The proposed system has the advantage of conducting dehumidification and regeneration simultaneously. A mathematical model is developed for the proposed system to investigate its performance under different climatic, design, and operating conditions.
The present research paper has been divided into different sections. The scope of the present work and international practices are introduced in the Introduction
Section 1 while
Section 2 discusses the desiccant-based air conditioning system.
Section 3 provides technical details about the proposed liquid desiccant system. The mathematical formulations of the problem are given in
Section 4 and the results are discussed in
Section 5. Finally, the findings of the study are summarized in
Section 6.
2. Desiccant-Based Air Conditioning Systems
Desiccant dehumidification systems can dehumidify air without cooling it below its dew point temperature, unlike conventional air conditioning systems. These systems can remove moisture at higher temperatures, thus eliminating the need for reheating and can prove to be more energy efficient for the removal of latent heat [
13]. Desiccant systems work near ambient pressure and can be scaled down to small capacity, unlike vapor absorption systems which are generally available above 35 kW cooling capacity [
14]. Liquid desiccant air conditioning systems have additional advantages like high density energy storage at near ambient conditions and flexibility of component layouts [
15]. On the other hand, there are some challenges like corrosion, carry over and low COP usually associated with this technology [
16,
17]. The major advantages of desiccant cooling systems can be summarized as:
Only air and water are required as working fluids. Chlorofluorocarbons are not required, thus, there is no adverse impact on the ozone layer.
The source of thermal energy can be diverse (i.e., solar, waste heat, natural gas). The electrical energy requirement can be less than 25% that of conventional refrigeration systems.
The sensible and latent loads can be controlled separately.
Emission of greenhouse gases (GHG) such as CO2 can be reduced significantly.
Since desiccant systems operate near atmospheric pressure, the maintenance and construction are simplified.
These systems can provide better indoor air quality.
Because of these advantages, many research efforts have been applied on the applications of desiccant cooling cycles [
18,
19]. The most popular desiccant cooling system is the Munters environmental control (MEC) cycle [
20]. This cycle is very attractive due to the suitability of relatively low temperature heat sources like solar energy for the regeneration of the desiccant. However, there are still two shortcomings that need to be addressed. First, the supply air temperature in such systems is 4 °C higher than that in a conventional all air system, which means that a 60% greater volume of air needed to be pumped and circulated through the system. As a result, fan energy demand, which is already high in a conventional all-air system [
21], would be further increased. This would compromise the energy savings effect of the system. Secondly, in hot and humid regions like Hong Kong, the effectiveness of desiccant dehumidification would be quite limited, which means that a heavier desiccant dehumidifier/wheel and/or a higher regenerating temperature are/is required to realize efficient dehumidification and cooling. The system would become bulky and the initial investment would be higher.
Since the 1950s, most of the studies related to liquid desiccant cooling have focused on direct contact between air and a liquid desiccant [
22,
23]. These direct liquid desiccant cooling systems have a significant drawback of desiccant carryover in the air streams. The liquid desiccant carryover in the air stream may affect indoor air quality and the health of occupants within the conditioned space. In addition, desiccant carryover can lead to higher maintenance costs and short life cycles because of equipment and ducting corrosion. The drawbacks mentioned above have limited the application of liquid desiccant cooling systems in different conditions [
24]. To overcome the problem of desiccant carryover, different liquid desiccant dehumidifier configurations have been proposed [
25]. One design to reduce the carryover problem is to use a low flow rate of process air in an internally cooled/heated dehumidifier [
26,
27]. The dehumidifier with indirect contact between air and liquid desiccant using membranes is another design which can help in eliminating the problem of desiccant carryover [
28]. The rotary type liquid desiccant cooling system is yet another configuration to overcome the drawbacks of liquid desiccant cooling systems mentioned above. In rotary type liquid desiccant cooling systems a rotary wheel embedded with a porous media is used to carry a liquid desiccant.
5. Results and Discussion
In the present work, six performance parameters are used to analyze the performance of proposed rotary liquid desiccant cooling system. These parameters are as follows:
The rate of moisture removal from the process air by the liquid desiccant cooling system is defined as moisture removal rate (
Mr):
The amount of latent and sensible load removed by the liquid desiccant cooling system is represented by sensible heat ratio (SHR):
where
Qsensible and
Qlatent are the sensible and latent load removal rate from the conditioned space, respectively.
The overall cooling provided by the desiccant system is defined as cooling capacity (CC). The difference of enthalpy between outdoor and supply air is used to represent overall CC because it includes both sensible and latent loads:
The overall performance of the system is represented by coefficient of performance (COP):
where, β equivalent conversion coefficient of electric power and thermal energy and its value is taken as 0.3.
The ratio between the CC and electrical energy consumption is given by electrical coefficient of performance (ECOP) while ratio between CC to consumption of thermal energy is represented by thermal coefficient of performance (TCOP):
The mass and energy balances for the liquid desiccant cooling system needs to be checked to ensure that the model conserves both energy and mass.
The effects of different key parameters on the performance of the proposed rotary liquid desiccant cooling system are discussed in this section. The parameters considered are effectiveness of evaporative cooler, temperature and humidity ratio of ambient air, ratio of mass flow rate, and regeneration temperature. The base values and ranges for each parameter studied in this paper are presented in
Table 3. These climatic parameters have been obtained from the long-term meteorological data measured at the Research Institute of the King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia. Only one parameter is varied in each case, keeping all other parameters constant at the reference values.
Although, the effectiveness of the evaporative cooler (ε
ev) has no effect on SHR and MRR because these parameters are controlled by the rotary desiccant dehumidifier, it has a significant effect on the electrical and thermal energy required for the liquid desiccant cooling system. In addition, ε
ev has strong impact on the capacity of the cooling equipment, and hence the system’s COP.
Table 4 shows the effect of ε
ev on the performance of the system. It is observed that the CC, COP, TCOP, and ECOP increase by 36%, 42%, 36% and 37%, respectively, when ε
ev increases from 0.35 to 0.9. It is clear that installing an evaporative cooler with high effectiveness, results in considerable savings in the operating and capital costs. Furthermore, the payback period of the system is expected to be shorter. Therefore, an evaporative cooler with high effectiveness is strongly recommended to control the sensible load in liquid desiccant cooling systems.
It is worth mentioning that an efficient control system should be installed for the cooling system used in the liquid desiccant cooling cycle. This is due to the fact that sometimes it is more beneficial to bypass the air flowing around the cooling system. For example, if the temperature of the air leaving the dehumidifier is lower than the supply air temperature, the evaporative cooler makes the temperature much lower than the supply demand temperature and reheating will be required to achieve comfort conditions. This cooling and reheating will cause a decrease in performance because of the corresponding increase in the energy consumption. Therefore, the operation of an evaporative cooler should be efficiently controlled by detecting the exit temperature from the dehumidifier at state point 2.
The increase of ambient air temperature causes an increase in dehumidification and cooling loads because of an increase in the potential of mass and heat transfer. In order to remove the total latent load of the conditioned space, a humidity ratio of about 10 g/kg is expected to achieve the goal depending on the indoor and outdoor ambient conditions. The proposed rotary liquid desiccant cooling system may not be able to meet latent load of the building with the reference parameters when the ambient air condition exceeds a certain temperature and humidity. Therefore, the system should be equipped with an efficient control system in order to have a better control of supply conditions according to outdoor and indoor conditions.
Figure 3a shows that the moisture removal rate increases linearly with ambient temperature due to the increase in potential for mass transfer. However, the sensible heat ratio (SHR) also increases with the increase in ambient air temperature, as shown in
Figure 3b.
The temperature of air at the exit of dehumidifier (state point 2) increases with ambient air temperature. This increase in temperature difference causes an increase in the enthalpy difference of the air across the rotary dehumidifier. This explains the increase that occurs in the cooling capacity of the system, as shown in
Table 5. The achieved improvement in the system performance parameters (CC, COP, ECOP, TCOP) is due to the fact that at higher ambient temperature, the amount of heat and mass transfer from the air to the desiccant increases. This enhancement of heat and mass transfer also tends to increase the amount of heat released from the air to the desiccant during the absorption process. Consequently, the thermal energy required to heat the regeneration air prior to entering the regeneration section of the rotary dehumidifier is reduced with ambient temperature. This leads to the improvement of the system performance parameters CC, COP, ECOP and TCOP. These results show that the proposed rotary liquid desiccant cooling system performs more efficiently in hot and humid climatic conditions.
The increase in humidity ratio of the ambient air results in an increased potential for mass transfer. In turn, this increase in mass transfer enhances the rate of moisture removal from the process air by the desiccant.
Figure 4 show that the moisture removal rate increases and sensible heat ratio decreases due to the increase in mass transfer potential. In fact, increasing the air inlet humidity ratio causes an increase in the driving force and hence increases the mass transfer potential within the dehumidifier. The partial vapor pressure is the governing factor for the mass transfer between process air and desiccant surface. As the inlet air humidity ratio increases, the partial pressure of water vapor in the air also increases. This enhances the difference between the partial vapor pressure of the inlet air stream and the desiccant surface which ultimately tend to increase the moisture absorbing capacity of the desiccant.
The effect of ambient humidity ratio on the performance of the system is shown in
Table 6. As discussed previously, the higher the ambient air humidity, the higher the CC of the system and the lower the thermal energy demand for the system. Therefore, the COP, ECOP and TCOP increase with increasing ambient air humidity ratio, as shown in
Table 6.
The air flow rate is one of the important parameters which have a strong effect on the performance of liquid desiccant cooling systems. There is no common optimum value of air flow rates that is applicable to different systems. Factors like heat and mass transfer coefficients should be considered to define the optimal value of flow rate because these factors may differ for different outdoor conditions and from system to system. The influence of the ratio between regeneration and process air flow rates on the system performance is shown in
Figure 5. In this case the process air flow rate value is fixed to the base value while the mass flow rate of regeneration air is varied. The COP and TCOP decreased by 40% and 42% as the ratio of the mass flow rate increased from 0.3 to 1, respectively. This may be explained as follows: when the regeneration air flow rate increases with process air flowing at a constant rate the input energy for regeneration tends to increase which in turn decreases the system performance. Consequently, more thermal energy is consumed to condition the regeneration air to the specified temperature before entering the regeneration portion. The CC and ECOP are not affected significantly by changing mass flow rate of regeneration air due to constant flow rate of process air stream.
The regeneration temperature is an important parameter for liquid desiccant cooling systems because it affects the performance of the overall system significantly. The input thermal energy increases with the increase in regeneration temperature which decreases both the thermal and overall COP of the system as shown in
Figure 6. Although a higher regeneration temperature value makes the moisture removal process faster, at the same time this higher temperature value tends to dry up the desiccant wheel before the completion of the regeneration period. Hence, some added energy is wasted and is not utilized during the absorption period for moisture removal. Secondly, the higher regeneration temperature value increases the input energy which decreases the COP of the cycle. A low regeneration temperature enhances the potential of these systems for use in solar applications. The COP and TCOP of the system decreased from 0.91 to 0.52 and 3.4 to 1, respectively, when the regeneration temperature increased from 50 to 85 °C.
It is observed from the above results that the system performance is largely affected by the variations of inlet air humidity ratio, mass flow rate of regeneration air, and regeneration temperature. System performance improvements are expected at lower regeneration temperatures and regeneration air mass flow rates as both of these have a direct effect on the required input thermal energy.