Accessing Colony Boundary Strengthening of Fully Lamellar TiAl Alloys via Micromechanical Modeling
Abstract
:1. Introduction
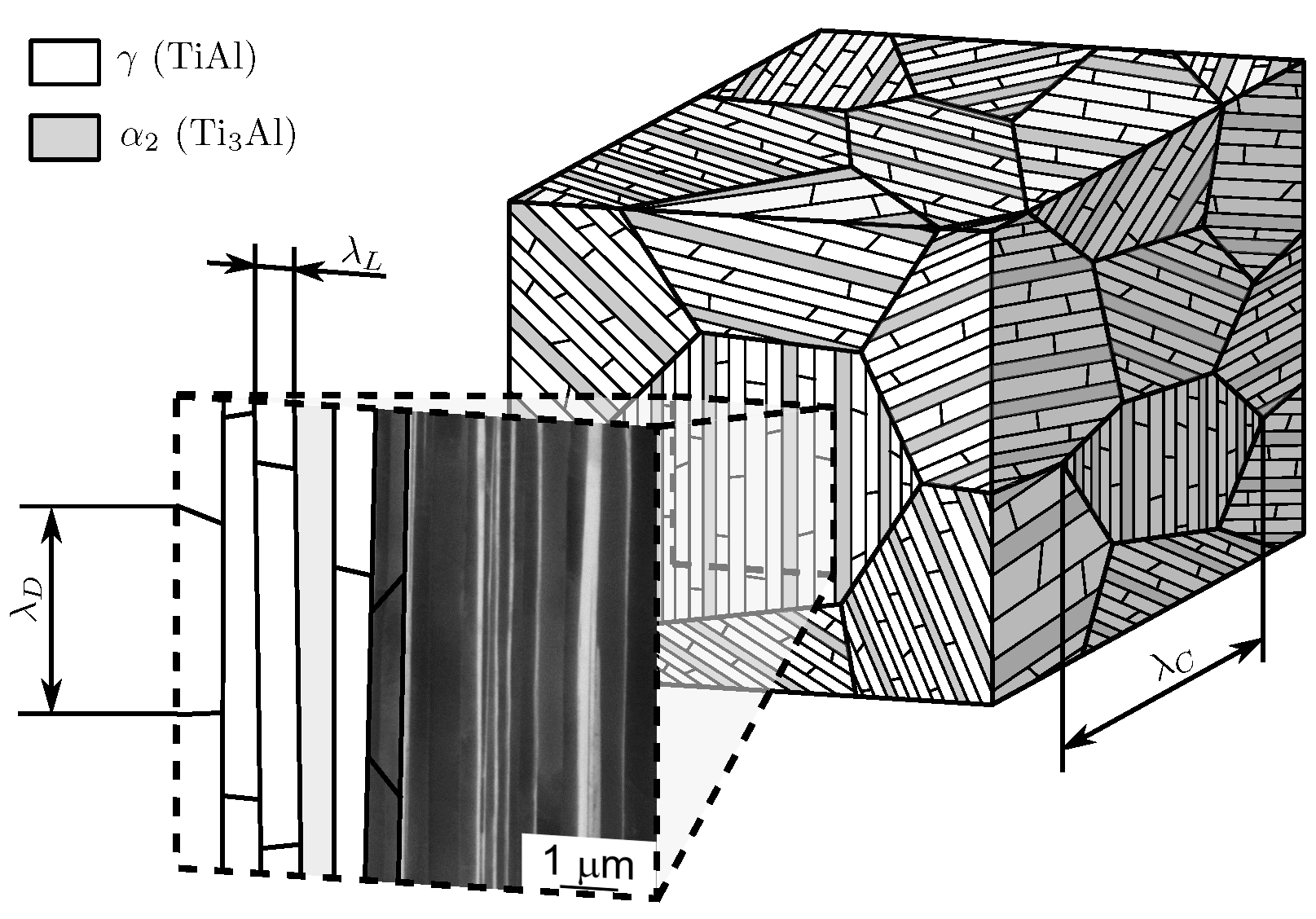
1.1. Microstructure and Micromechanics of Fully Lamellar TiAl
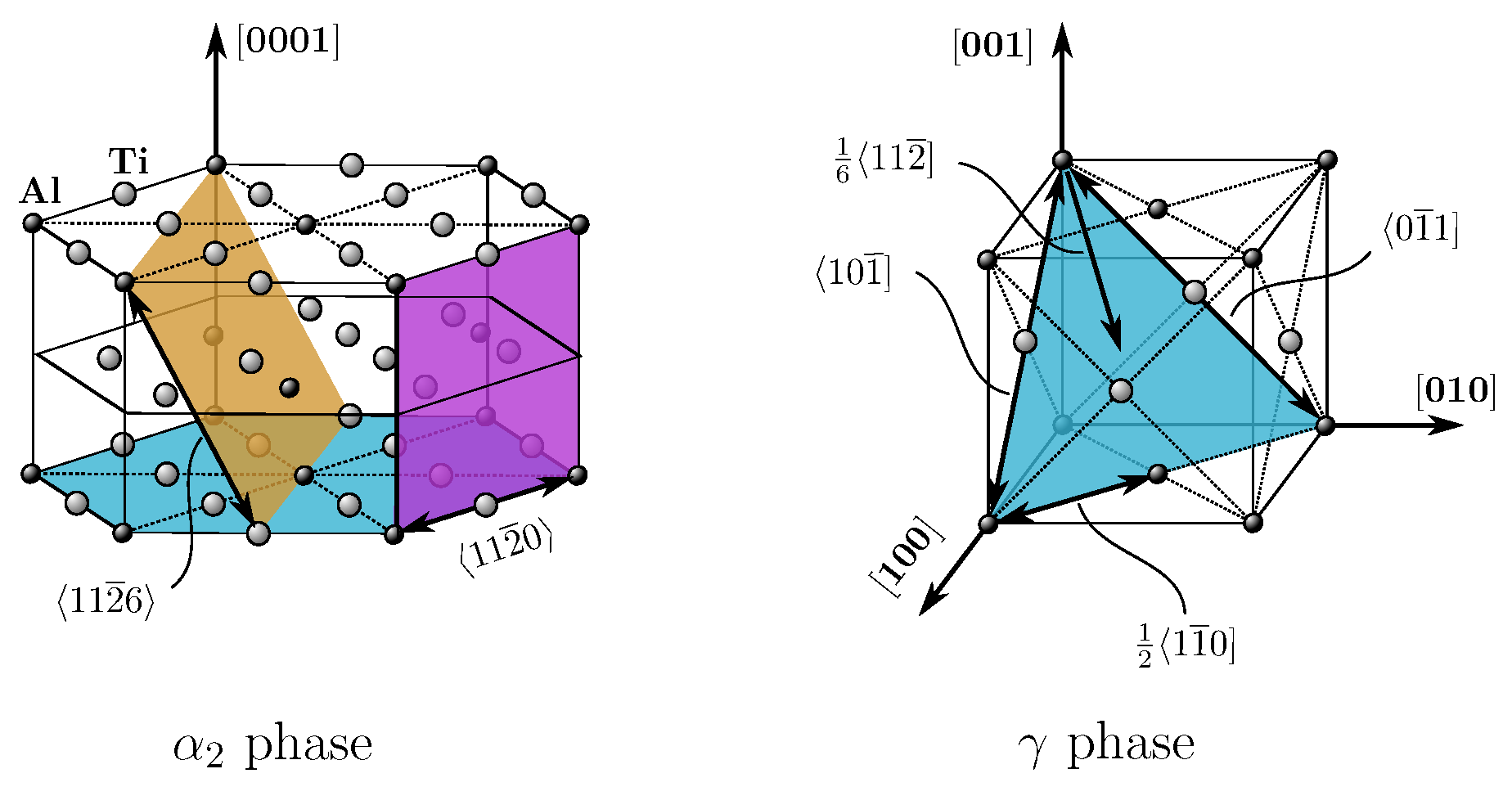
1.1.1. Lattice Structures and Orientation Relation
1.1.2. Influence of Microstructural Boundaries on Strength
- is a function of and , since strengths of slip/twinning systems in adjacent colonies are determined by lamella and domain boundary strengthening and
- experimentally determined values are only valid for the given combination of and , rendering identification of the functional relation unreasonably labor-intensive.
1.2. Scope of Present Paper
2. Modeling
2.1. Kinematics and Stress Measures
2.2. Thermomechanics and Temperature Evolution
2.3. Crystal Plasticity
2.3.1. Flow and Twinning Rule
Slip
Twinning
2.3.2. Defect Density Evolution
Dislocation Density Evolution
Twin Evolution
2.3.3. Critical Resolved Shear Stresses
Initial Slip/Twinning System Strength
Evolution of Slip System Strength
Evolution of Twinning System Strength
2.4. Helmholtz Free Energy
2.5. RVE Generation and Discretization
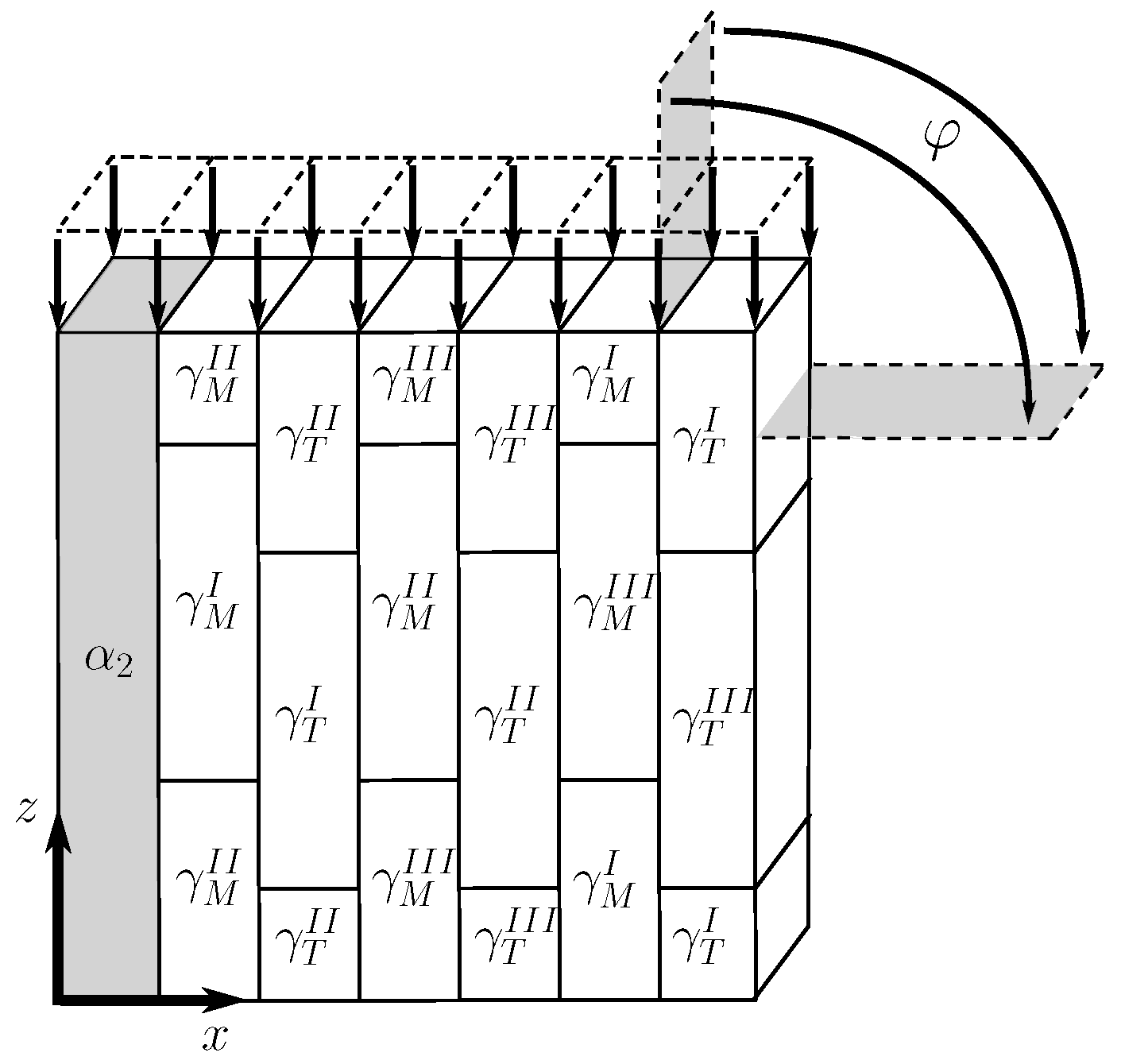
2.5.1. RVE of a Polysynthetically Twinned Crystal
2.5.2. RVE of a Polycolony Microstructure
3. Parameter Identification
3.1. Constitutive Assumptions
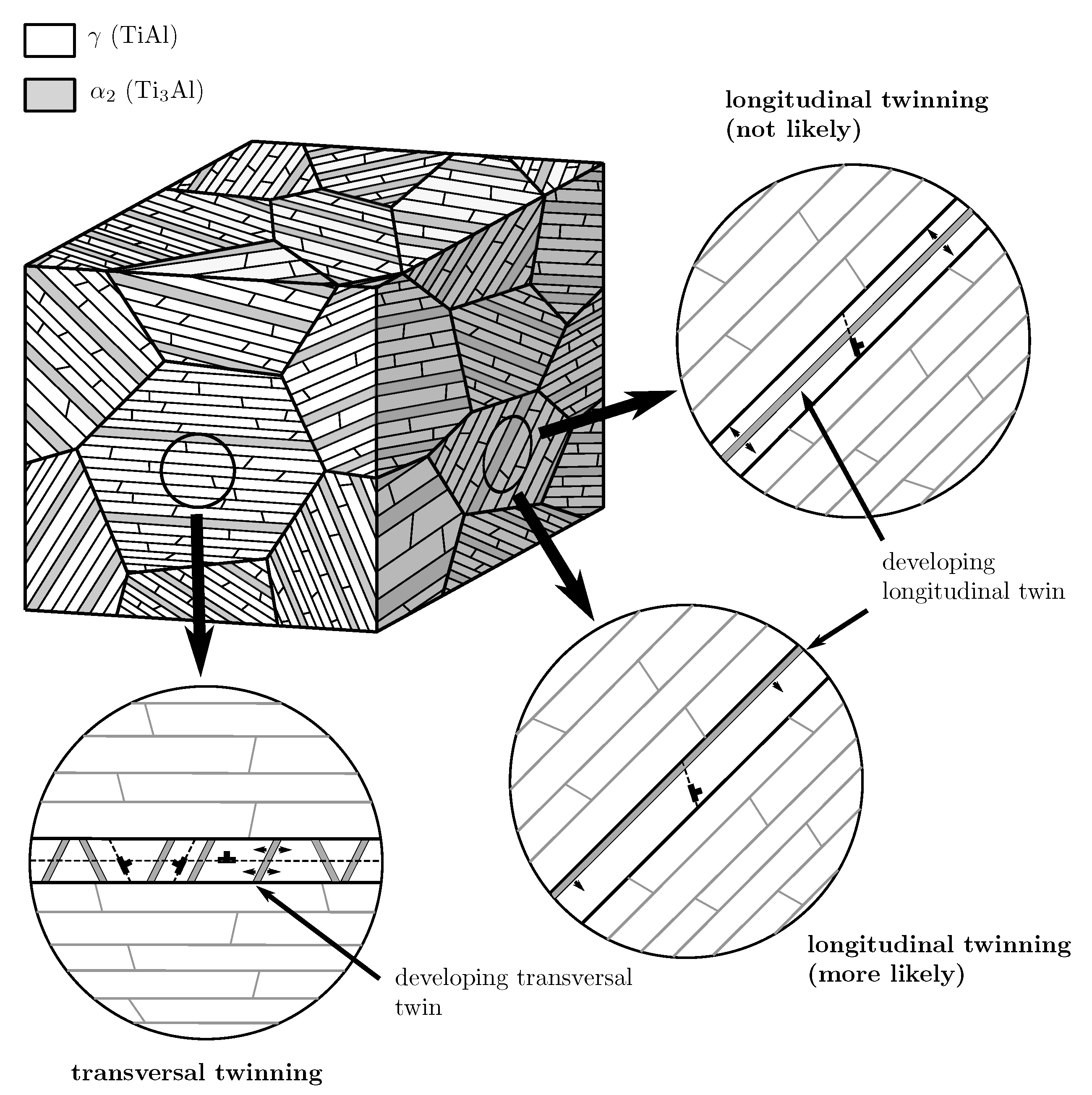
3.1.1. Morphological Classification
- longitudinal ( lamellar plane; lamellar plane),
- mixed ( lamellar plane;
lamellar plane) or
- transversal ( lamellar plane;
lamellar plane).
3.1.2. Hall–Petch Strengthening by Evolving Twins
3.1.3. Modeling Super Slip
Initial Critical Resolved Shear Stress
Taylor Hardening
3.1.4. Recovery
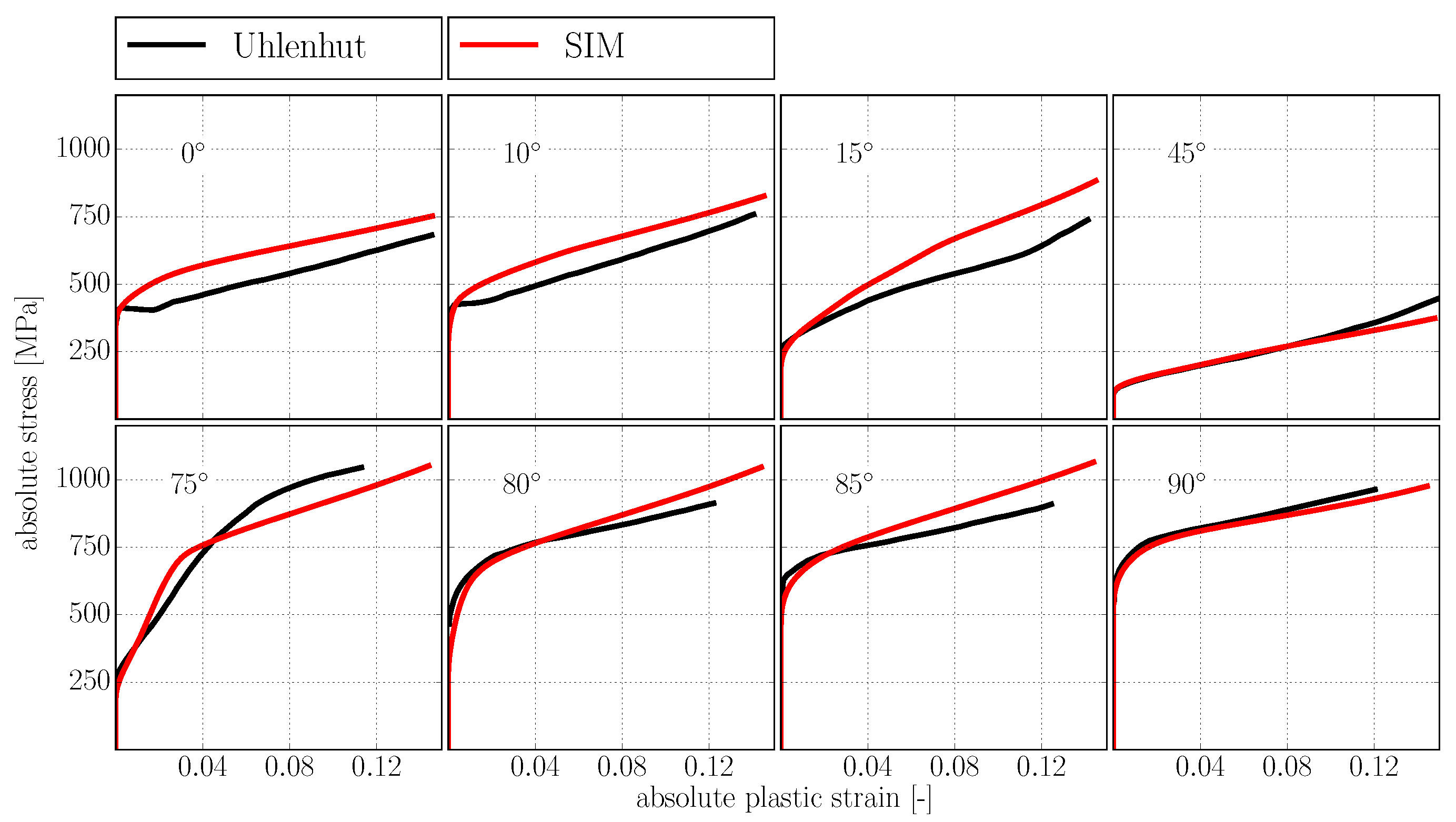
3.2. Model Parameters
3.2.1. Onset of Yield
3.2.2. Dislocation Accumulation and Hardening Interaction
3.3. Results
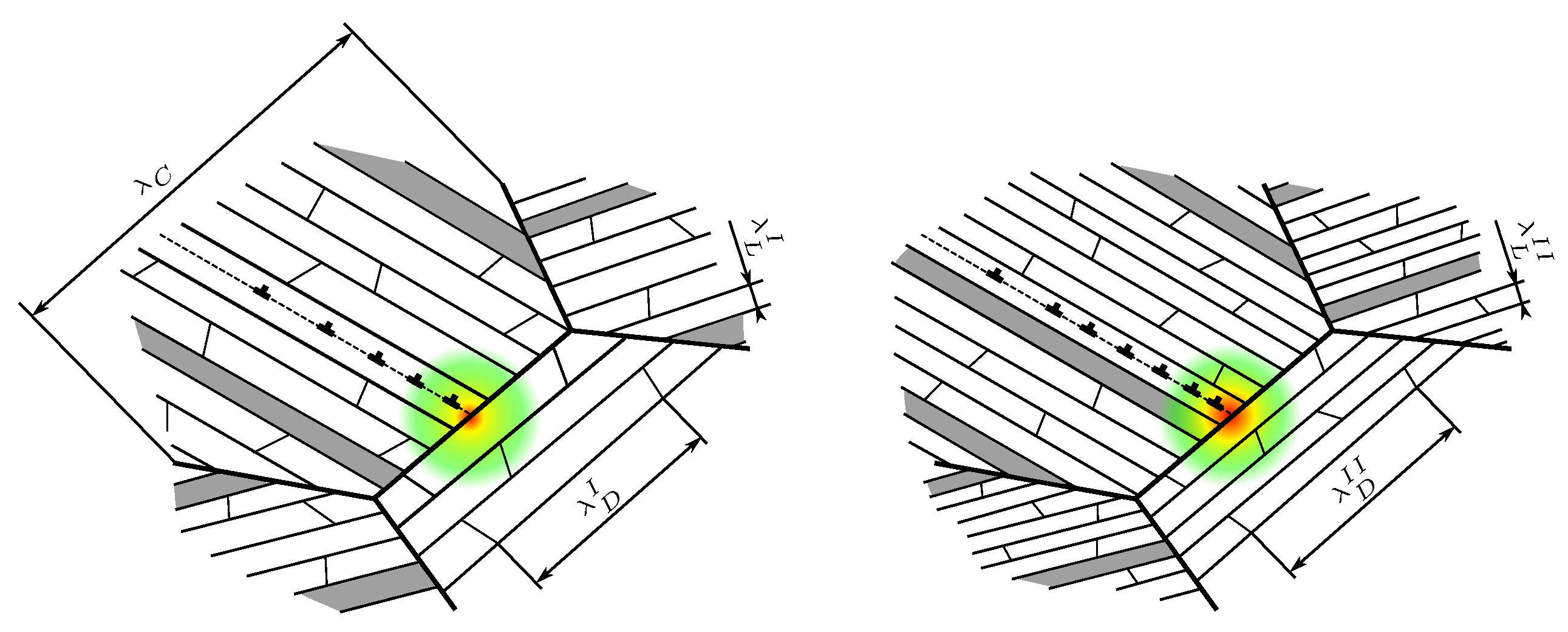
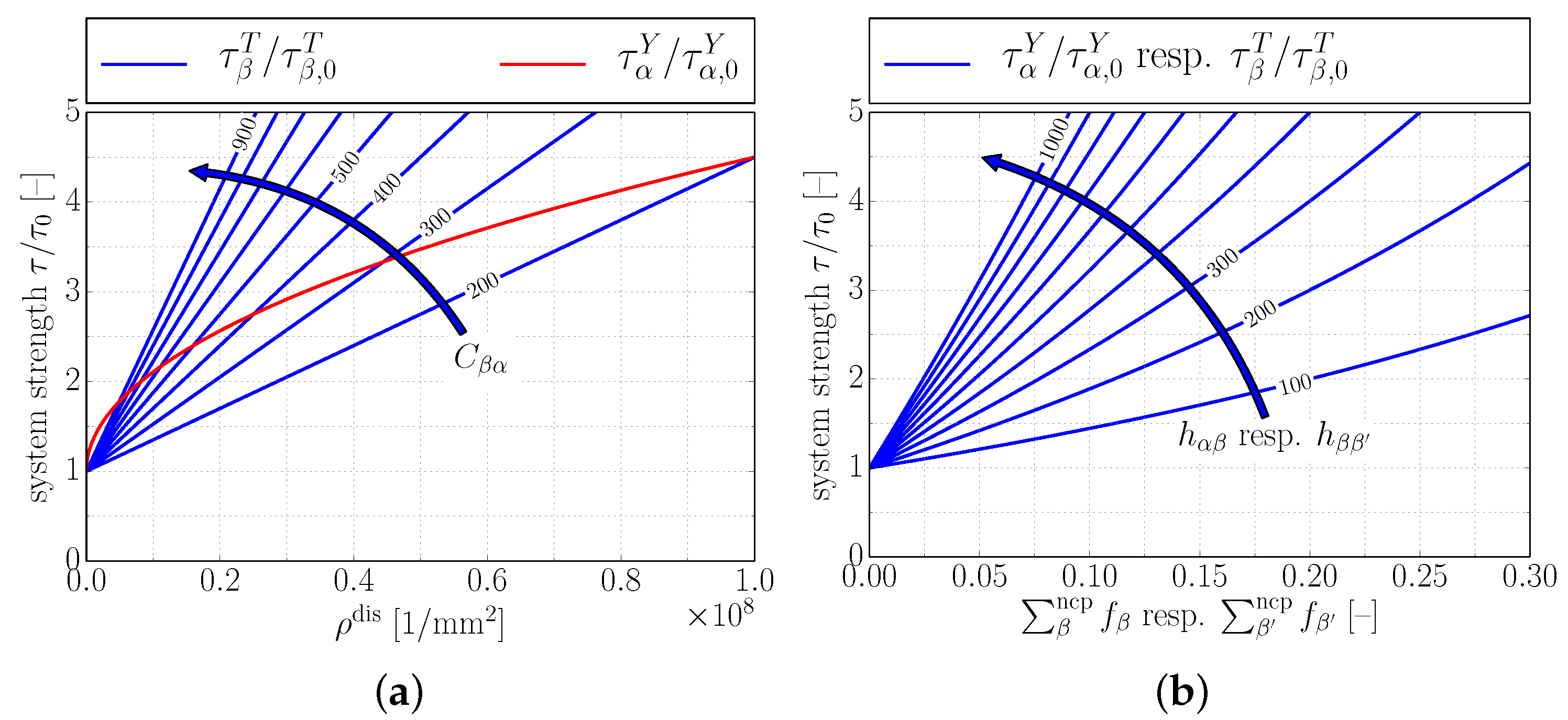
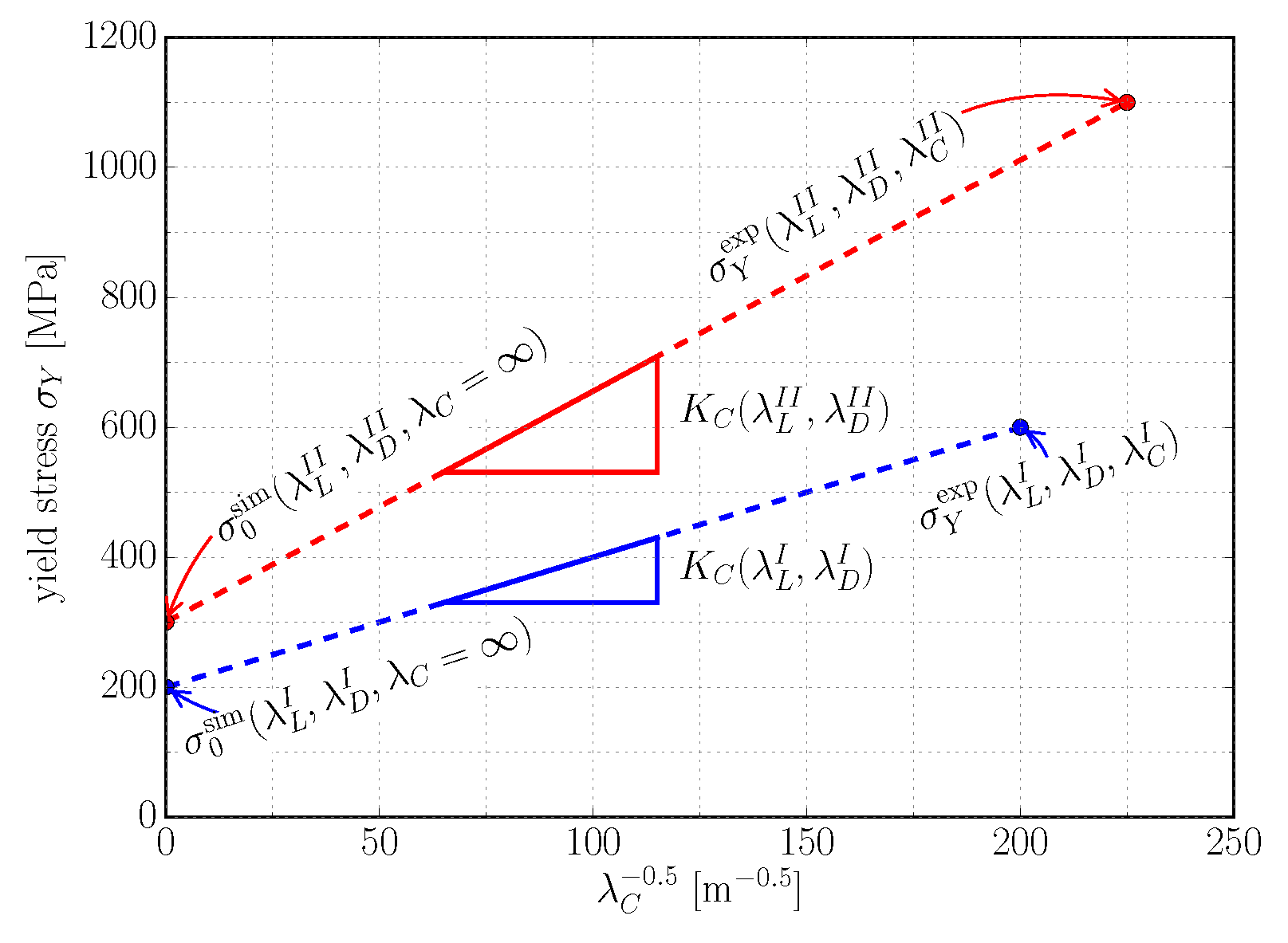
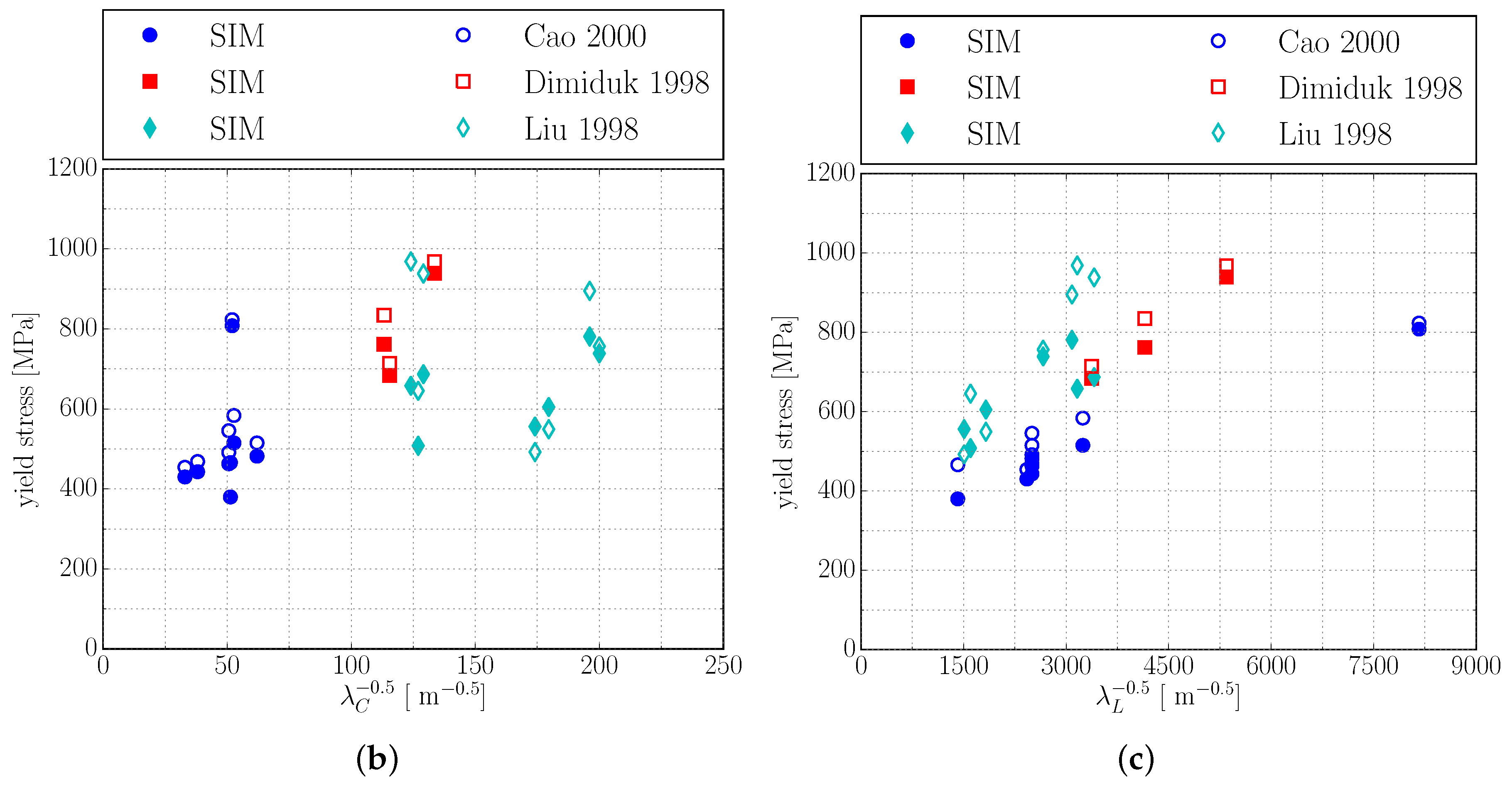
4. Determining the Hall–Petch Coefficient for Colony Boundary Strengthening
4.1. Calculation Scheme
4.2. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lasalmonie, A. Intermetallics: Why is it so difficult to introduce them in gas turbine engines? Intermetallics 2006, 14, 1123–1129. [Google Scholar] [CrossRef]
- Clemens, H.; Smarsley, W. Light-weight intermetallic titanium aluminides—status of research and development. Adv. Mater. Res. 2011, 278, 551–556. [Google Scholar] [CrossRef]
- Dimiduk, D.M. Gamma titanium aluminide alloys—An assessment within the competition of aerospace structural materials. Mater. Sci. Eng. 1999, A263, 281–288. [Google Scholar] [CrossRef]
- Appel, F.; Wagner, R. Microstructure and deformation of two-phase γ-titanium aluminides. Mater. Sci. Eng. 1998, R22, 187–268. [Google Scholar] [CrossRef]
- Appel, F.; Paul, J.; Oehring, M. Gamma Titanium Aluminide Alloys; Wiley-VCH Verlag & Co., KGaA: Weinheim, Germany, 2011. [Google Scholar]
- Lebensohn, R.; Uhlenhut, H.; Hartig, C.; Mecking, H. Plastic flow of γ-TiAl-based polysynthetically twinned crystals: Micromechanical modeling and experimental validation. Acta Mater. 1998, 46, 4701–4709. [Google Scholar] [CrossRef]
- Inui, H.; Oh, M.; Nakamura, A.; Yamaguchi, M. Ordered domains in tial coexisting with Ti3Al in the lamellar structure of Ti-rich TiAl compounds. Philos. Mag. A 1992, 66, 539–555. [Google Scholar] [CrossRef]
- Umakoshi, Y.; Nakano, T. The role of ordered domains and slip mode of α2 phase in the plastic behaviour of TiAl crystals containing oriented lamellae. Acta Metall. Mater. 1993, 41, 1155–1161. [Google Scholar] [CrossRef]
- Uhlenhut, H. Ursachen Plastischer Anisotropie von γ-TiAl-Basislegierungen. Ph.D. Thesis, Technische Universität Hamburg-Harburg, Hamburg, Germany, 1999. [Google Scholar]
- Liu, C.; Maziasz, P. Microstructural control and mechanical properties of dual-phase TiAl alloys. Intermetallics 1998, 6, 653–661. [Google Scholar] [CrossRef]
- Kishida, K.; Johnson, D.; Masuda, Y.; Umeda, H.; Inui, H.; Yamaguchi, M. Deformation and fracture of PST crystals and directionally solidified ingots of TiAl-based alloys. Intermetallics 1998, 6, 679–683. [Google Scholar] [CrossRef]
- Kim, Y.W. Strength and ductility in TiAl alloys. Intermetallics 1998, 6, 623–628. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Hazzledine, P.M.; Parthasarathy, T.A.; Seshagiri, S.; Mendiratta, M.G. The role of grain size and selected microstructural parameters in strengthening fully lamellar TiAl alloys. Metall. Mater. Trans. A 1998, 29, 37–47. [Google Scholar] [CrossRef]
- Cao, G.; Fu, L.; Lin, J.; Zhang, Y.; Chen, C. The relationships of microstructure and properties of a fully lamellar TiAl alloy. Intermetallics 2000, 8, 647–653. [Google Scholar] [CrossRef]
- Appel, F.; Lorenz, U.; Oehring, M.; Sparka, U.; Wagner, R. Thermally activated deformation mechanisms in micro-alloyed two-phase titanium aluminide alloys. Mater. Sci. Eng. A 1997, 233, 1–14. [Google Scholar] [CrossRef]
- Tang, J.; Huang, B.; He, Y.; Liu, W.; Zhou, K.; Wu, A. Hall–Petch relationship in two-phase TiAl alloys with fully lamellar microstructures. Mater. Res. Bull. 2002, 37, 1315–1321. [Google Scholar] [CrossRef]
- Maruyama, K.; Yamaguchi, M.; Suzuki, G.; Zhu, H.; Kim, H.Y.; Yoo, M.H. Effects of lamellar boundary structural change on lamellar size hardening in TiAl alloy. Acta Mater. 2004, 52, 5185–5194. [Google Scholar] [CrossRef]
- Butzke, J.; Bargmann, S. Thermomechanical modeling of polysynthetically twinned TiAl crystals. Philos. Mag. 2015, 95, 2607–2626. [Google Scholar] [CrossRef]
- Umakoshi, Y.; Nakano, T. Plastic behaviour ot TiAl crystals containing a single set of lamellae at high temperatures. ISIJ Int. 1992, 32, 139–1347. [Google Scholar] [CrossRef]
- Palomares-García, A.; Pérez-Prado, M.; Molina-Aldareguia, J. Effect of lamellar orientation on the strength and operating deformation mechanisms of fully lamellar TiAl alloys determined by micropillar compression. Acta Mater. 2017, 123, 102–114. [Google Scholar] [CrossRef]
- Palomares-García, A.; Sabirov, I.; Pérez-Prado, M.; Molina-Aldareguia, J. Effect of nanoscale thick lamellae on the micromechanical response of a TiAl alloy. Scr. Mater. 2017, 139, 17–21. [Google Scholar] [CrossRef]
- Gebhard, S.; Pyczak, F.; Göken, M. Microstructural and micromechanical characterisation of TiAl alloys using atomic force microscopy and nanoindentation. Mater. Sci. Eng. A 2009, 523, 235–241. [Google Scholar] [CrossRef]
- Maruyama, K.; Yamada, N.; Sato, H. Effects of lamellar spacing on mechanical properties of fully lamellar Ti-39.4mol % Al alloy. Mater. Sci. Eng. A 2001, 319-321, 360–363. [Google Scholar] [CrossRef]
- Maziasz, P.; Liu, C. Development of Ultrafine Lamellar Structures in Two-Phase γ-TiAl Alloys. Metall. Mater. Trans. A 1998, 29A, 105–117. [Google Scholar] [CrossRef]
- Parthasarathy, T.A.; Subramanian, P.R.; Mendiratta, M.G.; Dimiduk, D.M. Phenomenological observations of lamellar orientation effects on the creep behavior of Ti–48at.%Al PST Crystals. Acta Mater. 2000, 48, 541–551. [Google Scholar] [CrossRef]
- Zambaldi, C.; Roters, F.; Raabe, D. Analysis of the plastic anisotropy and pre-yielding of (γ/α2)-phase titanium aluminide microstructures by crystal plasticity simulation. Intermetallics 2011, 19, 820–827. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K. Modelling of texture evolution in metals accounting for lattice reorientation due to twinning. Eur. J. Mech. A Solids 2010, 29, 28–41. [Google Scholar] [CrossRef]
- Roos, A.; Chaboche, J.L.; Gélébart, L.; Crépin, J. Multiscale modelling of titanium aluminides. Int. J. Plast. 2004, 20, 811–830. [Google Scholar] [CrossRef]
- Kad, B.; Dao, M.; Asaro, R. Numerical simulations of plastic deformation and fracture effects in two phase γ-TiAl + α2-Ti3Al lamellar microstructures. Philos. Mag. A 1995, 71, 567–604. [Google Scholar] [CrossRef]
- Lebensohn, R. Modelling the role of local correlations in polycrystal plasticity using viscoplastic self-consistent schemes. Model. Simul. Mater. Sci. Eng. 1999, 7, 739–746. [Google Scholar] [CrossRef]
- Brockmann, R. Analysis of elastic-plastic deformation in TiAl polycrystals. Int. J. Plast. 2003, 19, 1749–1772. [Google Scholar] [CrossRef]
- Grujicic, M.; Cao, G.; Batchu, S. Crystal plasticity-based finite element analysis of deformation and fracture of polycrystalline lamellar γ-TiAl + α2-Ti3Al alloys. J. Mater. Sci. 2003, 38, 307–322. [Google Scholar] [CrossRef]
- Werwer, M.; Cornec, A. The role of superdislocations for modeling plastic deformation of lamellar TiAl. Int. J. Plast. 2006, 22, 1683–1698. [Google Scholar] [CrossRef]
- Schlögl, S.; Fischer, F. Numerical simulation of yield loci for PST crystals of TiAl. Mater. Sci. Eng. A 1997, 239, 790–803. [Google Scholar] [CrossRef]
- Kabir, M.; Chernova, L.; Bartsch, M. Numerical investigation of room-temperature deformation behavior of a duplex type γTiAl alloy using a multi-scale modeling approach. Acta Mater. 2010, 58, 5834–5847. [Google Scholar] [CrossRef]
- Parteder, E.; Siegmund, T.; Fischer, F.; Schlögl, S. Numerical simulation of the plastic behavior of polysynthetically twinned Ti-Al crystals. Mater. Sci. Eng. A 1995, 192–193, 149–154. [Google Scholar] [CrossRef]
- Cornec, A.; Kabir, M.; Huber, N. Numerical prediction of the stress-strain response of a lamellar γTiAl polycrystal using a two-scale modelling approach. Mater. Sci. Eng. A 2015, 620, 273–285. [Google Scholar] [CrossRef]
- Bartholomeusz, M.; Wert, J. Modeling creep deformation of a two-phase TiAI/Ti3AI alloy with a lamellar microstructure. Metall. Mater. Trans. A 1994, 25A, 2161–2171. [Google Scholar] [CrossRef]
- Marketz, W.; Fischer, F.; Clemens, H. Deformation mechanisms in TiAl intermetallics—Experiments and modeling. Int. J. Plast. 2003, 19, 281–321. [Google Scholar] [CrossRef]
- Héripré, E.; Caldemaison, D.; Roos, A.; Crépin, J. Microstrain analysis of titanium aluminides. Mater. Sci. Forum 2010, 638–642, 1330–1335. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Seghir, R.; Charkaluk, E.; Dufrenoy, P.; Bodelot, L. Thermomechanical couplings in crystalline plasticity under fatigue loading. Prodcedia Eng. 2010, 2, 1155–1164. [Google Scholar] [CrossRef]
- Bargmann, S.; Ekh, M. Microscopic temperature field prediction during adiabatic loading using gradient extended crystal plasticity. Int. J. Solids Struct. 2013, 50, 899–906. [Google Scholar] [CrossRef]
- Kalidindi, S. Incorporation of deformation twinning in crystal plasticity models. J. Mech. Phys. Solids 1998, 46, 267–290. [Google Scholar] [CrossRef]
- Pierce, D.; Asaro, R.; Needleman, A. Material rate dependence and local deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Schlögl, S.; Fischer, F. The role of slip and twinning in the deformation behaviour of polysynthetically twinned crystals of TiAl: A micromechanical model. Philos. Mag. A 1997, 75, 621–636. [Google Scholar] [CrossRef]
- Appel, F.; Sparka, U.; Wagner, R. Work hardening and recovery of gamma base titanium aluminides. Intermetallics 1999, 7, 325–334. [Google Scholar] [CrossRef]
- McBride, A.; Bargmann, S.; Reddy, B. A computational investigation of a model of single-crystal gradient thermoplasticity that accounts for the stored energy of cold work and thermal annealing. Comput. Mech. 2015, 55, 755–769. [Google Scholar] [CrossRef]
- Anand, L.; Gurtin, M.; Reddy, B. The stored energy of cold work, thermal annealing, and other thermodynamic issues in single crystal plasticity at small length scales. Int. J. Plast. 2015, 64, 1–25. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Wegmann, G.; Suda, T.; Maruyama, K. Deformation characteristics of polysynthetically twinned (PST) crystals during creep at 1150 K. Intermetallics 2000, 8, 165–177. [Google Scholar] [CrossRef]
- Remy, L. Kinetics of f.c.c. deformation twinning and its relationship to stress-strain behaviour. Acta Metall. 1978, 26, 443–451. [Google Scholar] [CrossRef]
- Kalidindi, S. Modeling anisotropic strain hardening and deformation textures in low stacking fault energy fcc metals. Int. J. Plast. 2001, 17, 837–860. [Google Scholar] [CrossRef]
- Proust, G.; Tomé, C.N.; Kaschner, G. Maodeling texture, twinning and hardening evolution during deformation of hexagonal materials. Acta Mater. 2007, 55, 2137–2148. [Google Scholar] [CrossRef]
- Beyerlein, I.; Tomé, C. A dislocation-based constitutive law for pure Zr including temperature effects. Int. J. Plast. 2008, 24, 867–895. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Beaudoin, A.; Chumlyakov, Y.; Maier, H.; Tomé, C. Modeling the deformation behavior of hadfield steel single and polycrystals due to twinning and slip. Acta Mater. 2000, 48, 2031–2047. [Google Scholar] [CrossRef]
- Werwer, M.; Cornec, A. Numerical simulation of plastic deformation and fracture in polysynthetically twinned (PST) crystals of TiAl. Comput. Mater. Sci. 2000, 19, 97–107. [Google Scholar] [CrossRef]
- Kim, Y.W. Microstructural evolution and properties of a forged gamma titanium aluminide alloy. Acta Metall. Mater. 1992, 40, 1121–1134. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K. Micromechanical Modelling of Metals and Alloys of High Specific Strength; Instytut Podstawowych Problemów Techniki Polskiej Akademii Nauk: Warszawa, Poland, 2011. [Google Scholar]
- Schlögl, S.; Fischer, F. Micromechanical modelling of TiAl intermetallics. Comput. Mater. Sci. 1996, 7, 34–39. [Google Scholar] [CrossRef]
- Inui, H.; Oh, M.; Nakamura, A.; Yamaguchi, M. Room-temperature tensile deformation of polysynthetically twinned (PST) crystals of TiAl. Acta Metall. Mater. 1992, 40, 3095–3104. [Google Scholar] [CrossRef]
- Schafrik, R. Dynamic elastic moduli of the titanium aluminides. Metall. Trans. A 1977, 8, 1003–1006. [Google Scholar] [CrossRef]
- Novoselova, T.; Malinov, S.; Sha, W.; Zhecheva, A. High-temperature synchrotron X-ray diffraction study of phases in a gamma TiAl alloy. Mater. Sci. Eng. A 2004, 371, 103–112. [Google Scholar] [CrossRef]
- Egry, I.; Brooks, R.; Holland-Moritz, D.; Novakovic, R.; Matsushita, T.; Ricci, E.; Seetharaman, S.; Wunderlich, R.; Jarvis, D. Thermophysical properties of γ-titanium aluminide: The European IMPRESS project. Int. J. Thermophys. 2007, 28, 1026–1036. [Google Scholar] [CrossRef]
- Zhang, W.; Reddy, B.; Deevi, S. Physical properties of TiAl-base Alloys. Scr. Mater. 2001, 45, 645–651. [Google Scholar] [CrossRef]


| Phase | ||||
| System | Mechanism | Classification | Index | |
| ordinary slip | longitudinal | 1 | 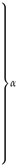 | |
| super slip | longitudinal | 2 | ||
| super slip | longitudinal | 3 | ||
| ordinary slip | mixed | 4 | ||
| super slip | mixed | 5 | ||
| super slip | mixed | 6 | ||
| ordinary slip | transversal | 7 | ||
| ordinary slip | transversal | 8 | ||
| super slip | transversal | 9 | ||
| super slip | transversal | 10 | ||
| super slip | transversal | 11 | ||
| super slip | transversal | 12 | ||
| twinning | longitudinal | 1 | 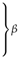 | |
| twinning | transversal | 2 | ||
| twinning | transversal | 3 | ||
| twinning | transversal | 4 | ||
| Phase | ||||
| System | Mechanism | Classification | Index | |
| basal slip | longitudinal | 1–3 | 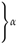 | |
| prismatic slip | mixed | 4–6 | ||
| pyramidal slip | transversal | 7–12 | ||
| Phase | Symbol | Value | Annotation | Ref. | |
|---|---|---|---|---|---|
| material parameters | E | [62] | |||
| [62] | |||||
| [63] | |||||
| [5] | |||||
| E | [62] | ||||
| [62] | |||||
| [63] | |||||
| / | [64] | ||||
| [65] | |||||
| [65] | |||||
| [65] | |||||
| model parameters | [18] | ||||
| 0.125 [MPa] | [18] | ||||
| [18] | |||||
| [18] | |||||
| 0.125 [MPa] | [18] | ||||
| [18] | |||||
| / | [18] | ||||
| n | [18] |
| Phase | Symb | Value | Unit | System Index (cf. Table 1) | Annotation | |
|---|---|---|---|---|---|---|
| dislocation accumulation | [] | 1–3 | ls | |||
| [] | 4–6 | ms | ||||
| [] | 7–12 | ts | ||||
| [] | 1–12 | all slip systems | ||||
| 0.05 | [–] | for 1–12 | all slip systems | |||
| [] | 4–6 | ms | ||||
| [] | 7–12 | ts | ||||
| [] | 4–12 | ms and ts | ||||
| 0.05 | [–] | 4–12 | ms and ts | |||
| hardening parameters | 0 | [MPa] | 1–3 and 1 | ls by lt | ||
| 100 | [MPa] | 4–12 and 1 | ms and ts by lt | |||
| 1500 | [MPa] | 1–6 and 2–4 | ls and ms by tt | |||
| 300 | [MPa] | 7–12 and 2–4 | ts by tt | |||
| 0 | [MPa] | 1 and 1 | lt by lt | |||
| 1500 | [MPa] | 1 and 2–4 | lt by tt | |||
| 300 | [MPa] | 2–4 and 2–4; | tt by tt | |||
| 100 | [MPa] | 2–4 and 1 | tt by lt | |||
| 900 | [–] | 1 and 1–12 | lt by all slip systems | |||
| 150 | [–] | 2–4 and 1–12 | tt by all slip systems |
| Composition | Content [Vol. %] | [m] | [m] | [m] | Ref. |
|---|---|---|---|---|---|
| Ti-45.3Al-2.1Cr-2Nb | 20 | 75 | 4.4 * | 0.088 | [13] |
| Ti-45.3Al-2.1Cr-2Nb | 29 | 78 | 2.9 * | 0.058 | [13] |
| Ti-45.3Al-2.1Cr-2Nb | 32 | 56 | 1.75 * | 0.035 | [13] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 260 | 8 * | 0.16 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 390 | 8 * | 0.16 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 690 | 8 * | 0.16 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 920 | 8.5 * | 0.17 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 370 | 0.75 * | 0.015 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 360 | 4.75 * | 0.095 | [14] |
| Ti-45.5Al-2Cr-1.5Nb-1V | 10 * | 380 | 25 * | 0.5 | [14] |
| Ti-47Al-2Cr-2Nb | 10 * | 65 | 5 * | 0.1 | [10] |
| Ti-47Al-2Cr-2Nb | 10 * | 62 | 19.5 * | 0.39 | [10] |
| Ti-47Al-2Cr-2Nb-0.15B | 10 * | 33 | 22 * | 0.44 | [10] |
| Ti-47Al-2Cr-1.8Nb-0.2W-0.15B | 10 * | 31 | 15 * | 0.3 | [10] |
| Ti-47Al-2Cr-1.8Nb-0.2W-0.15B | 10 * | 25 | 7.05 * | 0.141 | [10] |
| Ti-46Al-2Cr-1.8Nb-0.2W-0.15B | 10 * | 26 | 5.25 * | 0.105 | [10] |
| Ti-47Al-2Cr-1Nb-1Ta | 10 * | 60 | 4.3 * | 0.086 | [10] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnabel, J.E.; Bargmann, S. Accessing Colony Boundary Strengthening of Fully Lamellar TiAl Alloys via Micromechanical Modeling. Materials 2017, 10, 896. https://doi.org/10.3390/ma10080896
Schnabel JE, Bargmann S. Accessing Colony Boundary Strengthening of Fully Lamellar TiAl Alloys via Micromechanical Modeling. Materials. 2017; 10(8):896. https://doi.org/10.3390/ma10080896
Chicago/Turabian StyleSchnabel, Jan Eike, and Swantje Bargmann. 2017. "Accessing Colony Boundary Strengthening of Fully Lamellar TiAl Alloys via Micromechanical Modeling" Materials 10, no. 8: 896. https://doi.org/10.3390/ma10080896