A Compact Band-Pass Filter with High Selectivity and Second Harmonic Suppression
Abstract
:1. Introduction
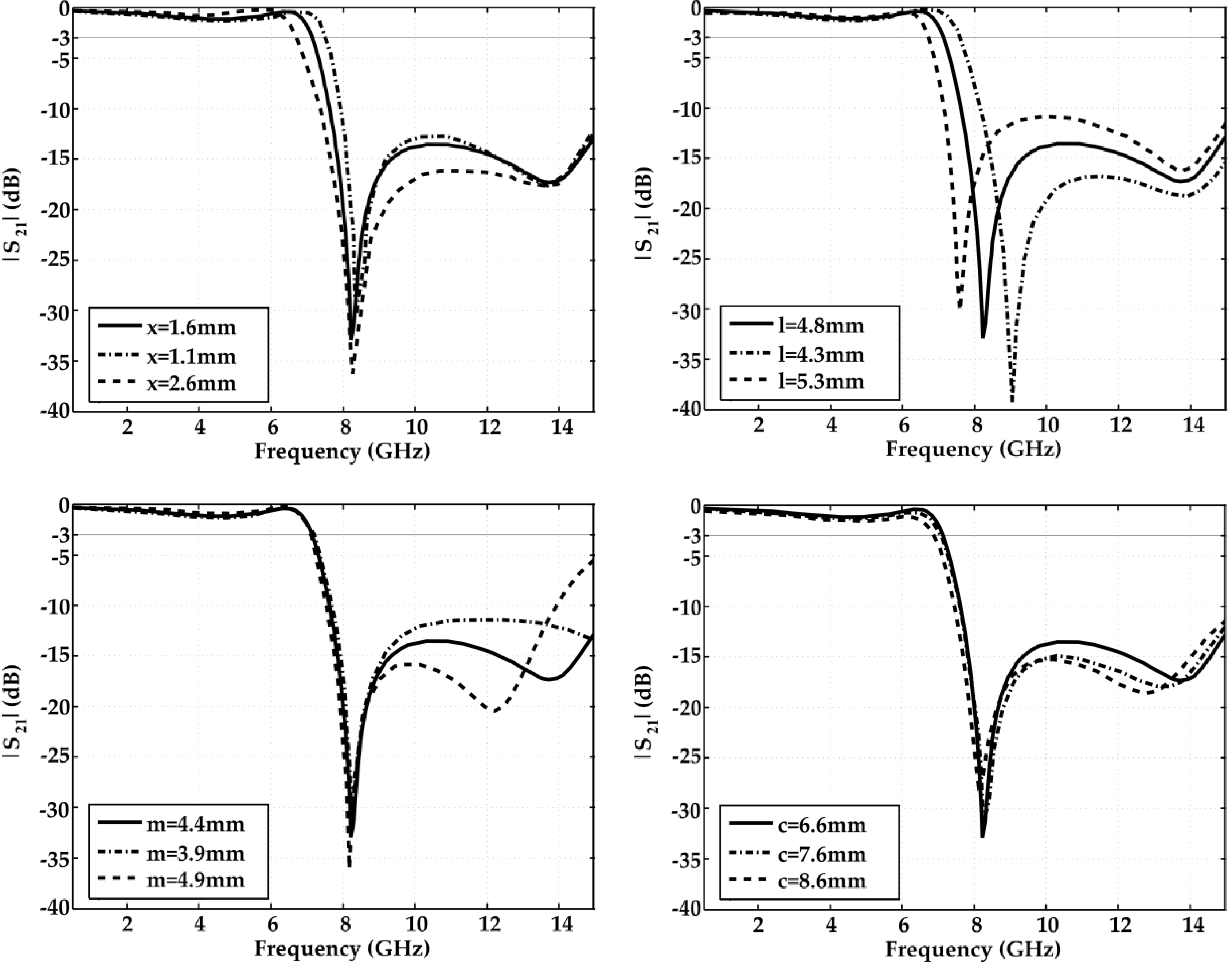
2. Resonant Element Design
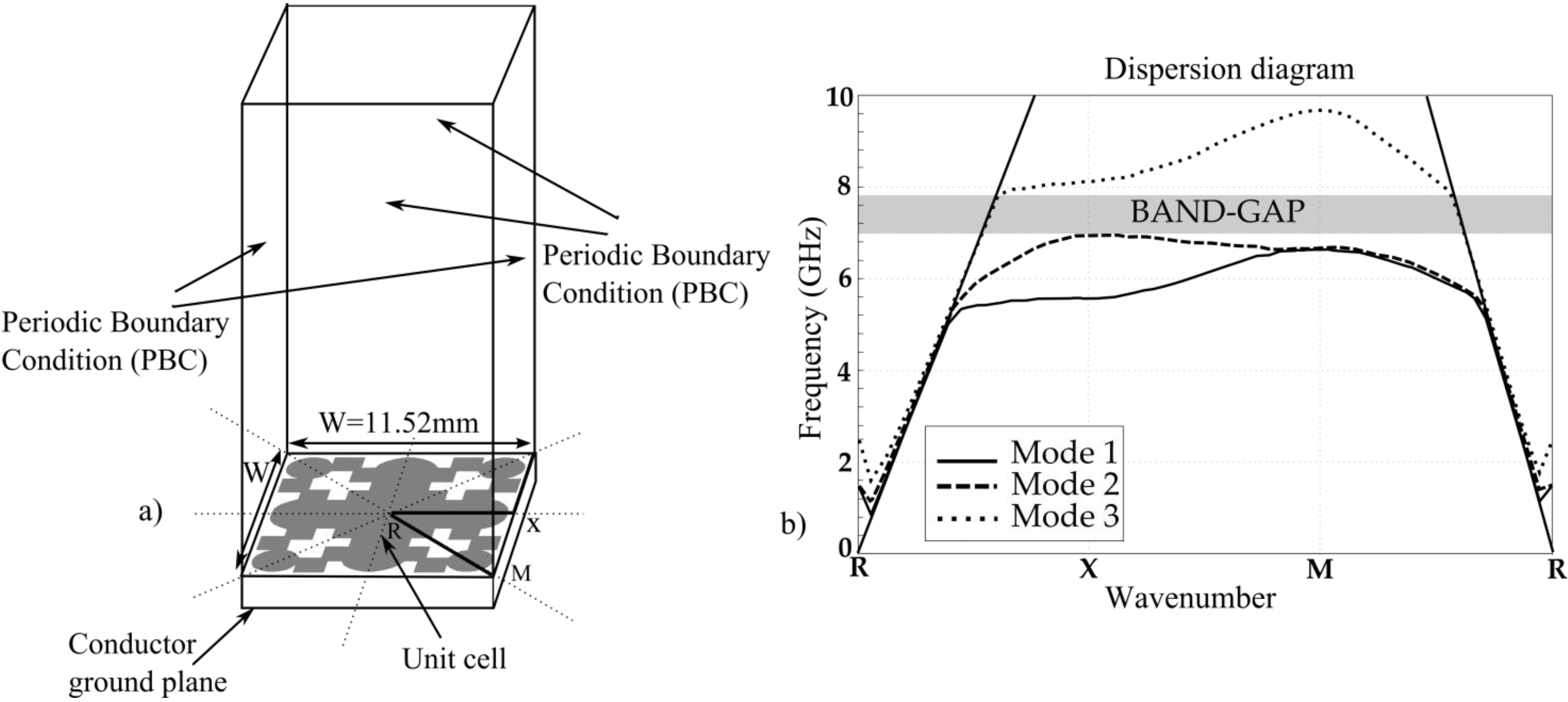
3. Filter Design
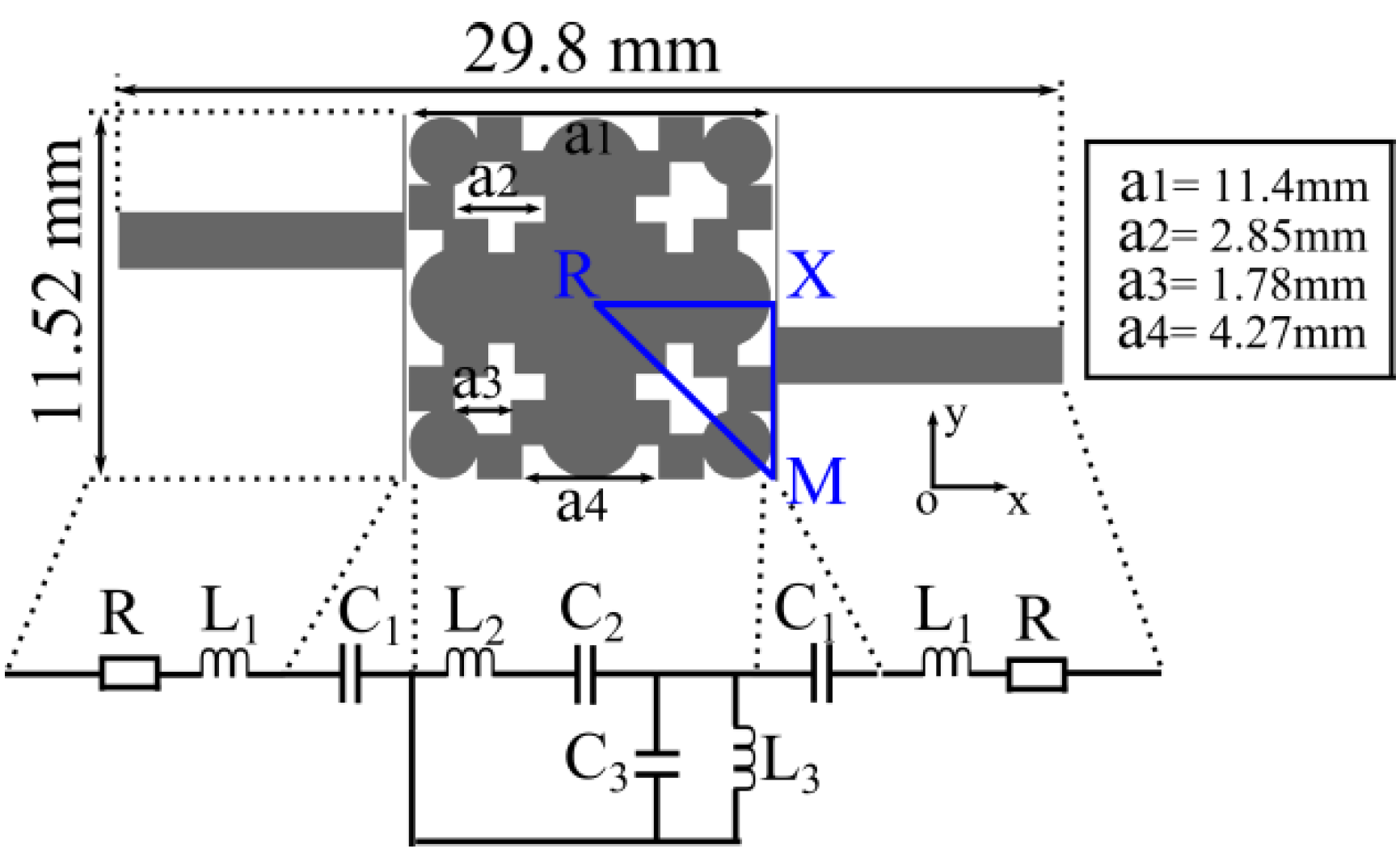
| Prototype | 3 dB | fc | BW(3 dB) | Q | Size (mm × mm) | Size (mm × mm) | ||
| flow(GHz) | fhigh(GHz) | GHz | % | |||||
| BPF | 6.25 | 6.62 | 6.44 | 0.37 | 5.57 | 17.40 | 29.80 × 11.52 * | 11.92 × 11.52 |
| 3-cells-oy BPF | 6.45 | 6.61 | 6.52 | 0.16 | 2.45 | 40.75 | 29.80 × 34.56 * | 11.92 × 34.56 |
| 3-cells-ox BPF | 6.55 | 6.67 | 6.62 | 0.12 | 1.81 | 55.16 | 52.84 ×11.52* | 34.96 × 11.52 |
| Square BPF | 6.13 | 7.30 | 6.70 | 1.17 | 17.4 | 5.72 | 29.80 ×11.52* | 11.92 × 11.52 |

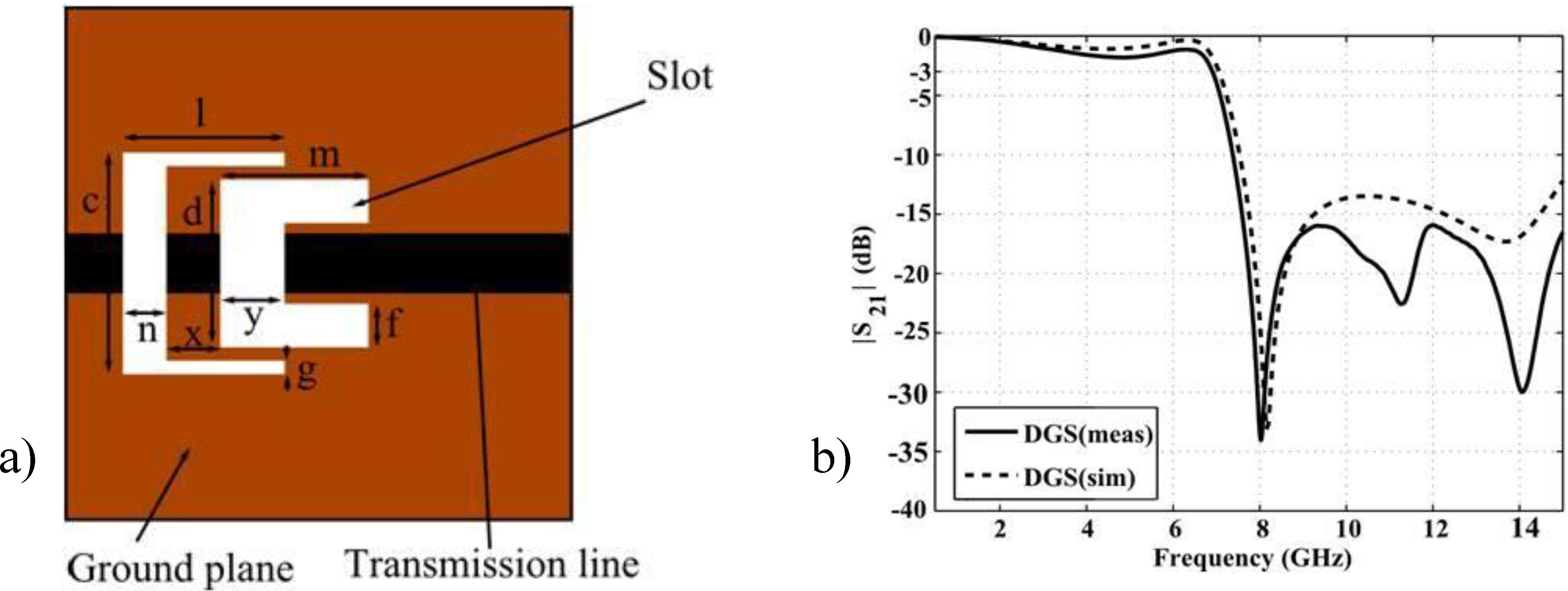
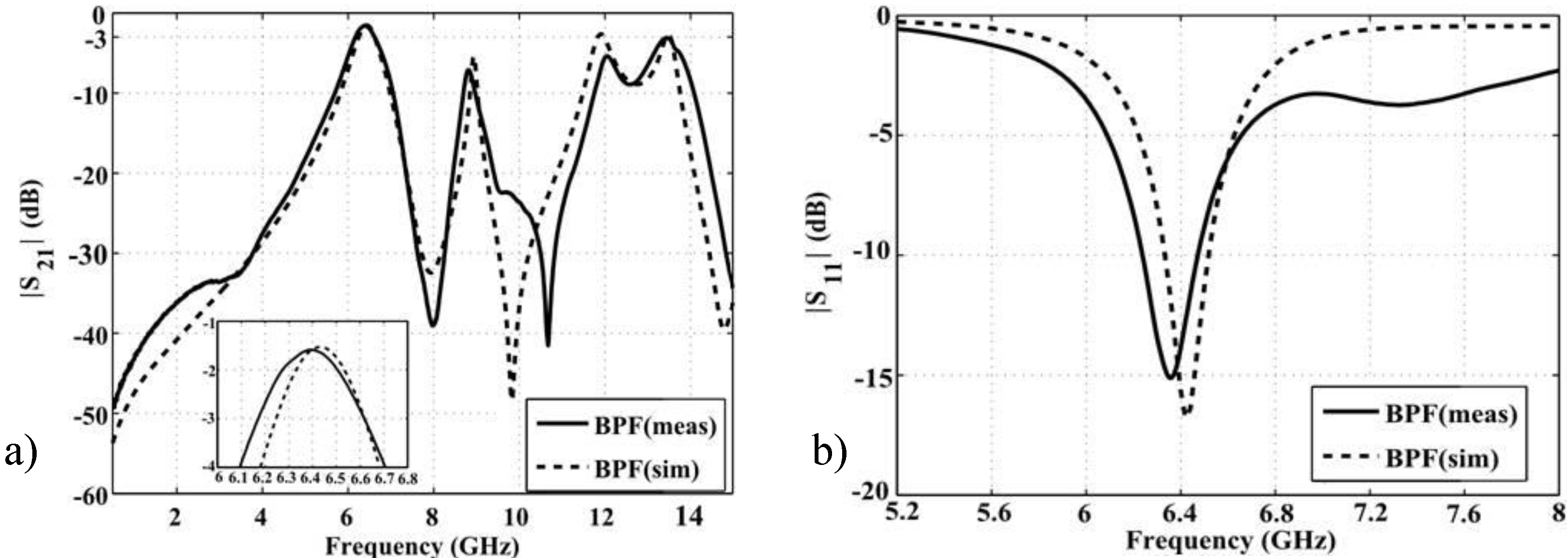
4. Results

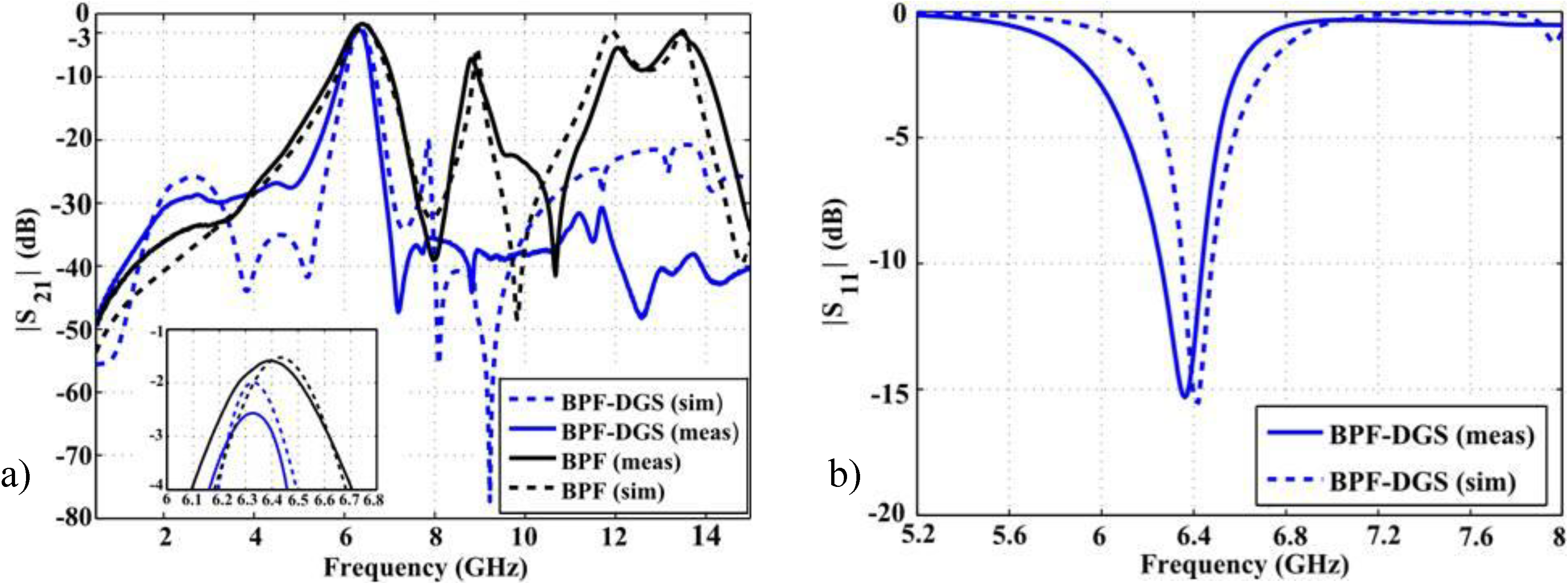
| Prototype | 3 dB | fc | BW(3 dB) | Q | Size (mm × mm) | Size λ—wavelength at the corresp. fc | ||
|---|---|---|---|---|---|---|---|---|
| flow(GHz) | fhigh(GHz) | GHz | % | |||||
| BPF | 6.25 | 6.62 | 6.44 | 0.37 | 5.75 | 17.40 | 29.8 × 11.52 * | 0.63λ × 0.25λ * |
| 11.92 × 11.52 | 0.25λ × 0.25λ | |||||||
| BPF-DGS | 6.23 | 6.40 | 6.33 | 0.17 | 2.76 | 36.38 | 29.8 × 11.52 | 0.63λ × 0.25λ |
| [31] | 5.46 | 5.84 | 5.65 | 0.38 | 6.72 | 14.80 | 46.2 × 11.5 | 0.87λ × 0.21λ |
| [35] | 5.58 | 5.83 | 5.71 | 0.25 | 4.46 | 22.80 | 40 × 10 | 0.76λ × 0.19λ |
| [35] | 5.39 | 6.02 | 5.71 | 0.63 | 11.14 | 9.06 | 40 × 10 | 0.76λ × 0.19λ |
| [36] | 5.88 | 6.12 | 6 | 0.24 | 4.05 | 25 | 15 × 13 | 0.3λ × 0.26λ |
| [32] | 6.63 | 6.96 | 6.8 | 0.33 | 4.9 | 20.6 | 20 × 22 | 0.45λ × 0.5λ |
| [33] | 5.09 | 5.35 | 5.25 | 0.26 | 4.9 | 20.2 | 45 × 14 | 0.79λ × 0.25λ |
| [34] | 5.14 | 5.38 | 5.25 | 0.24 | 4.57 | 21.8 | 19.8 × 17.9 | 0.35λ× 0.31λ |
| [37] | 4.78 | 5.61 | 5.2 | 0.83 | 16 | 6.26 | 26.3 × 9.9 | 0.45λ × 0.17λ |
| [38] | 5.54 | 5.86 | 5.7 | 0.32 | 5.6 | 17.81 | 26 × 8 | 0.5λ × 0.15λ |
| [39] | 1.36 | 1.49 | 1.42 | 0.13 | 9 | 10.9 | 22.14 × 5.08 | 0.1λ × 0.023λ |
| [40] | 2.84 | 4.2 | 3.4 | 1.36 | 40 | 2.5 | 20 × 15 | 0.22λ × 0.17λ |
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kam, M.S.; Mo, T.; Xue, Q.; Chan, C.H. A compact bandpass filter with two tuning transmission zeros using a CMRC resonator. IEEE Trans. Microw. Theory Tech. 2005, 53, 895–900. [Google Scholar] [CrossRef]
- Hettstedt, F.; Lehmann, T.; Knoechel, R. Novel dual mode microstrip bandpass-filter. IEEE Microw. Mag. 2009, 10, 155–157. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Chen, C.Y.; Chuang, H.R. Shunted-line stepped-impedance resonator. IEEE Microw. Mag. 2012, 13, 34–48. [Google Scholar]
- Boutejdar, A.; Omar, A.; Burte, E. Design and optimization of new compact tunable 2.4-GHz band pass filter using coupled λ/2 microstrip open loop resonators and memes-switch technique. Microw. Opt. Technol. Lett. 2013, 55, 2444–2450. [Google Scholar] [CrossRef]
- Boutejdar, A.; Al Sharkawy, M.; Omar, A.S. A simple transformation of improved WLAN band pass to low pass filter using defected ground structure (DGS), defected microstrip structure (DMS) and multilayer-technique. J. Microw. Optoelectron. Electromagn. Appl. 2013, 12, 111–130. [Google Scholar]
- Boutejdar, A. An improvement of defected ground structure lowpass/bandpass filters using h-slot resonators and coupling matrix method. J. Microw. Optoelectron. Electromagn. Appl. 2011, 10, 295–307. [Google Scholar] [CrossRef]
- Boutejdar, A.; Omar, A.S.; Senst, A.; Batmanov, A.; Burte, E.; Mikuta, R. A New Design of a Tunable WLAN-Band Pass Filter Using a Combination of Varactor Device, RF-Choke and Hairpin-Slottet Ground Structure (SGS). In Proceedings of 41th European Microwave Conference, Microwave Integrated Circuits Conference (EuMC) 2011, Manchester, UK, 10–11 October 2011; pp. 506–509.
- Matthaei, G.; Young, L.; Jones, E. Microwave Filters, Impedance Matching Networks, and Coupling Structures; Artech House: Boston, MA, USA, 1980. [Google Scholar]
- Kuan, H.; Lin, Y.-L.; Yang, R.-Y.; Chang, Y.-C. A multilayered parallel coupled microstrip bandpass filter with embedded SIR cells to have a broad upper rejection band. IEEE Microw. Wirel. Comp. Lett. 2010, 20, 25–27. [Google Scholar] [CrossRef]
- Matthaei, G.L. Design of parallel-coupled resonator filters. IEEE Microw. Mag. 2007, 8, 78–87. [Google Scholar] [CrossRef]
- Swanson, D.G. Narrow-band microwave filter design. IEEE Microw. Mag. 2007, 8, 105–114. [Google Scholar] [CrossRef]
- Hong, J.S.; Lancaster, M.J. Coupling of microstrip square open loop resonators for cross-coupled planar microwave filters. IEEE Trans. Microw. Theory Tech. 1996, 44, 2099–2109. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Chang, S.-F.; Chou, C.-Y.; Liu, K.-H. A reconfigurable bandpass-bandstop filter based on varactor-loaded closed-ring resonators. IEEE Microw. Mag. 2009, 10, 138–140. [Google Scholar] [CrossRef]
- Wang, H.; Chu, Q.-X. A narrow-band hairpin-comb two pole filter with source-load coupling. IEEE Trans. Microw. Theory Tech. 2010, 20, 372–374. [Google Scholar]
- Chen, C.-F.; Huang, T.-Y.; Wu, R.-B. Novel compact net-type resonators and their applications to microstrip bandpass filters. IEEE Trans. Microw. Theory Tech. 2006, 54, 755–762. [Google Scholar] [CrossRef]
- De Cos, M.E.; Álvarez, Y.; Hadarig, R.C.; Las-Heras, F. Novel SHF band uniplanar artificial magnetic conductor. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 44–47. [Google Scholar] [CrossRef]
- Hadarig, R.C.; de Cos, M.E.; Las-Heras, F. Microstrip patch antenna bandwidth enhancement using AMC/EBG structures. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Hadarig, R.C.; de Cos, M.E.; Las-Heras, F. Novel miniaturized artificial magnetic conductor. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 174–177. [Google Scholar] [CrossRef]
- De Cos, M.E.; Las-Heras, F. Novel flexible artificial magnetic conductor. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Mantash, M.; Tarot, A.C.; Collardey, S.; Mahdjoubi, K. Investigation of flexible textile antennas and amc reflectors. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Yang, F.R.; Ma, K.P.; Qian, Y.; Itoh, T. A uniplanar compact photonic-bandgap (UC-PBG) structure and its applications for microwave circuits. IEEE Trans. Microw. Theory Tech. 1999, 47, 1509–1514. [Google Scholar] [CrossRef]
- Yang, F.; Rahmat-Samii, Y. Electromagnetic Band-Gap Structures in Antenna Engineering; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Oskouei, D.H.; Forooraghi, K.; Hakkak, M. Guided and leaky wave characteristics of periodic defected ground structures. Prog. Electromagn. Res. 2007, 73, 15–27. [Google Scholar] [CrossRef]
- Sievenpiper, D.; Zhang, L.; Broas, R.F.J.; Alexopolous, N.G.; Yablonovitch, E. High impedance electromagnetic surface with a forbidden frequency band. IEEE Trans. Microw. Theory Tech. 1999, 47, 2059–2074. [Google Scholar]
- Caloz, C.; Itho, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; Wiley Interscience: New York, NY, USA, 2006. [Google Scholar]
- Karthikeyan, S.; Kshetrimayum, R.S. Harmonic suppression of parallel coupled microstrip line bandpass filter using CSRR. Prog. Electromagn. Res. Lett. 2009, 7, 193–201. [Google Scholar] [CrossRef]
- Naser-Moghadasi, M.; Alamolhoda, M. Spurious response suppression in hairpin filter using DMS integrated in filter structure. Prog. Electromagn. Res. 2011, 18, 221–229. [Google Scholar]
- Lopetegi, T.; Laso, M.A.A.G.; Hernández, J.; Bacaicoa, M.; Benito, D.; Garde, M.J.; Sorolla, M.; Guglielmi, M. New microstrip wiggly-line filters with spurious passband suppression. IEEE Trans. Microw. Theory Tech. 2001, 49, 1593–1598. [Google Scholar] [CrossRef]
- Kim, K.; Kingsley, N.D.; Morton, M.A.; Papapolymerou, J.; Tentzeris, M.M.; Yook, J.G.G. Fractal shaped microstrip coupled line band pass filters for suppression of 2nd harmonic. IEEE Microw. Theory Tech. 2005, 53, 2943–2948. [Google Scholar] [CrossRef]
- Woo, D.; Lee, T.; Lee, J.; Pyo, C.; Choi, W. Novel U slot and V slot DGSs for bandstop filter with improved Q factor. IEEE Trans. Microw. Theory Tech. 2006, 54, 2840–2847. [Google Scholar] [CrossRef]
- Su, B.; Huang, R. 5.8 GHz bandpass filter design using planar couple microstrip lines. Int. Conf. Commun. Circuits Syst. 2004, 2, 1204–1207. [Google Scholar]
- Wu, H.-W.; Yang, R.-Y. A new quad-band bandpass filter using asymmetric stepped impedance resonators. IEEE Microw. Wirel. Comp. Lett. 2011, 21, 203–205. [Google Scholar] [CrossRef]
- Chen, F.-C.; Chu, Q.-X. Design of compact tri-band bandpass filters using assembled resonators. IEEE Trans. Microw. Theory Tech. 2009, 57, 165–171. [Google Scholar] [CrossRef]
- Lee, C.H.; Chung, G.H.; Hsu, C.C. Balanced dual-band BPF with stub-loaded SIRs for common-mode suppression. IEEE Microw. Wirel. Comp. Lett. 2010, 20, 70–72. [Google Scholar] [CrossRef]
- Lugo, C.; Thompson, D.; Papapolymerou, J. Reconfigurable Bandpass Filter with Variable Bandwidth at 5.8 GHz Using a Capacitive Gap Variation Technique. In Proceedings of 33rd European Microwave Conference, Munich, Germany, 7–9 October 2003; pp. 923–926.
- Dong, Y.; Wu, C.-T.M.; Itoh, T. Miniaturised multi-band substrate integrated waveguide filters using complementary split-ring resonators. IET Microw. Antennas Propag. 2012, 6, 611–620. [Google Scholar] [CrossRef]
- Cheng, C.-M.; Yang, C.-F. Develop quad-band (1.57/2.45/3.5/5.2 GHz) bandpass filters on the ceramic substrate. IEEE Microw. Wirel. Comp. Lett. 2010, 20, 268–270. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Hsu, C.-Y. A simple and effective method for microstrip dual-band filters design. IEEE Microw. Wirel. Comp. Lett. 2006, 16, 246–248. [Google Scholar] [CrossRef]
- Lin, S.-C.; Wang, C.-H.; Chen, C.H. Novel patch-via-spiral resonators for the development of miniaturized bandpass filters with transmission zeros. IEEE Trans. Microw. Theory Tech. 2007, 55, 137–146. [Google Scholar] [CrossRef]
- Boutejdar, A.; Batmanov, A.; Machac, J.; Burte, E.; Omar, A.S. A New Transformation of Bandpass Filter to Bandstop Filter Using Multilayer-Technique and U-Defected Ground Structure (DGS). In Proceedings of 14th International Conference on Microwave Techniques, Prague, Czech Republic, 23–24 April 2008; pp. 1–4.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hadarig, R.C.; De Cos Gomez, M.E.; Las-Heras, F. A Compact Band-Pass Filter with High Selectivity and Second Harmonic Suppression. Materials 2013, 6, 5613-5624. https://doi.org/10.3390/ma6125613
Hadarig RC, De Cos Gomez ME, Las-Heras F. A Compact Band-Pass Filter with High Selectivity and Second Harmonic Suppression. Materials. 2013; 6(12):5613-5624. https://doi.org/10.3390/ma6125613
Chicago/Turabian StyleHadarig, Ramona Cosmina, Maria Elena De Cos Gomez, and Fernando Las-Heras. 2013. "A Compact Band-Pass Filter with High Selectivity and Second Harmonic Suppression" Materials 6, no. 12: 5613-5624. https://doi.org/10.3390/ma6125613





