Predicting the Trajectory of Replacements of SARS-CoV-2 Variants Using Relative Reproduction Numbers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nucleotide Sequences
2.2. Model of Advantageous Selection
2.3. Parameter Estimation from the Number of Sequences
2.4. Prediction of Relative Variant Frequency and Average Relative Reproduction Number
3. Results
3.1. Estimation of Relative Reproduction Number from Entire Observations
3.2. Relative Reproduction Number of Delta with Respect to Alpha Estimated from Partial Data
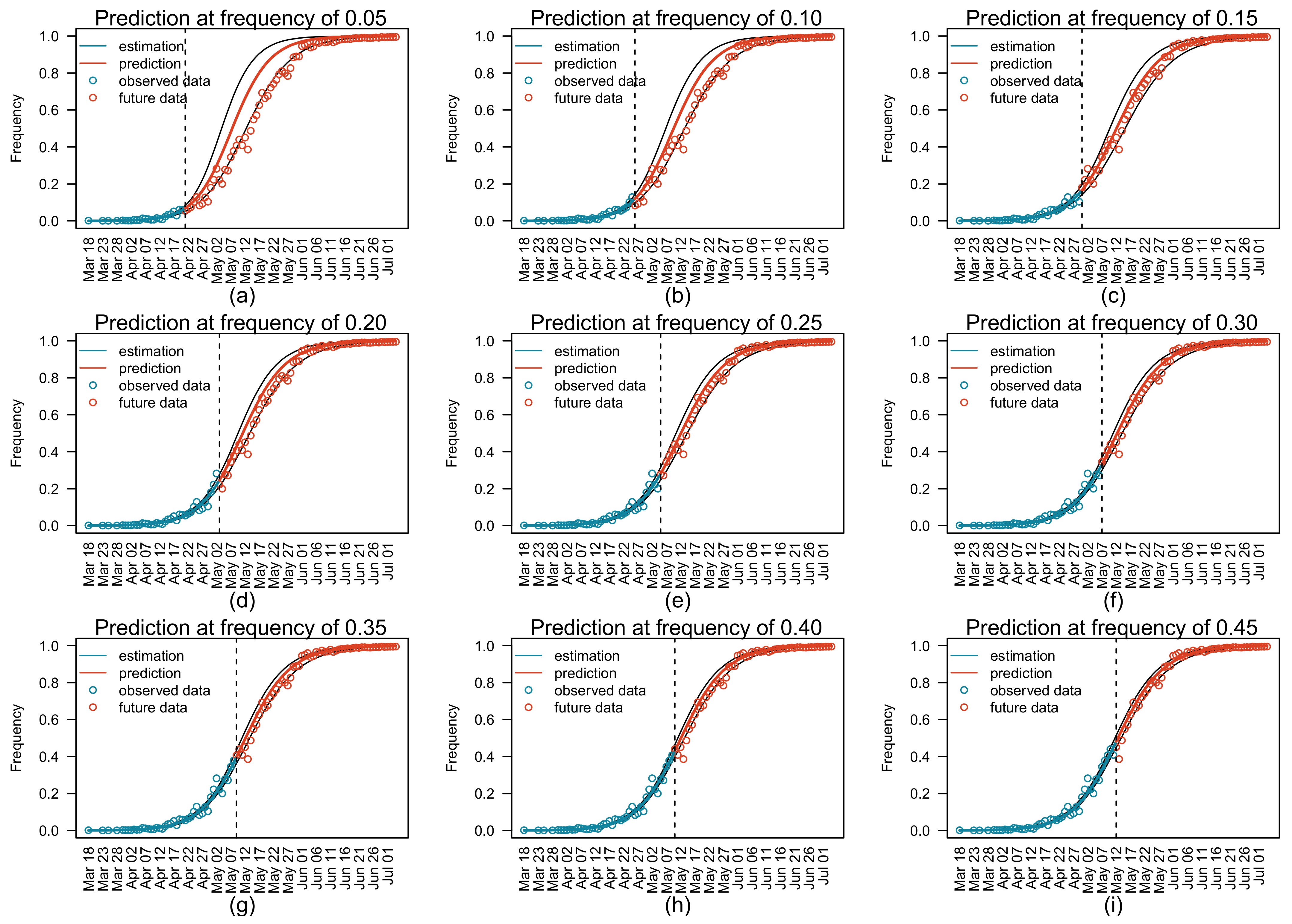
3.3. Prediction of Relative Variant Frequency in Future
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tao, K.; Tzou, P.L.; Nouhin, J.; Gupta, R.K.; de Oliveira, T.; Kosakovsky Pond, S.L.; Fera, D.; Shafer, R.W. The biological and clinical significance of emerging SARS-CoV-2 variants. Nat. Rev. Genet. 2021, 22, 757–773. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Tracking SARS-CoV-2 Variants. Available online: https://www.who.int/en/activities/tracking-SARS-CoV-2-variants/ (accessed on 28 February 2022).
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.C.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, A.; et al. Assessing transmissibility of SARS-CoV-2 lineage B.1.1.7 in England. Nature 2021, 593, 266–269. [Google Scholar] [CrossRef] [PubMed]
- Leung, K.; Shum, M.H.; Leung, G.M.; Lam, T.T.; Wu, J.T. Early transmissibility assessment of the N501Y mutant strains of SARS-CoV-2 in the United Kingdom, October to November 2020. Eurosurveillance 2021, 26, 2002106. [Google Scholar] [CrossRef]
- Ito, K.; Piantham, C.; Nishiura, H. Predicted dominance of variant Delta of SARS-CoV-2 before Tokyo Olympic Games, Japan, July 2021. Eurosurveillance 2021, 26, 2100570. [Google Scholar] [CrossRef] [PubMed]
- Ito, K.; Piantham, C.; Nishiura, H. Relative instantaneous reproduction number of Omicron SARS-CoV-2 variant with respect to the Delta variant in Denmark. J. Med. Virol. 2021, 94, 2265–2268. [Google Scholar] [CrossRef]
- Nishiura, H.; Ito, K.; Anzai, A.; Kobayashi, T.; Piantham, C.; Rodriguez-Morales, A.J. Relative reproduction number of SARS-CoV-2 Omicron (B.1.1.529) compared with Delta variant in South Africa. J. Clin. Med. 2021, 11, 30. [Google Scholar] [CrossRef]
- Morris, D.H.; Gostic, K.M.; Pompei, S.; Bedford, T.; Luksza, M.; Neher, R.A.; Grenfell, B.T.; Lassig, M.; McCauley, J.W. Predictive modeling of influenza shows the promise of applied evolutionary biology. Trends Microbiol. 2018, 26, 102–118. [Google Scholar] [CrossRef]
- Łuksza, M.; Lässig, M. A predictive fitness model for influenza. Nature 2014, 507, 57–61. [Google Scholar] [CrossRef]
- Huddleston, J.; Barnes, J.R.; Rowe, T.; Xu, X.; Kondor, R.; Wentworth, D.E.; Whittaker, L.; Ermetal, B.; Daniels, R.S.; McCauley, J.W.; et al. Integrating genotypes and phenotypes improves long-term forecasts of seasonal influenza A/H3N2 evolution. Elife 2020, 9, e60067. [Google Scholar] [CrossRef]
- Piantham, C.; Ito, K. Modeling the selective advantage of new amino acids on the hemagglutinin of H1N1 influenza viruses using their patient age distributions. Virus Evol. 2021, 7, veab049. [Google Scholar] [CrossRef]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar] [CrossRef]
- Leung, K.; Lipsitch, M.; Yuen, K.Y.; Wu, J.T. Monitoring the fitness of antiviral-resistant influenza strains during an epidemic: A mathematical modelling study. Lancet Infect. Dis. 2017, 17, 339–347. [Google Scholar] [CrossRef] [Green Version]
- Shu, Y.; McCauley, J. GISAID: Global initiative on sharing all influenza data—from vision to reality. Eurosurveillance 2017, 22, 30494. [Google Scholar] [CrossRef] [Green Version]
- Hadfield, J.; Megill, C.; Bell, S.M.; Huddleston, J.; Potter, B.; Callender, C.; Sagulenko, P.; Bedford, T.; Neher, R.A. Nextstrain: Real-time tracking of pathogen evolution. Bioinformatics 2018, 34, 4121–4123. [Google Scholar] [CrossRef] [Green Version]
- Rambaut, A.; Holmes, E.C.; O’Toole, A.; Hill, V.; McCrone, J.T.; Ruis, C.; du Plessis, L.; Pybus, O.G. A dynamic nomenclature proposal for SARS-CoV-2 lineages to assist genomic epidemiology. Nat. Microbiol. 2020, 5, 1403–1407. [Google Scholar] [CrossRef]
- Nishiura, H.; Linton, N.M.; Akhmetzhanov, A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020, 93, 284–286. [Google Scholar] [CrossRef]
- Ito, K.; Piantham, C.; Nishiura, H. Estimating relative generation times and reproduction numbers of Omicron BA.1 and BA.2 with respect to Delta variant in Denmark. Math. Biosci. Eng. 2022, 19, 9005–9017. [Google Scholar] [CrossRef]
- Rowan, T. Functional Stability Analysis of Numerical Algorithms; University of Texas: Austin, TX, USA, 1990. [Google Scholar]
- Johnson, S.G. NLopt, version 2.7.1; The NLopt Nonlinear-Optimization Package; GitHub, Inc.: San Francisco, CA, USA, 2021.
- Held, L.; Bové, D.S. Likelihood and Bayesian Inference, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020; 402p. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A globally convergent augmented lagrangian algorithm for optimization with general constraints and simple bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.R. Relative contagiousness of emerging virus variants: An analysis of the Alpha, Delta, and Omicron SARS-CoV-2 variants. Econom. J. 2022, 25, 739–761. [Google Scholar] [CrossRef]
- Figgins, M.D.; Bedford, T. SARS-CoV-2 variant dynamics across US states show consistent differences in effective reproduction numbers. medRxiv 2021. [Google Scholar] [CrossRef]
- Suzuki, R.; Yamasoba, D.; Kimura, I.; Wang, L.; Kishimoto, M.; Ito, J.; Morioka, Y.; Nao, N.; Nasser, H.; Uriu, K.; et al. Attenuated fusogenicity and pathogenicity of SARS-CoV-2 Omicron variant. Nature 2022, 603, 700–705. [Google Scholar] [CrossRef] [PubMed]
- Hart, W.S.; Miller, E.; Andrews, N.J.; Waight, P.; Maini, P.K.; Funk, S.; Thompson, R.N. Generation time of the alpha and delta SARS-CoV-2 variants: An epidemiological analysis. Lancet. Infect. Dis. 2022, 22, 603–610. [Google Scholar] [CrossRef]
- UK Health Security Agency. GOV.UK Coronavirus (COVID-19) in the UK. Available online: https://coronavirus.data.gov.uk/ (accessed on 12 November 2022).
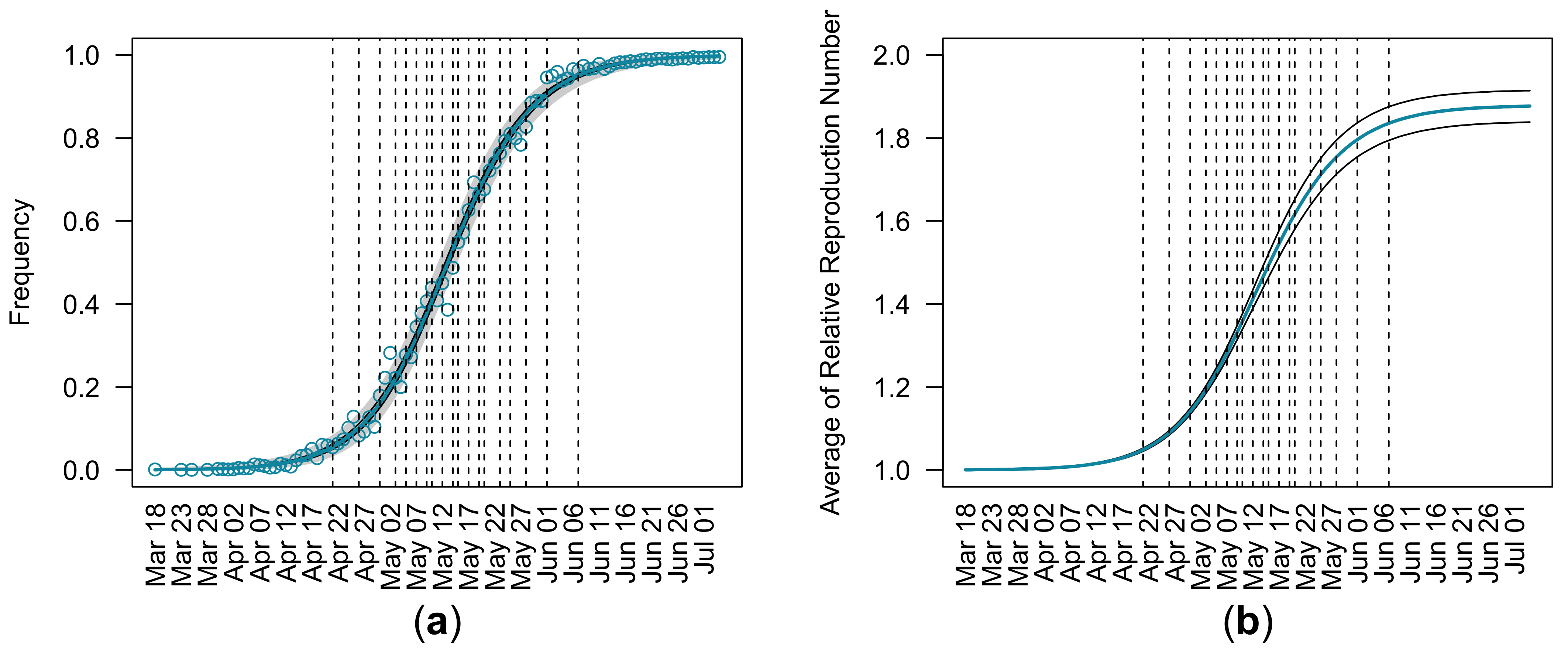

| (95% CI) | (95% CI) | (95% CI) | Log Likelihood |
|---|---|---|---|
| 1.88 (1.85, 1.91) | 0.0005 (0.0004, 0.0006) | 288.54 (202.96, 406.26) | −431.00 |
| Relative Frequency | Date When Delta Exceeded the Relative Frequency (95% CI) | Average Relative Reproduction Number w.r.t. Alpha (95% CI) |
|---|---|---|
| 0.05 | 2021-04-21 (2021-04-16, 2021-04-24) | 1.049 (1.045, 1.053) |
| 0.10 | 2021-04-26 (2021-04-23, 2021-04-29) | 1.090 (1.084, 1.095) |
| 0.15 | 2021-04-30 (2021-04-27, 2021-05-02) | 1.141 (1.134, 1.148) |
| 0.20 | 2021-05-03 (2021-04-30, 2021-05-05) | 1.193 (1.185, 1.203) |
| 0.25 | 2021-05-05 (2021-05-03, 2021-05-07) | 1.235 (1.223, 1.246) |
| 0.30 | 2021-05-07 (2021-05-05, 2021-05-09) | 1.281 (1.267, 1.295) |
| 0.35 | 2021-05-09 (2021-05-07, 2021-05-10) | 1.332 (1.314, 1.349) |
| 0.40 | 2021-05-10 (2021-05-08, 2021-05-12) | 1.358 (1.339, 1.377) |
| 0.45 | 2021-05-12 (2021-05-10, 2021-05-14) | 1.412 (1.389, 1.434) |
| 0.50 | 2021-05-14 (2021-05-12, 2021-05-15) | 1.467 (1.440, 1.493) |
| 0.55 | 2021-05-15 (2021-05-13, 2021-05-17) | 1.493 (1.465, 1.521) |
| 0.60 | 2021-05-17 (2021-05-15, 2021-05-19) | 1.545 (1.513, 1.577) |
| 0.65 | 2021-05-19 (2021-05-17, 2021-05-21) | 1.594 (1.559, 1.628) |
| 0.70 | 2021-05-20 (2021-05-18, 2021-05-23) | 1.617 (1.580, 1.652) |
| 0.75 | 2021-05-23 (2021-05-20, 2021-05-25) | 1.677 (1.638, 1.716) |
| 0.80 | 2021-05-25 (2021-05-23, 2021-05-28) | 1.712 (1.671, 1.751) |
| 0.85 | 2021-05-28 (2021-05-25, 2021-05-31) | 1.754 (1.713, 1.794) |
| 0.90 | 2021-06-01 (2021-05-29, 2021-06-05) | 1.796 (1.754, 1.837) |
| 0.95 | 2021-06-07 (2021-06-03, 2021-06-13) | 1.835 (1.794, 1.875) |
| Observed Relative Frequency | (95% CI) | (95% CI) | (95% CI) | Log Likelihood |
|---|---|---|---|---|
| 0.05 | 2.15 (2.00, 2.45) | 0.0002 (0.0001, 0.0003) | 834.12 (346.81, 2000.00 †) | −80.91 |
| 0.10 | 2.06 (1.92, 2.21) | 0.0002 (0.0001, 0.0004) | 581.40 (268.62, 1426.19) | −102.87 |
| 0.15 | 1.93 (1.83, 2.05) | 0.0004 (0.0002, 0.0006) | 399.87 (202.44, 832.82) | −123.23 |
| 0.20 | 1.97 (1.87, 2.08) | 0.0003 (0.0002, 0.0005) | 362.81 (188.91, 720.53) | −137.69 |
| 0.25 | 1.92 (1.83, 2.02) | 0.0004 (0.0002, 0.0006) | 307.07 (165.69, 575.00) | −148.88 |
| 0.30 | 1.91 (1.83, 2.00) | 0.0004 (0.0003, 0.0006) | 310.63 (170.09, 574.06) | −158.03 |
| 0.35 | 1.92 (1.85, 2.00) | 0.0004 (0.0003, 0.0006) | 328.39 (182.12, 607.05) | −166.02 |
| 0.40 | 1.93 (1.86, 2.00) | 0.0004 (0.0003, 0.0006) | 339.98 (189.18, 628.24) | −170.45 |
| 0.45 | 1.90 (1.84, 1.96) | 0.0004 (0.0003, 0.0006) | 315.00 (179.08, 565.97) | −180.84 |
| 0.50 | 1.86 (1.79, 1.92) | 0.0005 (0.0004, 0.0008) | 231.61 (136.25, 392.22) | −194.90 |
| 0.55 | 1.85 (1.79, 1.91) | 0.0006 (0.0004, 0.0008) | 234.52 (139.84, 401.81) | −198.95 |
| 0.60 | 1.86 (1.80, 1.91) | 0.0005 (0.0004, 0.0007) | 247.76 (147.88, 419.60) | −207.59 |
| 0.65 | 1.87 (1.81, 1.92) | 0.0005 (0.0004, 0.0007) | 248.77 (150.01, 415.23) | −217.85 |
| 0.70 | 1.86 (1.81, 1.91) | 0.0005 (0.0004, 0.0007) | 250.70 (152.17, 417.80) | −222.51 |
| 0.75 | 1.86 (1.82, 1.91) | 0.0005 (0.0004, 0.0007) | 271.02 (164.92, 448.18) | −235.19 |
| 0.80 | 1.87 (1.82, 1.91) | 0.0005 (0.0004, 0.0007) | 285.77 (174.67, 473.56) | −244.46 |
| 0.85 | 1.84 (1.81, 1.89) | 0.0006 (0.0004, 0.0007) | 250.12 (159.20, 426.80) | −261.43 |
| 0.90 | 1.86 (1.82, 1.90) | 0.0005 (0.0004, 0.0007) | 238.70 (154.56, 365.00) | −284.10 |
| 0.95 | 1.88 (1.85, 1.92) | 0.0005 (0.0004, 0.0006) | 209.79 (142.17, 313.90) | −321.85 |
| Target Date | Final Estimate of Relative Frequency | Number of Predictions † | Absolute Errors in Predicted Relative Frequency | |
|---|---|---|---|---|
| Median | Maximum | |||
| 14 May 2021 | 0.50 | 7 | 0.060 | 0.092 |
| 20 May 2021 | 0.70 | 11 | 0.023 | 0.060 |
| 1 June 2021 | 0.90 | 15 | 0.004 | 0.034 |
| Target Relative Frequency | Final Estimate of Date | Number of Predictions † | Absolute Errors of Predicted Dates | |
|---|---|---|---|---|
| Median | Maximum | |||
| 0.50 | 14 May 2021 | 7 | 1 | 2 |
| 0.70 | 20 May 2021 | 11 | 1 | 2 |
| 0.90 | 1 June 2021 | 15 | 1 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piantham, C.; Ito, K. Predicting the Trajectory of Replacements of SARS-CoV-2 Variants Using Relative Reproduction Numbers. Viruses 2022, 14, 2556. https://doi.org/10.3390/v14112556
Piantham C, Ito K. Predicting the Trajectory of Replacements of SARS-CoV-2 Variants Using Relative Reproduction Numbers. Viruses. 2022; 14(11):2556. https://doi.org/10.3390/v14112556
Chicago/Turabian StylePiantham, Chayada, and Kimihito Ito. 2022. "Predicting the Trajectory of Replacements of SARS-CoV-2 Variants Using Relative Reproduction Numbers" Viruses 14, no. 11: 2556. https://doi.org/10.3390/v14112556
APA StylePiantham, C., & Ito, K. (2022). Predicting the Trajectory of Replacements of SARS-CoV-2 Variants Using Relative Reproduction Numbers. Viruses, 14(11), 2556. https://doi.org/10.3390/v14112556







