Determination of Inherent Dissolution Performance of Drug Substances
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
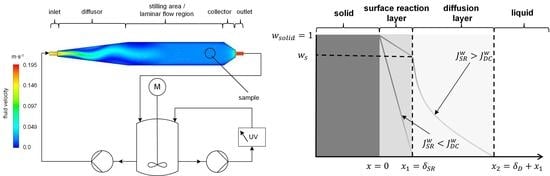
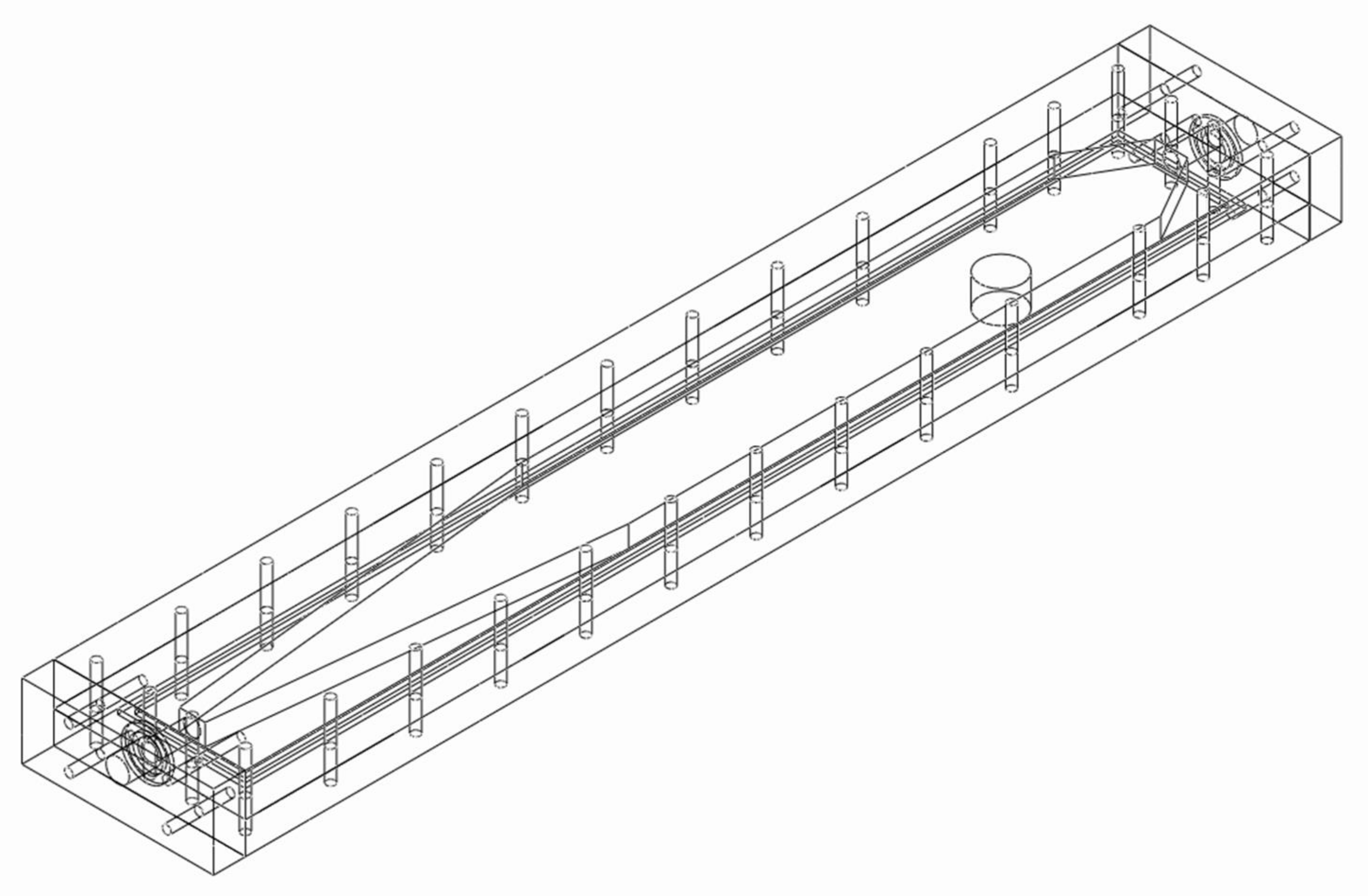
2.2. Design of the Flow Channel
2.3. Dissolution Experiments in the Flow Channel
3. Results and Discussion
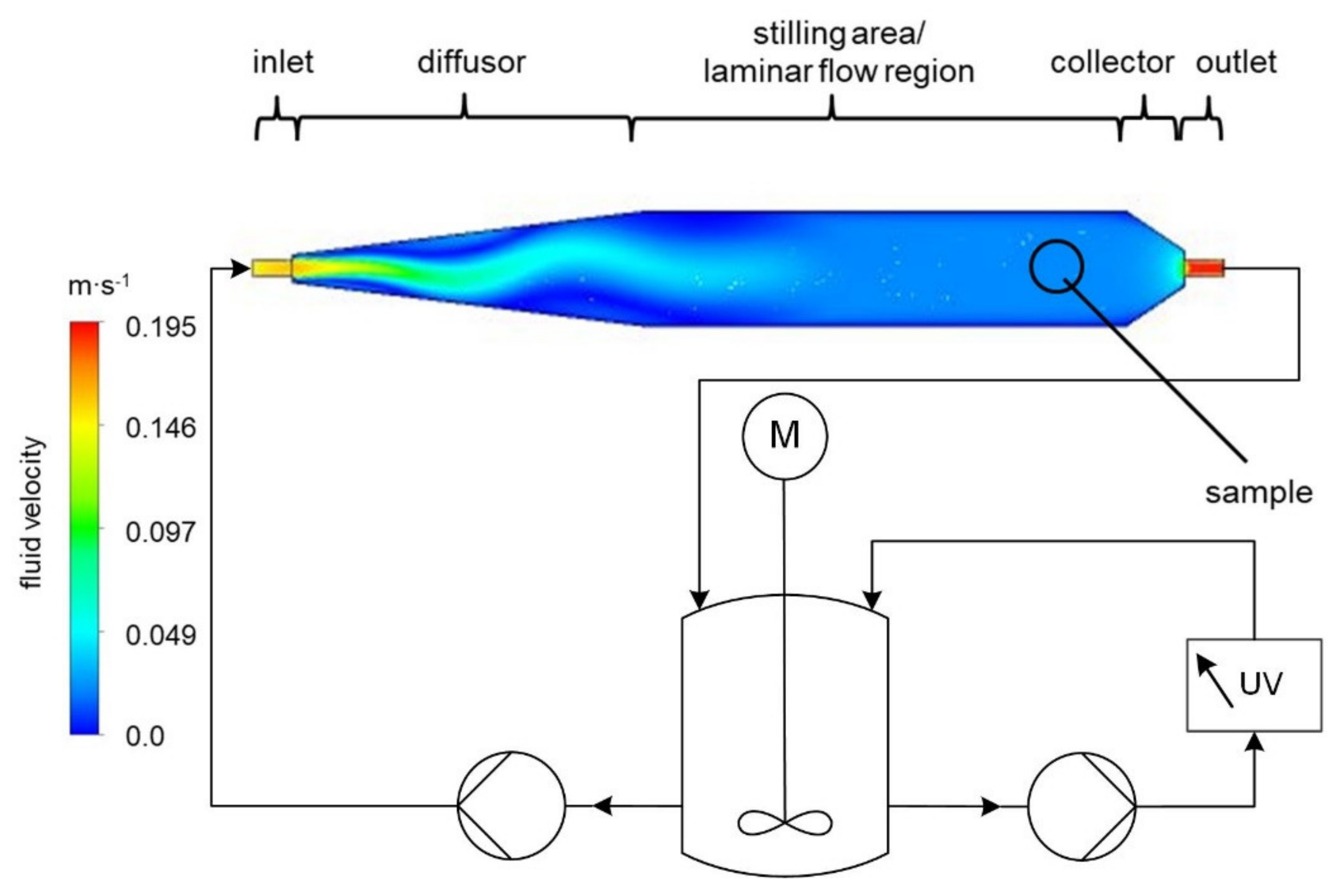
3.1. Experimental Setup
3.2. Measuring Protocol
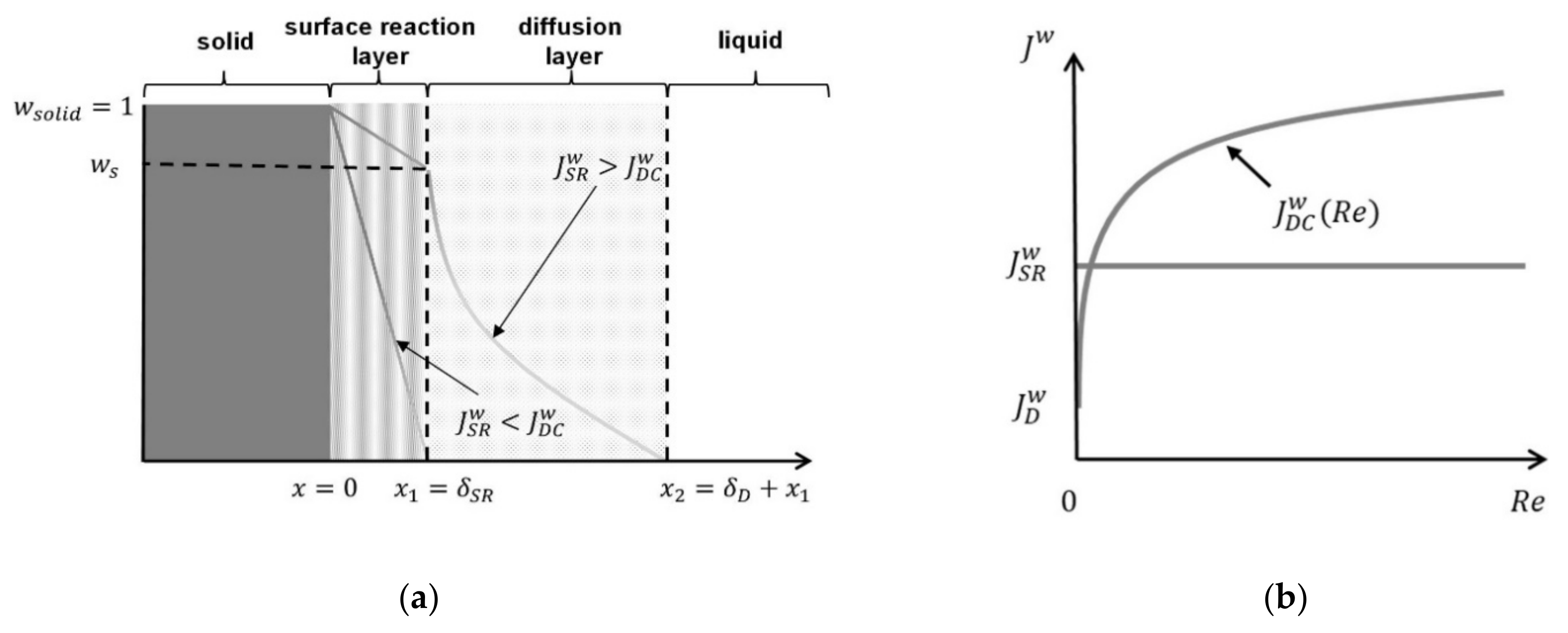
3.3. Modeling
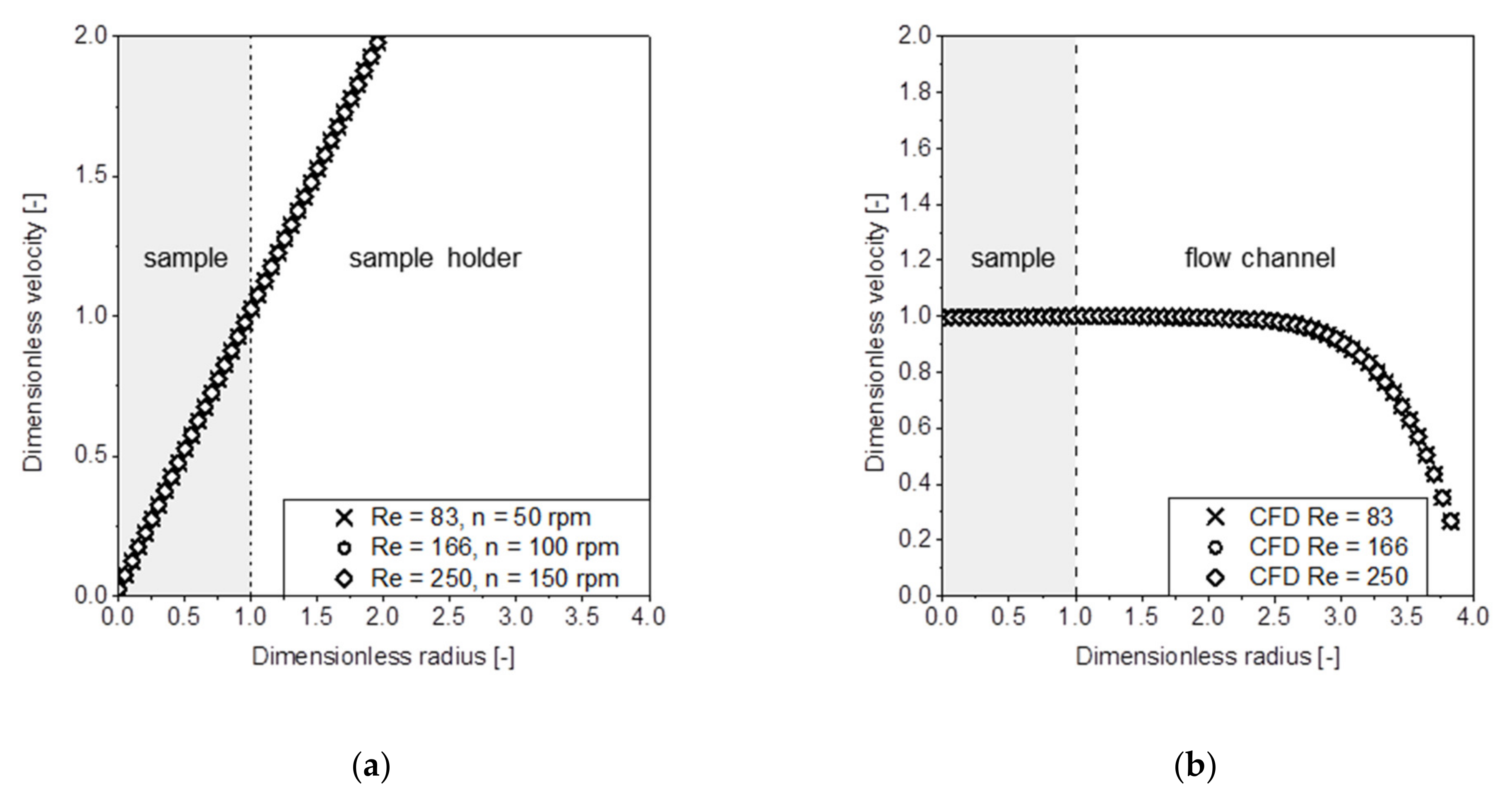
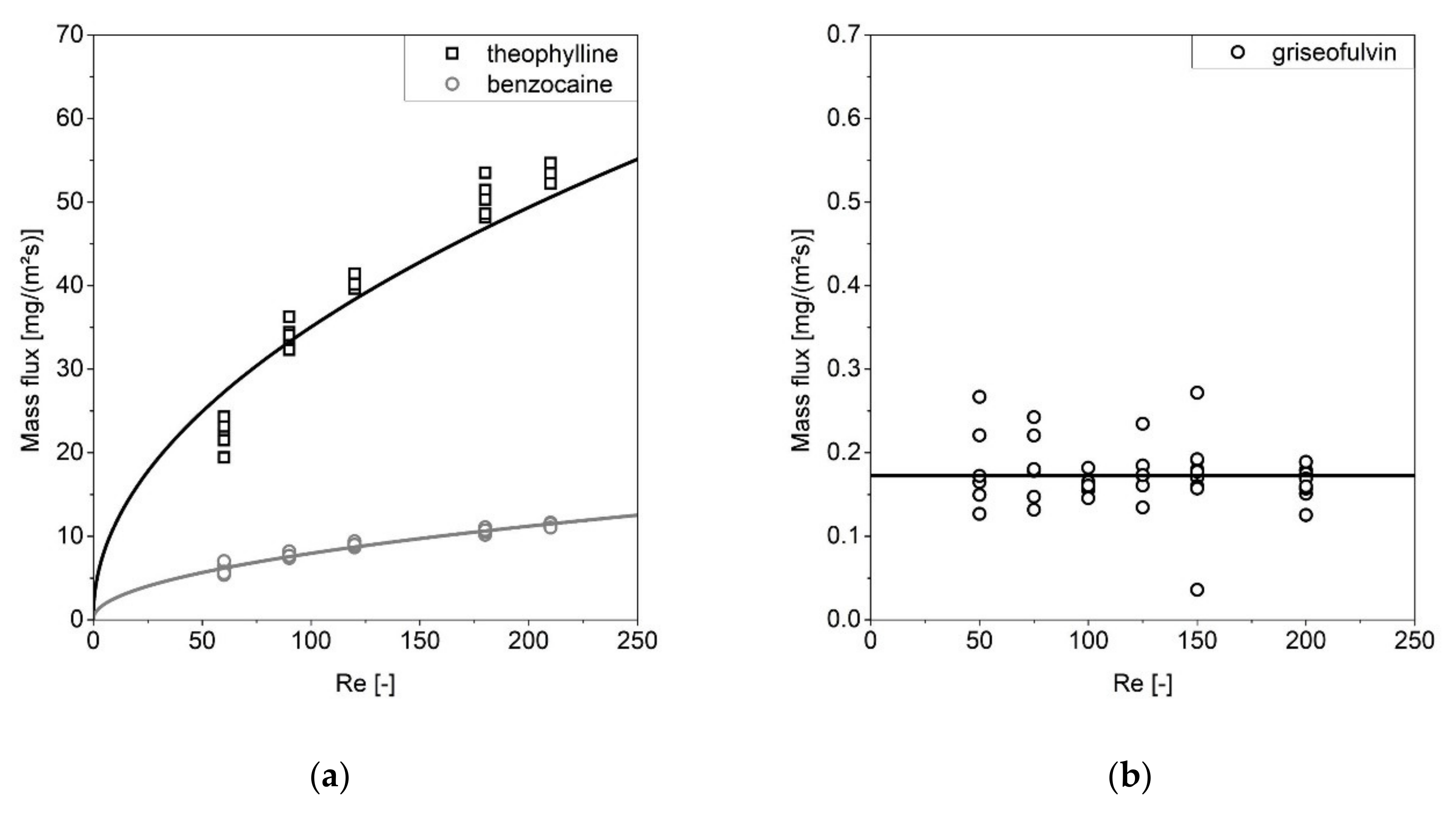
3.4. Model Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Description | SI Unit |
|---|---|---|
| A | area | m2 |
| a | width | m |
| b | height | m |
| ci | concentration of the species i | mol∙m−3 |
| D | diffusion coefficient | m2∙s−1 |
| Dhydr | hydrodynamic diameter | m |
| J | molar flux | mol∙m−2∙s−1 |
| Jw | mass flux per area | kg∙m−2∙s−1 |
| JwD | diffusive mass flux per area | kg∙m−2∙s−1 |
| JwDC | diffusive–convective mass flux per area | kg∙m−2∙s−1 |
| JwSR | surface reaction mass flux per area | kg∙m−2∙s−1 |
| k | Fick’s law coefficient | mol2∙s∙kg−1∙m−3 |
| kB | Boltzmann constant | kg∙m2∙s−1∙K−1 |
| kSR | phase transition coefficient | m2∙s−1 |
| linlet | inlet length of the channel | m |
| Mi | molar mass of the species i | kg∙mol−1 |
| p | pressure | kg∙m−1∙s−2 |
| Re | Reynolds number | - |
| rmol | molar radius | m |
| rsample | sample radius | m |
| Sc | Schmidt number | - |
| Sh | Sherwood number | - |
| T | temperature | °K |
| U | circumference | m |
| volume flow | m3 | |
| v | fluid velocity | m∙s−1 |
| vmax | maximum velocity | m∙s−1 |
| w | weight fraction | - |
| wbulk | weight fraction in the bulk liquid | - |
| ws | weight fraction at the saturation concentration | - |
| wi | weight fraction of the species i | - |
| wsolid | weight fraction of the solid | - |
| x | coordinate in the axial direction | m |
| δD | diffusion layer thickness | m |
| δSR | interfacial thickness | m |
| η | dynamic viscosity | kg∙m−1∙s−1 |
| µ | chemical potential | - |
| ρtotal | total density of the binary substance system | kg∙m−3 |
| ρsolid | density of the solute | kg∙m−3 |
| ρl | density of the liquid | kg∙m−3 |
| λ | pipe flow resistance | - |
References
- Lipinski, C. Poor aqueous solubility—an industry wide problem in drug discovery. Am. Pharm. Rev. 2002, 5, 82–85. [Google Scholar]
- Kawabata, Y.; Wada, K.; Nakatani, M.; Yamada, S.; Onoue, S. Formulation design for poorly water-soluble drugs based on biopharmaceutics classification system: Basic approaches and practical applications. Int. J. Pharm. 2011, 420, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Schwebel, H.J.; Van Hoogevest, P.; Leigh, M.L.; Kuentz, M. The apparent solubilizing capacity of simulated intestinal fluids for poorly water-soluble drugs. Pharm. Dev. Technol. 2010, 16, 278–286. [Google Scholar] [CrossRef] [PubMed]
- Amidon, G.L.; Lennernäs, H.; Shah, V.P.; Crison, J.R. A Theoretical Basis for a Biopharmaceutic Drug Classification: The Correlation of in Vitro Drug Product Dissolution and in Vivo Bioavailability. Pharm. Res. 1995, 12, 413–420. [Google Scholar] [CrossRef] [Green Version]
- Leane, M.; Pitt, K.; Reynolds, G. The Manufacturing Classification System (MCS) Working Group A proposal for a drug product Manufacturing Classification System (MCS) for oral solid dosage forms. Pharm. Dev. Technol. 2015, 20, 12–21. [Google Scholar] [CrossRef]
- Leane, M.; Pitt, K.; Reynolds, G.K.; Dawson, N.; Ziegler, I.; Szepes, A.; Crean, A.M.; Agnol, R.D.; Sy, T.M.C. Manufacturing classification system in the real world: Factors influencing manufacturing process choices for filed commercial oral solid dosage formulations, case studies from industry and considerations for continuous processing. Pharm. Dev. Technol. 2018, 23, 964–977. [Google Scholar] [CrossRef]
- Noyes, A.A.; Whitney, W.R. The Rate of Solution of Solid Substances in their Own Solutions. J. Am. Chem. Soc. 1897, 19, 930–934. [Google Scholar] [CrossRef] [Green Version]
- Hixson, A.W.; Crowell, J.H. Dependence of Reaction Velocity upon Surface and Agitation. Ind. Eng. Chem. 1931, 23, 1160–1168. [Google Scholar] [CrossRef]
- Higuchi, T. Rate of Release of Medicaments from Ointment Bases Containing Drugs in Suspension. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef]
- Siepmann, J.; Faisant, N.; Akiki, J.; Richard, J.; Benoit, J.P. Effect of the size of biodegradable microparticles on drug release: Experiment and theory. J. Control. Release 2004, 96, 123–134. [Google Scholar] [CrossRef]
- Goepferich, A.; Langer, R. Modeling monomer release from bioerodible polymers. J. Control. Release 1995, 33, 55–69. [Google Scholar] [CrossRef]
- Hasa, D.; Perissutti, B.; Voinovich, D.; Abrami, M.; Farra, R.; Fiorentino, S.M.; Grassi, G.; Grassi, M. Drug nanocrystals: Theo-retical background of solubility increase and dissolution rate enhancement. Chem. Biochem. Eng. Q. 2014, 28, 247–258. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Phys. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Papadopoulou, V.; Valsami, G.; Macheras, P. Development of a reaction-limited model of dissolution: Application to official dissolution tests experiments. Int. J. Pharm. 2008, 355, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Paus, R.; Prudic, A.; Lübbert, C.; Sadowski, G. A novel approach for analyzing the dissolution mechanism of solid dis-persions. Pharm. Res. 2015, 32, 2559–2578. [Google Scholar] [PubMed]
- Saylor, D.M.; Kim, C.-S.; Patwardhan, D.V.; Warren, J.A. Diffuse-interface theory for structure formation and release behavior in controlled drug release systems. Acta Biomater. 2007, 3, 851–864. [Google Scholar] [CrossRef] [PubMed]
- Rickard, D.; Sjoeberg, E.L. Mixed kinetic control of calcite dissolution rates. Am. J. Sci. 1983, 283, 815–830. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.-J.; Steinbach, I.; Karma, A.; Tong, X. Modeling Melt Convection in Phase-Field Simulations of Solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Juanes, R. A phase field model of unsaturated flow. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Zuo, P.; Zhao, Y.-P. A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries. Phys. Chem. Chem. Phys. 2015, 17, 287–297. [Google Scholar] [CrossRef]
- Compton, R.G.; Pritchard, K.L.; Unwin, P.R. The dissolution of calcite in acid waters: Mass transport versus surface control. Freshw. Biol. 1989, 22, 285–288. [Google Scholar] [CrossRef]
- Issa, M.G.; Ferraz, H.G. Intrinsic Dissolution as a Tool for Evaluating Drug Solubility in Accordance with the Biopharmaceutics Classification System. Dissolution Technol. 2011, 18, 6–13. [Google Scholar] [CrossRef]
- Missel, P.J.; Stevens, L.E.; Mauger, J.W. Reexamination of Convective Diffusion/Drug Dissolution in a Laminar Flow Channel: Accurate Prediction of Dissolution Rate. Pharm. Res. 2004, 21, 2300–2306. [Google Scholar] [CrossRef] [PubMed]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Menter, F. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Missel, P.J.; Stevens, L.E.; Mauger, J.W. Dissolution of Anecortave Acetate in a Cylindrical Flow Cell: Re-Evaluation of Con-vective Diffusion/Drug Dissolution for Sparingly Soluble Drugs. Pharm. Dev. Technol. 2005, 9, 453–459. [Google Scholar] [CrossRef]
- Peltonen, L.; Liljeroth, P.; Heikkilä, T.; Kontturi, K.; Hirvonen, J. Dissolution testing of acetylsalicylic acid by a channel flow method—correlation to USP basket and intrinsic dissolution methods. Eur. J. Pharm. Sci. 2003, 19, 395–401. [Google Scholar] [CrossRef]
- Shah, A.C.; Nelson, K.G. Evaluation of a Convective Diffusion Drug Dissolution Rate Model. J. Pharm. Sci. 1975, 64, 1518–1520. [Google Scholar] [CrossRef]
- Obot, N.T. Determination of Incompressible Flow Friction in Smooth Circular and Noncircular Passages: A Generalized Approach Including Validation of the Nearly Century Old Hydraulic Diameter Concept. J. Fluids Eng. 1988, 110, 431–440. [Google Scholar] [CrossRef]
- Greco, K.; Bergman, T.L.; Bogner, R. Design and characterization of a laminar flow-through dissolution apparatus: Comparison of hydrodynamic conditions to those of common dissolution techniques. Pharm. Dev. Technol. 2010, 16, 75–87. [Google Scholar] [CrossRef]
- Boetker, J.P.; Rantanen, J.; Rades, T.; Müllertz, A.; Østergaard, J.; Jensen, H. A New Approach to Dissolution Testing by UV Imaging and Finite Element Simulations. Pharm. Res. 2013, 30, 1328–1337. [Google Scholar] [CrossRef] [PubMed]
- Ward-Smith, A.J. Internal Fluid Flow-The Fluid Dynamics of Flow in Pipes and Ducts; Oxford University Press: Oxford, UK, 1980; Volume 81, p. 38505. [Google Scholar]
- Sommer, C. Die Größenabhängigkeit der Gleichgewichtsgeschwindigkeit von Partikeln beim Transport in Mikrokanälen. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2014. [Google Scholar]
- Wibel, W.; Erhard, P. Experiments on the Laminar/Turbulent Transition of Liquid Flows in Rectangular Micro Channels. In Proceedings of the International Conference on Nanochannels,Microchannels, and Minichannels, Puebla, Mexico, 18–20 June 2007. [Google Scholar]
- European Pharmacopoeia Commission. European Pharmacopoeia Ninth Edition (PhEur 9.0); European Directorate for the Quality of Medicines: Strasbourg, France, 2016. [Google Scholar]
- Whitman, W.G. The two film theory of gas absorption. Int. J. Heat Mass Transf. 1962, 5, 429–433. [Google Scholar] [CrossRef]
- Peter, A.; Julio, D.P. Atkins’ Physical Chemistry, 8th ed.; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 1960; Volume 413. [Google Scholar]
- Murzin, D.Y.; Salmi, T. Catalytic Kinetics; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 0080455468. [Google Scholar]
- Pohlhausen, E. Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibung und kleiner Wärmelei-tung. ZAMM-J. Appl. Math. Mech. 1921, 1, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Stokes, G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Philos. Soc. 1856, 9, 51. [Google Scholar]
- Satterfield, C.N.; Sherwood, T.K. The Role of Diffusion in Catalysis; Addison-Wesley: Boston, MA, USA, 1963. [Google Scholar]
- Brauer, H.; Sucker, D. Umströmung von Platten, Zylindern und Kugeln. Chem. Ing. Tech. 1976, 48, 665–671. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sleziona, D.; Mattusch, A.; Schaldach, G.; Ely, D.R.; Sadowski, G.; Thommes, M. Determination of Inherent Dissolution Performance of Drug Substances. Pharmaceutics 2021, 13, 146. https://doi.org/10.3390/pharmaceutics13020146
Sleziona D, Mattusch A, Schaldach G, Ely DR, Sadowski G, Thommes M. Determination of Inherent Dissolution Performance of Drug Substances. Pharmaceutics. 2021; 13(2):146. https://doi.org/10.3390/pharmaceutics13020146
Chicago/Turabian StyleSleziona, Dominik, Amelie Mattusch, Gerhard Schaldach, David R. Ely, Gabriele Sadowski, and Markus Thommes. 2021. "Determination of Inherent Dissolution Performance of Drug Substances" Pharmaceutics 13, no. 2: 146. https://doi.org/10.3390/pharmaceutics13020146
APA StyleSleziona, D., Mattusch, A., Schaldach, G., Ely, D. R., Sadowski, G., & Thommes, M. (2021). Determination of Inherent Dissolution Performance of Drug Substances. Pharmaceutics, 13(2), 146. https://doi.org/10.3390/pharmaceutics13020146