On the Analysis and Torque Enhancement of Flux-Switching Permanent Magnet Machines in Electric Power Steering Systems
Abstract
:1. Introduction
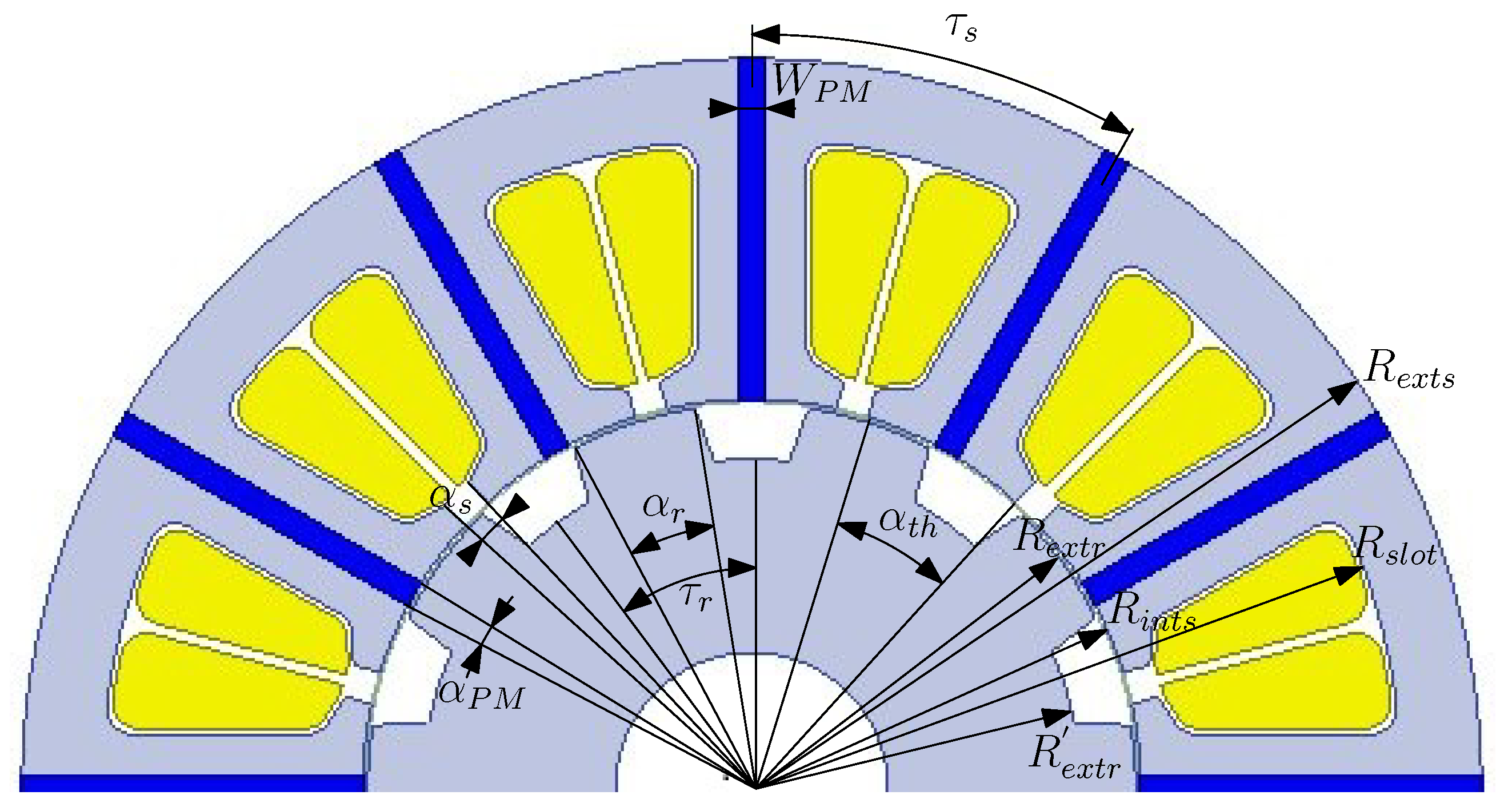
2. Analytical Formulation of FSPMM Features
2.1. PM Air Gap Flux Density
- , , and are the magnet remanence, relative permeability, and width, respectively;
- is the angular PM width at the air-gap stator inner border;
- g is the air gap thickness, with .
2.2. Permeance Functions
2.2.1. Stator Permeance Functions
Permeance Function Accounting for the Slotting Effect
Permeance Function Accounting for the PM Flux Concentrating Arrangement
2.2.2. Rotor Permeance Function
2.3. Improvement of the Accuracy of the PM Air Gap Flux Density Prediction
2.3.1. Correction Allied to the Rotor Position Variation
2.3.2. Saturation Correction Function
- The nonlinear behavior of the iron due to the magnetic saturation which is commonly accounted for using the B–H curve,
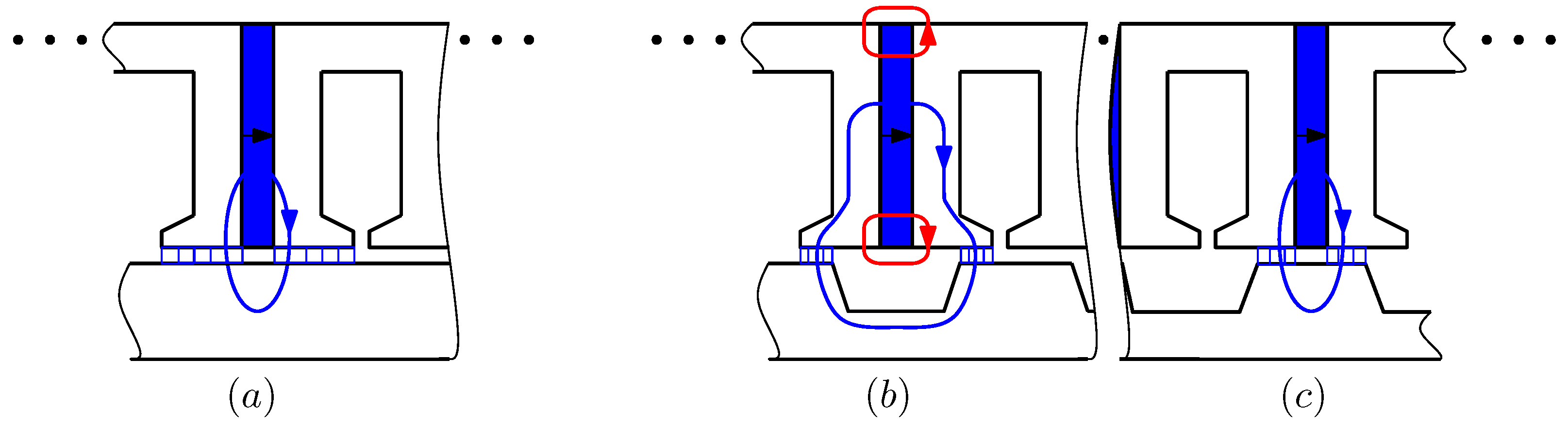
- The deformation of the flux tube within the air gap due to the fringing effect, as illustrated in Figure 3.
2.4. Armature Magnetic Reaction
2.5. Torque Formulation
- is the equivalent no-load air gap flux density;
- is the active length of the machine;
- is the number of coils per phase;
- is the winding factor;
- and are the permeance correction and leakage flux factors, respectively, [18];
- is the armature current quadrature component.
3. Case Study
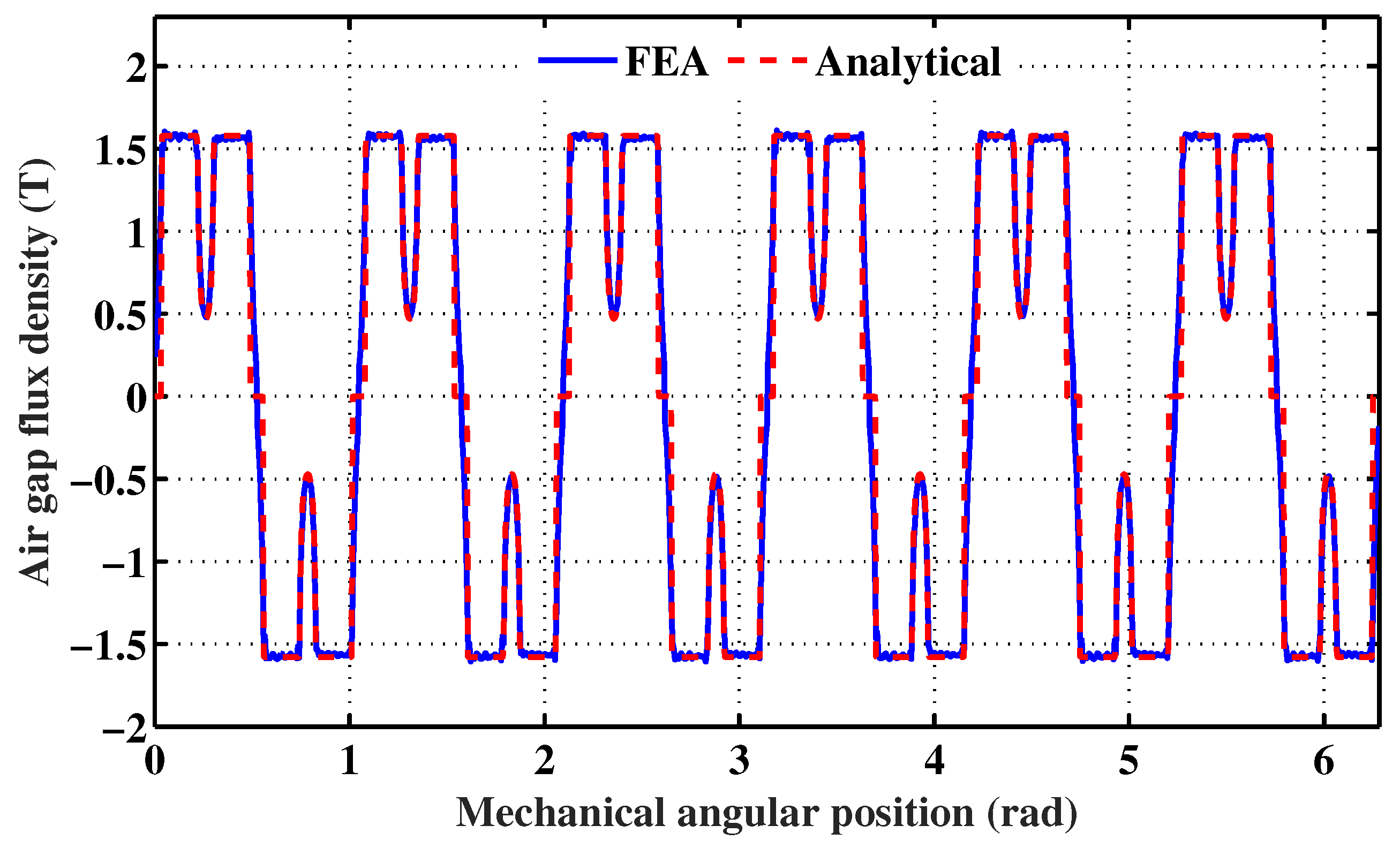
3.1. Analysis Assuming a Linear Magnetic Circuit
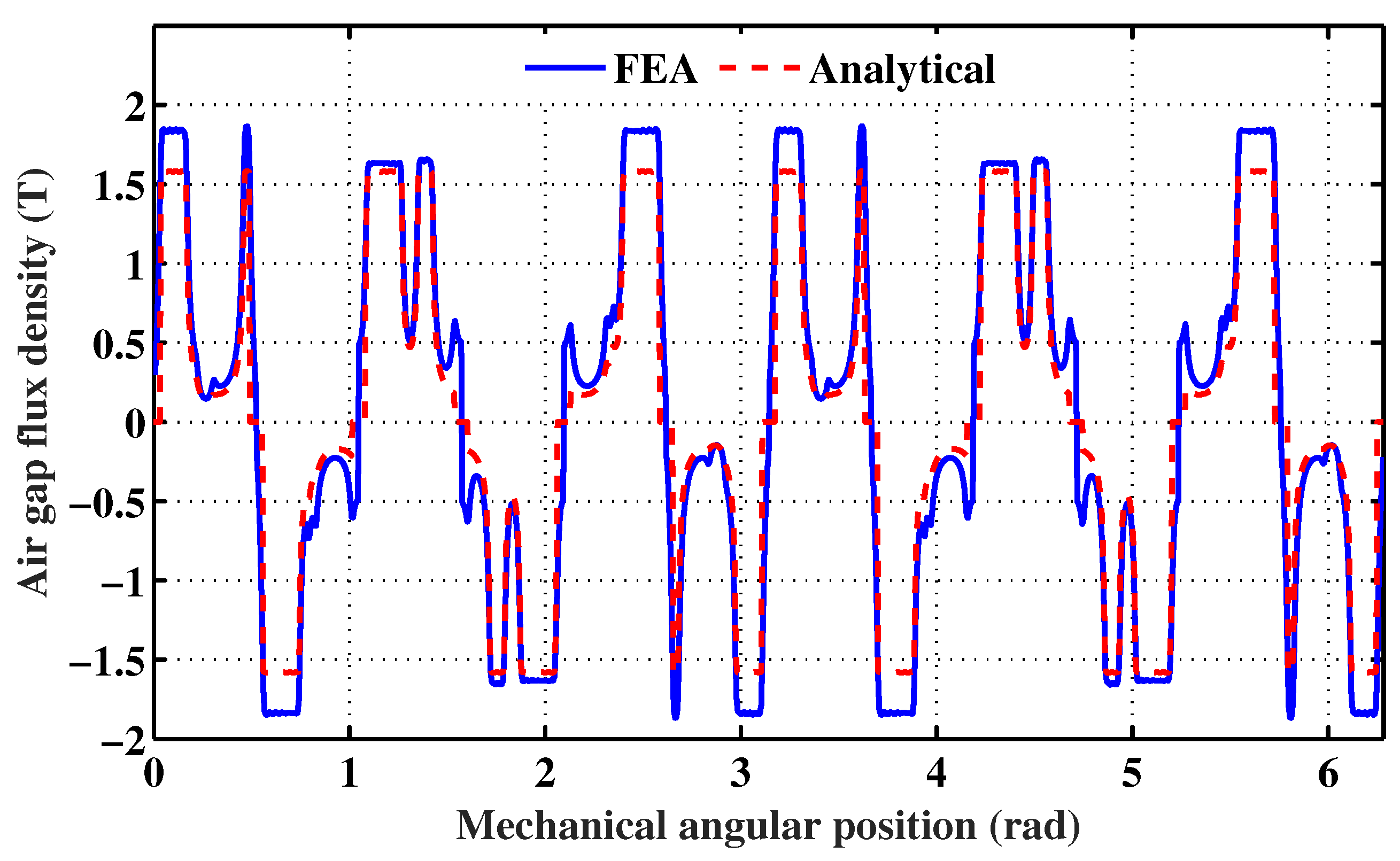
3.2. Analysis with the Magnetic Saturation Taken into Account
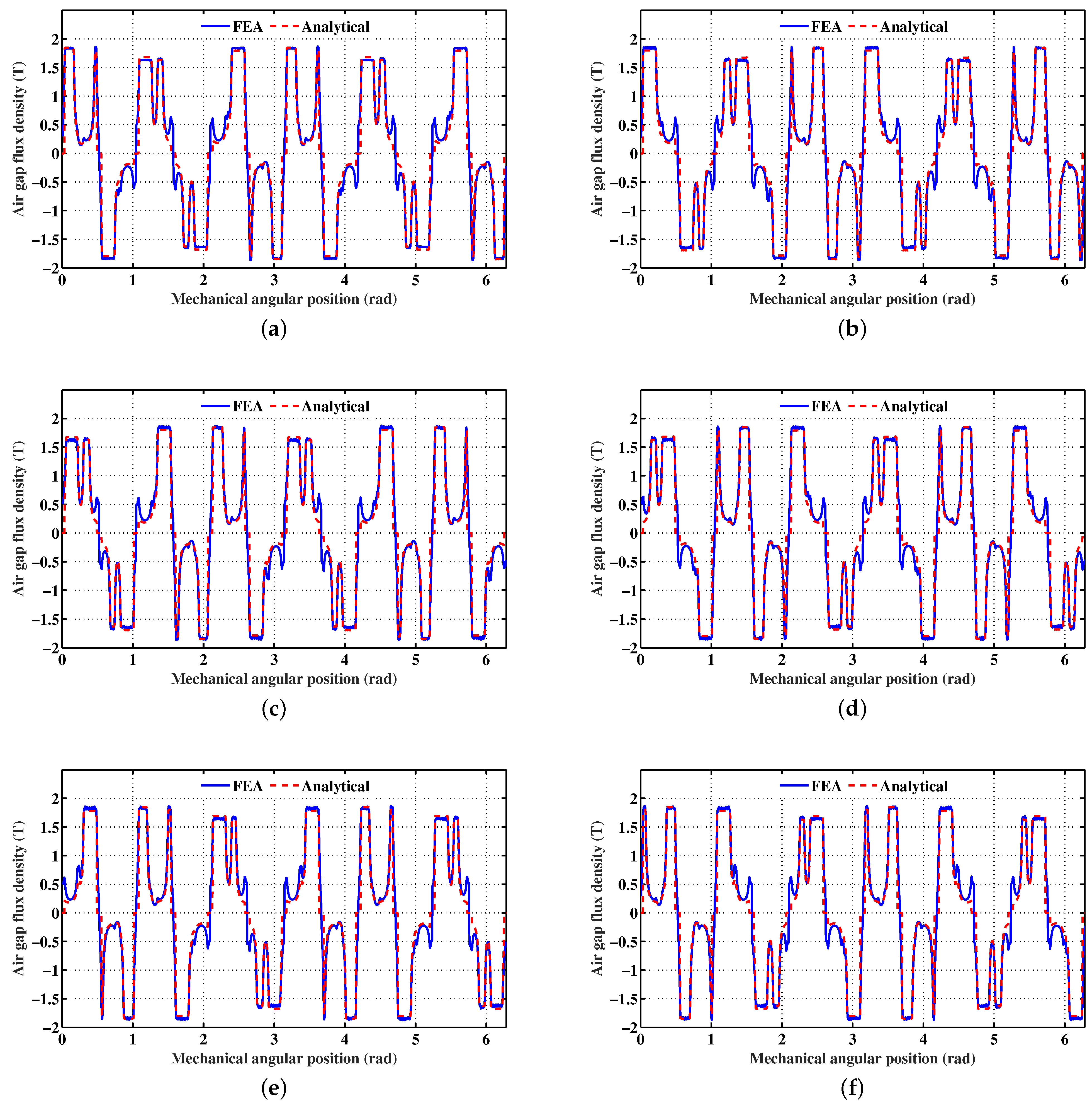
3.2.1. PM Air Gap Flux Density
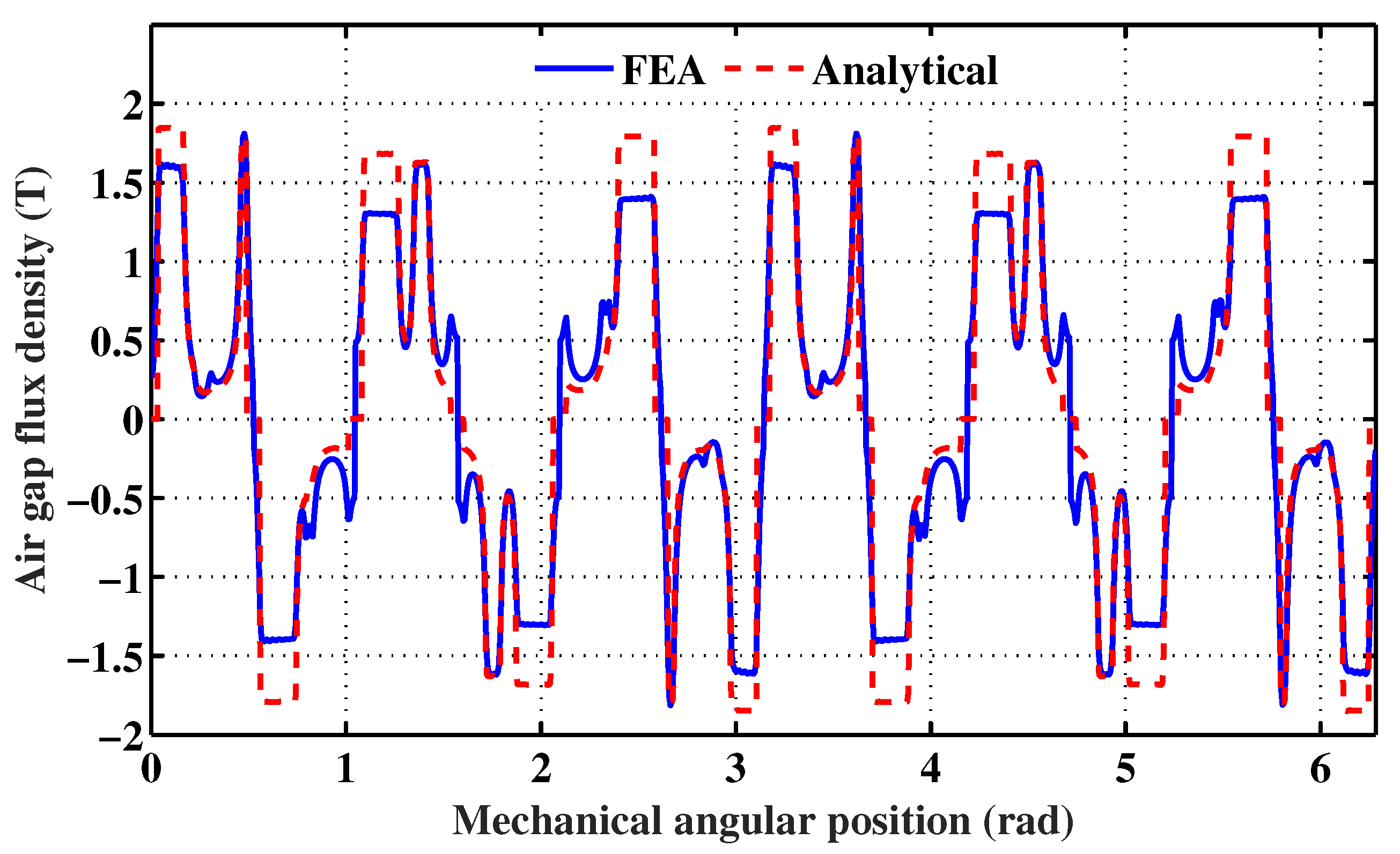
3.2.2. Armature Magnetic Reaction
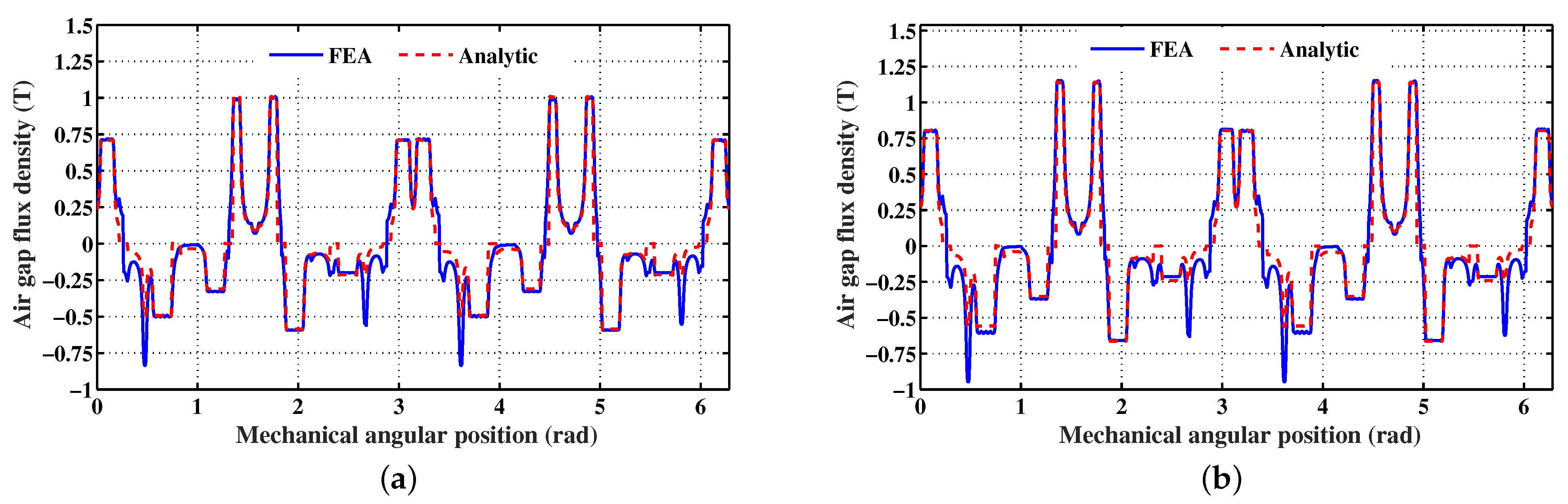
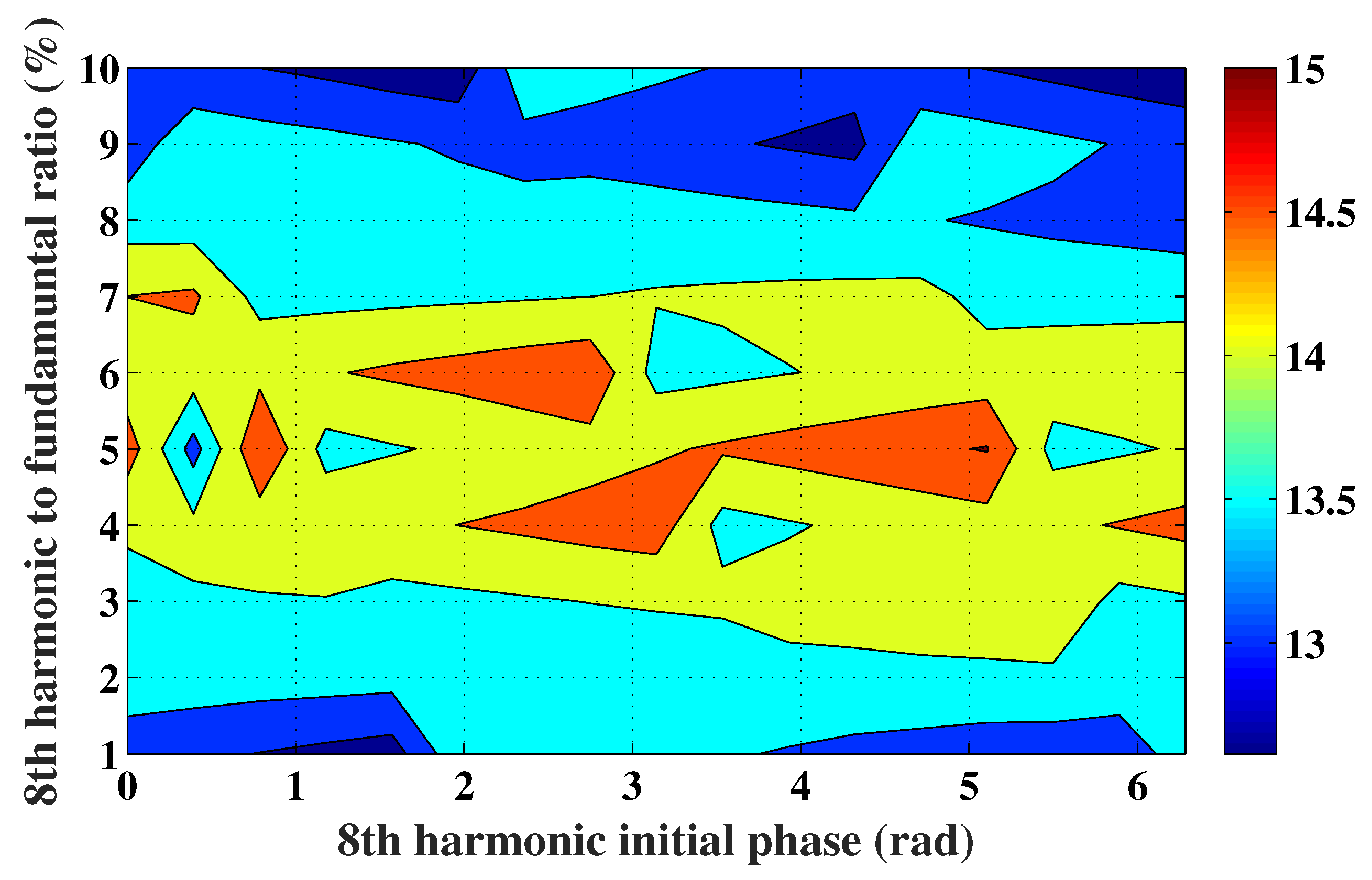
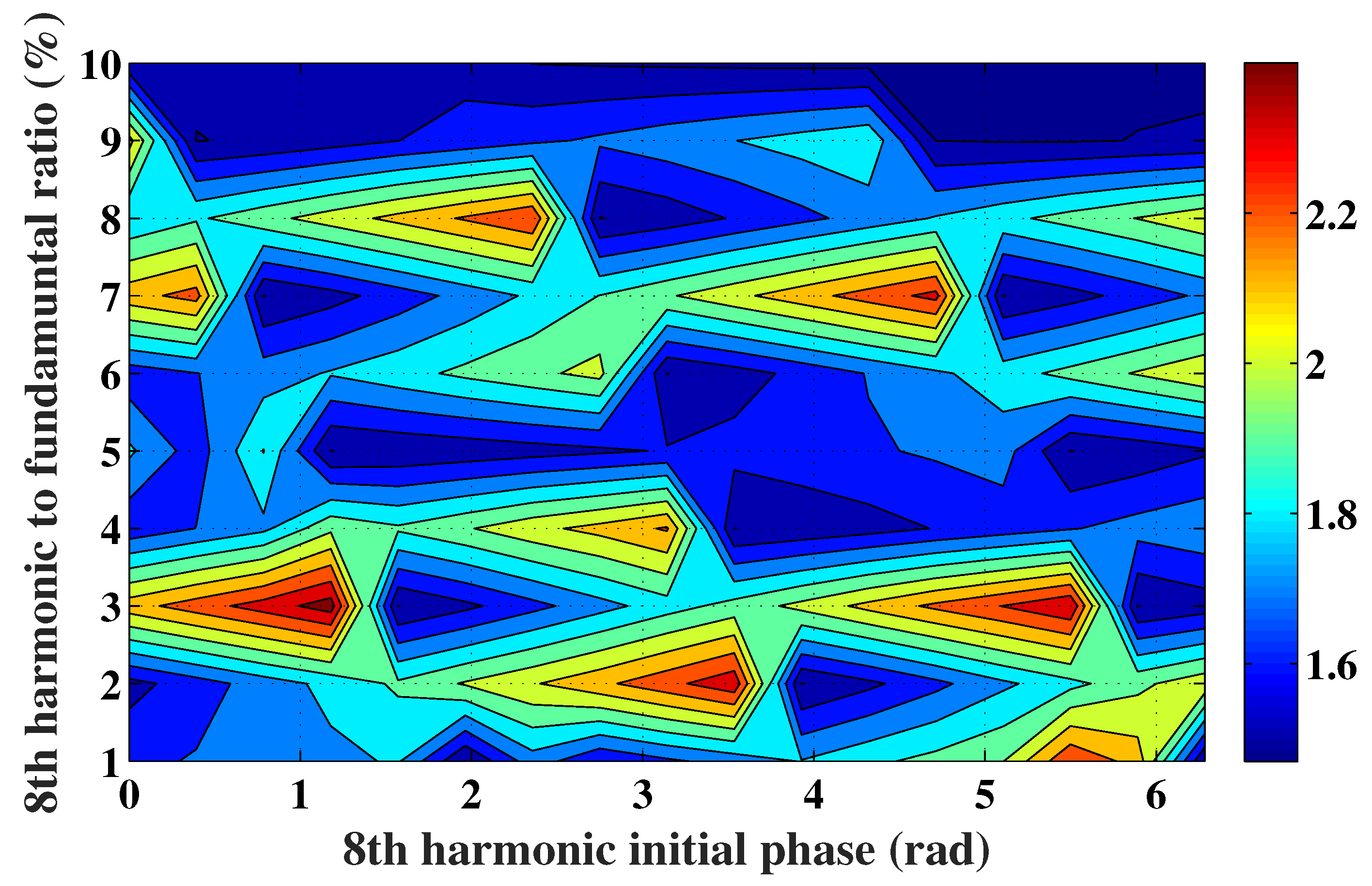
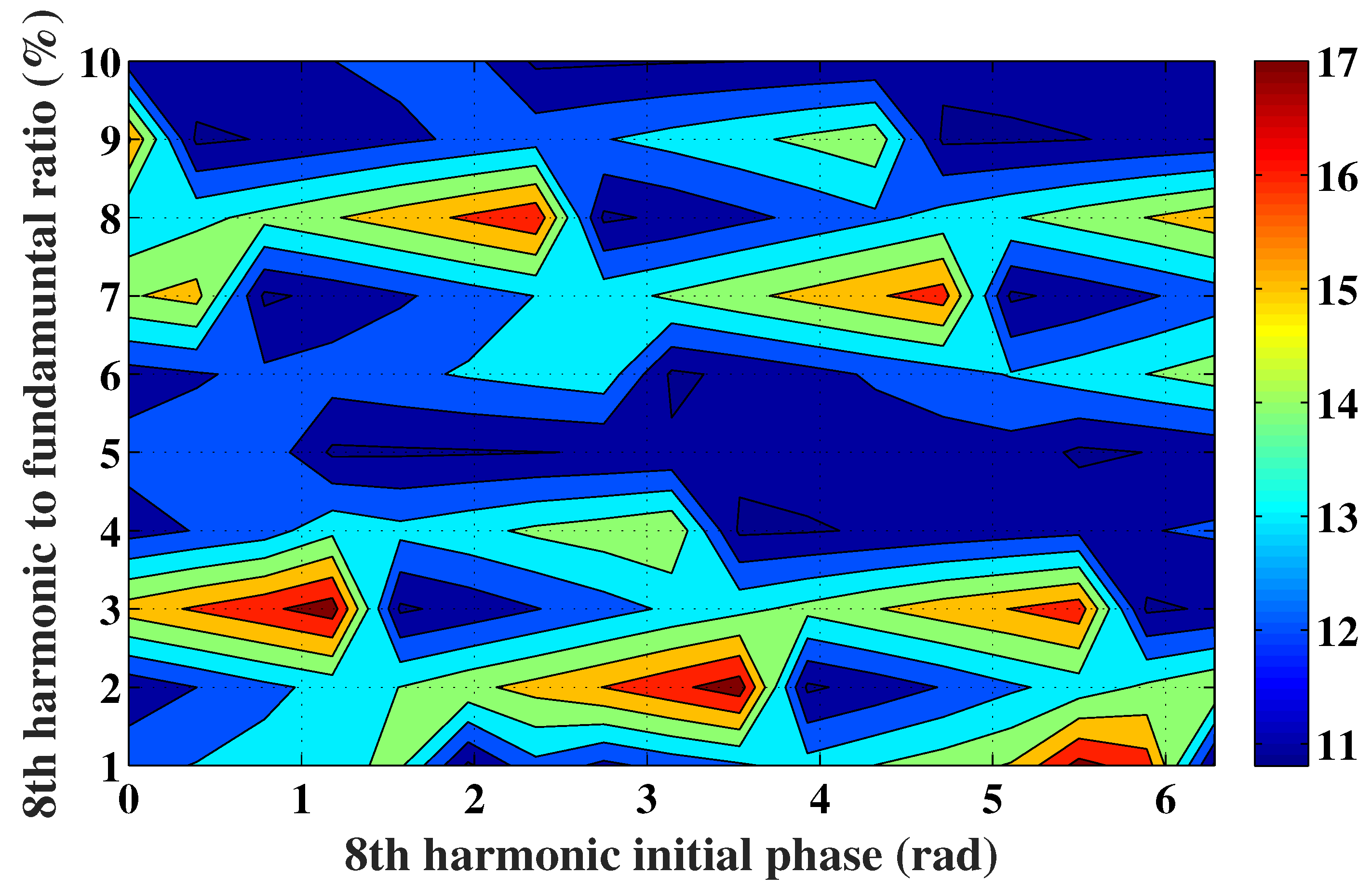
3.2.3. Torque Production Enhancement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rauch, S.E.; Johnson, L.J. Design principles of flux-switch alternators [includes discussion]. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1955, 74, 1261–1268. [Google Scholar] [CrossRef]
- Hua, W.; Cheng, M.; Zhu, Z.Q.; Howe, D. Analysis and optimization of back EMF waveform of a flux-switching permanent magnet motor. IEEE Trans. Energy Convers. 2008, 23, 727–733. [Google Scholar] [CrossRef]
- Gysen, B.L.J.; Ilhan, E.; Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. Modeling of flux switching permanent magnet machines with Fourier analysis. IEEE Trans. Magn. 2010, 46, 1499–1502. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wang, X.; Jung, S.-Y. Reduction on cogging torque in flux-switching permanent magnet machine by teeth notching schemes. IEEE Trans. Magn. 2012, 48, 4228–4231. [Google Scholar] [CrossRef]
- Yan, J.; Lin, H.; Feng, Y.; Zhu, Z.Q.; Jin, P.; Guo, Y. Cogging torque optimization of flux-switching transverse flux permanent magnet machine. IEEE Trans. Magn. 2013, 49, 2169–2172. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Zhu, Z.Q. Analysis of air-gap field modulation and magnetic gearing effects in switched flux permanent magnet machines. IEEE Trans. Magn. 2015, 51, 8105012. [Google Scholar] [CrossRef]
- Zeng, Z.; Shen, Y.; Lu, Q.; Gerada, D.; Wu, B.; Huang, X.; Gerada, C. Flux-density harmonics analysis of switched-flux permanent magnet machines. IEEE Trans. Magn. 2019, 55, 8103607. [Google Scholar] [CrossRef]
- Zhao, W.; Pan, X.; Ji, J.; Xu, L.; Zheng, J. Analysis of PM eddy current loss in four-phase fault-tolerant flux-switching permanent-magnet machines by air-gap magnetic field modulation theory. IEEE Trans. Ind. Electron. 2020, 67, 5369–5378. [Google Scholar] [CrossRef]
- Hu, J.; Liu, F.; Li, Y. An improved sub-domain model of flux switching permanent magnet machines considering harmonic analysis and slot shape. IEEE Access 2021, 9, 55260–55270. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, Y. Permanent magnet parameter design and performance analysis of bearingless flux switching permanent magnet motor. IEEE Trans. Ind. Electron. 2020, 68, 4153–4163. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, Z.Q.; Wang, C.; Hua, W.; Wang, K.; Zhang, W. Influence of rotor iron bridge position on DC-winding-induced voltage in wound field switched flux machine having partitioned stators. Chin. J. Electr. Eng. 2021, 7, 20–28. [Google Scholar] [CrossRef]
- Chen, C.; Ren, X.; Li, D.; Qu, R.; Liu, K.; Zou, T. Torque performance enhancement of flux-switching permanent magnet machines with dual sets of magnet arrangements. IEEE Trans. Transp. Electrif. 2021, 7, 2623–2634. [Google Scholar] [CrossRef]
- Bianchi, N.; Pre, M.D.; Bolognani, S. Design of a fault-tolerant IPM motor for electric power steering. IEEE Trans. Veh. Technol. 2006, 55, 1102–1111. [Google Scholar] [CrossRef]
- Saha, S.; Kim, S.-A.; Cho, Y.-H. Optimal Rotor shape design for minimizing cogging torque of spoke type BLAC motor for EPS. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 1313–1318. [Google Scholar]
- Liu, C.-T.; Hwang, C.-C.; Chiu, Y.-W. Design of a coaxially magnetic-geared linear actuator for electric power steering system applications. IEEE Trans. Ind. Appl. 2017, 53, 2401–2408. [Google Scholar] [CrossRef]
- Park, H.-J.; Lim, M.-S.; Lee, C.-S. Magnet shape design and verification for SPMSM of EPS system using cycloid curve. IEEE Access 2019, 7, 137207–137216. [Google Scholar] [CrossRef]
- Yang, H.; Ademi, S.; Paredes, J.; McMahon, R.A. Comparative study of motor topologies for electric power steering system. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021. [Google Scholar]
- Chaen, J.T.; Zhu, Z.Q. Winding configurations and optimal stator and rotor pole combination of flux-switching PM brushless AC Machines. IEEE Trans. Energy Convers. 2010, 25, 293–302. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Souissi, A.; Abdennadher, I. Analytical based enhancement of the torque production capability of flux switching PM machines. In Proceedings of the Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monaco, Monte-Carlo, 8–10 May 2019; pp. 1–6. [Google Scholar]





| Parameter | Symbol | Value |
|---|---|---|
| Number of phases | q | 3 |
| Number of stator slots | 12 | |
| Number of rotor slots | 10 | |
| Number of coils per phase | 4 | |
| Number of turns per coil | 120 | |
| PM remanence | 1.1 T | |
| PM relative permeability | 1.04457 | |
| PM width | 2.5 mm | |
| Stator outer radius | 67 mm | |
| Stator inner radius | 35.8 mm | |
| Stator slot radius | 59.7 mm | |
| Rotor outer radius | 35.3 mm | |
| Rotor slot radius | 34.8 mm | |
| Stack length | 100 mm | |
| Stator slot pitch | 30° | |
| Rotor slot pitch | 36° | |
| Stator tooth opening | 25.2° | |
| Stator slot opening | 4.8° | |
| Stator PM opening | 4° | |
| Rotor tooth opening | 16.92° |
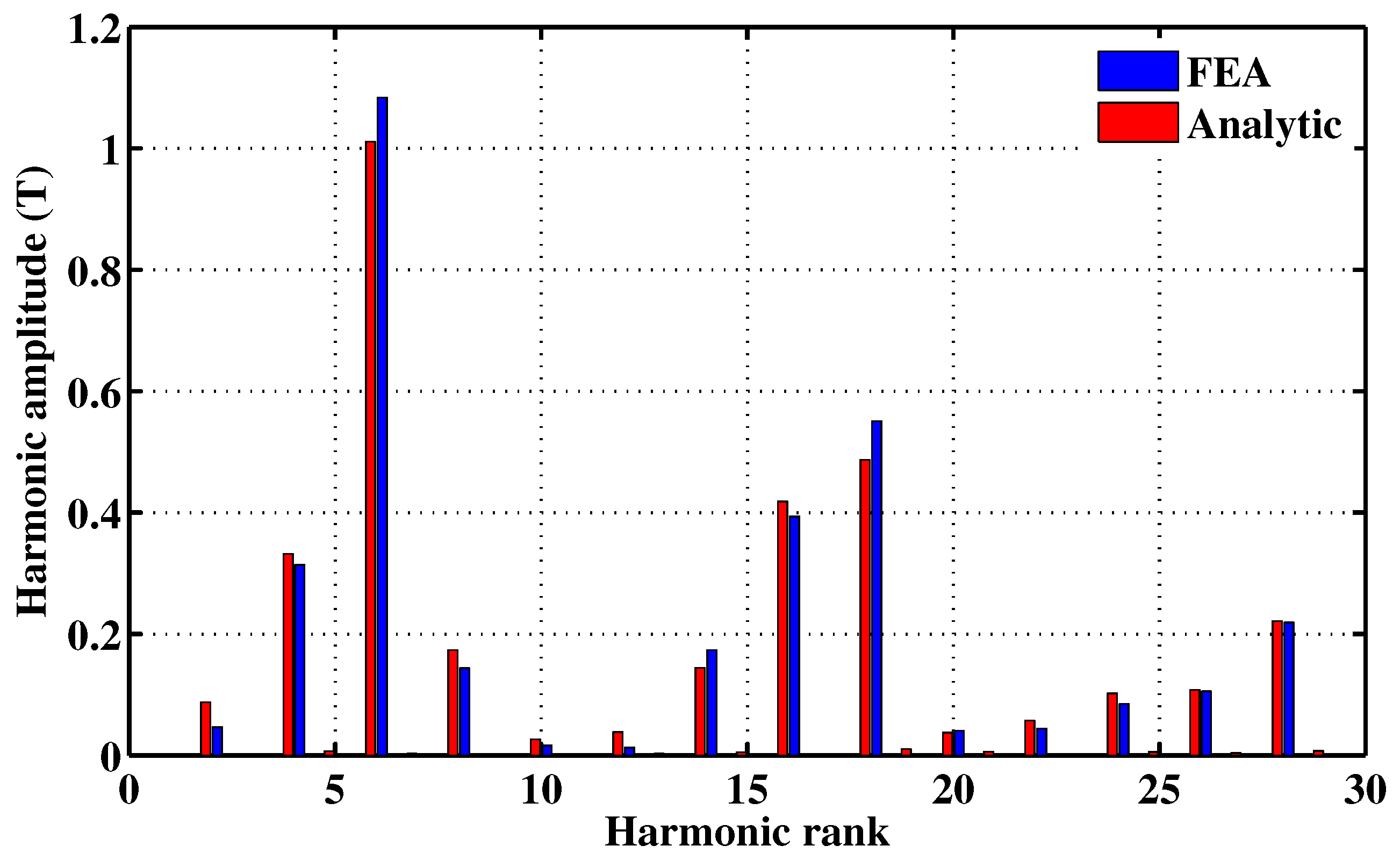
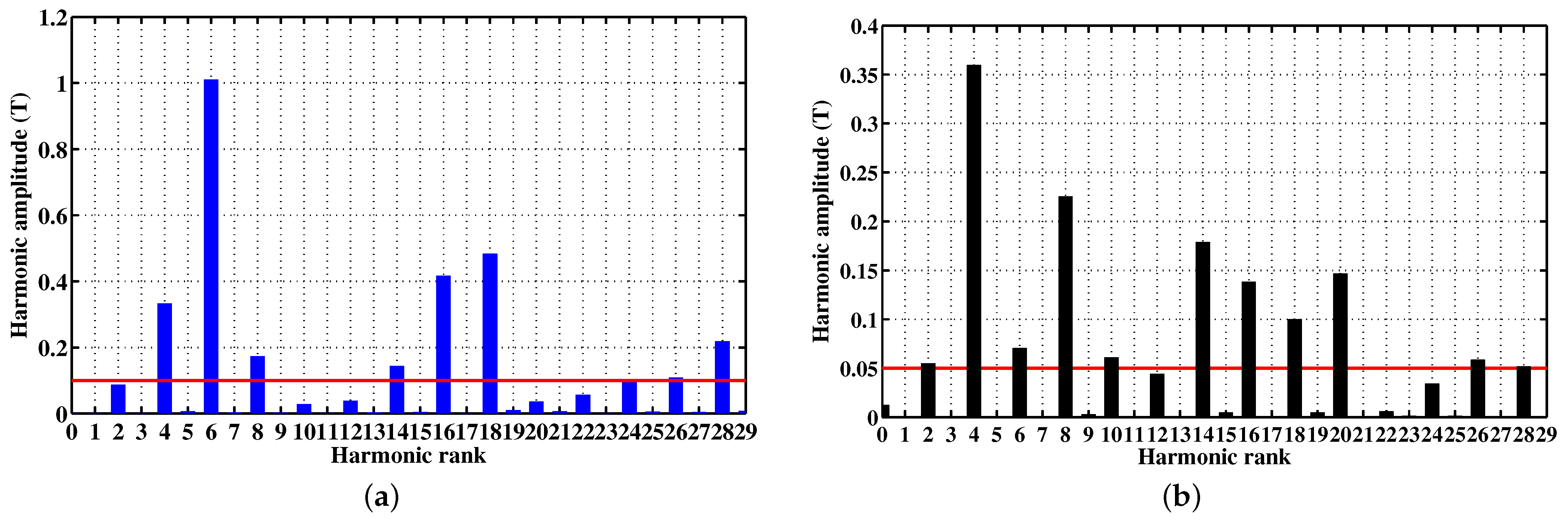
| RMF Dominant Harmonic Rank | PM Harmonic RMF Amplitude (T) | Rotation Direction | Armature Harmonic RMF Amplitude (T) | Rotation Direction |
|---|---|---|---|---|
| 4 | 0.33 | forward | 0.36 | forward |
| 6 | 1.01 | constant | 0.07 | static |
| 8 | 0.17 | backward | 0.23 | backward |
| 14 | 0.14 | forward | 0.18 | forward |
| 16 | 0.42 | forward | 0.14 | forward |
| 18 | 0.48 | constant | 0.1 | static |
| 28 | 0.22 | forward | 0.052 | forward |
| Analytic Torque | FEA Torque | |||
|---|---|---|---|---|
| Mean (Nm) | Ripple (%) | Mean (Nm) | Ripple (%) | |
| with injection of 8th harmonic | 15.2 | 6.9 | 15 | 11.9 |
| without injection of 8th harmonic | 13.9 | 7.5 | 13.8 | 10.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkefi, A.; Souissi, A.; Abdennadher, I.; Masmoudi, A. On the Analysis and Torque Enhancement of Flux-Switching Permanent Magnet Machines in Electric Power Steering Systems. World Electr. Veh. J. 2022, 13, 64. https://doi.org/10.3390/wevj13040064
Abdelkefi A, Souissi A, Abdennadher I, Masmoudi A. On the Analysis and Torque Enhancement of Flux-Switching Permanent Magnet Machines in Electric Power Steering Systems. World Electric Vehicle Journal. 2022; 13(4):64. https://doi.org/10.3390/wevj13040064
Chicago/Turabian StyleAbdelkefi, Anis, Amal Souissi, Imen Abdennadher, and Ahmed Masmoudi. 2022. "On the Analysis and Torque Enhancement of Flux-Switching Permanent Magnet Machines in Electric Power Steering Systems" World Electric Vehicle Journal 13, no. 4: 64. https://doi.org/10.3390/wevj13040064





