Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Data
2.2.1. Satellite Precipitation Products
2.2.2. Rain Gauge Data
2.3. Methodology
2.3.1. Spatial Downscaling Method
2.3.2. Evaluation Metrics
3. Results
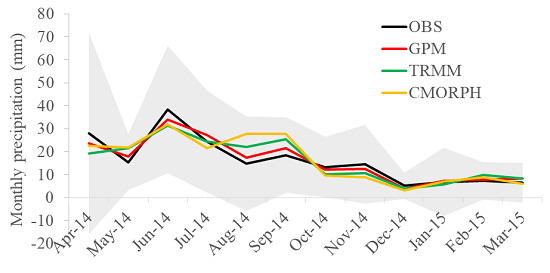
3.1. Accuracy in Describing Regional Precipitation
3.2. Accuracy in Describing Spatial Distribution of Precipitation
3.3. Elevation Impact Analyses
3.4. Contingency Statistics
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wheater, H.S.; Isham, V.S.; Cox, D.R.; Chandler, R.E.; Kakou, A.; Northrop, P.J.; Oh, L.; Onof, C.; Rodriguez-Iturbe, I. Spatial-temporal rainfall fields: Modelling and statistical aspects. Hydrol. Earth Syst. Sci. 2000, 4, 581–601. [Google Scholar] [CrossRef]
- Wilheit, T.T. Some comments on passive microwave measurement of rain. Bull. Am. Meteorol. Soc. 1986, 67, 1226–1232. [Google Scholar] [CrossRef]
- Boe, J.; Terray, L.; Cassou, C.; Najac, J. Uncertainties in european summer precipitation changes: Role of large scale circulation. Clim. Dyn. 2009, 33, 265–276. [Google Scholar] [CrossRef]
- Chung, C.T.; Power, S.B.; Arblaster, J.M.; Rashid, H.A.; Roff, G.L. Nonlinear precipitation response to el niño and global warming in the indo-pacific. Clim. Dyn. 2014, 42, 1837–1856. [Google Scholar] [CrossRef]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang. 2012, 112, 881–899. [Google Scholar] [CrossRef]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bohner, J. General climatic controls and topoclimatic variations in central and high Asia. Boreas 2006, 35, 279–295. [Google Scholar] [CrossRef]
- Domrös, M.; Peng, G. The Climate of China; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hu, Z.Y.; Hu, Q.; Zhang, C.; Chen, X.; Li, Q.X. Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in Central Asia. J. Geophys. Res. Atmos. 2016, 121, 5648–5663. [Google Scholar] [CrossRef]
- Schiemann, R.; Luthi, D.; Vidale, P.L.; Schar, C. The precipitation climate of Central Asia—Intercomparison of observational and numerical data sources in a remote semiarid region. Int. J. Climatol. 2008, 28, 295–314. [Google Scholar] [CrossRef]
- Lioubimtseva, E.; Cole, R. Uncertainties of climate change in arid environments of Central Asia. Rev. Fish. Sci. 2006, 14, 29–49. [Google Scholar] [CrossRef]
- Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol. 2005, 25, 693–712. [Google Scholar] [CrossRef] [Green Version]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Turk, F.J.; Miller, S.D. Toward improved characterization of remotely sensed precipitation regimes with modis/amsr-e blended data techniques. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1059–1069. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Su, F.G.; Gao, H.L.; Huffman, G.J.; Lettenmaier, D.P. Potential utility of the real-time TMPA-rt precipitation estimates in streamflow prediction. J. Hydrometeorol. 2011, 12, 444–455. [Google Scholar] [CrossRef]
- Xue, X.W.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based multi-satellite precipitation analysis over the wangchu basin of bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Yang, Y.F.; Luo, Y. Evaluating the performance of remote sensing precipitation products CMORPH, persiann, and TMPA, in the arid region of northwest China. Theor. Appl. Climatol. 2014, 118, 429–445. [Google Scholar] [CrossRef]
- Bellerby, T.J. Satellite rainfall uncertainty estimation using an artificial neural network. J. Hydrometeorol. 2007, 8, 1397–1412. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Habib, E. Accounting for uncertainties of the TRMM satellite estimates. Remote Sens. 2009, 1, 606–619. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N.; Bagtzoglou, A.C. On latin hypercube sampling for efficient uncertainty estimation of satellite rainfall observations in flood prediction. Comput. Geosci. 2006, 32, 776–792. [Google Scholar] [CrossRef]
- Duan, Y.; Wilson, A.M.; Barros, A.P. Scoping a field experiment: Error diagnostics of TRMM precipitation radar estimates in complex terrain as a basis for iphex2014. Hydrol. Earth Syst. Sci. 2015, 19, 1501–1520. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated multi-satellite retrievals for GPM (IMERG) technical documentation. NASA/GSFC Code 2015, 612, 47. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. Nasa global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. Version 2015, 4, 30. [Google Scholar]
- Liu, Z. Comparison of integrated multisatellite retrievals for GPM (IMERG) and TRMM multisatellite precipitation analysis (TMPA) monthly precipitation products: Initial results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Liu, C.T.; Zipser, E.J. The global distribution of largest, deepest, and most intense precipitation systems. Geophys. Res. Lett. 2015, 42, 3591–3595. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Zhang, L.; Win, K.W.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data-sparse mountainous watershed in myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Chen, F.R.; Li, X. Evaluation of IMERG and TRMM 3B43 monthly precipitation products over mainland China. Remote Sens. 2016, 8, 18. [Google Scholar] [CrossRef]
- Lu, X.; Wei, M.; Tang, G.; Zhang, Y. Evaluation and correction of the TRMM 3B43v7 and GPM 3IMERGM satellite precipitation products by use of ground-based data over Xinjiang, China. Environ. Earth Sci. 2018, 77, 209. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Tang, G.Q.; Long, D.; Yong, B.; Zhong, L.Z.; Wan, W.; Hong, Y. Similarity and error intercomparison of the GPM and its predecessor-TRMM multisatellite precipitation analysis using the best available hourly gauge network over the Tibetan Plateau. Remote Sens. 2016, 8, 17. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.Q.; Yang, L.; Hu, H.C.; Lu, H.; Hou, A.Z. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Wei, G.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, J.; Su, J. Evaluation of satellite-based precipitation products from IMERG V04A and V03D, CMORPH and TMPA with gauged rainfall in three climatologic zones in China. Remote Sens. 2017, 10, 30. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Z.; Shen, Y.; Zhang, S.; Shi, R. Evaluation of satellite rainfall estimates over the Chinese mainland. Remote Sens. 2014, 6, 11649–11672. [Google Scholar] [CrossRef]
- Zhao, T.; Yatagai, A. Evaluation of TRMM 3B42 product using a new gauge-based analysis of daily precipitation over China. Int. J. Climatol. 2014, 34, 2749–2762. [Google Scholar] [CrossRef]
- Kim, J.H.; Ou, M.L.; Park, J.D.; Morris, K.R.; Schwaller, M.R.; Wolff, D.B. Global precipitation measurement (GPM) ground validation (GV) prototype in the korean peninsula. J. Atmos. Ocean. Technol. 2014, 31, 1902–1921. [Google Scholar] [CrossRef]
- Golian, S.; Moazami, S.; Kirstetter, P.E.; Hong, Y. Evaluating the performance of merged multi-satellite precipitation products over a complex terrain. Water Resour. Manag. 2015, 29, 4885–4901. [Google Scholar] [CrossRef]
- Chen, X. Retrieval and Analysis of Evapotranspiration in Central Areas of Asia; China Meteorological News Pres: Beijing, China, 2012; p. 8. [Google Scholar]
- Duque, J.C.; Ramos, R.; Suriñach, J. Supervised regionalization methods: A survey. Int. Reg. Sci. Rev. 2007, 30, 195–220. [Google Scholar] [CrossRef] [Green Version]
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725–731. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.G.; Yang, D.Q.; Hao, Z.C. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.M.; Hu, J.J.; Gebregiorgis, A.S.; Xue, X.W.; Zhang, X.H. Inter-comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef]
- Huffman, G.; Adler, R.; Bolvin, D.; Nelkin, E. The TRMM Multi-Satellite Precipitation Analysis (TMPA). Chapter in Satellite Applications for Surface Hydrology; Hossain, F., Gebremichael, M., Eds.; Springer Verlag: Berlin/Heidelberg, Germany, 2009. Available online: ftp://meso.gsfc.nasa.gov/agnes/huffman/papers/TMPA_hydro_rev.pdf (accessed on 12 January 2017).
- GPM IMERG. Available online: https://pmm.nasa.gov/data-access/downloads/GPM (accessed on 12 January 2017).
- TRMM 3B42V7. Available online: https://pmm.nasa.gov/data-access/downloads/TRMM (accessed on 15 January 2017).
- CMORPH. Available online: https://rda.ucar.edu/datasets/ds502.0/ (accessed on 15 January 2017).
- Daily Precipitation Data. Available online: http://222.82.235.66/RadarDoc/WeatherService.aspx (accessed on 15 January 2017).
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Ren, Z.; Zhao, P.; Zhang, Q.; Zhang, Z.; Cao, L.; Yang, Y.; Zou, F.; Zhao, Y.; Zhao, H.; Chen, Z. Quality control procedures for hourly precipitation data from automatic weather stations in China. Meteorol. Mon. 2010, 36, 123–132. [Google Scholar]
- GPCC. Available online: https://kunden.dwd.de/GPCC/Visualizer (accessed on 17 January 2017).
- Blacutt, L.A.; Herdies, D.L.; de Goncalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and combined scheme datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef] [Green Version]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of precipitation forecast skill scores to bilinear interpolation and a simple nearest-neighbor average method on high-resolution verification grids. Weather Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A statistical topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical relationships between topography and precipitation patterns. J. Clim. 1994, 7, 1305–1315. [Google Scholar] [CrossRef]
- GTOPO30. Available online: http://eros.usgs.gov (accessed on 17 January 2017).
- Tian, Y.D.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114, 1–15. [Google Scholar] [CrossRef]
- El Kenawy, A.M.; Lopez-Moreno, J.I.; McCabe, M.F.; Vicente-Serrano, S.M. Evaluation of the TMPA-3B42 precipitation product using a high-density rain gauge network over complex terrain in northeastern Iberia. Glob. Planet. Chang. 2015, 133, 188–200. [Google Scholar] [CrossRef] [Green Version]
- Jenks, G.F.; Caspall, F.C. Error on choroplethic maps: Definition, measurement, reduction. Ann. Assoc. Am. Geogr. 1971, 61, 217–244. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M.; Dozier, J. Climatic and hydrologic changes in the Tien Shan, Central Asia. J. Clim. 1997, 10, 1393–1404. [Google Scholar] [CrossRef]
- Tang, H.; Micheels, A.; Eronen, J.T.; Ahrens, B.; Fortelius, M. Asynchronous responses of east Asian and indian summer monsoons to mountain uplift shown by regional climate modelling experiments. Clim. Dyn. 2013, 40, 1531–1549. [Google Scholar] [CrossRef]
- Baldwin, J.; Vecchi, G. Influence of the tian shan on arid extratropical Asia. J. Clim. 2016, 29, 5741–5762. [Google Scholar] [CrossRef]
- Bothe, O.; Fraedrich, K.; Zhu, X. Precipitation climate of Central Asia and the large-scale atmospheric circulation. Theor. Appl. Climatol. 2012, 108, 345–354. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM day-1 IMERG and TMPA version-7 legacy products over mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R. Validation of TRMM precipitation radar through comparison of its multiyear measurements with ground-based radar. J. Appl. Meteorol. Climatol. 2009, 48, 804–817. [Google Scholar] [CrossRef]
- Durden, S.L.; Haddad, Z.S.; Kitiyakara, A.; Li, F.K. Effects of nonuniform beam filling on rainfall retrieval for the TRMM precipitation radar. J. Atmos. Ocean. Technol. 1998, 15, 635–646. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Sorg, A.; Huss, M.; Rohrer, M.; Stoffel, M. The days of plenty might soon be over in glacierized Central Asian catchments. Environ. Res. Lett. 2014, 9, 104018. [Google Scholar] [CrossRef] [Green Version]
- Yin, G.; Chen, X.; Tiyip, T.; Shao, H.; Bai, L.; Hu, Z.; Zhang, C.; Xu, T. A comparison study between site-extrapolation-based and regional climate model-simulated climate datasets. Geogr. Res. 2015, 34, 631–643. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, W. Complex climatic and CO2 controls on net primary productivity of temperate dryland ecosystems over Central Asia during 1980–2014. J. Geophys. Res. Biogeosci. 2017, 122, 2356–2374. [Google Scholar] [CrossRef]







| Spatial/Temporal Resolutions | Temporal Extent | Coverage | Data Sources | |
|---|---|---|---|---|
| GPM IMERG | 0.1°/0.5 h | 2014–present | 60°N–60°N | [48] |
| TRMM 3B42V7 | 0.25°/3 h | 1998–2015 | 50°N–50°N | [49] |
| CMORPH | 0.07°/0.5 h | 2002–present | 60°N–60°N | [50] |
| Observations ≥ Threshold | Observations < Threshold | Total | |
|---|---|---|---|
| Estimates ≥ Threshold | H | F | Estimated yes |
| Estimates < Threshold | M | Z # | Estimated no |
| Total | Observed yes | Observed no | total |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. https://doi.org/10.3390/rs10101543
Zhang C, Chen X, Shao H, Chen S, Liu T, Chen C, Ding Q, Du H. Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sensing. 2018; 10(10):1543. https://doi.org/10.3390/rs10101543
Chicago/Turabian StyleZhang, Chi, Xi Chen, Hua Shao, Shuying Chen, Tong Liu, Chunbo Chen, Qian Ding, and Haoyang Du. 2018. "Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area" Remote Sensing 10, no. 10: 1543. https://doi.org/10.3390/rs10101543
APA StyleZhang, C., Chen, X., Shao, H., Chen, S., Liu, T., Chen, C., Ding, Q., & Du, H. (2018). Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sensing, 10(10), 1543. https://doi.org/10.3390/rs10101543