Extrinsic Calibration of 2D Laser Rangefinders Based on a Mobile Sphere
Abstract
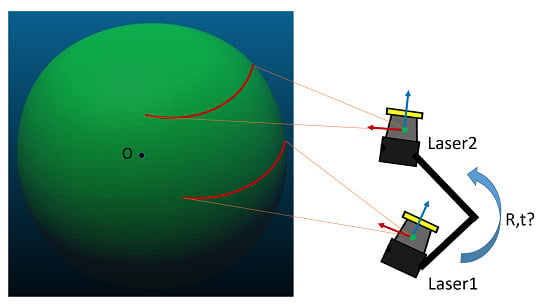
:1. Introduction
2. Calibration Approach
2.1. Calculation of the Spherical Center
2.1.1. Point Cloud Filtering
2.1.2. RANSAC Circle Model Fitting
2.1.3. Extrapolation of the Spherical Center
2.2. CP Matching
2.3. Calibration
2.3.1. Calibration Model
2.3.2. Solution of Equations
2.4. Processing Procedure
3. Experiments and Discussion
3.1. Data Introduction
3.2. Circle Model Fitting and the Distribution of CPs
3.3. Calibration and Analysis
3.4. Robustness and Accuracy Validation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Scanning Range Finder Utm-30lx Product Page. Available online: http://www.hokuyo-aut.jp/02sensor/07scanner/utm_30lx.html (accessed on 20 April 2018).
- Pouliot, N.; Richard, P.L.; Montambault, S. Linescout power line robot: Characterization of a utm-30lx lidar system for obstacle detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 24 December 2012; pp. 4327–4334. [Google Scholar]
- Demski, P.; Mikulski, M.; Koteras, R. Characterization of Hokuyo Utm-30lx Laser Range Finder for an Autonomous Mobile Robot; Springer: Heidelberg, Germany, 2013; pp. 143–153. [Google Scholar]
- Mader, D.; Westfeld, P.; Maas, H.G. An integrated flexible self-calibration approach for 2d laser scanning range finders applied to the Hokuyo utm-30lx-ew. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 5, 385–393. [Google Scholar] [CrossRef]
- Navvis Digitizing Indoors—Navvis. Available online: http://www.navvis.com (accessed on 20 April 2018).
- Google Cartographer Backpack. Available online: https://opensource.google.com/projects/cartographer (accessed on 20 April 2018).
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2d lidar slam. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Lehtola, V.V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.P. Comparison of the selected state-of-the-art 3d indoor scanning and point cloud generation methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Virtanen, J.P.; Kukko, A.; Kaartinen, H.; Hyyppä, H. Localization of mobile laser scanner using classical mechanics. ISPRS J. Photogramm. Remote Sens. 2015, 99, 25–29. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Loam: Lidar odometry and mapping in real-time. In Proceedings of the Robotics: Science and Systems Conference, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Fernández-Moral, E.; González-Jiménez, J.; Arevalo, V. Extrinsic calibration of 2d laser rangefinders from perpendicular plane observations. I. J. Robot. Res. 2015, 34, 1401–1417. [Google Scholar] [CrossRef]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the Intelligent Vehicles Symposium, Baden-Baden, Germany, 5–9 June 2011; pp. 163–168. [Google Scholar]
- Miller, I.; Campbell, M.; Huttenlocher, D. Efficient unbiased tracking of multiple dynamic obstacles under large viewpoint changes. IEEE Trans. Robot. 2011, 27, 29–46. [Google Scholar] [CrossRef]
- Leonard, J.; How, J.; Teller, S.; Berger, M.; Campbell, S.; Fiore, G.; Fletcher, L.; Frazzoli, E.; Huang, A.; Karaman, S. A perception-driven autonomous urban vehicle. J. Field Robot. 2008, 25, 727–774. [Google Scholar] [CrossRef] [Green Version]
- Huang, A.S.; Antone, M.; Olson, E.; Fletcher, L.; Moore, D.; Teller, S.; Leonard, J. A high-rate, heterogeneous data set from the darpa urban challenge. Int. J. Robot. Res. 2010, 29, 1595–1601. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Spletzer, J.R. On-line calibration of multiple lidars on a mobile vehicle platform. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 279–284. [Google Scholar]
- Underwood, J.; Hill, A.; Scheding, S. Calibration of range sensor pose on mobile platforms. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3866–3871. [Google Scholar]
- Pereira, M.; Silva, D.; Santos, V.; Dias, P. Self calibration of multiple lidars and cameras on autonomous vehicles. Robot. Auton. Syst. 2016, 83, 326–337. [Google Scholar] [CrossRef]
- Pcl Turorials: Filtering a Pointcloud Using a Passthrough Filter. Available online: http://www.pointclouds.org/documentation/tutorials/passthrough.php#passthrough (accessed on 15 June 2018).
- Meng, Y.; Zhang, H. Registration of point clouds using sample-sphere and adaptive distance restriction. Vis. Comput. 2011, 27, 543–553. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography; ACM: New York, NY, USA, 1981; pp. 726–740. [Google Scholar]
- Draper, D. Assessment and propagation of model uncertainty. J. R. Stat. Soc. 1995, 57, 45–97. [Google Scholar]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A 1987, 5, 1127–1135. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-d point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [PubMed]
- Barfoot, T.D. A matrix lie group approach. In State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Hassani, S. Representation of Lie Groups and Lie Algebras; Springer International Publishing: Basel, Switzerland, 2013; pp. 953–985. [Google Scholar]
- Varadarajan, V.S. Lie Groups, Lie Algebras, and Their Representations; Springer: New York, NY, USA, 1974. [Google Scholar]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef]
- Jiang, G.W.; Wang, J.; Zhang, R. A close-form solution of absolute orientation using unit quaternions. J. Zhengzhou Inst. Surv. Mapp. 2007, 3, 193–195. [Google Scholar]
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. Icp registration using invariant features. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 90–102. [Google Scholar] [CrossRef]
- Du, L.; Zhang, H.; Zhou, Q.; Wang, R. Correlation of coordinate transformation parameters. Geod. Geodyn. 2012, 3, 34–38. [Google Scholar]
- Wang, X.; Liu, D.; Zhang, Q.; Huang, H. The iteration by correcting characteristic value and its application in surveying data processing. J. Heilongjiang Inst. Technol. 2001, 15, 3–6. [Google Scholar]
- Vosselman, G.; Maas, H.G. Airborne and Terrestrial Laser Scanning. International Journal of Digital Earth. 2010, 4, 183–184. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of the Residential Interior Decoration; China Architecture & Building Press: Beijing, China, 2015.












| Item | Technology Performance |
|---|---|
| Measurement Principle | Time of Flight |
| Light Source | Laser Semiconductor λ = 905 nm Laser Class 1 |
| Detection Range | Guaranteed Range: 0.1~30 m (White Kent Sheet) Maximum Range: 0.1~60 m |
| Detection Object | Minimum Detectable Width at 10 m: 130 mm (varies with distance) |
| Measurement Resolution | 1 mm |
| Intrinsic Accuracy(Precision) | 0.1–10 m: σ < 10 mm 10–30 m: σ < 30 mm (White Kent Sheet) Under 3000 lx: σ < 10 mm (White Kent Sheet up to 10 m) Under 100,000 lx: σ < 30 mm (White Kent Sheet up to 10 m) |
| Scan Angle | 270° |
| Angular Resolution | 0.25° (360°/1440) |
| Scan Speed | 25 ms (motor speed: 2400 rpm) |
| Sensor | Intrinsic Accuracy (mm) | Absolute Mean Error (mm) | Standard Deviation (mm) | ||
|---|---|---|---|---|---|
| Previous Solution | Sick LMS151 | 12 | (0, 1) | 68 | 34 |
| Our Solution | Hokuyo UTM-30LX | 10 | (0, ) | 12 | 14 |
| Subset | CP Pairs | RMS (m) | Mean (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | Euclidean Metric | X | Y | Z | Euclidean Metric | |||
| 1st | 308 | (0, 1) | 0.0147 | 0.0119 | 0.0171 | 0.0255 | 2 × 108 | 7 × 109 | 5 × 108 | 0.0213 |
| 2nd | 178 | (0, ) | 0.0092 | 0.0086 | 0.0060 | 0.0140 | 2 × 107 | 1 × 107 | −3 × 108 | 0.0121 |
| Dataset | Point | RMS (m) | Mean (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | Number | X | Y | Z | Euclidean Metric | X | Y | Z | Euclidean Metric | |
| 1 | Training | 99 | 0.0102 | 0.0087 | 0.0063 | 0.0148 | −2.9 × 10−8 | −3.5 × 10−9 | −6.2 × 10−9 | 0.0129 |
| Test | 98 | 0.0090 | 0.0087 | 0.0071 | 0.0144 | 3.0 × 10−4 | −4.0 × 10−4 | −9.0 × 10−4 | 0.0123 | |
| 2 | Training | 814 | 0.0061 | 0.0118 | 0.0054 | 0.0144 | −7.1 × 10−9 | −2.4 × 10−7 | −2.7 × 10−7 | 0.0130 |
| Test | 814 | 0.0059 | 0.0123 | 0.0053 | 0.0147 | −1.4 × 10−4 | 2.4 × 10−4 | 1.4 × 10−4 | 0.0133 | |
| 3 | Training | 755 | 0.0058 | 0.0112 | 0.0050 | 0.0135 | 1.5 × 10−8 | −7.6 × 10−9 | −2.2 × 10−8 | 0.0120 |
| Test | 755 | 0.0062 | 0.0150 | 0.0052 | 0.0141 | 3.3 × 10−4 | −4.8 × 10−4 | −1.9 × 10−4 | 0.0125 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Liu, J.; Wu, T.; Huang, W.; Liu, K.; Yin, D.; Liang, X.; Hyyppä, J.; Chen, R. Extrinsic Calibration of 2D Laser Rangefinders Based on a Mobile Sphere. Remote Sens. 2018, 10, 1176. https://doi.org/10.3390/rs10081176
Chen S, Liu J, Wu T, Huang W, Liu K, Yin D, Liang X, Hyyppä J, Chen R. Extrinsic Calibration of 2D Laser Rangefinders Based on a Mobile Sphere. Remote Sensing. 2018; 10(8):1176. https://doi.org/10.3390/rs10081176
Chicago/Turabian StyleChen, Shoubin, Jingbin Liu, Teng Wu, Wenchao Huang, Keke Liu, Deyu Yin, Xinlian Liang, Juha Hyyppä, and Ruizhi Chen. 2018. "Extrinsic Calibration of 2D Laser Rangefinders Based on a Mobile Sphere" Remote Sensing 10, no. 8: 1176. https://doi.org/10.3390/rs10081176