A Review of Ten-Year Advances of Multi-Baseline SAR Interferometry Using TerraSAR-X Data

Abstract

Since its launch in 2007, TerraSAR-X has continuously provided spaceborne synthetic aperture radar (SAR) images of our planet with unprecedented spatial resolution, geodetic, and geometric accuracy. This has brought life to the once inscrutable SAR images, which deterred many researchers. Thanks to merits like higher spatial resolution and more precise orbit control, we are now able to indicate individual buildings, even individual floors, to pinpoint targets within centimeter accuracy. As a result, multi-baseline SAR interferometric (InSAR) techniques are flourishing, from point target-based algorithms, to coherent stacking techniques, to absolute positioning of the former techniques. This article reviews the recent advances of multi-baseline InSAR techniques using TerraSAR-X images. Particular focus was put on our own development of persistent scatterer interferometry, SAR tomography, robust estimation in distributed scatterer interferometry and absolute positioning using geodetic InSAR. Furthermore, by introducing the applications associated with these techniques, such as 3D reconstruction and deformation monitoring, this article is also intended to give guidance to wider audiences who would like to resort to SAR data and related techniques for their applications.

1. Introduction

1.1. Overview of Multi-Baseline InSAR

Since its launch in 2007, TerraSAR-X has continuously revealed synthetic aperture radar (SAR) images of unprecedented high resolution from space. This has brought life to the once obscure and sometimes inscrutable SAR images that deterred many researchers. Figure 1 shows a comparison of the medium resolution ERS image and a high resolution TerraSAR-X spotlight image of the same area in Las Vegas. Individual buildings are for the first time interpretable by the naked eye from spaceborne SAR images, because the 1-m resolution in spotlight mode is well beyond the inherent scale of the 3-m floor height typical of urban infrastructure. This marks the start of an era of urban infrastructure monitoring using spaceborne SAR images. Currently, the staring spotlight mode provides images with a resolution up to 25 cm, from which the mapping of individual window edges is even possible. This breakthrough in spatial resolution, together with the precise orbit determination with sub-centimeter accuracy [1,2], positions TerraSAR-X images as a perfect dataset for long-term repeated monitoring of large areas with precision and high resolution.

Among the many promising InSAR techniques that prospered in the past decade, multi-baseline, especially multi-pass, InSAR techniques are undoubtedly one of the jewels in the crown. They build up invaluable data cubes of long-term image time series. For example, the TerraSAR-X revisit time of 11 days allows monthly deformation signals of the Earth’s surface, such as ground subsidence, to be retrieved using techniques like persistent scatterer interferometry (PSI). For monitoring dense urban areas, SAR tomography (TomoSAR) and its differential form, D-TomoSAR inversion, are the most competent techniques because of their capability of layover separation. They generate point clouds with density comparable to that of a LiDAR. Both PSI and TomoSAR produce highly accurate parameter estimates, because they work on highly coherent point targets. Therefore, they are often the workhorses for deformation monitoring and 3D reconstruction, especially in urban areas. To complement these techniques, distributed scatterer (DS)-based techniques, such as SqueeSAR [4], robust InSAR optimization (RIO) [5] and coherence tomography enable dense monitoring of deformation in areas of low interferometric coherence, such as volcanic areas. Among them, some algorithms, such as RIO, address the statistical robustness of estimators to ensure the reliability of the accuracy of the estimates in operational processing over large areas. Despite the many advantages of multi-baseline InSAR, they are still relative measures, as the estimates are often relative to a local reference point whose 3D position is unknown. Such differential operation is often performed in multi-baseline InSAR in order to mitigate some common phase errors, such as atmospheric delay. It was only until recently, that geodetic InSAR [6] bridged the gap between multi-baseline InSAR techniques and absolute positioning using SAR imaging geodesy [7] to produce absolute 3D (and higher dimensional) InSAR point clouds. It is an important piece of the components of the ecosystem of Earth observation using SAR data. Multi-baseline InSAR techniques that were once only a relative measure can now be employed as geodetic techniques to provide centimeter-level absolute positioning and millimeter-level relative deformation monitoring.

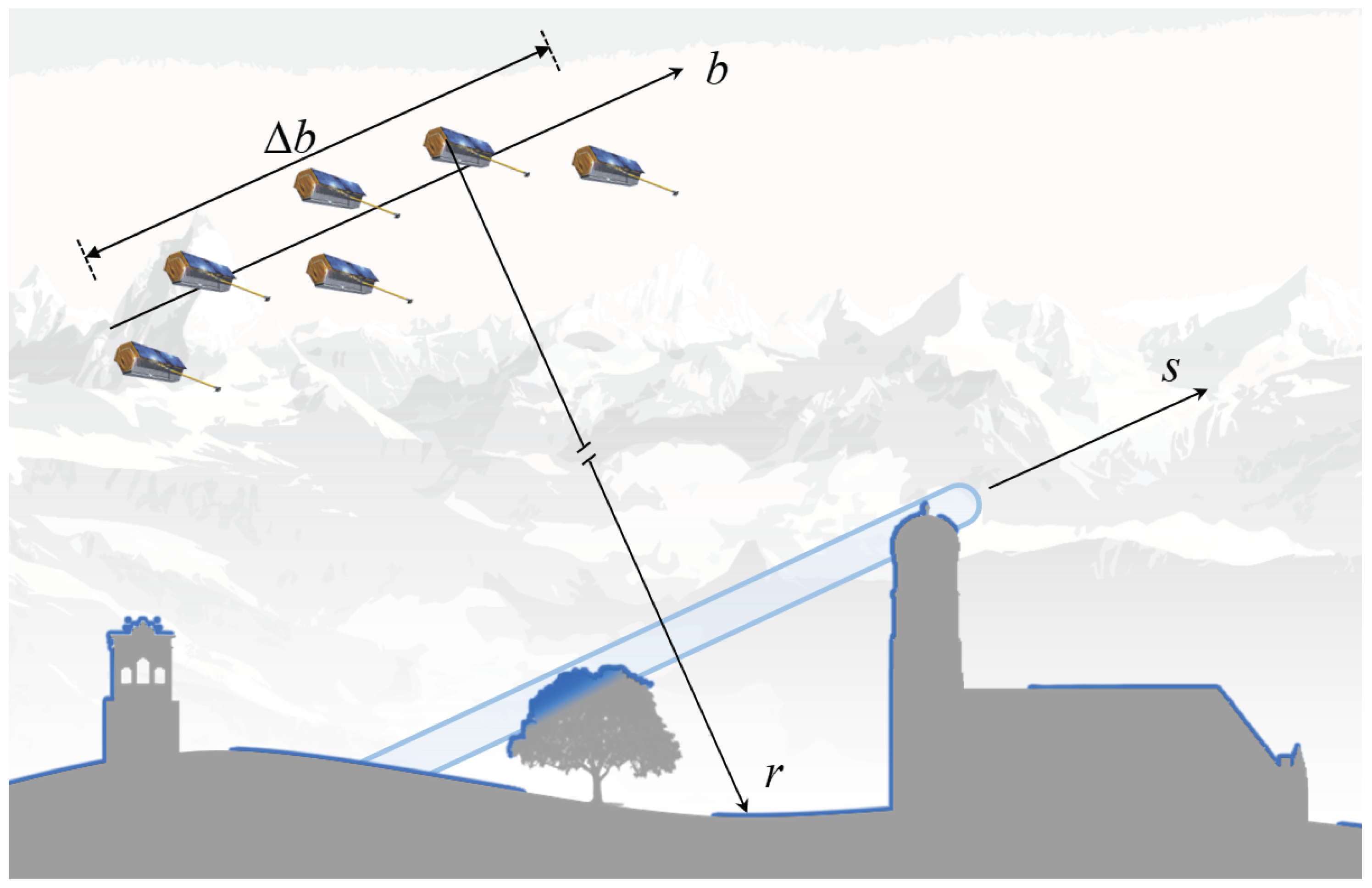
1.2. Principle of Multi-Baseline InSAR

InSAR is the technique of using SAR as an interferometer. Multi-baseline InSAR techniques exploit the interferometric phase (i.e., the phase difference) of multiple complex-valued SAR images. These images are acquired at different satellite positions, time, or frequency, and hence, they create spatial, temporal baselines, or $\Delta$k-radar when forming interferograms. For TerraSAR-X images, such multi-baseline configuration is usually acquired in a repeat-pass manner (hence “multi-pass”), except if the twin satellite TanDEM-X was employed. Figure 2 shows the multi-baseline InSAR configuration in an urban scenario at a fixed azimuth position. The TerraSAR-X satellite flies perpendicular into the screen/paper. The term r indicates the line of sight (LOS), i.e., the slant range direction, of the sensor; s is the elevation direction that is perpendicular to the range and azimuth. The blue outline on the surface indicates the area illuminated by radar pulses. The elongated ellipse is the range-elevation tube within which all the objects are imaged into a single pixel in the focused SAR image. The cross-section of the tube naturally depends on the range and azimuth resolution of the sensor. The extent of the tube $\Delta s$ is much larger than the dimension of the cross-section because of the large distance between the sensor and the object, as well as the small angular diversity among different acquisitions. Therefore, it is common that several objects, such as a building roof, tree and ground, are layovered in a single pixel in a TerraSAR-X image.

If one considers a single phase center in the range-azimuth-elevation tube without layover (i.e., single scatterer model), the absolute interferometric phase of the n-th measurement in a multi-baseline InSAR stack is [9]:

$${\varphi }_n=-\frac{4\pi }{\lambda }\frac{b_{n}s}{R}+{\varphi }_{defo}+{\varphi }_{atmo}+{\varphi }_{error},$$

(1)

where $\lambda$ is the wavelength of the SAR electromagnetic wave, $b_n$ is the baseline of the n-th image, s is the elevation of the single scatterer and R is the nominal range which is the distance of the SAR sensor to a zero-elevation point. The deformation phase ${\varphi }_{defo}$ is often modeled as a function $d\left(t_n\right)$ (e.g., linear or periodic) of the acquisition time $t_n$. The interferometric phase is always delayed due to atmospheric propagation. In multi-baseline InSAR, such atmospheric phase delay ${\varphi }_{atmo}$ is mitigated by subtracting a nearby reference point. This renders multi-baseline InSAR a relative measure, unless the absolute position of the reference point is known a priori.

Based on Equation (1), the forward system model of multi-baseline InSAR measurement can be expressed as Equation (2), where $g_n$ is the pixel value at the n-th image, and $\gamma \left(s\right)$ is the reflectivity profile along the elevation direction. Since a far-field antenna acts like a Fourier transform to the signal in the resolution cell, each measurement is actually the Fourier transform at a specific frequency that is linearly proportional to the perpendicular baseline $b_n$ to the master satellite position. This is also known as the system model for TomoSAR [10,11,12,13].

$$g_n=\underset{\Delta s}{\int }\gamma \left(s\right)exp\left(-j\frac{4\pi b_n}{\lambda R}s\right)ds.$$

(2)

In the case of differential TomoSAR (D-TomoSAR), Equation (2) is extended into higher dimensions [14,15,16].

Equation (2) can be written in a more compact matrix form as:

$$\mathbf{g}=\mathbf{R}\mathsf{\gamma },$$

(3)

where $\mathbf{R}$ and $\mathsf{\gamma }$ are the discretized Fourier matrix and the reflectivity profile along the direction s, respectively. Estimating $\mathsf{\gamma }$ is essentially a spectral estimation problem. In the case of PSI- or DS-based interferometry that assumes a single phase center in the resolution cell, it is basically a spectral estimation of a single frequency. Equation (3) will degenerate to either Equation (4) for the deterministic PS mode or Equation (5) for the stochastic DS model.

$$\mathbf{g}=\mathbf{r}\left(s_1\right){\gamma }_1,$$

(4)

$$E\left(\mathbf{g}{\mathbf{g}}^H\right)=\mathbf{r}\left(s_1\right){\mathbf{C}}_{\mathbf{g}\mathbf{g}}\mathbf{r}{\left(s_1\right)}^H,$$

(5)

where $s_1$ is the elevation of the single phase center, $\mathbf{r}\left(s_1\right)$ is the column in $\mathbf{R}$ associated with $s_1$, ${\gamma }_1$ is the complex-valued brightness of the PS and ${\mathbf{C}}_{\mathbf{g}\mathbf{g}}$ is the covariance matrix of the DS.

1.3. The Structure of This Paper

The rest of this article introduces the recent development of the aforementioned techniques, each in its respective section. In Section 2, we introduce the development of PS-based methods following their improvements in estimates accuracy that in turn refers to the reconstructed point density, as well as the reduction of the required number of images for a reliable estimation. Section 3 focuses on the development of robust InSAR techniques based on DS. Section 4 focuses on the evolution of TerraSAR-X absolute positioning from a single target to many targets and eventually to the fusion with multi-baseline InSAR.

2. Advances in Point Scatterer-Based Methods

This section focuses on the advances of PS-based methods, i.e., PSI and TomoSAR/D-TomoSAR in urban areas. Their development mainly focuses on the improvement of estimation accuracy, which in turn increases the density of the retrieved point cloud or reduces the number of interferograms required for a reliable estimation.

Both PSI and TomoSAR utilize a single-master configuration to extract time-coherent scatterers from SAR images. The major difference between the two methods is the number of scatterers that are assumed within a resolution cell, which requires different spectral estimators to be employed in the parameter retrieval. However, over the past two decades, PSI has made substantial development, so that it usually refers to a full processing chain including interferogram formation and reference network construction. Therefore, PSI is often employed as a preprocessing step for TomoSAR. Several variations of PSI that differ in algorithmic details have been introduced in recent years. For a full review of these techniques the reader is referred to [17]. Although the specifics of existing PSI algorithms are different, the following workflow is widely acknowledged:

Step 1

Differential interferogram formation: From a stack of $N+1$ co-registered SAR images, a master acquisition is selected. Subsequently N interferograms are computed, while their topographic phase components are removed using a reference digital elevation model (DEM).

Step 2

Reference network construction: Scatterers presumed to be the most phase-stable ones are selected. The detection can be carried out using various methods, such as thresholding on the amplitude dispersion index (ADI) [18] or on the signal-to-clutter ratio (SCR) [19]. These PS candidates are connected to form a reference network. Through the PS double-difference phase measurements, i.e., difference in time and space, differential topography and differential motion parameters are estimated on arcs.

Step 3

Atmospheric phase estimation: The differential topography estimates are integrated with respect to an arbitrarily chosen reference point so that the topographic phase components are removed from the interferometric phases. The remaining phase contributions include deformation, atmosphere, and noise. Then a low-pass filtering in the spatial domain and a high-pass filtering in the temporal domain extracts the atmospheric component, which is interpolated over the entire scene and subtracted from the differential interferograms.

Step 4

PS densification: Additional PS are computed from the corrected differential interferograms. These PS are connected to the nearest point(s) in the reference network and their modeled parameters are estimated.

Step 5

PS geocoding: The DEM height of each PS is added to its differential height estimate. The radar timing of each PS and its updated height are geocoded using satellite orbit and a reference ellipsoid to represent the PS coordinates in a common geodetic coordinate system.

The processing steps for TomoSAR are similar to those of PSI, except the fourth step is replaced with higher-order spectral estimators that can be enumerated as followings.

• The full reflectivity profile is reconstructed using higher-order spectral estimation techniques.
• The scatterers’ positions and motion parameters are determined by detecting maxima on the reflectivity profile.

2.1. Overview of Advances

For each of the steps delineated above, numerous improvements have been suggested in the literature. For example, in the reference network step, [20,21] consider the geometry of the connections among arcs to construct a redundant reference network, while dense differential PS pairs were used in [22] to form the network. In terms of network inversion, to robustly retrieve the topography and deformation estimates of the PS in the reference network, a ${\ell }_1$ norm outlier rejection scheme was proposed after the LAMBDA estimation [23]. In [24,25], numerical weather data were used to simulate and mitigate tropospheric delay. For a detailed comparison of widely used PSI techniques, the interested reader is referred to [21].

The development of TomoSAR has been mainly focused on the improvement of the spectral estimator and the scatterer detector. Studies have been conducted to improve the maximum likelihood estimator (MLE) by restricting the support of the signal (i.e., nonlinear least square) [3,13], by ${\ell }_2$ norm regularization (i.e., the Tikhonov method) [15], and by ${\ell }_1$ norm regularization (i.e., compressive sensing-based method) [26,27]. The SL1MMER algorithm proposed in [27] was also recently extended to the M-SL1MMER [28], which exploits group sparsity in the urban environment. M-SL1MMER achieves a comparable result with far fewer images than SL1MMER and other algorithms. Several studies have also addressed the efficiency and robustness of the detection of scatterers. For example, [29] describes the optimal detection of multiple scatterers, and [27,30,31,32] address scatterer detection in the super-resolution regime where the distance among scatterers is less than the elevation resolution.

In general, TomoSAR is so far the most competent multi-baseline InSAR method for urban area monitoring. However, the relatively high computational cost limits it for extensive uses like PSI, especially for the CS-based TomoSAR algorithms. Therefore, combining PSI and TomoSAR has also been proposed to improve the computational efficiency of TomoSAR processing [22,33,34]. Only recently, an efficient sparse recovery algorithm was proposed, which made city-scale 3D/4D reconstruction directly using SL1MMER operational [35].

2.2. Very High Resolution PSI

PSI is undoubtedly the workhorse for deformation monitoring of large areas, owing to its computational efficiency and reliability in the accuracy of the deformation estimates. As mentioned earlier, estimating the unknown elevation and deformation parameters in PSI is a spectral estimation of a single frequency. The spectral estimator is essentially a periodogram that can be expressed as follows.

$$\widehat{\mathsf{\theta }}=\underset{\mathsf{\theta }}{argmax}\left\{\left|\frac{1}{N}\sum _{n=1}^N{g}_{n}exp\left(-j{\varphi }_n\left(\mathsf{\theta }\right)\right)\right|\right\}\approx \underset{\mathsf{\theta }}{argmax}\left\{\left|\frac{1}{N}\sum _{n=1}^N\frac{g_n}{\left|g_n\right|}exp\left(-j{\varphi }_n\left(\mathsf{\theta }\right)\right)\right|\right\},$$

(6)

where $\mathsf{\theta }$ denotes the parameters, including the elevation s and the deformation parameters, and ${\varphi }_n\left(\mathsf{\theta }\right)$ is the modeled phase of the PS in the n-th image (i.e., Equation (1)). Often, the amplitude of $\mathbf{g}$ is dropped in the estimation [18], since it barely changes the estimates for PS of high signal-to-noise ratio (SNR).

Employing very high resolution (VHR) PSI, it is now possible to detect very localized deformation patterns even on different parts of a single building [36]. Apart from its deformation monitoring capability, VHR PSI leads to detailed 3D reconstruction of urban areas owing to the high density PSI point clouds. It can typically produce 40,000 to 100,000 PS per square kilometer using TerraSAR-X high resolution spotlight images [37,38]. The 3D reconstruction capability has even been strengthened by the geometrical fusion of PSI point clouds obtained from different viewing geometries, i.e., along-heading and cross-heading orbits [39]. Especially in the case of cross-heading orbits, that is, the combination of point clouds from ascending and descending orbits, point cloud fusion provides a shadow-free point cloud of the observed area. It also allows a decomposition of the raw LOS PSI deformation measurements into 3D displacement vectors in geodetic coordinate system [36,40,41].

2.3. Differential TomoSAR

Unlike PSI, D-TomoSAR retrieves the full reflectivity profile $\mathsf{\gamma }$, and detects prominent peaks from it. Therefore, D-TomoSAR is inherently a more competent method for urban area monitoring than PSI. The MLE (under complex Gaussian noise) of $\mathsf{\gamma }$ can be expressed as follows.

$${\widehat{\mathsf{\gamma }}}_{MLE}=\underset{\mathsf{\gamma }}{argmin}\frac{1}{2}{∥\mathbf{g}-\mathbf{R}\mathsf{\gamma }∥}_2^2.$$

(7)

During the last decade, we have developed a suite of algorithms named Tomo-GENESIS [42] to address both the methodological and practical aspects of D-TomoSAR. For example, the Tomo-GENESIS suite includes both conventional linear estimators [15] and the compressive sensing (CS)-based estimator that works in the superresolving regime [27,30,31], as well as a computationally efficient processing pipeline [22], the fusion of TomoSAR point clouds from multiple aspects [43] and 3D object reconstruction from TomoSAR point clouds [44,45,46].

2.3.1. Conventional (Non-Superresolving) D-TomoSAR

For spaceborne data, the number of acquisitions is usually far less than the discretization of $\mathsf{\gamma }$. Therefore, Equation (3) is often under-determined. A popular method before the invention of CS-based TomoSAR techniques to regularize the equation system was to employ the ${\ell }_2$ norm regularization that is also known as Tikhonov regularization. The regularized estimator is shown as follows.

$${\widehat{\mathsf{\gamma }}}_{{\ell }_2}=\underset{\mathsf{\gamma }}{argmin}\frac{1}{2}{∥\mathbf{g}-\mathbf{R}\mathsf{\gamma }∥}_2^2+{\lambda }_{{\ell }_2}{∥\mathsf{\gamma }∥}_2^2,$$

(8)

where ${\lambda }_{{\ell }_2}$ is the regularization parameter. We have implemented the estimator using singular value decomposition with Wiener filtering on the system matrix $\mathbf{R}$. Therefore this algorithm is also known as SVD-Wiener in the community [15].

This type of estimator is also a maximum a posteriori (MAP) estimator. It is the optimal Bayesian estimator that minimizes posterior expected loss. Experiments showed promising performance on TerraSAR-X image stacks [13]. However, in the classical Nyquist–Shannon sampling regime, the resolution of the reconstructed reflectivity profile is limited by the so-called Rayleigh resolution (see Equation (9)) [15] that is governed by the spread of the baseline $\Delta b$.

$${\rho }_s=\frac{\lambda R}{2\Delta b}.$$

(9)

2.3.2. Super-Resolving D-TomoSAR

For dense urban areas, closely spaced objects often coexist in a range-azimuth-elevation resolution cell. These objects cannot be resolved by conventional tomographic inversion algorithms. This is where CS-based super-resolving tomographic inversion comes to play, as it can achieve super-resolution in the estimate of $\mathsf{\gamma }$, if it is sparse. The CS-based TomoSAR estimator can be generally expressed in a similar form as Equation (8), except that the ${\ell }_2$ regularization term is replaced by the signal sparsity term, i.e., the ${\ell }_0$ norm. Because of the nonconvexity of the ${\ell }_0$ norm, it is often relaxed by the ${\ell }_1$ norm in optimization, such as the SL1MMER “scale-down by ${\ell }_1$ norm minimization, model selection, and estimation reconstruction” algorithm proposed in [27]. The ${\ell }_2$ + ${\ell }_1$ norm estimator can be expressed as follows.

$${\widehat{\mathsf{\gamma }}}_{{\ell }_0}=\underset{\mathsf{\gamma }}{argmin}\frac{1}{2}{∥\mathbf{g}-\mathbf{R}\mathsf{\gamma }∥}_2^2+{\lambda }_K{∥\mathsf{\gamma }∥}_1,$$

(10)

where ${\lambda }_K$ is a regularization parameter (K being the sparsity, i.e., the number of discrete scatterers). In practice, the minimization of the ${\ell }_0$ norm is often relaxed by the ${\ell }_1$ norm for better convexity in the optimization.

Because of their super-resolving ability and the robustness of the ${\ell }_1$ norm minimization, CS-based D-TomoSAR algorithms are the state of the art in term of the accuracy of the parameter estimate and the performance of scatterer detection. This in turn increases the density of the reliable points. Figure 3 is a comparison of the point cloud retrieved by PSI and SL1MMER of the same building (Bellagio Hotel, Las Vegas). SL1MMER retrieves many more points than PSI. Yet, CS-based algorithms are less computationally efficient than the conventional TomoSAR. To cope with large area processing, we enriched Tomo-GENESIS with an approach [22,47] that integrates PSI, conventional TomoSAR, and super-resolving TomoSAR. Recently, we have developed a fast and accurate ${\ell }_1$-regularized least square solver with application to D-TomoSAR [35]. This new solver offers a speedup of one or two orders of magnitude than typical second order cone programming. With above-mentioned advances, we are able to reconstruct a high-quality TomoSAR point cloud of an entire city with density comparable to that of LiDAR. For a better overview of the capability of the aforementioned methods,

Table 1. Comparison of the typical density of the point cloud reconstructed by PSI and D-TomoSAR using TerraSAR-X high resolution spotlight image stack.

	Density (thousand/km${}^2$)
PSI [38]	40–100
D-TomoSAR (non-superresolving) [15]	150–250
D-TomoSAR (SL1MMER) [48]	500–1500

summarizes the typical density of the point cloud reconstructed by PSI and D-TomoSAR using a TerraSAR-X high resolution sliding spotlight image stack.

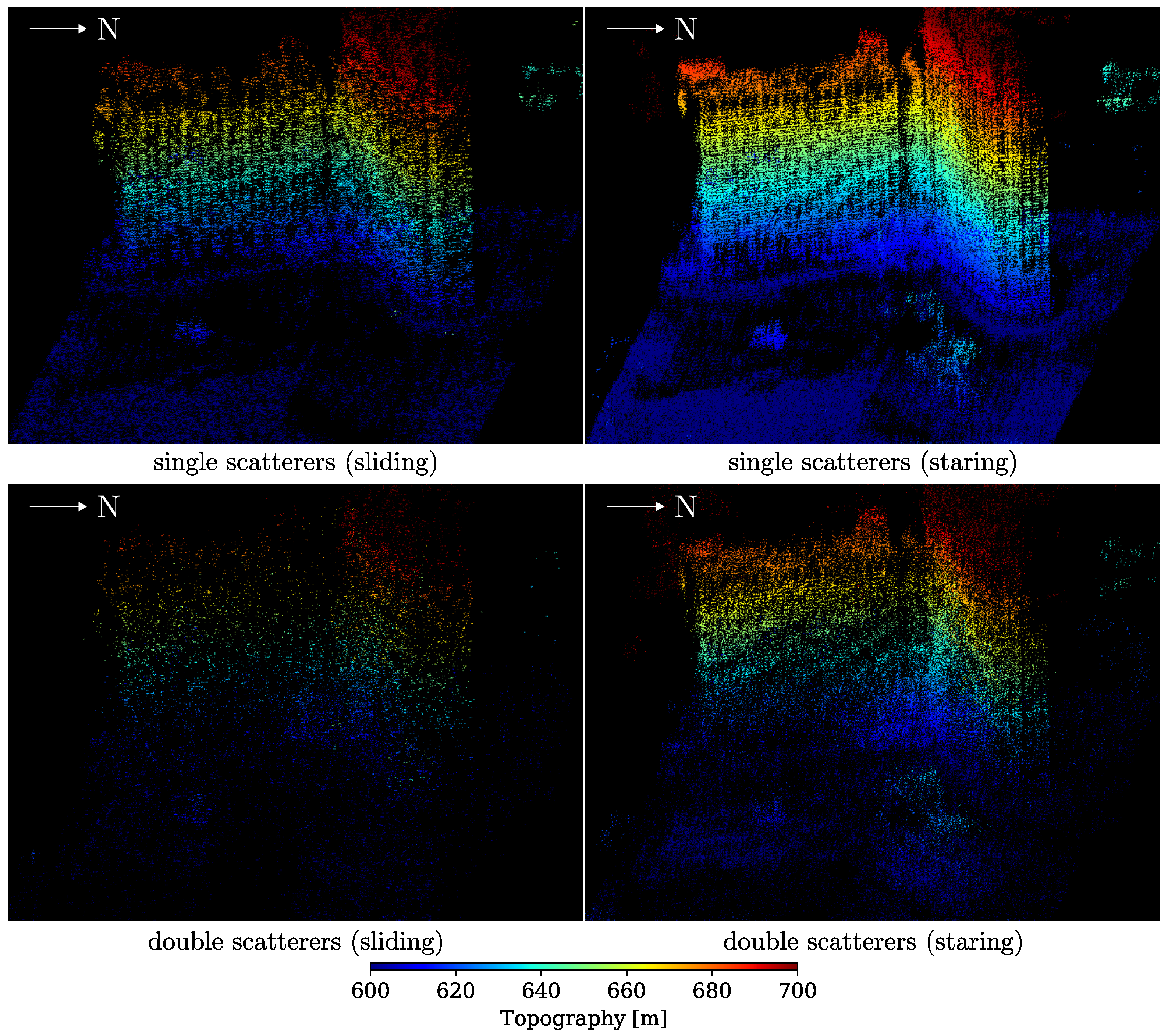
2.3.3. Staring Spotlight TomoSAR

In spotlight modes, the radar beam is steered back and forth toward a common reference target in order to increase its illumination time $t_{\mathrm{AP}}$ (see Figure 4). The beam sweep rate controls the balance between the scene spatial extent and the azimuth resolution. In the TerraSAR-X sliding spotlight mode, the radar beam is swept at a moderate rate with a squint angle range up to $\pm 0.75$ degrees [49]. While in its staring spotlight mode, the beam sweep rate is set to equal the frequency modulation (FM) rate of the reference target. In other words, the radar beam is configured to exactly follow the target over time and the squint angle range can be up to ca. $\pm 2.2$ degrees. As a result, the azimuth resolution is maximized. Nevertheless, the improved azimuth resolution comes at the cost of reduced scene extent: the time span of a focused image $\Delta t_{\mathrm{image}}$ is considerably shorter. Needless to say, the slant range resolution stays unchanged for both modes, as long as the same range bandwidth is employed during imaging.

The transition from sliding to staring spotlight requires several adaptations in SAR focusing and InSAR processing. In the staring spotlight mode, the satellite can no longer be assumed to be standing still during chirp transmission and reception, or to follow a linear trajectory. In addition, variations of tropospheric and ionospheric delay within the large squint angle span also need to be corrected. Another major challenge is to estimate Doppler centroid frequency as a function of focused image time. The TerraSAR-X multimode SAR processor [50,51] and the integrated wide area processor [24,25] were revised accordingly.

For PSI and TomoSAR in urban areas, the improved azimuth resolution has at least two advantages. PSs in the same resolution cell in the sliding spotlight mode may be resolved in different resolution cells in the staring spotlight mode. This leads to an increase in the density of the resulted 4D point cloud. Furthermore, the clutter in each resolution cell may be significantly suppressed, thanks to the increased azimuth resolution. Consequently, the SCR of PSs increases, which in turn leads to a better lower bound on the variance of elevation estimates [52].

In order to demonstrate these improvements, we processed two interferometric stacks of the City of Las Vegas in the sliding and staring spotlight modes using the SL1MMER algorithm. Each stack consists of 12 scenes acquired from October 2014 to February 2015. In each mode, 11 coregistered complex interferograms were used for the TomoSAR reconstruction of two regions of interests (ROIs).

One of the ROIs is a relatively flat region that was selected mainly for the assessment of relative vertical accuracy. The mean intensity maps in both modes are shown in Figure 5a. In the staring spotlight mode, point-like targets, such as the six bright points aligned at each side of the central field, are more focused. Even for DS, clutter appears to be more suppressed and thus the boundaries between areas of different smoothness are easier to recognize. This indicates an increased SCR. As a result, the reconstructed TomoSAR point cloud from staring spotlight images has a significant increase in the number of points compared to that of the sliding spotlight images. Indeed, the total number of scatterers in the staring spotlight is approximately $5.5$ times as high, and the scatterer density is up to circa $13.5$ million points per km${}^2$ in this small region. In addition, the better SCR also improves the relative accuracy of height estimates. In fact, the relative accuracy of height estimates using staring spotlight images is approximately $1.7$ times as high [48].

Another ROI contains two high-rise buildings (Hilton Grand Vacations on the Las Vegas Strip), which were chosen as a demonstration of layover separation. The mean intensity maps are shown in Figure 5b. Similarly, point-like targets stand out more prominently from clutter in the staring spotlight mode and the regularities on the building facades are more clearly visible. The TomoSAR point clouds of single and double scatterers are shown in Figure 6. For this ROI, a substantial increase in the number of (single and double) scatterers was also observed. The scatterer density in the staring spotlight mode is approximately $5.1$ times as high, see

Table 2. Statistics of the point clouds in Figure 6.

	Sliding	Staring	Ratio ${}^1$
No. of single scatterers	$148,646$	$740,656$	$4.98$
No. of double scatterers	$21,576$	$124,546$	$5.77$
Total no. of scatterers	$170,222$	$865,202$	$5.08$
Single-to-double-scatterer ratio	$6.89$	$5.95$	$1.16$
Scatterer density (million/km${}^2$)	$1.56$	$7.91$	$5.08$

${}^1$ The ratio was calculated by dividing the larger by the smaller value.

. The number of double scatterers in the staring spotlight mode almost rivals the number of single scatterers in the sliding spotlight mode.

2.3.4. Point Cloud Fusion

Both PSI and D-TomoSAR deliver 4D point clouds relative to their reference points. They need to be co-registered when considering the results from multiple SAR image stacks. Although general point cloud fusion is a classic topic in the computer vision field, there is very little literature addressing InSAR point cloud fusion, especially for point clouds from image stacks of cross-heading orbits. This is because the fusion of two point clouds requires the identification of common points in the two point clouds. There is theoretically no common point from such two point clouds due to the cross-heading geometry.

The first attempt to fuse cross-heading TerraSAR-X point clouds in an urban area was presented in [36]. This algorithm employs RANSAC to robustly match the ground points of two cross-heading TerraSAR-X PSI point clouds. The point correspondences are found by searching closely spaced point pairs on the ground surface. Therefore, this algorithm does not address the exact point correspondence. To find the exact point correspondence, Wang and Zhu detected the end positions of L-shaped facades in the two TomoSAR point clouds where the two point clouds converge [43]. In [6,53], the authors located dozens of pairs of street lampposts in two point clouds as point correspondences, additionally taking into account the diameter of the lampposts.

The fusion of along-heading (either both ascending or both descending) InSAR point clouds is less challenging. Classical point cloud co-registration methods such as iterative closest point (ICP) can be directly applied. Gernhardt et al. have demonstrated the direct application of ICP on multiple InSAR point clouds of a volcano [39].

2.3.5. 3D Motion Decomposition

A natural step after the fusion of multiple D-TomoSAR point clouds from different aspects is the decomposition of the 1D LOS displacement vector into its original 3D motion components. A 3D deformation vector in a geographic coordinate system is highly beneficial to improving the interpretation of the deformation pattern. A 3D motion decomposition algorithm was proposed and validated on four TomoSAR point clouds in [54]. The method relies on either geometrical [39,43] or geodetic fusion [6,55] of multi-aspect TomoSAR point clouds as input. It estimates the 3D motion components of the queried point target by inclusion of observations from all different viewing geometries and robust inversion with ${\ell }_1$ norm minimization in a local neighborhood. The method allows for highly detailed and shadow-free 3D deformation monitoring, as has been demonstrated in [54]. An example of seasonal motion decomposition on a small test site in Berlin is demonstrated in Figure 7, where it shows the vertical (up), and horizontal (east-west) linear deformation of a railway bridge.

2.3.6. Object Reconstruction

Due the development described above, the quality of TomoSAR point cloud, including point density and relative accuracy, has become sufficient for the reconstruction of 3D models of individual objects. We have developed a suite of algorithms that have proved effective for tasks ranging from reconstructing vertical facade [44,45] (see Figure 8), to the detection and reconstruct of a LOD1 model of individual buildings [46,56].

2.4. Object-Based InSAR Algorithms

The reconstruction of such high quality dense point clouds, as in aforementioned examples, are only possible with a stack of fairly high number of images. In practice, we are often faced with a limited number of images. In such situations, a proper algorithm should exploit information from neighboring pixels in order to reduce the number of images needed for a reliable reconstruction, such as adaptive filtering and nonlocal filtering that have been extensively described in previous literature, such as [4,57,58] and [59,60,61], respectively. However, this section goes beyond these pixel cluster-based methods. It focuses on the recent development of object-based algorithms that explicitly exploit geometric and semantic information to support parameter retrieval in multi-baseline InSAR. To this end, this section introduces the M-SL1MMER algorithm [28], which exploits the freely available building footprint from OpenStreetMap (OSM), and RoMIO (Robust Multi-pass InSAR via Object-based low rank decomposition) [62,63], which exploits the smoothness prior and low rank property of the InSAR data stack of individual objects.

2.4.1. M-SL1MMER

Multiple-snapshot SL1MMER (M-SL1MMER) is an extension of the original SL1MMER algorithm for joint tomographic reconstruction of resolution cells containing scatterers that share, up to quantization errors, the same height (hereafter referred to as “iso-height resolution cells”) [28]. Similar approaches based on multiple snapshots or polarimetric channels can be found, for example, in [64,65,66].

In M-SL1MMER, the iso-height resolution cells are detected by projecting the freely available OSM building footprint [67] to the SAR image, and shifting it toward the near range direction until it reaches the top of the building. Each shifted position of the footprint represents a cluster of iso-height resolution cells. Let a specific iso-height cluster contain M resolution cells; the InSAR measurements ${\mathbf{g}}_m\in {\mathbb{C}}^N$ (N being the number of interferograms) of the m-th resolution cell can be approximated with the linear model (see Equation (3)) ${\mathbf{g}}_m\approx {\mathbf{R}}_m{\mathsf{\gamma }}_m$ for all $m=1,\dots ,M$. In addition, we assume without loss of generality that ${\mathbf{R}}_1\approx \cdots \approx {\mathbf{R}}_M$ and rewrite the M linear models in the more compact form $\mathbf{G}\approx \mathbf{R}\mathsf{\Gamma }$, where the m-th columns of $\mathbf{G}$ and $\mathsf{\Gamma }$ equal ${\mathbf{g}}_m$ and ${\mathsf{\gamma }}_m$, respectively. A key element of M-SL1MMER involves solving the following ${\ell }_{2,1}$ regularization problem:

$$\widehat{\mathsf{\Gamma }}=\underset{\mathsf{\Gamma }}{arg\; min}\frac{1}{2}{\parallel \mathbf{R}\mathsf{\Gamma }-\mathbf{G}\parallel }_F^2+{\lambda }_{2,1}{\parallel \mathsf{\Gamma }\parallel }_{2,1},$$

(11)

where ${\parallel ·\parallel }_F$ and ${\parallel \mathsf{\Gamma }\parallel }_{2,1}={\sum }_{i=1}^L{\parallel {\mathsf{\gamma }}^i\parallel }_2$ denote the Frobenius and ${\ell }_{2,1}$ norms, respectively, and ${\mathsf{\gamma }}^i$ is the i-th row of $\mathsf{\Gamma }$. The ${\ell }_{2,1}$ norm is known to promote the entries of $\mathsf{\Gamma }$ to be jointly sparse among columns. In other words, nonzero rows can be expected in $\widehat{\mathsf{\Gamma }}$ or its submatrices. Solving the minimization problem in (11) is followed by model selection and amplitude debiasing independently for each resolution cell, as in the SL1MMER algorithm (see Section 2.3).

As a practical demonstration, we reconstructed the elevation of two high-rise buildings using 6 TanDEM-X bistatic sliding spotlight interferograms. The elevation estimates of the upper and lower layers are depicted in Figure 9. In the case of layover, the higher and lower scatterers can be found in the upper and lower layers, respectively. The smooth color transition on the reconstructed building facades already indicates its high quality. Roof-facade and facade-ground interactions are clearly visible in the near and far range, respectively. This can also be observed in the elevation difference map under layover (see Figure 10). The color change from deep blue (near range) to cyan (far range) corresponds to increasing elevation distance between building roof and facade.

2.4.2. RoMIO

As a complement to M-SL1MMER, RoMIO does not necessarily require explicit information of the footprints of the objects in the image. It is a more general framework that exploits the low rank property of InSAR phase tensor, because the low rankness of a tensor describes its information entropy, which requires looser signal support than the explicit iso-height line required in M-SL1MMER. RoMIO filters the InSAR data tensor by robustly minimizing its rank. Therefore, it can be regarded as a filtering step in prior to multi-baseline InSAR algorithms. The core RoMIO estimator can be expressed as follows.

$$\{\widehat{\mathcal{X}},\widehat{\mathcal{E}}\}=\underset{\mathcal{X},\mathcal{E}}{arg\; min}\mathrm{rank}\left(\mathcal{X}\right)+{\lambda }_{rank}{\parallel \mathcal{E}\parallel }_0,s.t.\mathcal{X}+\mathcal{E}=\mathcal{G},$$

(12)

where $\mathcal{G}$ is the observed InSAR phase tensor, $\mathcal{X}$ and $\mathcal{E}$ model the tensor of the true signal, and the sparse outliers, respectively, $\widehat{\mathcal{X}},\widehat{\mathcal{E}}$ are the recovered outlier-free phase tensor and the estimated outlier tensor, respectively, $\mathrm{rank}\left(\mathcal{X}\right)$ refers to the multilinear rank of $\mathcal{X}$, and ${\lambda }_{rank}$ is the regularization parameter. In practice, the multilinear rank and the ${\ell }_0$ norm are relaxed by the tensor nuclear norm ${\parallel \mathcal{X}\parallel }_{\ast }$ and ${\ell }_1$ norm, respectively.

RoMIO reaches filtering performance comparable to state-of-the-art filtering algorithms, i.e., nonlocal means filtering [59,61]. However, it outperforms nonlocal means filtering by a factor of two in terms of the interferometric phase variance when the interferogram is corrupted by 50% outliers [63]. The merit of this extreme robustness in turn improves parameter estimation in multi-baseline InSAR algorithms. In typical settings of the TerraSAR-X high-resolution spotlight image stack, i.e., 10–20 images, SNR of 0–5 dB, a combination RoMIO and PSI outperforms the original PSI by a factor of 10 to 30 in the accuracy of the linear deformation estimates [63].

While optimizing the deformation parameters using multi-baseline InSAR algorithms, e.g., PSI, RoMIO can also make use of the explicit support of objects, such as a given segmentation mask of the SAR image. RoMIO includes a spatial regularization term, e.g., smoothness, of the 2D matrices of the parameters in the estimator [62]. A general form of such regularized estimators can be expressed as follows.

$$\{\widehat{\mathbf{S}},\widehat{\mathbf{P}}\}=\underset{\mathbf{S},\mathbf{P}}{arg\; min}\frac{1}{2}{\parallel \mathcal{W}\odot (\mathcal{G}-\overline{\mathcal{G}}(\mathbf{S},\mathbf{P}))\parallel }_F^2+{\lambda }_{TV}f(\mathbf{S},\mathbf{P}),$$

(13)

where $\mathbf{S}$ and $\mathbf{P}$ are the matrices of the elevation and deformation parameters. Similar to other MAP estimators, e.g., Equation (8), the first term on the right-hand side of the estimator is a data fidelity term that calculates a weighted log likelihood between the observed InSAR phase tensor $\mathcal{G}$ and the modeled tensor $\overline{\mathcal{G}}$, where $\mathcal{W}$ denotes an optional weighting tensor, and ⊙ denotes the element-wise product between two tensors. An example of the weighting tensor can be a tensor comprised of coherence matrices of each interferogram. Pixels of higher coherence are given higher weights. The function $f(\mathbf{S},\mathbf{P})$ denotes the regularization term that represents the spatial prior of $\mathbf{S}$ and $\mathbf{P}$. The regularization parameter ${\lambda }_{T}V$ controls the balance between these two terms. In [62], we made use of the popular total variation as a smoothness prior.

3. Advances in Robust Estimation

3.1. Overview of Advances

Robust estimation in multi-baseline InSAR was sporadically mentioned in previous literature. Some examples include using an adaptive window to improve the covariance matrix estimation [4,57,68], improving the PSI reference network by ${\ell }_1$ norm minimization [23,24], and robust detection of multiple scatterers in TomoSAR [31,33]. However, it was not systematically addressed until [5]. Wang and Zhu pointed out that, due to the existence of non-Gaussian samples and unmodeled phase, e.g., the atmospheric phase, robust estimation in multi-baseline InSAR lies on the following two fundamental problems:

• covariance matrix estimation for DS, due to the existence of non-Gaussian and nonstationary samples
• phase history parameters estimation for both DS and PS, due to observations with large unmodeled phase

The impact of non-robust covariance estimation and the existence of nonstationary phase on parameter estimation in multi-baseline InSAR has been confirmed in several recent works, such as [69,70,71,72], and [58,73], respectively. The following sections will elaborate on these two points. The development of robust estimation is greatly associated with DS-based InSAR. Please refer to [74] for a recent review of DS-based InSAR techniques.

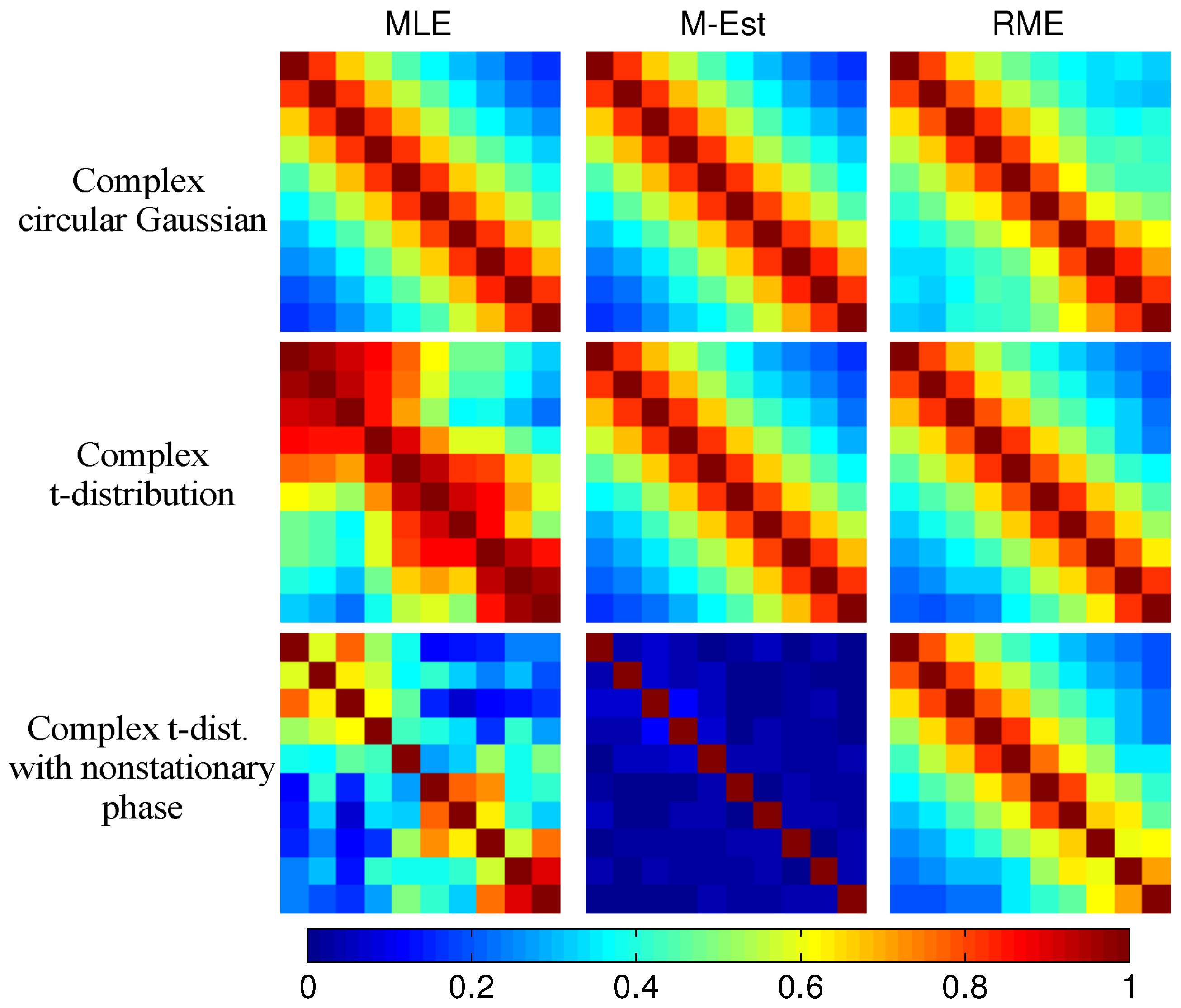
3.2. Robust Covariance Matrix Estimation

The estimation of the covariance matrix of a pixel is usually carried out by the sample covariance matrix. Its estimator is shown in Equation (14), where $\mathbf{g}$ is the multivariate observation, and $\mathbf{G}$ is the matrix consisting of M spatial samples, that is $\mathbf{G}=\left[{\mathbf{g}}_1,{\mathbf{g}}_2,\dots ,{\mathbf{g}}_M\right]$. Equation (14) is also the MLE if the samples are complex circular Gaussian (CCG) distributed. Unfortunately, this equation does not always hold in real data. This is why a robust estimator is necessary. A robust covariance estimator should consider the following two scenarios (and the mixture of both):

• the selected samples are non-Gaussian (possibly heavily tailed distribution)
• the expected interferometric phase of the samples is nonstationary, e.g., very strong underlying topographic phase

  $${\widehat{\mathbf{C}}}_{\mathbf{gg}}=\frac{1}{M}\sum _{m=1}^M{\mathbf{g}}_m{\mathbf{g}}_m^H=\frac{1}{M}\mathbf{G}{\mathbf{G}}^H$$

  (14)

The following content will summarize the robust covariance estimators, focusing on the points above.

3.2.1. Non-Gaussian Samples

For the first scenario, [5] proposed that the sample covariance matrix can be made more robust by an M-estimator, which is essentially an iterative reweighted sample covariance matrix [75,76]:

$${\widehat{\mathbf{C}}}_{k+1}=\frac{1}{M}\sum _{m=1}^{M}w\left({\mathbf{g}}_m^H{\widehat{\mathbf{C}}}_k^{-1}{\mathbf{g}}_m\right){\mathbf{g}}_m{\mathbf{g}}_m^H,$$

(15)

where m and k are the sample index and the iteration index, respectively, and $w\left(x\right)$ is a weighting function of the negative log-likelihood of the sample ${\mathbf{g}}_m$ to the CCG probability density function (PDF). The weighting function down-weights highly deviated samples whose log-likelihood is small. Equation (15) is solved iteratively. The authors of [5] also proposed an approximation to drop the iterative process, which is the sign covariance matrix (SCM) [77,78]. Extending it to complex number, it is:

$${\widehat{\mathbf{C}}}_{SCM}=\frac{1}{M}\sum _{m=1}^M{∥{\mathbf{g}}_m∥}^{-2}{\mathbf{g}}_m{\mathbf{g}}_m^H$$

(16)

SCM is an engineering solution for fast processing under the general M-estimator’s framework. The weighting function is replaced by the inverse of the ${\ell }_2$ norm of the sample. Therefore, only the direction (or sign) of each multivariate sample is considered.

3.2.2. Non-Gaussian Samples with Nonstationary Interferometric Phase

It is often the case that the interferometric phase of the selected samples are not stationary, due to varying topography and motion or other factors. Usually, this type of deterministic phase is estimated and mitigated in prior to covariance estimation. For example, [58] proposed a multi-resolution defringe algorithm to mitigate such nonstationary phase.

Nevertheless, poor estimates significantly affect the covariance matrix estimation. Therefore, [5] proposed a new covariance estimator rank M-estimator (RME) for complex multivariate. The RME is derived by replacing the multivariate $\mathbf{g}$ with its rank $\mathbf{r}$ in Equation (15):

$${\widehat{\mathbf{C}}}_{RME,k+1}=\frac{1}{M}\sum _{m=1}^{M}w\left(x_m\left({\widehat{\mathbf{C}}}_{RME,k}\right)\right){\widehat{\mathbf{r}}}_m.{\widehat{\mathbf{r}}}_m^H$$

(17)

The complex rank vector $\mathbf{r}$, analogous to its real number version [78], is defined as follows:

$${\widehat{\mathbf{r}}}_m=\frac{1}{J}\sum _{j=1}^J\frac{{\mathbf{g}}_m\odot {\mathbf{g}}_j^{\ast }}{∥{\mathbf{g}}_m\odot {\mathbf{g}}_j^{\ast }∥},$$

(18)

where ${\mathbf{g}}_j$ is a direct neighborhood sample of ${\mathbf{g}}_m$, and ⊙ denotes the Hadamard product. The multiplication of the complex conjugate of a direct neighbor mitigates the nonstationary interferometric phase of ${\mathbf{g}}_m$. Due to the multiplication, the RME is a fourth-order descriptor of the sample statistics. An element-wise square root on $\left|{\widehat{\mathbf{C}}}_{RME}\right|$ should be performed in order to obtain the second-order momentum. It was proven that the element-wise square root of $\left|{\widehat{\mathbf{C}}}_{RME}\right|$ approaches $\left|{\widehat{\mathbf{C}}}_{\mathbf{g}\mathbf{g}}\right|$ asymptotically under CCG distribution when calculating the rank using one neighborhood sample [5].

3.2.3. Comparison

We compared the sample covariance matrix, M-Estimator, and the RME under three different scenarios: (1) multivariate CCG, (2) a heavily tailed multivariate distribution (complex t-distribution), and (3) nonstationary multivariate complex t-distribution. For each scenario, 1000 ten-acquisition vectors were simulated according to the distribution and a predefined coherence matrix that has a exponential decay of the coherence w.r.t. the temporal baseline. In the last scenario, linear phase fringes with ten different fringe frequencies randomly picked within [0 $\pi$/10] were added to the phases of the ten acquisitions.

The results are shown in Figure 11, where each row corresponds to the three scenarios, respectively. The top left subplot can be regarded as the ground truth, because MLE is the optimal estimator under CCG, and is asymptotically unbiased. All three estimators can preserve the correct shape of the covariance matrix under CCG. The MLE fails in the second scenario, where the samples are contaminated by outliers. The coherence is usually overestimated because of the large amplitude of the outliers. In the last scenario, both MLE and M-estimator are not capable of dealing with nonstationary phases. Heavy underestimation occurs because of the summation of the complex numbers with non-constant phases. The estimates of M-estimator are extremely low due to more summation operations caused by the iterative process. Last but not least, RME is invariant to such nonstationary phase, and hence maintains good performance in all conditions.

A quantitative experiment shows that the robust estimator is extremely effective for samples with low coherence. At true coherence of 0.2, M-estimator outperforms the Gaussian MLE by a factor of 1.1 to 2.3, and a factor of 1 to 10, in terms of the accuracy and the bias, respectively, under a wide range of outlier percentages [5].

3.3. Robust Phase History Parameters Retrieval

A robust covariance matrix estimate alone is not sufficient for a robust estimation of the phase history parameters, i.e., elevation, and motion parameters, because a multi-pass InSAR observation $\mathbf{g}\in {\mathbb{C}}^{\mathrm{N}}$ may contain an unmodeled phase, e.g., uncompensated atmospheric phase, unmodeled motion phase, etc. The following content provides examples of robust estimators for the retrieval of the phase history parameters of both PS and DS.

3.3.1. Robust PS Estimator

The general form of the MLE of PS phase history parameters can be expressed as follows:

$${\widehat{\mathsf{\theta }}}_{MLE}=\underset{\mathsf{\theta }}{argmin}{∥\mathbf{g}-\overline{\mathbf{g}}\left(\mathsf{\theta }\right)∥}_2^2,$$

(19)

where $\overline{\mathbf{g}}\left(\mathsf{\theta }\right)$ is the modeled PS signal. Equation (19) is shown to be equivalent to Equation (6) in [79]. Similar to the robust covariance estimator, it can be robustified by an M-estimator:

$${\widehat{\mathsf{\theta }}}_{M-est}=\underset{\mathsf{\theta }}{argmin}\sum _{i=1}^N\rho \left(Re\left[{\epsilon }_i\left(\mathsf{\theta }\right)\right]/{\sigma }_R\right)+\rho \left(Im\left[{\epsilon }_i\left(\mathsf{\theta }\right)\right]/{\sigma }_I\right),$$

(20)

where the residual ${\mathsf{\epsilon }}_i\left(\mathsf{\theta }\right)$ equals $g_i-{\overline{g}}_i\left(\mathsf{\theta }\right)$, $Re\left[·\right]$, $Im\left[·\right]$ are the real and imaginary parts of a complex number, and ${\sigma }_R$ and ${\sigma }_I$ are the standard deviations of the real and imaginary parts of the residual, respectively. The function $\rho \left(x\right)$ is the so-called robust loss function that can be derived from the PDF of the contaminated distribution of $\mathbf{g}$, if it is known. However, it is usually unknown in practice. We shall use stable empirical functions instead, e.g., the Tukey biweight function.

3.3.2. Robust DS Estimator

According to [80], the MLE of DS phase history parameters can be expressed as follows:

$${\widehat{\mathsf{\theta }}}_{\mathit{MLE}}=\underset{\mathsf{\theta }}{argmin}\left\{{\mathbf{g}}^H\mathsf{\Phi }\left(\mathsf{\theta }\right){\left|\mathbf{C}\right|}^{-1}\mathsf{\Phi }{\left(\mathsf{\theta }\right)}^H\mathbf{g}\right\}$$

(21)

where $\mathsf{\Phi }$ is a diagonal matrix of the modeled interferometric phase. If stationarity is assumed for a DS and its neighborhood, one can treat a cluster of DSs as a single PS by averaging them, as proposed in SqueeSAR [4]. Then, the robustified DS estimator is identical to Equation (20).

However, if the objective is a full inversion of individual single-look DS observation (without averaging) without the strict assumption of phase stationarity, the robustified estimator is shown in [5] to be in the following form:

$${\widehat{\mathsf{\theta }}}_{\mathit{M}-\mathit{est}}=\underset{\mathsf{\theta }}{argmin}\left\{{\mathsf{\epsilon }}^H\left(\mathsf{\theta }\right)\mathbf{W}\left(\overline{\mathsf{\epsilon }}\right)\mathsf{\epsilon }\left(\mathsf{\theta }\right)\right\},$$

(22)

where the residuals $\mathsf{\epsilon }\left(\mathsf{\theta }\right)$ is shown in Equation (23). It is whitened by a robust covariance matrix estimate, e.g., ${\widehat{\mathbf{C}}}_{RME}$. The matrix $\mathbf{W}\in {\mathbb{R}}^{N\times N}$ is a diagonal robust weighting matrix computed from the mean residual $\overline{\mathsf{\epsilon }}$. Because of possible outliers in the residual, $\overline{\mathsf{\epsilon }}$ should also be robustly estimated, for example by a robust weighted averaging of $\mathsf{\epsilon }\left(\mathsf{\theta }\right)$ of the selected samples.

$$\mathsf{\epsilon }\left(\mathsf{\theta }\right)={\left|{\widehat{\mathbf{C}}}_{RME}\right|}^{-0.5}\mathsf{\Phi }{\left(\mathsf{\theta }\right)}^H\mathbf{g}$$

(23)

To summarize, Equation (22) is a joint estimation of the phase parameters of individual single-look DS observations in a neighborhood. It is solved iteratively. Its computation should begin with initial estimates of each sample in the neighborhood (assumed to be the same), which jointly determine the initial weighting matrix. The same weighting matrix is used to retrieve the parameters of each single-look DS in the neighborhood, and is updated on the basis of all the estimates upon finishing one iteration.

To demonstrate the robustness of the estimator, Figure 12 shows the linear deformation rate of the volcano Stromboli, Italy, estimated by the robust DS phase history parameter retrieval method. Parameter estimation in active volcanic areas is challenging due to strong decorrelation, and the varying deformation model. In the experiment, only 16 interferograms acquired in 2008 were used. We can see that scatterers over 50% of the surface area were retrieved, although most of them did not undergo any significant deformation. The crater shows an uplift of 10 cm/year, and the southern slope undergoes a subsidence of up to 20 cm/year. This may suggest certain displacement of the magma underneath the volcano.

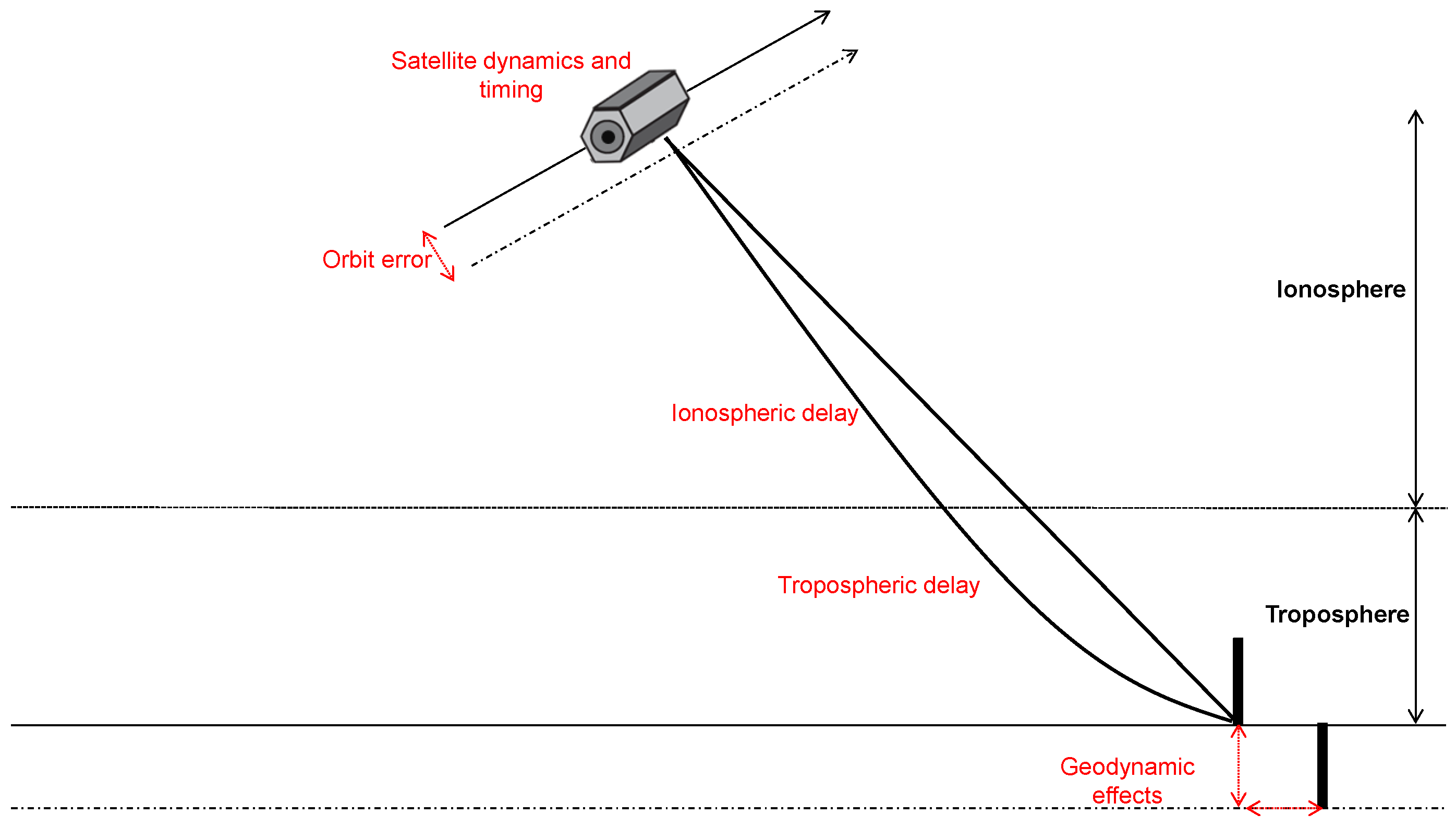
4. Advances in Absolute Positioning

A unique feature of TerraSAR-X is its precise orbit determination and high precision range measurements, which allows for an unprecedented 2D localization accuracy of image pixels below one meter. In recent years, this level of accuracy has been further improved by thorough consideration of the most prominent error factors affecting range and azimuth measurements of SAR, a method termed SAR imaging geodesy [7,81]. SAR imaging geodesy is seen as a great leap in SAR technology, because it extends the applications of SAR to the geodetic positioning domain rather than the imaging domain. Two of the numerous application examples of SAR imaging geodesy are geodetic stereo SAR [82], a method that retrieves the precise 3D absolute position of a target by combining its 2D radar timings from different orbit tracks, and a framework called geodetic InSAR [6], in which multi-baseline InSAR and stereo SAR are combined to achieve absolute 4D InSAR point clouds. A brief introduction to the two methods is given below, and the most recent advances of these techniques and their new applications are described.

The SAR imaging geodesy method aims at attaining 2D absolute pixel localization [7]. A single pixel in a focused complex SAR image is localized, in across-track, by range ${\tau }_{rg}$ and, in along-track, by azimuth $t_{az}$ times. For a point target inside the mentioned pixel, the following equations read:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\tau }_{rg}=\frac{2R}{c}+\delta {\tau }_{SD}+\delta {\tau }_O+\delta {\tau }_F+\delta {\tau }_I+\delta {\tau }_T+\delta {\tau }_G\\ \hfill t_{az}=t+\delta t_{SD}+\delta t_O+\delta t_F+\delta t_G,\end{array}\end{array}$$

(24)

where R is the geometric distance from the sensor to the center of the pixel in meters and c is the speed of light in vacuum; the other terms are all expressed in seconds. The raw acquisition time is denoted by t and the timing error terms subscripted by $SD$, O, F, I, T and G represent delays caused by satellite dynamics, orbit inaccuracies, feature localization error, ionospheric delay, tropospheric delay, and geodynamic effects, respectively. The magnitude of individual errors range from a couple of centimeters for the ionospheric effect, if the satellite operates in X-band, followed by decimeter regimes for satellite dynamic effects and geodynamic effects for both components, to up to a few meters for the tropospheric effect, depending on the weather conditions and the average incidence angle of the acquired SAR images. Some of the mentioned errors and their effects on SAR measurements are shown in Figure 13. The curved propagation path shown in Figure 13 is highly exaggerated for visualization purposes only. In order to remove the mentioned timing errors, the imaging geodesy method exploits the highly precise orbit data of TerraSAR-X and Tandem-X [1,2,83], utilizes a highly sophisticated SAR processor to avoid unnecessary approximations [84], precisely extracts targets with sub-pixel sensitivity [85,86], and corrects the path delay and geodynamic errors by global numerical weather data [81,87] and state-of-the-art geodetic models [88].

By combining the ${\tau }_{rg}$ and $t_{az}$ of the same target visible in SAR images acquired from two or more different viewing geometries, the stereo SAR method determines the 3D position of the target (see Figure 14). The 2D radar timing coordinates of a particular target in the SAR image $x_T=(t_{az},{\tau }_{rg})$ are linked to their corresponding 3D coordinates on the surface of the Earth ${\mathbf{X}}_T=(X,Y,Z)$ by the range-Doppler equation system [85]:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill |{\mathbf{X}}_S-{\mathbf{X}}_T|-c·{\tau }_{rg}=0\\ \hfill \frac{{\dot{\mathbf{X}}}_S({\mathbf{X}}_S-{\mathbf{X}}_T)}{|{\dot{\mathbf{X}}}_S\left|\right|{\mathbf{X}}_S-{\mathbf{X}}_T|}=0\end{array}\end{array}$$

(25)

with ${\mathbf{X}}_S$ and ${\dot{\mathbf{X}}}_S$ denoting the position and the velocity vector of the satellite relative to $t_{az}$, and ${\tau }_{rg}$ being the calibrated two-way traveled time from the satellite to the target. The variable $t_{az}$ is implicitly included in the second equation relating the state-vector of the satellite to the time of the acquisition using a polynomial model [82]. The estimation of the coordinates is performed by least squares adjustment plus stochastic modeling of timing observations using the variance component estimation (VCE) [82]. The relative accuracy of the estimated coordinates depends on the SCR of the target, the precision of the external atmospheric and geodynamic corrections, the degree of difference in the combined viewing geometries, and the number of SAR acquisitions.

4.1. Overview of Advances

SAR imaging geodesy was first named in 2011 by Eineder et al., since the method incorporates correction principles used in geodesy with SAR [7]. Schubert et al. reported on the correction of atmospheric delays by local height dependent models in [90]. Gisinger studied the effect of utilizing different mapping functions for converting the zenith atmospheric delays into the radar line of sight in [91]. These methods used the local GNSS zenith path delays for atmospheric corrections. Cong et al. introduced atmospheric correction through the 3D integration of weather data obtained from the European Center for Medium-Range Weather Forecasts (ECMWF) and using global TEC maps [81]. Apart from atmospheric errors, calibration of internal electronic delays of the SAR sensor was investigated in [7] and the precision of azimuth timing was improved by calibrating the sensor’s internal clock rate [92]. The most prominent geodynamic effects, such as solid earth tides, pole tides, and continental drifts, were included in further studies [7,81,86,93]. In order to improve the localization precision into sub-centimeter regimes, Balss et al. further modeled geodynamic effects with smaller magnitudes, such as atmospheric pressure loading, ocean tidal loading, ocean pole tides, and atmospheric tidal loading [94]. In all the studies, the geodynamic effects were considered by the state-of-the-art models of the IERS 2010 convention [88]. The already precise orbit of TerraSAR-X [83] has been further improved by modeling the non-gravitational forces and also solar radiation pressure modeling [1]. The world-wide reproducibility of high precision measurements was demonstrated in [95] and an operational processor called the SAR Geodesy Processor (SGP) was introduced in [87]. Relative to applications, the high precision ranging measurement of TerraSAR-X has been exploited for maritime purposes [96,97]. In terms of achievable accuracy, SAR imaging geodesy is capable of localizing corner reflectors with 1.16 cm and 1.85 cm range and azimuth standard deviations, respectively [98].

The first results on 3D localization of CRs by means of stereo SAR was reported in [99]. Although 3D positioning using multi-aspect TerraSAR-X images had been previously demonstrated in [100,101,102], the results in [99] were unique in the sense that the stereo processing was carried out on thoroughly calibrated range and azimuth timings. Gisinger et al. demonstrated the applicability of the geodetic stereo SAR method not only on CRs but on opportunistic non-ideal scatterers such as PS in an urban area [82]. The manually extracted scatterers could be localized with 3D precision better than 10 cm [82], which paved the way for new geodetic applications such as secular ground movement estimation using natural PS [103,104], high precision mapping of road networks (DriveMark) [105], and highly precise automatic SAR Ground Control Point (GCP) generation [89,106,107,108,109]. In terms of achievable accuracy, geodetic stereo SAR is able to localize corner reflectors with 3D precision better than 4 cm and an absolute accuracy of 2–3 cm when compared to independently surveyed reference positions [82].

4.2. Geodetic InSAR

The geodetic InSAR approach integrates the capabilities of multi-baseline InSAR with SAR imaging geodesy and stereo SAR techniques. The goal of the framework is to tackle the shortcomings of both methods: the relative estimates of all InSAR approaches and the small number of points that can be absolutely localized by geodetic stereo SAR. Therefore, it tends to achieve absolute positioning of a large number of scatterers by exploiting the advantages of both techniques. In the following, the workflow of the geodetic InSAR technique is described and some example applications are demonstrated.

4.2.1. SAR GCP Generation

The first major part of the procedure is concerned with extraction of GCPs from multi-aspect SAR images. This includes [89]:

Step 1

Detection and matching of identical PS from SAR images acquired from different orbits. In the reference geodetic SAR tomography technique this task was performed manually [6]. At the current state of the framework, the identification of common PS can be carried out using the PSI multi-track fusion algorithm [39] for same-heading tracks and utilizing high resolution optical data [106] or external geospatial road network data [109] for cross-heading tracks. A combination of all the mentioned methods for automatic detection of large number of GCPs was used in [89].

Step 2

Precise timing extraction of PS from stacks of non-coregistered SLC images. This is done by PTA [85,86].

Step 3

PS visibility check and initial outlier removal. The time series of phase noise approximated by SCR of each PS [19] is analyzed and the outliers are robustly removed by the adjusted box plot method [110].

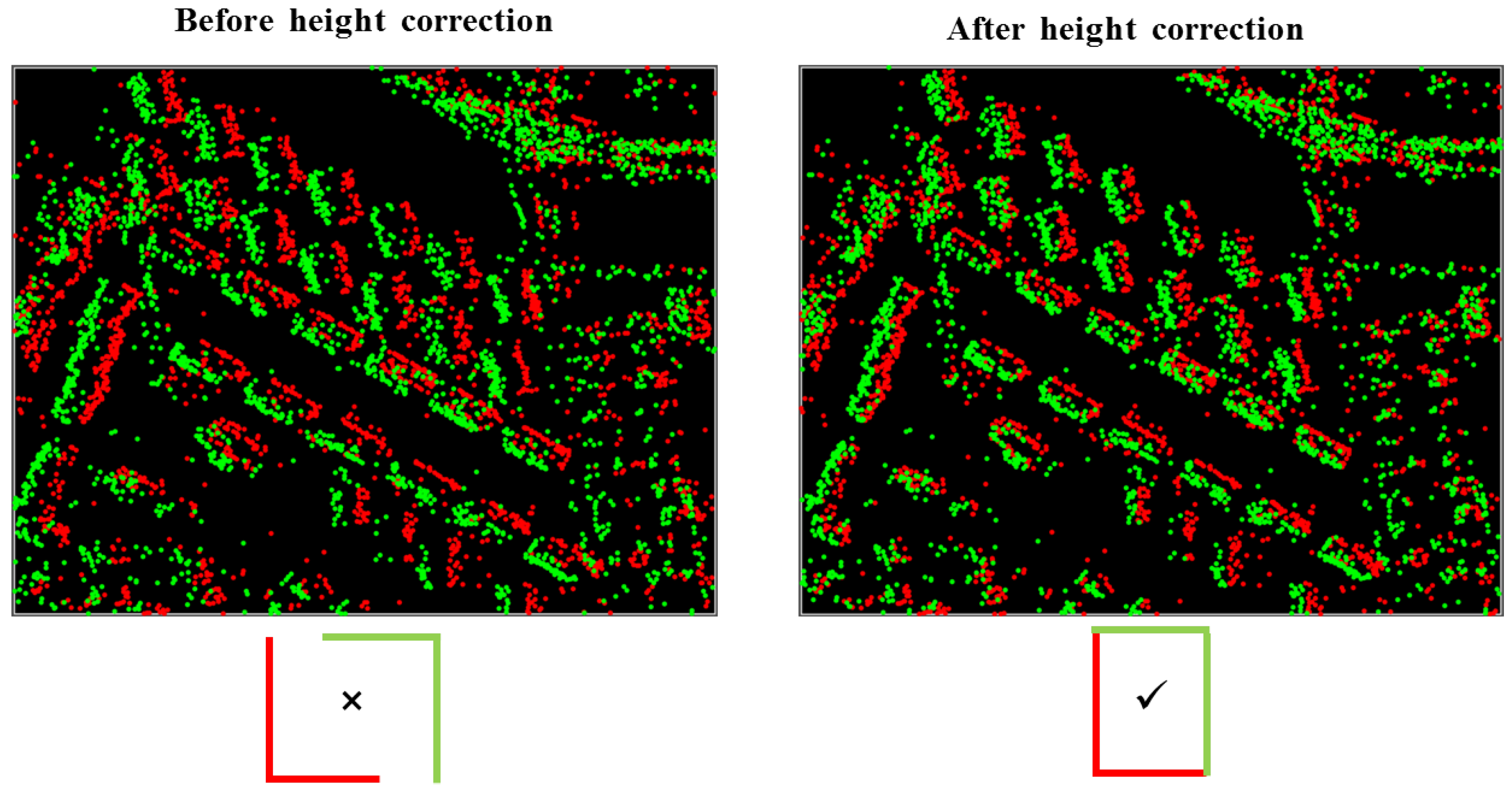
Step 4

Correction of PS timings in the stack of images using imaging geodesy.

Step 5

Absolute 3D positioning of each PS by the stereo SAR method [82]. The posterior quality measures of the observations and the estimates are also reported in this step.

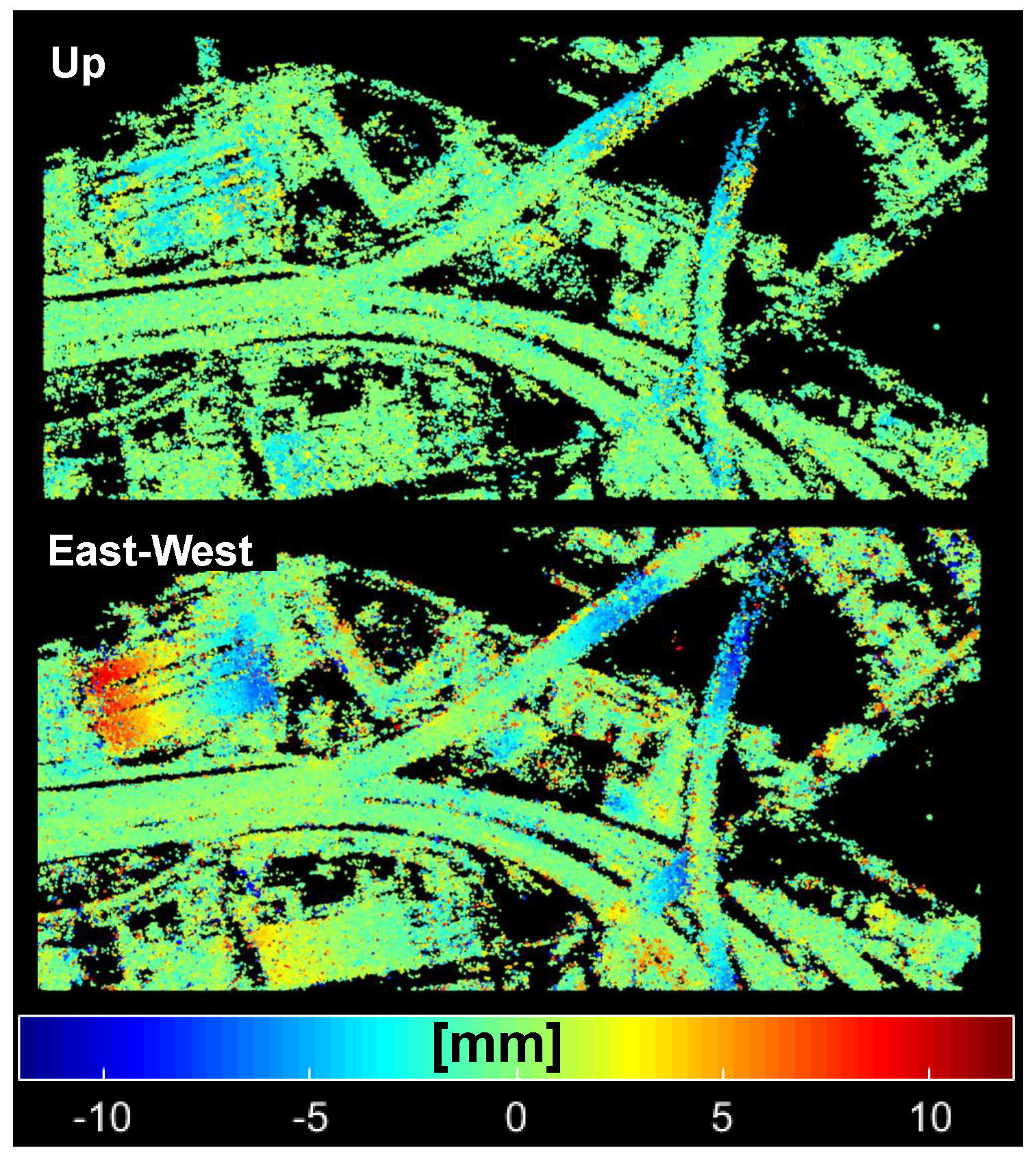
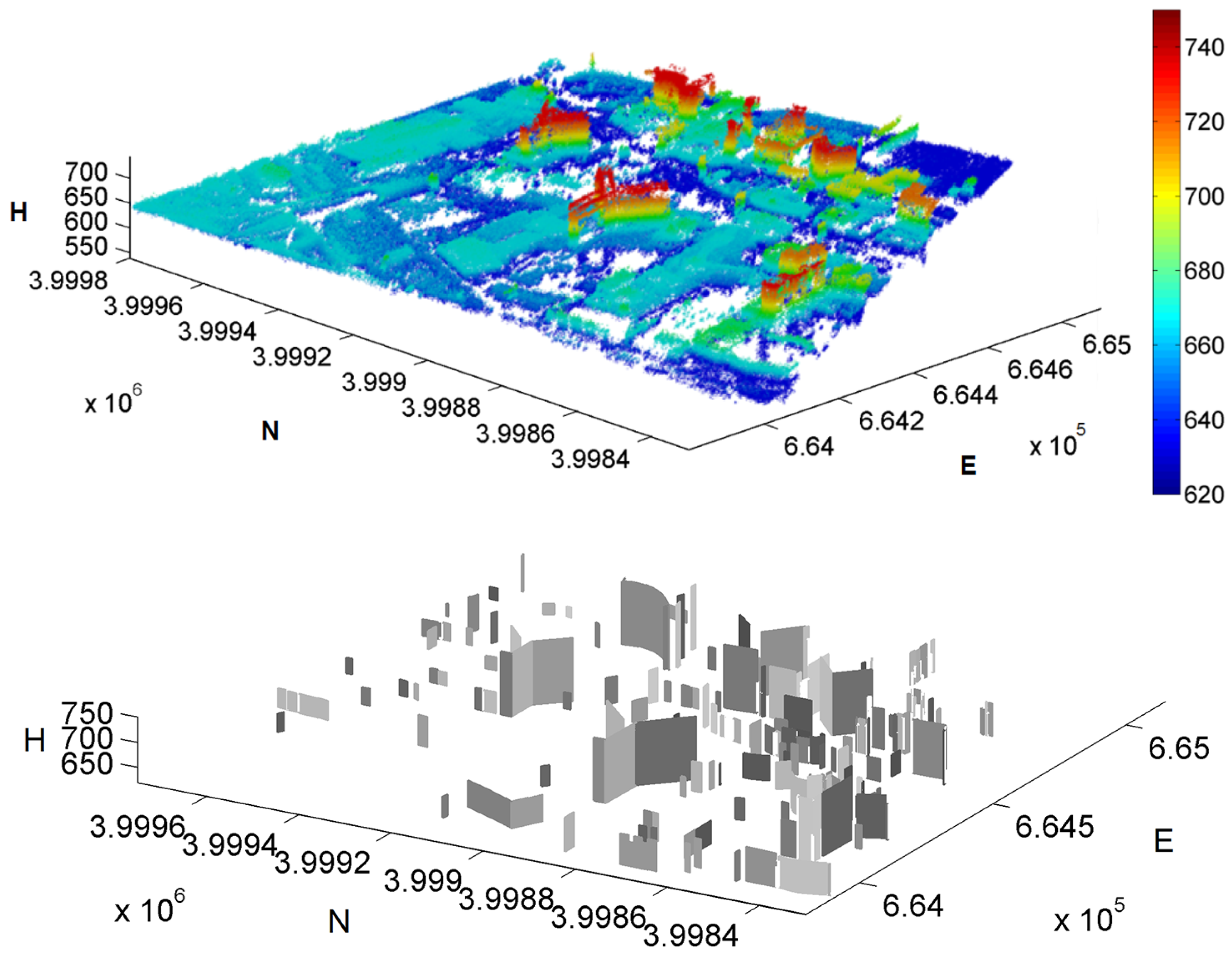
4.2.2. Absolute Localization of InSAR Point Clouds

The main objective of the geodetic InSAR framework is to resolve the DEM error of the reference point with respect to which the topography and deformation parameters are estimated [20,21,40]. The geodetic InSAR approach can overcome this problem, to some extent, in two ways dependent on the number of available GCPs. If only a small number of GCPs are available, the best candidate will be chosen as the reference point during PSI/TomoSAR processing and at the final stage the geocoded coordinates of all points in the point clouds are shifted toward the absolute coordinates of this point [6]. If a large number of GCPs are available, for instance using the GCP generation approaches in [89,107], the DEM error of the reference point is approximated as a post-processing step. Therefore, the difference in ellipsoidal heights of GCPs and their corresponding geocoded PS heights are calculated and a height offset is robustly estimated. The height offset is added to the geocoded PS heights and an updated geocoding is carried out which results in absolute coordinates of the InSAR point cloud [111].

4.2.3. Applications

To conclude this subsection, a few examples and applications of the geodetic InSAR framework are demonstrated below.

Figure 15 shows the city of Oulu in Finland overlaid by 2049 GCPs obtained from four stacks of TerraSAR-X high resolution spotlight images.

The GCPs are color-coded based on the underlying geometry configuration used for their localization, where AA, DD, and AD stand for ascending-ascending, descending-descending and ascending-descending orbits, respectively; ADAD means that scatterers were localized from all the four viewing geometries. It is observed that the entire central area of Oulu is covered with the generated GCPs. The candidates from the same-heading geometries stem from built areas, while the ones from cross-heading orbits include the bases of lamp poles, street lights, and traffic lights. The statistics of the generated GCPs are reported in

Table 3. Averaged statistics based on the stereo SAR least squares estimated 3D coordinate standard deviations in Oulu. The letters A and D stand for ascending and descending geometries, respectively. The sample mean and standard deviation are denoted by $\mu$ and $\sigma$ and $S_{\left[ENH\right]}$ represents the local coordinates standard deviations within a 95% confidence level [89].

Geometry	Number of Scatterers	${\mathit{\mu }}_{{\mathbf{s}}_{\mathbf{E}}}\left(\mathbf{cm}\right)$	${\mathit{\mu }}_{{\mathbf{s}}_{\mathbf{N}}}\left(\mathbf{cm}\right)$	${\mathit{\mu }}_{{\mathbf{s}}_{\mathbf{H}}}\left(\mathbf{cm}\right)$	${\mathit{\sigma }}_{{\mathbf{s}}_{\mathbf{E}}}\left(\mathbf{cm}\right)$	${\mathit{\sigma }}_{{\mathbf{s}}_{\mathbf{N}}}\left(\mathbf{cm}\right)$	${\mathit{\sigma }}_{{\mathbf{s}}_{\mathbf{H}}}\left(\mathbf{cm}\right)$
AA	565	17.73	5.04	15.87	11.98	2.63	11.09
DD	1417	15.08	3.80	16.71	10.38	2.10	11.30
AD	24	2.26	2.50	1.75	0.99	1.11	0.83
ADAD	43	1.17	1.40	1.12	0.42	0.55	0.37

, which demonstrate the extremely high potential of TerraSAR-X for precise 3D positioning.

Comparison with a reference LiDAR point cloud shows that we can achieve a horizontal absolute accuracy of 20 cm using just a single GCP to correct the geocoding of an InSAR point cloud [6,55]. Therefore, employing over one thousand GCPs, as shown previously, can achieve extremely high absolute accuracy, presumably in the order of centimeter. In order to demonstrate this, a close comparison of two cross-heading InSAR point clouds before and after height correction is shown in Figure 16, where the red and green points represent the PS of descending and ascending tracks, respectively. It can be seen that after the calibration of the height of the reference point using the GCPs, the endpoint of building facades correctly match.

To give an impression of the fused TomoSAR point cloud of a large area, Figure 17 shows a result obtained by fusing four TomoSAR point clouds of Berlin obtained from two pairs of cross-heading high resolution TerraSAR-X spotlight images that are fused by selecting an identical GCP as the reference point of all point clouds. The point cloud has in total 63 million scatterers in an area of 50 km${}^2$. Such shadow-free highly detailed TomoSAR point clouds can be further utilized to reconstruct dynamic 3D and 4D city models [44,45,46,112].

5. Conclusions and Outlook

This paper provides a review of the multi-baseline InSAR techniques in the scope of TerraSAR-X data. It covers the evolution of multi-baseline InSAR techniques, particularly with respect to improving the relative estimation accuracy, introducing robustness to the estimators, and achieving accurate absolute positioning of scatterers, which includes bridging the absolutely located scatterers with the relative measures obtained from multi-baseline techniques. Particular focus was placed on our own development work, specifically SL1MMER, M-SL1MMER, Tomo-GENESIS (TomoSAR), RIO (robust estimation), RoMIO (object-based InSAR), and geodetic InSAR (absolute positioning).

Looking into the future, the next generation spaceborne SAR missions, including high resolution wide swath (HRWS) and Tandem-L, will simultaneously possess high resolution and global coverage, which would enable novel applications such as monitoring global changes. Retrieving geo-parameters from these data will require not only new technological approaches to manage large amounts of data, but also new analysis methods. In the following, we would like to point out some promising future directions:

• Big data management technologies: So far, besides big missions, such as global TanDEM-X DEM generation, scientists are dealing with SAR data in the order of up to terabytes. However, this is about to change. Already today, petabytes of Sentinel-1 data are openly accessible to the public. Yet, only very limited groups are capable of national-scale InSAR data processing, to say nothing about global. To be prepared for the future, novel big geo-data management technologies are of high relevance.
• Fast and accurate parameter inversion algorithms: The development of inversion algorithms should keep up with the pace of data growth. For example, as a pre-study of Tandem-L, sequential interferometric phase estimators are proposed instead of full covariance matrix inversion to tackle the challenge of big InSAR data [72]. Fast solvers are demanded for many advanced parameter inversion models that often involve non-convex, nonlinear, and complex-valued optimization problem, such as CS-based tomographic inversion, or low rank complex tensor decomposition. Besides aforementioned model-based inversion methods, recently, data-driven machine learning/deep learning methods have boosted the baseline performances in many remote sensing problems [113], mostly in classification and detection tasks, yet its potential in InSAR processing or more generally in geoparamater estimation is not yet exploited at all. This deserves more attention of the community.
• Complicated motion: Up to now, only limited motion models, such as linear, seasonal or a combination of several basic models, are considered for deformation estimations of InSAR. There are also studies using model order selection to detect different types of motion either being embedded in the estimation [114] or considered as a post-processing [115]. However, the actual motion can be far more complex than any model can describe. The weekly repeat cycle and long-term monitoring capability of future sensors will enable retrieving much more complex motion models, and even allow performing classification of different types of motions and detecting anomalies. This calls for more sophisticated algorithms.
• Data assimilation: At present, the interferometric stack is usually a static cube of interferograms. As Sentinel-1 provides global coverage every six days, new stacking and multi-pass InSAR concepts should be able to include new images without excessive computational burden. This requires development of the data assimilation strategy, as well as novel inversion algorithms that only require the new measurements and the previous estimates for updating the parameters of interest.
• Multi-sensor data fusion: In the Copernicus era, it is standard that more than one data source, such as SAR and optical, is available at any test site. Intelligent use of the complementary peculiarities of the ever-increasing number of diverse remote sensing sensors and other geo-data sources has become the natural choice for many applications [116]. Some preliminary work in the community demonstrated that introducing the geometric prior or semantic prior to InSAR or TomoSAR reconstruction could significantly reduced the number of required SAR data while retaining the estimation accuracy [28,63]. This is definitely a promising future direction.