Modelling the L-Band Snow-Covered Surface Emission in a Winter Canadian Prairie Environment
Abstract
:1. Introduction
2. Site and Data
3. Emission Models
3.1. WALOMIS
3.2. DMRT-ML
3.3. LS-MEMLS-1L
3.4. Soil Emission Model
4. Results
4.1. Frozen Soil Permittivity
4.2. WALOMIS Gaussian Noise Parameterization
4.3. Footprint Integration
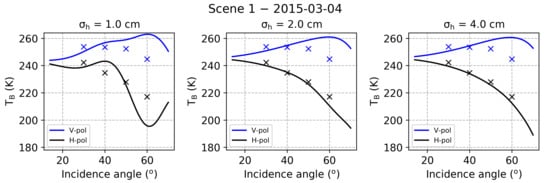
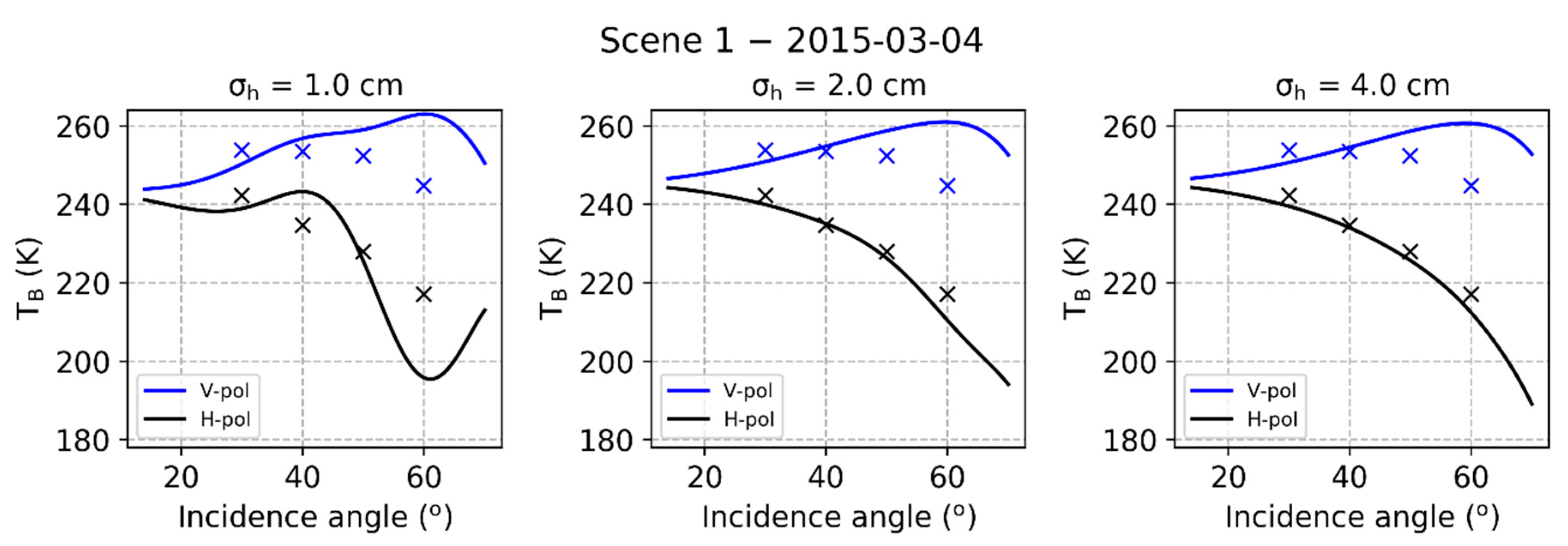
4.4. Snow Emission Model Intercomparison
5. Discussion
5.1. Soil Permittivity Parameterization
5.2. WALOMIS Gaussian Noise Parameterization
5.3. Footprint Integration
5.4. Snow Emission Model Intercomparison
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Lagerloef, G.; deCharon, A.; Lindstrom, E. Ocean salinity and the Aquarius/SAC-D mission: A new frontier in ocean remote sensing. Mar. Technol. Soc. J. 2013, 47, 26–30. [Google Scholar] [CrossRef]
- SMAP Handbook, Mapping Soil Moisture and Freeze/Thaw from Space. Available online: https://smap.jpl.nasa.gov/system/internal_resources/details/original/178_SMAP_Handbook_FINAL_1_JULY_2014_Web.pdf (accessed on 5 September 2018).
- Rautiainen, K.; Parkkinen, T.; Lemmetyinen, J.; Schwank, M.; Wiesmann, A.; Ikonen, J.; Derksen, C.; Davydov, S.; Davydova, A.; Boike, J.; et al. SMOS prototype algorithm for detecting autumn soil freezing. Remote Sens. Environ. 2016, 180, 346–360. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Schwank, M.; Kontu, A.; Ménard, C.B.; Mätzler, C.; Drusch, M.; Wiesmann, A.; Ikonen, J.; Pulliainen, J. Detection of soil freezing from L-band passive microwave observations. Remote Sens. Environ. 2014, 147, 206–218. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Derksen, C.; Brucker, L.; Langlois, A.; Mialon, A.; Kerr, Y.H. Evaluation of Spaceborne L-Band Radiometer Measurements for Terrestrial Freeze/Thaw Retrievals in Canada. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4442–4459. [Google Scholar] [CrossRef]
- Derksen, C.; Xu, X.; Dunbar, S.R.; Colliander, A.; Kim, Y.; Kimball, J.S.; Black, T.A.; Euskirchen, E.; Langlois, A.; Loranty, M.M.; et al. Retrieving landscape freeze/thaw state from Soil Moisture Active Passive (SMAP) radar and radiometer measurements. Remote Sens. Environ. 2017, 194, 48–62. [Google Scholar] [CrossRef]
- Schwank, M.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Pulliainen, J.; Lemmetyinen, J.; Drusch, M. Snow density and ground permittivity retrieved from L-band radiometry: A synthetic analysis. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3833–3845. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Derksen, C.; Toose, P.; et al. Snow density and ground permittivity retrieved from L-Band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Mäkynen, M.; Drusch, M. Sea ice thickness retrieval from SMOS brightness temperatures during the Arctic freeze-up period. Geophys. Res. Lett. 2012, 39, L05501. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.-J.; Richaume, P.; Schwank, M. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A.; Ding, K.-H. Scattering of Electromagnetic Waves, Vol. 1: Theories and Applications; Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Picard, G.; Brucker, L.; Roy, A.; Dupont, F.; Fily, M.; Royer, A.; Harlow, C. Simulation of the microwave emission of multilayered snowpacks using the Dense Media Radiative transfer theory: The DMRT-ML model. Geosci. Model Dev. 2013, 6, 1061–1078. [Google Scholar] [CrossRef]
- Pulliainen, J.T.; Grandell, J.; Hallikainen, M.T. HUT snow emission model and its applicability to snow water equivalent retrieval. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1378–1390. [Google Scholar] [CrossRef]
- Schwank, M.; Rautiainen, K.; Mätzler, C.; Stähli, M.; Lemmetyinen, J.; Pulliainen, J.; Vehviläinen, J.; Kontu, A.; Ikonen, J.; Ménard, C.B.; et al. Model for microwave emission of a snow-covered ground with focus on L band. Remote Sens. Environ. 2014, 154, 180–191. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground -based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Leduc-Leballeur, M.; Picard, G.; Milaon, A.; Arnaud, L.; Lefebvre, E.; Possenti, P.; Kerr, Y.H. Modeling L-band brightness temperature at dome C in Antarctica and comparison with SMOS observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4022–4032. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M.; Mätzler, C. Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sens. 2017, 9, 1185. [Google Scholar] [CrossRef]
- Hofer, R.; Mätzler, C. Investigations on snow parameters by radiometry in the 3- to 60-mm wavelength Region. J. Geophys. Res. 1980, 85, 453–460. [Google Scholar] [CrossRef]
- Schwank, M.; Stähli, M.; Wydler, H.; Leuenberger, J.; Mätzler, C.; Member, S.; Flühler, H. Microwave L-Band Emission of Freezing Soil. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1252–1261. [Google Scholar] [CrossRef]
- Mätzler, C. Applications of the interactions of micowaves with natural snow cover. Remote Sens. Rev. 1987, 2, 259–392. [Google Scholar] [CrossRef]
- Montpetit, B.; Royer, A.; Roy, A.; Langlois, L.; Derksen, D. Snow microwave emission modeling of ice lenses within a snowpack using the microwave emission model for layered snowpacks. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4705–4717. [Google Scholar] [CrossRef]
- Rees, A.; Lemmetyinen, J.; Derksen, C.; Pulliainen, J.; English, M. Observed and modelled effects of ice lens formation on passive microwave brightness temperatures over snow covered tundra. Remote Sens. Environ. 2010, 114, 116–126. [Google Scholar] [CrossRef]
- Leduc-Leballeur, M.; Picard, G.; Macelloni, G.; Arnaud, L.; Brogioni, M.; Mialon, A.; Kerr, Y.H. Influence of snow surface properties on L-band brightness temperature at Dome C, Antarctica. Remote Sens. Environ. 2017, 199, 427–436. [Google Scholar] [CrossRef]
- Chabot, M.; Lindsay, J.; Rowlandson, T.; Berg, A.A. Comparing the Use of Terrestrial LiDAR Scanners and Pin Profilers for Deriving Agricultural Roughness Statistics. Can. J. Remote Sens. 2018, 1–16. [Google Scholar] [CrossRef]
- Lindsay, J.B. Whitebox GAT: A case study in geomorphometric analysis. Comput. Geosci. 2016, 95, 75–84. [Google Scholar] [CrossRef]
- Toose, P.; Roy, A.; Solheim, F.; Derksen, C.; Royer, A.; Walker, A. Radio frequency interference mitigating hyperspectral L-band radiometer. Geosci. Instrum. Method Data Syst. 2017, 6, 39–51. [Google Scholar] [CrossRef]
- West, R.D.; Winebrenner, D.P.; Tsang, L.; Rott, H. Microwave emission from density-stratified Antarctic firn at 6 cm wavelength. J. Glaciol. 1996, 42, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Tsang, L.; Kong, J.A. Scattering of Electromagnetic Waves, Vol. 3: Advanced Topics; Wiley-Interscience: Paris, France, 2001. [Google Scholar]
- Tsang, L.; Kong, J.; Shin, R. Theory of Microwave Remote Sensing; Wiley-Interscience: New York, NY, USA, 1987. [Google Scholar]
- Tan, S.; Aksoy, M.; Brogioni, M.; Macelloni, G.; Durand, M.; Jezek, K.C.; Wang, T.-L.; Tsang, L.; Johnson, J.T.; Drinkwater, M.R.; et al. Physical models of layered polar firn brightness temperatures from 0.5 GHz to 2 GHz. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3681–3691. [Google Scholar] [CrossRef]
- Jin, Y. Electromagnetic Scattering Modelling for Quantitative Remote Sensing; World Scientific: Singapore, 1994. [Google Scholar]
- Naderpour, R.; Schwank, M.; Mätzler, C.; Lemmetyinen, J.; Steffen, K. Snow Density and Ground Permittivity Retrieved From L-Band Radiometry: A Retrieval Sensitivity Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3148–3161. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Pulliainen, J.; Vehvilainen, J.; Drusch, M.; Kontu, A.; Kainulainen, J.; Seppänen, J. L-band radiometer observations of soil processes in boreal and subarctic environments. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1483–1497. [Google Scholar] [CrossRef]
- Wegmüller, U.; Mätzler, C. Rough bare soil reflectivity model. IEEE Trans. Geosci. Remote 1999, 37, 1391–1395. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Derksen, C.; Rowlandson, T.; Berg, A.; Lemmetyinen, J.; Royer, A.; Tetlock, E.; Helgason, W.; Sonnentag, O. Spatial Variability of L-Band Brightness Temperature during Freeze/Thaw Events over a Prairie Environment. Remote Sens. 2017, 9, 894. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.-K. Microwave dielectric behavior of wet soil—Part I: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]
- Mironov, V.L.; De Roo, R.D.; Savin, I.V. Temperature-dependable microwave dielectric model for an Arctic soil. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2544–2556. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W. Modelling blowing snow redistribution to prairie wetlands. Hydrol. Process. 2009, 23, 2557–2569. [Google Scholar] [CrossRef]
- Li, L.; Pomeroy, J. Estimates of threshold wind speeds for snow transport using meteorological data. J. Appl. Meteorol. 1999, 36, 205–213. [Google Scholar] [CrossRef]






| Dates | Snow Depth (cm) | Snow Bulk Density (kg m−3) | Air Temperature (°C) | Magna Probe Mean Snow Depth and Standard Deviation (cm) | ||
|---|---|---|---|---|---|---|
| Scene 1 | Scene 3 | Scene 1 | Scene 3 | |||
| 2014-12-7 | 20 | 20 | 230 | 230 | −6.6 | 12 ± 5 |
| 2014-12-19 | 14 | 18 | 460 | 490 | −9.0 | - |
| 2015-1-11 | 26 | 28 | 226 | 563 | −20.2 | 18 ± 10 |
| 2015-2-9 | 12 | 30 | 360 | 480 | −13.9 | 18 ± 7 |
| 2015-3-4 | 36 | 31 | 283 | 358 | −16.8 | 25 ± 7 |
| RMSE for TBV-pol (K) | RMSE for TBH-pol (K) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 30° | 40° | 50° | 60° | All | 30° | 40° | 50° | 60° | All | |
| WALOMIS | 4.6 | 2.9 | 7.8 | 15.4 | 9.1 | 6.9 | 7.8 | 10.2 | 12.9 | 9.7 |
| DMRT-ML | 4.1 | 2.6 | 7.7 | 14.8 | 8.8 | 5.9 | 7.0 | 11.0 | 15.7 | 10.5 |
| LS-MEMLS-1L | 2.5 | 3.8 | 9.2 | 16.1 | 9.6 | 3.7 | 4.3 | 7.3 | 11.2 | 7.2 |
| Std for TBV-pol (K) | Std for TBH-pol (K) | |||||||
|---|---|---|---|---|---|---|---|---|
| 30° | 40° | 50° | 60° | 30° | 40° | 50° | 60° | |
| WALOMIS | 3.8 | 3.1 | 2.6 | 2.5 | 6.7 | 7.5 | 8.1 | 10.1 |
| DMRT-ML | 3.1 | 2.5 | 2.3 | 2.4 | 5.6 | 6.8 | 8.6 | 11.1 |
| LS-MEMLS-1L | 2.6 | 2.5 | 2.4 | 2.4 | 2.9 | 2.9 | 2.8 | 2.8 |
| Measures | 2.3 | 2.7 | 2.9 | 4.2 | 5.3 | 7.8 | 11.3 | 13.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, A.; Leduc-Leballeur, M.; Picard, G.; Royer, A.; Toose, P.; Derksen, C.; Lemmetyinen, J.; Berg, A.; Rowlandson, T.; Schwank, M. Modelling the L-Band Snow-Covered Surface Emission in a Winter Canadian Prairie Environment. Remote Sens. 2018, 10, 1451. https://doi.org/10.3390/rs10091451
Roy A, Leduc-Leballeur M, Picard G, Royer A, Toose P, Derksen C, Lemmetyinen J, Berg A, Rowlandson T, Schwank M. Modelling the L-Band Snow-Covered Surface Emission in a Winter Canadian Prairie Environment. Remote Sensing. 2018; 10(9):1451. https://doi.org/10.3390/rs10091451
Chicago/Turabian StyleRoy, Alexandre, Marion Leduc-Leballeur, Ghislain Picard, Alain Royer, Peter Toose, Chris Derksen, Juha Lemmetyinen, Aaron Berg, Tracy Rowlandson, and Mike Schwank. 2018. "Modelling the L-Band Snow-Covered Surface Emission in a Winter Canadian Prairie Environment" Remote Sensing 10, no. 9: 1451. https://doi.org/10.3390/rs10091451
APA StyleRoy, A., Leduc-Leballeur, M., Picard, G., Royer, A., Toose, P., Derksen, C., Lemmetyinen, J., Berg, A., Rowlandson, T., & Schwank, M. (2018). Modelling the L-Band Snow-Covered Surface Emission in a Winter Canadian Prairie Environment. Remote Sensing, 10(9), 1451. https://doi.org/10.3390/rs10091451