Modeling and Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution
Abstract
:1. Introduction
2. Methodology
3. Data and Processing Strategy
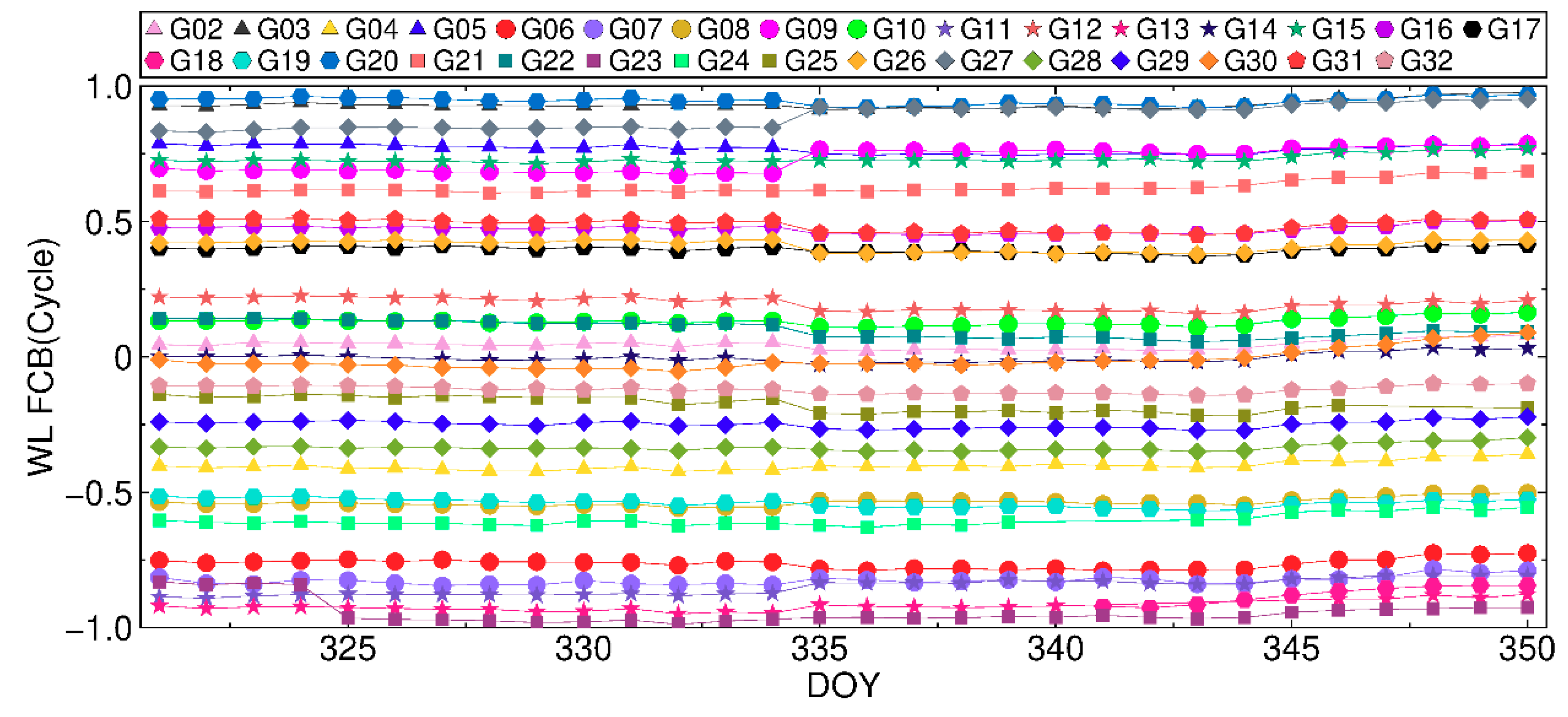
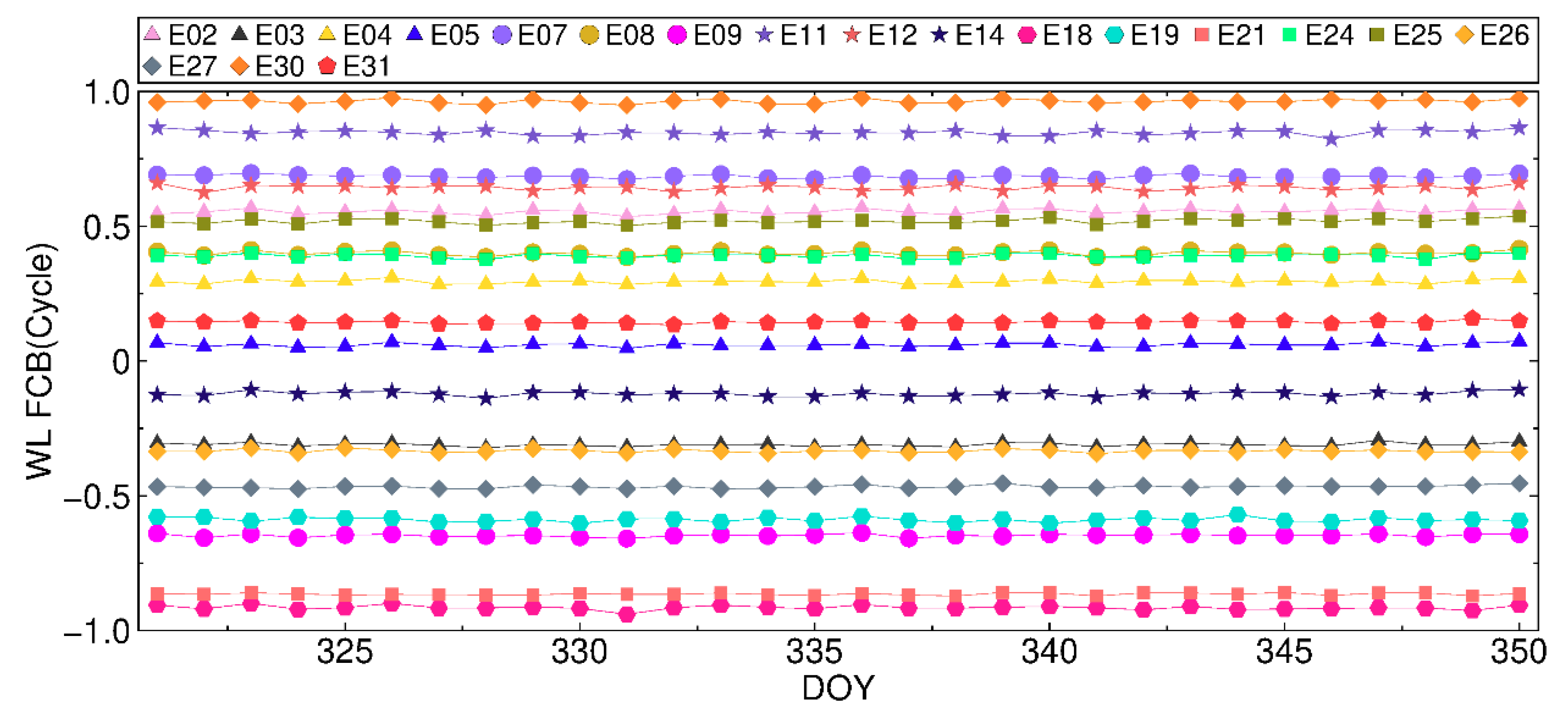
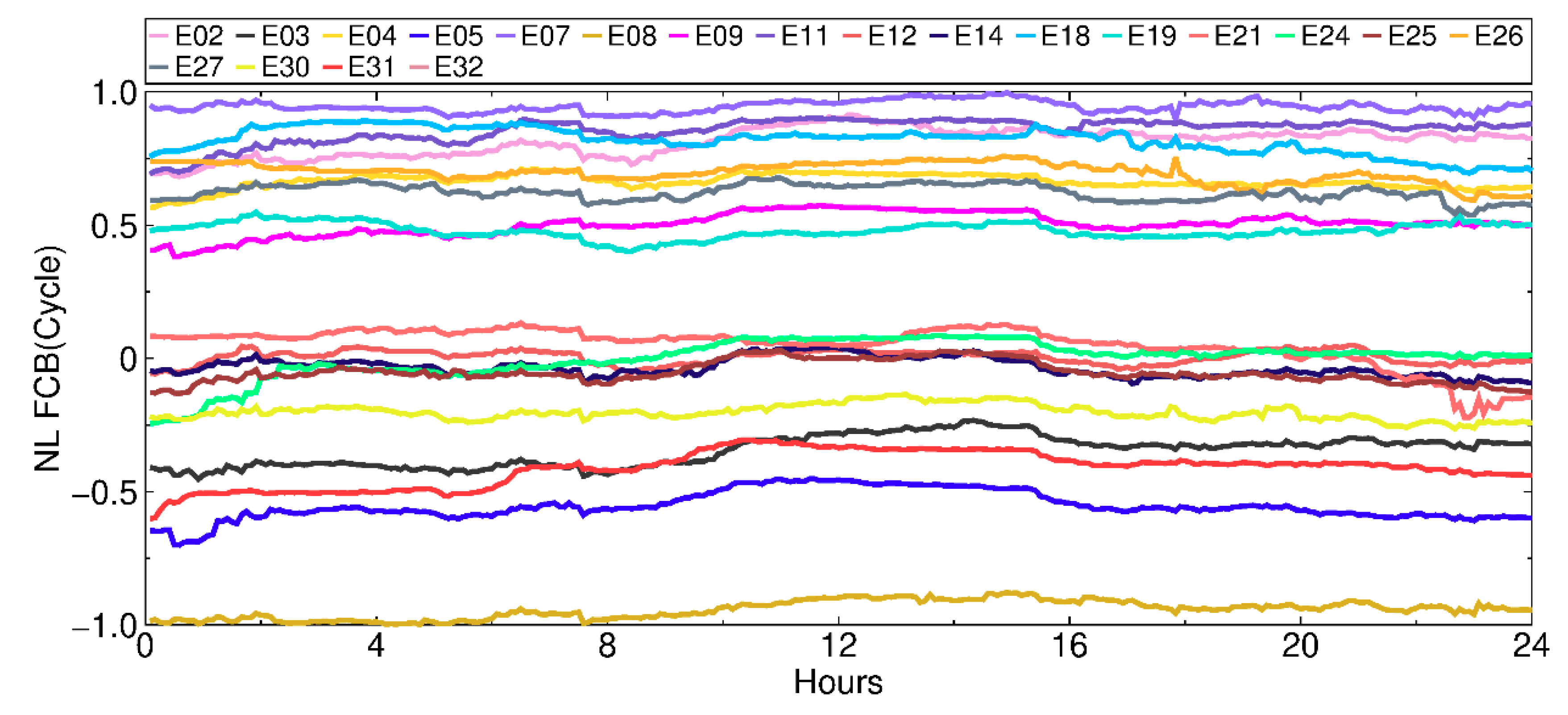
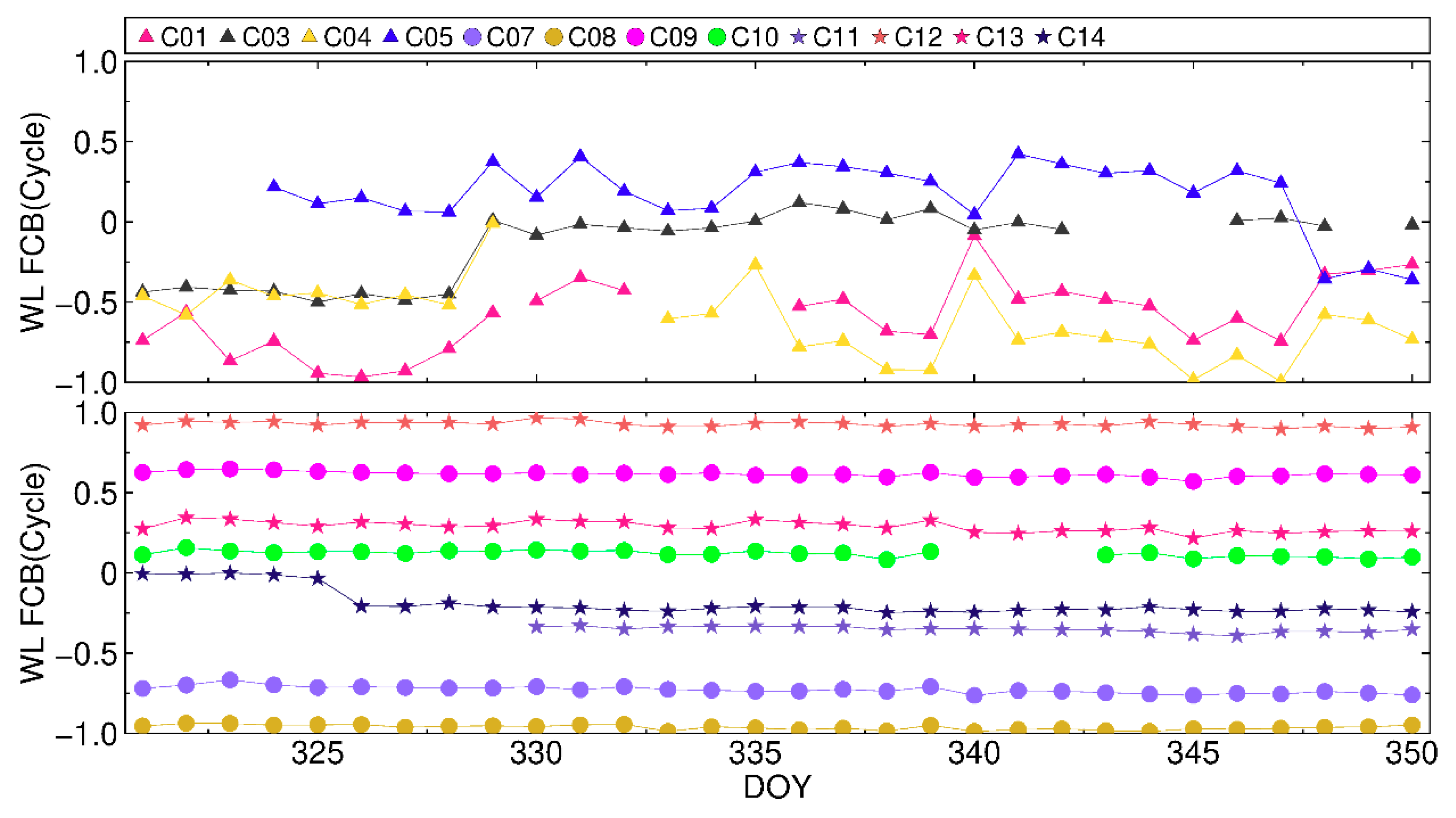
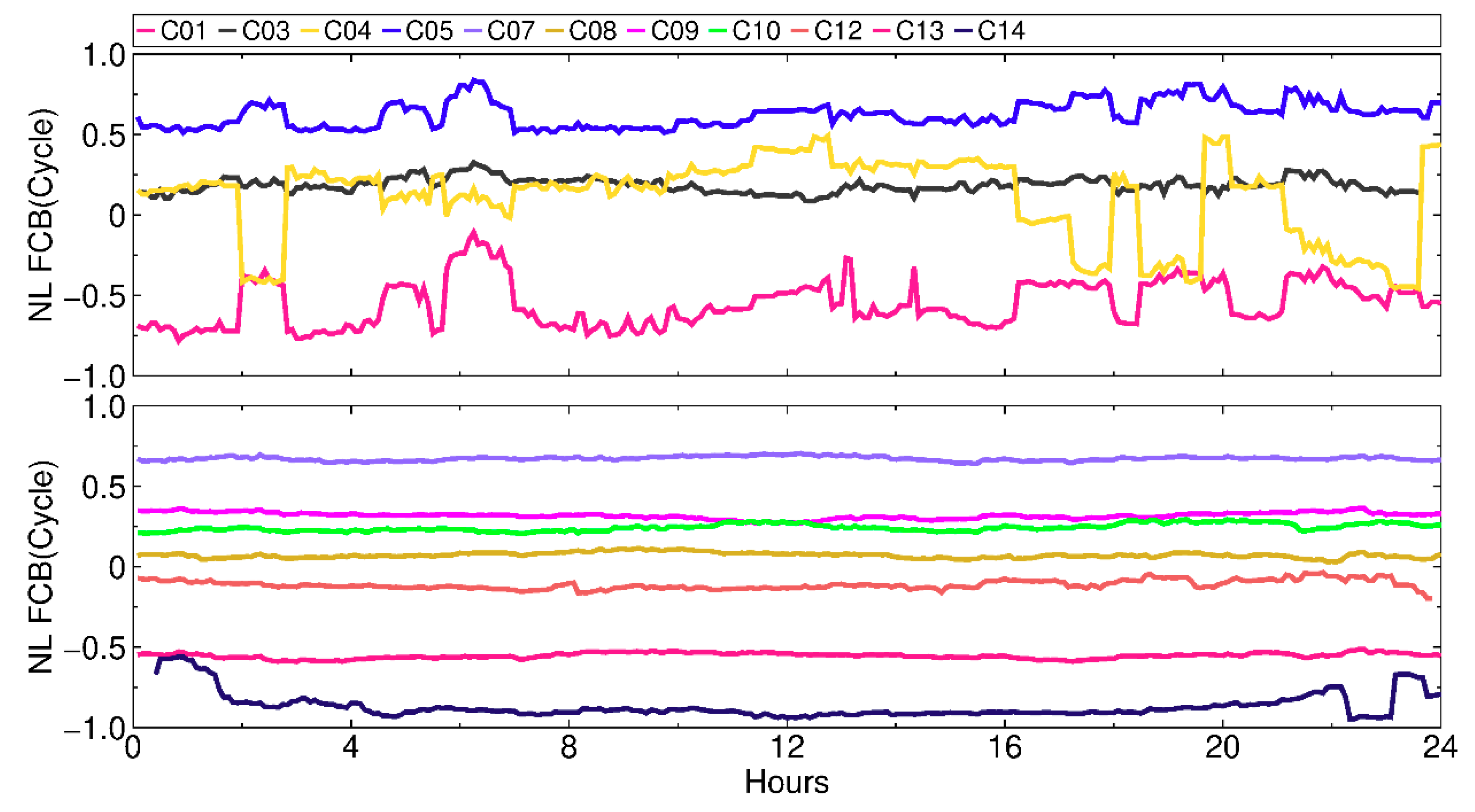
4. FCB Estimation
4.1. GPS FCB
4.2. Galileo FCB
4.3. BDS FCB
5. PPP AR Results and Analysis
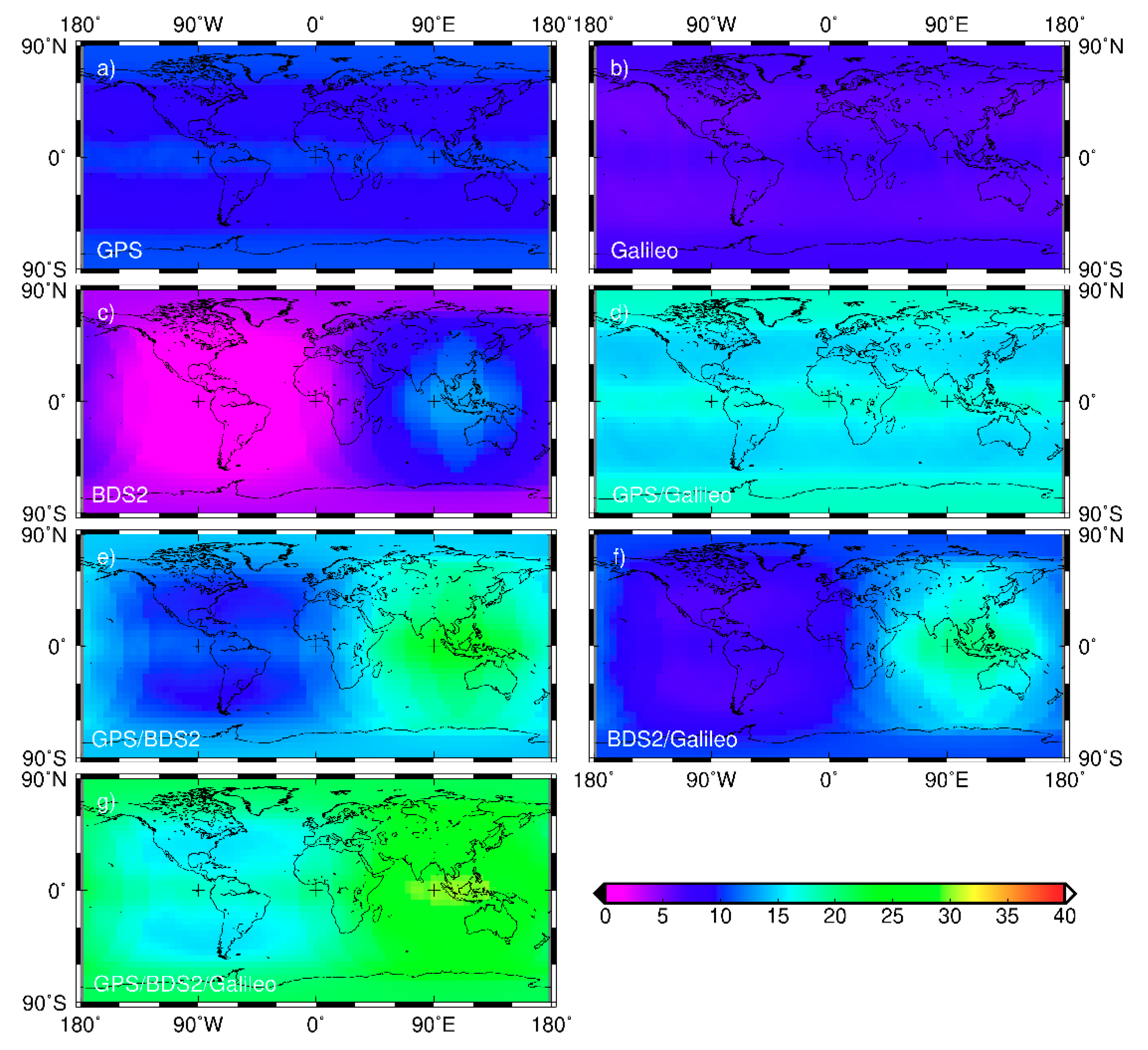
5.1. Evaluation of Satellite Availability and PDOP
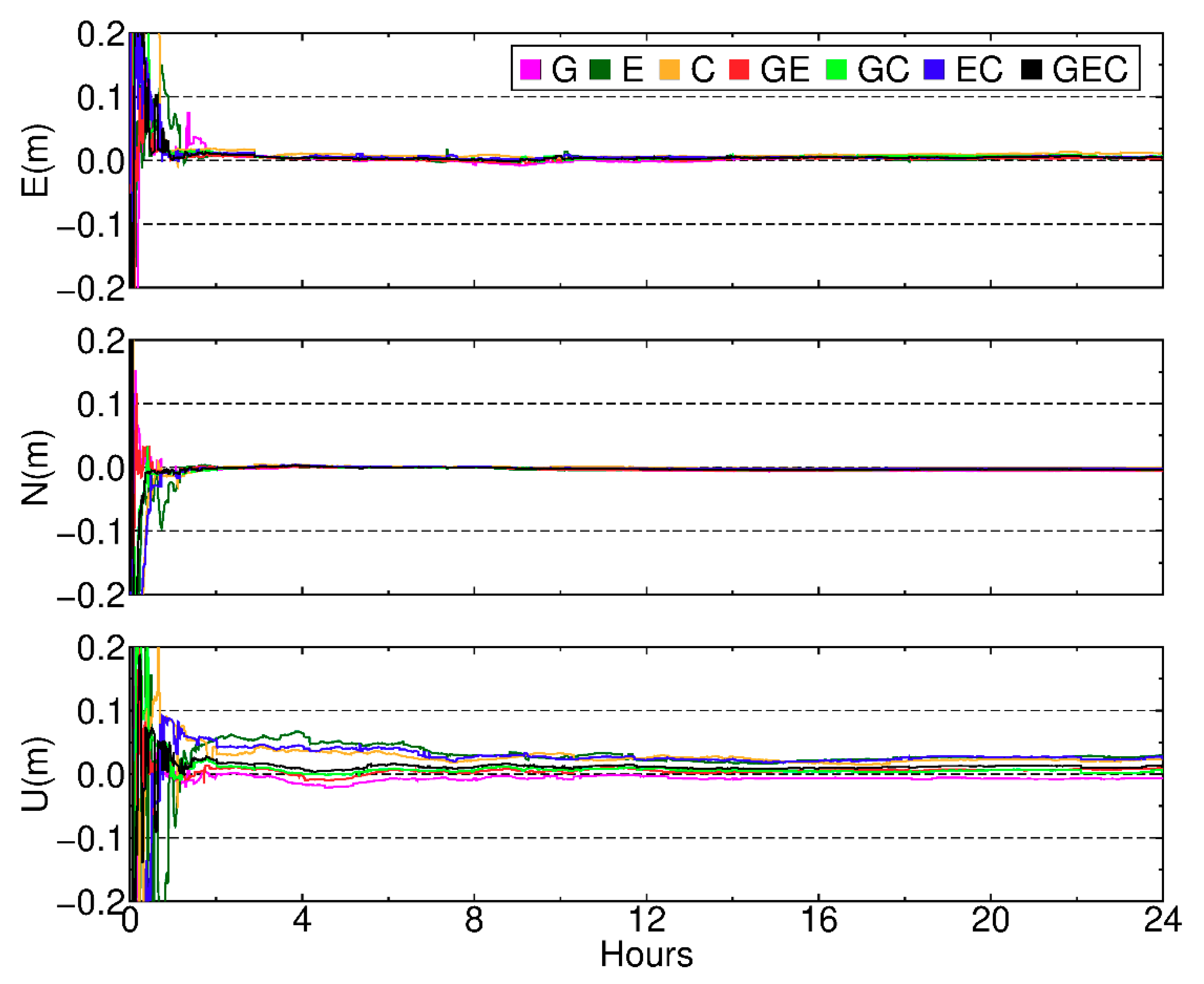
5.2. Performance of PPP AR
6. Discussions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Ge, M.; Helse, S.; Wickert, J.; Bender, M. Real-time GPS sensing of atmospheric water vapor: Precise point positioning with orbit, clock, and phase delay corrections. Geophys. Res. Lett. 2014, 41, 3615–3621. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geod. 2019, 93, 977–991. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, K. Performance analysis of precise point positioning using Real-time orbit and clock products. J. Glob. Position. Syst. 2004, 3, 95–100. [Google Scholar] [CrossRef]
- Le, A.Q.; Tiberius, C. Single-frequency precise point positioning with optimal filtering. GPS Solut. 2007, 11, 61–69. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Performance analysis of precise point positioning based on combined GPS and GLONASS. In Proceedings of the ION GNSS, 25–28 September 2007; pp. 858–865. [Google Scholar]
- Melgard, T.; Vigen, E.; Jong, K.D.; Lapucha, D.; Visser, H.; Oerpen, O. G2-The first real-time GPS and GLONASS precise orbit and clock service. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 9 September 2001; Volume 5538, pp. 1885–1891. [Google Scholar]
- Li, X.; Zhang, X.; Guo, F. Study on precise point positioning based on combined GPS and GLONASS. In Proceedings of the ION GNSS, Savannah, GA, USA, 22–25 September 2009; pp. 2449–2459. [Google Scholar]
- Li, P.; Zhang, X. Modeling and Performance Analysis of GPS/GLONASS/BDS Precise Point Positioning. In Proceedings of the China Satellite Navigation Conference, Nanjing, China, 21–23 May 2014; pp. 251–263. [Google Scholar]
- Li, W.; Teunissen, P.J.G.; Zhang, B.; Verhagen, S. Precise point positioning using GPS and COMPASS observations. In Proceedings of the China Satellite Navigation Conference, Wuhan, China, 15–17 May 2013; pp. 367–378. [Google Scholar]
- Shen, X.; Gao, Y. Analyzing the impacts of Galileo and modernized GPS on precise point positioning. In Proceedings of the ION GPS, Portland, OR, USA; 2006; Volume 49, pp. 1532–1539. [Google Scholar]
- Cao, W.; Hauschild, A.; Steigenberger, P.; Langley, R.B.; Urquhart, L.; Santos, M. Performance evaluation of integrated GPS/GIOVE precise point positioning. In Proceedings of the ION NTM, San Diego, CA, USA, March 2010; pp. 540–552. [Google Scholar]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Kleusberg, A. GPS Observation Equations and Positioning Concepts. In Lecture Notes in Earth Sciences: GPS for Geodesy; Springer: Berlin/Heidelberg, Germany, 1996; Volume 60, pp. 175–217. [Google Scholar]
- Gabor, M.J.; Nerem, R.S. GPS Carrier Phase Ambiguity Resolution Using Satellite-Satellite Single Differences. In Proceedings of the ION GPS 1999, Nashville, TN, USA, 14–17 September 1999; pp. 1569–1578. [Google Scholar]
- Gabor, M.J.; Nerem, R.S. Characteristics of Satellite-Satellite Single Difference Widelane Fractional Carrier Phase Biases. In Proceedings of the ION GPS 2000, Salt Lake City, UT, USA, 19–22 September 2000; pp. 396–406. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Collins, P.; Lahaye, F.; Herous, P.; Bisnath, S. Precise point positioning with AR using the decoupled clock model. In Proceedings of the ION GNSS. Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Geng, J.; Teferle, F.N.; Shi, C.; Meng, X.; Dodson, A.H.; Liu, J. Ambiguity resolution in precise point positioning with hourly data. GPS Solut. 2009, 13, 263–270. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Alan, H.D.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Liu, Y.; Song, W.; Lou, Y.; Ye, S.; Zhang, R. GLONASS phase bias estimation and its PPP ambiguity resolution using homogeneous receivers. GPS Solut. 2017, 21, 427–437. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, S.; Song, W.; Lou, Y.; Chen, D. Integrating GPS and BDS to shorten the initialization time for ambiguity-fixed PPP. GPS Solut. 2017, 21, 333–343. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Guo, F. Ambiguity resolved precise point positioning with GPS and BeiDou. J. Geod. 2017, 91, 25–40. [Google Scholar]
- Li, X.; Li, X.; Yuan, Y.; Zhang, K.; Zhang, X.; Wickert, J. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo. J. Geod. 2017, 92, 579–608. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, W.; Li, Z.; Chen, H.; Zhao, W. Comparison of convergence time and positioning accuracy among BDS, GPS and BDS/GPS precise point positioning with ambiguity resolution. Adv. Space Res. 2019, 63, 3489–3504. [Google Scholar] [CrossRef]
- Melbourne, W.G. The case for ranging in GP S-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985. [Google Scholar]
- Wübbena, G. Software developments for geodetic positioning with GPS using TI-4100 code and carrier measurements. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985. [Google Scholar]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603. [Google Scholar]
- Blewitt, G. An automatic editing algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, W.; Chen, H.; Zhao, W.; Huo, L.; Huang, L.; Chen, Q. An analysis of inter-system biases in BDS/GPS precise point positioning. GPS Solut. 2019, 23, 116. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. 2009. Available online: http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf (accessed on 15 January 2019).
- Hauschild, A.; Montenbruck, O.; Sleewaegen, J.M.; Huisman, L.; Teunissen, P. Characterization of Compass M-1 signals. GPS Solut. 2012, 16, 117–126. [Google Scholar] [CrossRef]
- Perello Gisbert, J.V.; Batzilis, N.; Risueno, G.L.; Rubio, J.A. GNSS payload and signal characterization using a 3 m dish antenna. In Proceedings of the ION GNSS, Nashville, TN, USA, 9 December 2012; pp. 347–356. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Riley, S. A COMPASS for Asia: First experience with the BeiDou-2 regional navigation system. In Proceedings of the Poster at IGS Workshop, Olsztyn, Poland, 23–27 July 2012. [Google Scholar]
- Montenbruck, O.; Rizos, C.; Weber, R.; Weber, G.; Neilan, R.; Hugentobler, U. Getting a grip on multi-GNSS—the international GNSS service MGEX campaign. GPS World 2013, 24, 44–49. [Google Scholar]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]






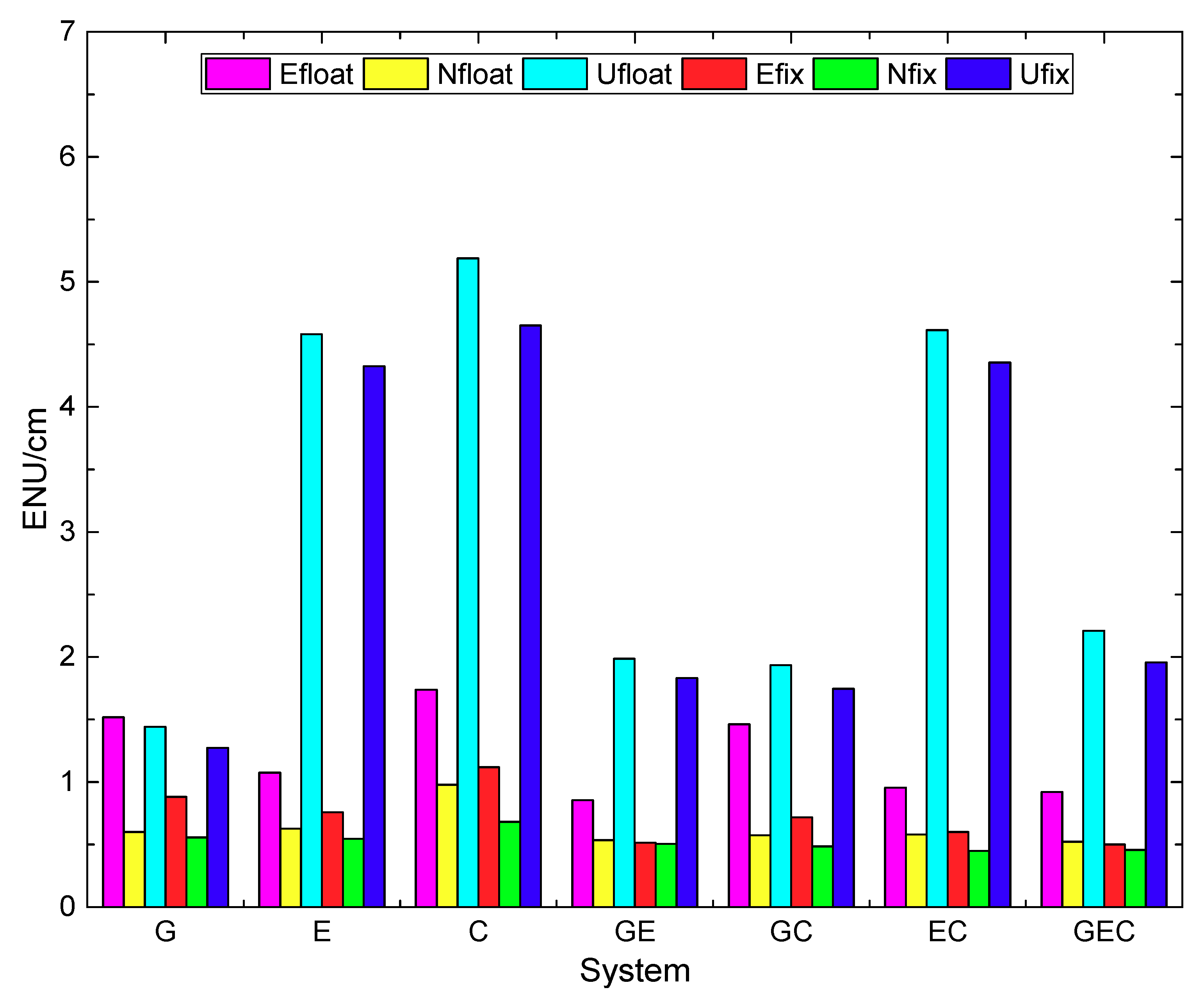
| System | Efloat | Nfloat | Ufloat | Efix | Nfix | Ufix |
|---|---|---|---|---|---|---|
| G | 1.52 | 0.60 | 1.44 | 0.88 | 0.56 | 1.27 |
| E | 1.08 | 0.63 | 4.58 | 0.76 | 0.55 | 4.33 |
| C | 1.74 | 0.98 | 5.19 | 1.12 | 0.68 | 4.65 |
| GE | 0.86 | 0.53 | 1.98 | 0.51 | 0.50 | 1.83 |
| GC | 1.46 | 0.57 | 1.93 | 0.72 | 0.49 | 1.75 |
| EC | 0.95 | 0.58 | 4.61 | 0.60 | 0.45 | 4.36 |
| GEC | 0.92 | 0.52 | 2.21 | 0.50 | 0.46 | 1.96 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Chen, H.; Jiang, W.; Xi, R.; Zhao, W.; Song, C.; Zhou, X. Modeling and Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution. Remote Sens. 2019, 11, 2693. https://doi.org/10.3390/rs11222693
Liu X, Chen H, Jiang W, Xi R, Zhao W, Song C, Zhou X. Modeling and Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution. Remote Sensing. 2019; 11(22):2693. https://doi.org/10.3390/rs11222693
Chicago/Turabian StyleLiu, Xuexi, Hua Chen, Weiping Jiang, Ruijie Xi, Wen Zhao, Chuanfeng Song, and Xingyu Zhou. 2019. "Modeling and Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution" Remote Sensing 11, no. 22: 2693. https://doi.org/10.3390/rs11222693






