Soil Moisture Estimate Uncertainties from the Effect of Soil Texture on Dielectric Semiempirical Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Descriptions
2.2. Soil Texture Grouping Over All Soil Texture Cases
2.3. Methods of Soil Moisture Estimate
- 1:
- Mironov–Dobson
- 2:
- Wang–Dobson
- 3:
- SSMDM–Dobson
- 4:
- Mironov–Wang
- 5:
- SSMDM–Wang
- 6:
- Mironov–SSMDM
- The soil texture changes from clay to silt, and the sand content remains constant: from ‘H’ (clay) to ‘H1’ (clay), from ‘H’ (clay) to ‘C1’ (loam), from ‘H’ (clay) to ‘E1’ (silt), and from ‘H’ (clay) to ‘I’ (silt).
- The soil texture changes from sand to silt, and the clay content remains constant: from ‘I’(sand) to ‘E1’ (sand), from ‘I’ (sand) to ‘A’ (loam), from ‘I’ (sand) to ‘H1’ (silt), and from ‘I’ (sand) to ‘H’ (silt).
- The soil texture changes from sand to clay, and the silt content remains constant: from ‘H’ (sand) to ‘H1’ (sand), from ‘H’ (sand) to ‘H’ (loam), from ‘H’ (sand) to ‘E1’ (clay), and from ‘H’ (sand) to ‘I’ (clay).
3. Results and Analysis
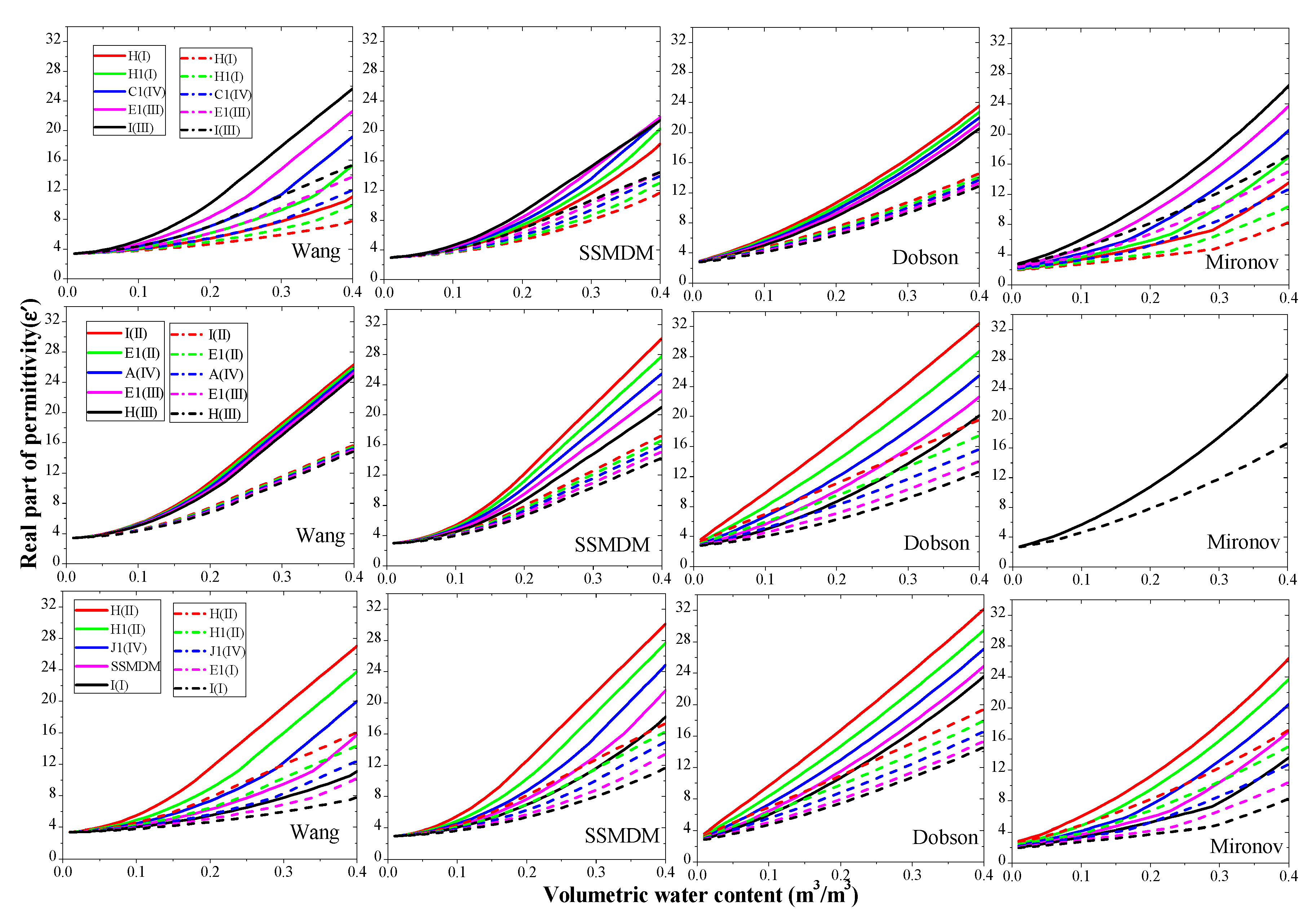
3.1. The Effect of Soil Texture on Models
3.1.1. Different Ways Considering Soil Texture
- The distinction between bound water and bulk water
- The dielectric properties of dry soil
- The dielectric properties of bulk water
- The dielectric properties of bound water
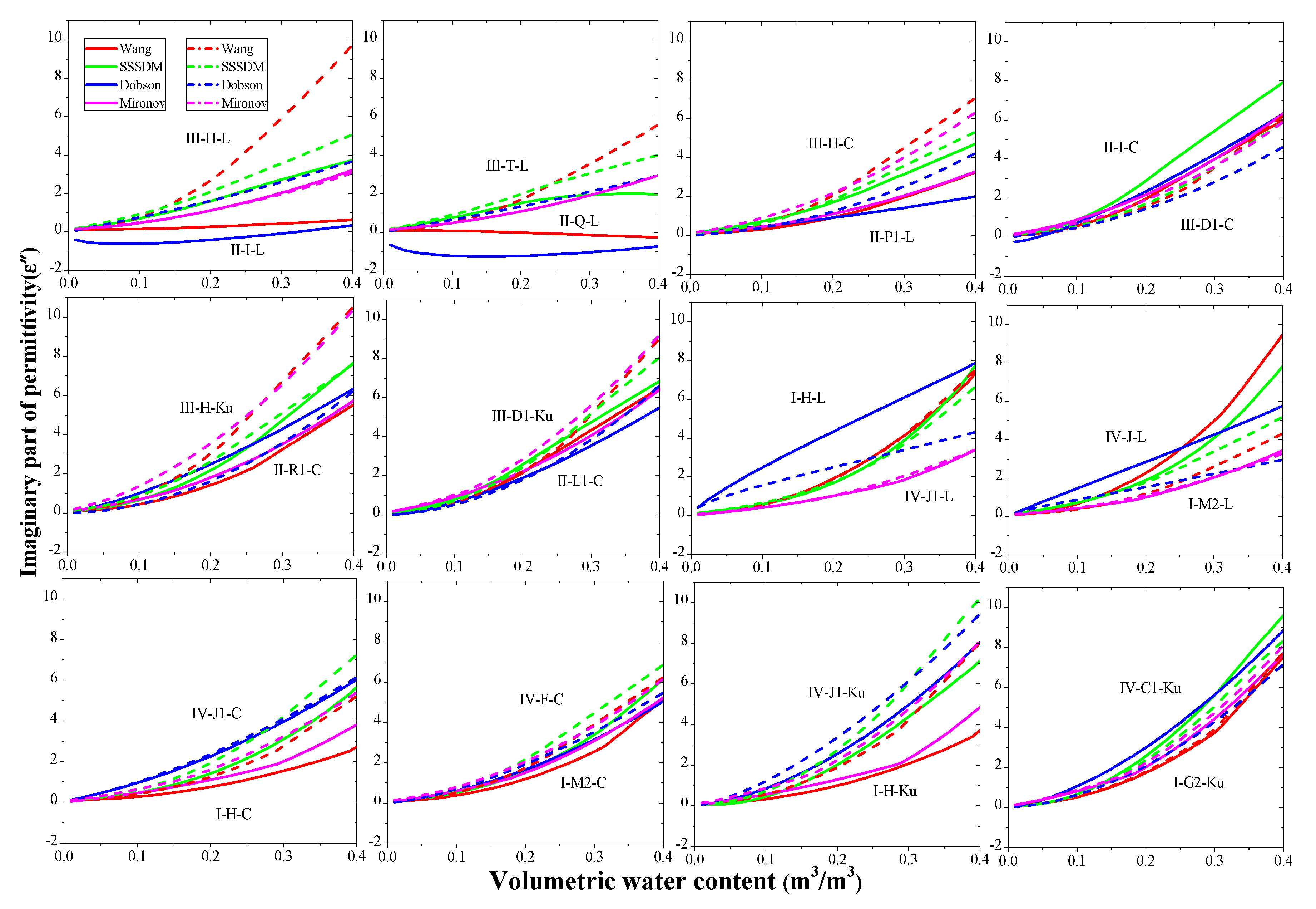
3.1.2. Simulation Differences and Reliability Evaluation
3.2. Soil Moisture Estimate Uncertainties
3.2.1. Soil Moisture Estimate Uncertainties from Soil Dielectric Model Discordance
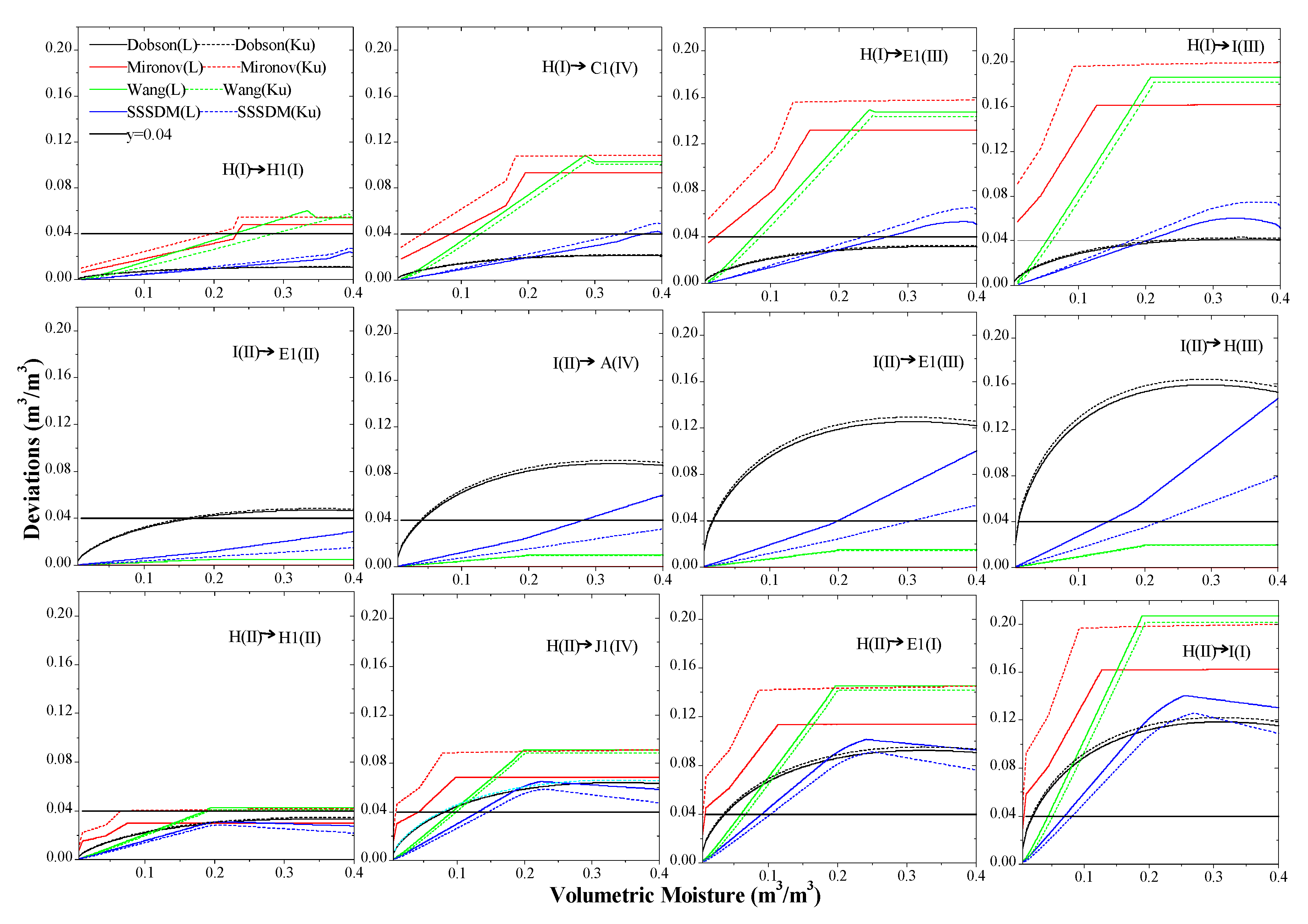
3.2.2. Soil Moisture Estimate Uncertainties from Soil Texture Discordance
4. Discussion and Conclusions
- For soil texture cases under the condition of 55% ≤ silt content ≤ 70% with low sand content, and 50% ≤ silt content ≤ 55%, the discrepancies between these four SEMs are small, and similar results can be achieved with all of them when chosen for soil moisture retrieval algorithms, except a few cases under the condition of 50% ≤ silt content ≤ 55% with high clay content (about >40%), where soil moisture estimation deviations are a little higher than 0.04 m3/m3 due to the discrepancies between the Dobson and Wang model at low soil moisture.
- For soil texture cases under the condition of silt content ≥ 15% with low clay content for soil texture cases in Section II, and silt content ≥ 20% with low clay content for soil texture cases in Section IV, with the exception of the Dobson model at low and medium volumetric water content due to the lack of distinction between bound water and bulk water, the discrepancies between the Wang, Mironov, and SSMDM models are small, and similar results are achieved.
- For soil texture cases under the condition of silt content ≥ 15% with high clay content for soil texture cases in Section II and silt content ≥ 20% with high clay content for soil texture cases in Section IV, the deviations will exceed the 4% volumetric water content requirement between the Dobson model and another model at low or medium water volumetric water content due to the lack of distinction between bound water and bulk water, and between the Wang and other models (i.e., Mironov or SSMDM model) at low water volumetric water content; whereas the discrepancies between the Mironov and SSMDM models are small. And these two SEMs for soil moisture retrieval algorithms can be considered firstly because both of them consider the dielectric properties of FSW. However, these soil texture cases lack validation with experimental data, and more accurate experimental data are needed to assess them.
- The Mironov model, in which the clay percentage is the sole input parameter of soil texture, may introduce some uncertainties for soil texture cases with a large proportion of a certain component. For soil texture cases under the condition of 55% ≤ silt content ≤ 70% with high sand content and silt content > 70% at low frequencies, the discrepancies between the Dobson and SSMDM models are small. Either of these two SEMs for soil moisture retrieval algorithms can be tested firstly. Moreover, for these soil texture cases at high frequencies (about >10 GHz), the discrepancies between the Wang and SSMDM models are small. Either of these two SEMs for soil moisture retrieval algorithms can be tested firstly. However, all analyses are based on theory and lack validation with experimental data, and more accurate experimental data are needed to assess this.
- For soil texture cases under the condition of silt content < 15% in Section II, silt content < 20% in Section IV, and all soil texture cases in Section I, we cannot provide reliable recommendations due to insufficient experimental data. The SSMDM can be tested firstly due to its better theoretical principle; however, the selection of the most appropriate model may largely depend on soil water content. Thus, more accurate experimental data are needed to provide a proposal.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| <0.04 | >0.04 | ||
|---|---|---|---|
| Mironov-Dobson ‘1′ | I Clay content ≥ 50%) | Some cases at high moisture when silt content ≥ 45%, or rare cases at very low and very high moisture when clay content ≤ 55% | Other cases |
| II (Sand content ≥ 50%) | When silt content ≥ 35%, or 25% ≤ silt content < 35% with low clay content, or some cases at low and high moisture for other samples | When silt content < 10% or some samples when 10% ≤ silt content ≤ 20% with high clay content except for rare cases at very low moisture, or other cases at medium moisture for other samples | |
| III (Silt content ≥ 50%) | Other cases | Some cases at relatively high moisture when silt content > 70% or 55% < silt content ≤ 70% with high sand content, or some cases at low or low and medium moisture when silt content ≤ 55% with high clay content | |
| IV (Clay content < 50% and Sand content < 50% and Silt content < 50%) | When silt content ≥ 40% and clay content ≤ 20%, or silt content ≥ 40% and (silt content minus clay content) ≥ 15% at low frequencies, or at relatively high moisture for other samples | When clay content ≥ 35% and silt content ≤ 20% or clay content ≥ 45% and silt content ≤ 30%, or at relatively low moisture for other samples except for rare cases at very low moisture for low frequencies | |
| Wang-Dobson ‘2′ | I | When VWC ≤ 0.08, or some cases when 0.08 < VWC < 0.16 for all samples | When VWC ≥ 0.16, or other cases when 0.08 < VWC < 0.16 for all samples |
| II | When silt content ≥ 45%, or some samples when 40% ≤ silt content < 45% with low clay content, or some cases at low and high moisture for other samples | When silt content ≤ 20% except a few cases at very low moisture, some samples when 20% < silt content ≤ 30% with high clay content, or other cases at medium moisture for other samples | |
| III | Other cases | Some cases at high moisture when silt content > 70%, or 65% < silt content ≤ 70% with high sand content, or rare cases at very low moisture for high frequencies with high clay content, or some cases at medium or high moisture when silt content ≤ 55% with high clay content | |
| IV | When silt content ≥ 45% and clay content ≤ 15%, or at low moistures for samples with high sand content and low silt content, or at low and high moisture with low sand content and high silt content | Other cases | |
| SSMDM-Dobson ‘3′ | I | At high frequencies when silt content ≥ 40%, or when VWC ≤ 0.07 for all samples, or some cases when VWC > 0.07 | When VWC ≥ 0.12 with clay content ≥ 75% except for rare cases at very high moisture for high frequencies, or some cases over other samples when VWC > 0.7 |
| II | When silt content ≥ 45%, or other cases at low and high moisture for other samples | When silt content ≤ 15% at high frequencies, and some cases at medium moisture for other samples | |
| III | Other cases | Some cases at high moisture for high frequencies when silt content ≥ 85% | |
| IV | When silt content ≥ 45% at high frequencies, or at relatively lower and higher moisture for other samples | Other cases | |
| Mironov-Wang ‘4′ | I | Other cases, the transition point: 0.05 (high silt content)–0.11 (high clay content) at L-band; 0.15–0.33 at Ku-band | Low moisture, or rare cases for samples with high clay content in the vicinity of 0.4 m3/m3 at low frequencies and low and medium moisture at high frequencies |
| II | At low frequencies, or when clay content ≤ 20% except for rare cases at low moisture for high frequencies, or some cases at medium and high moisture when clay content > 20% | Some cases at low moisture for high frequencies when clay content > 20%, the transition point at Ku-band is 0.13 m3/m3 when clay content is 45% | |
| III | Other cases | Rare cases at high moisture for high frequencies when silt > 95%, or some cases at low moisture for samples with high clay content. The highest transition point at L-, Ku-bands are 0.04 and 0.13 when clay content is 45% | |
| IV | Other cases | Rare cases at very low moisture for low frequencies, or at low moisture for high frequencies for samples with high clay content. The highest transition point at Ku-band is 0.13 | |
| SSMDM-wang ‘5′ | I | When 0.06 ≤ VWC ≤ 0.17, or some cases when 0.02 < VWC < 0.06 or VWC > 0.17 | When VWC ≤ 0.02, and VWC ≥ 0.28 at Ku-band, and some other cases when 0.02 < VWC < 0.06 or VWC > 0.17 |
| II | When silt content ≥ 15% and clay content ≤ 30%, or silt content (0–15%) matches the clay content (5–25%) except for rare cases at low moisture for high frequencies and very high moisture for samples with relatively high clay content, and other cases at low and medium moisture for other samples | Other cases | |
| III | Other cases | Rare cases at low moisture for high frequencies, or samples with high clay content for low frequencies, or some cases at high moisture for low frequencies when silt content ≥ 80%, or 70% ≤ silt content < 80% with high sand content, or for high frequencies when silt content ≥ 95% with low clay content | |
| IV | When silt content ≥ 20% and clay content ≤ 40% except for rare cases at very low and high moistures at high frequencies, or other cases for other samples | Some cases for other samples at relatively lower moisture for low frequencies, or at low and high moisture for high frequencies | |
| Mironov-SSMDM ‘6′ | I | At low frequencies with high silt content, or relatively low clay content with relatively high silt content except for rare cases at very low moisture, or some cases at some VWCs for other samples | When relatively high clay content with low silt content, and cases at other VWCs for other samples |
| II | When silt content ≥ 15% and clay content ≤ 30% except for rare cases at low moisture for high frequencies, or silt content (0–15%) match clay content (25–35%) at high frequencies except for rare cases at very low moisture, or other cases for other samples | At high frequencies when clay content is closed to 50%, or some cases at high moisture for low frequencies, or some case at low and high moisture for other samples | |
| III | Other cases | Rare cases at low moisture for samples with high clay content at high frequencies, or some cases at high moisture when silt content > 80% or 75% ≤ silt content < 80% with high sand content | |
| IV | When silt content ≥ 20% except for rare cases at low moisture for high frequencies with high clay content, or other cases for other samples | Some cases for other samples at relatively lower moisture for low frequencies and at low and high moisture for high frequencies |
References
- Brunfeldt, D.R.; Ulaby, F.T. Measured microwave emission and scattering in vegetation canopies. IEEE Trans. Geosci. Remote Sens. 1984, 22, 520–524. [Google Scholar] [CrossRef]
- Mo, T.; Choudhury, B.J.; Schmugge, T.J.; Wang, J.R.; Jackson, T.J. A model for microwave emission from vegetation-covered fields. J. Geophys. Res. Space Phys. 1982, 87, 11229. [Google Scholar] [CrossRef]
- Abdulla, S.; Mohammed, A.-K.; Al-Rizzo, H. The complex dielectric constant of Iraqi soils as a function of water content and texture. IEEE Trans. Geosci. Remote Sens. 1988, 26, 882–885. [Google Scholar] [CrossRef]
- Curtis, J.O.; Weiss, C.A.; Everett, J.B. Effect of Soil Composition on Complex Dielectric Properties; Technical Report EL-95-34; U.S. Army Corps of Engineers Waterways Experiment Station: Vicksburg, MS, USA, 1995. [Google Scholar]
- Narayanan, R.M.; Rhoades, D.W.; Hoffmeyer, P.D.; Curtis, J.O. Comparative Study of Dielectric Constant Measurements of Soils using Different Techniques. In Proceedings of the International Symposium for Spectral Sensing Research (ISSSR’94), San Diego, CA, USA, 15–16 July 1994. [Google Scholar]
- Hallikainen, M.; Ulaby, F.; Dobson, M.; El-Rayes, M.; Wu, L.K. Microwave Dielectric Behavior of Wet Soil-Part 1: Empirical Models and Experimental Observations. IEEE Trans. Geosci. Remote Sens. 1985, 23, 25–34. [Google Scholar] [CrossRef]
- Dobson, M.; Ulaby, F.; Hallikainen, M.; El-Rayes, M. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Mironov, V.L.; Dobson, M.C.; Kaupp, V.H.; Komarov, S.A.; Kleshchenko, V.N. Generalized refractive mixing dielectric model for moist soils. IEEE Trans. Geosci. Remote Sens. 2004, 42, 773–785. [Google Scholar] [CrossRef]
- Mironov, V.L.; Kosolapova, L.G.; Fomin, S.V. Soil Dielectric Model Accounting for Contribution of Bound Water Spectra through Clay Content . Progress in Electromagnetics Research Symposium (Piers), Hangzhou, China. PIERS Online 2008, 4, 31–35. Available online: http://www.piers.org/piersonline/pdf/Vol4No1Page31to35.pdf (accessed on 20 July 2020).
- Mironov, V.; Kosolapova, L.; Fomin, S.V. Physically and Mineralogically Based Spectroscopic Dielectric Model for Moist Soils. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2059–2070. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric Properties of Soils in the 0.3–1.3-GHz Range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807, Correction in 1995, 33, 1340. [Google Scholar] [CrossRef]
- Wang, J.R.; Schmugge, T.J. An Empirical Model for the Complex Dielectric Permittivity of Soils as a Function of Water Content. IEEE Trans. Geosci. Remote Sens. 1980, 18, 288–295. [Google Scholar] [CrossRef] [Green Version]
- Behari, J. Microwave dielectric behaviour of wet soils. Geoderma 2005, 133, 478–479. [Google Scholar]
- Liu, J.; Liu, Q.; Li, H.; Du, Y.; Cao, B. An Improved Microwave Semiempirical Model for the Dielectric Behavior of Moist Soils. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6630–6644. [Google Scholar] [CrossRef]
- Fernández-Gálvez, J. Errors in soil moisture content estimates induced by uncertainties in the effective soil dielectric constant. Int. J. Remote Sens. 2008, 29, 3317–3323. [Google Scholar] [CrossRef]
- Saleh, K.; Wigneron, J.-P.; Waldteufel, P.; De Rosnay, P.; Schwank, M.; Calvet, J.-C.; Kerr, Y. Estimates of surface soil moisture under grass covers using L-band radiometry. Remote Sens. Environ. 2007, 109, 42–53. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Laguerre, L.; Kerr, Y.H. A simple parameterization of the L-band microwave emission from rough agricultural soils. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1697–1707. [Google Scholar] [CrossRef]
- De Rosnay, P.; Drusch, M.; Boone, A.; Balsamo, G.; Decharme, B.; Harris, P.; Kerr, Y.; Pellarin, T.; Polcher, J.; Wigneron, J.-P. AMMA Land Surface Model Intercomparison Experiment coupled to the Community Microwave Emission Model: ALMIP-MEM. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Kerr, Y.; De Rosnay, P.; Wigneron, J.-P.; Calvet, J.-C.; Lemaitre, F. A Simple Model of the Bare Soil Microwave Emission at L-Band. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1978–1987. [Google Scholar] [CrossRef]
- Wentz, F.J.; Vine, D.M.L. Algorithm Theoretical Basis Document (ATBD) Aquarius Level-2 Radiometer Algorithm: Revision 1. RSS Technical Report 012208. 2008. Available online: http://oceancolor.gsfc.nasa (accessed on 20 July 2020).
- Bircher, S.; Balling, J.E.; Skou, N.; Kerr, Y.H. Validation of SMOS Brightness Temperatures during the HOBE Airborne Campaign, Western Denmark. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1468–1482. [Google Scholar] [CrossRef] [Green Version]
- Mialon, A.; Richaume, P.; Leroux, D.; Bircher, S.; Al Bitar, A.; Pellarin, T.; Wigneron, J.P.; Kerr, Y.H. Comparison of Dobson and Mironov Dielectric Models in the SMOS Soil Moisture Estimate Algorithm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3084–3094. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Chanzy, A.; Kerr, Y.H.; Lawrence, H.; Shi, J.; Escorihuela, M.J.; Mironov, V.; Mialon, A.; Demontoux, F.; De Rosnay, P.; et al. Evaluating an Improved Parameterization of the Soil Emission in L-MEB. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1177–1189. [Google Scholar] [CrossRef]
- O’Neill, P.; Chan, S.; Njoku, E.; Jackson, T.; Bindlish, R. SMAP Algorithm Theoretical Basis Document Level 2 & 3 Soil Moisture (Passive) Data Products, JPL D-66480, Jet Propulsion Laboratory, Pasadena, CA, USA. 2014. Available online: https://smap.jpl.nasa.gov/system/internal_resources/details/original/275_L2_3_SM_P_RevA_web.pdf (accessed on 20 July 2020).
- Owe, M.; Van De Griend, A.A. Comparison of soil moisture penetration depths for several bare soils at two microwave frequencies and implications for remote sensing. Water Resour. Res. 1998, 34, 2319–2327. [Google Scholar] [CrossRef]
- Srivastava, P.K.; O’Neill, P.; Cosh, M.; Kurum, M.; Lang, R.; Joseph, A. Evaluation of Dielectric Mixing Models for Passive Microwave Soil Moisture Estimate Using Data From ComRAD Ground-Based SMAP Simulator. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4345–4354. [Google Scholar] [CrossRef]
- Laymon, C.; Crosson, W.; Jackson, T.; Manu, A.; Tsegaye, T. Ground-based passive microwave remote sensing observations of soil moisture at S-band and L-band with insight into measurement accuracy. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1844–1858. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Wagner, N.; Emmerich, K.; Bonitz, F.; Kupfer, K. Experimental Investigations on the Frequency- and Temperature-Dependent Dielectric Material Properties of Soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2518–2530. [Google Scholar] [CrossRef]
- Van Dam, R.; Borchers, B.; Hendrickx, J.M.H. Methods for prediction of soil dielectric properties: A review. Def. Sec. 2005, 5794, 188–198. [Google Scholar] [CrossRef]
- Brovelli, A.; Cassiani, G. Effective permittivity of porous media: A critical analysis of the complex refractive index model. Geophys. Prospect. 2008, 56, 715–727. [Google Scholar] [CrossRef]
- Robinson, D.A. Measurement of the Solid Dielectric Permittivity of Clay Minerals and Granular Samples Using a Time Domain Reflectometry Immersion Method. Vadose Z. J. 2015, 3, 705–713. [Google Scholar] [CrossRef]
- Stogryn, A. Equations for Calculating the Dielectric Constant of Saline Water (Correspondence). IEEE Trans. Microw. Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]
- Lane, J.A.; Saxton, J.A. Dielectric dispersion in pure polar liquids at very high radio frequencies—III.The effect of electrolytes in solution. Proc. Royal Soc. London. S. A Math. Phys. Sci. 1952, 214, 531–545. [Google Scholar]




| Sources of Measurements | Sand (%) | Silt (%) | Clay (%) | Sources of Measurements | Sand (%) | Silt (%) | Clay (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| From ref [25] | Forest soil | 57.4 | 32.1 | 10.5 | From ref [27] | Silt loam | 8 | 71 | 21 |
| Natural soil | 72.2 | 24.3 | 3.5 | From ref [26] | Sandy loam | 62 | 24 | 14 | |
| Sand soil | 92.7 | 6.7 | 0.6 | From ref [23] | silty clay loam | 11 | 62 | 27 | |
| From ref [12] | Harlingen clay | 2.0 | 37.0 | 61.0 | From ref [7] | Sample 1 | 51.51 | 35.06 | 13.43 |
| F2 | 56.0 | 26.7 | 17.3 | Sample 2 | 41.96 | 49.51 | 8.53 | ||
| H7 | 19.3 | 46.0 | 34.7 | Sample 3 | 30.63 | 55.89 | 13.48 | ||
| Yuma sand | 100 | 0 | 0 | Sample 4 | 17.16 | 63.84 | 19.00 | ||
| Vernon clay loam | 16.0 | 56.0 | 28.0 | Sample 5 | 5.02 | 47.60 | 47.38 | ||
| Miller clay | 3.0 | 35.0 | 62.0 | From ref [10] | Silty sand (D) | 77 | 9 | 14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, Q. Soil Moisture Estimate Uncertainties from the Effect of Soil Texture on Dielectric Semiempirical Models. Remote Sens. 2020, 12, 2343. https://doi.org/10.3390/rs12142343
Liu J, Liu Q. Soil Moisture Estimate Uncertainties from the Effect of Soil Texture on Dielectric Semiempirical Models. Remote Sensing. 2020; 12(14):2343. https://doi.org/10.3390/rs12142343
Chicago/Turabian StyleLiu, Jing, and Qinhuo Liu. 2020. "Soil Moisture Estimate Uncertainties from the Effect of Soil Texture on Dielectric Semiempirical Models" Remote Sensing 12, no. 14: 2343. https://doi.org/10.3390/rs12142343






