Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data
Abstract
:1. Introduction
2. Methods
2.1. Study Site and Data
2.2. Estimating Tree Variables from LiDAR Imagery
2.3. Nonlinear Mixed-Effects DBH Estimation Model
2.4. Predictor Variables
2.5. Base Model
2.6. Parameter Effects
2.7. Determining the Structure of the Between Sub-Sample Plot Variance–Covariance Matrix ()
2.8. Determining Structure of Within Sub-Sample Plot Variance–Covariance Matrix ()
2.9. Model Estimation
2.10. Subject-Specific Prediction
- (i)
- DBH of 1-10 randomly selected trees per sub-sample plot (random).
- (ii)
- DBH of 1-10 medium-size trees per sub-sample plot (medium).
- (iii)
- DBH of 1-10 the largest trees per sub-sample plot (largest).
- (iv)
- DBH of 1-10 the smallest trees per sub-sample plot (smallest).
2.11. Model Evaluation
2.12. Model Application
3. Results
3.1. Base Model
3.2. Generalized NLME DBH Estimation Model
3.3. Parameter Estimation
- ,
- ,
- ,
- ,
- and was an identity matrix. All other parameters and predictors in this model are the same as defined earlier.
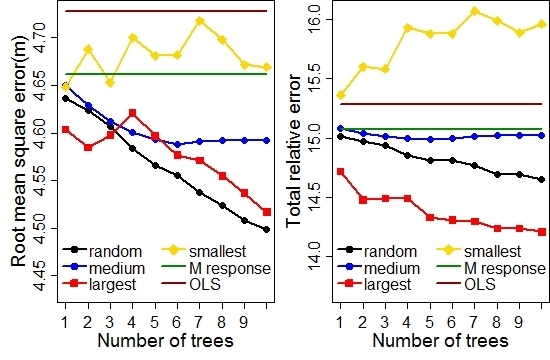
3.4. Subject-Specific DBH Prediction
3.5. Model Evaluation
3.6. Model Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Variance | CPA | LH | ||||||
|---|---|---|---|---|---|---|---|---|
| Function | AIC | −2LL | LR | p value | AIC | −2LL | LR | p value |
| 1 | 2382 | −1180 | 2382 | −1180 | ||||
| PF | 2363 | −1169 | 21.56 | <0.0001 | 2360 | −1168 | 24.42 | <0.0001 |
| EF | 2366 | −1171 | 18.39 | <0.0001 | 2361 | −1169 | 22.87 | <0.0001 |
| CPF | 2365 | −1169 | 21.55 | <0.0001 | 2362 | −1168 | 24.42 | <0.0001 |
References
- Crecente-Campo, F.; Tomé, M.; Soares, P.; Dieguez-Aranda, U. A generalized nonlinear mixed-effects height-diameter model for Eucalyptus globulus L. in northwestern Spain. For. Ecol. Manag. 2010, 259, 943–952. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Lei, Y.; Wang, G.; Bi, H.; Tang, S.; Song, X. Comparison of seemingly unrelated regressions with multivariate errors-in-variables models for developing a system of nonlinear additive biomass equations. Trees 2016, 30, 839–857. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Sharma, R.P.; Pang, L.; Wang, G. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China. For. Ecol. Manag. 2017, 384, 34–43. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A generalized interregionalnonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 384, 34–43. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenerg. 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Broadbent, E.N.; Asner, G.P.; Peña-Claros, M.; Palace, M.; Soriano, M. Spatial partitioning of biomass and diversity in a lowland Bolivian forest: Linking field and remote sensing measurements. For. Ecol. Manag. 2008, 255, 2602–2616. [Google Scholar] [CrossRef]
- Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manag. 2008, 255, 2416–2433. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. For. Res. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to estimating tree height via LiDAR in closed-canopy forests: A parable from western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Vauhkonen, J.; Mehtätalo, L.; Packalén, P. Combining tree height samples produced by airborne laser scanning and stand management records to estimate plot volume in Eucalyptus plantations. Can. J. For. Res. 2011, 41, 1649–1658. [Google Scholar] [CrossRef]
- Duncanson, L.; Cook, B.; Hurtt, G.; Dubayah, R. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative Assessment of the Performance of Individual Tree Crowns Delineation Algorithms from ALS Data in Tropical Forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.R. Allometric equations to predict the total aboveground biomass of radiata pine trees. Ann. For. Sci. 2010, 67, 806. [Google Scholar] [CrossRef] [Green Version]
- Rombouts, J.; Ferguson, I.S.; Leech, J.W. Campaign and site effects in LiDAR prediction models for site-quality assessment of radiata pine plantations in South Australia. Int. J. Remote Sens. 2010, 31, 1155–1173. [Google Scholar] [CrossRef]
- Herrera-Fernández, J.J.; Campos, J.J.; Kleinn, C. Site productivity estimation using height-diameter relationships in Costa Rican secondary forests. For. Syst. 2004, 13, 295–303. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- Calama, R.; Montero, G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef] [Green Version]
- Schabenberger, O.; Gregoire, T.G. A conspectus on estimating function theory and its application to recurrent modelling issues in forest biometry. Silva Fenn. 1995, 29, 49–70. [Google Scholar] [CrossRef] [Green Version]
- West, P.W.; Ratkowsky, D.A.; Davis, A.W. Problems of hypothesis testing of regressions with multiple measurements from individual sampling units. For. Ecol. Manag. 1984, 7, 207–224. [Google Scholar] [CrossRef]
- Meng, S.X.; Huang, S. Improved calibration of nonlinear mixed-effects models demonstrated on a height growth function. For. Sci. 2009, 55, 239–248. [Google Scholar]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Lindstrom, M.J.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef] [PubMed]
- Vonesh, E.F.; Chinchilli, V.M. Linear and Nonlinear Models for the Analysis of Repeated Measurements; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Adame, P.; Río, M.D.; Cañellas, I. A mixed nonlinear height diameter model for Pyrenean oak (Quercus pyrenaica Willd.). For. Ecol. Manag. 2008, 256, 88–98. [Google Scholar] [CrossRef]
- Dang, H.Z.; Zhao, Y.S.; Chen, X.W. Law of the water transfer process of water—Conversation forest in Qilian Mountains. Chin. J. Eco-Agric. 2004, 12, 43–46. [Google Scholar]
- Ma, Y.J.; Wang, J.Y.; Liu, X.M.; Pei, W.; Jin, M. Status of Forestry Ecosystem and Protection Countermeasure in the Protection Areas in Qilian Mountains. J. Northwest For. 2005, 20, 5–8. [Google Scholar]
- Pang, Y.; Chen, E.; Liu, Q.; Xiao, Q.; Zhong, K.; Li, X.; Ma, M. WATER: Dataset of airborne LiDAR mission at the super site in the Dayekou watershed flight zone on Jun. 23, 2008. In Chinese Academy of Forestry; Institute of Remote Sensing Applications, Chinese Academy of Sciences; Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences; Heihe Plan Science Data Center: Lanzhou, China, 2008. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. Aprogressive morphological filter for removing nonground measurements fromairborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in asavanna Woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Yu, B.; Huang, C.; Wu, Q.; Wu, J. Automated extraction of groundsurface along urban roads from mobile laser scanning point clouds. Remote Sens. Lett. 2016, 7, 170–179. [Google Scholar] [CrossRef]
- Liu, Q. Study on the Estimation Method of Forest Parameters Using Airborne LiDAR. Ph.D. Dissertation, Chinese Academy of Forestry, Beijing, China, 2009. [Google Scholar]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Li, Z.; Chen, E.; Pang, Y.; Wu, H. Extracting individual tree heights and crowns using airborne LIDAR data. J. Beijing For. Univ. 2008, 30, 83–89. [Google Scholar]
- Liu, Q.; Fu, L.; Wang, G.; Li, S.; Li, Z.; Chen, E.; Pang, Y.; Hu, K. Improving Estimation of Forest Canopy Cover by Introducing Loss Ratio of Laser Pulses Using Airborne LiDAR. IEEE Trans. Geosci. Remote 2019, 58, 567–585. [Google Scholar] [CrossRef]
- Davidian, M.; Giltinan, D.M. Nonlinear Models for Repeated Measurement Data; Chapmanand Hall: New York, NY, USA, 1995. [Google Scholar]
- Nilsson, M. Estimation of tree heights and stand volume using an airborne lidar system. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
- Huuskonen, S.; Miina, J. Stand-level growth models for young scots pine stands in Finland. For. Ecol. Manag. 2007, 241, 49–61. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS, 3rd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Yang, Y.; Huang, S.; Meng, S.X.; Trincado, G.; VanderSchaaf, C.L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands. Can. J. For. Res. 2009, 39, 2203–2214. [Google Scholar] [CrossRef]
- Fang, Z.; Bailey, R.L. Nonlinear mixed-effect modeling for Slash pine dominant height growth following intensive silvicultural treatments. For. Sci. 2001, 47, 287–300. [Google Scholar]
- Calama, R.; Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (pinus pinea): A calibrating approach. Silva Fenn. 2005, 39, 37–54. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.Z.; Li, Y.; Fu, L.Y. Statistical Foundation for Biomathematical Models, 2nd ed.; Higher Education Press: Beijing, China, 2015. [Google Scholar]
- De-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating marginal and conditional predictions of taper models in the absence of calibration data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Temesgen, H.; Monleon, V.J.; Hann, D.W. Analysis and comparison of nonlinear tree height prediction strategies for Douglas-fir forests. Can. J. For. Res. 2008, 38, 553–565. [Google Scholar] [CrossRef] [Green Version]
- Nord-Larsen, T.; Meilby, H.; Skovsgaard, J.P. Site-specific height growth models for six common tree species in Denmark. Scand. J. For. Res. 2009, 24, 194–204. [Google Scholar] [CrossRef]
- Timilsina, N.; Staudhammer, C.L. Individual tree-based diameter growth model of slash pine in Florida using nonlinear mixed modeling. For. Sci. 2013, 59, 27–31. [Google Scholar] [CrossRef]
- Wang, J.Y.; Ju, K.J.; Fu, H.E.; Chang, X.X.; He, H.Y. Study on biomass of water conservation forest on North Slope of Qilian Mountains. J. Fujian Coll. For. 1998, 18, 319–325. [Google Scholar]
- Zeng, W.S.; Zhang, H.R.; Tang, S.Z. Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—A case study for Masson pine (Pinus massoniana) in southern China. Can. J. For. Res. 2011, 41, 1547–1554. [Google Scholar] [CrossRef]
- Hall, R.J.; Morton, R.T.; Nesby, R.N. A Comparison of existing models for DBH estimation for large-scale photos. For. Chron. 1989, 65, 114–116. [Google Scholar] [CrossRef] [Green Version]
- Gering, L.R.; May, D.M. The relationship of diameter at breast height and crown diameter for four species groups in Hardin county, Tennessee. South. J. Appl. For. 1995, 19, 177–181. [Google Scholar] [CrossRef] [Green Version]
- Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. An allometric model for estimating DBH of isolated and clustered Eucalyptus trees from measurements of crown projection area. For. Ecol. Manag. 2014, 326, 125–132. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Zhu, G.; Li, H.; Hong, L.; Guo, H.; Duan, G.; Shen, C.; Lei, Y.; Li, Y.; et al. Comparing height–age and height–diameter modelling approaches for estimating site productivity of natural uneven-aged forests. Forestry 2018, 91, 419–433. [Google Scholar] [CrossRef]
- Castedo-Dorado, F.C.; Diéguez-Aranda, U.; Anta, M.B.; Rodríguez, M.S.; Gadow, K.V. A generalized height-diameter model including random components for radiate pine plantations in northwestern Spain. For. Ecol. Manag. 2006, 229, 202–213. [Google Scholar] [CrossRef]
- Zhang, W.; Ke, Y.; Quackenbush, L.J.; Zhang, L. Using error-in-variable regression to predict tree diameter and crown width from remotely sensed imagery. Can. J. For. Res. 2010, 40, 1095–1108. [Google Scholar] [CrossRef]






| Variable | Mean | SD | Min | Max |
|---|---|---|---|---|
| DBH (cm) | 23.46 | 8.35 | 2.50 | 81.10 |
| LH (m) | 6.95 | 1.90 | 1.96 | 11.30 |
| CPA (m2) | 7.43 | 2.06 | 2.94 | 13.50 |
| SCD | 0.79 | 0.06 | 0.67 | 0.89 |
| Models | ||||
|---|---|---|---|---|
| Model (4) | 0.0000 | 4.8070 | 4.8070 | 0.6244 |
| Model (5) | 0.7426 | 4.9460 | 5.0010 | 0.5934 |
| Model (6) | 0.0040 | 4.7150 | 4.7150 | 0.6386 |
| Model (7) | −0.0043 | 4.7190 | 4.7190 | 0.6381 |
| Parameters | Model (7) | Model (18) | Model (19) | |
|---|---|---|---|---|
| Fixed-effects parameters | 12.90 | 16.64 | 15.98 | |
| −0.0954 | −0.1141 | −0.1083 | ||
| −0.0458 | −0.0346 | −0.0372 | ||
| 0.5681 | 0.9495 | 0.8702 | ||
| Variance components | - | 0.2713 | 0.3543 | |
| - | 0.0020 | 0.0013 | ||
| - | 0.0014 | 0.0152 | ||
| - | 0.0124 | 0.0296 | ||
| - | −0.0058 | 0.0068 | ||
| - | −0.0230 | 0.0064 | ||
| - | - | 0.6189 | ||
| 4.7360 | 4.4150 | 4.3480 | ||
| Model performance | AIC | 2391 | 2382 | 2360 |
| −2LL | −1191 | −1180 | −1168 |
| Model | ||||
|---|---|---|---|---|
| Model (7) | 0.1101 | 4.6530 | 4.7280 | 0.6122 |
| Model (19) | ||||
| M response | 0.0843 | 4.6570 | 4.6620 | 0.6335 |
| Sub-sample plot level | −0.0307 | 4.4210 | 4.4210 | 0.6815 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Duan, G.; Ye, Q.; Meng, X.; Luo, P.; Sharma, R.P.; Sun, H.; Wang, G.; Liu, Q. Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data. Remote Sens. 2020, 12, 1066. https://doi.org/10.3390/rs12071066
Fu L, Duan G, Ye Q, Meng X, Luo P, Sharma RP, Sun H, Wang G, Liu Q. Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data. Remote Sensing. 2020; 12(7):1066. https://doi.org/10.3390/rs12071066
Chicago/Turabian StyleFu, Liyong, Guangshuang Duan, Qiaolin Ye, Xiang Meng, Peng Luo, Ram P. Sharma, Hua Sun, Guangxing Wang, and Qingwang Liu. 2020. "Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data" Remote Sensing 12, no. 7: 1066. https://doi.org/10.3390/rs12071066