Using the Global Hydrodynamic Model and GRACE Follow-On Data to Access the 2020 Catastrophic Flood in Yangtze River Basin
Abstract
:1. Introduction
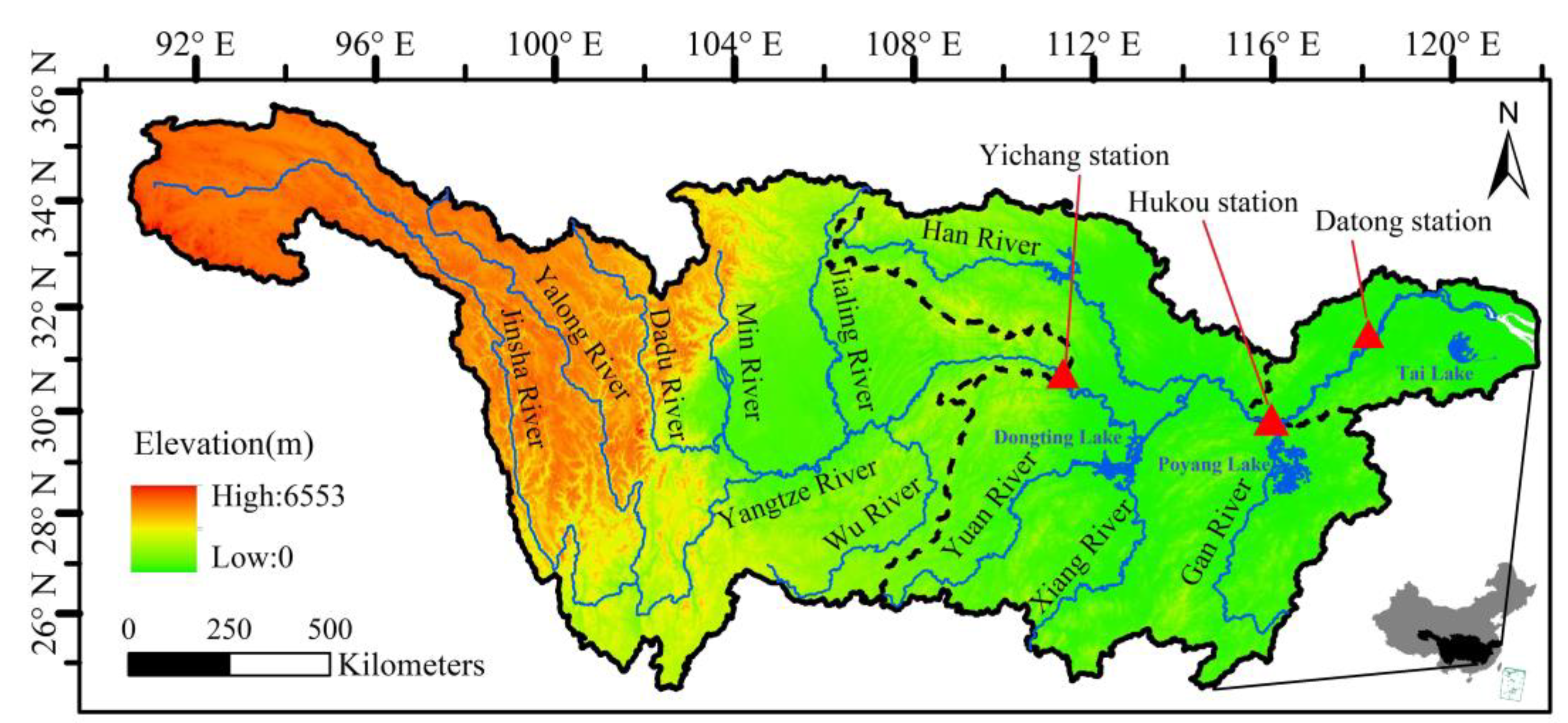
2. Study Area
3. Data and Methods
3.1. Data
3.1.1. Remote Sensing Products
3.1.2. Reanalysis Dataset
3.1.3. Model Outputs
3.1.4. In Situ Observations
3.2. Methods
3.2.1. Water Balance Equation
3.2.2. Uncertainty and Error Analysis
3.2.3. CaMa-Flood Hydrodynamic Model
3.2.4. Flood Potential Index
3.2.5. Time Series Decomposition
4. Results
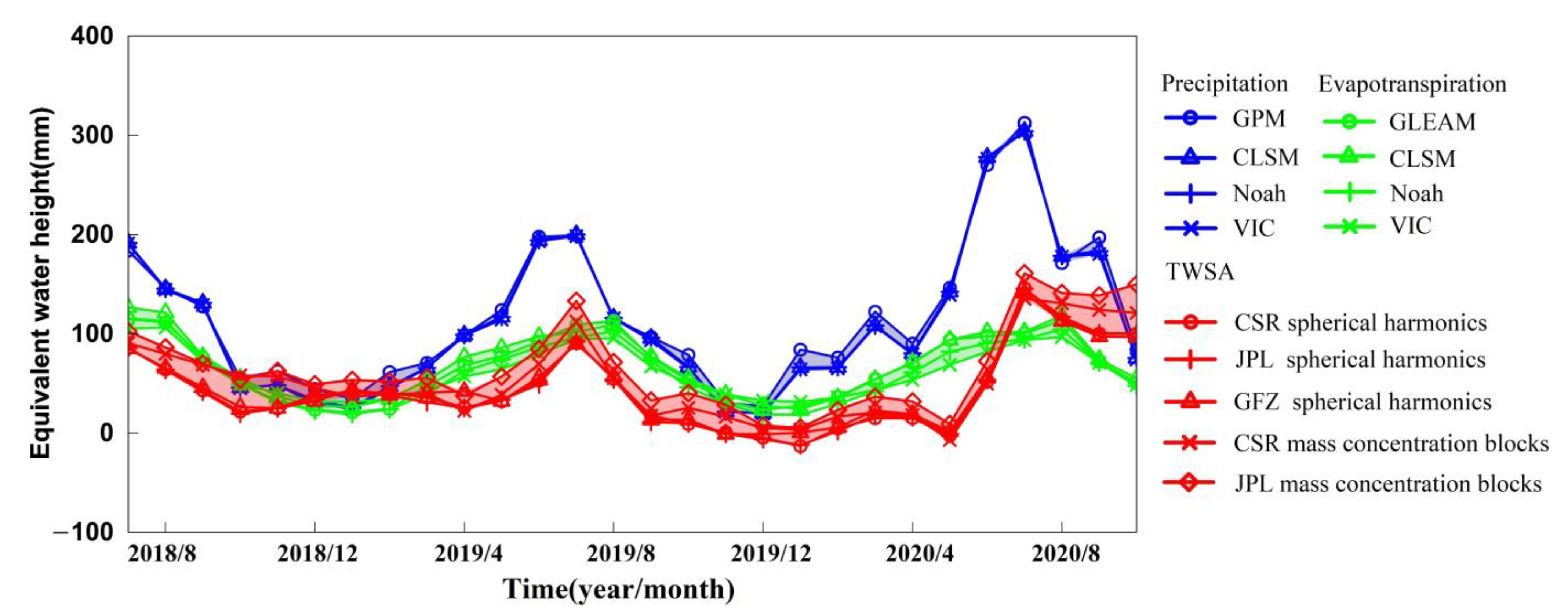
4.1. Uncertainty Analysis
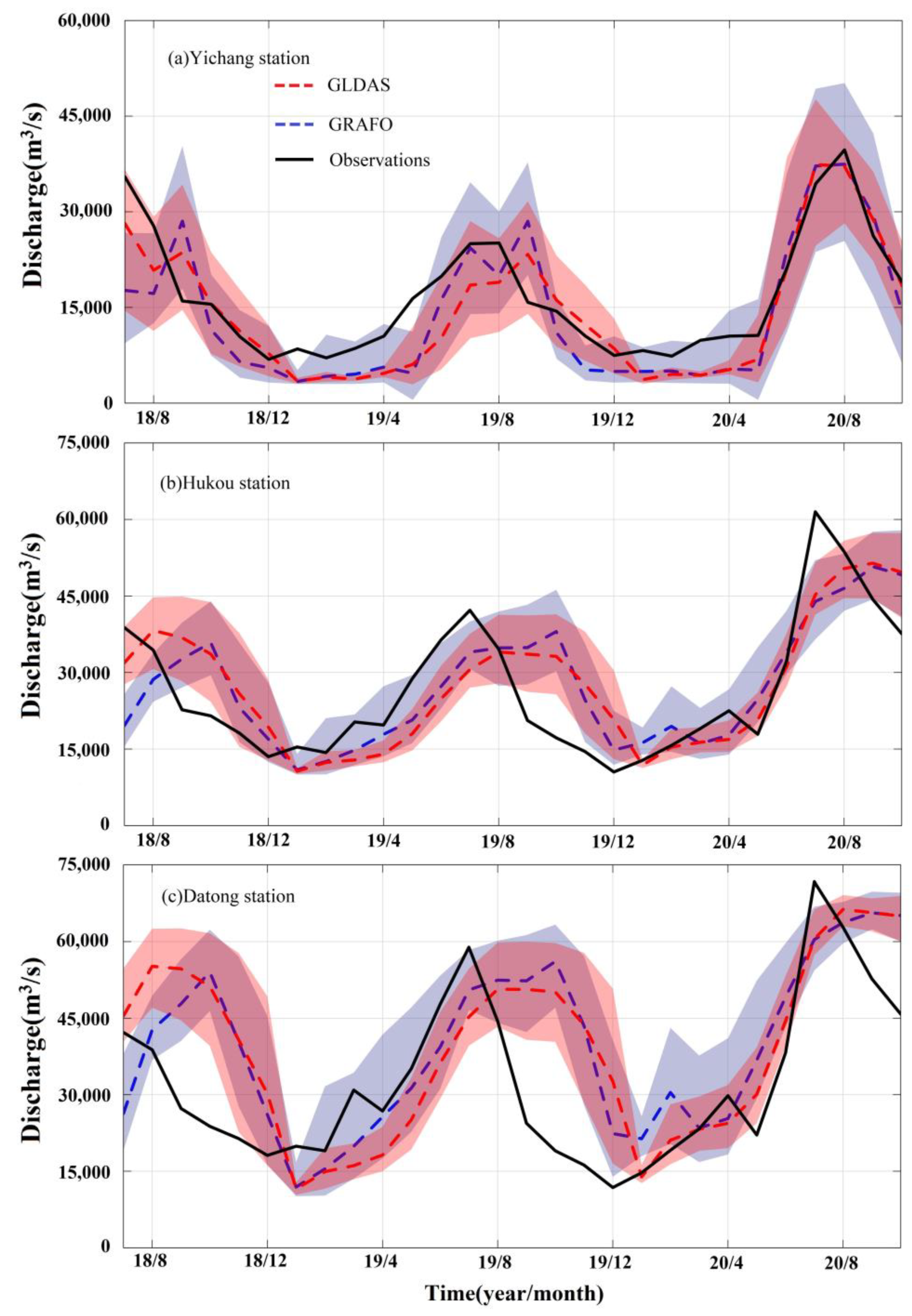
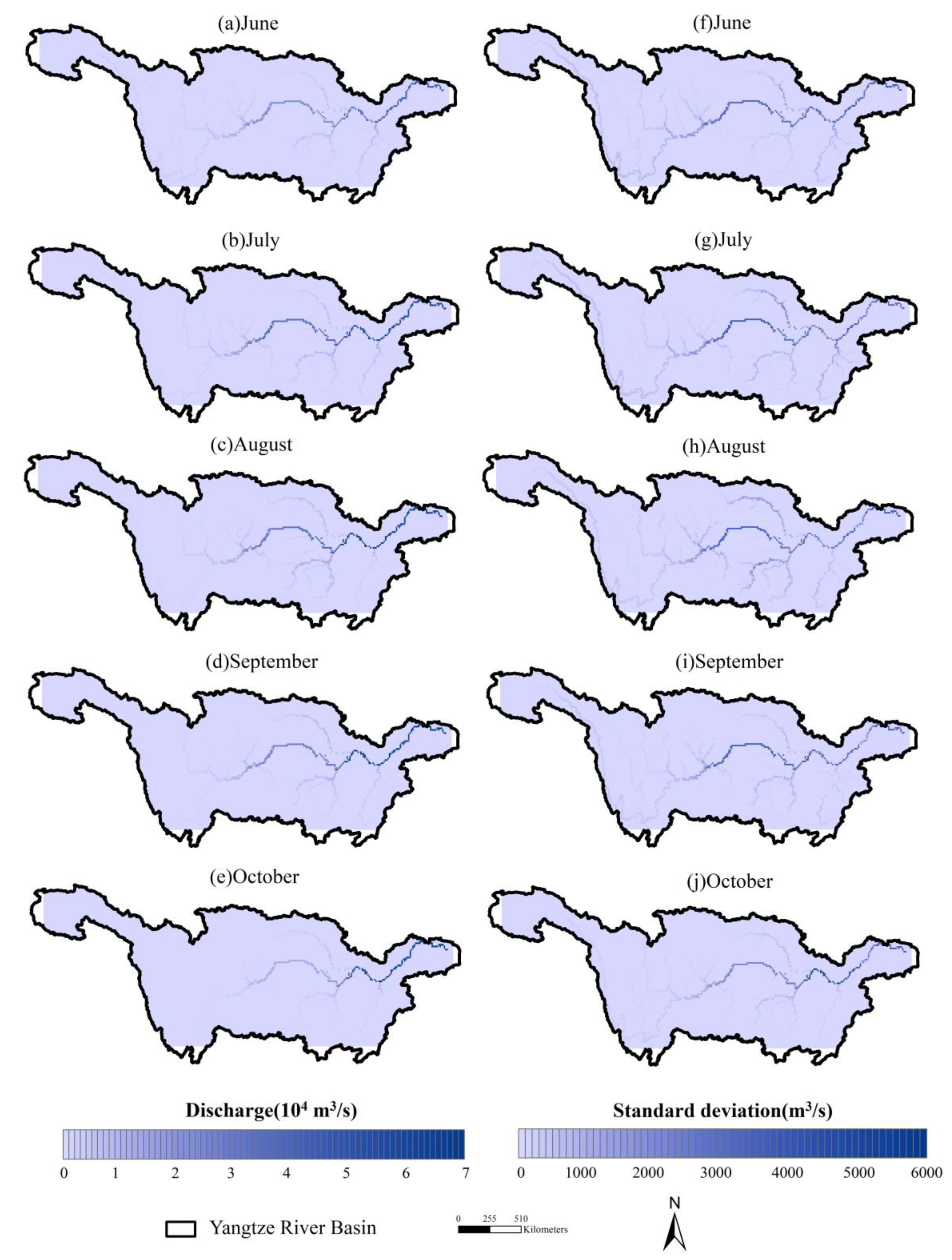
4.2. Evaluation of Discharge
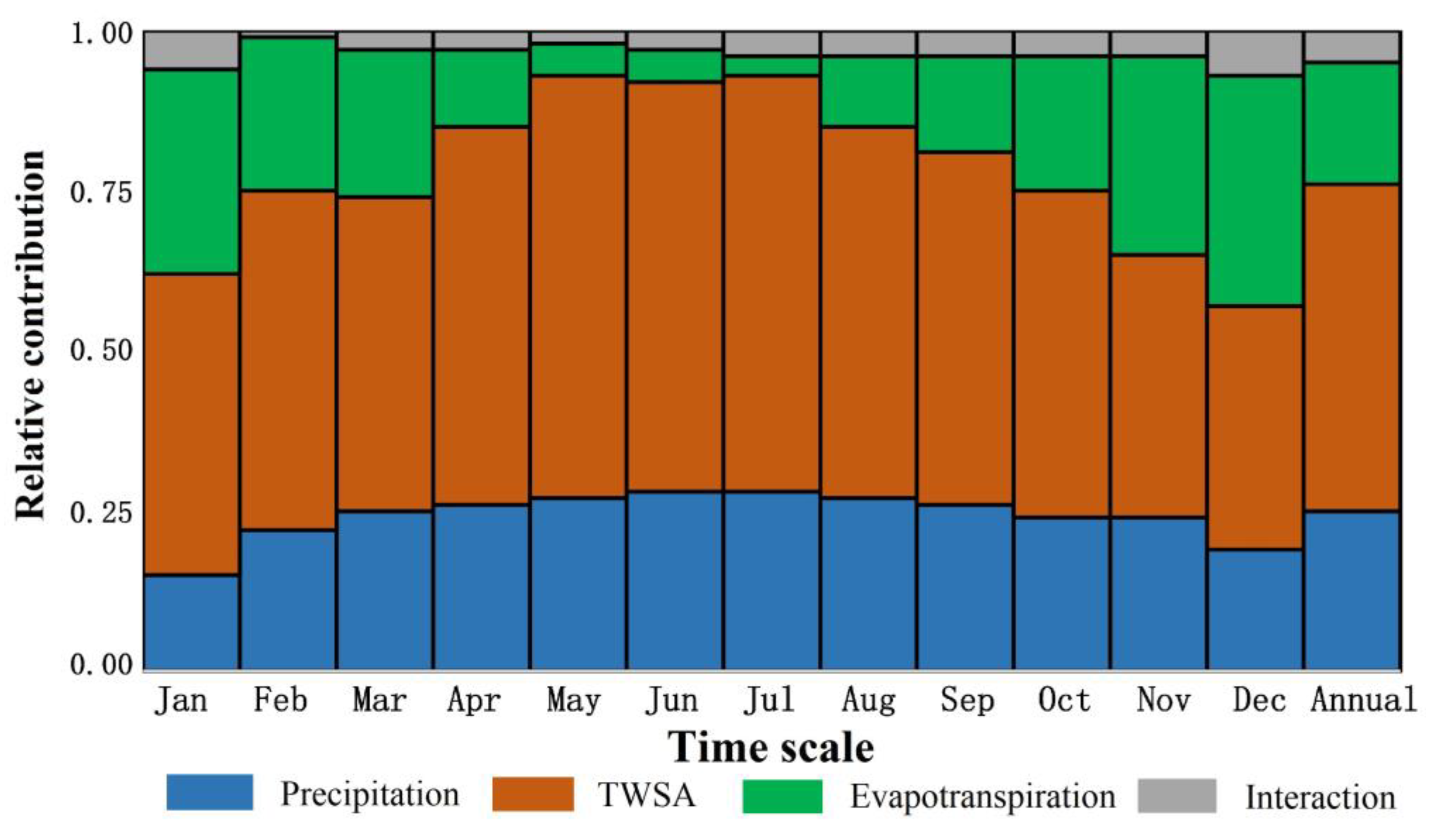
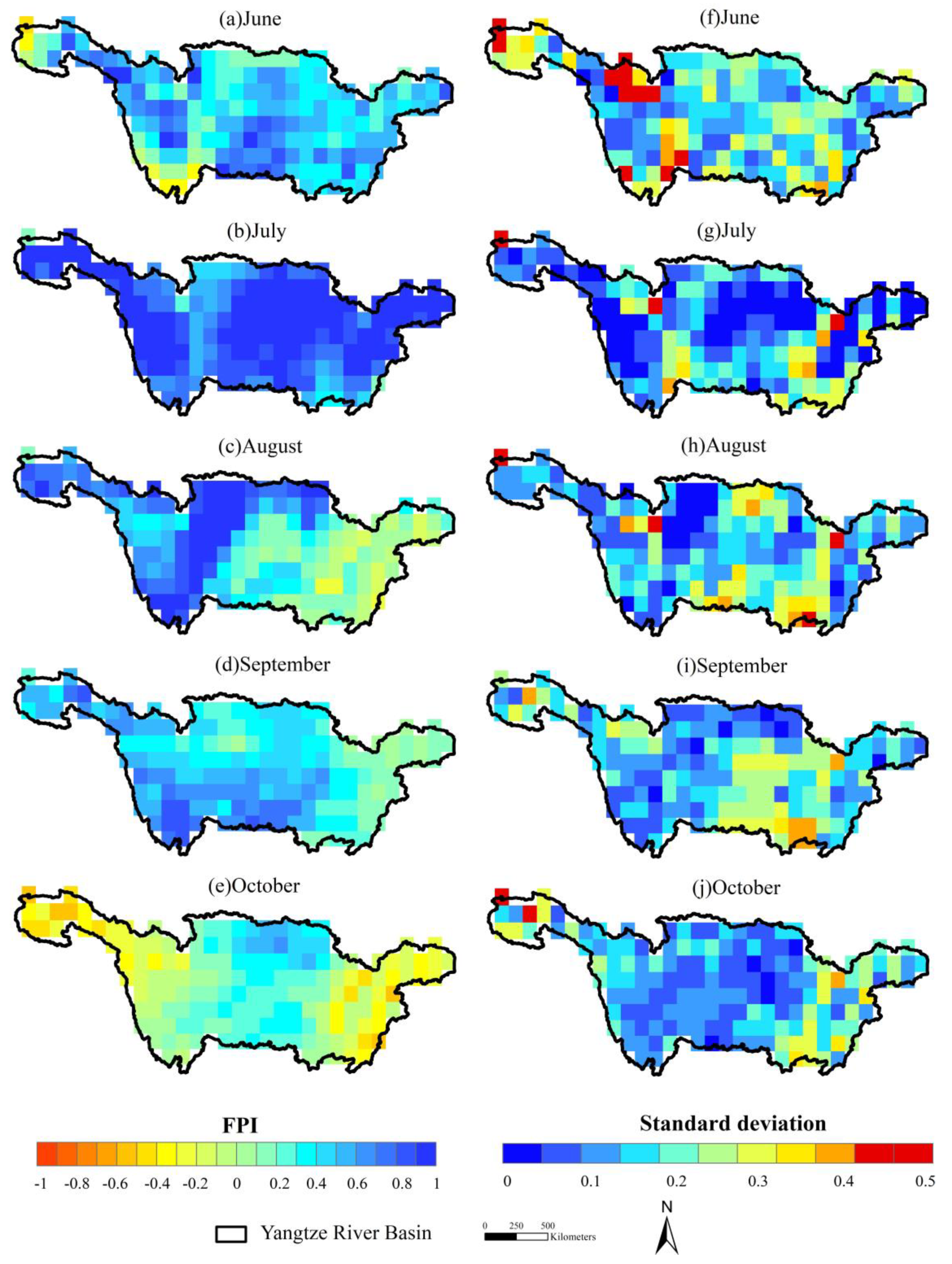
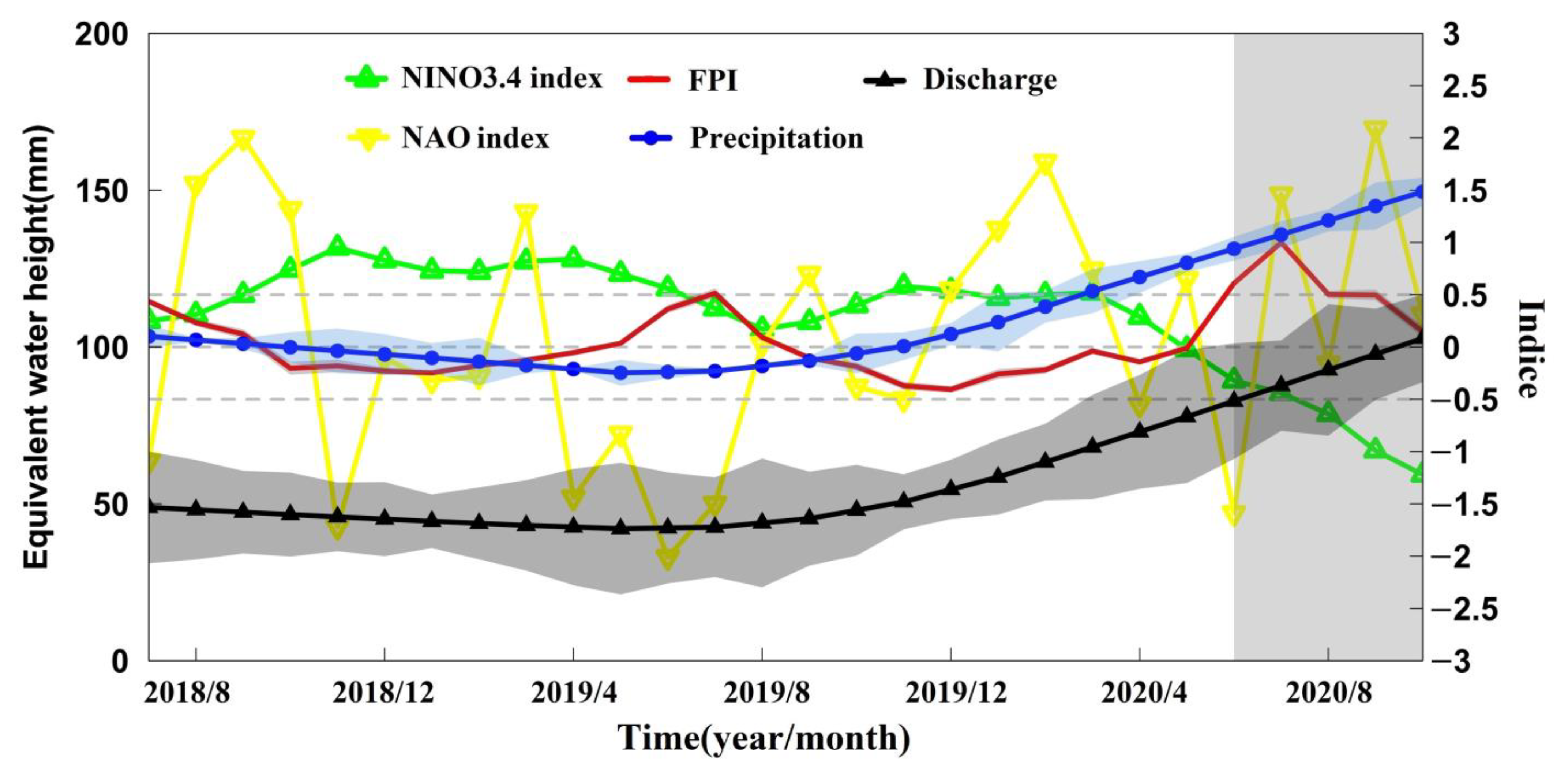
4.3. The 2020 Flood
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards. 2007, 42, 125–148. [Google Scholar] [CrossRef]
- Milly, P.; Wetherald, R.T.; Dunne, K.A. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, J.; Chen, J. A new era of flood control strategies from the perspective of managing the 2020 Yangtze River flood. Sci. China Earth Sci. 2021, 64, 1–9. [Google Scholar] [CrossRef]
- Chen, J.L.; Tapley, B.; Rodell, M.; Seo, K.; Wilson, C.; Scanlon, B.; Pokhrel, Y. Basin-scale river runoff estimation from GRACE gravity satellites, climate models, and in situ observations: A case study in the Amazon Basin. Water Resour. Res. 2020, 56, e2020WR028032. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Liu, D.; Chen, J.; Shen, Y.; Xu, C. Blending multi-satellite, atmospheric reanalysis, and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2021, 593, 125878. [Google Scholar] [CrossRef]
- Zhao, C.S.; Zhang, C.B.; Yang, S.T. Calculating e-flow using UAV and ground monitoring. J. Hydrol. 2017, 552, 351–365. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Bosilovich, M. The global land data assimilation system. Bull. Amer. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Lou, H.; Wang, P.; Yang, S. Combining and comparing an unmanned aerial vehicle and multiple remote sensing satellites to calculate long-term river discharge in an ungauged water source region on the Tibetan Plateau. Remote Sens. 2020, 12, 2155. [Google Scholar] [CrossRef]
- Scanlon, B.; Zhang, Z.; Save, H.; Sun, A.; Schmied, H.; Beek, V.; Wiese, D.; Wada, Y.; Long, D.; Reedy, R. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [Green Version]
- Sichangi, A.W.; Wang, L.; Yang, K. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Wang, P.; Lou, H. Estimating river discharges in ungauged catchments using the slope-area method and unmanned aerial vehicle. Water 2019, 11, 2361. [Google Scholar] [CrossRef] [Green Version]
- Yeh PJ, F.; Swenson, S.C. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment. Water Resour. Res. 2006, 42, W12203. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Zheng, G.; He, X. Estimating total discharge in the Yangtze River basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef] [Green Version]
- Frappart, F.; Ramillien, G.; Ronchail, J. Changes in terrestrial water storage versus rainfall and discharges in the Amazon basin. Int. J. Climatol. 2013, 33, 3029–3046. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.A.; Jin, S. Lake level change and total water discharge in East Africa Rift Valley from satellite-based observations. Glob. Planet. Chang. 2014, 117, 79–90. [Google Scholar] [CrossRef]
- Beamer, J.P.; Hill, D.F.; Arendt:, A. High-resolution modeling of coastal freshwater discharge and glacier mass balance in the Gulf of Alaska watershed. Water Resour. Res. 2016, 52, 3888–3909. [Google Scholar] [CrossRef] [Green Version]
- Mouyen, M.; Longuevergne, L.; Steer, P. Assessing modern river sediment discharge to the ocean using satellite gravimetry. Nat. Commun. 2018, 9, 3384. [Google Scholar] [CrossRef] [Green Version]
- Khan, R.; Usmani, M.; Akanda, A. Long-range River discharge forecasting using the gravity recovery and climate experiment. J. Water Resour. Plan. Manag. 2018, 145, 06019005. [Google Scholar] [CrossRef]
- Lorenz, C.; Kunstmann, H.; Devaraju, B.; Tourian, M.J.; Sneeuw, N.; Riegger, J. Large-scale runoff from landmasses: A global assessment of the closure of the hydrological and atmospheric water balances. J. Hydrometeorol. 2014, 15, 2111–2139. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36, L23402. [Google Scholar] [CrossRef] [Green Version]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 589–593. [Google Scholar] [CrossRef]
- Molodtsova, T.; Molodtsov, S.; Kirilenko, A. Evaluating flood potential with GRACE in the United States. Nat. Hazards Earth Syst. Sci. 2016, 16, 1011–1018. [Google Scholar] [CrossRef] [Green Version]
- Idowu, D.; Zhou, W. Performance evaluation of a potential component of an early flood warning system-a case study of the 2012 flood, lower Niger River Basin, Nigeria. Remote Sens. 2019, 11, 1970. [Google Scholar] [CrossRef] [Green Version]
- Jaggi, A.; Weigelt, M.; Flechtner, F.; Guentner, A. European gravity service for improved emergency management, EGSIEM-from concept to implementation. Geophys. J. Int. 2019, 218, 1572–1590. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, Y.Y.; Xia, J.; Sun, S.X. Identification of drought events in the major basins of Central Asia based on a combined climatological deviation index from GRACE measurements. Atmos. Res. 2020, 244, 105105. [Google Scholar] [CrossRef]
- Ciracì, E.; Velicogna, I.; Swenson, S. Continuity of the mass loss of the world’s glaciers and ice caps from the GRACE and GRACE Follow-on missions. Geophys. Res. Lett. 2020, 47, e2019GL086926. [Google Scholar] [CrossRef]
- Ghobadi-Far Han, S.; McCullough, C.; Wiese, D.; Watkins, M. GRACE Follow-On laser ranging interferometer measurements uniquely distinguish short-wavelength gravitational perturbations. Geophys. Res. Lett. 2020, 47, e2020GL089445. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.-C.; Allgeyer, S. GRACE gravitational measurements of tsunamis after the 2004, 2010, and 2011 great earthquakes. J. Geod. 2020, 94, 65. [Google Scholar] [CrossRef]
- Wegener, H.; Mueller, V.; Heinzel, G.; Misfeldt, M. Tilt-to-length coupling in the GRACE Follow-On laser ranging interferometer. J. Spacecr. Rockets. 2020, 57, 1362–1372. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.; Wang, Y.; Zhang, Y.; Wang, J. Individual and combined impacts of future land-use and climate conditions on extreme hydrological events in a representative basin of the Yangtze River delta, China. Atmos. Res. 2019, 236, 104805. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascon. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Amer. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution blended analysis for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Feng, J.; Li, J.; Liao, H.; Zhu, J. Simulated coordinated impacts of the previous autumn North Atlantic Oscillation, NAO and winter El Niño on winter aerosol concentrations over eastern China. Atmos. Chem. Phys. 2019, 19, 10787–10800. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.; Lievens, H.; Schalie, R.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin, USA using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Vetter, T.; Huang, S.; Aich, V.; Yang, T.; Wang, X.; Krysonova, V.; Hattermann, F. Multi-model climate impact assessment and intercomparison for three large-scale river basins on three continents. Earth Syst. Dynam. 2015, 6, 17–43. [Google Scholar] [CrossRef] [Green Version]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Livezey, R.E.; Chen, W.Y. Statistical field significance and its determination by Monte Carlo techniques. Mon. Weather Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef] [Green Version]
- Ventura, V.; Paciorek, C.J.; Risbey, J.S. Controlling the proportion of falsely rejected hypotheses when conducting multiple tests with climatological data. J. Clim. 2004, 17, 4343–4356. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Kanae, S.; Kim, H.; Oki, T. A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 2011, 47, W04501. [Google Scholar] [CrossRef]
- Zhao, F.; Veldkamp, T.; Frieler, K.; Schewe, J.; Leng, G. The critical role of the routing scheme in simulating peak river discharge in global hydrological models. Environ. Res. Lett. 2017, 12, 075003. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Zhou, F.; Xu, Y.; Chen, Y.; Xu, C.; Gao, Y.; Du, J. Hydrological response to urbanization at different spatiotemporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Jin, E.K.; Kinter, J.L.; Wang, B. Current status of ENSO prediction skill in coupled ocean–atmosphere models. Clim. Dyn. 2008, 31, 647–664. [Google Scholar] [CrossRef]
- Zou, Y.; Xi, X. On the role of the south Pacific subtropical high at the onset of El Niño events. Atmos. Chem. Phys. Discuss. 2018, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Fedorov, A.V. Exceptionally strong easterly wind burst stalling El Niño of 2014. Proc. Natl. Acad. Sci. USA 2016, 113, 2005–2010. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, K.; Gu, P.; Febg, H.; Yin, Y.; Chen, W.; Cheng, B. Changes in precipitation extremes in the Yangtze River basin during 1960–2019 and the association with global warming, ENSO, and local effects. Sci. Total Environ. 2021, 760, 144244. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.K.; Yu, J.Y.; Johnson, K.R. Pacific and Atlantic controls of the relationship between mainland southeast Asia and east China interannual precipitation variability. Clim. Dyn. 2020, 54, 4279–4292. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gentine, P.; Sullivan, S.C.; Gu, L.; He, S.; Chen, J.; Liu, P. Does the hook structure constrain future flood intensification under anthropogenic climate warming? Water Resour. Res. 2021, 57, e2020WR028491. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Cui, L.L.; Ma, Y.; Du, H.Q.; Wen, K.M. Trends in temperature extremes and their association with circulation patterns in China during 1961–2015. Atmos. Res. 2018, 212, 259–272. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Guo, S.; Yin, J.; Gu, L.; Xiong, F. Using the Global Hydrodynamic Model and GRACE Follow-On Data to Access the 2020 Catastrophic Flood in Yangtze River Basin. Remote Sens. 2021, 13, 3023. https://doi.org/10.3390/rs13153023
Xiong J, Guo S, Yin J, Gu L, Xiong F. Using the Global Hydrodynamic Model and GRACE Follow-On Data to Access the 2020 Catastrophic Flood in Yangtze River Basin. Remote Sensing. 2021; 13(15):3023. https://doi.org/10.3390/rs13153023
Chicago/Turabian StyleXiong, Jinghua, Shenglian Guo, Jiabo Yin, Lei Gu, and Feng Xiong. 2021. "Using the Global Hydrodynamic Model and GRACE Follow-On Data to Access the 2020 Catastrophic Flood in Yangtze River Basin" Remote Sensing 13, no. 15: 3023. https://doi.org/10.3390/rs13153023







