Investigation of the Shielding and Attenuation Effects of a Dynamical High-Density Chaff Cloud on the Signal Based on Voxel Splitting

Abstract

Chaff jamming is a widely used passive interference method. A chaff cloud diffusion model for the widespread chaff cloud was presented. The high-density chaff cloud aerodynamic model can rapidly predict the chaff elements’ time-varying spatial orientation, location, and overall spatial distribution. Basing on these pieces of information, the radar cross section (RCS) for the single chaff fibre can be obtained based on the method of moments (MoM). For high-density chaff clouds, the attenuation and shielding effects on the signal must be considered. This paper proposed a voxel splitting method in rotated coordinates, dividing the chaff cloud into rectangular cells with one side perpendicular to the direction of radar entry. The varied polarized RCS features of the chaff cloud were simulated and analysed on this foundation. By dividing the chaff cloud into dynamic voxels and considering the uneven density distribution of the chaff cloud and the signal attenuation in each segment caused by the continuous fluctuating shape, fine-grained simulations of the chaff cloud radar echoes can be performed.

1. Introduction

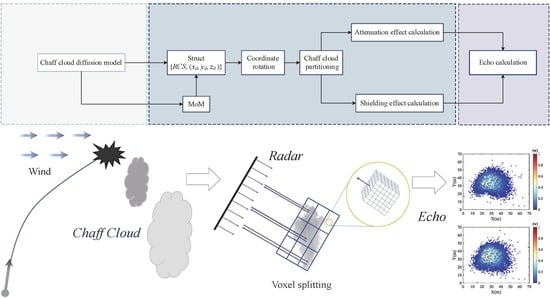
A chaff cloud is an aerial reflection target cloud made up of a huge number of metal filaments or metallic coated fibres. Electronic countermeasures to radar detection and air motion measurements take full advantage of this technology [1,2,3]. Chaff clouds interfere with radar mainly by creating a target-like spoof signal or by masking the signal of a real target. After chaff fibres are released into space, its position and attitude constantly change over time. The consequent RCS of the chaff cloud also varies with time. These changes eventually affect radar echoes of the chaff cloud. To estimate the radar echo of the chaff cloud, three parts are differentiated: (1) the Chaff kinetic model determines the orientation, position of chaff elements, and the density distribution of the chaff cloud; (2) the electromagnetic scattering model calculates the RCS based on the chaff orientation and the radar parameters; (3) the radar echo model calculates the radar echo from the chaff RCS and the relative distance to the radar.

Kinematic diffusion properties of chaff clouds are the basis for the study of radar echoes from the chaff cloud. There are many models of chaff motion based on experimental research and aerodynamic knowledge currently. Marcus [4] proposed a chaff cloud model (CCM) and described the helical motion model. Seo [5] introduced an aerodynamic model of the chaff based on the six degree-of-freedom (6 DOF) equations of motion, which provided a functional simulation of the angular variation and motion of the chaff. The above models provided a good simulation of the movement of the chaff in the absence of wind, but the consideration of diffusion and movement under wind conditions in real scenarios were slightly lacking. Knott [6] and Arnott [7] gave a model for the general first-order motion of the chaff under the influence of wind, based on an analysis of the forces on the chaff in the air. We have combined existing research with simulation of chaff movement under the influence of wind, diffusion due to helical rotation, and changes in attitude angle. The chaff fiber has a high aspect ratio with length and ultra-fine radius. The electromagnetic scattering theory of thin metal wires can be used to calculate the RCS of a single fiber. The wire moment method is used to determine the segmented induced current, and the backscattering cross-section can then be calculated [8,9,10]. In practice, the RCS calculation for a huge chaff quantity using the MoM [10] is time-consuming. To solve this problem, we used parallel for loops to fully exploit the multi-core performance of the computer and keep the overall time of the simulation within an acceptable limit.

When the distance between each chaff fiber is larger than $2\lambda$, the effect of mutual coupling can be ignored. Normally, a chaff cloud contains hundreds of thousands to millions of chaffs and the mutual coupling effect should be fully considered. Kownacki [11] and Marcus [8] described the effects of electromagnetic wave propagation through a unit volume chaff cloud, and the resulting shielding effect of the cloud. Zhang [12] built the bistatic RCS model of a high-density spherical chaff cloud based on the vector transport theory of random media. The above study is about the regular shaped chaff cloud, but in fact the shape and position of the chaff cloud change constantly during their movement. Seo [5] introduced a generalized equivalent conductor (GEC) method to calculate the RCS of the chaff cloud. Due to the uneven density of the chaff cloud, it is necessary to divide the chaff cloud into sub-small blocks to consider the mutual coupling effect of each part separately. Seo [5] used octree to segment the chaff cloud. Depending on our tests, the segmentation efficiency decreases dramatically when the sub-block size differs too much from the overall size. Pinchot [13] divided the chaff cloud into 3D cells according to the principle of solid angle elements in the spherical coordinate system. For the study of radar echoes from chaff clouds, the research focused on the effect of chaff motion on the spectral characteristics [14,15,16,17].

According to existing research, the following problems need to be solved for chaff cloud radar echo simulation: (1) The influence of the attenuation effect of the chaff cloud on the electromagnetic signal is fully considered in the calculation of the chaff cloud echoes; (2) a more flexible and efficient voxel partitioning algorithm is required to accommodate radar echo simulation of large areas with numerous elements in the chaff cloud. In this paper, to ensure that the projection plane perpendicular to the incident wave was easy to obtain and that the length of the incident wave through each voxel was the same, we created a rotational coordinate system based on the incident wave direction and converted the chaffs to the rotational coordinate system; the chaff cloud can be voxel split according to the direction of the coordinate axes. The method of partitioning by position is extremely efficient in the calculation of blocks for large areas.

This article is organized as follows: Section 2 describes the aerodynamic model. The method of moments (MoM) is recommended to determine the surface current and the RCS of fibers subsequently. In Section 3, the shielding and attenuation models for high-density chaff clouds are analyzed. Afterwards, the coordinate rotation and voxel splitting methods are presented.

In Section 4, simulations of the chaff cloud mobility under various atmospheric conditions are shown, firstly. The fluctuation of the chaff cloud polarization properties with the angle of incidence and time is examined on this basis. The attenuation impact of the chaff strip cloud on electromagnetic waves is then simulated for various radar frequencies, polarization conditions, and the different total number of elements. Finally, chaff cloud echoes are simulated, with an emphasis on the impacts of radar incidence angle and polarized echoes.

2. Chaff Kinetic Model and the Electromagnetic Scattering Reckoning

The RCS of a fibre is related to the radar observation angle and flight carriage of the fibre. During chaff fibre diffusion, it includes vertical and horizontal motion and a quasi-steady-state spiral. The diffusion model is utilized to determine the orientation distributions of elements within a chaff cloud, the RCS of which can be calculated. The chaff cloud diffusion model based on aerodynamic principles is given in this section. Afterwards, the electromagnetic (EM) scattering method is investigated to achieve the RCS of a single chaff fibre.

2.1. Chaff Cloud Diffusion Model

Because of their extraordinarily wide aspect ratios, chaff fibres have a remarkable aerodynamic property in that they can linger in the air for a long time. The initial velocity of the chaff cloud as it bursts open is rather high, and it will be susceptible to more air resistance. The horizontal velocity gradually changes and eventually converges to the wind speed. Meanwhile, chaff fibres continue to fall due to the combined effects of gravity and lift. In practice, non-rigid thin metallic wires inevitably undergo bending or torsion, causing helicoidal motion due to the unequal force induced by shape change.

As illustrated in Figure 1, the axes of the reference coordinate system are parallel to those of the global coordinate system, respectively. U is the wind speed at the height of the fibre, and V is the speed of the fibre displacement. The midpoint of the chaff is located at the origin of the reference coordinate system. Assuming the orientation vector of the chaff fibre is d, θ and φ are the zenith and azimuth angles of the chaff fibre’s orientation, separately. The chaff dynamic equations in the reference coordinate system are given by [6,7]:

$$\{\begin{array}{l}m\frac{dV}{dt}=\mathit{F}-mgz,\\ \mathit{F}=\frac{\rho C_{D}A}{2}\left(U-V\right)\left|U-V\right|,\end{array}$$

(1)

where ρ is the density of air [18] and m denotes the mass of a chaff fibre. The predicted area of chaff on the plane perpendicular to the velocity plane is defined as A, which is the characteristic frontal area of the body. The chaff drag coefficient C_D is calculated using the following equation [7]:

$$C_D=10.5{(\frac{\left|V\right|D\rho }{\mu })}^{-0.63}$$

(2)

where D is the chaff diameter, and $\mu$ is the dynamic viscosity of air.

Due to slight bending in the fibre and horizontal movement accompanied by directional change, the fibre’s descent is in the form of a helix [19]. It is assumed that the rotational velocity is Ω; then the radius of the circular trajectory is written [4,6,19]:

$$R=\sqrt{V_x^2+V_y^2}/\mathsf{\Omega }$$

(3)

where $V_x$ and $V_y$ are the horizontal components of the chaff motion velocity and the probability density that a given fiber will have a rotational velocity $\mathsf{\Omega }$ can be written as [4]:

$$\begin{array}{cc}F\left(\mathsf{\Omega }\right)=\frac{2}{{\mathsf{\Omega }}_{\mathit{e}}}\left(1-\frac{\mathsf{\Omega }}{{\mathsf{\Omega }}_{\mathit{e}}}\right),& 0<\mathsf{\Omega }<\end{array}{\mathsf{\Omega }}_{\mathit{e}}$$

(4)

A time interval is determined, assuming that the chaff speed is stable for a period of time. The spatial position of the fibre at different times can be obtained according to the above formula.

The orientation distribution of the chaff has an essential effect on diffusion and descent. As for the azimuth and zenith angles, this paper used typical statistical distributions to generate them [20]:

$$\begin{array}{cc}F\left({\theta }_c\right)=\frac{1}{\sqrt{2\mathit{\pi }{\mathit{\sigma }}^2}}\exp \left[\frac{{\left({\theta }_{\mathit{c}}-{\theta }_0\right)}^2}{2{\sigma }^2}\right],& F({\mathit{\phi }}_{\mathit{c}})\end{array}=\frac{1}{2\mathit{\pi }}$$

(5)

The majority of chaff attitudes in the steady state, according to the measured data and the simulation results, are horizontal [5,6,7,19]. In this paper, ${\theta }_c$ is generated with the mean value ${\theta }_0={90}^{\circ }$ and the variation ${\sigma }^2={10}^{\circ }$. The above angular distribution is only a reasonable assumption based on existing research.

2.2. Chaff Radar Cross Section

The chaff fibre can be represented as a wire in the EM calculation procedure, since it is a narrow cylinder with a high aspect ratio and a very thin section radius [10]. In the plane-wave field, according to the boundary condition, the electric field on the conductor surface is zero. It is known that there is an induced current on the surface of the chaff, as shown in Figure 2.

Dividing the chaff into N segments using the pulse basis function $f_n$, the expression for the surface current on the chaff fibre is the following:

$$I={\displaystyle \sum _{n=0}^N{I}_n{f}_n}\begin{array}{cc}& n=0,1,...,N\end{array}$$

(6)

A coordinate system is established with the chaff axis $l$ as the z-axis. For a chaff irradiated by a plane wave with the incident direction at an angle $\theta$ to the z-axis, the following equation is derived from the boundary conditions [21] (p. 83):

$$j\omega \mu {\displaystyle \underset{L}{\int }\left[1+\frac{1}{k^2}\frac{{\partial }^2}{\partial z^2}\right]}I\left(z^{\prime }\right)G\left(z,z^{\prime }\right)d{z}^{\prime }=E_{inc}\cdot l$$

(7)

The above equation is discretized by the weight function ${\omega }_m=\delta \left(z-z_m\right)$ and substituting (6), the matrix form can be written as: $\left[Z\right]\left[I\right]=\left[V\right]$ [22]. Furthermore, using MoM, the induced current distribution can be calculated. Finally, the chaff RCS can subsequently be calculated from the scattered field generated by the induced current and the known incident field.

The above calculations are performed in the chaff local coordinate system, where each chaff has its own local coordinate system during diffusion. Whereas the radar polarization is defined in the global coordinate system, the conversion of the two coordinate systems is analysed next. A diagram of the coordinate system conversion is shown in Figure 3. The incident wave and vector direction in the global coordinate $\left(x_G,y_G,z_G\right)$ is $\left({\theta }_i^G,{\varphi }_i^G\right)$. The chaff attitude angle in the global coordinate system is $\left({\theta }_d^G,{\phi }_d^G\right)$. The direction vector of the chaff’s long axis is written as:

$$d=\left(\cos {\phi }_d^G\sin {\theta }_d^G,\sin {\phi }_d^G\sin {\theta }_d^G,\cos {\theta }_d^G\right)$$

(8)

The incident wave vector is defined as:

$$k_i=(\sin {\theta }_i^G\cos {\varphi }_i^G,\sin {\theta }_i^G\sin {\varphi }_i^G,-\cos {\theta }_i^G)$$

(9)

The polarization vector of the incident wave electric field is defined as:

$$H_i=\left(-\sin {\varphi }_i^G,\cos {\varphi }_i^G\right)$$

(10)

$$V_i=(-\cos {\theta }_i^G\cos {\varphi }_i^G,-\cos {\theta }_i^G\sin {\varphi }_i^G,\sin {\theta }_i^G)$$

(11)

The direction vector of the chaff local coordinate system can be expressed as:

$$\begin{array}{l}{z}_L=d\hfill \\ y_L=z_L\times k_i/\left|z_L\times k_i\right|\hfill \\ x_L=y_L\times z_L\hfill \end{array}$$

(12)

Subsequently, the polarization vector in the local coordinate system can be written as:

$$h_i=y_L$$

(13)

$$v_i=h_i\times k_i$$

(14)

The polarization angle $\mathsf{\Phi }$ [23] required for the line MoM can be calculated using geometric relations by the equation below:

$$\cos \mathsf{\Phi }=\left[\begin{array}{cc}{H}_i\cdot v_i& V_i\cdot v_i\end{array}\right]$$

(15)

The MoM and the angular relationship can be used to calculate the RCS of a chaff with varied polarizations. Figure 4 shows the RCS of a single chaff back-scattered at an attitude angle $\left({30}^{\circ },{60}^{\circ }\right)$ as a function of incident wave angle.

Variations of polarized RCS with incident angle for 500 chaff fibres with uniformly distributed attitude angles are given in Figure 5. To reduce the effect of randomly generated chaff attitude angles, the results in the graphs are averaged over 10 calculations. Figure 5a shows $\varphi =0^{\circ }$ and $\theta$ variation and Figure 5b shows $\theta =0^{\circ }$ and $\varphi$ variation. The zenith angle $\theta$ of the incident wave has a substantial influence on the vertical and cross-polarization RCS, as shown in Figure 5, but the horizontal polarization RCS fluctuates very little with the incident wave angle. We conducted experiments based on the simulation parameters in [24], repeated the calculations 10 times, and averaged them to reduce uncertainty. The comparison results are shown in

Table 1. Comparison of computed RCS (dBsm) of a spherical chaff cloud.

Direction	${\mathit{k}}_{\mathit{s}\mathit{c}}$	${\mathit{u}}_{\mathit{s}\mathit{c}}$	Analytical [25]	Computed [24]	This Paper
mono	x	z	21.30 dBsm	21.32 dBsm	21.14 dBsm

. The simulation result we calculated has an error of 0.84% with the analytical value [25] and the simulation result in [24], which can prove the validity of the calculation.

3. The Signal Attenuation Model of the Chaff Cloud

Because one component of the chaff cloud is blocked by another, it cannot operate as an electromagnetic wave scatterer. The chaff blocking effect occurs when the chaff in front of a high-density section of the chaff cloud stops the chaff behind it from receiving electromagnetic energy. The attenuation effect occurs when an EM wave passes through a chaff cloud and loses energy owing to scattering by the chaff [24].

For a sufficiently diffuse cloud of randomly oriented chaff particles, which have an uneven spatial density distribution, there is also a position difference in the attenuation degree of the signal. The attenuation of the signal for a unit volume chaff cloud of area $1{\mathrm{m}}^2$ with a thickness of $\mathrm{dx}$ along the direction of the incident wave can be calculated according to the following equation [26]:

$$P_{out}=P_{in}\exp \left(-{\displaystyle \sum _{i=1}^{N_V}{\sigma }_i\cdot \mathrm{dx}}\right)$$

(16)

where $P_{in}$ is the signal power at incidence terminal, ${\sigma }_i$ is the RCS for a single chaff in the grid cuboid, $N_V$ is the total amount in the volume units, and $dx$ is the chaff cloud thickness along the incident direction.

According to (16), supposing the attenuation coefficient of each cell is $\Gamma$, the double distance attenuation of each region can be written as:

$$\mathsf{\Lambda }(r,c,p)={\left({\displaystyle \prod _{n=1}^p\mathsf{\Gamma }(r,c,n)}\right)}^2$$

(17)

As the chaff cloud density increases, chaffs will block each other. The shielding effect between chaffs will make the total RCS per unit volume smaller than the sum of all unit RCS superposition [11,25,27]; $A_c$ is assumed to be the projected area of the chaff cloud-resolving cell perpendicular to the incident wave. According to the absorption theory, the shielding model of a chaff cloud is given as follows [26]:

$${\sigma }_s=A_C\left[1-\exp (-{\sigma }_T)\right]$$

(18)

$${\sigma }_T={\displaystyle {\sum }_{i=1}^{N_V}{\sigma }_i/Ac}$$

(19)

where $N_V$ is the total number of dipoles in the grid cuboid and the RCS of each chaff is ${\sigma }_i$.

Using statistics ${\sigma }_s=0.153{\lambda }^{2}N$ [25] to estimate the shielding effect, the shielding curves for different incident wave frequencies are given in Figure 6. As the frequency increases, the chaff density required to reach the limit value is greater. Furthermore, the shielding effect decreases rapidly as the chaff density decreases. The shielding effect is only apparent at the stage when the chaff is first spread out and the density is very high.

One opposite face of the voxel needs to be perpendicular to the incident wave when calculating the RCS of the chaff voxel. Chaff coordinates can be rotated to the same or opposite direction of the z-axis and the incoming wave direction (red line) using coordinate rotation, as shown in Figure 7, so that the edge of the voxel can be parallel to the coordinate system vector during segmentation.

Assume that the chaff coordinate matrix is $\left[x_c,y_c,z_c\right]$. The direction of the incident wave is $\left({\theta }_i,{\phi }_i\right)$. According to the order of z-y-x, a new coordinate matrix $\left[{x^{\prime }}_c,{y^{\prime }}_c,{z^{\prime }}_c\right]$ can be obtained by rotating counterclockwise. The rotation matrix is indicated in (19). And the rotation coordinates can be calculated according to the Equation (20).

$$R(\rho ,\theta ,\phi )=\left[\begin{array}{ccc}\cos (\theta )\cos (\phi )& \cos (\theta )\sin (\phi )& -\sin (\phi )\\ \cos (\rho )\sin (\phi )+\sin (\rho )\sin (\theta )\cos (\phi )& \cos (\rho )\cos (\phi )-\sin (\rho )\sin (\theta )\sin (\phi )& \sin (\rho )\cos (\theta )\\ \sin (\rho )\sin (\phi )+\cos (\rho )\sin (\theta )\cos (\phi )& \cos (\phi )\sin (\rho )+\cos (\rho )\sin (\theta )\sin (\phi )& \cos (\rho )\cos (\theta )\end{array}\right]$$

(20)

$$\left[{x^{\prime }}_c,{y^{\prime }}_c,{z^{\prime }}_c\right]=\left[x_c,y_c,z_c\right]\cdot R(0,{\theta }_i,{\phi }_i)$$

(21)

For voxel partitioning of chaff clouds, the octree algorithm is often utilized [5]. The octree algorithm allows adaptive control of voxel size depending on the density of the point cloud, is flexible in use, and has important applications in voxel segmentation. In this paper, it is necessary to control the segmentation of voxels of the same size, and this requirement leads to a reduction in efficiency of the octree algorithm. Therefore, we improved the voxel segmentation algorithm for the above problem. The following is the segmentation approach employed in this study:

(1)

Determine the range of the axis-aligned bounding box (AABB) [28] from the upper and lower limits of the coordinates of the chaff cloud in a rotating coordinate system;

(2)

The preset voxel cell sizes $V_x$, $V_y$ and $V_z$, and the bounding box ranges $\left[\min ({x^{\prime }}_c),\min ({y^{\prime }}_c),\min ({z^{\prime }}_c)\right]$ and $\left[\max ({x^{\prime }}_c),\max ({y^{\prime }}_c),\max ({z^{\prime }}_c)\right]$, are used to determine the range for each voxel. Floor operations are used to turn the chaff coordinates and the center coordinates of each voxel into serial numbers. Each chaff’s location, velocity, and RCS information may then be stored as a structure in the associated voxel-based on its serial number.

(3)

Because the point cloud coordinates sorting has no effect on the form of the point cloud, each chaff is sorted in x-y-z order.

(4)

Place the information for each fibre into the corresponding grid according to the desired rectangular grid size.

(5)

The coordinates are reversed and rotated back to the original position.

We presented a comparison between the above method and the octree method for voxel partitioning under different experimental conditions in

Table 2. Time-consuming comparison of voxel segmentation for regions of different sizes using two methods.

L(m)	n	Octree	This Paper	Speedup
10	500,000	0.71 s	0.74 s	0.96
20	500,000	4.05 s	0.66 s	6.13
40	500,000	44.1 s	0.75 s	58.8
60	500,000	44.77 s	1.01 s	44.32
80	500,000	1638.5 s	1.27 s	1290
100	500,000	1616.9 s	1.76 s	918.69

. The computer configuration used in the experiment is: Intel Xeon W-2245, 32 GB DDR4 memory, Win10 system, and MATLAB 2021b software. The dimensions of the voxel size are 1 m square. The area of the square where random elements are located has the side length L and the total number of elements is n. The time taken for this experiment is the sum of the coordinate rotation and voxel partitioning time. The rotation angle is (45°, 45°). The efficiency advantage of the method in this paper becomes progressively more apparent as the area to be segmented increases. Generally, the chaff movement process scatters the area in the range of tens to hundreds of meters, and the method of this paper is appropriate to the chaff cloud.

According to the above operation and Equations (9)–(11), the RCS and attenuation coefficient of each grid cuboid can be obtained. Eventually, the signal received by the monostatic radar from the chaff cloud is given by [14]:

$$s(t)={\displaystyle \sum _{i=1}^{N_x}{\displaystyle \sum _{j=1}^{N_y}{\displaystyle \sum _{k=1}^{N_z}\sqrt{{\sigma }_s(i,j,k)}}}}\mathsf{\Lambda }(i,j,k)\exp \left[-j(2\pi f_{0}t+\mathsf{\Phi }(i,j,k))\right]$$

(22)

$$\mathsf{\Phi }(i,j,k)=4\pi R(i,j,k)/\mathit{\lambda }$$

(23)

where $\lambda$ is the wavelength of the radar and $R(i,j,k)$ is the range from the radar to each voxel center.

Figure 8 depicts the flow chart for the chaff cloud radar echoes simulation. For a simulation with a total simulation time of T and time intervals of $\Delta t$, the dynamic chaff cloud radar echo simulation steps are as follows.

Step 1: Calculation of chaff attitude angles and spatial positions using the chaff cloud diffusion model.

Step 2: Calculation of the RCS using the MoM based on the chaff fibers’ attitude;

Step 3: Rotation of the spatial coordinates of each fiber and voxelization of the chaff cloud in the rotated coordinate system.

Step 4: Calculation of the shielding RCS and power attenuation for each grid cuboid.

Step 5: Calculation of radar echoes.

Step 6: If the $t_n$ is less than the pre-defined total duration of the simulation T, then $t_{n+1}=t_n+\Delta t$ and the simulation returns to the first step and is calculated in sequence. If $t_n>T$, the simulation is terminated.

4. Electromagnetic Scattering Results and Analysis

The physical dimensions of the chaff elements are 14.475 mm length and 12.5 μm radius. This is a typical chaff specification, which has a first resonant frequency of 10 GHz. All the chaff clouds analyzed afterwards are composed of this dipole unless otherwise specified. In the chaff cloud motion simulation, the number of chaff fibres is set to 500,000. We suppose the initial distribution of the chaff cloud is the spherical shape and each chaff fiber has an initial velocity along its radius. In an environment with wind speeds of (5, 5, 0) m/s and (10, 10, 0) m/s, falling at the initial position of (0, 0, 500) m, the spatial density distributions of chaff clouds after 30 s are illustrated in Figure 9.

As can be seen from the diagram, chaff clouds undergo a density buildup in the wind direction due to wind action. In environments with different wind speeds, the overall manifestation is a different diffuse area due to the increased force gap between the elements in the chaff cloud. Due to the different attitude angles of the chaffs, the lifting forces differ, which is reflected in the slow fall of the chaffs close to the horizontal and the fast fall of the chaffs close to the vertical, forming an angularly stratified inverted conical chaff cloud pattern.

Figure 10 shows the variation of the polarization RCS with the changing angle of incidence for one million chaffs moving for 30 s. The VV polarization RCS reduces rapidly with rising θ because the chaff attitude is mostly horizontal. The HH polarization RCS varies little with the angle of incidence and remains at a high value. This is explained by the fact that the majority of fibres within the chaff cloud tend to be horizontal.

The horizontally polarized electric field vector excites a greater induced current, which has a greater induced electric field in the horizontal direction. Since the azimuth of the chaff is random, the chaff cloud RCS does not vary significantly.

Figure 11 exhibits the polarization RCS over time for 500,000 chaffs with different radar incidence angles. Because the chaffs are not entirely distributed at the beginning of the motion, the shielding effect between them is visible. In the constant diffusion state, the RCS of the chaff cloud fluctuates just slightly and is slightly smaller than the theoretical analysis.

The signal attenuation by the chaff cloud is shown in Figure 12 for various incident wave frequencies. The simulation parameters are as follows: atmospheric wind speed = (5, 5, 0) m/s, resolution cell = 1 × 1 m², ${\theta }_i={30}^{\circ }$ and ${\phi }_i=0^{\circ }$. The horizontal coordinates are the serial numbers of the resolution cells along with the longitudinal extension in the direction of the incident plane, and the vertical coordinates are the signal power after the chaff cloud has attenuated it. The attenuation of the spread-out chaff cloud for the incident wave at 5 GHz, with chaff elements of 1,000,000, 500,000, and 1,000,000, respectively, are presented in Figure 12a–c. The incident wave at 10 GHz is given in Figure 12d–f, with chaff elements of the 1,000,000, 500,000, and 1,000,000, respectively. The graph shows that when the total number of chaffs rises, the number of cells with severe attenuation increases, and the maximum attenuation increases at the same time. To obtain the same amount of interference for higher frequency radar signals, additional chaffs are necessary.

Figure 13 shows the three-dimensional distribution of the echo amplitude for 500,000 chaffs under varied polarized incident wave conditions and wind speeds of (5, 5, 0) m/s. The incident wave zenith angle ${\theta }_i={30}^{\circ }$, HH polarization and VV polarization echo amplitude distributions are shown in Figure 13a,b. The incident wave zenith angle ${\theta }_i={60}^{\circ }$, HH polarization and VV polarization echo amplitude distributions are shown in Figure 13c,d, respectively. As can be seen in Figure 13, the region impacted by the chaff cloud varies based on the ${\theta }_i$ of incidence. The distribution of strong locations of the echoes is also affected by the polarization of the radar.

5. Conclusions

The attenuation of signals in high-density chaff clouds is investigated in this work using the diffusion model and the electromagnetic model. The issue of unequal chaff density distribution and a method for estimating the attenuation coefficient in a sub-region are investigated. The main contribution of the proposed scheme is the fast partitioning of the chaff cloud within it by creating a rotating coordinate system as opposed to the traditional method of partitioning in a global coordinate system. In the simulation, the voxel partitioning method in this paper has a great improvement in computational efficiency compared to the octree method. The scheme in this paper takes full account of the influence of the projection surface of the chaff cloud over the distance travelled by the electromagnetic wave on the calculation of the attenuation and shielding effects. The electromagnetic scattering characteristics of high-density chaff clouds are then examined, as well as the echo simulation method. Different polarizations, radar incident frequencies, and total numbers of chaff are considered in the simulation. After that, simulated analysis of radar echoes in complex settings with target and ground-sea clutter can be performed.