Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters
Abstract
:1. Introduction
2. Methodological Background: Data Reduction Principles, Forward/Inverse Methodology
2.1. The Fourier Pair: Spectrum, , Interferogram,
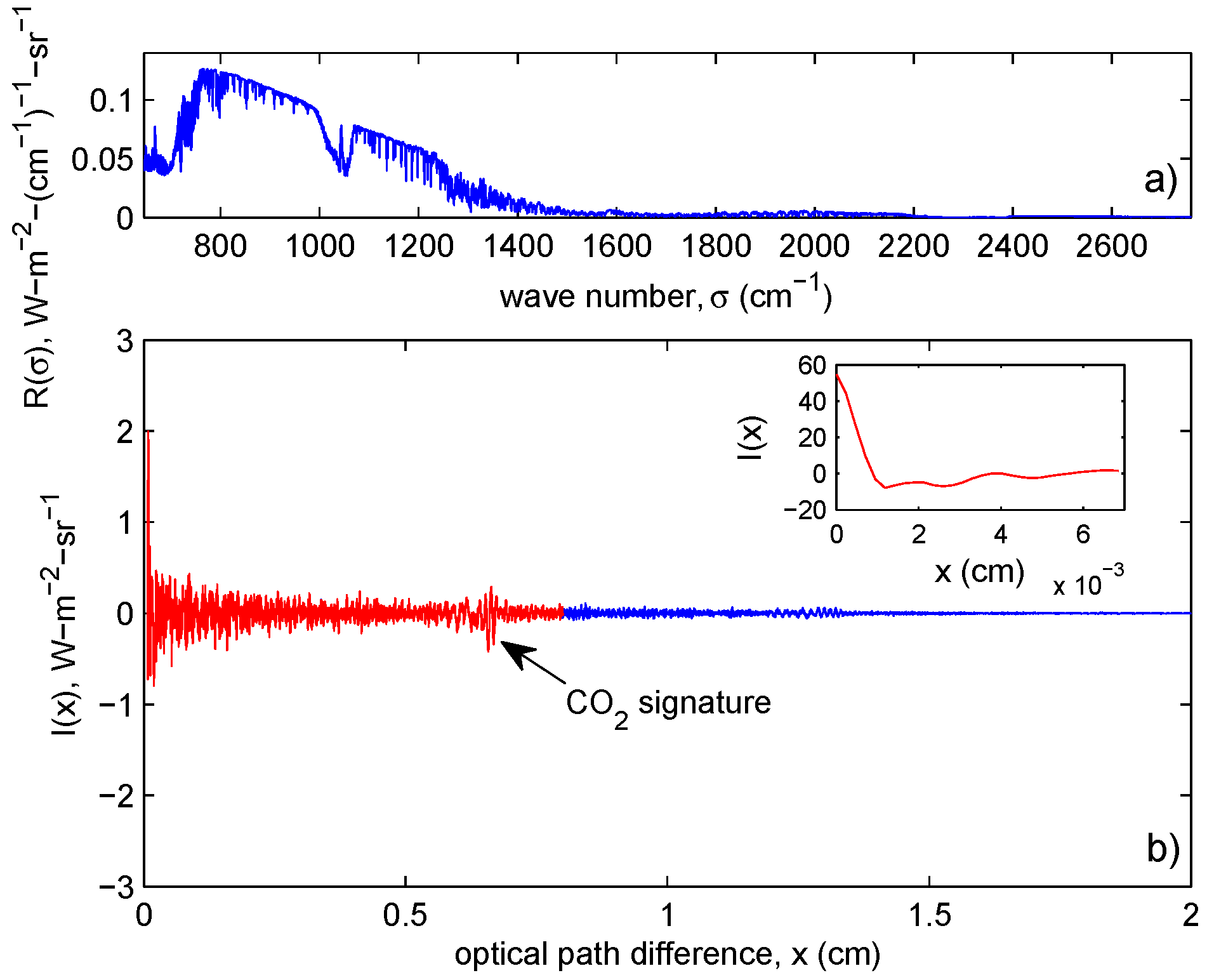
- Fourier transform the spectrum to the interferogram domainFigure 1. Example of IASI observed spectrum, , shown in panel (a), and its mathematical Fourier transform, , shown in panel (b). The behaviour of close to is shown in the inset. The interferogram interval [0,0.8] cm has been drawn in red in panel (b).Figure 1. Example of IASI observed spectrum, , shown in panel (a), and its mathematical Fourier transform, , shown in panel (b). The behaviour of close to is shown in the inset. The interferogram interval [0,0.8] cm has been drawn in red in panel (b).
- cut the interferogram at a new
- transform back the truncated interferogram to the spectral domain.

2.2. Forward and Inverse Modeling
3. Data Reduction Applied to IASI
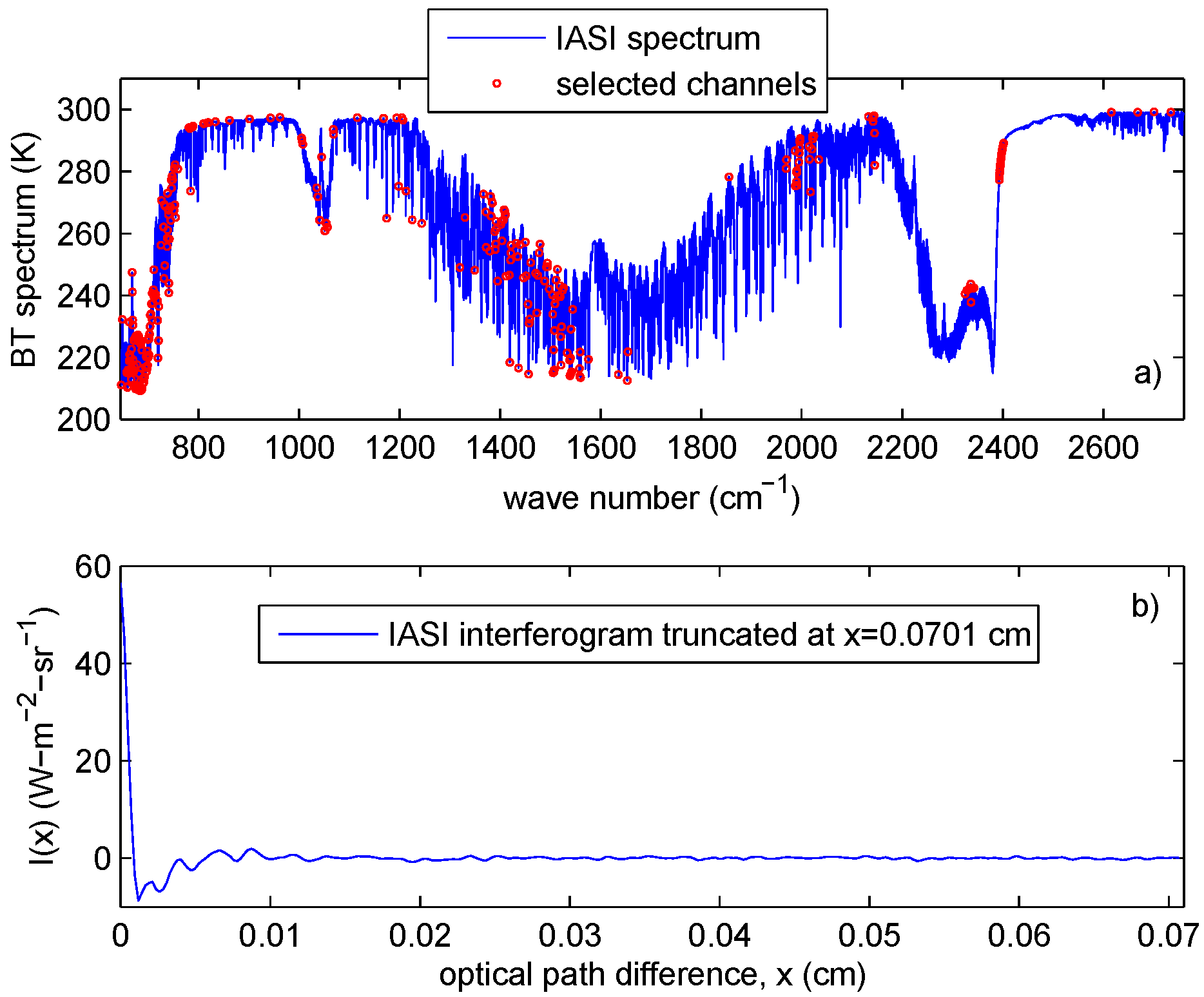
- I-method, the method which is based on the truncation of the interferogram at point below the IASI maximum path difference of 2 cm,
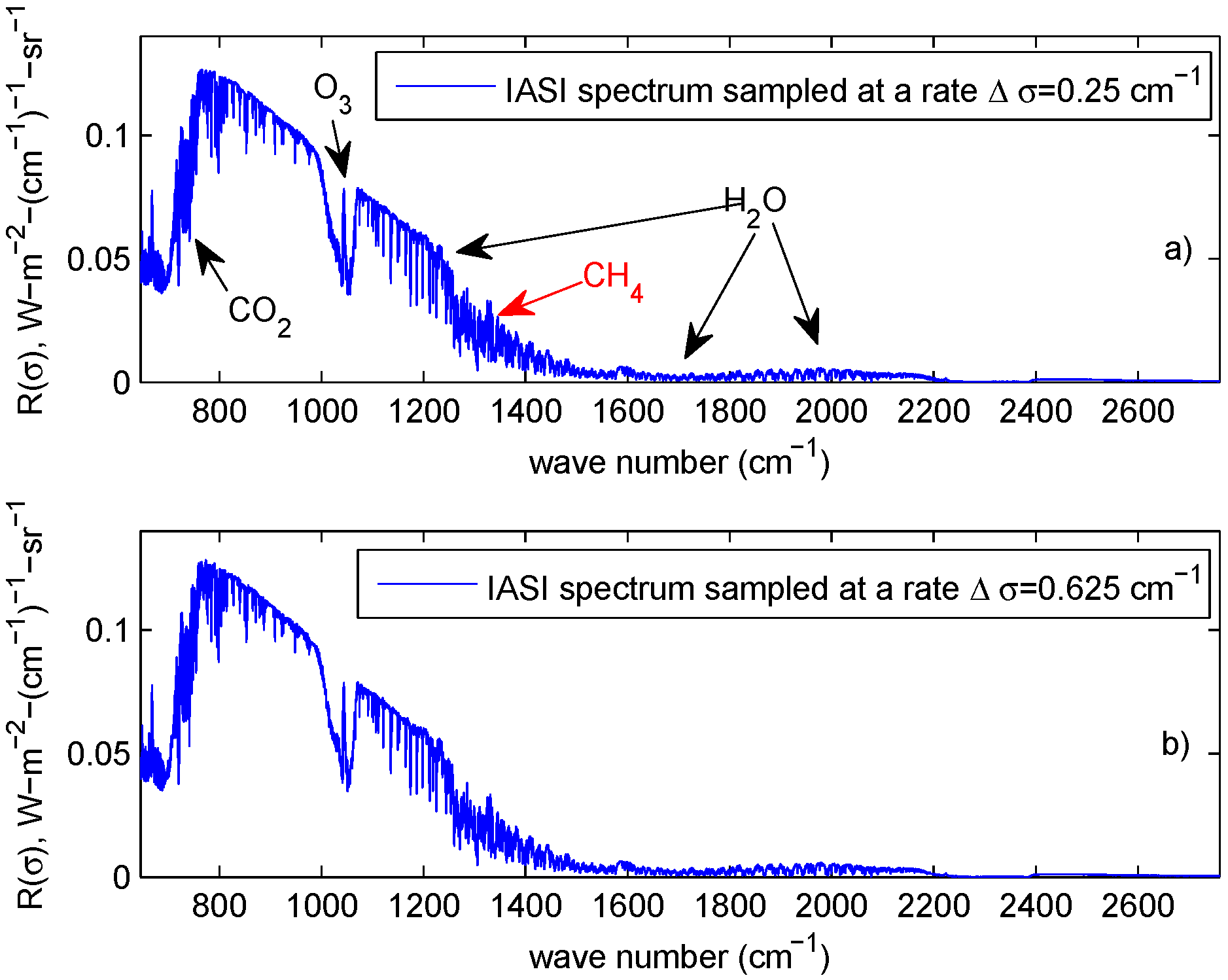
- R-method, the method which is based on the selection of sparse spectral channels from the IASI spectrum at its nominal sampling cm.
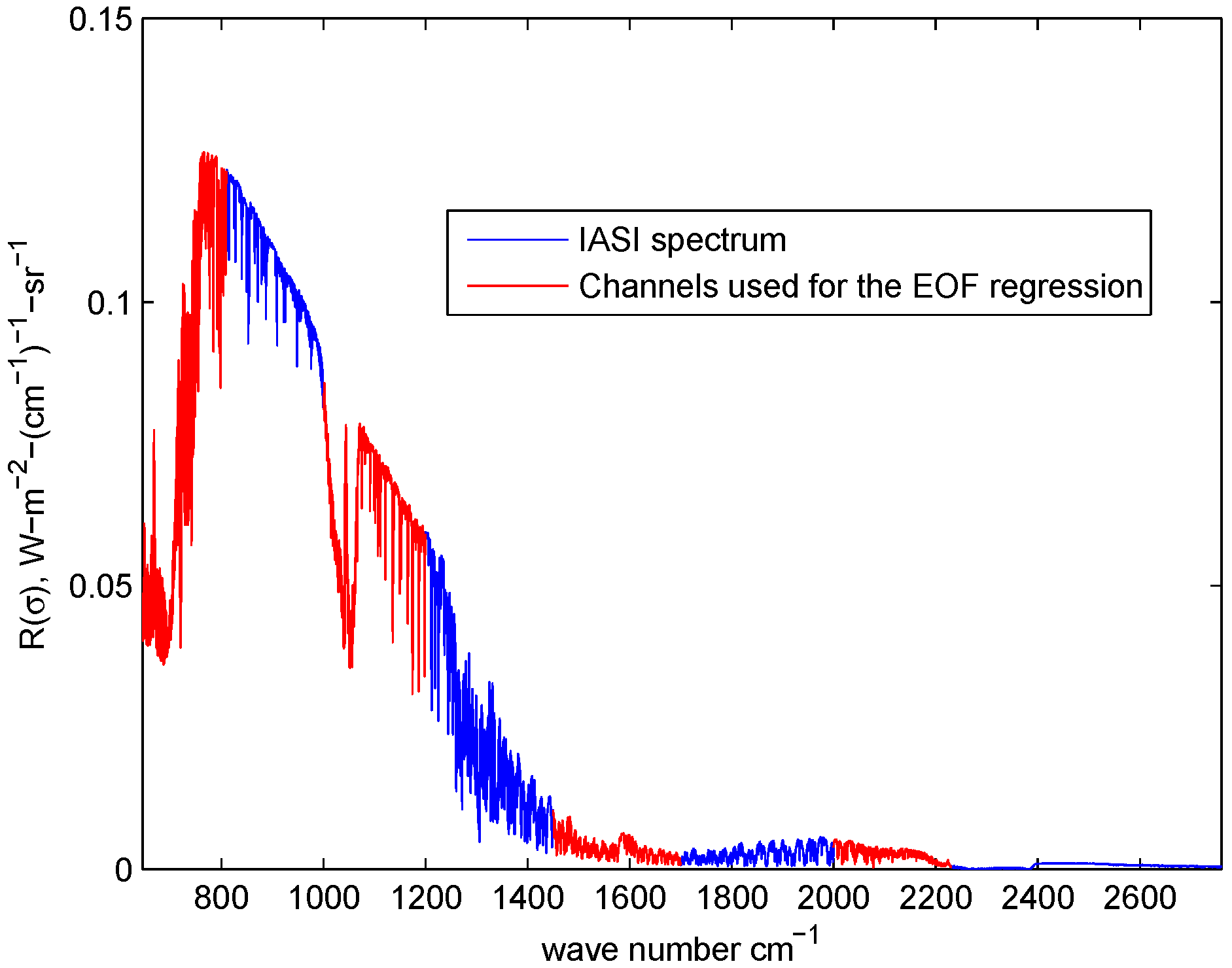
3.1. Data Reduction of a Factor 2.5
- the absorption band of CO and part of the atmospheric window (range from 645 to 830 cm)
- the ozone band at 9.6 μm
- the atmospheric window from 1,100 to 1,200 cm
- the core of the absorption band of HO at 6.7 μm
- the portion of the spectrum from 2,000 to 2,230 cm, this includes a part of the NO/CO absorption band at 4.3 μm
- 810 to 1,000 cm because of unknown contamination from CFC absorption;
- 1,200 to 1,450 because of strong contamination by CH;
- 2,230 to 2,760, because of spectroscopic issues such as CO line and continuum absorption uncertainty, e.g., [16], non LTE effects and sun contribution during the day.
3.2. Data Reduction of a Factor
4. Results: Assessment of the Retrieval Capability of the I-method and R-method
4.1. A Case Study in Simulation
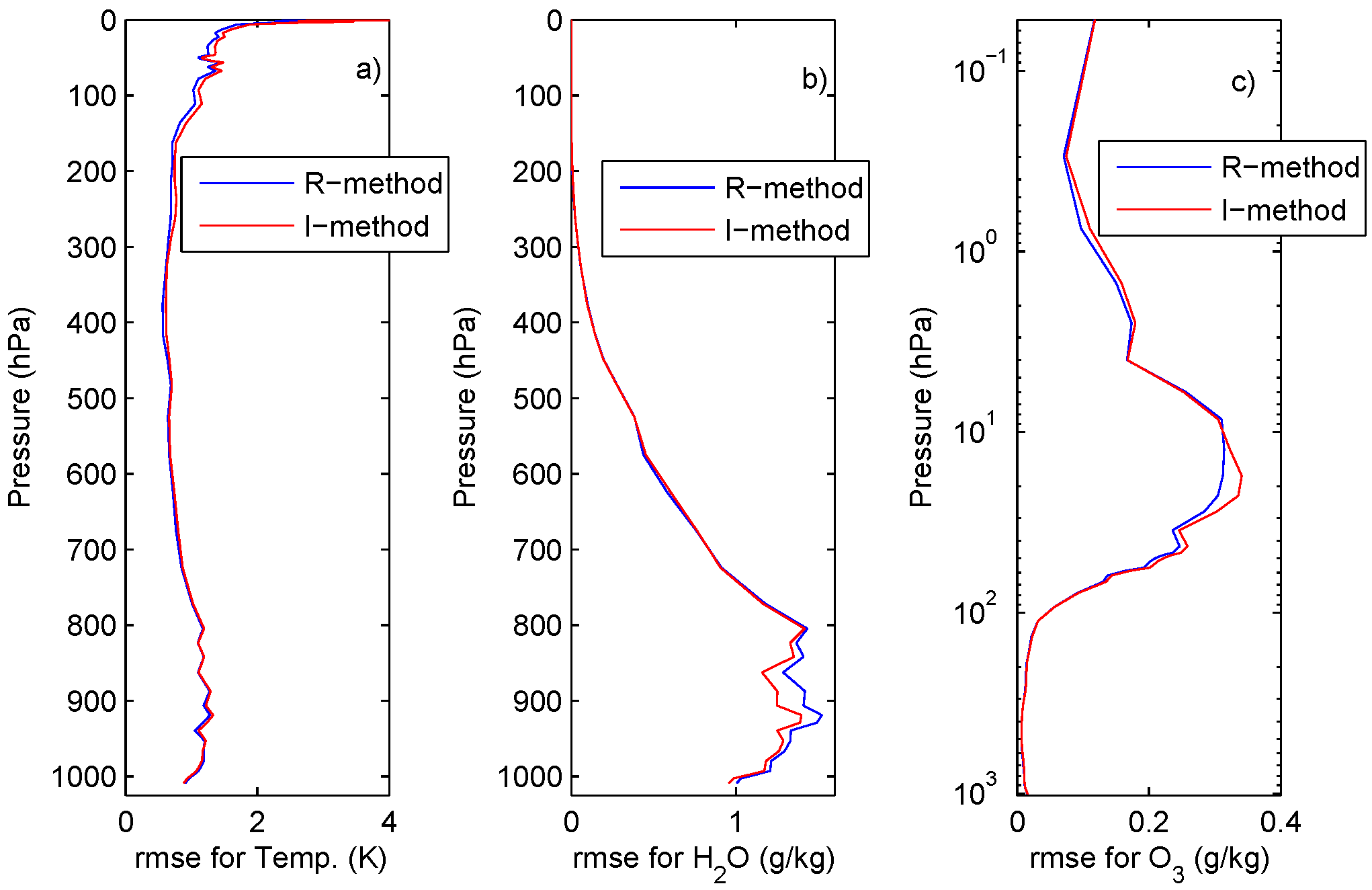

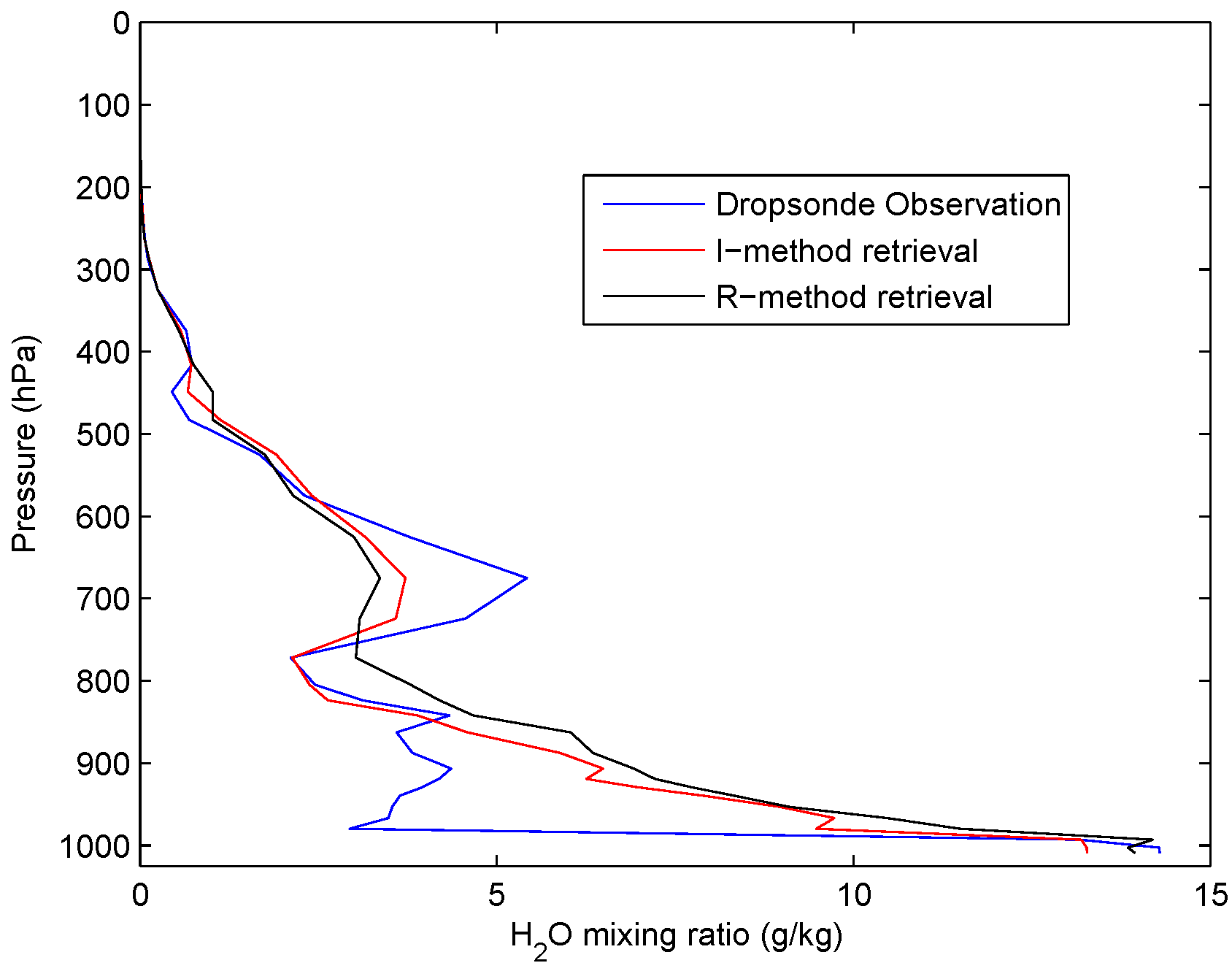
4.2. The JAIVEx Case Study
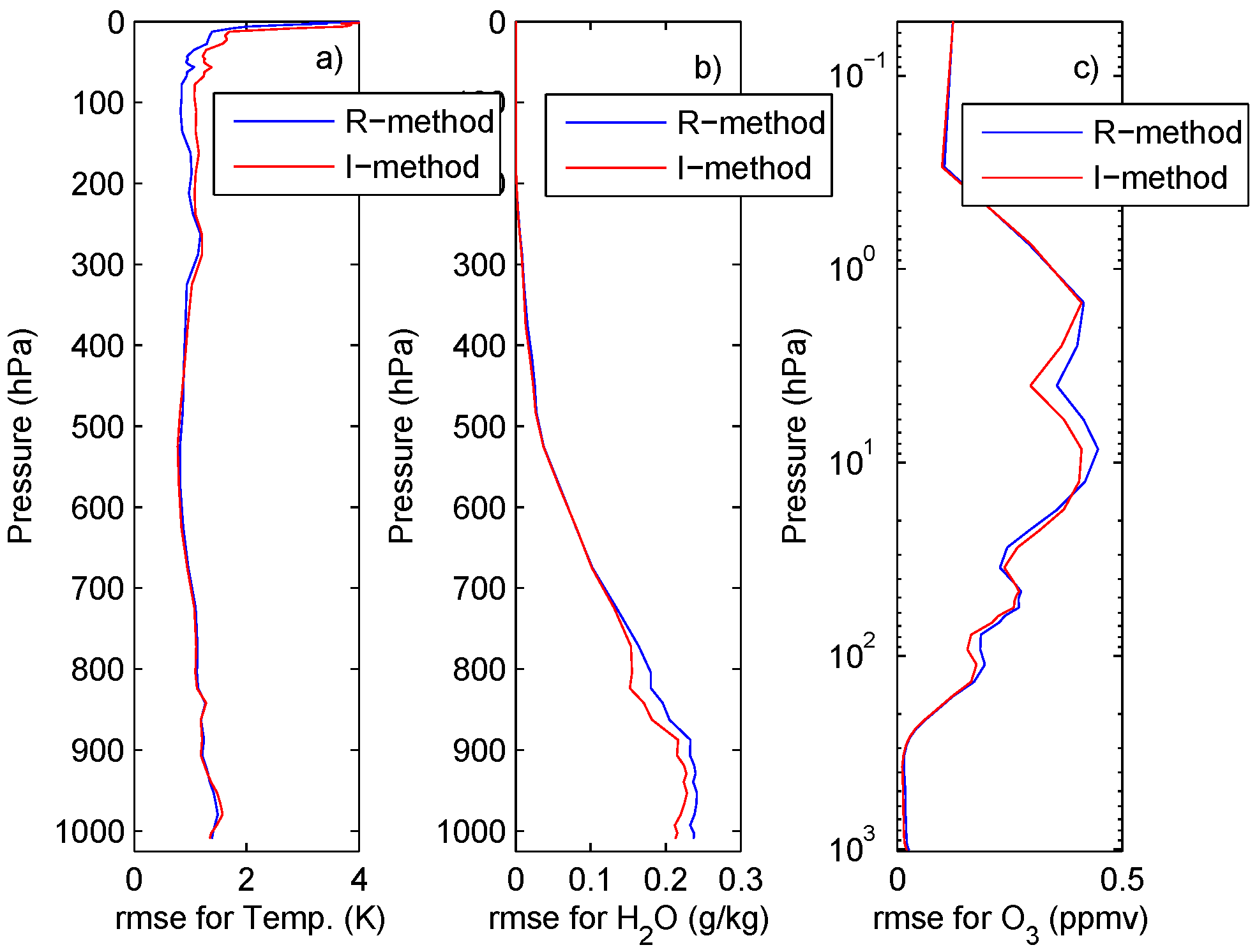

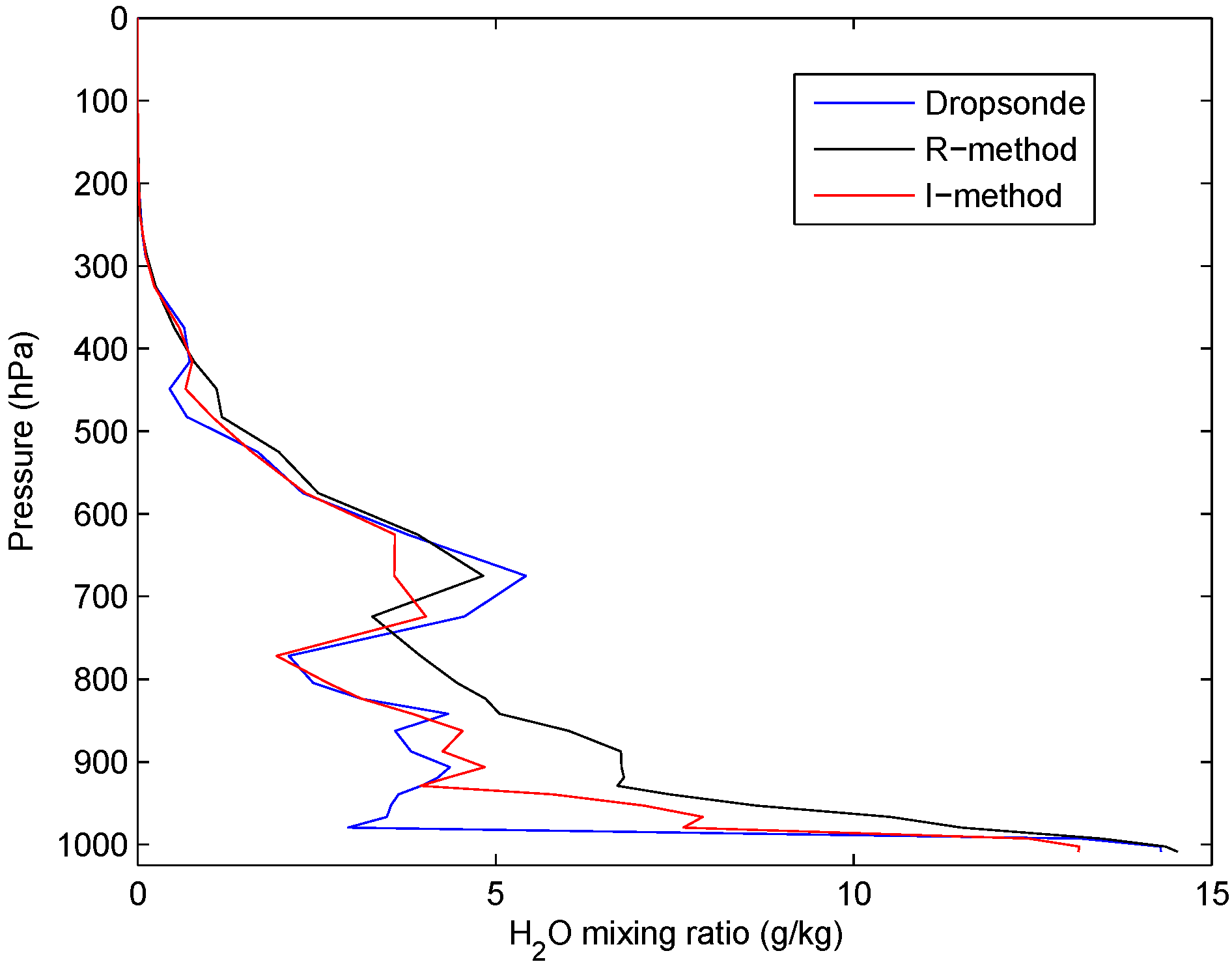
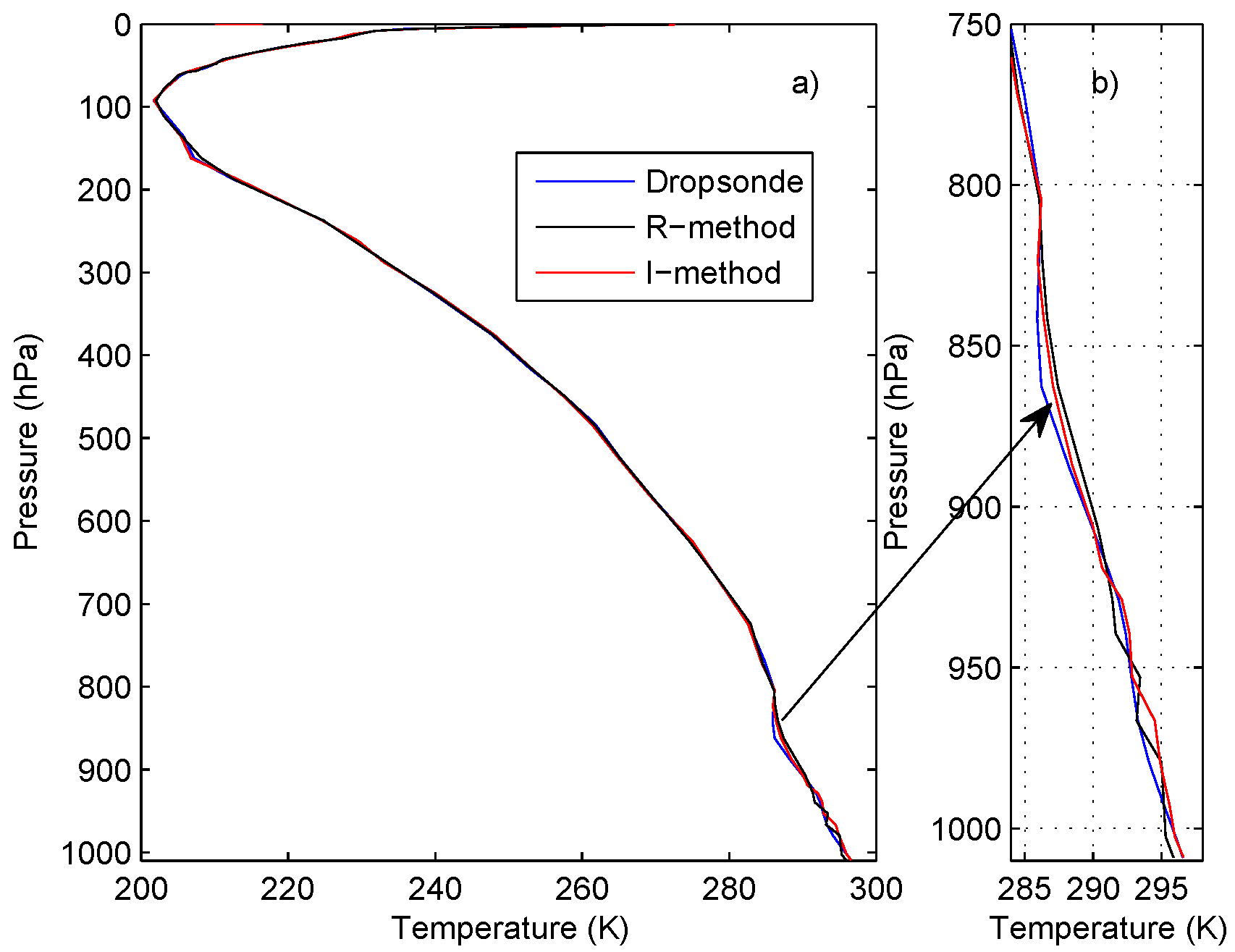
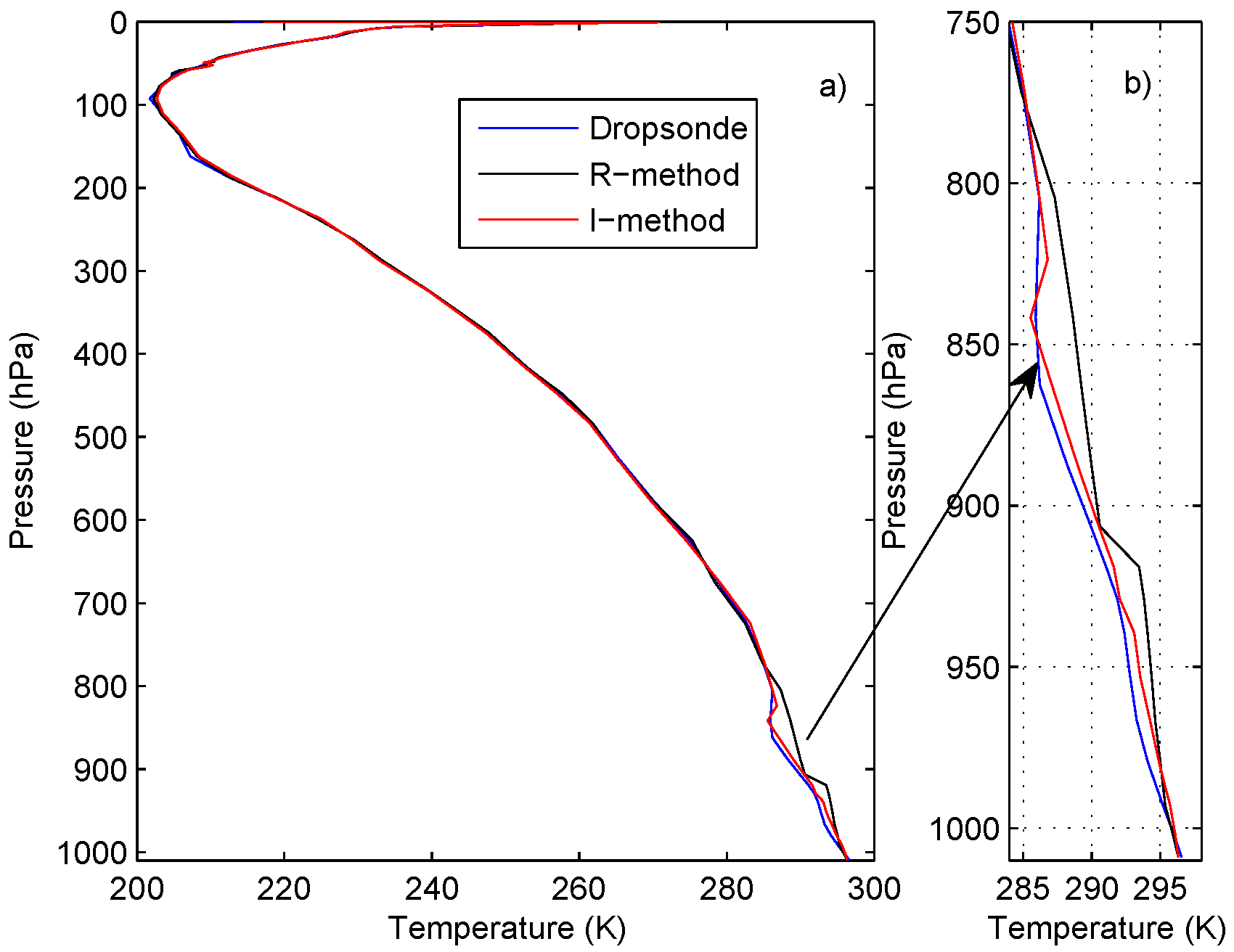
4.3. The Tropical Case Study
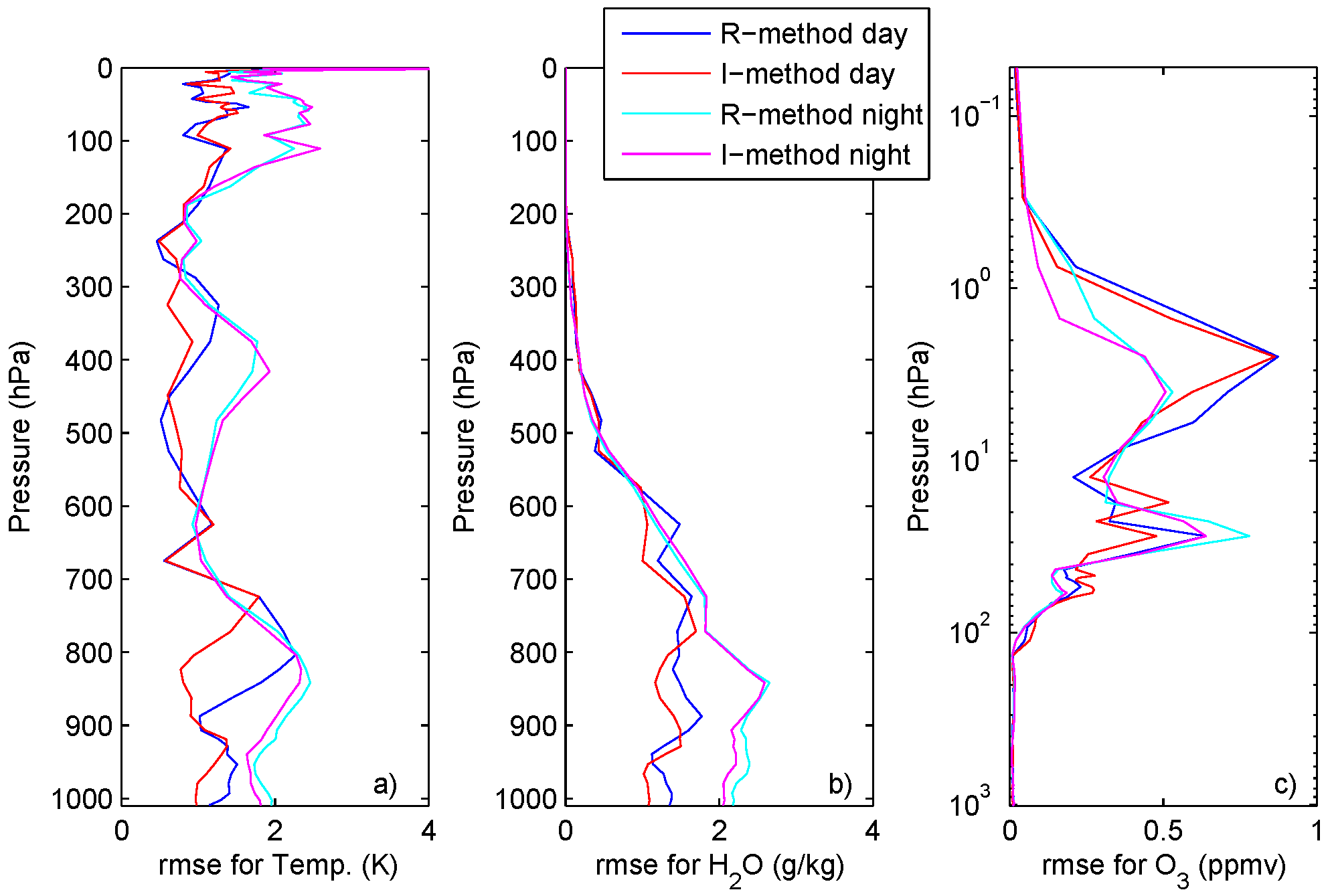
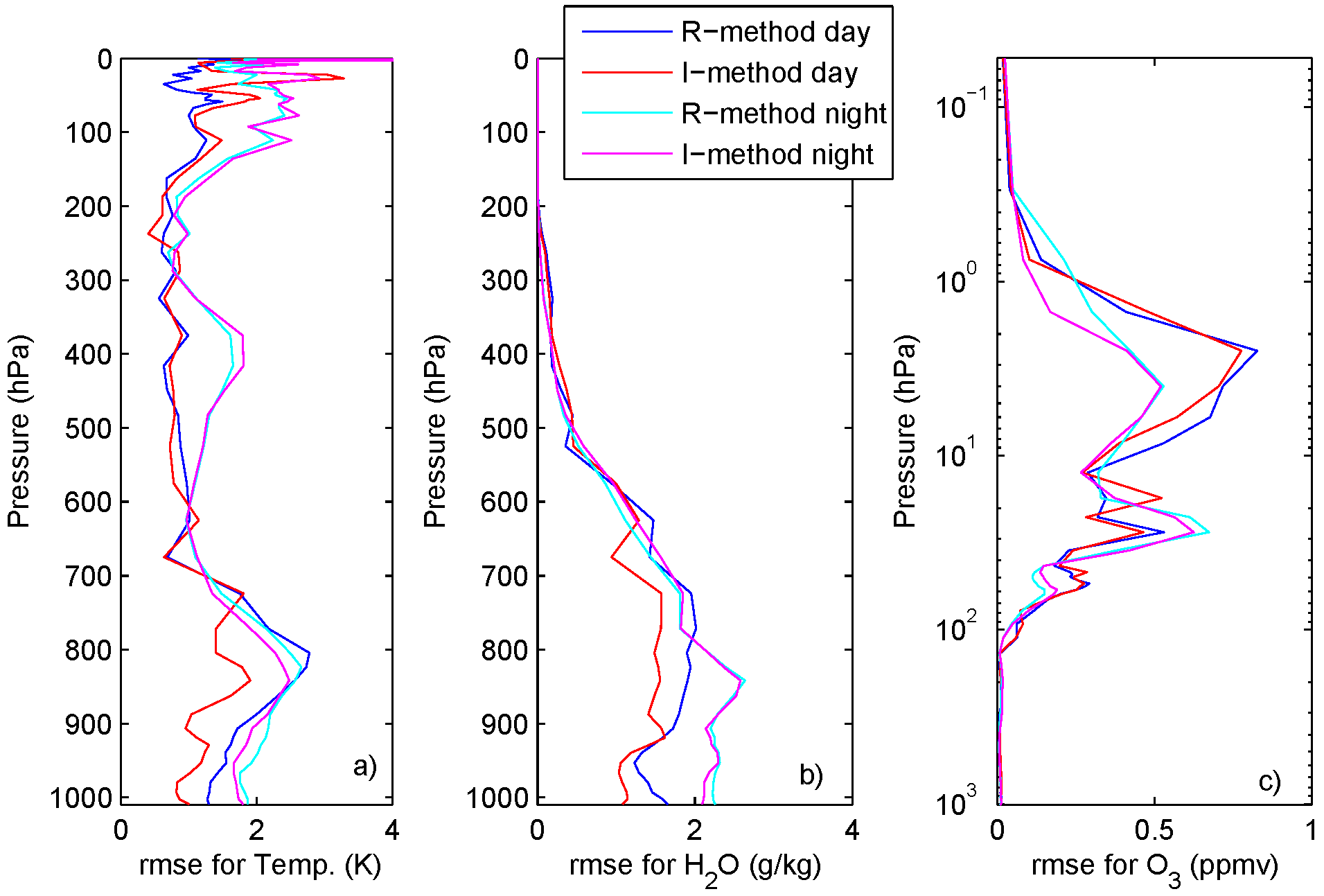
5. Discussion and Conclusions

Acknowledgements
References and Notes
- Richter, A.; Wagner, T. The IASI instrument onboard the METOP Satellite: First results. Atmos. Chem. Phys. 2009. Special Issue. Available online: http://www.atmos-chem-phys.net/special_issue123.html (accessed on 29 September 2010).
- Collard, A.D.; McNally, A.P. The assimilation of Infrared Atmospheric Sounding Interferometer radiances at ECMWF. Q. J. R. Meteorol. Soc. 2009, 135, 1044–1058. [Google Scholar] [CrossRef]
- Robinson, E.A.; Silvia, M.T. Digital Foundation of Time Series Analysis: Wave-Equation Space-Time Processing; Holden-Day: San Francisco, CA, USA, 1981; Volume 2. [Google Scholar]
- Collard, A.D. Selection of IASI channels for use in numerical weather prediction: The assimilation of Infrared Atmospheric Sounding Interferometer radiances at ECMWF. Q. J. R. Meteorol. Soc. 2007, 133, 1977–1991. [Google Scholar] [CrossRef]
- Kaplan, L.D.; Chahine, M.T.; Susskind, J.; Searle, L.E. Spectral band passes for a high precision satellite sounder. Appl. Opt. 1977, 16, 322–325. [Google Scholar] [CrossRef] [PubMed]
- Kyle, T.G. Temperature soundings with partially scanned interferograms. Appl. Opt. 1977, 16, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.L.; Howell, H.B.; Woolf, H.M. The use of interferometric radiance measurements for the sounding the atmosphere. Appl. Opt. 1979, 36, 566–575. [Google Scholar]
- Huang, H.-L.; Antonelli, P. Application of principal component analysis to high- resolution infrared measurements compression and retrieval. J. Appl. Metereo. 2001, 40, 365–388. [Google Scholar]
- Serio, C.; Masiello, G.; Grieco, C. EOF regression analytical model with applications to the retrieval of atmospheric temperature and gas constituents concentration from high spectral resolution infrared observations. In Environmental Modelling: New Research; Findley, P.N., Ed.; Nova Science Publishers, Inc.: Hauppagauge, NY, USA, 2009; pp. 51–88. [Google Scholar]
- Goldberg, M.D.; Qu, Y.; McMillin, L.M.; Wolf, W.; Zhou, L.; Divakarla, M. AIRS near-real-time products and algorithms in support of operational numerical weather prediction. IEEE Trans. Geosci. Remote Sens. 2003, 41, 379–389. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C. Dimensionality-reduction approach to the thermal radiative transfer equation inverse problem. Geophys. Res. Lett. 2004, 31, L11105. [Google Scholar] [CrossRef]
- Serio, C.; Esposito, F.; Masiello, G.; Pavese, G.; Calvello, M.R.; Grieco, G.; Cuomo, V.; Buijs, H.L.; Roy, C.B. Interferometer for ground-based observations of emitted spectral radiance from the troposphere: evaluation and retrieval performance. Appl. Opt. 2008, 47, 3909–3919. [Google Scholar] [PubMed]
- Zhou, D.K.; Smith, W.L.; Li, J.; Howell, H.B.; Cantwell, G.W.; Larar, A.M.; Knuteson, R.O.; Tobin, D.C.; Revercomb, H.E.; Bingham, G.E.; Tsou, J-.J.; Mango, S.A. Thermodynamic product retrieval methodology and validation for NAST-I. Appl. Opt. 2002, 41, 6957–6970. [Google Scholar] [CrossRef] [PubMed]
- Amato, U.; Masiello, G.; Serio, C.; Viggiano, M. The σ-IASI code for the calculation of infrared atmospheric radiance and its derivatives. Environ. Model. Software 2002, 17, 651–667. [Google Scholar] [CrossRef]
- Grieco, G.; Masiello, G.; Matricardi, M.; Serio, C.; Summa, D.; and Cuomo, V. Demonstration and validation of the φ-IASI inversion scheme with NAST-I data. Q. J. R. Meteorol. Soc. 2007, 133, 217–232. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Carissimo, A.; Grieco, G. Application of ϕ-IASI to IASI: Retrieval products evaluation and radiative transfer consistency. Atmos. Chem. Phys. 2009, 9, 8771–8783. [Google Scholar] [CrossRef]
- Amato, U.; De Canditiis, D.; Serio, C. Effect of apodization on the retrieval of geophysical parameters from Fourier-Transform Spectrometers. Appl. Opt. 1998, 37, 6537–6543. [Google Scholar] [CrossRef] [PubMed]
- Chevalier, F. Sampled Database of 60 Levels Atmospheric Profiles from the ECMWF Analysis; Technical Report; ECMWF EUMETSAT SAF programme Research Report 4; ECMWF: Shinfield Park, Reading, UK, 2001. [Google Scholar]
- Taylor, J.P. Joint Airborne IASI Validation Experiment. Available online: http://badc.nerc.ac.uk/data/jaivex/ (accessed on 29 September 2010).
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Grieco, G.; Masiello, G.; Serio, C. Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sens. 2010, 2, 2323-2346. https://doi.org/10.3390/rs2102323
Grieco G, Masiello G, Serio C. Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sensing. 2010; 2(10):2323-2346. https://doi.org/10.3390/rs2102323
Chicago/Turabian StyleGrieco, Giuseppe, Guido Masiello, and Carmine Serio. 2010. "Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters" Remote Sensing 2, no. 10: 2323-2346. https://doi.org/10.3390/rs2102323
APA StyleGrieco, G., Masiello, G., & Serio, C. (2010). Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sensing, 2(10), 2323-2346. https://doi.org/10.3390/rs2102323