Estimating Canopy Nitrogen Concentration in Sugarcane Using Field Imaging Spectroscopy

Abstract

The retrieval of nutrient concentration in sugarcane through hyperspectral remote sensing is widely known to be affected by canopy architecture. The goal of this research was to develop an estimation model that could explain the nitrogen variations in sugarcane with combined cultivars. Reflectance spectra were measured over the sugarcane canopy using a field spectroradiometer. The models were calibrated by a vegetation index and multiple linear regression. The original reflectance was transformed into a First-Derivative Spectrum (FDS) and two absorption features. The results indicated that the sensitive spectral wavelengths for quantifying nitrogen content existed mainly in the visible, red edge and far near-infrared regions of the electromagnetic spectrum. Normalized Differential Index (NDI) based on FDS_(750/700) and Ratio Spectral Index (RVI) based on FDS_(724/700) are best suited for characterizing the nitrogen concentration. The modified estimation model, generated by the Stepwise Multiple Linear Regression (SMLR) technique from FDS centered at 410, 426, 720, 754, and 1,216 nm, yielded the highest correlation coefficient value of 0.86 and Root Mean Square Error of the Estimate (RMSE) value of 0.033%N (n = 90) with nitrogen concentration in sugarcane. The results of this research demonstrated that the estimation model developed by SMLR yielded a higher correlation coefficient with nitrogen content than the model computed by narrow vegetation indices. The strong correlation between measured and estimated nitrogen concentration indicated that the methods proposed in this study could be used for the reliable diagnosis of nitrogen quantity in sugarcane. Finally, the success of the field spectroscopy used for estimating the nutrient quality of sugarcane allowed an additional experiment using the polar orbiting hyperspectral data for the timely determination of crop nutrient status in rangelands without any requirement of prior cultivar information.

1. Introduction

Sugarcane (Saccharum spp. hybrid) is one of the most important economic crops in Thailand. It is used to produce sugar and to generate power [1]. The precise estimation of the annual sugarcane yield is necessary to balance the amount of sugarcane used by these two competing industries and, consequently, to establish proper policies regarding its use. Several physical and chemical factors, such as nitrogen, cultivars, climate, soil and water availability, influence sugarcane growth [2] and need to be considered in any yield estimation model. Nitrogen is one of the most significant macronutrients associated with sugarcane yield due to its impact on leaf and stalk growth [3]. Sugarcane accumulates most of its nitrogen from the initial growth stages up to canopy closure [4,5]. An adequate nitrogen supply will improve the leaf area index and the chlorophyll concentration [6].

In general, several approaches to measure nutrient status in the plant have been developed and evaluated. The most common method is performed in the laboratory using leaf samples collected in the field [7]. Non-destructive field measurements of N status have been proposed, e.g., using leaf color charts or chlorophyll meters [8,9]. With the availability of remotely sensed data, these measurements enable the indirect determination of the amount of nitrogen available to crops on a large spatial scale. Such technology has proven to be useful for estimating biochemical parameters [10–15], plant species discrimination [16–18] and crop disease monitoring [19,20].

However, the first method requires more leaf samples from the field, which is a laborious, lengthy and destructive process [21]. The second technique is practical only at the leaf level and is limited to evaluating plant quality in a large area. In contrast, the estimation of biochemical parameters through remotely sensed data could provide a rapid and low-cost solution for diagnosing the spatial variability of crop field properties. Satellite images with a spectral resolution broader than 100 nm are not suitable for estimating the biophysical and biochemical status of crops due to the associated combinations of spectral reflectance [22]. To solve this problem, field spectroscopy or hyperspectral remote sensing with narrow spectral bands (<10 nm) over a contiguous range should be considered [22]. In fact, previous studies using a predictive approach based on hyperspectral remote sensing mainly focused on a single crop species [10,23,24] or one age group [25]. Few studies have attempted to apply hyperspectral data to determine the status of sugarcane nutrients at the foliar or canopy level [26–29]. As applications of hyperspectral data are in the infancy stage, studies are needed to achieve a better understanding of sugarcane spectral information. Thus, the estimation of the nitrogen characteristics of sugarcane with mixed cultivars at the canopy level is a challenge in remote sensing [30].

The aim of this study was to develop an estimation model that could explain the nitrogen variations in sugarcane. The field spectroscopy data were analyzed to investigate whether they contained adequate information for determining the nitrogen concentration in sugarcane with several cultivars. Original reflectance was transformed into a first-derivative spectrum (FDS) and two absorption features. Narrow vegetation indices and Stepwise Multiple Linear Regression (SMLR) were applied to compute the estimation models. Subsequently, the relationships between the measured nitrogen concentration and the spectral reflectance were explored. In addition, effects of canopy architecture on the spectral signature and the model precision were analyzed. This research will be expanded to include an additional experiment using polar orbiting hyperspectral data for the timely determination of crop nutrient status without any requirement of prior cultivar information.

2. Materials and Methods

2.1. Field Experimental Design

The two study sites are located in the Watthana Nakhon district (plot 1) and Mueang Sakaeo district (plot 2), Sakaeo Province, in the eastern region of Thailand (102°15′E, 13°45′N) (Figure 1). Sugarcane is the most dominant crop in this area with approximately ten different cultivars. Experimental plots, which were 36 m wide and 76 m long with a total area of 0.27 ha were designed based on a Randomized Complete Block (RCB) with three replications. The soil textures of the two plots were different (loamy sand and loamy clay, respectively). Experimental factors were controlled, including sugarcane cultivars, amount of nitrogen fertilizer (74 kg per ha), sowing date (end of March), and water supply (

Table 1. Characteristics of the experimental plots used in this study.

	Plot 1	Plot 2
Location	13.866°N 102.287°E	13.710°N 102.214°E
Soil texture	loamy sand	loamy clay
Annual precipitation, mm (2010)	1,268.2	1,296.6
Annual air temperature, °C (2010)	22.91/35.14 (Min/Max)	22.8/34.08 (Min/Max)
Plot size	36 m × 76 m	36 m × 76 m

). Based on the RCB design, we assumed that the influences of sunlight, soil moisture and temperature were equally distributed. Three sugarcane cultivars with different leaf orientations were investigated, namely KK-3 (planophile), K84-200 (erectophile) and LK92-11 (combined structure). Cultural management followed the local standard practice in sugarcane production. Samples collected from plot 1 and plot 2 were randomly separated and pooled into two groups for model calibration and model validation.

2.2. Measurements of Hyperspectral Reflectance

In December 2010, the canopy spectral reflectance was measured using a Fieldspec® 3 spectroradiometer (Analytical Spectral Devices, Boulder, CO, USA) [31], with a spectral range of 400–2,500 nm, and sampling intervals of 1.4 nm between wavelengths of 400 and 1,050 nm and 2 nm between wavelengths of 1,050 and 2,500 nm (

Table 2. Characteristics of the sensor, wavelength covering and spectral resolution used in this study.

Sensor	Wavelength (nm)	Spectral Resolution (nm)	Number of Bands
Fieldspec® 3 spectroradiometer	400–1,050	1.4	465
	1,050–2,500 *	2	560

^*The spectral regions between 1355–1450 nm, 1800–1950 nm and 2420–2500 nm, which are associated with the water absorption, were excluded from the analysis.

). However, the spectral regions between 1,355–1,450 nm, 1,800–1,950 nm and 2,420–2,500 nm, which are associated with the water absorption, were excluded from the analysis [22,32]. Canopy spectral data were collected by pointing a fiber optic cable with a 25° Field Of View (FOV) at the nadir position from a height of 1.5 m above the canopy (the height of sugarcane is 3–4 m at nine months of age). After nine months, the canopy is fully covered without any effect of soil brightness. The ground area observed by the sensor had a diameter of approximately 65 cm, which was large enough to cover one canopy tiller without being influenced by the surroundings. Spectral measurements were made on a clear sunny day between 10:00 a.m. and 2:00 p.m. local time (GMT+7) to minimize atmospheric perturbations and Bi-directional Reflectance Distribution Function (BRDF) effects [33]. Twenty-five replicate spectral measurements were taken for each tiller, which enabled noise reduction by averaging the spectra [34]. Relative reflectance spectra were calculated by dividing the leaf radiance by the reference radiance from a spectralon white reference panel for each wavelength. Measurements of the hyperspectral reflectance were conducted on 10 samples in each subplot, all of which were randomly selected from rows 5, 6, 7, 8 and 9 for a total of 90 samples per experimental site (180 in total).

2.3. Determination of Nitrogen Concentration

The first and second fully expanded leaves from the top of two random shoots for one tiller were collected. The midrib was removed from the leaf blade because the presence of the midrib resulted in a decreased concentration of nitrogen [35,36]. Four fresh leaves were oven-dried at 75 °C for 24 h and then ground up and oven-dried again at 75 °C for 24 h, resulting in a leaf powder. The total nitrogen concentration in sugarcane foliar was measured using the Kjeldahl method. The leaf powder was digested by 98% sulfuric acid (w/w) at 380 °C until the solution was transparent. Nitrogen was measured with a Nitrogen Distillation Apparatus using Kjeltec™ 2200 Auto distillation [37] and expressed as both milligrams per gram (mg/g) and a percentage of nitrogen.

2.4. Spectral Transformations

2.4.1. First-Derivative Transformation

FDS was calculated and used as a variable in the estimation model. FDS is commonly used to enhance absorption features that might be masked by interfering background absorptions and canopy background effects [38]. A derivative was taken to determine the slope of the spectrum (rate of change of reflectance with wavelength). This technique is useful for reducing the effects of multiple scattering of radiation due to sample geometry and surface roughness [39]. FDS can be derived by Equation (1).

$$\mathit{FDS}=(R_{\lambda (j+1)}-R_{\lambda (j)})/\mathrm{\Delta }\lambda$$

(1)

where the FDS is the first-derivative transformation at a wavelength i midpoint between wavebands j and j + 1. R_λ(j) is the reflectance at the j waveband, R_{λ(j + 1)} is the reflectance at the j + 1 waveband and Δλ is the difference in wavelength between j and j + 1.

2.4.2. Calculation of Absorption Features

Nitrogen exhibits absorption features in the visible, near-infrared and shortwave-infrared regions [23]. The continuum-removed reflectance R′_(λi) is obtained by dividing the reflectance value R_(λi) of each waveband i in the absorption feature by the reflectance level of the continuum line (convex hull) R_c(λi) at the corresponding wavelength i:

$${R^{\prime }}_{(\lambda )}=\frac{R_{(\lambda i)}}{R_{c(\lambda i)}}$$

(2)

The first and last spectral data values are on the hull; therefore, the first and last values of the continuum-removed spectrum are equal to 1. The output curves have values between 0 and 1, where the absorption pits are enhanced. In this study, only three regions of the wavelength were used, including R420–R530, R550–R750 and R1116–R1284, which are known as the pigment and water content absorption zones. Two variables proposed in [40,41] were used as variables in this study:

• Continuum-Removed Derivative Reflectance (CRDR) was calculated by applying a first-derivative transformation to the continuum-removed reflectance spectrum R′.

  $$\mathit{CRDR}=({R^{\prime }}_{\lambda (j+1)}-{R^{\prime }}_{\lambda (j)})/\mathrm{\Delta }\lambda$$

  (3)
• The band depth (BD) was calculated by subtracting the continuum-removed reflectance at wavelength i from 1:

  $$B{D}_{(\lambda i)}=1-{R^{\prime }}_{\lambda i}$$

  (4)

2.5. Univariate Approach: Narrow Vegetation Indices

Narrow vegetation indices were computed from all possible two-wavelength combinations involving the 1,025 wavelengths using FDS, CRDR and BD. These 1,025 discrete bands allowed a calculation of N*N (1,050,625 indices). The two most widely used vegetation indices in estimating agricultural and ecological variables are the Ratio Spectral Index (RSI) and the Normalized Differential Index (NDI) [15,32,42–44]. Equations (5) and (6) are the equations used to calculate the vegetation index. Relationships between the vegetation index and the N-determinant value were investigated in this step.

$$\text{RSI}={\lambda }_1/{\lambda }_2$$

(5)

$$\text{NDI}=({\lambda }_1-{\lambda }_2)/({\lambda }_1+{\lambda }_2)$$

(6)

where λ₁: FDS, CRDR and BD between 400–2,500 nm., and λ₂: FDS, CRDR and BD between 400–2,500 nm.

2.6. Multivariate Approach: Stepwise Multiple Linear Regression

SMLR was used to estimate the nitrogen concentration in sugarcane from the measured reflectance spectra. The idea was to identify the spectral wavebands that provide the best correlation with different chemical compounds present in the leaf or canopy [22,23,41,45,46]. The estimation models were calculated based on three independent variables: FDS, CRDR and BD. A SMLR starts with no predictors (wavelength) in the regression equation. At each step, it adds the most statistically significant wavelength (wavelength with the highest or lowest p-value) [33]. p-values to enter and remove wavelengths were set at 0.01 and 0.02, respectively. The maximum number of selected wavelengths was fixed at five to avoid an over fitting problem. The multicollinearity of variables was tested using a variance inflation factor (VIF) that must be lower than three [33].

2.7. Model Validation

Two approaches were adopted to evaluate the predictive accuracy: validation by (1) an independent data set and (2) a 10-fold cross technique. Performances of the estimation models were summarized and reported in terms of the coefficient of determination (R²), the Root Mean Square Error of the Estimate (RMSE) and the Relative Error (RE), as illustrated by Equations (7) and (8) [47].

$$\mathit{RMSE}=\sqrt{\frac{\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}{n}}$$

(7)

$$\mathit{RE}=\frac{100}{\overline{y}}\sqrt{\frac{\sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}{n}}$$

(8)

where ŷ_i and y_i are the estimated and measured crop variables, respectively, and n is the number of samples. The RMSE provides an estimate of the modeling error and is expressed in original measurement units.

3. Results and Discussion

3.1. Variations in Nitrogen Concentration and Hyperspectral Canopy Reflectance

3.1.1. Variations in Nitrogen Concentration

Table 3. Descriptive statistics of the nitrogen concentration measured in the laboratory.

Data Set	Sample	Min (%N)	Max (%N)	Mean (%N)	Std Deviation (%N)
Calibration	90	1.142	1.483	1.313	0.098
Validation	90	1.148	1.457	1.319	0.084
Pooled	180	1.142	1.483	1.316	0.091
By Cultivar
LK92-11	60	1.251	1.415	1.333	0.046
KK-3	60	1.275	1.483	1.395	0.062
K84-200	60	1.142	1.322	1.221	0.051

shows the number of samples used and the statistics associated with the nitrogen concentration measured in the laboratory. We tested the hypothesis that the mean nitrogen concentrations in sugarcane between the three cultivars were significantly different, viz. the null hypothesis Ho: μ1 = μ2 = μ3 and the alternate hypothesis Ha: μ1≠ μ2 ≠ μ3, where μ1, μ2, and μ3 are the mean observed nitrogen concentrations for LK92-11, KK-3 and K84-200, respectively. The results of the one-way analysis of variance (ANOVA) indicated that the means of the observed nitrogen concentration between the three cultivars were significantly different (P < 0.00001). A post-hoc Scheffe test was used to check for any significant difference between the nitrogen concentrations of cultivars. The overall result from these tests was that the mean nitrogen concentrations were significantly different between all cultivars (P < 0.00001).

3.1.2. Hyperspectral Canopy Reflectance

The canopy spectral reflectance values of the three cultivars, shown in Figure 2(a), were averaged. The mean spectra (n = 60) between K84-200 and KK-3 are obviously discriminated, while the difference is subtle between LK92-11 and K84-200. Moreover, the spectral reflectance of the erectophile canopy (K84-200) is lower than that of the planophile canopy (KK-3). The highest variations occur in the near-infrared (650–700 nm) and shortwave-infrared regions, which are mainly absorbed by the water (1,300–1,400 nm). An averaged FDS is illustrated in Figure 2(b). This figure clearly displays the variations in the magnitude and position of the absorption features between the three cultivars.

3.2. Relationships between the Nitrogen Concentration and Narrow Vegetation Index

The correlation coefficients between all possible wavelength pairs with R² ≥ 0.6 are displayed in a correlation plot (Figure 3). The highest correlation regions between the NDI and RVI based on the FDS and the nitrogen concentration were highlighted in the range of 630–750 nm, i.e., the near-infrared and red edge regions. Wavelengths between 675 and 750 nm in the CRDR also constitute the sensitive band for determining the nitrogen status.

Table 4. Performances of narrow vegetation indices calculated from different independent variables for estimating nitrogen concentration in sugarcane with the combined cultivars.

VI	Variable	λ1/λ2 (nm)	Calibration Data Set (N = 90)		Validation Data Set (N = 90)		Pooled Data Set (N = 180)
			R2c	RMSEc	R2v	RMSEv	R2cv	RMSEcv
NDI	FDS	750/700	0.82	0.041	0.73	0.044	0.78	0.043
	CRDR	748/690	0.82	0.041	0.73	0.043	0.78	0.043
	BD	748/680	0.81	0.042	0.70	0.047	0.76	0.045
RVI	FDS	724/700	0.80	0.043	0.73	0.044	0.78	0.043
	CRDR	748/630	0.83	0.041	0.73	0.044	0.78	0.043
	BD	748/670	0.82	0.042	0.70	0.048	0.76	0.045

λ: Selected wavelength in nm; RMSE_c, RMSE_v and RMSE_cv: root mean square error of calibration, validation and relative cross-validation with a 10-fold cross technique, respectively, expressed as %N; R²_cv: relative cross-validated coefficient of determination with a 10-fold cross technique; fit between estimated and observed values at the 0.01 level was considered highly significant.

illustrates the model accuracy estimated by the NDI and the RVI, using the combined cultivar data set. The predictive performance of the NDI was slightly higher than that of the RVI. In this experiment, the NDI based on the FDS_(750/700) and the RVI based on the FDS_(724/700) yielded the highest accuracy, with R² values of 0.73 and 0.78, RMSE_cv values of 0.044 and 0.043% N and RE values of 3.34 and 3.27%N for the validation data set and the pooled data set, respectively. The regression equations are Y = 0.37x + 1.39 and Y = 0.14x + 1.04.

The scatter plots in Figure 4 illustrate the comparison between the measured and estimated nitrogen concentration determined by four models. We found that the region of 510–540 nm and 700–800 nm are the sensitive regions for characterizing the nitrogen status.

Table 5. Performances of narrow vegetation indices calculated from different independent variables for estimating nitrogen concentration in sugarcane with the separated cultivar.

VI	Variable	LK92-11 (N = 60)			KK-3 (N = 60)			K84-200 (N = 60)
		λ1	λ2	R2v	λ1	λ2	R2v	λ1	λ2	R2v
NDI	FDS	748	728	0.81	718	710	0.91	712	706	0.80
	CRDR	570	748	0.80	736	712	0.90	712	700	0.79
	BD	748	584	0.78	716	710	0.92	746	680	0.75
RVI	FDS	748	728	0.79	718	710	0.90	724	692	0.82
	CRDR	748	510	0.78	712	574	0.91	712	700	0.82
	BD	748	586	0.78	716	710	0.91	712	678	0.76

λ: Selected wavelength in nm; R²_v: root mean square error of calibration, validation; fit between estimated and observed values at the 0.01 level was considered highly significant.

shows the capability of narrow vegetation indices to estimate the nitrogen concentration in sugarcane with the separated cultivars. Partitioning data into the individual cultivars can improve the model precision. The proposed model can mostly explain the nitrogen variation of KK-3, with an accuracy of approximately 90%. Wavelengths between 700 and 750 nm are best suited for predicting nitrogen quality. Selected wavelengths and regression equations are summarized in

Table 6. List of regression models developed by the vegetation indices using the different data sets.

Data set	VI	Variablewavelength	Regression Model	R2v
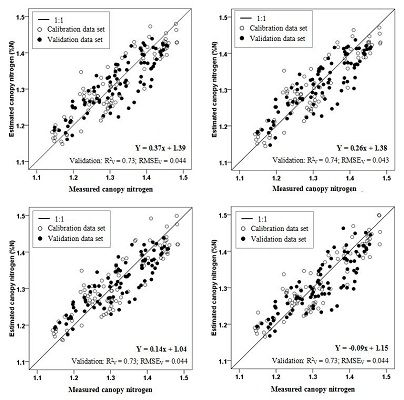
Combined cultivars	NDI	FDS750,700	Y = 0.37x + 1.39	0.73
		CRDR748,690	Y = 0.26x + 1.38	0.73
		BD748,680	Y = 9.64× + 10.77	0.70
	RVI	FDS724,700	Y = 0.14x + 1.04	0.73
		CRDR748,630	Y = −0.09x + 1.15	0.73
		BD748,670	Y = 18.79x + 1.12	0.70
Separated cultivar - LK92-11	NDI	FDS748,728	Y = 0.95x + 1.71	0.79
		CRDR570,748	Y = 0.11x + 1.12	0.80
		BD748,584	Y = 4.58x + 5.72	0.78
	RVI	FDS748,728	Y = 0.93x + 0.93	0.79
		CRDR748,510	Y = 0.24x + 1.21	0.78
		BD748,586	Y = 9.05x + 1.14	0.78
Separated cultivar - KK-3	NDI	FDS718,710	Y = 1.59x + 1.09	0.91
		CRDR736,712	Y = 0.44x + 1.39	0.90
		BD716,710	Y = 4.18x + 1.73	0.92
	RVI	FDS718,710	Y = 0.53x + 0.61	0.90
		CRDR712,574	Y = 0.61x + 2.05	0.91
		BD716,710	Y = 2.45x – 0.7	0.91
Separated cultivar - K84-200	NDI	FDS712,706	Y = 1.45x + 1.18	0.80
		CRDR712,700	Y = 0.75x + 1.23	0.79
		BD746,680	Y = 3.47x + 4.59	0.75
	RVI	FDS724,692	Y = 0.08x + 1.07	0.82
		CRDR712,700	Y = 0.39x + 0.84	0.82
		BD712,678	Y = 0.63x + 0.86	0.76

.

3.3. Relationships between the Nitrogen Concentration and Spectral Wavelength Determined by a SMLR Technique

The number of selected spectral wavelengths, used to estimate the nitrogen concentration by SMLR, ranges from two to five. Using the FDS as an independent variable, SMLR selected five sensitive wavelengths, centered at the visible, red edge and far near-infrared regions of the electromagnetic spectrum. The best model yielded R² values of 0.80 and 0.86, RMSE values of 0.038 and 0.033%N and RE values of 2.88 and 2.50%N validated by an independent data set and a pooled data set, respectively. The regression equation is Y = 212.76x₁ – 471.9x₂ – 31.98x₃ + 133.78x₄ – 115.86x₅ + 1.4. The selected wavelengths for each data set are summarized in

Table 7. Performance of stepwise multiple linear regression in estimating the nitrogen concentration in sugarcane with combined cultivar.

Variable	Wavelength (nm)	Calibration Data set (N = 90)		Validation Data set (N = 90)		Pooled Data Set (N = 180)
		R2c	RMSEc	R2v	RMSEv	R2cv	RMSEcv
FDS	410, 430, 720, 754,1216	0.90	0.030	0.80	0.038	0.86	0.033
CRDR	748, 1158, 1184, 1216, 1276	0.89	0.033	0.64	0.053	0.78	0.043
BD	748, 1262	0.83	0.040	0.70	0.047	0.77	0.044

λ: Selected wavelength in nm; RMSE_c, RMSE_v and RMSE_cv: root mean square error of calibration, validation and relative cross-validation with a 10-fold cross technique, respectively, expressed as %N; R²_cv: relative cross-validated coefficient of determination with a 10-fold cross technique; fit between estimated and observed values at the 0.01 level was considered highly significant.

. The CRDR and BD variables cannot be used to improve the model precision for determining the nitrogen concentration compared with the FDS. Relationships between the measured and estimated nitrogen concentration were determined from the combined and separated cultivar data sets and are depicted in Figure 5(a,b). However, the predictive models developed by a SMLR technique exhibited a higher accuracy than those developed based on the narrow vegetation indices, as indicated by the higher R² and lower RMSE associated with the former.

Table 8. Selected wavelengths and coefficients of determination between the observed nitrogen concentration and the spectral reflectance of separated cultivar.

Variable	LK92-11 (N = 60)		KK-3 (N = 60)		K84-200 (N = 60)
	Wavelength (nm)	R2cv	Wavelength (nm)	R2cv	Wavelength (nm)	R2cv
FDS	670, 754, 1,266, 1,494, 2,313	0.86	750, 1,104, 1,572, 1,586, 2,153	0.93	552, 1,032, 1,284, 1,604, 2,359	0.80
CRDR	656, 704, 1,266	0.79	598, 674, 740, 1,228	0.92	678, 746, 1,128	0.80
BD	684, 748, 1,228	0.82	552, 736	0.92	746	0.78

R²_cv: relative cross-validated coefficient of determination with a 10-fold cross technique; fit between estimated and observed values at the 0.01 level was considered highly significant.

summarizes the performance of SMLR in estimating the nitrogen concentration of separated cultivars using the different independent variables, including FDS, CRDR and BD. The sensitive wavelengths were shifted from the shortwave to the middle-infrared region. The proposed model can mostly explain the nitrogen variations of KK-3 (94%), LK92-11 (86%) and K84-200 (80%). Partitioning of data into cultivar could increase the estimation capability of the method applied in this research. The selected wavelengths and regression equations used are listed in

Table 9. List of regression models developed by SMLR from the different data sets.

Data set	Variable	Regression Model	R2v
Combined cultivars	FDS	Y = 212.76x1 – 471.9x2 – 31.98x3 + 133.78x 4 – 115.86x5 + 1.4	0.80
	CRDR	Y = 55.77x1 + 19.0x2 + 61.92x3 – 73.5x 4 – 34.25x5 + 1.26	0.64
	BD	Y = 25.26x1 – 3.7x2 + 1.19	0.70
Separated cultivar -LK92-11	FDS	Y = 520.59x1 + 14.794x2 – 97.004x3 + 95.08x 4 – 63.49x5 + 1.347	0.86
	CRDR	Y = 33.04x1 – 18.84x2 – 32.51x3 + 1.72	0.79
	BD	Y = −0.47x1 + 17.86x2 – 0.7845x3 + 1.62	0.82
Separated cultivar-KK-3	FDS	Y = 67.4x1 – 24.64x2 – 136.2x3 – 168.34x4 – 42.007x 5 + 1.4153	0.93
	CRDR	Y = −14.27x1 – 105.25x2 + 23.31x3 + 8.84x4 + 1.004	0.92
	BD	Y = −3.31x1 + 2.26x2 + 1.17	0.92
Separated cultivar - K84-200	FDS	Y = −194.8x1 + 138.92x2 – 94.52x3 – 213.97x 4 – 22.31x5 + 1.29	0.80
	CRDR	Y = −64.57x1 + 25.36x2 + 6.34x3 + 28.04x4 + 1.08	0.80
	BD	Y = 7.86x1 + 1.12	0.78

.

3.4. Discussion

3.4.1. Utility of the Methods Used in this Study in Estimating the Nitrogen Concentration

Results from this research indicate that field spectroscopy data contains adequate information for determining the nitrogen concentration in sugarcane with combined cultivars. The univariate method has illustrated that the red edge region contains the sensitive wavelengths for explaining the nitrogen variations in sugarcane canopy. This region has been shown to be insensitive to atmospheric and background effects [11], and to be related to chlorophyll [14]. Since, there is a positive strong relationship between nitrogen concentration and chlorophyll [48]. The proposed models using FDS, CRDR and BD as independent variables could explain between 70% and 83% the variation of nitrogen concentration in standing sugarcane canopies. The model RMSE values range from 0.048–0.043%N. The modified estimation model, generated by a SMLR technique using FDS, yields the highest correlation coefficient value of 0.86 and a RMSE value of 0.033 with sugarcane canopy nitrogen concentration. The estimation model developed by SMLR yields a higher correlation coefficient with nitrogen content as compared to the model computed by narrow vegetation indices. This is because the two-wavelength index uses only a limited amount of the spectral information. These results are consistent with those of previous studies [10,33]. In addition, we found that the estimation models developed from the FDS exhibited a higher correlation with the observed nitrogen concentration than those generated from the CRDR and BD. This conclusion agrees with the results of previous studies [26].

3.4.2. Wavelength Selection

The estimation model with the highest predictive accuracy was developed by SMLR technique. The selected wavelengths, including the spectral bands centered at 410, 430, 720, 754 and 1216 nm, were used to predict the nutrient quality in sugarcane. Wavelengths in the visible region (λ = 410 nm and 430 nm), selected for nitrogen concentration estimation, are related to pigment absorption [22]. Several publications have shown a strong correlation between the concentration of nitrogen and chlorophyll a and b [10,22,23,26,43]. Nitrogen is directly related to the photosynthetic process. A strong relationship between chlorophyll absorption bands and nitrogen concentration is therefore expected [10]. Two wavelengths in the shorter region of the red edge (λ = 720 nm) and in the longer region of the red edge (λ = 754 nm), selected by the estimation model, are in agreement with the known nitrogen absorption bands [22]. The wavelength centered at 720 nm is the critical point on the red-edge around which there is the maximum change in the slope of the reflectance spectra per unit. It is also considered as the sensitive band to the temporal variations in crop growth, vegetation stress, and chlorophyll & nitrogen status of plants [42,43,49]. Whereas the wavelength centered at 754 nm is sensitive to the variations of chlorophyll and nitrogen. The last wavelength in the Far Near-Infrared Region (FNIR) (λ = 1,216 nm), is selected as an estimator and is sensitive to plant moisture. The most rapid change falls into the spectra with a change in wavelength in FNIR [50,51]. The wavelength 1,216 nm, which yields the high correlation with the N status, is in disagreement with [26] who found that wavelengths between 1,300–1,350 nm were strongly related to the leaf nitrogen concentration in sugarcane.

3.4.3. Effects of Plant Morphology and Structure on the Spectral Response

The structure of the plant canopy has a significant bearing on its spectral signature [43]. The leaf orientation of the KK-3, K84-200 and LK92-11 cultivar, which were tested in this study, exhibits the planar, erect and mixed structures, respectively. The proposed estimation models in this study could explain most of the nitrogen variations (>90%) in planophile canopy (KK-3). On the other hand, the model precision was quite low in the mixed structures, ∼80–86% (LK92-11), and in the erectophile structure, ∼78–80% (K84-200). Thenkabail et al. [43] concluded that the planophile structure (30 degrees) contributes to a significantly greater reflectance in the near infrared and to a greater absorption in the red when compared with the erectophile structure (65 degree). This summary is consistent with the measured reflectance spectra used in this study, as shown in Figure 2(a). Usually, the Leaf Area Index (LAI) value of planophile structures is higher than that of mixed and erectophiles, which results in the difference of the density of light radiation reaching the mature leaves down the stalk [52]. LAI, therefore, directly influences the spectral profile of sugarcane canopy. In addition, effects from soil brightness on the reflectance spectra of planophile structures are lower than those of other structures. The canopy structure should be taken into consideration when mapping crop nutrient status in rangelands with combined cultivars. This recommendation is consistent with that of the previous study [10].

3.4.4. Performance Comparison of Proposed Models with Previous Models

Most of the previous publications developed models for estimating the nitrogen variations in paddy rice, wheat, cotton or grass, but only in a few cases in sugarcane [26,28]. The previous experiments estimating the nitrogen concentration from hyperspectral data were conducted at the leaf level. In vegetation canopies, near-infrared reflectance is much higher than that for the single leaves. As most of the radiation at near-infrared wavelengths passes through the single leaves, the multiple leaf layers of a canopy have an additive effect on the reflectance [53]. Part of the radiation transmitted by the first leaf layer is reflected back onto subsequent layers [54]. At the canopy level, there are several factors that influence the spectral reflectance, e.g., wind, the solar azimuth angle, light intensity, and canopy architecture [26]. In this paper, the estimation model was developed from the reflectance spectra measured over the sugarcane canopy. Therefore, it is not reasonable to apply the regression equation, published in previous studies, to the data used in this study.

Table 10. The estimation models for estimating nitrogen concentration in sugarcane from field spectroscopy compared with previous publications (unit: % nitrogen).

Spectral Parameter	Regression Equation	Validation		No. of Samples	Study Level	Reference
		R2	RMSE
RVI (FDS741, FDS1323)	Y = −0.237x + 0.587	0.74	0.084	25	Leaf	[26]
RVI (R740, R720)	Y = 0.73x + 0.753	0.81	0.103	37	Leaf	[28]
NDI (FDS750, FDS700)	Y = 0.37x + 1.39	0.78	0.043	90	Canopy	This paper
RVI (FDS724, FDS700)	Y = 0.14x + 1.04	0.78	0.043	90	Canopy	This paper
FDS (410, 430, 720, 754,1216) *	Y = 212.76x1 – 471.9x2 – 31.98x3 + 133.78x 4 – 115.86x5 + 1.4	0.86	0.033	90	Canopy	This paper

^*developed by SMLR technique.

shows the estimation models to estimate sugarcane nitrogen concentration from field spectroscopy. Based on the results in this study, the performance of the estimation models was more stable and reliable than in previous studies, because of the higher correlation, lower estimation error and the higher number of samples used.

4. Conclusions

The optimal goal of this paper was to develop an estimation model that could explain the nitrogen variations in sugarcane with combined cultivars. Reflectance spectra were measured over the sugarcane canopy. Derivative spectra and absorption features were used as independent variables in univariate and multivariate approaches. The most important conclusions that could be drawn from this study are as follows:

• Stepwise multiple linear regression could explain the nitrogen variations in sugarcane canopy better than a narrow vegetation index. This technique utilizes more than two wavelengths from the entire spectral region (400–2,500 nm) to estimate the dependent variable.
• First Derivative Spectrum (FDS) showed a better relationship with canopy nitrogen concentration than Continuum-Removed Derivative Reflectance (CRDR) and Band Depth (BD) when the models were developed with multivariate approaches and validated with a combined cultivar data set.
• It was concluded that a First Derivative Spectrum (FDS) has potential when used to estimate the nitrogen content in sugarcane with combined cultivars at the maturity stage (9–12 months).
• Visible, red edge and far near-infrared regions contain more information on canopy nitrogen concentration of combined sugarcane cultivars compared to other parts of the electromagnetic spectrum.
• Canopy architecture directly influences the spectral response and the predictive precision. Canopy structure, therefore, should be taken into consideration when mapping sugarcane nutrient quality in rangelands with combined cultivars.
• In the case of a known cultivar, partitioning the data into cultivars could increase the estimation capability of the method applied in this research.
• The modified estimation model, generated by SMLR technique from FDS centered at 410, 426, 720, 754, and 1,216 nm, yields the highest correlation coefficient value of 0.86 and RMSE value of 0.033%N (n = 90) with nitrogen concentration in sugarcane. This result is much better than those of the previous studies.

Overall, since the field spectroscopy data used in this study was measured over the sugarcane canopy under natural atmospheric conditions, the success of field spectroscopy used for estimating nutrient quality in sugarcane allows an additional experiment using the polar orbiting hyperspectral data for the timely determination of crop nutrient status in rangelands without any requirement of the prior cultivar information.