Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data
Abstract
:1. Introduction
2. Lake Qinghai Settings

3. Satellite Data Used and Methodology
3.1. Satellite Data
3.1.1. ICESat/GLAS
3.1.2. Optical Satellite Images
3.2. Methodology
3.2.1. ICESat Data Processing
3.2.2. Surface Area Extraction

3.2.3. Estimating Water Volume Variations
3.2.4. Validation

4. Results
4.1. ICESat/GLA14-Derived Water Levels

| Date | ICEsat Elevation | In situ Measurement | Date | ICEsat Elevation | In situ Measurement |
|---|---|---|---|---|---|
| 10/14/2003 | 3193.34 | 3193.42 | 06/23/2006 | 3193.70 | 3193.67 |
| 10/18/2003 | 3193.43 | 3193.42 | 10/27/2006 | 3193.68 | 3193.75 |
| 10/22/2003 | 3193.44 | 3193.41 | 10/30/2006 | 3193.87 | 3193.75 |
| 11/16/2003 | 3193.33 | 3193.33 | 11/24/2006 | 3193.62 | 3193.69 |
| 02/19/2004 | 3193.16 | 3193.27 | 03/13/2007 | 3193.68 | 3193.60 |
| 02/22/2004 | 3193.18 | 3193.27 | 03/17/2007 | 3193.77 | 3193.60 |
| 03/18/2004 | 3193.05 | 3193.21 | 04/11/2007 | 3193.65 | 3193.62 |
| 05/20/2004 | 3193.13 | 3193.20 | 10/04/2007 | 3193.77 | 3193.83 |
| 06/17/2004 | 3193.31 | 3193.25 | 10/08/2007 | 3193.74 | 3193.84 |
| 10/06/2004 | 3193.39 | 3193.40 | 11/02/2007 | 3193.85 | 3193.87 |
| 11/03/2004 | 3193.35 | 3193.33 | 02/19/2008 | 3193.74 | 3193.74 |
| 11/08/2004 | 3193.34 | 3193.32 | 02/22/2008 | 3193.87 | 3193.74 |
| 02/20/2005 | 3193.13 | 3193.20 | 02/27/2008 | 3194.01 | 3193.74 |
| 02/24/2005 | 3193.15 | 3193.19 | 03/18/2008 | 3193.71 | 3193.74 |
| 05/22/2005 | 3193.13 | 3193.22 | 10/06/2008 | 3193.94 | 3193.92 |
| 05/26/2005 | 3193.19 | 3193.24 | 10/09/2008 | 3193.92 | 3193.93 |
| 10/23/2005 | 3193.86 | 3193.79 | 10/14/2008 | 3193.68 | 3193.92 |
| 10/27/2005 | 3193.82 | 3193.79 | 12/14/2008 | 3193.73 | 3193.76 |
| 11/21/2005 | 3193.63 | 3193.72 | 03/10/2009 | 3193.66 | 3193.73 |
| 02/24/2006 | 3193.76 | 3193.63 | 03/14/2009 | 3193.80 | 3193.73 |
| 02/27/2006 | 3193.73 | 3193.63 | 03/18/2009 | 3193.59 | 3193.73 |
| 03/24/2006 | 3193.68 | 3193.63 | 04/08/2009 | 3193.66 | 3193.74 |
| 05/26/2006 | 3193.60 | 3193.61 | 10/02/2009 | 3194.02 | 3194.09 |
| 05/29/2006 | 3193.75 | 3193.62 |
4.2. Surface Area Changes



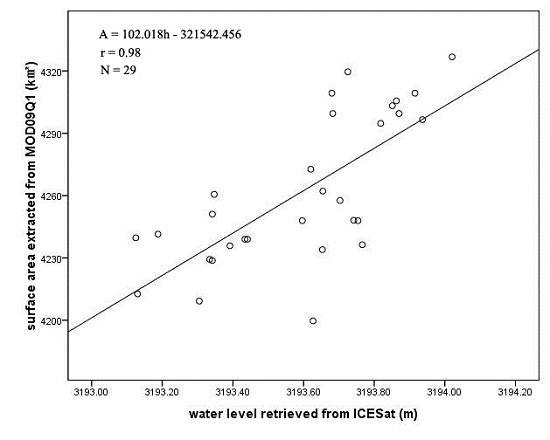
4.3. Relationship between Water Level and Surface Area


4.4. Water Volume Variations


5. Discussion
5.1. The Accuracy of In Situ Measurements

5.2. The Extension of Our Study



5.3. Comparison with Similar Studies

| Source | Water Level (m) | Surface Area (km2) | Delta Volume (km3) | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| HYDROWEB | 0.10 | 0.13 | 17.49 | 21.34 | 1.04 | 1.18 |
| Our study | 0.07 | 0.09 | 6.21 | 7.81 | 0.48 | 0.60 |
5.4. The Limitations and Applicability of Our Study
6. Conclusion
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Abdallah, H.; Bailly, J.S.; Baghdadi, N.; Lemarquand, N. Improving the assessment of ICESatwater altimetry accounting for autocorrelation. ISPRS. J. Photogramm. Remote Sens. 2011, 66, 833–844. [Google Scholar]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Calmant, S.; Seyler, F.; Crétaux, J.F. Monitoring continental surface waters by satellite altimetry. Surv. Geophys. 2008, 29, 247–269. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhope, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef] [Green Version]
- Medina, C.E.; Gomez-Enri, J.; Alonso, J.J.; Villares, P. Water level fluctuations derived from ENVISAT Radar Altimeter (RA-2) and in situ measurements in a subtropical waterbody: Lake Izabal (Guatemala). Remote Sens. Environ. 2008, 112, 3604–3617. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Xu, K.Q.; Yang, Y.H.; Qi, L.H.; Hayashi, S.; Watanabe, M. Measuring water storage fluctuations in Lake Dongting, China, by Topex/Poseidon satellite altimetry. Environ. Monit. Assess. 2006, 115, 23–37. [Google Scholar] [CrossRef] [PubMed]
- Song, C.Q.; Huang, B.; Ke, L.H. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- GLCF. MODIS Water Mask. Available online: http://landcover.org/data/watermask (accessed on 27 October 2014).
- Kropacek, J.; Braun, A.; Kang, S.C.; Feng, C.; Ye, Q.H.; Hochschild, V. Analysis of lake level changes in Nam Co in central Tibet utilizing synergistic satellite altimetry and optical imagery. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 3–11. [Google Scholar] [CrossRef]
- Deniz, O.; Yidiz, M.Z. The ecological consequences of level changes in Lake Van. Water Resour. 2007, 34, 707–711. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Xie, H.J.; Duan, S.Q.; Tian, M.Z.; Yi, D.H. Water level variation of Lake Qinghai from satellite and in situ measurements under climate change. J. Appl. Remote Sens. 2011, 5, 053532–053532. [Google Scholar]
- Phan, V.H.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 12–22. [Google Scholar] [CrossRef]
- Wang, X.W.; Gong, P; Zhao, Y.Y; Xu, Y.; Cheng, X.; Niu, Z.G.; Luo, Z.C.; Huang, H.B.; Sun, F.D.; Li, X.W. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
- Yan, L.J.; Qi, W. Lakes in Tibetan Plateau extraction from remote sensing and their dynamic changes. Acta Geosci. Sin. 2012, 33, 65–74. [Google Scholar]
- Liu, J.S.; Wang, S.Y.; Yu, S.M.; Yang, D.Q.; Zhang, L. Climate warming and growth of high-elevation inland lakes on the Tibetan Plateau. Global Planet. Change 2009, 67, 209–217. [Google Scholar] [CrossRef]
- Ye, Q.H.; Yao, T.D.; Naruse, R.J. Glacier and lake variations in the MapamYumco basin, western Himalayas, Tibetan Plateau, from 1974 to 2003 using remote sensing and GIS technologies. J. Glaciology. 2008, 54, 933–935. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- LEGOS. HYDROWEB. Available online: http://www.legos.obs-mip.fr/soa/hydrologie/hydroweb/ (accessed on 27 October 2014).
- Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry datasets and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Li, X.Y.; Xu, H.Y.; Sun, Y.L.; Zhang, D.S.; Yang, Z.P. Lake-level change and water balance analysis at Lake Qinghai, west China during recent decades. Water Resour. Man. 2007, 21, 1505–1516. [Google Scholar] [CrossRef]
- Jia, S.F.; Zhu, W.B.; Lv, A.F.; Yan, T.T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodynamics 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Abshire, J.; Sun, X.; Riris, H.; Sirota, J.; McGarry, J.; Palm, S.; Yi, D.; Liiva, P. Geoscience Laser Altimeter System (GLAS) on the ICESat mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Kwok, R.; Zwally, H.J.; Yi, D. ICESat observations of Arctic sea ice: A first look. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Zwally, H.J.; Yi, D.H.; Kwok, R.; Zhao, Y.H. ICESat measurements of sea ice freeboard and estimates of sea ice thickness in the Weddell Sea. J. Geophys .Res.-Oceans 2008, 113. [Google Scholar] [CrossRef]
- Chipman, J.W.; Lillesand, T.M. Satellite-based assessment of the dynamics of new lakes in southern Egypt. Int. J. Remote. Sens. 2007, 28, 4365–4379. [Google Scholar] [CrossRef]
- Song, C.Q.; Huang, B.; Ke, L.H.; Richards, K.S. Seasonal and abrupt changes in the water level of closed lakes on the Tibetan Plateau and implications for climate impacts. J. Hydrol. 2014, 514, 131–144. [Google Scholar] [CrossRef]
- Adalbert, A.; Jean-Francois, C.; Muriel, B.N.; Rodrigo, A.R. Remote sensing-derived bathymetry of Lake Poopo. Remote Sens. 2014, 6, 407–420. [Google Scholar]
- Baghdadi, N.; Lemarquand, N.; Abdallah, H.; Bailly, J.S. The relevance of GLAS/ICESat elevation data for the monitoring of River Networks. Remote Sens. 2011, 3, 708–720. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Xie, H.J.; Kang, S.C.; Yi, D.H.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Berry, P.A.M. Two decades of inland water monitoring using satellite radar altimetry. In Proceedings of 2006 15 Years of Progress in Radar Altimetry, Venice, Italy, 1 March 2006; pp. 1–8.
- Urban, T.J.; Schutz, B.E.; Neuenschwander, A.L. A survey of ICESat coastal altimetry applications: Continental coast, open ocean island, and inland rivers. Terr. Atmos. Ocean. Sci. 2008, 19, 1–19. [Google Scholar] [CrossRef]
- Braun, A.; Cheng, K.; Csatho, B.; Shum, C.K. ESat Laser Altimetry in the Great Lakes. In Proceedings of 2004 Annual Meeting of the Institute of Navigation, Dayton, OH, USA, 7–9 June 2004; pp. 409–416.
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Eric, M.; Yasir, A.M.; Zheng, D.; Pieter, V.Z. Estimation of reservoir discharges from Lake Nasser and Roseires Reservoir in the Nile Basin using satellite altimetry and imagery data. Remote Sens. 2014, 6, 7522–7545. [Google Scholar] [CrossRef]
- Zhang, B.L.; Jia, R.C.; Zhang, Q.; Cheng, G. The water body area changes of Dalainur Lake based on satellite images of remote sensing. Res. Soil Water Conserv. 2011, 18, 196–199. [Google Scholar]
- Michishita, R.; Jiang, Z.B.; Xu, B. Monitoring two decades of urbanization in the Poyang Lake area, China through spectral unmixing. Remote Sens. Environ. 2012, 117, 3–18. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.L.; Vogelmann, J.E.; Gao, F.; Jin, S.M. A simple and effective method for filling gaps in Landsat ETM plus SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- EXELIS. Visual Information Solution. Available online: http://www.exelisvis.com (accessed on 27 October 2014).
- Pat, S.; Esad, M.; Gyanesh, C. SCL Gap-Filled Products Phase One Methodology. Available online: http://landsat.usgs.gov/documents/SLC_Gap_Fill_Methodology.pdf (accessed on 27 October 2014).
- Jang, K.; Kang, S.; Kim, J.; Lee, C.B.; Kim, T.; Kim, J.; Hirata, R.; Saigusa, N. Mapping evapotranspiration using MODIS and MM5 Four-Dimensional Data Assimilation. Remote Sens. Environ. 2010, 114, 657–673. [Google Scholar] [CrossRef]
- Bhang, K.J.; Schwartz, F.W.; Braun, A. Verification of the vertical error in C-band SRTM DEM using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans. Geosci. Remote Sens. 2007, 45, 36–44. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Jackson, T.; Chen, D.; Cosh, M.; Li, F.; Anderson, M.; Walthall, C.; Doriaswamy, P.; Hunt, E.R. Vegetation water content mapping using Landsat data derived normalized difference water index for corn and soybeans. Remote Sens. Environ. 2004, 92, 475–482. [Google Scholar] [CrossRef]
- Lacaux, J.P.; Tourre, Y.M.; Vignolles, C.; Ndione, J.A.; Lafaye, M. Classification of ponds from high-spatial resolution remote sensing: Application to Rift Valley Fever epidemics in Senegal. Remote Sens. Environ. 2007, 106, 66–74. [Google Scholar] [CrossRef]
- Xu, H.Q. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote. Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Soti, V.; Tran, A.; Bailly, J.-S.; Puech, C.; Seen, D.L.; Bégué, A. Assessing optical earth observation systems for mapping and monitoring temporary ponds in arid areas. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 344–351. [Google Scholar] [CrossRef] [Green Version]
- Ouma, Y.; Tateishi, R. A water index for rapid mapping of shoreline changes of five East African Rift Valley lakes: An empirical analysis using Landsat TM and ETM+ data. Int. J. Remote. Sens. 2006, 27, 3153–3181. [Google Scholar] [CrossRef]
- Verdin, J.P. Remote sensing of ephemeral water bodies in Western Niger. Int. J. Remote. Sens. 1996, 17, 733–748. [Google Scholar] [CrossRef]
- Richardson, A.J.; Everitt, J.H. Using spectra vegetation indices to estimate rangeland productivity. Geocarto Int. 1992, 1, 63–69. [Google Scholar] [CrossRef]
- Davranche, A.; Lefebvre, G.; Poulin, B. Wetland monitoring using classification trees and SPOT-5 seasonal time series. Remote Sens. Environ. 2010, 114, 552–562. [Google Scholar] [CrossRef] [Green Version]
- Birkett, C.M.; Beckley, B. Investigating the performance of the Jason-2/OSTM radar altimeter over lakes and reservoirs. Mar. Geodesy 2010, 33, 204–238. [Google Scholar] [CrossRef]
- Guo, H.R.; Jiao, W.H.; Yang, Y.X. The systematic difference and its distribution between the 1985 national height datum and the global quasigeoid. Acta Geod. Cartogr. Sin. 2004, 33, 100–104. [Google Scholar]
- Mercier, F.; Cazenave, A.; Maheu, C. Interannual lake level fluctuations (1993–1999) in Africa from Topex/Poseidon: Connections with ocean–atmosphere interactions over the Indian Ocean. Global Planet. Change 2002, 32, 141–163. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Jia, S.; Lv, A. Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data. Remote Sens. 2014, 6, 10457-10482. https://doi.org/10.3390/rs61110457
Zhu W, Jia S, Lv A. Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data. Remote Sensing. 2014; 6(11):10457-10482. https://doi.org/10.3390/rs61110457
Chicago/Turabian StyleZhu, Wenbin, Shaofeng Jia, and Aifeng Lv. 2014. "Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data" Remote Sensing 6, no. 11: 10457-10482. https://doi.org/10.3390/rs61110457
APA StyleZhu, W., Jia, S., & Lv, A. (2014). Monitoring the Fluctuation of Lake Qinghai Using Multi-Source Remote Sensing Data. Remote Sensing, 6(11), 10457-10482. https://doi.org/10.3390/rs61110457