Next Article in Journal
A Survey of Algorithmic Shapes
Next Article in Special Issue
Monitoring Natural Ecosystem and Ecological Gradients: Perspectives with EnMAP
Previous Article in Journal
A Global Grassland Drought Index (GDI) Product: Algorithm and Validation
Previous Article in Special Issue
Capability of Spaceborne Hyperspectral EnMAP Mission for Mapping Fractional Cover for Soil Erosion Modeling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 7
Issue 10
10.3390/rs71012737
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Potential of Pan-Sharpened EnMAP Data for the Assessment of Wheat LAI

by
Bastian Siegmann
*,
Thomas Jarmer
,
Florian Beyer
and
Manfred Ehlers
Institute for Geoinformatics and Remote Sensing, University of Osnabrueck, Barbarastraße 22b, Osnabrueck 49076, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2015, 7(10), 12737-12762; https://doi.org/10.3390/rs71012737
Submission received: 28 May 2015 / Revised: 2 September 2015 / Accepted: 22 September 2015 / Published: 28 September 2015
(This article belongs to the Special Issue The Environmental Mapping and Analysis Program (EnMAP) Mission: Preparing for Its Scientific Exploitation)
Browse Figures
Versions Notes

Abstract

:
In modern agriculture, the spatially differentiated assessment of the leaf area index (LAI) is of utmost importance to allow an adapted field management. Current hyperspectral satellite systems provide information with a high spectral but only a medium spatial resolution. Due to the limited ground sampling distance (GSD), hyperspectral satellite images are often insufficient for precision agricultural applications. In the presented study, simulated hyperspectral data of the upcoming Environmental Mapping and Analysis Program (EnMAP) mission (30 m GSD) covering an agricultural region were pan-sharpened with higher resolution panchromatic aisaEAGLE (airborne imaging spectrometer for applications EAGLE) (3 m GSD) and simulated Sentinel-2 images (10 m GSD) using the spectral preserving Ehlers Fusion. As fusion evaluation criteria, the spectral angle (αspec) and the correlation coefficient (R) were calculated to determine the spectral preservation capability of the fusion results. Additionally, partial least squares regression (PLSR) models were built based on the EnMAP images, the fused datasets and the original aisaEAGLE hyperspectral data to spatially predict the LAI of two wheat fields. The aisaEAGLE model provided the best results (R2cv = 0.87) followed by the models built with the fused datasets (EnMAP–aisaEAGLE and EnMAP–Sentinel-2 fusion each with a R2cv of 0.75) and the simulated EnMAP data (R2cv = 0.68). The results showed the suitability of pan-sharpened EnMAP data for a reliable spatial prediction of LAI and underlined the potential of pan-sharpening to enhance spatial resolution as required for precision agriculture applications.

Graphical Abstract

1. Introduction

Ecological conditions and current management techniques have a strong influence on the spatial heterogeneity of agricultural fields. One of the most important challenges in modern agriculture is the development and implementation of an adapted field treatment to avoid over- and/or undersupply of agricultural inputs, a frequent cause for ecological problems and economic drawbacks. Multi- and hyperspectral remote sensing data can help to overcome these problems. In this context, imaging airborne and satellite sensors provide spatial, spectral, and temporal information of agricultural fields that can be used to identify infield variability and can support decision making in precision agriculture [1,2,3,4,5].
Fast, cost-effective and non-destructive assessment of relevant biochemical and structural vegetation properties is of utmost importance to characterize the crop status at leaf and canopy level. In this regard, parameters like chlorophyll content, above ground biomass dry matter, nitrogen status, canopy water content and leaf area index (LAI) provide important information for describing current growth conditions, and thus can be converted into yield-driving state variables (e.g., dry mass increase), which were used for the re-parameterization of agricultural production models [6,7,8,9]. The LAI is one of the most important plant parameters and serves as an essential variable for assimilating remote sensing data into crop growth models [10,11]. It is defined as the ratio of the total one-sided leaf surface area per unit soil surface area [12]. As an indicator for the current biotic and abiotic conditions, the LAI provides information about the photosynthetic “potential” of plants and is an important input parameter for yield modeling, since it is significantly influenced by yield-limiting and -reducing factors such as plant diseases and mismanagement [13,14,15].
Hyperspectral image data acquired from satellites (e.g., Earth Observing-1 Hyperion) provide high-resolution spectral information, which are useful for many applications in agricultural modeling [16]. In contrast, the spatial resolution of the data is often unsuitable for precision agriculture because of its ground sampling distance (GSD = 30 m), which means that a single pixel represents an averaged spectral reflectance signature of a large area [17,18]. This is especially a problem for monitoring the small-scale intra-field variability of crops, which is important to identify areas affected by stress, diseases and physical damage [1,19,20]. Additionally, remote sensing data with high spatial and spectral resolution serve as a vital information source for applying an adapted field treatment on sub-field scale and thus, allow a more precise management practice (e.g., fertilization [21], irrigation [22]).
Currently, there is no scientific or commercial satellite system available that provides hyperspectral image data with a higher spatial resolution than 30 m. To overcome this limitation, pan-sharpening can be used as an adequate method to enhance the spatial resolution of these datasets. In this context, multi- or hyperspectral image data of lower spatial resolution containing numerous spectral bands are fused with a panchromatic image of higher spatial resolution [23,24,25,26]. In recent years, different methods have been introduced for merging hyperspectral and panchromatic/multispectral images. Zhang [25] and Zhang et al. [27] developed different methods working in the wavelet domain that enable the direct fusion of multispectral and hyperspectral datasets to improve the spatial resolution of the latter (tested on AVIRIS airborne data). Chen et al. [17] introduced a generalized pan-sharpening approach that divides the hyperspectral dataset into several spectral regions and subsequently, each spectral region of the hyperspectral dataset is merged with a corresponding multispectral dataset using any state-of-the-art pan-sharpening technique. To interpolate missing spectral data in the multispectral image, the method is using the ratio image-based spectral resampling (RIBSR) before both images are fused. The method was tested on simulated hyperspectral HYDICE data in combination with a Landsat TM dataset. Furthermore, Delalieux et al. [26] used a method based on spectral mixture analysis to fuse hyperspectral airborne data (APEX) of high spectral resolution with higher spatial resolution thermal camera images acquired by an unmanned aerial vehicle (UAV). A detailed overview of the different fusion techniques applied on hyperspectral data can be found in [27,28].
The above-mentioned studies, however, were mostly not focused on a specific application but rather on the development and validation of new algorithms. Until now, only a few studies focusing on precision agriculture have been conducted using fused multispectral satellite data [29,30] or merged multi- and hyperspectral information acquired from different platforms (satellite, aircraft, UAV) [26,31] to assess crop conditions.
For this reason, in this study we fused simulated EnMAP (Environmental Mapping and Analysis Program) data covering an agricultural area with panchromatic datasets derived from the airborne hyperspectral scanner aisaEAGLE (airborne imaging spectrometer for applications EAGLE) (GSD = 3 m) as well as from simulated Sentinel-2 data (GSD = 10 m). In this context, the Ehlers Fusion was applied to merge the EnMAP image data with the different panchromatic datasets. This pan-sharpening technique was used because of its special design, which allows the spatial improvement of multi-/hyperspectral images by simultaneously preserving its spectral characteristics [23]. Furthermore, the Ehlers Fusion has proven to be well suited for multi-sensor image fusion because it provided a good compromise in terms of spectral preservation and spatial improvement compared to other state-of-the-art pan-sharpening techniques [23,32,33,34].
Given the above-described background, the major goals of this study were:
(1)
To prove the spatial enhancement as well as the spectral preservation capability of pan-sharpening when applied to hyperspectral EnMAP data.
(2)
To investigate the potential of the fusion results for a precise spatial intra-field assessment of wheat LAI for precision agriculture applications.

2. Study Area

The study area (11°54′E, 51°47′N) is part of one of the most important agricultural regions in Germany and is located in the federal state of Saxony-Anhalt (Figure 1). The region is distinctly dry with 430 mm mean annual precipitation because of its location in the rain shadow of the Harz Mountains. The mean annual temperature varies between 8 and 9 °C. The study area has an altitude of 70 m above sea level and is characterized by a thin Loess layer up to 1.2 m deep, which covers a slightly undulated tertiary plain. Predominant soil types of the region are Chernozems in conjunction with Cambisols and Luvisols. Within the study area, LAI assessment was carried out for two selected fields (A and B) with sizes of 80 ha and 50 ha, respectively.
Remotesensing 07 12737 g001 1024
Figure 1. Location of the test site in the federal state of Saxony-Anhalt in Germany with the two investigated wheat fields (red polygons) and the sampled plots within the fields (yellow dots).
Figure 1. Location of the test site in the federal state of Saxony-Anhalt in Germany with the two investigated wheat fields (red polygons) and the sampled plots within the fields (yellow dots).
Remotesensing 07 12737 g001

3. Data and Pre-Processing

3.1. Field Data

Two field campaigns were conducted in the study area in 7–10 May 2011 and 24–25 May 2012. Prior to the field campaigns, satellite data of former years were used to develop a representative sampling strategy. In total, 71 winter wheat plots (each with a size of 0.25 m2) distributed across the observed fields were sampled (36 in 2011, 35 in 2012) (cf. Figure 1). The LAI was measured non-destructively with a LAI 2000 (LI-COR Inc., Lincoln, NE, USA). For each plot, six measurements were recorded and afterwards mean values were calculated using all measurements within the standard deviation of the mean. Thus, it was possible to obtain a representative value for each plot and to exclude outliers from further investigations. Due to different stages of plant development in 2011 (stem elongation—EC (Eucarpia Code) 31–34) and in 2012 (ear emergence—EC 51–60), a wide range of LAI was covered.

3.2. Airborne Data

Parallel to the field campaigns, image data of the test site were acquired by the airborne hyperspectral scanner aisaEAGLE (Specim Ltd., Oulu, Finland) on 10 May 2011 and 24 May 2012. The aisaEAGLE system is a hyperspectral push-broom scanner covering the VNIR spectral range.
The image data have a GSD of 3 m with 124 spectral bands in the wavelength range of 400–970 nm. For data correction, the ROME destriping algorithm [35] was used to reduce miscalibration effects, present as deficient lines along track in the images. Afterwards, an atmospheric correction was conducted using MODTRAN4 (MODerate resolution atmospheric TRANsmission) to transfer the radiance values of each pixel to reflectance data [36]. Additionally, an empirical line correction, with spectral ground measurements of different dark and bright targets collected at the test site during the time of aisaEAGLE overpass, was necessary to remove spectral artifacts, which remained within the data after atmospheric correction [37]. The geometric correction as well as the orthorectification of the aisaEAGLE data was performed with ENVI (Environment for Visualizing Images). Afterwards, twelve spectral bands at the beginning of the aisaEAGLE spectral range (400–450 nm) were deleted because of high noise of the sensor system in this spectral region leaving 112 spectral bands for further analysis. Figure 2a shows the processed aisaEAGLE data subsets covering the two investigated wheat fields.
Furthermore, the 112 spectral bands covering the VNIR spectral range (450–970 nm) were averaged to generate panchromatic images (aisaEAGLE pan) out of the aisaEAGLE data (Figure 2b). These datasets were a requirement for the subsequent pan-sharpening of the EnMAP data.

3.3. Simulated Satellite-Data

Image data of the German hyperspectral satellite EnMAP (scheduled for launch in 2018) and ESA’s multispectral satellite Sentinel-2 (launch date 23 June 2015) were simulated from the aisaEAGLE datasets of the study site acquired in 2011 and 2012. The simulations were conducted using the EnMAP end-to-end simulation tool (EeteS) [38]. The tool consists of a complete forward (EnMAP Scene Simulator) and backward processing scheme (Onboard Calibration, L1 Processor, L2 Processor) as well as a detailed physical sensor model of EnMAP, which allows the simulation of realistic EnMAP data. A detailed description of EeteS is given in Segl et al. [38,39] and Guanter et al. [40]. Although the software was especially developed to simulate EnMAP data, the flexible modular structure of EeteS can easily be adapted to simulate image date of other sensors (e.g., Sentinel-2). Thus, EeteS offers the possibility to investigate the potential of future satellite missions for numerous applications and supports the development of new sensor designs.
As results of the simulations, two EnMAP (Figure 2c) and two Sentinel-2 (Figure 2d) datasets (one each in 2011 and 2012) were generated, which have the specific sensor characteristics of EnMAP and Sentinel-2, respectively. Due to the different GSDs of the single spectral bands, which will be provided by Sentinel-2, only the four spectral bands with the highest spatial resolution of 10 m (band 2: 458–522 nm, band 3: 543–577 nm, band 4: 650–680 nm, and band 8: 785–900 nm [41]) were further used for pan-sharpening the EnMAP data. Comparable to the aisaEAGLE data, panchromatic images (Sentinel-2 pan) for both years were created out of the Sentinel-2 scenes by averaging the four Sentinel-2 spectral bands (Figure 2e). Afterwards, the simulated EnMAP and Sentinel-2 datasets were cropped to match the spatial dimensions of the aisaEAGLE datasets covering the investigated fields. Dependent on the GSD of the panchromatic image used for pan-sharpening, the EnMAP data had to be resampled (with cubic convolution) to the same spatial resolution (aisaEAGLE pan: 3 m, Sentinel-2 pan: 10 m). Finally, after conducting all pre-processing steps, the different datasets were prepared for merging the simulated EnMAP data with the panchromatic aisaEAGLE as well as the panchromatic Sentinel-2 images using the Ehlers Fusion.
Remotesensing 07 12737 g002 1024
Figure 2. Image data of the investigated fields (Field A—2011 and Field B—2012; yellow polygons) with specific sensor characteristics. (a) aisaEAGLE (airborne imaging spectrometer for applications EAGLE) data; (b) panchromatic datasets based on aisaEAGLE; (c) simulated EnMAP (Environmental Mapping and Analysis Program) data; (d) simulated Sentinel-2 data, and (e) panchromatic datasets based on Sentinel-2 simulations.
Figure 2. Image data of the investigated fields (Field A—2011 and Field B—2012; yellow polygons) with specific sensor characteristics. (a) aisaEAGLE (airborne imaging spectrometer for applications EAGLE) data; (b) panchromatic datasets based on aisaEAGLE; (c) simulated EnMAP (Environmental Mapping and Analysis Program) data; (d) simulated Sentinel-2 data, and (e) panchromatic datasets based on Sentinel-2 simulations.
Remotesensing 07 12737 g002

4. Methodology

4.1. Ehlers Fusion

The Ehlers Fusion was developed specifically for a spectral characteristics preserving image merging [32]. It is based on an IHS (intensity, hue, saturation) transform coupled with a Fourier domain filtering and therefore belongs to the hybrid image fusion methods [24].
The principal idea behind a spectral characteristics preserving image fusion is that the high-resolution image has to sharpen the multi-/hyperspectral image without adding new grey level information to its spectral components. An ideal fusion algorithm would enhance high-frequency changes such as edges and grey level discontinuities in an image without altering the spectral components in homogeneous regions [23]. To facilitate these demands, two prerequisites have to be addressed. First, spectral and spatial information need to be separated. Second, the spatial information content has to be manipulated in a way that allows an adaptive enhancement of the images. This is achieved by a combination of color and Fourier transforms. For optimal separation of spatial and spectral information, use is made of an IHS transform. This technique is extended to include more than three bands by using multiple IHS transforms until the number of bands is exhausted. If the assumption of spectral characteristics preservation holds true, there is no dependency on the selection or order of bands for the IHS transform. Subsequently, Fourier transforms of the intensity component and the panchromatic image allow an adaptive filter design in the frequency domain. Using fast Fourier transform (FFT) techniques, the spatial components to be enhanced or suppressed can be directly accessed. The intensity spectrum is filtered with a low-pass filter, whereas the spectrum of the high-resolution image is filtered with an inverse high-pass filter. After filtering, the images are transformed back into the spatial domain with an inverse FFT and added together to form a fused intensity component with the low-frequency information from the spatial low-resolution multi-/hyperspectral image and the high-frequency information from the spatial high-resolution panchromatic image. This new intensity component has to be histogram matched to the original intensity component for mapping it into the value range of the original image. Afterwards, the fused and histogram matched intensity component and the original hue and saturation components of the multi-/hyperspectral image form a new IHS image. Finally, an inverse IHS transformation produces a fused RGB image that contains the spatial resolution of the panchromatic image and the spectral characteristics of the multi-/hyperspectral image. These steps can be repeated with successive three band selections until all bands are fused with the panchromatic image. The order of bands and the inclusion of spectral bands for more than one IHS transform are not critical because of the color preservation of the procedure [23]. The entire fusion procedure is presented in Figure 3.
Since the visual interpretation of the fusion results can be considered as very subjective and always depends on the experiences of the human interpreter two statistical evaluation criteria were calculated to measure the spectral preservation of the results. These methods are objective, quantitative and reproducible. First, the spectral angle (αspec) between corresponding pixel of the original aisaEAGLE data and the fusion results were determined [42]. αspec can be calculated in hyper-dimensional space for all bands of two pixels (two spectral curves) at once. An angle of 0 indicates an ideal fusion result while larger angles imply a poorer spectral preservation [43]. αspec was calculated (per pixel) to determine the spectral performance achieved by the Ehlers Fusion in order to identify spatial differences of spectral preservation in the fusion results.
α s p e c   =   c o s − 1 ( ∑ i = 1 n t i   r i ∑ i = 1 n t i 2   ∑ i = 1 n r i 2 )
  • where n = the number of spectral bands
  •    ti = fused spectrum
  •    ri = original spectrum
Remotesensing 07 12737 g003 1024
Figure 3. Scheme of the Ehlers Fusion with i1, i2, i3 ∈ {1, 2,…, n}.
Figure 3. Scheme of the Ehlers Fusion with i1, i2, i3 ∈ {1, 2,…, n}.
Remotesensing 07 12737 g003
As a second evaluation criterion, the correlation coefficient (R) was calculated for corresponding bands of the original data and the fusion results. In contrast to αspec, R was determined to evaluate the goodness of spectral preservation achieved for every single band. R has a value range from −1 to 1, where 1 indicates a perfect match for two compared spectral bands.
R   =   ( ∑ i n ( t i − µ t )   ( r i − µ r ) ∑ i n t i 2   ∑ i n r i 2 )
  • where n = the number of spectral bands
  •    ti = fused spectrum
  •    ri = original spectrum
  •    µt/r = mean of t or r

4.2. Partial Least Squares Regression

For predicting the LAI of the two investigated fields, partial least squares regression (PLSR) was used. PLSR was originally developed for chemical applications, but it has also been adapted to remote sensing data for many years to derive biophysical and biochemical parameters from reflectance spectra, e.g., [44,45,46,47].
Model building was carried out using the wide kernel-PLSR algorithm [48]. In this context, spectra of the image pixels corresponding to the geographic location of the different sampled wheat plots were extracted from the aisaEAGLE, the simulated EnMAP and the fused data for model calibration and validation. The maximum number of allowed latent variables (rank) was set to 10 and the Akaike information criterion (AIC) was calculated for the different PLSR models to determine the model with the optimum number of latent variables [49]. As criteria for regression model accuracy the coefficient of determination (R2) and the root mean squared error (RMSE) were calculated. A two-tailed t-test was conducted to determine whether there are significant differences between coupled RMSE values. Furthermore, the residual prediction deviation (RPD) was determined as an additional indicator for the robustness of the regression models. The RPD represents the ratio of the standard deviation of the observed LAI and the RMSE of the predictions [50]. Williams [51] developed a RPD scale based on high-resolution NIR laboratory spectra with different value classes for applications in food chemistry. Due to the lower spectral resolution of the data used in this study, a RPD scale with the following value limits suggested by Dunn et al. [52] was applied instead to evaluate the robustness of the regression models: RPD < 1.6, poor model; RPD = 1.6–2.0, acceptable model; RPD > 2.0, excellent model.
First, PLSR models were generated based on the aisaEAGLE and the EnMAP data. Leave-one-out cross-validation (cv) was performed to determine the model quality. Applying this validation technique, each sample was predicted by a regression model that was built using all remaining (n − 1) samples [53]. Second, PLSR models were built based on the fusion results. Thus, the potential of pan-sharpened EnMAP data to derive LAI could be examined. In analogy to the models calibrated with the aisaEAGLE and the simulated EnMAP data, the AIC was calculated to determine the optimal number of latent variables and leave-one-out cross-validation was conducted to ascertain regression model quality.

5. Results and Discussion

5.1. Image Fusion Results

Figure 4 illustrates the fusion results achieved with the Ehlers method for the different years in comparison to the original aisaEAGLE datasets (Figure 4a). A predefined filter design for rural regions was used in the fusion process to take into account the predominant land cover of the investigated area. As a result of merging simulated EnMAP data with an aisaEAGLE or Sentinel-2 panchromatic band, fused datasets were created, which have the spectral characteristics of EnMAP (82 spectral bands) and the spatial resolution of aisaEAGLE pan (Figure 4b) or Sentinel-2 pan (Figure 4c), respectively.
Remotesensing 07 12737 g004 1024
Figure 4. Comparison of the aisaEAGLE datasets with the fusion results. Displayed images in RGB (863/652/548 nm): (a) original aisaEAGLE datasets; (b) EnMAP–aisaEAGLE fusion; and (c) EnMAP–Sentinel-2 fusion. The two investigated fields are indicated by the yellow polygons.
Figure 4. Comparison of the aisaEAGLE datasets with the fusion results. Displayed images in RGB (863/652/548 nm): (a) original aisaEAGLE datasets; (b) EnMAP–aisaEAGLE fusion; and (c) EnMAP–Sentinel-2 fusion. The two investigated fields are indicated by the yellow polygons.
Remotesensing 07 12737 g004
As a first step, a visual analysis of the fusion results was conducted. In this context, the aisaEAGLE–EnMAP fusion result of 2011 showed a plausible spatial enhancement compared to the EnMAP data and a good agreement with the original aisaEAGLE image. In contrast, the aisaEAGLE–EnMAP fusion of 2012 appeared more blurred. This was particularly evident for the villages with their small-scale structures in the northern and southeastern part of the image. Both EnMAP–aisaEAGLE fusion results show some artifacts. Due to the frequency content of the image from 2012, these artifacts are less notable. The results of the EnMAP–Sentinel-2 fusion showed a similar trend. The result from 2011 seemed to be sharper compared to the result achieved for the images from 2012. Furthermore, the lower spatial resolution of Sentinal-2 provoked fewer artifacts in the result images in comparison to the EnMAP–aisaEAGLE fusion results. In terms of visual evaluation, the color infrared composites (RGB 863/652/548 nm) of all fusion results provided reasonable color preservation. This kind of interpretation, however, can be regarded as very subjective and only allowed the analysis of a single three-band combination. For a more objective spectral evaluation αspec was calculated using corresponding pixel from the original aisaEAGLE datasets and the fused images. In this context, the original aisaEAGLE datasets (112 bands) first had to be resampled to match the spectral resolution of the fusion results (82 bands). Second, due to the different spatial resolution of the original aisaEAGLE data (3 m GSD) and the EnMAP–Sentinel-2 fusion results (10 m GSD), a spatial resampling of the aisaEAGLE GSD to 10 m was necessary. Thus, the datasets were prepared to apply a pixel-based αspec determination.
Based on the computed αspec map of each fusion result, descriptive statistics were calculated for all pixel values and additionally only for the pixel values covering the investigated wheat fields (Table 1). The minimum αspec values determined for the EnMAP–aisaEAGLE fusion and the EnMAP–Sentinel-2 fusion were nearly the same for the pixel values covering the investigated fields and the pixel values of the entire images. In contrast, the maximum αspec values showed distinct differences. In 2012, the maximum angles for each image were much higher compared to 2011. This fact suggested that the overall spectral preservation yielded a higher level of accuracy for both fused datasets in 2011. Furthermore, it became obvious that the maximum αspec values were distinctly lower for the observed fields than for the pixels of the entire fused scenes. From the spectral point of view it can therefore be concluded that the fusion procedure worked much better for the investigated fields. One reason for this is the relatively large spectral homogeneity of the observed fields in comparison to the entire scene which was characterized by numerous land cover types, and thus by a distinctly higher spectral heterogeneity. This finding was also confirmed by the mean of the αspec maps. Again, the values were lower for the investigated fields than for the entire scenes. However, there were some differences between both years. In 2011, the mean values were lower for the entire scenes. Taking into account only the pixel covering the investigated fields, the situation was reversed. Both the EnMAP–aisaEAGLE fusion results and the EnMAP–Sentinel-2 fusion results provided slightly lower αspec mean values in 2012 than in 2011. This finding indicated a slightly better spectral preservation of the fusion results achieved for the fields in 2012.
Table
Table 1. Image and field statistics of αspec maps (in degree) for both years.
Table 1. Image and field statistics of αspec maps (in degree) for both years.
MinMaxMeanSD
Year20112012201120122011201220112012
αspec Image (aisaEAGLE fusion)0.560.6082.49170.464.516.744.348.79
αspec Field (aisaEAGLE fusion)0.561.0126.5735.173.022.652.491.28
αspec Image (Sentinel-2 fusion)0.550.5339.61167.323.634.513.547.94
αspec Field (Sentinel-2 fusion)0.581.0621.8213.342.502.331.841.02
Since this study focused on wheat fields, Figure 5 only illustrates the pixel-based calculated spectral angles of the investigated fields. Due to waterlogging in early spring, which allowed no plant growth, two drainless hollows in the southeastern and in the northern part of the field investigated 2011 were masked and not considered for further analysis.
Remotesensing 07 12737 g005 1024
Figure 5. αspec maps based on (a) EnMAP–aisaEAGLE fusion and (b) EnMAP–Sentinel-2 fusion for 2011 and 2012.
Figure 5. αspec maps based on (a) EnMAP–aisaEAGLE fusion and (b) EnMAP–Sentinel-2 fusion for 2011 and 2012.
Remotesensing 07 12737 g005
In accordance with the calculated mean values, the αspec maps of the EnMAP–Sentinel-2 fusion results (Figure 5b) seemed to have a slightly higher proportion of blue pixels compared to the corresponding EnMAP–aisaEAGLE fusion results (Figure 5a). Blue and dark blue pixel represent small spectral angles, and thus indicate an excellent spectral preservation. In general, the 2012 fusion results showed a better spectral preservation capability. One reason might be the more advanced plant development stage in 2012 compared to 2011, resulting in a spectrally more homogeneous surface, which caused less problems in the fusion process. Only small areas with less vegetation in the western part of the field and two larger areas in the south and east provided higher spectral angles and therefore a poorer spectral preservation compared to the rest of the field. Furthermore, some fusion artifacts present as horizontal edges crossing the middle part of the field were recognized in the EnMAP–aisaEAGLE fusion result. That was most likely the result of the insufficient correction of defective image lines during aisaEAGLE pre-processing (cf. Section 3.2).
In comparison to 2012, the αspec maps based on the fusion results of 2011 had a distinctly higher number of cyan pixels indicating only a medium quality spectral preservation. The yellow, orange and red areas at the edges of the drainless hollows in both αspec maps of 2011 representing regions with large spectral angles, and thus a poor spectral preservation. In these transition areas, the spectral reflection was characterized by a small-scaled and fast changing mixture of vegetation and soil resulting in a spectral inhomogeneous surface structure, which apparently led to problems during the fusion. Additionally, the same problem was detected at the western edge of the wheat field in the EnMAP–aisaEAGLE fusion result of 2011. In this area, the sharp spectral transition of the wheat field to the neighboring field covered with bare soil could properly not be reproduced in the fusion result. In the EnMAP–Sentinel-2 fusion result the problem was less pronounced. One reason for this was possibly the lower spatial resolution of Sentinel-2 and therefore the lower spatial fusion ratio of 1:3 in comparison to the EnMAP–aisaEAGLE fusion with a ratio of 1:10.
Besides the pixel-based performance of the fusion procedure that provided information on the spatial distribution of the spectral preservation capability, it was equally important to determine the spectral quality of the single bands. Therefore, the correlation coefficient (R) was calculated for every spectral band of the fusion results. Similar to the αspec calculations, R was computed for the entire images and also solely for the investigated fields. Table 2 shows the general results for the EnMAP–aisaEAGLE and the EnMAP–Sentinel-2 fusions. In this context, the mean value provided the most important information. Consistent with the results of the αspec analysis, the EnMAP–Sentinel-2 fusion produced a better spectral preservation which was confirmed by a higher correlation average across all spectral bands compared to the mean R determined for the EnMAP–aisaEAGLE fusion. In contrast to the mean αspec results, mean r, however, was higher for the entire images in comparison to the investigated fields. This fact suggested that other land cover types in the fused images were better spectrally preserved than the investigated fields. With respect to single band analysis, Figure 6 illustrates the correlation of every spectral band of the EnMAP–aisaEAGLE (Figure 6a) as well as the EnMAP–Sentinel-2 fusion (Figure 6b) with the original aisaEAGLE bands. It can be seen that on average the EnMAP–Sentinel-2 fusion for complete images as well as for the fields showed a higher correlation than the EnMAP–aisaEAGLE fusion.
Table
Table 2. Image statistics based on calculated correlation coefficients (R) taking into account all spectral bands of EnMAP (82 bands, 450–975 nm) for the entire images and for only the investigated fields.
Table 2. Image statistics based on calculated correlation coefficients (R) taking into account all spectral bands of EnMAP (82 bands, 450–975 nm) for the entire images and for only the investigated fields.
Correlation Coefficient (R)MinMaxMeanSD
ImageFieldImageFieldImageFieldImageField
R EnMAP–aisaEAGLE fusion0.770.500.850.870.820.750.020.11
R Field EnMAP–Sentinel-2 fusion0.800.660.910.920.880.830.030.08
While the correlation of all spectral bands for the entire images displayed a relatively constant and high level in both fusion cases, the shape of the graph representing the R of the investigated fields indicated a different behavior in some spectral regions. In the near-infrared domain, the graphs showing only the field specific correlation had a high conformity with the graphs of the entire images. In contrast, the correlation coefficients were distinctly lower in the blue range of the visible light. A possible reason for this can be the very low reflectance of green vegetation in the blue part of the spectrum, which has an impact on the histogram match applied to the fused intensity component matching it to the original intensity component during the Ehlers Fusion. The same problem appeared in the red domain of visible light. However, it was less pronounced because reflectance in this spectral range was on average a little higher. An additional reason for the low correlation coefficients in the blue and red part of visible light can be the chosen procedure to generate the artificial panchromatic images. In future studies it has to be investigated whether an averaged panchromatic image based on weighted spectral bands is better suited for the fusion procedure.
Remotesensing 07 12737 g006 1024
Figure 6. Correlation coefficients (R) calculated between the original aisaEAGLE datasets and the fusion results for the single spectral bands: (a) based on the entire images; and (b) limited to the pixels covering the two investigated fields. The red dashed lines represent typical green vegetation reflectance spectra added for better interpretation and understanding purpose.
Figure 6. Correlation coefficients (R) calculated between the original aisaEAGLE datasets and the fusion results for the single spectral bands: (a) based on the entire images; and (b) limited to the pixels covering the two investigated fields. The red dashed lines represent typical green vegetation reflectance spectra added for better interpretation and understanding purpose.
Remotesensing 07 12737 g006
Furthermore, only considering the fields a sharp decline of correlation in both fusion cases was detected for the spectral bands in the red edge range. This can also be explained by one of the operations during the fusion process. To conduct the IHS transforms each time three successive spectral bands were used. In the red edge range, these bands had a strongly deviating level of reflectance height caused by the steep increase of green vegetation reflectance in this spectral region. This probably had a negative impact on the generated intensity component, which was necessary for the further steps in the fusion procedure. Less pronounced the same effect was also detected for the spectral bands around 940 nm. This fact can also be explained by an abrupt change of the reflectance level of green vegetation because of a small water vapor absorption band in this spectral range [54].
Although there are still some problems, the first EnMAP–aisaEAGLE and EnMAP–Sentinel-2 fusion results were promising. However, in this study all used datasets are based on aisaEAGLE airborne data. As a consequence, all datasets exhibit the same acquisition conditions (e.g., same day and time, same atmospheric conditions, same sensor view angles), and are optimal co-registered to each other. In future work, the pan-sharpening of real EnMAP images with real Sentinel-2 data may cause problems which could not be considered in this study. In this context, the co-registration of images from different sensors is not a question of great concern anymore. New sensors with high geometric stability and new rectification/registration methods no longer work with the standard polynomial approach provide geometric registration accuracy with subpixel accuracy [55,56]. In contrast to that, different acquisition dates and atmospheric conditions can lead to major problems during the pan-sharpening process. Nevertheless, using simulated data in this study, acquired under exactly the same conditions, can also be regarded as an advantage. Thus, it was possible to identify problems caused by the applied pan-sharpening algorithm itself.

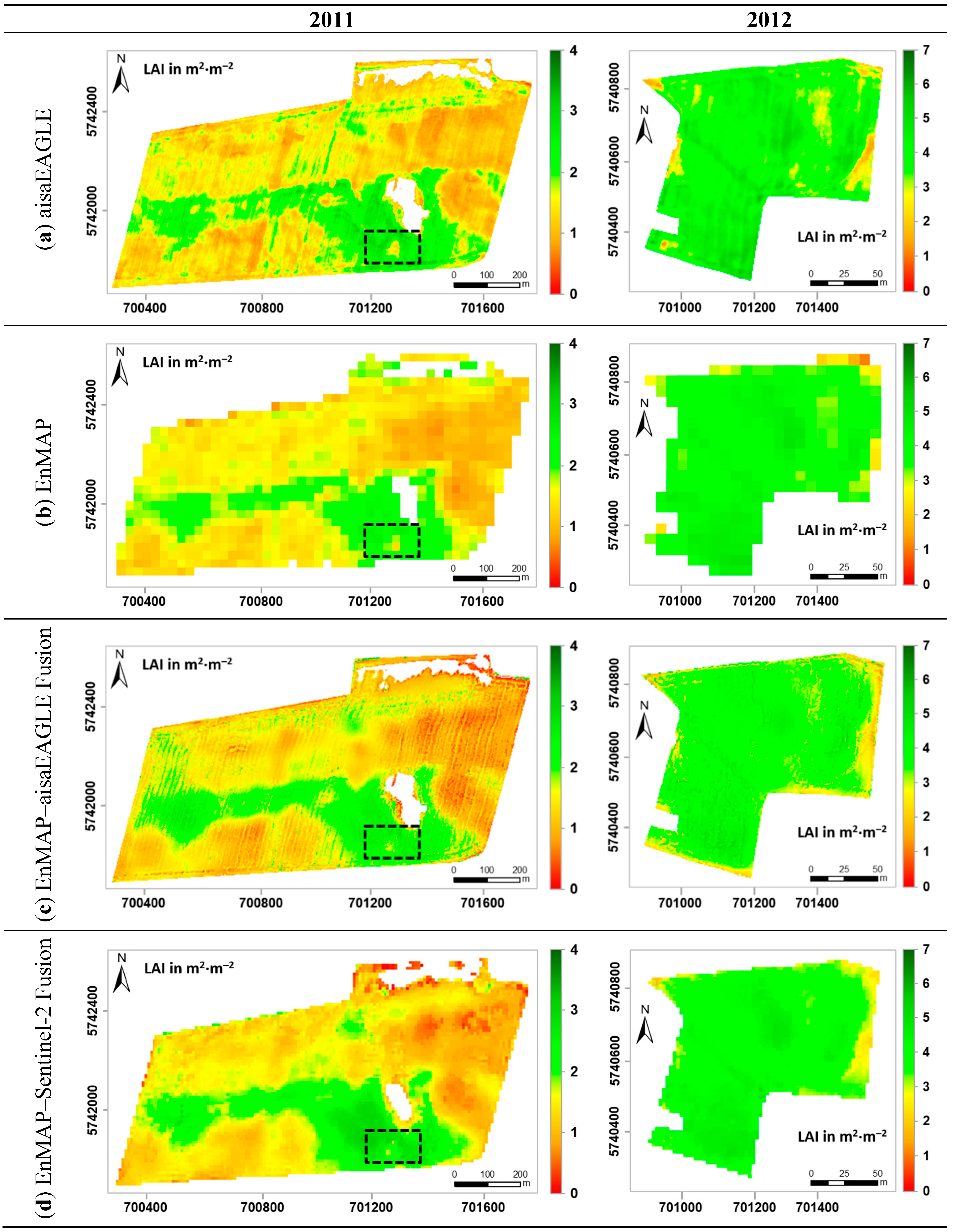
5.2. LAI Retrieval

Besides the evaluation of the fusion results, the LAI was spatially predicted as an additional criterion measuring the quality of the fusion results. LAI values of all wheat plots were measured between 0.50 m2·m−2 at minimum and 5.70 m2·m−2 at maximum during the field campaigns. The calculated average was 2.70 m2·m−2. LAI values measured in 2011 were relatively low because of the early stage of plant development (stem elongation—EC 31–34). In 2012, the measured LAI values covered a wider range and the mean was distinctly higher than in 2011. This was due to the advanced stage of plant development (ear emergence—EC 51–60) during the measurement campaign where also a more pronounced variability of the wheat stands was observed. Descriptive statistics of the winter wheat samples for both years are summarized in Table 3. Furthermore, the cross-validated results of all PLSR models (all correlations between measured and predicted values were statistically significant with p < 0.01) are summarized in Table 4 while Figure 7 illustrates the scatterplot of the models.
Table
Table 3. Descriptive statistics of winter wheat leaf area index (LAI) (in m2·m−2).
Table 3. Descriptive statistics of winter wheat leaf area index (LAI) (in m2·m−2).
nMinMaxMeanSD
36 (2011)0.503.351.490.65
35 (2012)1.915.703.950.83
71 (2011 & 2012)0.505.702.701.44
Table
Table 4. Cross-validated results of LAI predictions with PLSR based on aisaEAGLE, EnMAP, EnMAP–aisaEAGLE fusion, EnMAP + aisaEAGLE pan, EnMAP–Sentinel-2 fusion and EnMAP + Sentinel-2 pan.
Table 4. Cross-validated results of LAI predictions with PLSR based on aisaEAGLE, EnMAP, EnMAP–aisaEAGLE fusion, EnMAP + aisaEAGLE pan, EnMAP–Sentinel-2 fusion and EnMAP + Sentinel-2 pan.
n = 71R2cvRMSEcvRPDcv
aisaEAGLE0.870.512.81
EnMAP0.670.831.75
EnMAP–aisaEAGLE fusion0.750.731.99
EnMAP + aisaEAGLE pan0.710.761.88
EnMAP–Sentinel-2 fusion0.750.722.01
EnMAP + Sentinel-2 pan0.680.811.80
Remotesensing 07 12737 g007 1024
Figure 7. Scatterplots of predicted (cross-validated) and measured LAI for winter wheat based on partial least squares regression (PLSR) models for (a) aisaEAGLE, (b) EnMAP, (c) EnMAP–aisaEAGLE fusion, (d) EnMAP + aisaEAGLE pan, (e) EnMAP–Sentinel-2 fusion, and (f) EnMAP + Sentinel-2 pan. The solid red line represents the regression line while the dotted grey line represents the 1:1 line.
Figure 7. Scatterplots of predicted (cross-validated) and measured LAI for winter wheat based on partial least squares regression (PLSR) models for (a) aisaEAGLE, (b) EnMAP, (c) EnMAP–aisaEAGLE fusion, (d) EnMAP + aisaEAGLE pan, (e) EnMAP–Sentinel-2 fusion, and (f) EnMAP + Sentinel-2 pan. The solid red line represents the regression line while the dotted grey line represents the 1:1 line.
Remotesensing 07 12737 g007
First, PLSR models were calibrated based on the simulated EnMAP data and the original aisaEAGLE hyperspectral images, which were spectrally resampled to match the 82 spectral bands of EnMAP. The cross-validated (cv) aisaEAGLE model provided a high R2cv of 0.87 and a low RMSEcv of a half LAI unit (RMSEcv = 0.51). According to Dunn et al. [52], the calculated RPDcv of 2.81 indicated excellent model quality. In contrast, the model performance of the EnMAP model was at a distinctly lower level of accuracy (R2cv = 0.67, RMSEcv = 0.83). The RPDcv of 1.75 was clearly lower than 2, which only suggested an acceptable model performance [52]. The scatterplot of the EnMAP model (Figure 7b) also illustrates the less robust model calibration, which can be observed by a larger offset and a gain with a higher deviation from one compared to the aisaEAGLE model (Figure 7a). Furthermore, the scattering, especially of higher LAI, is more pronounced in the scatterplot of the EnMAP model. Although the EnMAP model performance was poorer, the result showed a higher quality than expected. In the process of model calibration and validation, EnMAP pixels with a size of 900 m2 were used in combination with corresponding LAI measurements only representing plots of a quarter square meter size each. This mismatch apparently had less influence on parameter predictability, which possibly indicated a less strong change of LAI over medium distances within the investigated fields.
Second, PLSR model building was conducted on the basis of the fused EnMAP–aisaEAGLE and the fused EnMAP–Sentinel-2 datasets. Moreover, these PLSR models were compared to additional PLSR models calibrated with the EnMAP spectral reflectance of each plot extended by another spectral band holding the grey value of the same plot extracted from the aisaEAGLE pan image (EnMAP + aisaEAGLE pan model) and Sentinel-2 pan image (EnMAP + Sentinel-2 pan model), respectively. In this context, it was examined whether the spatial enhancement as the result of the fusion process or the additional panchromatic information served as the more important factor improving LAI prediction based on EnMAP spectral information. The model built for the EnMAP–aisaEAGLE fusion resulted in a slightly higher model performance (R2cv = 0.75, RMSEcv = 0.73) compared to the EnMAP + aisaEAGLE pan model (R2cv = 0.71, RMSEcv = 0.76). A similar trend was obtained comparing the EnMAP–Sentinel-2 fusion model (R2cv = 0.75, RMSEcv = 0.72) and the EnMAP + Sentinel-2 pan model (R2cv = 0.68, RMSEcv = 0.81). In this case, differences regarding model performance were already distinctly larger. In general, the regression models built with the fused datasets led to better LAI predictions. This finding was confirmed by RPDcv values of approximately 2 for the fused datasets, which, according to Dunn et al. [52], indicated a model calibration very close to excellent.
While the RMSE of the aisaEAGLE model showed a significant difference to the other models (p-value < 0.05), the p-values of the t-tests determined for the fusion (EnMAP–aisaEAGLE fusion, EnMAP–Sentinel-2 fusion) and pan models (EnMAP + aisaEAGLE pan, EnMAP + Sentinel-2 pan) were over 0.05 indicating no significant difference between the compared RMSE values. Hence, it cannot be concluded that the fusion models statistically performed better than the comparable pan models. Nevertheless, the fusion models enable much higher spatial data resolution and consequently a more differentiated spatial LAI prediction, which is required for precision farming applications.
Due to the nearly equal regression functions and calculated model evaluation criteria, the EnMAP–aisaEAGLE fusion and the EnMAP–Sentinel-2 fusion models have almost identical scatterplots (Figure 7c,e). Although the quality of both models were considerably lower than of the original aisaEAGLE model, an improved LAI prediction was possible in comparison to the EnMAP model. A reason for the equal performance of the fusion models can be the spatial fusion ratio. The higher the ratio, the more difficult the filtering of the intensity component in Fourier space becomes. For this reason, the fusion ratio of 1:3 in case of the EnMAP–Sentinel-2 fusion was obviously well suited for a robust LAI estimation of the investigated fields. Using a higher ratio like 1:10 in EnMAP–aisaEAGLE fusion allowed no additional improvement of LAI prediction. The two models based on the EnMAP data extended by the panchromatic information also provided more accurate model results compared to the model solely calibrated with EnMAP spectral information. In contrast to the fused spectral data used for model building which only contained the spatial information of the panchromatic images, the LAI prediction improvement achieved with the EnMAP + aisaEAGLE pan as well as the EnMAP + Sentinel-2 pan model can only be explained by the additional spectral information of the panchromatic band. Furthermore, a reason for the better model performance of the EnMAP + aisaEAGLE pan model can be the higher number of narrow spectral bands covering a wider spectral range (112 spectral bands, 450–970 nm, bandwidth: ~4.5 nm) used for generating the panchromatic band. The Sentinel-2 panchromatic band, however, only consisted of the averaged spectral information of four broad spectral bands and therefore is less representative for the entire VNIR range. As a consequence, the model quality was only negligibly higher compared to the EnMAP model. In this context, the fusion of EnMAP data with a higher resolution panchromatic dataset seemed to be better suited to predict the LAI than using PLSR models calibrated with the EnMAP spectral bands extended with the additional information of a panchromatic image. Moreover, the most operational satellites have panchromatic bands only covering small parts of the EnMAP spectral range (e.g., Landsat 8 pan: 500–680 nm, 15 m GSD [57], SPOT 6/7 pan: 450–745 nm, 5 m GSD [58]). The spatial information of these bands will offer a high potential for pan-sharpening EnMAP images but only provide limited additional spectral information, which would be helpful for the retrieval of plant parameters.
Due to the fact that all models were based on aisaEAGLE data or simulated data from these datasets, the scatterplots show high similarities. A general trend is the overestimation of low values and the underestimation of high values. This suggests a successful pan-sharpening because the fused datasets obviously contain spectral information comparable to those of the simulated EnMAP data as well as the original aisaEAGLE hyperspectral data.
Finally, the calibrated regression models were applied to the corresponding images. Figure 8 shows the LAI maps of both fields based on the different models. Since the EnMAP + aisaEAGLE pan as well as the EnMAP + Sentinel-2 pan model provided lower model accuracies compared to the fusion results, the spatial LAI predictions of these models are not presented.
The spatial LAI prediction from the regression model based on the original aisaEAGLE datasets (Figure 8a) served as reference for the LAI estimates achieved by the other regression models. The LAI maps derived from the aisaEAGLE data show a very detailed spatial LAI distribution across the fields. In both years, the tram lines caused by agricultural machinery were clearly visible. In 2011, the LAI was lower because of the earlier stage of plant development.
The field investigated in 2012 had a much more homogeneous LAI distribution. The maps based on the EnMAP model (Figure 8b) also represented the general LAI structure of the fields. Small variations, however, could not be detected. The reason for this was the lower spatial resolution of the simulated EnMAP data in comparison to the aisaEAGLE datasets. In contrast, the maps derived from the aisaEAGLE–EnMAP fusion results (Figure 8c) enabled a more detailed spatial LAI assessment and showed more precise correspondence with the aisaEAGLE maps. However, in 2011 areas with low LAI in the eastern and southwestern part of the field and areas with high LAI around the drainless hollow in the south were underestimated. In 2012, the largest differences occurred at the southern and eastern edge of the field where the LAI again was underestimated. In general, the spatial improvement by a factor of ten seemed to be problematic. In this context, the LAI map of 2012 showed some unrealistic structures. These structures reflected artifacts caused by the fusion process using images with a distinctly different GSD, and thus a high fusion ratio (1:10). Although the LAI map of 2011 had no visible artifacts, the spatial improvement appeared exaggerated. This fact indicated that the filter settings for the high pass pan filter were set to a frequency that was probably too low, and thus included too much spatial information from the pan images during the fusion process. The LAI maps of both years derived from the EnMAP–Sentinel-2 fusion results (Figure 8d) provided a more realistic LAI distribution within the fields. Due to the lower spatial resolution, very small-scaled structures within the field, which can be detected in the aisaEAGLE LAI maps, cannot be recognized. In contrast to the EnMAP LAI maps, however, more detailed LAI predictions were possible. The EnMAP–Sentinel-2 LAI map of 2012 showed a high agreement with the aisaEAGLE LAI map of 2012. The map of 2011 also reflected the spatial pattern of LAI very well. Only two areas with low LAI in the northern part of the field were underestimated in comparison to the corresponding areas in the aisaEAGLE LAI map.
As an additional criterion evaluating the fusion results, a profile covering an area with highly variable LAI over a short distance was extracted from all LAI maps of 2011. In Figure 8, the area of interest was bordered with a dashed black line in all LAI maps. Figure 9 illustrates the enlarged areas with the profiles on the right side and the scatterplot with the extracted LAI of the pixels on the left side. The black graph represents the reference profile of the aisaEAGLE LAI map. The profile has a length of 180 m, which corresponds to 60 pixels, and thus 60 LAI values. At the beginning, the LAI was higher than 3 and then gradually decreased to a value of approximately 1.25. After 75 m, the LAI increased again sharply and then leveled at a value of about 2.25 with slight fluctuations. The red graph showed the profile extracted from the EnMAP LAI map. Due to the spatial resolution one EnMAP pixel corresponded to 10 aisaEAGLE pixels. Therefore, the EnMAP profile could not reflect the curve of the aisaEAGLE profile in detail. Especially the representation of sharp LAI changes was not possible in this context. The shape of the EnMAP–aisaEAGLE fusion LAI profile was well in accordance with the aisaEAGLE profile. Only very low values in the middle of the profile were overestimated. The same problem was also observed for the EnMAP–Sentinel-2 fusion profile. Again, lower values were overestimated. However, in contrast to the EnMAP–aisaEAGLE fusion, higher LAI values were also, on average, a little overestimated in the EnMAP–Sentinel-2 fusion result. The problem with lower values was probably caused by the abrupt change in LAI from high to low values and back over a short distance that cannot be reflected by the fusion results. In contrast, the EnMAP graph shows a distinctly better match with the aisaEAGLE graph in the considered transition area. Therefore, it seems the fusion algorithm has some difficulties to deal with these abrupt changes. Furthermore, again the large spatial resolution ratio of the fused images, which did not allow a realistic representation of small-scale patterns, leads to a certain overestimation of low values in the EnMAP–aisaEAGLE fusion profile.
Remotesensing 07 12737 g008 1024
Figure 8. Spatial LAI prediction based on (a) aisaEAGLE; (b) EnMAP; (c) EnMAP–aisaEAGLE fusion and (d) EnMAP–Sentinel-2 fusion. The dashed rectangle indicates the area presented in Figure 9.
Figure 8. Spatial LAI prediction based on (a) aisaEAGLE; (b) EnMAP; (c) EnMAP–aisaEAGLE fusion and (d) EnMAP–Sentinel-2 fusion. The dashed rectangle indicates the area presented in Figure 9.
Remotesensing 07 12737 g008
Remotesensing 07 12737 g009 1024
Figure 9. LAI profile for a specific area of the field investigated in 2011 based on (a) aisaEAGLE (black); (b) EnMAP (red); (c) EnMAP–aisaEAGLE fusion (blue) and (d) EnMAP–Sentinel-2 fusion (orange).
Figure 9. LAI profile for a specific area of the field investigated in 2011 based on (a) aisaEAGLE (black); (b) EnMAP (red); (c) EnMAP–aisaEAGLE fusion (blue) and (d) EnMAP–Sentinel-2 fusion (orange).
Remotesensing 07 12737 g009

6. Conclusion and Outlook

Remote sensing can be regarded as one of the key tools in precision agriculture because it allows the spatial assessment of important crop parameters, and thus supports decision making for an adapted intra-field treatment. Nowadays, a large number of remote sensing sensors are available that have different spatial, spectral and temporal resolutions. For a temporal high-resolution monitoring of agricultural crops over a growing season, pan-sharpening offers the possibility of filling in gaps of missing suitable datasets by combining spatial and spectral characteristics of different remote sensing sensors, with sensor characteristics that would be less beneficial for precision agriculture if not used in an integrated manner.
This study investigated the potential of merging hyperspectral EnMAP data with panchromatic bands derived from aisaEAGLE airborne and Sentinel-2 satellite data using the spectral preserving Ehlers method. Different PLSR regression models were developed to predict the LAI of winter wheat. The fusion models provided higher model accuracies (EnMAP–aisaEAGLE fusion: R2cv = 0.75, EnMAP–Sentinel-2 fusion R2cv = 0.75) compared to the pan models (EnMAP + aisaEAGLE pan: R2cv = 0.71, EnMAP + Sentinel-2 pan: R2cv = 0.68) and the EnMAP model (R2cv = 0.67), respectively. Although the RMSE values of the models showed no significant differences, the more precise spatial LAI predictions of the investigated wheat fields were possible on the basis of fusion models. Therefore, the fused datasets are deemed to be better suited for applications in precision agriculture where an exact LAI assessment is a decisive factor (e.g., for yield modeling). However, the study also showed some problems that occurred during the data fusion process, which can be explained by the methodology that the Ehlers Fusion is based on. In this context, the fusion ratio of the fused datasets had a substantial impact on fusion results, and thus on LAI prediction. The fused EnMAP–aisaEAGLE dataset (fusion ratio: 1:10, GSD: 3 m) did not lead to a more precise LAI estimate in comparison to the prediction based on the EnMAP-Sentinel 2 datasets (fusion ratio: 1:3, GSD: 10 m). Thus, in future studies, one of the tasks will be the identification of an optimal spatial fusion ratio. Furthermore, the problem of the poor preservation of spectral bands within the red edge spectral region of green vegetation has to be solved. This is especially important for the determination of plant parameters like LAI, chlorophyll content and above ground biomass dry matter, which have major influence on this spectral region.
As a next step panchromatic bands of operational satellites (e.g., Landast 8 (GSD: 15 m) [57], ALI (GSD: 10 m) [59]) or simulated panchromatic bands from multispectral satellite information (e.g., RapidEye (GSD: 5 m) [60], Sentinel-2 (GSD: 10/20 m) [41]) need to be integrated in the fusion process to test the capability of the Ehlers Fusion under more realistic conditions. Additionally, the SWIR part of the sensor should be included in the fusion procedure. Thus, the prediction of other plant (e.g., canopy water content) and soil parameters (e.g., soil organic carbon) would be possible. In this regard, it has to be examined if a spectral preserving fusion of the SWIR range can be conducted using a panchromatic band only covering the VNIR range.
In this study, only the Ehlers Fusion was tested, showing the potential of pan-sharpened EnMAP data for precision agriculture. In future research, more attention has to be paid to an inter-comparison of the Ehlers method with other techniques allowing the fusion of hyperspectral datasets like the Hyper Color Space (HCS) Resolution Merge introduced by Padwick et al. [61] or the Wavelet-Based Bayesian Fusion developed by Zhang [25] and Zhang et al. [27]. Besides an inter-comparison, uniform fusion evaluation criteria have to be defined to ensure an objective validation of the fusion results. A large number of criteria measuring the spectral preservation already exist but there is still a great demand for meaningful spatial evaluation criteria.

Acknowledgments

This work was funded by the German Aerospace Center (DLR) with financial resources of the Federal Ministry of Economics and Technology on the basis of a decision of the German Parliament, grant number 50 EE 1014. We would like to thank the Helmholtz Centre for Environmental Research Leipzig (UFZ) and the Humboldt University at Berlin for making their field instruments available. Special thanks go to Mr. Wagner and the Wimex GmbH, owner of the investigated fields, for their cooperation and their support. Additionally, we want to thank Karl Segl, Rudolf Richter, Daniel Doktor, Sascha Klonus, Sabine Hornberg, Holger Lilienthal, Nicole Richter, Thomas Selige, Anne Bodemann, Martin Kanning, Thorben Jensen and Yevgeniya Filippovska for their assistance in field during data collection and data pre-processing.

Author Contributions

Bastian Siegmann and Thomas Jarmer were responsible for the field data collection. Bastian Siegmann, with input from Thomas Jarmer, Florian Beyer and Manfred Ehlers, designed and conducted substantial parts of the analysis and wrote the article. The article was improved by the contributions of all coauthors at various stages of the analysis and writing process.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Moran, M.S.; Inoue, Y.; Barnes, E.M. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 1997, 61, 319–346. [Google Scholar] [CrossRef]
  2. Gebbers, R.; Adamchuck, V. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
  3. Seelan, K.S.; Laguetta, S.; Casady, G.M.; Seielstad, G.A. Remote sensing applications for precision agriculture: A learning community approach. Remote Sens. Environ. 2003, 88, 157–169. [Google Scholar] [CrossRef]
  4. Zhang, N.; Wang, M.; Wang, N. Precision agriculture—A worldwide overview. Comput. Electron. Agric. 2002, 36, 113–132. [Google Scholar] [CrossRef]
  5. Zarco-Tejada, P.J.; Ustin, S.L.; Whiting, M.L. Temporal and spatial relationships between within-field yield variability in cotton and high-spatial hyperspectral remote sensing imagery. Agron. J. 2005, 97, 641–653. [Google Scholar] [CrossRef]
  6. Cox, S. Information technology: The global key to precision agriculture and sustainability. Comput. Electron. Agric. 2002, 36, 93–111. [Google Scholar] [CrossRef]
  7. Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
  8. Schueller, J.K. A review and integrating analysis of spatially-variable control of crop production. Fertil. Res. 1992, 33, 1–34. [Google Scholar] [CrossRef]
  9. Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm. Remote Sens. 1992, 47, 145–161. [Google Scholar] [CrossRef]
  10. Machwitz, M.; Giutarini, L.; Bossung, C.; Frantz, D.; Schlerf, M.; Lilienthal, H.; Wandera, L.; Matgen, P.; Hoffmann, L.; Udelhoven, T. Enhanced biomass prediction by assimilating satellite data into a crop growth model. Environ. Model. Softw. 2014, 62, 437–453. [Google Scholar] [CrossRef]
  11. Moulin, S.; Bondeau, A.; Delécolle, R. Combining agricultural crop models and satellite observation: From field to regional scales. Int. J. Remote Sens. 1998, 19, 1021–1036. [Google Scholar] [CrossRef]
  12. Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 4th ed.; Elsevier/Academic Press: London, UK, 2013; p. 418. [Google Scholar]
  13. Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
  14. Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
  15. Daughtry, C.S.T.; Gallo, K.P.; Goward, S.N.; Prince, S.D.; Kustas, W.D. Spectral estimates of absorbed radiation and phytomass production in corn and soybean canopies. Remote Sens. Environ. 1992, 39, 141–152. [Google Scholar] [CrossRef]
  16. Dale, L.M.; Thewis, A.; Boudry, C.; Rotar, I.; Dardenne, P.; Baeten, V.; Fernández Pierna, J.A. Hyperspectral imaging applications in agriculture and agro-food product quality and safety control: A review. Appl. Spectrosc. Rev. 2013, 48, 142–159. [Google Scholar] [CrossRef]
  17. Chen, Z.; Pu, H.; Wang, B. Fusion of hyperspectral and multispectral images: A novel framework based on generalization of pan-sharpening methods. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1418–1422. [Google Scholar] [CrossRef]
  18. Mayumi, N.; Iwasaki, A. Image sharpening using hyperspectral and multispectral data. IEEE Int. Geosci. Remote Sens. Symp. 2011. [Google Scholar] [CrossRef]
  19. Johnson, B. Effects of pansharpening on vegetation indices. ISPRS Int. J. Geo-Inf. 2014, 3, 507–522. [Google Scholar] [CrossRef]
  20. Pinter, P.J., Jr.; Hatfield, J.L.; Schepers, J.S.; Barnes, E.M.; Moran, M.S.; Daughtry, C.S.T.; Upchurch, D.R. Remote Sensing for Crop Management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar] [CrossRef]
  21. Baret, F.; Houlès, V.; Guérif, M. Quantification of plant stress using remote sensing observations and crop models: The case of nitrogen management. J. Exp. Bot. 2007, 58, 869–880. [Google Scholar] [CrossRef] [PubMed]
  22. Vuolo, F.; Essl, L.; Atzberger, C. Costs and benefits of satellite-based tools for irrigation management. Front. Environ. Sci. 2015, 3, 1–12. [Google Scholar] [CrossRef]
  23. Ehlers, M.; Klonus, S.; Astrand, P.; Rosso, P. Multi-sensor image fusion for pansharpening in remote sensing. Int. J. Image Data Fusion 2010, 1, 25–45. [Google Scholar] [CrossRef]
  24. Pohl, C.; van Genderen, J. Structuring contemporary remote sensing image fusion. Int. J. Image Data Fusion 2015, 6, 3–21. [Google Scholar] [CrossRef]
  25. Zhang, Y. Wavelet-based Bayesian fusion of multispectral and hyperspectral images using Gaussian scale mixture model. Int. J. Image Data Fusion 2012, 3, 23–37. [Google Scholar] [CrossRef]
  26. Delalieux, S.; Zarco-Tejada, P.J.; Tits, L.; Jiménez Bello, M.Á.; Intrigliolo, D.S.; Somers, B. Unmixing-based fusion of hyperspatial and hyperspectral airborne imagery for early detection of vegetation stress. IEEE Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2571–2582. [Google Scholar] [CrossRef]
  27. Zhang, Y.; de Backer, S.; Scheunders, P. Noise-resistant wavelet-based Bayesian fusion of multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3834–3843. [Google Scholar] [CrossRef]
  28. Chaudhuri, S.; Kotwal, K. Hyperspectral Image Fusion, 1st ed.; Springer: New York, NY, USA, 2013; p. 191. [Google Scholar]
  29. Zurita-Milla, R.; Clevers, J.G.P.W.; Shaepman, M.E. Unmixing-based Landsat TM and MERIS FR data fusion. IEEE Geosci. Remote Sens. Lett. 2008, 5, 453–457. [Google Scholar] [CrossRef] [Green Version]
  30. Amorós-López, J.; Gómez-Chova, L.; Alonso, L.; Guanter, L.; Zurita-Milla, R.; Moreno, M.; Camps-Valls, G. Multitemporal fusion of Landsat/TM and ENVISAT/MERIS for crop monitoring. Int. J. Appl. Earth Obs. Geoinformation 2013, 23, 132–141. [Google Scholar] [CrossRef]
  31. Gevaert, C.M.; Tang, J.; García-Haro, F.J.; Suomalainen, J.; Kooistra, L. Combining hyperspectral UAV and multispectral Formosat-2 imagery for precision agriculture applications. In Proceedings 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014.
  32. Klonus, S.; Ehlers, M. Image fusion using the Ehlers spectral characteristics preserving algorithm. GIScience Remote Sens. 2007, 44, 93–116. [Google Scholar] [CrossRef]
  33. Ling, Y.; Ehlers, M.; Usery, E.L.; Madden, M. FFT-enhanced IHS transform method for fusing high-resolution satellite images. ISPRS J. Photogramm. Remote Sens. 2007, 61, 381–392. [Google Scholar] [CrossRef]
  34. Jawak, S.D.; Luis, A.J. A comprehensive evaluation of PAN-sharpening algorithms coupled with resampling methods for image synthesis of very high resolution remotely sensed satellite data. Adv. Remote Sens. 2013, 2, 332–344. [Google Scholar] [CrossRef]
  35. Rogaß, C.; Spengler, D.; Bochow, M.; Segl, K.; Lausch, A.; Doktor, D.; Roessner, S.; Behling, R.; Wetzel, H.U.; Kaufmann, H. Reduction of radiometric miscalibration-application to pushbroom sensors. Sensors 2011, 11, 6370–6395. [Google Scholar] [CrossRef] [PubMed]
  36. Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
  37. Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
  38. Segl, K.; Guanter, L.; Rogass, C.; Kuester, T.; Roessner, S.; Kaufmann, H.; Sang, B.; Mogulsky, V.; Hofer, S. EeteS—The EnMAP end-to-end simulation tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 522–530. [Google Scholar] [CrossRef]
  39. Segl, K.; Guanter, L.; Kaufmann, H. Simulation of spatial sensor characteristics in the context of the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3046–3054. [Google Scholar] [CrossRef]
  40. Guanter, L.; Segl, K.; Kaufmann, H. Simulation of optical remote sensing scenes with application to the EnMAP hyperspectral mission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2340–2351. [Google Scholar] [CrossRef]
  41. Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/resolutions/radio-metric (accessed on 7 May 2015).
  42. Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
  43. Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S Data-Fusion Contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef] [Green Version]
  44. Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
  45. Jarmer, T. Spectroscopy and hyperspectral imagery for monitoring summer barley. Int. J. Remote Sens. 2013, 34, 6067–6078. [Google Scholar] [CrossRef]
  46. Pu, R. Comparing canonical correlation analysis with partial least squares regression in estimating forest leaf area index with multitemporal landsat TM imagery. GIScience Remote Sens. 2013, 49, 92–116. [Google Scholar] [CrossRef]
  47. Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, in press. [Google Scholar]
  48. Rännar, S.; Geladi, P.; Lidgren, F.; Wold, S. A PLS kernel algorithm for data sets with many variables and fewer objects. Part 1: Theory and algorithm. J. Chemom. 1994, 8, 111–124. [Google Scholar] [CrossRef]
  49. Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
  50. Malley, D.F.; Martin, P.D.; Ben-Dor, E. Application in analysis of soils. In Near-Infrared Spectroscopy in Agriculture, 1st ed.; Roberts, C.A., Workman, J., Jr., Reeves, J.B., III, Eds.; American Society of Agronomy; Crop Science Society of America; Soil Science Society of America: Madison, WI, USA, 2004; pp. 729–783. [Google Scholar]
  51. Williams, P.C. Implementation of near-infrared technology. In Near-Infrared Technology in the Agricultural and Food Industries, 2nd ed.; Williams, P., Norris, K., Eds.; American Association of Cereal Chemists: St. Paul, MN, USA, 2001; pp. 145–169. [Google Scholar]
  52. Dunn, B.W.; Beecher, H.G.; Batten, G.D.; Ciavarella, S. The potential of near-infrared reflectance spectroscopy for soil analysis: A case study from the Riverine plain of South-Eastern Australia. Aust. J. Exp. Agric. 2002, 42, 607–614. [Google Scholar] [CrossRef]
  53. Otto, M. Chemometrics: Statistics and Computer Application in Analytical Chemistry, 2nd ed.; Wiley-VCH: New York, NY, USA, 2007; p. 343. [Google Scholar]
  54. Rollin, M.E.; Milton, E.J. Processing of high spectral resolution reflectance data for the retrieval of canopy water content information. Remote Sens. Environ. 1998, 65, 86–92. [Google Scholar] [CrossRef]
  55. Ehlers, M. Rectification and registration. In Integration of Remote Sensing and GIS, 1st ed.; Star, J.L., Estes, J.E., McGwire, K.C., Eds.; Cambridge University Press: Cambridge UK, 1997; pp. 13–36. [Google Scholar]
  56. Ehlers, M.; Jacobsen, K.; Schiewe, J. High Resolution Image Data and GIS. In ASPRS Manual of GIS, 1st ed.; Madden, M., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2009; pp. 721–777. [Google Scholar]
  57. Landsat Science. Available online: http://landsat.gsfc.nasa.gov/?p=5771 (accessed on 7 May 2015).
  58. SPOT 6 SPOT 7 Technical Sheet. Available online: http://www2.geo-airbusds.com/files/pmedia/public/r12317_9_spot6–7_technical_sheet.pdf (accessed on 7 May 2015).
  59. Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
  60. Black Bridge Imagery Products. Available online: http://www.blackbridge.com/geomatics/products/rapideye.html (accessed on 13 May 2015).
  61. Padwick, C.; Deskevich, M.; Pacifici, F.; Smallwood, S. WorldView-2 pan-sharpening. In Proceedings of the 2010 ASPRS Annual Conference, San Diego, CA, USA, 26–30 June 2010.

Share and Cite

MDPI and ACS Style

Siegmann, B.; Jarmer, T.; Beyer, F.; Ehlers, M. The Potential of Pan-Sharpened EnMAP Data for the Assessment of Wheat LAI. Remote Sens. 2015, 7, 12737-12762. https://doi.org/10.3390/rs71012737

AMA Style

Siegmann B, Jarmer T, Beyer F, Ehlers M. The Potential of Pan-Sharpened EnMAP Data for the Assessment of Wheat LAI. Remote Sensing. 2015; 7(10):12737-12762. https://doi.org/10.3390/rs71012737

Chicago/Turabian Style

Siegmann, Bastian, Thomas Jarmer, Florian Beyer, and Manfred Ehlers. 2015. "The Potential of Pan-Sharpened EnMAP Data for the Assessment of Wheat LAI" Remote Sensing 7, no. 10: 12737-12762. https://doi.org/10.3390/rs71012737

APA Style

Siegmann, B., Jarmer, T., Beyer, F., & Ehlers, M. (2015). The Potential of Pan-Sharpened EnMAP Data for the Assessment of Wheat LAI. Remote Sensing, 7(10), 12737-12762. https://doi.org/10.3390/rs71012737

Article Metrics

Back to TopTop