Consistency between In Situ, Model-Derived and High-Resolution-Image-Based Soil Temperature Endmembers: Towards a Robust Data-Based Model for Multi-Resolution Monitoring of Crop Evapotranspiration
Abstract
:1. Introduction
2. Sites and Data Description
2.1. Site and In Situ Data Description
2.1.1. R3 Perimeter



2.1.2. Urgell Site
2.1.3. Yaqui Site
2.2. Remote Sensing Data
2.2.1. ASTER
2.2.2. Formosat-2
2.2.3. LST, Fractional Green Vegetation Cover, NDVI and Surface Albedo
3. Models
3.1. SEB-1S: An EF Model (EF_SEB-1S)

3.2. Image-Based Tends Algorithm (Tends_RS)

3.3. Model-Derived Tends (Tends_EBsoil)
3.3.1. Soil Energy Balance Model
3.3.2. Aerodynamic Resistance Formulations for Bare Soil
3.3.3. Vegetation Tends

3.4. Validation Strategy
4. Results and Discussion
4.1. Modeled Soil Tends
4.1.1. Direct Validation Using In Situ Measurements
| Time | RMSE (C) | Bias (C) | R (-) | Slope (-) | ||||
|---|---|---|---|---|---|---|---|---|
| RI | MO | RI | MO | RI | MO | RI | MO | |
| 10:30 a.m. | 3.2 | 2.3 | −1.8 | −1.2 | 0.93 | 0.96 | 0.82 | 0.99 |
| 11:00 a.m. | 3.3 | 2.3 | −2.2 | −1.7 | 0.97 | 0.98 | 0.79 | 0.94 |
| 11:30 a.m. | 4.2 | 2.7 | −2.5 | −1.9 | 0.95 | 0.98 | 0.74 | 0.90 |
| Mean | 3.6 | 2.4 | −2.2 | −1.6 | 0.95 | 0.97 | 0.78 | 0.94 |



4.1.2. Consistency with Remotely-Sensed Soil Tends
| Day | Site | Bias (C) | Bias (C) | ||
|---|---|---|---|---|---|
| RI | MO | RI | MO | ||
| 30 December | Yaqui | −0.84 | 0.23 | 2.4 | 1.3 |
| 23 February | Yaqui | −3.0 | −0.80 | 3.8 | 2.8 |
| 10 March | Yaqui | −7.7 | −0.21 | 0.40 | 1.8 |
| 11 April | Yaqui | −9.0 | −5.7 | 4.6 | 3.6 |
| 27 April | Yaqui | −14 | −2.2 | 2.8 | 4.3 |
| 6 May | Yaqui | −10 | −8.8 | −2.8 | − 3.9 |
| 13 May | Yaqui | −9.3 | −6.0 | 2.6 | 0.90 |
| 16 August | Urgell | −8.3 | −4.0 | 5.2 | 4.4 |
| 3 October | Urgell | −7.8 | −7.6 | 2.6 | 1.3 |
| All (mean) | Yaqui | −7.7 | −3.4 | 2.0 | 1.5 |
| All (σ) | Yaqui | 4.4 | 3.5 | 2.5 | 2.7 |
| All (mean) | Urgell | −8.0 | −5.8 | 3.9 | 2.8 |
| RMSD (C) | R (-) | Slope (-) | ||||||
|---|---|---|---|---|---|---|---|---|
| RI | MO | RS_1km | RI | MO | RS_1km | RI | MO | RS_1km |
| 6.4 | 4.1 | 6.7 | 0.97 | 0.97 | 0.92 | 0.58 | 0.76 | 0.55 |
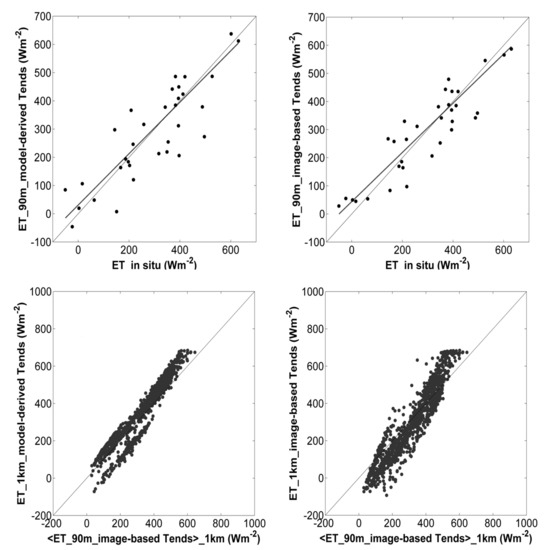
4.2. Application to ET Estimation at 90-m and 1-km Resolutions


| Date | RMSD (W·m) | Bias (W·m) | R (-) | Slope (-) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | MO | RS | RI | MO | RS | RI | MO | RS | RI | MO | RS | |
| 30th Dec | 48 | 55 | 47 | 46 | 54 | 5.3 | 0.98 | 0.98 | 0.96 | 1.3 | 1.2 | 2.0 |
| 23 February | 64 | 58 | 78 | 57 | 55 | 2.0 | 0.94 | 0.96 | 0.94 | 1.1 | 0.98 | 1.7 |
| 10 March | 61 | 36 | 99 | −46 | 31 | −73 | 0.99 | 0.97 | 0.97 | 1.5 | 1.1 | 1.8 |
| 11 April | 71 | 57 | 91 | 24 | 37 | 41 | 0.97 | 0.98 | 0.96 | 1.6 | 1.4 | 1.7 |
| 27 April | 122 | 63 | 79 | −102 | 57 | 24 | 0.99 | 0.99 | 0.98 | 1.6 | 1.2 | 1.7 |
| 6 May | 127 | 95 | 82 | −126 | −93 | −52 | 0.98 | 0.98 | 0.93 | 1.2 | 1.1 | 1.6 |
| 13 May | 42 | 28 | 67 | −38 | 23 | −53 | 0.98 | 0.97 | 0.95 | 1.2 | 1.0 | 1.4 |
| All (mean) | 77 | 56 | 78 | −27 | 23 | −15 | 0.98 | 0.98 | 0.95 | 1.4 | 1.1 | 1.7 |
| All (σ) | 34 | 21 | 17 | 72 | 53 | 44 | 0.01 | 0.01 | 0.01 | 0.22 | 0.12 | 0.19 |
4.3. A Mixed Modeling Remote Sensing Approach for Improved Tends and ET estimates
| Configuration | RMSD (W·m) | Bias (W·m) | R (-) | Slope (-) |
|---|---|---|---|---|
| MO | 59 | 23 | 0.95 | 1.1 |
| RS | 79 | −15 | 0.93 | 1.3 |
| MX_αends_1km | 52 | 25 | 0.96 | 1.1 |
| MX_αends_90m | 43 | 9.3 | 0.96 | 1.0 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| α | Surface albedo | |
| Bare soil albedo | ||
| Green vegetation albedo | ||
| Senescent vegetation albedo | ||
| Threshold albedo, computed as the average between and | ||
| Average of all albedo values | ||
| αends_90m | Albedo endmembers at 90-m resolution | |
| αends_1km | Albedo endmembers at 1-km resolution | |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer | |
| Specific heat of air at constant pressure | (J·kg·K) | |
| Saturated vapor pressure at temperature T | (Pa) | |
| Soil emissivity | ||
| η | Stability coefficient | |
| EF | Evaporative fraction | |
| ET | Evapotranspiration | (W·m) |
| ET_IS | Evapotranspiration given by in situ measurements | (W·m) |
| ET_90m_RS | Evapotranspiration estimated at 90-m resolution, by using image-based temperature endmembers as input | (W·m) |
| ET_90m_EBsoil | Evapotranspiration estimated at 90-m resolution, by using model-derived temperature endmembers as input | (W·m) |
| ET_1km_RS | Evapotranspiration estimated at 1-km resolution, by using image-based temperature endmembers as input | (W·m) |
| ET_1km_EBsoil | Evapotranspiration estimated at 1-km resolution, by using model-derived temperature endmembers as input | (W·m) |
| ET_1km_MX | Evapotranspiration estimated at 1-km resolution, by using as input the temperature endmembers derived from mixed-modeling | (W·m) |
| Fractional green vegetation cover | ||
| Average of all fractional green vegetation cover values | ||
| g | Gravitational constant | (m·s) |
| G | Ground heat flux | (W·m) |
| γ | Psychrometric constant | (Pa·K) |
| Soil sensible heat flux | (W·m) | |
| k | Von Kármán constant | |
| LST | Land surface temperature | (C) |
| Soil latent heat flux | (W·m) | |
| Monin–Obukhov length | (m) | |
| MO | Monin–Obukhov | |
| NDVI | Normalized Difference Vegetation Index | |
| Stability correction factor for heat transport | ||
| Stability correction factor for momentum transport | ||
| Aerodynamic resistance to heat transfer | (s·m) | |
| Aerodynamic resistance to heat transfer based on the Richardson number | (s·m) | |
| Aerodynamic resistance to heat transfer based on the Monin–Obukhov length | (s·m) | |
| Soil evaporation resistance | (s·m) | |
| ρ | Air density | (kg·m) |
| RI | Richardson | |
| Richardson number | ||
| RMSD | Root mean square difference | |
| RMSE | Root mean square error | |
| Incident atmospheric radiation at large wavelengths | (W·m) | |
| Incident solar radiation at short wavelengths | (W·m) | |
| Surface net radiation | (W·m) | |
| SEB-1S | Surface energy balance-mono-source | |
| σ | Stefan–Boltzmann constant | (W·m·K) |
| Surface (0–5 cm) soil moisture | (m·m) | |
| Soil moisture at field capacity | (m·m) | |
| SMC | Meteorological Service of Catalonia | |
| Air temperature | (C) | |
| Maximum surface temperature | (C) | |
| Tends | Temperature endmembers | (C) |
| Tends_IS | Soil temperature endmembers measured in situ | (C) |
| Tends_RS_90m | Soil temperature endmembers derived from 90-m resolution images | (C) |
| Tends_RS_1Km | Soil temperature endmembers derived from 1-km resolution images | (C) |
| Tends_EBsoil | Model-derived soil temperature endmembers | (C) |
| Temperature of a fully dry bare soil | (C) | |
| Maximum soil temperature, derived from the mixed modeling approach | (C) | |
| Temperature of a fully wet bare soil | (C) | |
| Temperature of fully water-stressed vegetation | (C) | |
| Temperature of well-watered vegetation | (C) | |
| Wind speed | (ms) | |
| Friction velocity | (ms) | |
| UTC | Coordinated Universal Time | |
| WC | Automatic weather station of Golmes | |
| XEMA | Automatic weather station network | |
| Roughness length for momentum transfer over bare soil | (m) | |
| Reference height at which the wind speed is measured | (m) |
Appendix
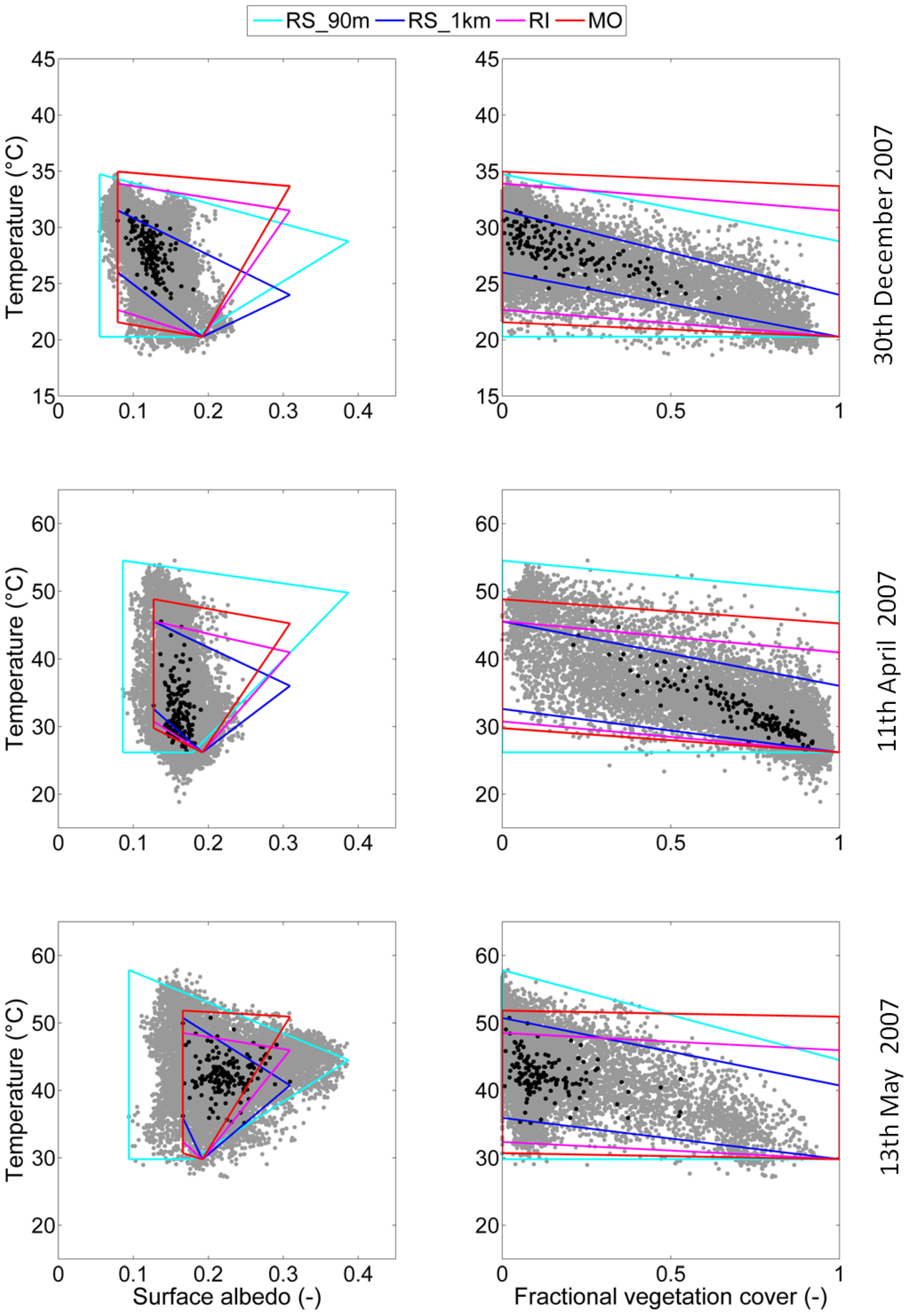
A. Image-Based Temperature Endmembers Algorithm
- (if ) is set to the air temperature ;
- (if ) is set to the maximum temperature () observed within the study area.
- The minimum soil temperature is defined as the intercept at α = of the line passing through the point (, ) and the point with α < , such that the slope of the line is maximum (meaning that all of the other data points with α < are located above the wet surface edge), with being the average between and . In the original version of SEB-1S, this threshold was set to .
- The maximum vegetation temperature is defined as the intercept at α = of the line passing through (, ) and the point with α > , such that the slope of the line is maximum (meaning that all of the other data points with α > are located below the dry surface edge) with being the average of all α values within the study area.
- (if = 1) is set to the air temperature ;
- (if = 0) is set to .
- The minimum soil temperature is computed as the intercept (at = 0) of the line passing through the point (1, ) and the point with , such that the slope of the line is maximum (meaning that all of the other data points with are located above the wet surface edge) with being the average of all values within the study area. In the original version of SEB-1S, the threshold value () was set to 0.5. It is now computed for each day separately.
- The maximum vegetation temperature is defined as the intercept (at = 1) of the line passing through the point (0, ) and the point with , such that the slope of the line is maximum (meaning that all of the other data points with are located below the dry surface edge).
B. Energy Balance Model for Bare Soil
C. Aerodynamic Resistance Modeling (MO Formulation)
References
- Garrido, A.; Llamas, M.; Varela-Ortega, C.; Novo, P.; Rodgriguez-Casado, R.; Aldaya, M. Water footprint and virtual water trade in Spain: Policy implications. Nat. Resource Manag. Policy 2010, 35. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Allen, R.G. Using the FAO-56 dual crop coefficient method over an irrigated region as part of an evapotranspiration intercomparison study. J. Hydrol. 2000, 229, 27–41. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Bausch, W.C.; Neale, C. Spectral inputs improve corn crop coefficients and irrigation scheduling. Trans. ASAE 1989, 32, 1901–1908. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Integration of the GG model with SEBAL to produce time series of evapotranspiration of high spatial resolution at watershed scales. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSG-SEVERI data in the Senegal River basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts-VI method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Merlin, O. An original interpretation of the surface temperature-albedo space to estimate crop evapotranspiration (SEB-1S). Hydrol. Earth Syst. Sci. 2013, 17, 3623–3637. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Singh, V.P. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ. 2012, 121, 370–388. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the “Triangle Method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.L. How sensitive is SEBAL to changes in input variables, domain sizes and satellite sensor? J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Scalon, B.R. Deriving theoretical boundaries to address scale dependencies of triangle models for evapotranspiration estimation. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Yang, Y.; Shang, S. A hybrid dual-source scheme and trapezoid framework-based evapotranspiration model (HTEM) using satellite images: algorithm and model test. J. Geophys. Res. Atm. 2013, 118, 2284–2300. [Google Scholar] [CrossRef]
- de Tomás, A.; Nieto, H.; Guzinski, R.; Salas, J.; Sandholt, I.; Berliner, P. Validation and scale dependencies of the triangle method for the evaporative fraction estimation over heterogeneous areas. Remote Sens. Environ. 2014, 152, 493–511. [Google Scholar] [CrossRef]
- Venturini, V.; Bisht, G.; Islam, S.; Jiang, L. Comparison of evaporative fractions estimated from AVHRR and MODIS sensors over South Florida. Remote Sens. Environ. 2004, 93, 77–86. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Er-Raki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Hoedjes, J.; Karrou, H.; Mougenot, B.; et al. Monitoring wheat phenology and irrigation in Central Morocco: on the use of relationship between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- iButtonLink Technology. Available online: http://www.ibuttonlink.com/products/ds1921g (accessed on 3 February 2014).
- Merlin, O.; Escorihuela, M.J.; Mayoral, M.A.; Hagolle, O.; Al Bitar, A.; Kerr, Y. Self-calibrated evaporation-based disaggregation of SMOS soil moisture: an evaluation study at 3 km and 100 m resolution in Catalunya, Spain. Remote Sens. Environ. 2013, 130, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J.; et al. Inter-comparison of four remote sensing based surface energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 895–963. [Google Scholar] [CrossRef]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Dedieu, G.; Garatuza, J.; Kerr, Y. Disaggregation of MODIS surface temperature over an agricultural area using a time series of Formosat-2 images. Remote Sens. Environ. 2010, 114, 2500–2512. [Google Scholar] [CrossRef] [Green Version]
- Fieuzal, R.; Duchemin, B.; Jarlan, L.; Zribi, M.; Baup, F.; Merlin, O.; Hagolle, O.; Garatuza-Payan, J. Combined use of optical and radar satellite data for the monitoring of irrigation and soil moisture of wheat crops. Hydrol. Earth Syst. Sci. 2011, 15, 1117–1129. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, S.; Hook, S.; Khale, A. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Schmugge, T.J. Applications of passive microwave observations of surface soil moisture. J. Hydrol. 1998, 212–213, 188–197. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Leroy, M.; Begué, A.; Hautecoeur, O.; Santer, R. Hemispherical reflectance and albedo estimates from the accumulation of across track sun synchroneous satellite data. J. Geophys. Res. 1999, 104, 221–232. [Google Scholar]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; Kzemipour, F. Albedo and LAI estimates from FORMOSAT-2 data for crop monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Gómez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of evapotranspiration over the Alpilles/ReSeDA experimental site using airborne POLDER sensor and a thermal camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Gómez, M.; Jiménez-Munoz, J.C.; Olioso, A.; Chehbouni, G. A simple algorithm to estimate evapotranspiration from DAIS data: Application to the DAISEX campaigns. J. Hydrol. 2005, 315, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Sobrino, J.A.; Gómez, M.; Jiménez-Munoz, J.C.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA-AVHRR images for the Iberian Peninsula. Remote Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Fan, L.; Liu, S.; Bernhofer, C.; Liu, H.; Berger, F.H. Regional land surface energy fluxes by satellite remote sensing in the Upper Xilin River watershed (Inner Mongolia, China). Theor. Appl. Climatol. 2007, 88, 231–245. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; Liang, S. Mapping daily evapotranspiration over a Mediterranean vineyard watershed. IEEE Geosci. Remote Sens. Lett. 2011, 8, 168–172. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC) - Model. J. Irrig. Drain. Eng. ASCE 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Sellers, P.J.; Heiser, M.D.; Hall, F.G. Relations between surface conductance and spectral vegetation indices at intermediate (100 m2 to 15 km2) length scales. J. Geophys. Res. 1992, 97, 19033–19059. [Google Scholar] [CrossRef]
- Kustas, W.P.; Schmugge, T.J.; Humes, K.S.; Jackson, T.J.; Parry, R.; Weltz, M.A.; Moran, M.S. Relationships between evaporative fraction and remotely sensed vegetation index and microwave brightness temperature for semiarid rangelands. J. Appl. Meteor. 1993, 32, 1781–1790. [Google Scholar] [CrossRef]
- Crow, W.T.; Kustas, W.P.; Prueger, J.H. Monitoring root-zone soil moisture through the assimilation of a thermal remote sensing-based soil moisture proxy into a water balance model. Remote Sens. Environ. 2008, 112, 1268–1281. [Google Scholar] [CrossRef]
- Monteith, J.L. Principles of Environmental Physics; Edward Arnold Press: London, UK, 1973; p. 241. [Google Scholar]
- Choudhury, B.; Reginato, R.J.; Idso, S.B. An analysis of infrared temperature observations over wheat and calculation of latent heat flux. Agric. For. Meteor. 1986, 37, 75–88. [Google Scholar] [CrossRef]
- Lee, H. Notes and correspondence: improvement of surface flux calculation in the atmospheric surface layer. J. Appl. Meteor. 1997, 36, 1416–1423. [Google Scholar] [CrossRef]
- Yang, K.; Tamai, N.; Koike, T. Analytical solution of surface layer similarity equations. J. Appl. Meteor. 2001, 40, 1647–1653. [Google Scholar] [CrossRef]
- Liu, Y.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: A case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sens. Environ. 2006, 105, 115–128. [Google Scholar] [CrossRef]
- Carlson, T.N.; Capehart, W.J.; Gillies, R.R. A new look at the simplified method for remote-sensing of daily evapotranspiration. Remote Sens. Environ. 1995, 54, 161–167. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observation. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL) 1 Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar]
- Senay, G.; Bohms, S.; Singh, R.; Gowda, P.; Velpuri, N. Operational evapotranspiration mapping using remote sensing and weather datasets: A New parametrization for the SSEB approach. J. Am. Water Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Ishikawa, H. Turbulent flux transfer over bare soil surfaces: Characteristics and parameterization. J. Appl. Meteor. 2008, 40, 276–290. [Google Scholar] [CrossRef]
- Liu, S.; Mao, D.; Jia, L. Evaluating parameterizations of aerodynamic resistance to heat transfer using field measurements. Hydrol. Earth Syst. Sci. 2007, 11, 769–783. [Google Scholar] [CrossRef]
- Gonzales-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteor. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Minacapilli, M.; Agnese, C.; Blanda, F.; Cammalleri, C.; Ciraolo, G.; D’Urso, G.; Iovino, M.; Pumo, D.; Provenzano, G.; Rallo, G. Estimation of actual evapotranspiration of Mediterranean perennial crops by means of remote-sensing based surface energy balance models. Hydrol. Earth Syst. Sci. 2009, 13, 1061–1074. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Wood, E.; McCabe, M.; Su, Z. Evaluation of remotely sensed evapotranspiration over the CEOP EOP-1 reference sites. J. Meteorol. Soc. Jpn 2007, 85A, 439–459. [Google Scholar] [CrossRef]
- Nishida, K.; Nemani, R.R.; Glassy, J.M.; Running, S.W. Development of an evapotranspiration index from Aqua/MODIS for monitoring surface moisture status. IEEE Trans. Geosci. Remote Sens. 2003, 41, 493–501. [Google Scholar] [CrossRef]
- Merlin, O.; Walker, J.P.; Chehbouni, A.; Kerr, Y. Towards deterministic downscaling of SMOS soil moisture using MODIS derived soil evaporative efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Chehbouni, G.; Walker, J.P.; Panciera, R.; Kerr, Y. A simple method to disaggregate passive microwave based soil moisture. IEEE Trans. Geosc. Remote Sens. 2008, 46, 786–796. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Chirouze, J.; Olioso, A.; Jarlan, L.; Chehbouni, G.; Boulet, G. An image-based four-source surface energy balance model to estimate crop evapotranspiration from solar reflectance/thermal emission data (SEB-4S). Agric. For. Meteor. 2014, 184, 188–203. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Daughtry, C.S.T. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteor. 1989, 49, 205–223. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefan, V.G.; Merlin, O.; Er-Raki, S.; Escorihuela, M.-J.; Khabba, S. Consistency between In Situ, Model-Derived and High-Resolution-Image-Based Soil Temperature Endmembers: Towards a Robust Data-Based Model for Multi-Resolution Monitoring of Crop Evapotranspiration. Remote Sens. 2015, 7, 10444-10479. https://doi.org/10.3390/rs70810444
Stefan VG, Merlin O, Er-Raki S, Escorihuela M-J, Khabba S. Consistency between In Situ, Model-Derived and High-Resolution-Image-Based Soil Temperature Endmembers: Towards a Robust Data-Based Model for Multi-Resolution Monitoring of Crop Evapotranspiration. Remote Sensing. 2015; 7(8):10444-10479. https://doi.org/10.3390/rs70810444
Chicago/Turabian StyleStefan, Vivien Georgiana, Olivier Merlin, Salah Er-Raki, Maria-José Escorihuela, and Said Khabba. 2015. "Consistency between In Situ, Model-Derived and High-Resolution-Image-Based Soil Temperature Endmembers: Towards a Robust Data-Based Model for Multi-Resolution Monitoring of Crop Evapotranspiration" Remote Sensing 7, no. 8: 10444-10479. https://doi.org/10.3390/rs70810444
APA StyleStefan, V. G., Merlin, O., Er-Raki, S., Escorihuela, M.-J., & Khabba, S. (2015). Consistency between In Situ, Model-Derived and High-Resolution-Image-Based Soil Temperature Endmembers: Towards a Robust Data-Based Model for Multi-Resolution Monitoring of Crop Evapotranspiration. Remote Sensing, 7(8), 10444-10479. https://doi.org/10.3390/rs70810444